Statistical Inference for the Weibull Distribution Based on δ-Record Data

Abstract

We consider the maximum likelihood and Bayesian estimation of parameters and prediction of future records of the Weibull distribution from $\delta$-record data, which consists of records and near-records. We discuss existence, consistency and numerical computation of estimators and predictors. The performance of the proposed methodology is assessed by Montecarlo simulations and the analysis of monthly rainfall series. Our conclusion is that inferences for the Weibull model, based on $\delta$-record data, clearly improve inferences based solely on records. This methodology can be recommended, more so as near-records can be collected along with records, keeping essentially the same experimental design.

1. Introduction

Informally, a record is an extraordinary value of a variable, which surpasses all of its kind. Records are very popular in fields such as sports, climatology, finance or insurance. In mathematical terms, given a sequence of real-valued observations $X_1,X_2,\dots ,$ we define $X_1$ as the first record, by convention, and we say that $X_n$ is an upper record (or simply a record) if $X_n>M_{n-1}$ holds, where $M_{n-1}=max\{X_1,\dots ,X_{n-1}\}$, for $n\ge 2$. Records have been extensively studied in Extreme Value Theory and their probabilistic properties, mainly under the assumption of independent and identically distributed observations, with continuous underlying distribution, are well known. This classical setting has significant symmetry which greatly simplifies calculations because it implies that all orderings of observations are equally likely. On the other hand, departures from symmetry, such as the existence of a trend in the sequence of observations, brings about technical complexities which require the use of more sophisticated mathematical tools. For general information on record theory, see Reference [1] or Reference [2].

In parallel, statistical inference for record data has developed considerably, impelled by the availability of many data sets of records and also because, in contexts such as destructive stress-testing, efficient sampling schemes (in terms of the number of broken units) yield record series. There is a vast literature on inference for record data and the interested reader can consult, for example, References [3,4,5].

A serious problem with record data is relative scarceness, since a sequence of n iid observations has only about $logn$ records. So extra data may be needed and a reasonable option is near-record data, which can be available along with records. By near-record data we mean observations that are close to being records, in a sense to be made precise. Our working hypothesis is this: if one uses statistical methods specifically designed for record data but feels that the record series is too short, then a sound option is to incorporate near-records. Of course, the methodology has to be adapted to handle the new data, along with records. In this paper we show how this can be done, in the particular case of the Weibull model. We assess via simulations the impact of the additional information and present an application to real data. Various definitions of near-records have been proposed, for example, in References [6,7,8]. In this paper we consider near-records in the sense of Reference [7], which are closely related to $\delta$-records. The latter were independently defined in Reference [9], as natural and tractable generalizations of records, which are as easily collected as records. Their probabilistic properties have been studied in References [9,10,11,12,13,14].

Concerning the statistical applications of $\delta$-records, their likelihood function for a continuous distribution was first published in Reference [10], with results on maximum likelihood estimation (MLE) for the exponential and Weibull distributions. In Section 4.3 of the above cited paper, a variant of the sequential stress-testing scheme is proposed to collect $\delta$-records, which we briefly describe here. Suppose we wish to test, say, tensile strength. In a classical sampling scheme, all items are stressed until they break. In the more efficient sequential testing, each item is stressed up to the maximum level that a previous item broke and this yields a sequence of (lower) records. The proposed variant consists in stressing the items further than the previous record, by a fixed value $\delta >0$, to obtain a sequence of lower $\delta$-records. The likelihood of lower $\delta$-records can be easily obtained by adapting the ideas from the theory of standard (upper) $\delta$-records; see Reference [10] for details. Additionally, Bayesian and MLE methods, for parameter estimation and prediction of future records in the geometric distribution, were presented in Reference [15]. A conclusion to be drawn from results in these papers is that inference methods based on $\delta$-records outperform their corresponding record-only versions.

The main objective of the present paper is to investigate properties of inferences based on $\delta$-records for the Weibull model, such as strong consistency of the MLE of parameters, maximum likelihood prediction (MLP) of records and Bayesian estimation and prediction of records. The reason for focusing on the Weibull distribution is twofold: First, the model and recently introduced variants are widely used in applications; see References [16,17]. Second, inference for its parameters using records has drawn significant attention in recent years; see References [4,5,18,19,20,21,22,23,24].

In our analysis we consider two cases: known and unknown shape parameter, while the scale parameter is always assumed unknown. According to References [25,26] and [27] (Section 14.2), in many practical problems it is not unreasonable to assume that the shape parameter is known or, at least, it is one among a small number of values. We do not analyze the situation of known scale parameter since, according to the literature, it is not considered natural and very few papers deal with it; see Section 14.2.2 in Reference [27]. It is important to warn the reader that, while statistical inference based on records from a Weibull distribution, with known shape parameter, can be reduced to inference from the exponential distribution (via power transform), this is not the case for $\delta$-records. See Remark 2.

We assess the impact of $\delta$-records in parameter estimation and prediction of new records, by means of Montecarlo simulation and the analysis of real data. We perform comparative analyses of estimators and predictors based on $\delta$-records, in a variety of settings. In particular, we show that the performance of estimators and predictors is improved when using $\delta$-record data with respect to only record data. Regarding real data, we analyze cumulative rainfall information recorded at the Castellote weather station in Spain; see Reference [10].

The paper is organized as follows: Section 2 is devoted to preliminary definitions and notation. MLE and MLP of future records are developed in Section 3; we show existence of estimators and predictors and prove the strong consistency of the MLE of the scale parameter, if the shape parameter is known. Results of simulation are presented in Section 3.4, showing that $\delta$-records bring about noticeable improvement in estimation and prediction. The analysis of real data is presented in Section 3.5. Section 4 is devoted to Bayesian inference. We compute Bayes estimators and highest posterior density (HPD) intervals of parameters, using two different priors in the case of both parameters unknown. Then we consider Bayesian prediction of future records. Results from simulations and real data are shown in Section 4.5 and Section 4.6. In Section 5 we present our conclusions.

We end this introduction with some comments about the novelty of results presented in this paper. We remark first that, while the expressions for the likelihood of the sample of $\delta$-records and for the MLE of the parameters were first obtained in Reference [10], the remaining results are new, in the context of continuous distributions. These novel results include strong consistency of the MLE of the scale parameter (under known shape parameter); the development of a frequentist strategy for the prediction of future records and the proof of existence of predictors. In the Bayesian framework we develop the estimation of parameters, under a variety of choices of prior distributions, also complemented with a consistency result and, finally, we propose and analyze a method for predicting new records.

2. Preliminaries

Let $X_n$, $n\ge 1,$ be a sequence of independent and identically distributed (iid) random variables, with common distribution function $F_{\theta }$ and density $f_{\theta }$, where $\theta$ is a parameter. Let $M_n=max\{X_1,\dots ,X_n\}$, $n\ge 1,$ be the sequence of partial maxima.

Definition 1.

Let $X_1$ be a record by convention and, for $n\ge 2$, $X_n$ is a (upper) record if $X_n>M_{n-1}$. The indexes $L(n)$, corresponding to record observations, are called record times. That is, $L(1)=1$ and for $n\ge 2$, $L(n)=min\{m>L(n-1):X_m>M_{m-1}\}$. Records (or record-values) $R_n$ are defined by $R_n=X_{L(n)},n\ge 1$.

Definition 2.

Let δ be a fixed, real parameter. Let $X_1$ be a δ-record by convention and, for $n\ge 2$, $X_n$ is a δ-record if $X_n>M_{n-1}+\delta$.

The sequences of $\delta$-record times and $\delta$-records are defined analogously as for records. Note that if $\delta =0$, $\delta$-record are just records. If $\delta >0$, $\delta$-records are a subsequence of records and, on the contrary, if $\delta <0$, records are a subsequence of $\delta$-records. So, the only statistically relevant situation is $\delta <0$, since $\delta$-records contain all records plus the so-called near-records (in the sense of Reference [7]). Given $\delta <0$, $X_n$ is a $\delta$-near-record (or simply near-record) if $X_n\in (M_{n-1}+\delta ,M_{n-1}]$. In other words, near-records are close to being records but are not records. It is clear also that near records are not symmetrically clustered around records. In the rest of the paper we assume $\delta \le 0$.

Definition 3.

 

(i) A near-record $X_n$ is said to be associated to the m-th record $R_m$, if $L(m)<n<L(m+1)$.

(ii) The number of near-records associated to $R_m$ is denoted by $S_m$.

(iii) If $S_m>0$, the vector of near-records associated to $R_m$ is denoted by $(Y_{m,1},\dots ,Y_{m,S_m})$.

(iv) The sample is defined by the vector $\mathbf{T}=({\mathit{R}}_n,{\mathbf{S}}_n,{\mathbf{Y}}_n)$, where ${\mathit{R}}_n=(R_1,\dots ,R_n)$, ${\mathbf{S}}_n=(S_1,\dots ,S_n)$ and ${\mathbf{Y}}_n=(Y_{1,1},\dots ,Y_{1,S_1},\dots ,Y_{n,1},\dots ,Y_{n,S_n})$.

When referring to the sample as a random object we use bold upper-case letters, otherwise we use $\mathbf{t}=({\mathbf{r}}_n,{\mathbf{s}}_n,{\mathbf{y}}_n)$. Note that $\mathbf{T}$ contains a fixed number n of records (R), plus the counts (S) and respective values (Y) of all near-records associated to each record. So, $\mathbf{T}$ has random length, depending on the (random) numbers $S_i$ of near-records associated to each record $R_i$. In turn, the distribution of $S_i$ depends in a non trivial way on $\delta$ and is also affected by the tail behavior of $F_{\theta }$. For example, the number of near-records obviously increases with the absolute value of $\delta$. On the other hand, if $F_{\theta }$ is heavy-tailed, there will tend to be fewer near-records. Laws of large numbers and central limit theorems, for the number of near-records, can be found in References [28,29]. Normalizing sequences of asymptotic results in Example 4 of Reference [10], may serve as proxies for the expected values of the number of near-records, for the Weibull distribution.

2.1. Likelihood of $\delta$-Record Observations

Proposition 1.

Let ${\overline{F}}_{\theta }(x)=1-F_{\theta }(x)$. The likelihood function of sample $\mathbf{T}$ is given by

$$L(\mathbf{t}|\theta )={\overline{F}}_{\theta }(r_n)\prod _{i=1}^n\frac{f_{\theta }(r_i)}{{\overline{F}}_{\theta }{(r_i+\delta )}^{s_i+1}}\prod _{j=1}^{s_i}{f}_{\theta }(y_{i,j}),$$

(1)

where $0<r_1<\cdots <r_n<\infty$, $s_i\in {\mathbb{Z}}_{+}=\{0,1,\dots \}$ and $y_{i,j}\in (r_i+\delta ,r_i)$, for $j=1,\dots ,s_i$, $i=1,\dots ,n$.

Proof. 

See Proposition 1 in Reference [10]. ☐

Remark 1.

Observe that in (1) the sample is assumed to contain all near-records associated to the last record $R_n$. To ensure that all near-records are present in the sample, the value of $R_{n+1}$ must be observed. As commented in Section 4.2.1 of Reference [10], the data may not contain all near-records associated to $R_n$, since $R_{n+1}$ is not observed. So, it is not known if some near-records associated to $R_n$ are missing and, in such situation, the likelihood has to be modified accordingly. It is easy to see that this amounts to substituting ${\overline{F}}_{\theta }(r_n)$ for ${\overline{F}}_{\theta }(r_n+\delta )$ in (1). Then the modified likelihood $\mathcal{L}$, of a possibly incomplete sample, is

$$\mathcal{L}(\mathbf{t}|\theta )={\overline{F}}_{\theta }(r_n+\delta )\prod _{i=1}^n\frac{f_{\theta }(r_i)}{{\overline{F}}_{\theta }{(r_i+\delta )}^{s_i+1}}\prod _{j=1}^{s_i}{f}_{\theta }(y_{i,j}).$$

(2)

In the rest of the paper, except in the analysis of real data, we work with L (thereby assuming that all near-records associated to $R_n$ have been collected). Results for L can be adapted to $\mathcal{L}$, with only minor modifications.

2.2. Density of Future Records

The prediction of a future record $R_m$, $m>n$, is based on the conditional density, given $\mathbf{T}$, as presented below.

Proposition 2.

The density of the m-th record $R_m$ conditional on $\mathbf{T}$, is given by

$$f_{R_m}(z|\mathbf{t},\theta )=\frac{{({\Lambda }_{\theta }(z)-{\Lambda }_{\theta }(r_n))}^{m-n-1}}{\Gamma (m-n)}\frac{f_{\theta }(z)}{{\overline{F}}_{\theta }(r_n)},$$

(3)

for $m>n$ and $z\ge r_n,$ where ${\Lambda }_{\theta }(z)=-log{\overline{F}}_{\theta }(z)$.

Proof. 

Conditionally on $R_n$, $R_m$ is independent of $\mathbf{T}$ (see Proposition 1 in Reference [10]). Therefore, the density of $R_m$ given $\mathbf{T}$ is the same as the density of $R_m$ given $R_n$, which proves the result. ☐

2.3. Weibull Distribution

We present here the likelihoods corresponding the Weibull distribution, with two parametrizations: $P_1$, for classical (frequentist) inference, and $P_2$, for Bayesian analysis. We find it convenient to work with these two parametrizations mainly because they are found in the literature, associated respectively to classical or Bayesian inferences. See, for example, the Weibull Distribution Handbook [27], where the author argues that $P_2$ separates parameters and has the advantage over $P_1$, of simplifying the algebra in Bayesian manipulations.

Definition 4.

Let the parametrizations $P_1,P_2$ of the Weibull distribution be defined respectively by

P₁ :

$f_{\lambda ,\beta }(x)={\lambda }^{-\beta }\beta x^{\beta -1}{e}^{-{(x/\lambda )}^{\beta }},F_{\lambda ,\beta }(x)=1-e^{-{(x/\lambda )}^{\beta }}$,

P₂ :

$f_{\alpha ,\beta }(x)=\alpha \beta x^{\beta -1}{e}^{-\alpha x^{\beta }},F_{\alpha ,\beta }(x)=1-e^{-\alpha x^{\beta }}$,

for $x\ge 0$ and $\lambda ,\alpha ,\beta >0$.

Parameter $\lambda$ in $P_1$ is the so-called scale parameter, while $\beta$ is known as shape parameter. In $P_2$ the scale parameter is given by ${\alpha }^{-1/\beta }$. From (1) we obtain the corresponding likelihoods

$$L_1(\mathbf{t}|\lambda ,\beta )={\lambda }^{-N\beta }{\beta }^N{e}^{-{\lambda }^{-\beta }G(\beta )}{J}^{\beta -1},$$

(4)

$$L_2(\mathbf{t}|\alpha ,\beta )={\alpha }^N{\beta }^N{e}^{-\alpha G(\beta )}{J}^{\beta -1},$$

(5)

where $N,G(\beta )$ and J are defined by

$$\begin{array}{cc}\hfill N& =n+\sum _{i=1}^n{s}_i,G(\beta )=\sum _{i=1}^n\left(r_i^{\beta }-{(r_i+\delta )}_{+}^{\beta }+\sum _{j=1}^{s_i}\left(y_{i,j}^{\beta }-{(r_i+\delta )}_{+}^{\beta }\right)\right)+r_n^{\beta }\mathrm{and}\hfill \\ \hfill J& =\prod _{i=1}^n{r}_i\left(\prod _{j=1}^{s_i}{y}_{i,j}\right),\mathrm{with}{(x)}_{+}:=max\{x,0\}.\hfill \end{array}$$

(6)

For possibly incomplete data, using (2), the corresponding likelihoods are (4) and (5), with $G(\beta )$ substituted by $\tilde{G}(\beta ):=G(\beta )-(r_n^{\beta }-{(r_n+\delta )}_{+}^{\beta })$.

3. Maximum Likelihood Analysis

This section is devoted to study the MLE of parameters and the MLP of future records. We begin with the MLE of parameters $\lambda ,\beta$, related to $P_1$ and, as commented before, we consider two cases: $\beta$ known and $\beta$ unknown. Throughout this section $\lambda$ is assumed unknown.

Remark 2.

Notice that if β is known, some inferences for λ can be reduced to the exponential distribution since, if X is Weibull distributed, then $X^{\beta }$ is exponentially distributed. However, this is not so for δ-records because, for $\beta \ne 1$, the β-th power of δ-records sampled from X, are not distributed as δ-records sampled from $X^{\beta }$. The reason being that δ-record extraction and power transform of the data are not symmetrical actions, in the sense that they do not commute. Therefore, the consistency result of Theorem 1, for $\beta \ne 1$, does not follow from the corresponding result for the exponential model ($\beta =1$).

The existence of the MLE of $\lambda ,\beta$ is established in Proposition 3. For ease of notation, we omit their dependence on $\mathbf{t}$. The set of solutions of a maximization problem is denoted argmax.

3.1. MLE of Parameters $\lambda ,\beta$

Proposition 3.

(i)  For all $\beta >0$, $arg\underset{\lambda }{max}{L}_1(\mathbf{t}|\lambda ,\beta )$ has a unique element

$$\widehat{\lambda }(\beta )={\left(\frac{G(\beta )}{N}\right)}^{1/\beta }.$$

(7)

(ii)  Let $\widehat{A}=arg\underset{\beta }{max}{L}_1(\mathbf{t}|\widehat{\lambda }(\beta ),\beta )$. Then $\widehat{A}\ne \varnothing$ and $(\widehat{\lambda }(\widehat{\beta }),\widehat{\beta })\in arg\underset{\lambda ,\beta }{max}{L}_1(\mathbf{t}|\lambda ,\beta )$, for any $\widehat{\beta }\in \widehat{A}$.

Proof. 

(i) (7) is obtained by solving $\frac{\partial log{L}_1}{\partial \lambda }=0$ for $\lambda$.

(ii) It can be shown that maximizing $log{L}_1(\mathbf{t}|\widehat{\lambda }(\beta ),\beta )$ over $\beta$ is equivalent to maximizing $h(\beta ):=log\beta -logG(\beta )+(\beta -1)(logJ)/N$ and that $\varnothing \ne arg\underset{\beta }{max}h(\beta )\subseteq [L,U]$, where $0<L={(log{r}_n-\frac{logJ}{N})}^{-1}/(3N+2)$ and $U=2{(log{r}_n-\frac{logJ}{N})}^{-1}(1+log(N+1))$. See Reference [10] for details. ☐

Remark 3.

Note that $\widehat{\lambda }(\beta )$ depends on all δ-records (records and near-records) in the sample $\mathbf{t}$. If, by chance, no near-records are observed ($s_i=0$, for $i=1,\dots ,n$), then

$$\widehat{\lambda }(\beta )={\left(\frac{{\sum }_{i=1}^n(r_i^{\beta }-{(r_i+\delta )}_{+}^{\beta })+r_n^{\beta }}{n}\right)}^{1/\beta },$$

which is in contrast with the case $\delta =0$, where the estimator depends only on the last record $r_n$.

The numerical computation of the MLE is straightforward. If $\beta$ is known, the explicit formula for the MLE of $\lambda$ is given in (7). If $\beta$ is unknown, the numerical maximization of $h(\beta )$ over $[L,U]$ must be carried out to find $\widehat{\beta }$, as explained in the proof of Proposition 3. Then $\widehat{\lambda }(\widehat{\beta })$ and $\widehat{\beta }$ are the MLE of $\lambda$ and $\beta$ respectively.

3.2. Strong Consistency

We state below the strong consistency of $\widehat{\lambda }(\beta )$, the MLE of $\lambda$ when $\beta$ is known. The proof of this result is split into several technical lemmas, presented in Section 6.1. Strong convergence as $n\to \infty$ is denoted $\stackrel{a.s.}{⟶}$.

Theorem 1.

$\widehat{\lambda }(\beta )\stackrel{a.s.}{⟶}\lambda$, for all $\lambda ,\beta >0$.

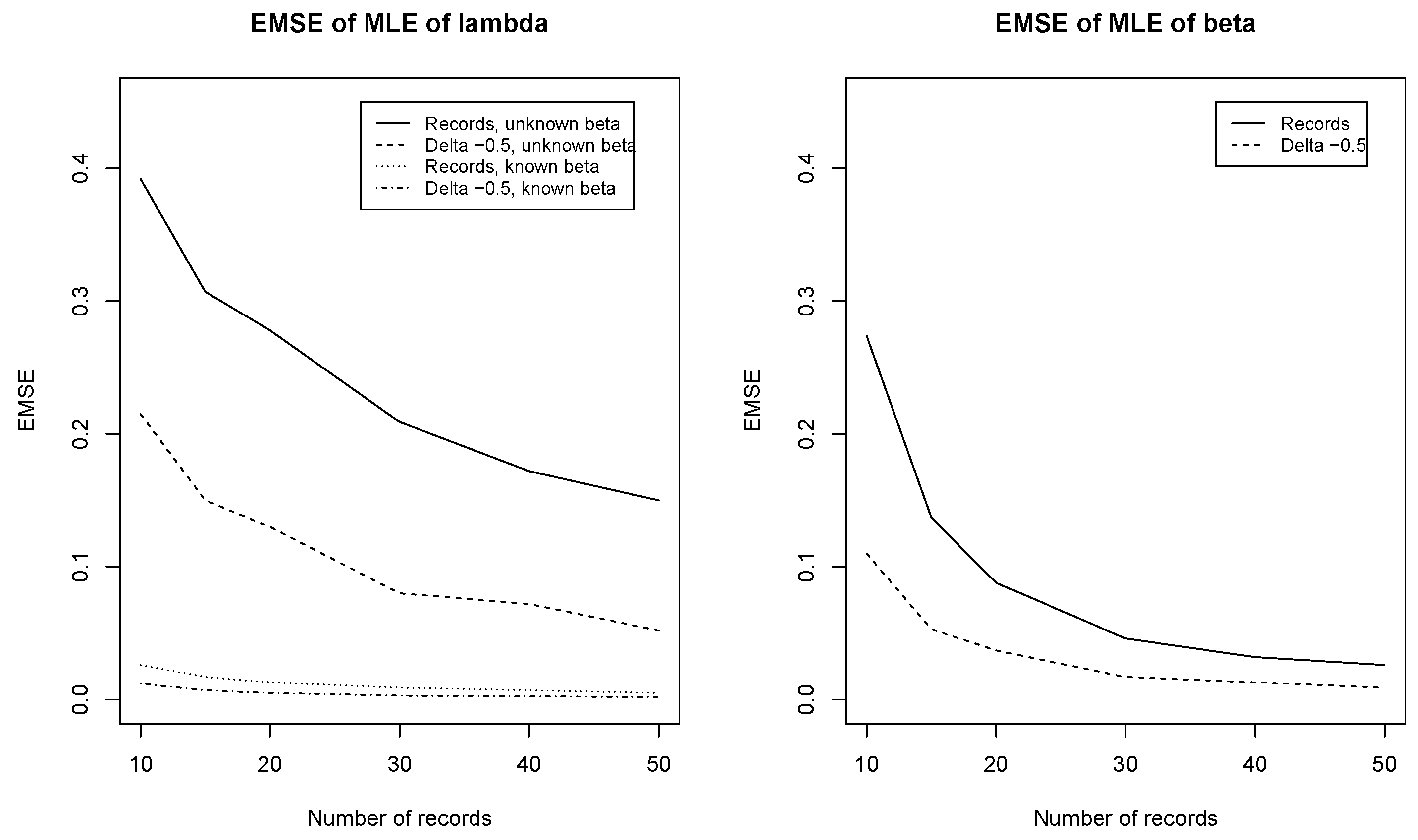
Remark 4.

If β is unknown, the question of consistency of $\widehat{\lambda }$ remains open. Nevertheless, we have run Montecarlo simulations which suggest that consistency also holds in this case. In the left panel of Figure 1, values of the EMSE of $\widehat{\lambda }$ are plotted versus n. It can be seen that $\widehat{\lambda }$ appears to be consistent, for unknown β (in mean square sense). We also observe that convergence in the case of known β is much faster (lower curves). Moreover, in both situations δ-records yield an EMSE smaller than records. On the right panel of Figure 1 we can see a steep descent of the EMSE of $\widehat{\beta }$, suggesting consistency of this estimator as well.

3.3. Maximum Likelihood Prediction of Future Records

The MLP of future records, as defined in Reference [30], consists in maximizing the so-called predictive likelihood function. The following definitions follows that idea, adapted to the sample $\mathbf{t}$ of $\delta$-records.

Definition 5.

Let the predictive likelihood of $R_m$ and θ be defined by $L^P(z,\mathbf{t}|\theta )=f_{R_m}(z|\mathbf{t},\theta )L(\mathbf{t}|\theta )$. In the case of the Weibull distribution, using parametrization $P_1$, we have, for $z\ge r_n$,

$$f_{R_m}(z|\mathbf{t},\lambda ,\beta )=\frac{{\lambda }^{-\beta (m-n)}\beta }{\Gamma (m-n)}{z}^{\beta -1}{e}^{-{\lambda }^{-\beta }(z^{\beta }-r_n^{\beta })}{(z^{\beta }-r_n^{\beta })}^{m-n-1},$$

and so,

$$L_1^P(z,\mathbf{t}|\lambda ,\beta ):=\frac{{\lambda }^{-(m-n+N)\beta }{\beta }^{N+1}}{\Gamma (m-n)}{z}^{\beta -1}{e}^{-{\lambda }^{-\beta }(z^{\beta }-r_n^{\beta }+G(\beta ))}{(z^{\beta }-r_n^{\beta })}^{m-n-1}{J}^{\beta -1}.$$

(8)

Definition 6.

The MLP of $R_m,m>n$, is defined by ${\tilde{R}}_m=\tilde{z}$, where $(\tilde{z},\tilde{\theta })\in arg\underset{z,\theta }{max}{L}^P(z,\mathbf{t}|\theta )$. In the case of the Weibull distribution, using parametrization $P_1$, we have

(i) ${\tilde{R}}_m=\tilde{z}(\beta )$, where $(\tilde{z}(\beta ),\tilde{\lambda }(\beta ))\in arg\underset{z,\lambda }{max}{L}_1^P(z,\mathbf{t}|\lambda ,\beta )$, if β is known, and

(ii) ${\tilde{R}}_m=\tilde{z}$, where $(\tilde{z},\tilde{\lambda },\tilde{\beta })\in arg\underset{z,\lambda ,\beta }{max}{L}_1^P(z,\mathbf{t}|\lambda ,\beta )$, if β is unknown.

Remark 5.

The estimators $\tilde{\lambda },\tilde{\beta }$ in Definition 6 are the so-called predictive maximum likelihood estimators of $\lambda ,\beta$, according to Reference [7]. Their properties are not investigated in this paper.

The existence of MLP of future records in the Weibull distribution is established in Proposition 4 and the corresponding proof is presented in Section 6.2.

Proposition 4.

 

(i) For all $\beta >0$, there is a unique pair $(\tilde{z}(\beta ),\tilde{\lambda }(\beta ))\in arg\underset{z,\lambda }{max}{L}_1^P(z,\mathbf{t}|\lambda ,\beta )$, given by

$$\tilde{z}(\beta )={\left(\rho +r_n^{\beta }\right)}^{\frac{1}{\beta }}and\tilde{\lambda }(\beta )={\left(\frac{\rho +G(\beta )}{N+m-n}\right)}^{\frac{1}{\beta }},$$

(9)

where $\rho =\frac{-b-\sqrt{b^2-4ac}}{2a}$, with

$$a=-(\beta N+1),b=-\beta (N+1)r_n^{\beta }+(\beta (m-n)-1)G(\beta )andc=\beta (m-n-1)r_n^{\beta }G(\beta ).$$

(10)

(ii) Let $\tilde{A}=arg\underset{\beta }{max}{L}_1^P(\tilde{z}(\beta ),\mathbf{t}|\tilde{\lambda }(\beta ),\beta )$. Then $\tilde{A}\ne \varnothing$ and $(\tilde{z}(\tilde{\beta }),\tilde{\lambda }(\tilde{\beta }),\tilde{\beta })\in arg\underset{z,\lambda ,\beta }{max}{L}_1^P(z,\mathbf{t}|\lambda ,\beta )$, for any $\tilde{\beta }\in \tilde{A}$.

Remark 6.

According to Proposition 4, if β is known, there is an explicit formula for the MLP of $R_m$, equal to $\tilde{z}(\beta )$ in (9). On the other hand, if β is unknown, $\tilde{z}(\beta )$ and $\tilde{\lambda }(\beta )$ are plugged in $L_1^P$ and a maximization problem in one real variable must be solved (numerically), namely $\underset{\beta }{max}{L}_1^P(\tilde{z}(\beta ),\mathbf{t}|\tilde{\lambda }(\beta ),\beta )$. This is straightforward since, as shown in Section 6.2, there is a compact interval containing a solution $\tilde{\beta }$. Finally, it suffices to replace β by $\tilde{\beta }$ in (9), to find the MLP.

Observe, also in Proposition 4, that, if $m=n+1$, then $b<0$ (because $G(\beta )\le (N+1)r_n^{\beta }$), $c=0$ and, consequently, $\rho =0$. Hence, regardless of β being known or unknown, ${\tilde{R}}_{n+1}=r_n$. See Section 6.2 for details.

3.4. Simulation Study

To assess the behavior of the MLE and MLP, we carry out Montecarlo simulations. For several values of $\lambda ,\beta$ and for $\delta =0,-0.5$, we generate ${10}^4$ samples of $n=5$ records and their near-records.

The MLE of the Weibull parameters using $\delta$-records were first studied in Section 4.1.1 of Reference [10]. A comparison of the accuracy of estimators, for $n=10$, $\lambda =1,\beta =2$ and $\delta =0,-0.5$ can be found in that paper. Throughout this paper we work in a different scenario, namely $n=5$, with several values of $\lambda ,\beta$ and $\delta =0,-0.5$.

The estimated mean square errors (EMSE) of the MLE of $\lambda ,\beta$ are computed as averages of the squared deviations of the MLE from the true values of the parameters. Results in

Table 1. Estimated Mean Square Errors (EMSE) of maximum likelihood estimators (MLE) $\widehat{\lambda },\widehat{\beta }$.

		Known $\mathit{\beta }$		Unknown $\mathit{\beta }$
		$\mathbf{\delta }=\mathbf{0}$	$\mathbf{\delta }=-\mathbf{0.5}$	$\mathbf{\delta }=\mathbf{0}$		$\mathbf{\delta }=-\mathbf{0.5}$
$\mathbf{\lambda }$	$\mathbf{\beta }$	EMSE $\widehat{\mathbf{\lambda }}(\mathbf{\beta })$	EMSE $\widehat{\mathbf{\lambda }}(\mathbf{\beta })$	EMSE $\widehat{\mathbf{\lambda }}$	EMSE $\widehat{\mathbf{\beta }}$	EMSE $\widehat{\mathbf{\lambda }}$	EMSE $\widehat{\mathbf{\beta }}$
	0.75	0.024	0.015	0.370	1.200	0.230	0.376
0.25	1	0.013	0.004	0.118	1.814	0.033	0.174
	1.5	0.005	0.001	0.032	4.187	0.001	0.067
	0.75	0.102	0.076	1.488	1.196	1.252	0.671
0.5	1	0.051	0.027	0.463	1.871	0.298	0.631
	1.5	0.022	0.006	0.128	3.688	0.038	0.388

show that, for $\beta$ known, the EMSE of $\widehat{\lambda }(\beta )$ is much lower for $\delta <0$ than for $\delta =0$ (only records). For $\beta$ unknown, the observed improvement is greater in $\widehat{\beta }$ than in $\widehat{\lambda }$. Regarding bias, it is known that the MLE of $\lambda$ and $\beta$, from record data, are biased; see Reference [23]. In the case of $\delta$-records our simulations show a small positive bias in the estimations of both parameters.

For MLP of future records we proceed as above in terms of the number of simulated samples, the number n of records and the values of $\lambda ,\beta$ and $\delta$. The record to be predicted is $R_7$ (that is $m=n+2$), which is the first interesting case for $m>5$, since ${\tilde{R}}_6=r_5$, as commented in Remark 6. For each run we simulate $R_7$ and compute the EMSE, as the average of squared deviations of ${\tilde{R}}_7$ from the simulated value of $R_7$. Results show that predictions based on records or on $\delta$-records tend to underestimate $R_7$. For example, given $\lambda =0.25$ and $\beta =1$, the mean of $R_7$ is 1.75; for $\delta =0$, the mean of ${\widehat{R}}_7$ is 1.39 while, for $\delta =-0.5$, the mean of ${\widehat{R}}_7$ is 1.47. The values of the EMSE are displayed in

Table 2. Estimated Mean Square Errors (EMSE) of ${\tilde{R}}_7$.

		Known $\mathit{\beta }$		Unknown $\mathit{\beta }$
$\mathbf{\lambda }$	$\mathbf{\beta }$	$\mathbf{\delta }=\mathbf{0}$	$\mathbf{\delta }=-\mathbf{0.5}$	$\mathbf{\delta }=\mathbf{0}$	$\mathbf{\delta }=-\mathbf{0.5}$
	0.75	1.462	1.353	1.739	1.525
0.25	1	0.223	0.193	0.260	0.213
	1.5	0.027	0.022	0.034	0.024
	0.75	5.893	5.591	6.963	6.445
0.5	1	0.884	0.793	1.072	0.917
	1.5	0.114	0.092	0.139	0.106

.

Although, in absolute terms, the advantage of $\delta$-records appears to be greater in estimation than in prediction, it should be borne in mind that there exists a positive lower bound of the EMSE of any predictor of $R_m$, based on past information, even if parameters were known. This is because the optimal mean square predictor, based on past information, is the conditional expectation with respect to the past. Indeed, let ${\mathcal{F}}_n$ be the $\sigma$-algebra generated by $\{X_k;k\le L(n+1)-1\}$ and $R_m^{*}$ a predictor based on the available information before record $R_{n+1}$ (that is, ${\mathcal{F}}_n$-measurable), then

$$E{(R_m^{*}-R_m)}^2\ge E{(E(R_m|{\mathcal{F}}_n)-R_m)}^2=E{(E(R_m|R_n)-R_m)}^2.$$

In particular, for the Weibull model, with $\beta =1$, $R_n$ is distributed as sums of n iid exponential random variables, with mean $\lambda$, hence

$$E{(R_m^{*}-R_m)}^2\ge E{(R_m-R_n-(m-n)\lambda )}^2=(m-n){\lambda }^2.$$

(11)

For example, if $m=7$, $n=5$ and $\lambda =0.5$, the bound in (11) is equal to 0.5. Therefore, when comparing the EMSE 0.884 ($\delta =0$) versus 0.793 ($\delta =-0.5$), in the penultimate line of Table 2, the bound should be taken into account. A fair estimate of the gain is obtained by subtracting 0.5 from each quantity and computing $(0.384-0.293)/0.384$, which yields a $23.7\%$ reduction, instead of just $10.3\%$, without such correction. An overall conclusion from Table 1 and Table 2 is that estimators and predictors, based on $\delta$-records, outperform those based on records only. This is coherent with the fact that there is more information in $\delta$-records than in records and also with results in Reference [15], where this property was also observed in the case of the geometric distribution.

3.5. Real Data

We compute estimations and predictions for the rainfall data mentioned in the introduction. The data consists of cumulative rainfall (measured in millimeters), from September to November, recorded at the Castellote weather station in Spain, between 1927 and 2000. The complete sample of 74 values is well fitted by a Weibull distribution, as can be seen in Table 3 and Figure 1 in Reference [10]. We have also run the Ljung-Box test to check the existence of autocorrelation, yielding a p-value of $0.621$. There are $n=5$ records in the sample and, for $\delta =-25$, $-50$ and $-75$, the number of $\delta$-records is 6, 9 and 18, respectively. For completeness we show the $\delta$-record data in

Table 3. Records and near-records ($\delta$-records) from Castellote rainfall data in millimeters. Near records are shown to the right of their corresponding records (in boldface).

$\mathit{\delta }$	$\mathit{\delta }$-Record Values
$0$	164.6, 184.9, 224.9, 247.1, 278.8
$-25$	164.6, 184.9, 164.7, 224.9, 247.1, 278.8
$-50$	164.6, 138.5, 184.9, 164.7, 224.9, 179.5, 247.1, 278.8, 230.5
$-75$	164.6, 138.5, 108.0, 184.9, 164.7, 130.1, 224.9, 179.5, 154.1, 151.1, 157.3,
	247.1, 278.8, 204.3, 230.5, 214.0, 206.0, 209.1

.

Since in real data applications, unlike in simulations, we do not know the values of the parameters, it is not clear how to assess the impact of $\delta$-records. This is also the case in predicting records, because no new record has been observed between the years 2000 and 2018. So, in order to measure the improvement of estimations and predictions due to $\delta$-records, we compare our results with those obtained from the complete sample of 74 values, taken as benchmarks. Note that the complete sample can be seen as the set of $\delta$-records with $\delta =-\infty$.

The MLE of $\lambda$ and $\beta$ were reported in Reference [10], showing that $\delta$-records give estimates closer to the benchmark than the estimates from records only. For completeness we present those results here, in the second and third columns of

Table 4. MLE $\widehat{\lambda },\widehat{\beta }$ and maximum likelihood prediction (MLP) ${\tilde{R}}_7,{\tilde{R}}_8,{\tilde{R}}_9$ for Castellote rainfall data.

$\mathit{\delta }$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\beta }}$	${\tilde{\mathit{R}}}_7$	${\tilde{\mathit{R}}}_8$	${\tilde{\mathit{R}}}_9$
0	185	3.93	289.3	298.5	306.6
−25	188	3.48	294.1	306.8	317.7
−50	182	3.44	293.4	305.9	316.7
−75	150	2.90	292.7	305.1	316.3
$-\infty$	130	2.04	305.2	328.6	349.9

.

Maximum likelihood prediction was not considered in Reference [10]. The results in Table 4 show that the prediction with delta-records is closer to the estimation using the complete sample, even though the gain is not as clear as in the case of estimation. Recall, however, that the predicted values for future records using the whole sample are not the real values (since they have not been observed yet). Conclusions on the advantage of using delta-records over records must be drawn from Montecarlo simulations in Section 3.4, rather than from this particular dataset. The reader interested in applications to real data can also see Section 4.2.2 in Reference [10], where the theory is adapted to lower records and lower $\delta$-records. This is readily done by taking advantage of the symmetry between the definitions of upper and lower records.

4. Bayesian Analysis

We develop the estimation of parameters and prediction of future records in the Bayesian framework. We use parametrization $P_2$ because it is frequently found in the literature on Bayesian analysis of the Weibull model; see Section 14.2 of Reference [27]. As in Section 3, we analyze the cases of $\beta$ known and unknown, while in this section $\alpha$ is assumed unknown. In all expressions below, $\alpha ,\beta$ are positive. Let the Gamma$(\mu ,p)$ density, with parameters $\mu ,p>0$, be denoted $\gamma (x|\mu ,p)={\mu }^p{x}^{p-1}{e}^{-\mu x}/\Gamma (p),x\ge 0$.

If $\beta$ is known, we assume that $\alpha$ has prior $\pi (\alpha )=\gamma (\alpha |a,b)$, which is easily checked to be conjugate. In the case of $\beta$ unknown, there seems to be no tractable conjugate family for $\alpha ,\beta$ and, among several alternatives found in the literature, we decided to follow Kundu [31] and Soland [32]. In Kundu’s approach $\alpha$ and $\beta$ have independent gamma distributions; in Soland’s approach, $\beta$ is discrete, taking values in a finite set and $\alpha$ conditional on $\beta$ is gamma distributed. Other options, not considered here, are found in References [33,34], where $\alpha$, as well as $\beta$ conditional on $\alpha$, have gamma distributions. Definitions of Kundu’s and Soland’s priors are given below.

Definition 7.

(i) Let Kundu’s prior ${\pi }_1$ be defined by ${\pi }_1(\alpha |\beta )=\gamma (\alpha |a,b)$ and ${\pi }_1(\beta )=\gamma (\beta |c,d)$, where $a,b,c,d$ are hyperparameters and $a,b$ do not depend on β.

(ii) Let Soland’s prior ${\pi }_2$ be defined by ${\pi }_2(\alpha |\beta ={\beta }_i)=\gamma (\alpha |a_i,b_i)$ and ${\pi }_2(\beta ={\beta }_i)=p_i$, where $a_i,b_i$ are hyperparameters and ${\beta }_i,p_i$ are positive known values, for $i=1,\dots ,k$, with ${\sum }_{i=1}^k{p}_i=1$.

For simplicity we write hereafter ${\pi }_2(\alpha |{\beta }_i),{\pi }_2({\beta }_i),$ and so forth, instead of ${\pi }_2(\alpha |\beta ={\beta }_i),{\pi }_2(\beta ={\beta }_i)$ and so forth. In what follows we determine the posterior distributions to be used in inferences, namely $\pi (\alpha |\mathbf{t})$ if $\beta$ is known and ${\pi }_j(\alpha ,\beta |\mathbf{t}),j=1,2$, if $\beta$ is unknown. Integrals with respect to $\alpha$ or $\beta$ are understood on $(0,+\infty )$ and so, the limits of the integrals are omitted.

4.1. Posterior Distributions

Suppose first that $\beta$ is known and recall that $\pi (\alpha )=\gamma (\alpha |a,b)$. From (5) we have $\pi (\alpha |\mathbf{t})\propto L_2(\mathbf{t}|\alpha ,\beta )\gamma (\alpha |a,b)\propto {\alpha }^{b+N-1}{e}^{-(a+G(\beta ))\alpha }$ and so, $\pi (\alpha |\mathbf{t})=\gamma (\alpha |a+G(\beta ),b+N)$.

If $\beta$ is unknown, using Kundu’s prior we obtain the posteriors

$$\begin{array}{cc}\hfill {\pi }_1(\alpha ,\beta |\mathbf{t})& \propto L_2(\mathbf{t}|\alpha ,\beta )\gamma (\alpha |a,b)\gamma (\beta |c,d)\propto {\alpha }^{b+N-1}{\beta }^{d+N-1}{e}^{-(a+G(\beta ))\alpha }{(J{e}^{-c})}^{\beta },\hfill \\ \hfill {\pi }_1(\alpha |\mathbf{t})& \propto {\alpha }^{b+N-1}\int {\beta }^{d+N-1}{e}^{-(a+G(\beta ))\alpha }{(J{e}^{-c})}^{\beta }d\beta ,\hfill \\ \hfill {\pi }_1(\beta |\mathbf{t})& \propto \Gamma (b+N)\frac{{\beta }^{d+N-1}{(J{e}^{-c})}^{\beta }}{{(a+G(\beta ))}^{b+N}},\hfill \end{array}$$

(12)

with common normalizing constant (numerically computed), given by

$$K_1:=\Gamma (b+N)\int \frac{{\beta }^{d+N-1}{(J{e}^{-c})}^{\beta }}{{(a+G(\beta ))}^{b+N}}d\beta .$$

(13)

For Soland’s prior we have, from (5) and Definition 7, the posteriors

$$\begin{array}{cc}\hfill {\pi }_2(\alpha ,{\beta }_i|\mathbf{t})& \propto L_2(\mathbf{t}|\alpha ,{\beta }_i){\pi }_2(\alpha |{\beta }_i){\pi }_2({\beta }_i)={\alpha }^{b_i+N-1}{\beta }_i^N{e}^{-(a_i+G({\beta }_i))\alpha }{J}^{{\beta }_i-1}\frac{a_i^{b_i}}{\Gamma (b_i)}{p}_i,\hfill \\ \hfill {\pi }_2(\alpha |\mathbf{t})& \propto \sum _{i=1}^k{\alpha }^{b_i+N-1}{\beta }_i^N{e}^{-(a_i+G({\beta }_i))\alpha }{J}^{{\beta }_i-1}\frac{a_i^{b_i}}{\Gamma (b_i)}{p}_i,\hfill \\ \hfill {\pi }_2({\beta }_i|\mathbf{t})& \propto \frac{p_i{\beta }_i^N{J}^{{\beta }_i-1}}{{\left(a_i+G({\beta }_i)\right)}^{b_i+N}}\frac{a_i^{b_i}\Gamma (b_i+N)}{\Gamma (b_i)},\hfill \end{array}$$

(14)

with common normalizing constant given by

$$K_2=\sum _{i=1}^k\frac{p_i{\beta }_i^N{J}^{{\beta }_i-1}}{{\left(a_i+G({\beta }_i)\right)}^{b_i+N}}\frac{a_i^{b_i}\Gamma (b_i+N)}{\Gamma (b_i)}.$$

(15)

4.2. Estimation of Hyperparameters in Soland’s Prior

A practical challenge with Soland’s prior is the choice of the hyperparameters $a_i,b_i$. We propose to estimate them, using the empirical-Bayes-type method described below, inspired by Reference [4].

For $j=1,\dots ,n$ and $i=1,\dots ,k$, consider the expectations

$$E({\overline{F}}_{\alpha ,\beta }(r_j)|{\beta }_i)=\int {\overline{F}}_{\alpha ,\beta }(r_j){\pi }_2(\alpha |{\beta }_i)d\alpha ={\left(\frac{a_i}{a_i+r_j^{{\beta }_i}}\right)}^{b_i},$$

(16)

$$E({\overline{F}}_{\alpha ,\beta }(R_j)|{\beta }_i)=\int E({\overline{F}}_{\alpha ,\beta }(R_j)|\alpha ,{\beta }_i){\pi }_2(\alpha |{\beta }_i)d\alpha =2^{-j}.$$

(17)

Note that the value $2^{-j}$ in (17) follows from ${\overline{F}}_{\alpha ,\beta }(R_j)$ being distributed as $e^{-{\sum }_{l=1}^j{\xi }_l}$, where ${\xi }_1,\dots ,{\xi }_j$ are iid exponential, with parameter one, so $E({\overline{F}}_{\alpha ,\beta }(R_j)|\alpha ,\beta )=E(e^{-{\sum }_{l=1}^j{\xi }_l})=2^{-j}$; see Reference [2]. Note also that (16) depends on $r_j$, the actual j-th record value of the sample, while (17) depends on the random variable $R_j$. Then $a_i,b_i$ can be estimated by choosing, if possible (as described in Lemma 1 below), two suitable records $r_j,r_l,j<l$ and solving for $a_i,b_i$ in the equations

$${\left(\frac{a_i}{a_i+r_j^{{\beta }_i}}\right)}^{b_i}=2^{-j},{\left(\frac{a_i}{a_i+r_l^{{\beta }_i}}\right)}^{b_i}=2^{-l}.$$

(18)

Lemma 1.

If there exist records $r_j,r_l,j<l$, such that $l{r}_j^{{\beta }_i}<j{r}_l^{{\beta }_i}$, then (18) has a solution.

Proof. 

Let $x=1/a_i$ and $y=b_i$, then (18) is equivalent to

$${\left(1+x{r}_j^{{\beta }_i}\right)}^y=2^j,{\left(1+x{r}_l^{{\beta }_i}\right)}^y=2^l.$$

(19)

Solving for y in (19) and equating we have $g_j(x):={(1+x{r}_j^{{\beta }_i})}^{1/j}=g_l(x):={(1+x{r}_l^{{\beta }_i})}^{1/l}$. Furthermore, observe that $g_j(0)=g_l(0)=1$ and that $g_j(x)/g_l(x)\to \infty$, as $x\to \infty$. Hence, if the derivatives satisfy $g_j^{\prime }(0)<g_l^{\prime }(0)$ or, equivalently, if ${\left(r_j/r_l\right)}^{{\beta }_i}<j/l$, there exists $x^{*}$ such that $g_j(x^{*})=g_l(x^{*})$. Finally, x is replaced by $x^{*}$ in either expression of (19) to solve for y. ☐

4.3. Bayes Estimators of Parameters $\alpha ,\beta$

Bayes estimators are defined under quadratic loss. In the case of known $\beta$, the estimator of $\alpha$ is denoted ${\widehat{\alpha }}_{{}_B}(\beta )$ and follows at once from $\pi (\alpha |\mathbf{t})=\gamma (\alpha |a+G(\beta ),b+N)$. So,

$${\widehat{\alpha }}_{{}_B}(\beta )=\frac{b+N}{a+G(\beta )}.$$

(20)

Credible intervals for $\alpha$ are readily obtained from $\pi (\alpha |\mathbf{t})$, as well. Additionally, it may be of interest the next result of consistency for ${\widehat{\alpha }}_{{}_B}(\beta )$, which follows from Theorem 1. See Reference [35] for a discussion on Bayesian consistency.

Corollary 1.

${\widehat{\alpha }}_{{}_B}(\beta )\stackrel{a.s.}{⟶}\alpha$, for all $a,b,\beta >0$.

Proof. 

From the definitions of $P_1,P_2$, we know that $\alpha ={\lambda }^{-\beta }$. Using this and (20), we can write ${\widehat{\alpha }}_{{}_B}(\beta )$ in terms of $\widehat{\lambda }(\beta )$ (the MLE of $\lambda$ in (7)) as ${\widehat{\alpha }}_{{}_B}(\beta )=\frac{b/N+1}{a/N+{(\widehat{\lambda }(\beta ))}^{\beta }}$. Last, Theorem 1 yields ${\widehat{\alpha }}_{{}_B}(\beta )\stackrel{a.s.}{⟶}{\lambda }^{-\beta }.$ ☐

If $\beta$ is unknown and Kundu’s prior is used, we (numerically) compute the Bayes estimators of $\alpha ,\beta$, denoted respectively ${\widehat{\alpha }}_{{}_B},{\widehat{\beta }}_{{}_B}$, by taking expectations of the posterior densities (12). We obtain

$${\widehat{\alpha }}_{{}_B}=K_1^{-1}\Gamma (b+N+1)\int \frac{{\beta }^{d+N-1}{(J{e}^{-c})}^{\beta }}{{(a+G(\beta ))}^{b+N+1}}d\beta ,{\widehat{\beta }}_{{}_B}=K_1^{-1}\Gamma (b+N)\int \frac{{\beta }^{d+N}{(J{e}^{-c})}^{\beta }}{{(a+G(\beta ))}^{b+N}}d\beta ,$$

(21)

where $K_1$ is defined in (13).

In the case of Soland’s prior, the Bayes estimators are also readily computed from (14), as

$${\widehat{\alpha }}_{{}_B}=K_2^{-1}\sum _{i=1}^k\frac{p_i{\beta }_i^N{a}_i^{b_i}{J}^{{\beta }_i-1}}{{\left(a_i+G({\beta }_i)\right)}^{b_i+N+1}}\frac{\Gamma (b_i+N+1)}{\Gamma (b_i)},{\widehat{\beta }}_{{}_B}=K_2^{-1}\sum _{i=1}^k\frac{p_i{\beta }_i^{N+1}{a}_i^{b_i}{J}^{{\beta }_i-1}}{{\left(a_i+G({\beta }_i)\right)}^{b_i+N}}\frac{\Gamma (b_i+N)}{\Gamma (b_i)},$$

(22)

where $K_2$ is defined in (15). It should be noted that in simulations and in the analysis of real data, using Soland’s prior, we prefer to estimate $\beta$ using ${\widehat{\beta }}_{{}_{\mathrm{MP}}}\in arg\underset{1\le i\le k}{max}{\pi }_2({\beta }_i|\mathbf{t})$, in order to stay within the set of possible $\beta$ values.

4.4. Prediction of Future Records

The Bayesian prediction of future records is based either on $f_{R_m}(z|\beta ,\mathbf{t})$, if $\beta$ is known, or on $f_{R_m}(z|\mathbf{t})$, if $\beta$ is unknown. In all densities below we assume that parameters are positive and $z\ge r_n$.

From (3) and using parametrization $P_2$, we have

$$f_{R_m}(z|\alpha ,\beta ,\mathbf{t})=\frac{{\alpha }^{m-n}{(z^{\beta }-r_n^{\beta })}^{m-n-1}\beta z^{\beta -1}}{\Gamma (m-n)}{e}^{-\alpha (z^{\beta }-r_n^{\beta })}.$$

First, if $\beta$ is known, we use the posterior $\pi (\alpha |\mathbf{t})$ to compute

$$\begin{array}{cc}{f}_{R_m}(z|\beta ,\mathbf{t})\hfill & =\int f_{R_m}(z|\alpha ,\beta ,\mathbf{t})\pi (\alpha |\mathbf{t})d\alpha \hfill \\ \hfill & =\frac{{(z^{\beta }-r_n^{\beta })}^{m-n-1}\beta z^{\beta -1}{(a+G(\beta ))}^{b+N}}{\Gamma (m-n)\Gamma (b+N)}\int {\alpha }^{m-n+b+N-1}{e}^{-\alpha (z^{\beta }-r_n^{\beta }+a+G(\beta ))}d\alpha \hfill \\ \hfill & =\frac{{(z^{\beta }-r_n^{\beta })}^{m-n-1}\beta z^{\beta -1}{(a+G(\beta ))}^{b+N}\Gamma (b+N+m-n)}{{(z^{\beta }-r_n^{\beta }+a+G(\beta ))}^{b+N+m-n}\Gamma (m-n)\Gamma (b+N)}.\hfill \end{array}$$

(23)

Then the Bayes predictor of $R_m$, given by ${\widehat{R}}_m(\beta )=E(R_m|\beta ,\mathbf{t})={\int }_{z_n}^{\infty }z{f}_{R_m}(z|\beta ,\mathbf{t})dz$, is numerically computed as

$${\widehat{R}}_m(\beta )=\frac{\beta {(a+G(\beta ))}^{b+N}\Gamma (b+N+m-n)}{\Gamma (m-n)\Gamma (b+N)}{\int }_{r_n}^{\infty }\frac{z^{\beta }{(z^{\beta }-r_n^{\beta })}^{m-n-1}}{{(z^{\beta }-r_n^{\beta }+a+G(\beta ))}^{b+N+m-n}}dz.$$

If $\beta$ is unknown we use ${\pi }_j(\alpha ,\beta )$ ($j=1$, for Kundu and $j=2$, for Soland) to compute

$$f_{R_m}(z|\mathbf{t})=\int \int f_{R_m}(z|\alpha ,\beta ,\mathbf{t}){\pi }_j(\alpha ,\beta |\mathbf{t})d\alpha d\beta ,$$

(24)

and the Bayes predictor is given by ${\widehat{R}}_m=E(R_m|\mathbf{t})={\int }_{z_n}^{\infty }z{f}_{R_m}(z|\mathbf{t})dz$. Bayesian prediction intervals are also readily obtained.

In the case of Kundu’s prior, from (12) and (24) we have

$$f_{R_m}(z|\mathbf{t})=K_1^{-1}\frac{\Gamma (N+m-n+b)}{\Gamma (m-n)}\int \frac{{\beta }^{N+d}{z}^{\beta -1}{(z^{\beta }-r_n^{\beta })}^{m-n-1}{(J{e}^{-c})}^{\beta }}{{(z^{\beta }-r_n^{\beta }+a+G(\beta ))}^{m-n+N+b}}d\beta .$$

(25)

In the case of Soland’s prior, from (14) and (24), we get

$$f_{R_m}(z|\mathbf{t})=\frac{K_2^{-1}}{\Gamma (m-n)}\sum _{i=1}^k\frac{{\beta }_i^{N+1}{z}^{{\beta }_i-1}{(z^{{\beta }_i}-r_n^{{\beta }_i})}^{m-n-1}{J}^{{\beta }_i-1}{a}_i^{b_i}{p}_i\Gamma (m-n+b_i+N)}{{(z^{{\beta }_i}-r_n^{{\beta }_i}+a_i+G({\beta }_i))}^{m-n+N+b_i}\Gamma (b_i)}.$$

4.5. Simulation Study

We assess here the performance of estimators, credible intervals and predictors. To that end, we simulate samples of $\delta$-records, with $n=5$ records. For each sample we compute estimators or predictors for records only ($\delta =0$) and for $\delta$-records ($\delta =-0.5$).

4.5.1. Known $\beta$

In

Table 5. EMSE of Bayes estimator ${\widehat{\alpha }}_{{}_B}(\beta )$; length (LHPD) and coverage (%CHPD) of highest posterior density (HPD) interval of parameter $\alpha$, with known $\beta$.

		$\mathit{\delta }=0$			$\mathit{\delta }=-0.5$
$\mathit{\pi }(\mathit{\alpha })$	$\mathit{\beta }$	EMSE	LHPD	%CHPD	EMSE	LHPD	%CHPD
	0.75	0.128	1.262	94.9	0.098	1.140	95.1
$\gamma (\alpha |4,4)$	1	0.131	1.263	94.7	0.090	1.077	95.0
	1.5	0.120	1.250	94.9	0.066	0.919	94.7
	0.75	0.224	1.719	94.9	0.162	1.500	95.0
$\gamma (\alpha |4,6)$	1	0.218	1.715	95.2	0.145	1.409	94.9
	1.5	0.222	1.719	94.9	0.107	1.206	94.6

we show results for the Bayes estimator ${\widehat{\alpha }}_{{}_B}(\beta )$, defined in (20) and 95% HPD intervals for $\alpha$. For several values of $a,b$ and $\beta$, we simulate ${10}^4$ independent observations of $\alpha$, from the Gamma$(a,b)$ distribution. Then, for each $\alpha$ we simulate a random sample of 5 records and their associated near-records and compute ${\widehat{\alpha }}_{{}_B}(\beta )$. The EMSE is computed as average of squared differences ${({\widehat{\alpha }}_{{}_B}(\beta )-\alpha )}^2$, over the ${10}^4$ simulation runs.

We report in Table 5 the mean coverage and average length of the ${10}^4$ HPD intervals. Regarding the coverage, as we sample $\alpha$ from its prior distribution, approximately $95\%$ of the intervals (both for records and $\delta$-records), contain the value of the parameter in the simulation. Since this happens in all the HPD we construct in this section, we do not include the coverage of the HPD intervals in the remaining tables. In all cases we observe that ${\widehat{\alpha }}_{{}_B}(\beta )$ and the HPD intervals based on $\delta$-records compare quite favorably with their counterparts based only on records ($\delta =0$), in terms of smaller EMSE and interval length.

Additionally, we analyze the frequentist coverage for particular values of the parameter. In order to do so, we take $\beta =1.5$ and fix a value of $\alpha$ in a grid from 0.2 to 2; we then simulate 200 samples of records (and $\delta$-records), compute the corresponding HPDs for $\alpha$, using a Gamma$(4,4)$ prior and check if they contain the value of $\alpha$. We repeat this for each value of $\alpha$. 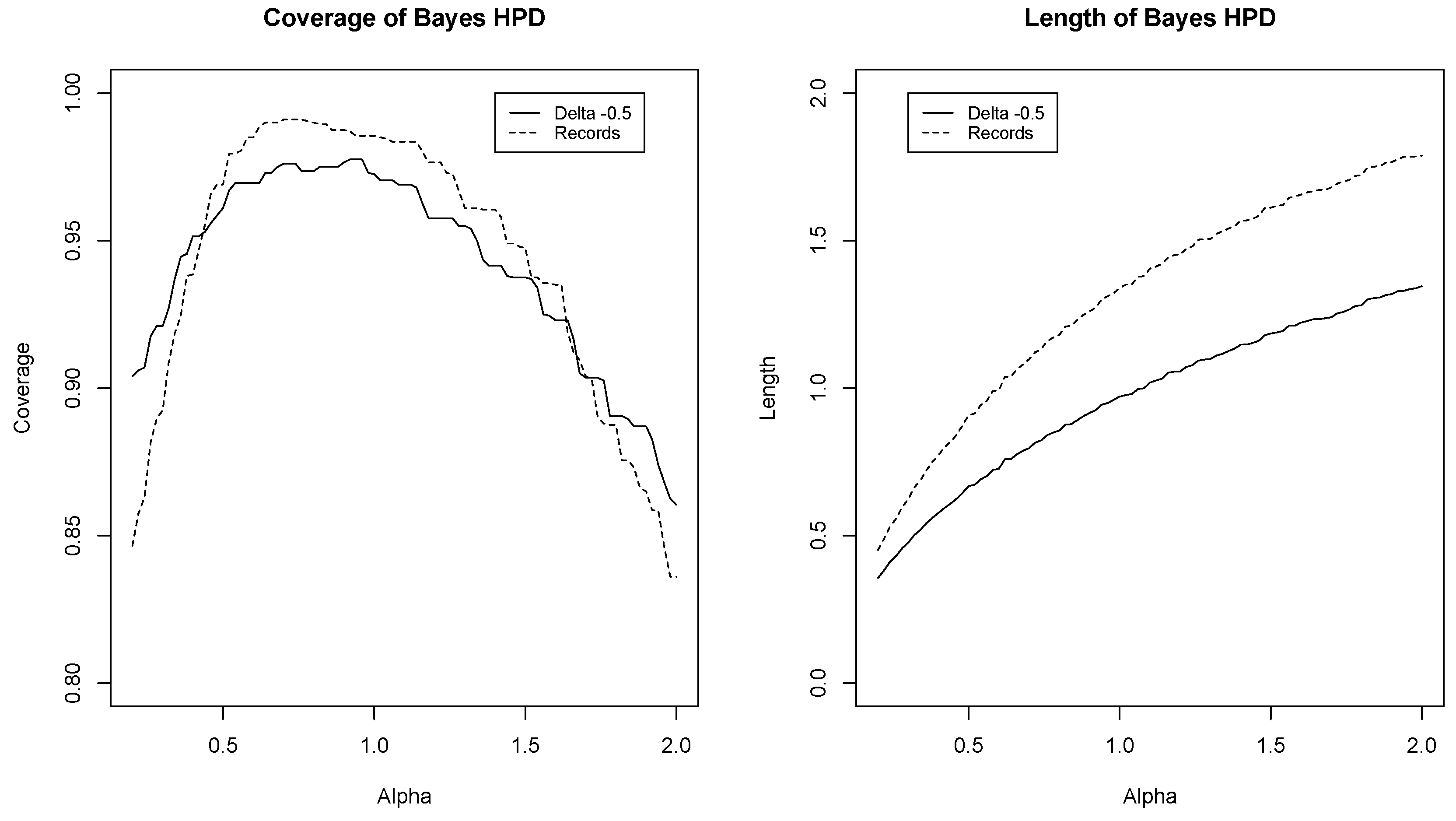Figure 2 (left) shows the coverage for $\alpha \in [0.2,2]$. We observe that $\delta$-records provide intervals with frequentist coverage closer to $95\%$ than records. The right plot in Figure 2 shows the average length of the intervals as a function of $\alpha$.

In the assessment of Bayes predictors of future records (known $\beta$), we consider different gamma priors for $\alpha$ and simulate ${10}^4$ values of $\alpha$. For each simulated $\alpha$ we generate a sample of $\delta$-records and the values of $R_6$ and $R_7$. Then we compute the EMSE of ${\widehat{R}}_6$ and ${\widehat{R}}_7$, as the average of the squared deviations ${({\widehat{R}}_6-R_6)}^2$ and ${({\widehat{R}}_7-R_7)}^2$, over the ${10}^4$ simulation runs. We also compute the lengths of the HPD intervals as the average of the lengths of the estimated intervals. The coverage of the intervals, defined as the proportion of runs where the simulated record is in the interval, is included as well. As in the case of estimation, since we sample $\alpha$ from the prior distribution in the simulations, approximately 95% of the intervals contain the corresponding record. So, we do not include the coverage in the rest of the tables for prediction.

Results are displayed in

Table 6. EMSE of Bayes predictors ${\widehat{R}}_6,{\widehat{R}}_7$; length (LHPD) and coverage (%CHPD) of HPD intervals for $R_6,R_7$, with known $\beta$.

		$\mathit{\delta }=0$						$\mathit{\delta }=-0.5$
		${\mathit{R}}_{\mathbf{6}}$			${\mathit{R}}_{\mathbf{7}}$			${\mathit{R}}_{\mathbf{6}}$			${\mathit{R}}_{\mathbf{7}}$
$\mathbf{\pi }(\mathbf{\alpha })$	$\mathbf{\beta }$	EMSE${\widehat{\mathit{R}}}_{\mathbf{6}}$	LHPD	%CHPD	EMSE${\widehat{\mathit{R}}}_{\mathbf{7}}$	LHPD	%CHPD	EMSE${\widehat{\mathit{R}}}_{\mathbf{6}}$	LHPD	%CHPD	EMSE${\widehat{\mathit{R}}}_{\mathbf{7}}$	LHPD	%CHPD
	0.75	35.094	12.225	94.9	111.424	21.297	94.8	34.931	12.147	94.7	110.946	21.092	94.8
$\gamma (\alpha |4,4)$	1	3.054	4.261	94.9	6.292	6.964	95.1	2.995	4.217	94.9	6.095	6.843	95.0
	1.5	0.227	1.368	95.4	0.491	2.140	94.6	0.219	1.335	95.3	0.454	2.058	94.9
	0.75	6.302	5.961	94.6	14.945	10.211	94.9	6.213	5.916	94.7	14.671	10.074	94.7
$\gamma (\alpha |4,6)$	1	0.902	2.516	94.7	1.965	4.081	94.9	0.883	2.485	94.8	1.910	3.985	94.7
	1.5	0.118	0.978	95.1	0.222	1.522	94.8	0.113	0.957	94.9	0.207	1.464	94.7

, where it is apparent that predictors are more accurate with $\delta$-records. While Table 5 shows a significant improvement in the estimation of $\alpha$, with the use of $\delta$-records, this improvement is less visible when forecasting future records. Nevertheless, as in the case of MLP, a fair comparison between the EMSE of predictions should take into account the lower bounds commented there. For instance, if $\beta =1$ and $\alpha$ is fixed, the bound is $(m-n)/{\alpha }^2$. Therefore, when $\alpha$ has a prior Gamma$(a,b)$, with $b>2$, the lower bound can be computed as

$${\int }_0^{\infty }\frac{m-n}{{\alpha }^2}\frac{1}{\Gamma (b)}{e}^{-a\alpha }{\alpha }^{b-1}{a}^{b}d\alpha =\frac{(m-n)a^2}{(b-1)(b-2)}.$$

In the particular case $a=b=4$, $m=7$, $n=5$, the bound is $16/3$. Then the gain with the use of $\delta$-records, once subtracted the lower bound, is $(6.292-6.095)/(6.292-16/3)=20.5\%$. That is, while the absolute gain of 0.2 may not seem relevant, relative to 6.292, it is so when the lower bound on the EMSE is taken into account.

4.5.2. Unknown $\alpha ,\beta$

We begin with Kundu’s prior ${\pi }_1$, described in Definition 7. For fixed $a,b,c,d$ we simulate ${10}^3$ pairs $(\alpha ,\beta )$ from ${\pi }_1(\alpha ,\beta )$ and, for each $(\alpha ,\beta )$ we generate a sample of 5 records and their near-records. Once the sample is observed, we numerically compute $K_1$ in (13), to obtain an approximation of ${\pi }_1(\alpha ,\beta |\mathbf{t})$. We then compute the Bayes estimators ${\widehat{\alpha }}_{{}_B},{\widehat{\beta }}_{{}_B}$ in (21) and the HPD intervals from ${\pi }_1(\alpha ,\beta |\mathbf{t})$. The EMSE are obtained as averages of the squared deviations ${({\widehat{\alpha }}_{{}_B}-\alpha )}^2$ and ${({\widehat{\beta }}_{{}_B}-\beta )}^2$, over the ${10}^3$ simulation runs. As in the case of known $\beta$, we observe in

Table 7. EMSE of Bayes estimators ${\widehat{\alpha }}_{{}_B}$, ${\widehat{\beta }}_{{}_B}$ and length (LHPD) of HPD intervals, using Kundu’s prior.

		$\mathit{\delta }=0$				$\mathit{\delta }=-0.5$
${\mathit{\pi }}_1(\mathit{\alpha })$	${\mathit{\pi }}_1(\mathit{\beta })$	EMSE ${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	LHPD $\mathit{\alpha }$	EMSE ${\widehat{\mathit{\beta }}}_{{}_{\mathit{B}}}$	LHPD $\mathit{\beta }$	EMSE ${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	LHPD $\mathit{\alpha }$	EMSE ${\widehat{\mathit{\beta }}}_{{}_{\mathit{B}}}$	LHPD $\mathit{\beta }$
	$\gamma (\alpha |8,6)$	0.179	1.488	0.048	0.731	0.152	1.389	0.036	0.662
$\gamma (\alpha |4,4)$	$\gamma (\alpha |6,6)$	0.192	1.485	0.080	0.970	0.160	1.363	0.058	0.850
	$\gamma (\alpha |6,8)$	0.173	1.456	0.105	1.205	0.139	1.310	0.080	1.049
	$\gamma (\alpha |8,6)$	0.293	1.904	0.045	0.747	0.219	1.717	0.033	0.640
$\gamma (\alpha |4,6)$	$\gamma (\alpha |6,6)$	0.288	1.899	0.078	0.997	0.220	1.690	0.051	0.830
	$\gamma (\alpha |6,8)$	0.269	1.888	0.111	1.247	0.206	1.620	0.077	1.020

that $\delta$-records have a positive effect, both in the accuracy of the estimations and in the length of the HPD intervals.

For Soland’s prior ${\pi }_2$ we choose the values ${\beta }_k\in \{0.5,0.75,1,1.25,1.5\}$ for $\beta$, with different prior probabilities and two different gamma distributions for $\alpha$, given $\beta ={\beta }_k$. The HPD intervals for $\beta$ are not computed since $\beta$ is discrete and takes only five different values. Results are shown in

Table 8. EMSE of Bayes estimator ${\widehat{\alpha }}_{{}_B}$ and of MP estimator ${\widehat{\beta }}_{{}_{\mathrm{MP}}}$ and length (LHPD) of HPD interval for $\alpha$, using Soland’s prior ${\pi }_2$.

		$\mathit{\delta }=0$			$\mathit{\delta }=-0.5$
${\mathit{\pi }}_2(\mathit{\alpha }|\mathit{\beta })$	${\mathit{\pi }}_2(\mathit{\beta })$	EMSE ${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	EMSE ${\widehat{\mathit{\beta }}}_{{}_{\mathbf{MP}}}$	LHPD $\mathit{\alpha }$	EMSE ${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	EMSE ${\widehat{\mathit{\beta }}}_{{}_{\mathbf{MP}}}$	LHPD $\mathit{\alpha }$
	$(\frac{4}{10},\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10})$	0.165	1.400	0.076	0.138	1.289	0.054
$\gamma (\alpha |4,4)$	$(\frac{1}{10},\frac{2}{10},\frac{4}{10},\frac{2}{10},\frac{1}{10})$	0.156	1.374	0.055	0.128	1.240	0.044
	$(\frac{1}{10},\frac{1}{10},\frac{2}{10},\frac{2}{10},\frac{4}{10})$	0.163	1.354	0.079	0.121	1.166	0.065
	$(\frac{4}{10},\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10})$	0.258	1.837	0.085	0.204	1.634	0.053
$\gamma (\alpha |4,6)$	$(\frac{1}{10},\frac{2}{10},\frac{4}{10},\frac{2}{10},\frac{1}{10})$	0.252	1.820	0.061	0.189	1.578	0.046
	$(\frac{1}{10},\frac{1}{10},\frac{2}{10},\frac{2}{10},\frac{4}{10})$	0.259	1.801	0.086	0.181	1.488	0.061

.

Simulation results of Bayes predictors of future records ($\alpha ,\beta$ unknown), using Kundu’s and Soland’s priors, are presented in

Table 9. Trimmed EMSE (TEMSE) of Bayes predictors and lengths (LHPD) of HPD intervals for $R_6,R_7$, using Kundu’s prior ${\pi }_1$.

		$\mathit{\delta }=0$				$\mathit{\delta }=-0.5$
${\mathit{\pi }}_1(\mathit{\alpha })$	${\mathit{\pi }}_1(\mathit{\beta })$	TEMSE ${\widehat{\mathit{R}}}_6$	LHPD ${\mathit{R}}_6$	TEMSE ${\widehat{\mathit{R}}}_7$	LHPD ${\mathit{R}}_7$	TEMSE ${\widehat{\mathit{R}}}_6$	LHPD ${\mathit{R}}_6$	TEMSE ${\widehat{\mathit{R}}}_7$	LHPD ${\mathit{R}}_7$
	$\gamma (\alpha |8,6)$	3318.601	42.805	24,215.125	58,844	3281.805	42.795	24198.502	58.309
$\gamma (\alpha |4,4)$	$\gamma (\alpha |6,6)$	45.326	14.270	415.003	27.315	45.724	14.013	414.015	26.771
	$\gamma (\alpha |6,8)$	1.997	3.735	7.296	7.446	1.917	3.602	6.885	7.288
	$\gamma (\alpha |8,6)$	134.211	19.175	1018.288	34.819	132.540	18.758	1006.229	34.279
$\gamma (\alpha |4,6)$	$\gamma (\alpha |6,6)$	10.079	7.689	67.697	16.994	9.830	7.636	64.405	16.586
	$\gamma (\alpha |6,8)$	0.664	2.266	2.539	4.221	0.702	2.201	2.534	4.032

and

Table 10. Trimmed EMSE (TEMSE) of Bayes predictors and lengths (LHPD) of HPD intervals for $R_6,R_7$, using Soland’s prior ${\pi }_2$.

		$\mathit{\delta }=0$				$\mathit{\delta }=-0.5$
${\mathit{\pi }}_2(\mathit{\alpha }|\mathit{\beta })$	${\mathit{\pi }}_2(\mathit{\beta })$	TEMSE ${\widehat{\mathit{R}}}_6$	LHPD ${\mathit{R}}_6$	TEMSE ${\widehat{\mathit{R}}}_7$	LHPD ${\mathit{R}}_7$	TEMSE ${\widehat{\mathit{R}}}_6$	LHPD ${\mathit{R}}_6$	TEMSE ${\widehat{\mathit{R}}}_7$	LHPD ${\mathit{R}}_7$
	$(\frac{4}{10},\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10})$	462.880	25.479	1069.877	41.557	462.968	25.420	1054.563	41.486
$\gamma (\alpha |4,4)$	$(\frac{1}{10},\frac{2}{10},\frac{4}{10},\frac{2}{10},\frac{1}{10})$	45.904	7.823	102.881	12.856	45.608	7.714	103.401	12.634
	$(\frac{1}{10},\frac{1}{10},\frac{2}{10},\frac{2}{10},\frac{4}{10})$	15.881	5.597	56.159	10.723	16.009	5.565	54.574	10.551
	$(\frac{4}{10},\frac{2}{10},\frac{2}{10},\frac{1}{10},\frac{1}{10})$	66.015	11.170	145.522	20.895	66.318	11.111	145.077	20.724
$\gamma (\alpha |4,6)$	$(\frac{1}{10},\frac{2}{10},\frac{4}{10},\frac{2}{10},\frac{1}{10})$	7.938	3.929	9.609	7.093	7.832	3.888	9.520	7.013
	$(\frac{1}{10},\frac{1}{10},\frac{2}{10},\frac{2}{10},\frac{4}{10})$	5.827	3.022	5.961	5.185	5.769	2.983	5.943	5.132

, respectively. As before, we proceed by simulating first the parameter values, from the prior distributions and then the sample of $\delta$-records and the values of future records. There is, however, a practical difficulty when computing the EMSE of predictors, since a few huge records, which actually appear in simulations, completely dominate the EMSE because it is just the average of squared deviations. Suppose, for example, that we use Kundu’s prior and that the values $\alpha =0.5,\beta =0.1$ have been obtained from ${\pi }_1(\alpha ,\beta )$. Then, the corresponding Weibull distribution has expectation $3.7\times {10}^9$, the value of $R_m$ will likely be very large and so, a huge value of ${({\widehat{R}}_m-R_m)}^2$ will be observed. These “outliers” make the EMSE, computed over all the simulation runs, a useless measure of performance. In order to avoid this problem, we compute the $5\%$ trimmed mean of ${({\widehat{R}}_m-R_m)}^2$, over the simulations. That is, we eliminate the $2.5\%$ smallest and largest values of ${({\widehat{R}}_m-R_m)}^2$ and compute the average with the remaining ones. The results in Table 9 and Table 10 show that $\delta$-records have an impact in the prediction of future records, as observed in the case of known $\beta$.

4.6. Real Data

Given that we do not have actual prior knowledge of the parameters, we decided to consider values around 2 for $\beta$ and around $1/2$ for $\alpha$, having only illustrative meaning. In Kundu’s prior ${\pi }_1$, we take $a=2,b=1,c=1,d=2$. For Soland’s prior ${\pi }_2$ we consider $\beta$ uniformly distributed on $\{1.5,1.75,2,2.25,2.5\}$ and in order to determine the values of $(a_i,b_i)$, we apply the method described before Lemma 1, if possible. Recall that in order to apply the method on ${\beta }_i$, there must exist a pair of records $r_j<r_l$ such that $l{r}_j^{{\beta }_i}<j{r}_l^{{\beta }_i}$. For ${\beta }_1=1.5$ and ${\beta }_2=1.75$, there exists no such pair of records while, for ${\beta }_3=2,{\beta }_4=2.25$ and ${\beta }_5=2.5$, the method can be applied and yields the following hyperparameter pairs (after rounding up to the nearest integer): $(40,20),(18,8)$ and $(13,5)$ for ${\beta }_3,{\beta }_4$ and ${\beta }_5$ respectively. For ${\beta }_1$ and ${\beta }_2$, where the method fails, we pick the value of the closest $\beta$, that is, $(40,20)$. For numerical convenience, we analyze rainfall data using decimeters instead of millimeters, so that the values of $\delta$ and ${\widehat{r}}_i$ are now divided by 100.

The results are shown in

Table 11. Bayes estimates ${\widehat{\alpha }}_{{}_B},{\widehat{\beta }}_{{}_B}$, Bayes predictions ${\widehat{R}}_6,{\widehat{R}}_7,{\widehat{R}}_8$ and HPD intervals, for rainfall data, using Kundu’s prior ${\pi }_1$.

$\mathit{\delta }$	${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	HPD $\mathit{\alpha }$	${\widehat{\mathit{\beta }}}_{{}_{\mathit{B}}}$	HPD $\mathit{\beta }$	${\widehat{\mathit{R}}}_6$	HPD ${\mathit{R}}_6$	${\widehat{\mathit{R}}}_7$	HPD ${\mathit{R}}_7$	${\widehat{\mathit{R}}}_8$	HPD ${\mathit{R}}_8$
0	0.41	[0.01, 1.05]	2.69	[1.21, 4.32]	3.04	[2.79, 3.61]	3.26	[2.79, 4.12]	3.47	[2.81, 4.58]
−0.25	0.41	[0.01, 1.04]	2.46	[1.06, 4.02]	3.13	[2.79, 3.87]	3.42	[2.79, 4.54]	3.24	[2.80, 3.84]
−0.50	0.39	[0.02, 0.97]	2.57	[1.19, 4.09]	3.07	[2.79, 3.67]	3.32	[2.79, 4.20]	3.55	[2.83, 4.68]
−0.75	0.48	[0.06, 1.05]	2.60	[1.44, 3.82]	2.98	[2.79, 3.37]	3.15	[2.79, 3.70]	3.32	[2.82, 4.00]
$-\infty$	0.58	[0.42, 0.74]	2.10	[1.72, 2.46]	3.05	[2.79, 3.54]	3.28	[2.80, 3.94]	3.50	[2.87, 4.30]

and

Table 12. Bayes estimation ${\widehat{\alpha }}_{{}_B}$, maximum probability estimation ${\widehat{\beta }}_{{}_{\mathrm{MP}}}$, Bayes predictions ${\widehat{R}}_6,{\widehat{R}}_7,{\widehat{R}}_8$ and HPD intervals (except $\beta$), for rainfall data, using Soland’s prior.

$\mathit{\delta }$	${\widehat{\mathit{\alpha }}}_{{}_{\mathit{B}}}$	HPD $\mathit{\alpha }$	${\widehat{\mathit{\beta }}}_{{}_{\mathbf{MP}}}$	${\widehat{\mathit{R}}}_6$	HPD ${\mathit{R}}_6$	${\widehat{\mathit{R}}}_7$	HPD ${\mathit{R}}_7$	${\widehat{\mathit{R}}}_8$	HPD ${\mathit{R}}_8$
0	0.39	[0.16, 0.62]	2.50	3.01	[2.79, 3.45]	3.21	[2.8, 3.79]	3.39	[2.85, 4.08]
−0.25	0.33	[0.15, 0.53]	2.50	3.04	[2.79, 3.53]	3.26	[2.8, 3.90]	3.47	[2.86, 4.22]
−0.50	0.34	[0.17, 0.52]	2.50	3.03	[2.79, 3.49]	3.24	[2.8, 3.84]	3.44	[2.86, 4.14]
−0.75	0.43	[0.27, 0.61]	2.50	2.98	[2.79, 3.34]	3.15	[2.8, 3.62]	3.31	[2.85, 3.86]
$-\infty$	0.47	[0.37, 0.56]	2.50	2.96	[2.79, 3.29]	3.12	[2.8, 3.54]	3.27	[2.85, 3.75]

. In both tables we observe that the estimates of the parameters using $\delta$-records, with $\delta =-0.75$, outperform those based on records only, because they are closer to results using the complete sample. As in maximum likelihood prediction, the gain in prediction of future records using $\delta$-records versus records is not clear; while there is some improvement using Soland’s prior, this is not the case for Kundu’s prior. This can be due to the surprising closeness of Kundu’s prediction using records to the prediction using the whole sample, which we believe happens by chance in this particular instance.

5. Final Comments

Professionals interested in statistical inferences for the Weibull model, based on record data, should consider the possibility of using $\delta$-records. We have presented in this paper the mathematical bases of the methodology, together with some theoretical results, such as consistency. We have also established the existence of estimators and predictors and discussed their numerical implementation so that researchers interested in applications can readily test the method on their own data. As commented above, we insist here that $\delta$-records can be collected, in many cases, by slightly modifying the experimental setup for records so that the additional cost related to extra data is kept low. The conclusions to be drawn from the simulations and the application to the rainfall data are that $\delta$-records improve inferences in the Weibull model. The impact is more notorious in MLE than in the Bayesian framework, possibly because of a strong influence of the priors. We believe that more investigation would be welcome for fine tuning this novel methodology. For example, it would be useful to have guidelines for the choice of $\delta$ and to explore the possibility of letting $\delta$ vary during data collection. Also, in the theoretical analysis of the model, it would be of interest to extend the consistency of Theorem 1 to the case of unknown shape parameter and study eventual asymptotic distributions; see Remark 4. These and other related topics will be considered in forthcoming papers.

6. Technical Results and Proofs

6.1. Consistency of the MLE $\widehat{\lambda }(\beta )$

The proof of Theorem 1 follows from Lemmas 2–7, related to the asymptotic behavior of $\delta$-records, which can be of independent interest. Strong convergence, as the appropriate index (usually n) tends to infinity, is denoted by $\stackrel{a.s.}{⟶}$; inequalities with random variables are understood in the almost sure sense. Recall that $R_m$ denotes the m-th record, while $S_m$ and $(Y_{m,1},\dots ,Y_{m,S_m})$ denote respectively the number and the vector of near-records associated to $R_m$.

Lemma 2.

If $\beta >1$ then $S_n/n^{\gamma }\stackrel{a.s.}{⟶}\infty$, for all $\gamma >0$.

Proof. 

It suffices to show that $S_n/{\varphi }_{n,k}\stackrel{a.s.}{⟶}\infty$, for $k\ge 1$, where ${\varphi }_{n,k}=(n-1)\cdots (n-k)$ is the k-th falling factorial of $n-1$. To that end we apply the Borel-Cantelli lemma to show that $P(S_n<{\varphi }_{n,k}M\mathrm{i}.\mathrm{o}.)=0$, for every integer $M>0$ (i.o. stands for infinitely often). Observe that $S_n$ conditional on $R_n$ is geometrically distributed (starting at 0), with parameter

$$p_n:=\frac{{\overline{F}}_{\lambda ,\beta }(R_n)}{{\overline{F}}_{\lambda ,\beta }(R_n+\delta )}=e^{-\alpha (R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta })},$$

(26)

where $\alpha ={\lambda }^{-\beta }$, that is, $P(S_n=k|R_n)={(1-p_n)}^k{p}_n,k\ge 0$; see Reference [10]. Noting that

$$R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta }\ge \beta (R_n-{(R_n+\delta )}_{+}){(R_n+\delta )}_{+}^{\beta -1}=|\delta |\beta {(R_n+\delta )}_{+}^{\beta -1},$$

from (26) we have $p_n\le e^{-\alpha |\delta |\beta {(R_n+\delta )}_{+}^{\beta -1}}$ and so,

$$P(S_n<{\varphi }_{n,k}M|R_n)=1-{(1-p_n)}^{{\varphi }_{n,k}M}\le {\varphi }_{n,k}M{p}_n\le {\varphi }_{n,k}M{e}^{-\alpha |\delta |\beta {(R_n+\delta )}_{+}^{\beta -1}}.$$

Now, since $R_n^{\beta }$ has Gamma$(\alpha ,n)$ distribution (see Reference [2]), we get

$$P(S_n<{\varphi }_{n,k}M)\le M{\int }_0^{\infty }{e}^{-\alpha |\delta |\beta {(t^{1/\beta }+\delta )}_{+}^{\beta -1}}{\varphi }_{n,k}\frac{{\alpha }^n{t}^{n-1}{e}^{-\alpha t}}{\Gamma (n)}dt.$$

Hence, knowing that the k-th factorial moment of a Poisson random variable with parameter $\mu$ is ${\mu }^k$, we have

$$\begin{array}{cc}\hfill \sum _{n=1}^{\infty }P(S_n<{\varphi }_{n,k}M)& \le M{\int }_0^{\infty }{e}^{-\alpha |\delta |\beta {(t^{1/\beta }+\delta )}_{+}^{\beta -1}}\alpha \sum _{n=1}^{\infty }{\varphi }_{n,k}\frac{{(\alpha t)}^{n-1}{e}^{-\alpha t}}{\Gamma (n)}dt\hfill \\ \hfill & =M{\int }_0^{\infty }\alpha {(\alpha t)}^k{e}^{-\alpha |\delta |\beta {(t^{1/\beta }+\delta )}_{+}^{\beta -1}}dt\hfill \\ \hfill & =M{\int }_0^{\infty }\alpha {(\alpha u^{\beta })}^k{e}^{-{\alpha |\delta |\beta (u+\delta )}_{+}^{\beta -1}}\beta u^{\beta -1}du<\infty ,\hfill \end{array}$$

and the conclusion follows. ☐

Lemma 3.

Let $U_n={\sum }_{j=1}^{S_n}(Y_{n,j}^{\beta }-{(R_n+\delta )}_{+}^{\beta }),n\ge 1$. Then, if $\beta >1$, $U_n/S_n\stackrel{a.s.}{⟶}{\lambda }^{\beta }$.

Proof. 

From Proposition 1 in Reference [10] we know that, conditional on $R_n$ and $S_n,S_n>0$, the random variables $Y_{n,1},\dots ,Y_{n,S_n}$ are iid, with common density function

$$g_{\lambda ,\beta }(y):=\frac{\alpha \beta y^{\beta -1}{e}^{-\alpha y^{\beta }}}{e^{-\alpha {(R_n+\delta )}_{+}^{\beta }}-e^{-\alpha R_n^{\beta }}},y\in ({(R_n+\delta )}_{+},R_n),n\ge 1,$$

with $\alpha ={\lambda }^{-\beta }$. Hence, letting $\mathcal{F}$ be the $\sigma$-algebra generated by the sequences $(R_n)$ and $(S_n)$, we obtain

$$\begin{array}{cc}\hfill E[Y_{n,j}^{\beta }|\mathcal{F}]& =\frac{1}{e^{-\alpha {(R_n+\delta )}_{+}^{\beta }}-e^{-\alpha R_n^{\beta }}}{\int }_{{(R_n+\delta )}_{+}}^{R_n}\alpha \beta y^{2\beta -1}{e}^{-\alpha y^{\beta }}dy\hfill \\ & =\frac{1}{e^{-\alpha {(R_n+\delta )}_{+}^{\beta }}-e^{-\alpha R_n^{\beta }}}{\int }_{{(R_n+\delta )}_{+}^{\beta }}^{R_n^{\beta }}\alpha t{e}^{-\alpha t}dt\hfill \\ & ={\displaystyle \frac{1}{\alpha }}-\frac{R_n^{\beta }{e}^{-\alpha R_n^{\beta }}-{(R_n+\delta )}_{+}^{\beta }{e}^{-\alpha {(R_n+\delta )}_{+}^{\beta }}}{e^{-\alpha {(R_n+\delta )}_{+}^{\beta }}-e^{-\alpha R_n^{\beta }}},\hfill \end{array}$$

and so, $E[Y_{n,j}^{\beta }-{(R_n+\delta )}_{+}^{\beta }|\mathcal{F}]=\frac{1}{\alpha }-K_n$, where $K_n:=\frac{R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta }}{e^{\alpha (R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta })}-1},j=1,\dots ,S_n.$ Let also

$$Z_{n,j}=Y_{n,j}^{\beta }-E[Y_{n,j}^{\beta }|\mathcal{F}]=Y_{n,j}^{\beta }-{(R_n+\delta )}_{+}^{\beta }-\frac{1}{\alpha }+K_n,j=1,\dots ,S_n,$$

(27)

and let $V_n={\sum }_{j=1}^{S_n}{Z}_{n,j},n\ge 1$. Then, by Tchebychev’s inequality, $P(|V_n|>ϵS_n|\mathcal{F})\le \frac{{\sigma }_n^2}{{ϵ}^2{S}_n}$, for all $ϵ>0$, where

$${\sigma }_n^2:=E(Z_{n,j}^2|\mathcal{F})=E({(Y_{n,j}^{\beta }-E(Y_{n,j}^{\beta }|\mathcal{F}))}^2|\mathcal{F})\le E(Y_{n,j}^{2\beta }|\mathcal{F})\le R_n^{2\beta },n\ge 1.$$

Furthermore, since the sequence $(R_n^{\beta })$ is distributed as the ordered points of a homogeneous Poisson process, with rate ${\lambda }^{-\beta }$ (see Reference [2]), the strong law of large numbers implies

$$\frac{R_n^{\beta }}{n}\stackrel{a.s.}{⟶}{\lambda }^{\beta },$$

(28)

and so $lim\; sup{\sigma }_n^2/n^2\le {\lambda }^{2\beta }$. Then, by Lemma 2, with $\gamma =4$, we have ${\sigma }_n^2/S_n=o(n^{-2})$. Therefore ${\sum }_{n=1}^{\infty }P(|V_n|>ϵS_n|\mathcal{F})<\infty$ and, by the (conditional) Borel-Cantelli lemma, $P(|V_n|>ϵS_n\mathrm{i}.\mathrm{o}.|\mathcal{F})=0$ and so $P(V_n/S_n\to 0|\mathcal{F})=1$. Then, taking expectation, we obtain $V_n/S_n\stackrel{a.s.}{⟶}0$. Finally, since $R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta }\ge |\delta |\beta {(R_n+\delta )}_{+}^{\beta -1}\stackrel{a.s.}{⟶}\infty$ (because $R_n\stackrel{a.s.}{⟶}\infty$ and $\beta >1$), we get $K_n\stackrel{a.s.}{⟶}0$. The conclusion now follows from the above convergence results and the identity $U_n/S_n=V_n/S_n+{\lambda }^{\beta }-K_n$. ☐

Lemma 4.

If $\beta =1$ then $\frac{1}{n}{\sum }_{i=1}^n{S}_i\stackrel{a.s.}{⟶}{e}^{-\delta /\lambda }-1$.

Proof. 

As stated in Lemma 2, conditionally on $(R_n)$, the random variables $S_i$ are independent and geometrically distributed, with parameter $p_i=e^{-\alpha (R_i-{(R_i+\delta )}_{+})}$, where $\alpha ={\lambda }^{-1}$. Let ${\tilde{S}}_i=S_i-(1-p_i)/p_i,i\ge 1$, then $E({\tilde{S}}_i|\mathcal{G})=0$, where $\mathcal{G}$ is the $\sigma$-algebra generated by $(R_n)$. Furthermore, observe that $p_i\ge e^{\delta \alpha }$ and $E({\tilde{S}}_i^4|\mathcal{G})\le 19p_i^{-4}$. So, the conditional fourth moment of ${\tilde{S}}_i$ is bounded above by $19e^{-4\alpha \delta }$ and the following (conditional) strong law of large numbers holds: $P\left(\frac{1}{n}{\sum }_{i=1}^n{\tilde{S}}_i\to 0|\mathcal{G}\right)=1$. Then, taking expectation and observing that $(1-p_n)/p_n=e^{\alpha (R_n-{(R_n+\delta )}_{+})}-1\stackrel{a.s.}{⟶}{e}^{-\alpha \delta }-1$, the conclusion follows. ☐

Lemma 5.

If $\beta =1$ then $\frac{1}{n}{\sum }_{i=1}^n{U}_i\stackrel{a.s.}{⟶}\lambda (e^{-\delta /\lambda }-1)+\delta$, with $U_i$ defined in Lemma 3.

Proof. 

Let $\mathcal{F},Z_{i,j},V_i$ and $\alpha$ be defined as in the proof of Lemma 3. Note that, conditionally on $\mathcal{F}$, the $Z_{i,j}$ are independent with mean 0 and also that $|Z_{i,j}|\le |\delta |$. It follows that $E(V_i^2|\mathcal{F})\le M{S}_i$ and $E(V_i^4|\mathcal{F})\le M{S}_i^2$, for some non-random constant $M>0$. Consequently, since the $V_i$ are also conditionally independent and centered, we have

$$E\left({\left(\sum _{i=1}^n{V}_i\right)}^4|\mathcal{F}\right)=\sum _{i=1}^{n}E(V_i^4|\mathcal{F})+6\sum _{i<j}E(V_i^2|\mathcal{F})E(V_j^2|\mathcal{F})\le M\sum _{i=1}^n{S}_i^2+6M^2\sum _{i<j}{S}_i{S}_j.$$

On the other hand, from (26) and $R_i-{(R_i+\delta )}_{+}\le -\delta$, we get

$$E(S_i^2|R_i)\le \frac{2}{p_i^2}\le 2e^{-2\alpha \delta },E(S_i{S}_j|R_i,R_j)=E(S_i|R_i)E(S_j|R_j)\le \frac{1}{p_i{p}_j}\le e^{-2\alpha \delta }.$$

(29)

Then, by Tchebychev’s inequality and (29),

$$\begin{array}{cc}\hfill P\left(\left|\frac{1}{n}\sum _{i=1}^n{V}_i\right|>ϵ\right)& \le \frac{E({({\sum }_{i=1}^n{V}_i)}^4)}{n^4{ϵ}^4}\hfill \\ \hfill & \le \frac{M}{n^4{ϵ}^4}\left(\sum _{i=1}^{n}E(S_i^2)+6M\sum _{i<j}E(S_i{S}_j)\right)\hfill \\ \hfill & \le \frac{M}{n^4{ϵ}^4}(2n{e}^{-2\alpha \delta }+3n^{2}M{e}^{-2\alpha \delta }),\hfill \end{array}$$

and it follows that $\frac{1}{n}{\sum }_{i=1}^n{V}_i\stackrel{a.s.}{⟶}0$. The conclusion is obtained if we show that

$$\frac{1}{n}\sum _{i=1}^n{S}_i\left(\frac{1}{\alpha }-\frac{R_i-{(R_i+\delta )}_{+}}{e^{\alpha (R_i-{(R_i+\delta )}_{+})}-1}\right)\stackrel{a.s.}{⟶}\frac{1}{\alpha }(e^{-\alpha \delta }-1)+\delta ,$$

but such convergence is implied by Lemma 4 and $R_n-{(R_n+\delta )}_{+}\stackrel{a.s.}{⟶}-\delta$. ☐

Lemma 6.

If $\beta <1$ then $\frac{1}{n}{\sum }_{i=1}^n{S}_i\stackrel{a.s.}{⟶}0$.

Proof. 

Let $N_n$ and $D_n$ be the number of records and of near-records among the first n observations, respectively, then it is clear that $S_1+\cdots +S_{N_n-1}\le D_n\le S_1+\cdots +S_{N_n}$. From Proposition 5.1 of Reference [28], we have $D_n/logn\stackrel{a.s.}{⟶}0$ and, noting that $N_{L(n)}=n$, where $L(n)$ is the n-th record time, we have

$$\frac{S_1+\cdots +S_{n-1}}{n}=\frac{S_1+\cdots S_{N_{L(n)}-1}}{N_{L(n)}}\le \frac{D_{L(n)}}{logL(n)}\frac{logL(n)}{N_{L(n)}}\stackrel{a.s.}{⟶}0,$$

where we have used $L(n)\stackrel{a.s.}{⟶}\infty$ and the well-known result $N_n/logn\stackrel{a.s.}{⟶}1$, thus proving the result. ☐

Lemma 7.

If $\beta <1$ then $\frac{1}{n}{\sum }_{i=1}^n{U}_i\stackrel{a.s.}{⟶}0$, where $U_i$ is defined in Lemma 3.

Proof. 

Since $\beta <1$, we have $Y_{i,j}^{\beta }-{(R_i+\delta )}_{+}^{\beta }\le R_i^{\beta }-{(R_i+\delta )}_{+}^{\beta }\le {|\delta |}^{\beta }$. Therefore, by Lemma 6, $\frac{1}{n}{\sum }_{i=1}^n{U}_i\le \frac{{|\delta |}^{\beta }}{n}{\sum }_{i=1}^n{S}_i\stackrel{a.s.}{⟶}0$. ☐

Proof of Theorem 1.

 

We divide the proof in three cases, depending on the tail behavior of $F_{\lambda ,\beta }$, that is, $\beta >1$, $\beta =1$, $\beta <1$. Recall that $U_i={\sum }_{j=1}^{S_i}\left(Y_{i,j}^{\beta }-{(R_i+\delta )}_{+}^{\beta }\right)$, then from (6) and (7),

$$\widehat{\lambda }(\beta )={\left(\frac{{\sum }_{i=1}^n\left(R_i^{\beta }-{(R_i+\delta )}_{+}^{\beta }+U_i\right)+R_n^{\beta }}{n+{\sum }_{i=1}^n{S}_i}\right)}^{\frac{1}{\beta }}.$$

(i) Case $\beta >1$. Note that, by Lemma 2 and (28),

$$\frac{{\sum }_{i=1}^n\left(R_i^{\beta }-{(R_i+\delta )}_{+}^{\beta }\right)+R_n^{\beta }}{n+{\sum }_{i=1}^n{S}_i}\le \frac{(n+1)R_n^{\beta }}{S_n}\stackrel{a.s.}{⟶}0.$$

Then convergence of $\widehat{\lambda }(\beta )$ to $\lambda$ is equivalent to

$$\frac{{\sum }_{i=1}^n{U}_i}{n+{\sum }_{i=1}^n{S}_i}\stackrel{a.s.}{⟶}{\lambda }^{\beta },$$

which follows from Lemmas 2 and 3.

(ii) Case $\beta =1$. From Lemma 4 we have $\frac{N}{n}=\frac{n+{\sum }_{i=1}^n{S}_i}{n}\stackrel{a.s.}{⟶}{e}^{-\delta /\lambda }.$ Also, since $R_n\stackrel{a.s.}{⟶}\infty$, we have $\frac{1}{n}{\sum }_{i=1}^n(R_i-{(R_i+\delta )}_{+})\stackrel{a.s.}{⟶}-\delta$ and the result follows from (28) and Lemma 5.

(iii) Case $\beta <1$. Note that $R_n^{\beta }-{(R_n+\delta )}_{+}^{\beta }\stackrel{a.s.}{⟶}0$, since $R_n\stackrel{a.s.}{⟶}\infty$ and $\beta <1$, so $\frac{1}{n}{\sum }_{i=1}^n(R_i^{\beta }-{(R_i+\delta )}_{+}^{\beta })\stackrel{a.s.}{⟶}0.$ This convergence, together with (28) and Lemmas 6 and 7, complete the proof. ☐

6.2. MLP of $R_m$

Proof of Proposition 4.

 

(i) For $z>r_n$, let $l_1(z,\lambda ,\beta )=log{L}_1^P(z,\mathbf{t}|\lambda ,\beta )$. Then

$$\begin{array}{cc}\hfill l_1(z,\lambda ,\beta )& =(m-n-1)log(z^{\beta }-r_n^{\beta })-log\Gamma (m-n)-\beta (m-n+N)log\lambda +(N+1)log\beta \hfill \\ \hfill & +(\beta -1)logz-{\lambda }^{-\beta }(z^{\beta }-r_n^{\beta }+G(\beta ))+(\beta -1)logJ.\hfill \end{array}$$

Solving for $\lambda$ in

$$\frac{\partial l_1}{\partial \lambda }=-\frac{\beta (m-n+N)}{\lambda }+\beta {\lambda }^{-(\beta +1)}(z^{\beta }-r_n^{\beta }+G(\beta ))=0,$$

we obtain the stationary point $\tilde{\lambda }(\beta )={\left(\frac{z^{\beta }-r_n^{\beta }+G(\beta )}{m-n+N}\right)}^{\frac{1}{\beta }}>0$, which is the unique element of $arg\underset{\lambda }{max}{l}_1(z,\lambda ,\beta )$, because $\frac{{\partial }_1^{2}l}{\partial {\lambda }^2}<0$ at $\tilde{\lambda }$, for all $z,\beta$. Thus, the problem $\underset{\lambda ,z}{max}{l}_1(z,\lambda ,\beta )$ is reduced to $\underset{z}{max}{l}_1(z,\tilde{\lambda }(\beta ),\beta )$ or, equivalently, to $\underset{z}{max}{\tilde{l}}_1(z)$, where

$$\begin{array}{cc}\hfill {\tilde{l}}_1(z):=& -(m-n+N)log(z^{\beta }-r_n^{\beta }+G(\beta ))+(N+1)log\beta \hfill \\ & +(m-n-1)log(z^{\beta }-r_n^{\beta })+(\beta -1)logz+\beta logJ.\hfill \end{array}$$

With the change of variable $x=z^{\beta }-r_n^{\beta }$, we get

$${\widehat{l}}_1(x):=-(m-n+N)log(x+G(\beta ))+(N+1)log\beta +(m-n-1)logx+\frac{\beta -1}{\beta }log(x+r_n^{\beta })+\beta logJ,$$

(30)

and $\underset{z>r_n}{max}{\tilde{l}}_1(z)$ is reduced to $\underset{x>0}{max}{\widehat{l}}_1(x)$. We now study the sign of the derivative

$$\frac{\partial {\widehat{l}}_1}{\partial x}=-\frac{N+m-n}{x+G(\beta )}+\frac{m-n-1}{x}+\frac{\beta -1}{\beta (x+r_n^{\beta })},$$

(31)

which is equal to the sign of the polynomial $q(x):=a{x}^2+bx+c$, with coefficients defined in (10).

We observe, since $a<0$ and $ac\le 0$, that q is concave on $\mathbb{R}$ and has real roots given by $\nu =\frac{-b+\sqrt{b^2-4ac}}{2a}\le 0$ and $\rho =\frac{-b-\sqrt{b^2-4ac}}{2a}\ge 0$. If $m=n+1$, then $c=0$ and $b=(\beta -1)G(\beta )-\beta (N+1)r_n^{\beta }<0$, because $G(\beta )\le (N+1)r_n^{\beta }$; see (6), for definitions of N and $G(\beta )$. Hence $\rho =-\frac{b+|b|}{2a}=0$. On the other hand, if $m>n+1$, then $c>0$ and $ac<0$, which clearly implies $\rho >0$. We summarize the above in terms of (31), denoting by $\tilde{z}(\beta )$ an element of $arg\underset{z}{max}{\tilde{l}}_1(z)$:

• If $m=n+1$, then $\rho =0$, $\frac{\partial {\widehat{l}}_1}{\partial x}$ is negative on $(0,+\infty )$ and so, ${\widehat{l}}_1(x)$ has no maximum on $(0,+\infty )$. In this case we do, however, define $\tilde{z}(\beta )=r_n$, that is, ${\tilde{z}}^{\beta }(\beta )=\rho +r_n^{\beta }$.
• If $m>n+1$, then $\rho >0$, $\frac{\partial {\widehat{l}}_1}{\partial x}$ is positive on $(0,\rho )$ and is negative on $(\rho ,+\infty )$. Hence ${\tilde{z}}^{\beta }(\beta )=\rho +r_n^{\beta }$.

(ii) Given the definitions of $\tilde{z}(\beta )$ and $\tilde{\lambda }(\beta )$, it only remains to prove that $\tilde{A}$ is nonempty, noting that $\tilde{A}=arg\underset{\beta }{max}{\widehat{l}}_1(\rho )$. By Lemma 8, ${\widehat{l}}_1(\rho )\to -\infty$, as $\beta \to 0^{+}$ and, by Lemma 10, ${\widehat{l}}_1(\rho )\to -\infty$, as $\beta \to +\infty$. This ensures that $\tilde{A}$ is nonempty, since ${\widehat{l}}_1(\rho )$ is a continuous function of $\beta >0$. ☐

Lemma 8.

(i) $\underset{\beta \to 0^{+}}{lim}\frac{\rho }{\beta }\to m-n-1$,

(ii) $\underset{\beta \to 0^{+}}{lim}{\widehat{l}}_1(\rho )\to -\infty$.

Proof. 

(i) Note that $r_n^{\beta }\to 1$ and $G(\beta )\to 1$, implying $a\to -1,b\to -1$, $c\to 0$ and $c/\beta \to m-n-1$, as $\beta \to 0^{+}$. Hence, the conclusion follows from

$$\frac{\rho }{\beta }=\frac{2c}{\beta \left(-b+\sqrt{b^2-4ac}\right)}\to m-n-1.$$

(32)

(ii) Let $m=n+1$ and recall that $\rho =0$. Then the conclusion is reached, since, as $\beta \to 0^{+}$,

$${\widehat{l}}_1(\rho )=(N+1)(log\beta -logG(\beta ))+\beta (log{r}_n+logJ)-log{r}_n\to -\infty .$$

On the other hand, if $m>n+1$, from $G(\beta )\to 1,\rho \to 0$, we have

$$\underset{\beta \to 0^{+}}{lim}{\widehat{l}}_1(\rho )=\underset{\beta \to 0^{+}}{lim}((N+1)log\beta +(m-n-1)log\rho )+\underset{\beta \to 0^{+}}{lim}\frac{\beta -1}{\beta }log(\rho +r_n^{\beta }).$$

(33)

The first limit in the RHS of (33) is $-\infty$ and the second is finite and can be computed from (32), since

$${(\rho +r_n^{\beta })}^{1/\beta }={\left(1+\beta \left(\frac{\rho }{\beta }+\frac{r_n^{\beta }-1}{\beta }\right)\right)}^{1/\beta }\to r_n{e}^{m-n-1}.$$

 ☐

Lemma 9.

Let $m>n+1$. Then there exist constants $A,B>0$ such that, for all $\beta >1$,

$$A{r}_n^{\beta }<\rho <B{r}_n^{\beta }.$$

(34)

Proof. 

Note that $G(\beta )=2r_n^{\beta }+o(r_n^{\beta })$, as $\beta \to +\infty$. Then, from (10), $a/\beta =-N+o(1)$, $b/\beta =r_n^{\beta }(K+o(1))$ and $c/\beta =2(m-n-1)r_n^{2\beta }(1+o(1))$, as $\beta \to +\infty$, where $K\ne 0$ is a constant. Then

$$\frac{\rho }{r_n^{\beta }}\to \frac{K+\sqrt{K^2+8N(m-n-1)}}{2N}>0,$$

and the conclusion follows. ☐

Lemma 10.

$\underset{\beta \to +\infty }{lim}{\widehat{l}}_1(\rho )=-\infty$.

Proof. 

Let $m>n+1$. From Lemma 9 and recalling that $r_n^{\beta }<G(\beta )\le (N+1)r_n^{\beta }$, we have

$$\begin{array}{cc}\hfill {\widehat{l}}_1(\rho )& \le -(m-n+N)log((A+1)r_n^{\beta })+(N+1)log\beta \hfill \\ \hfill & +(m-n-1)log(B{r}_n^{\beta })+\frac{\beta -1}{\beta }log((B+1)r_n^{\beta })+\beta logJ\hfill \\ \hfill & =\beta (logJ-Nlog{r}_n)+(N+1)log\beta +K+o(1)\to -\infty ,\hfill \end{array}$$

as $\beta \to +\infty$, where K is a constant and the limit is a consequence of the inequality $logJ<Nlog{r}_n$; see (6) for definitions of J and N. Now, if $m=n+1$, we have $\rho =0$ and

$$\begin{array}{cc}\hfill {\widehat{l}}_1(\rho )& =(N+1)(log\beta -logG(\beta ))+(\beta -1)log{r}_n+\beta logJ\hfill \\ \hfill & \le (N+1)(log\beta -\beta log{r}_n)+\beta (log{r}_n+logJ)-log{r}_n\hfill \\ \hfill & =(N+1)log\beta +\beta (logJ-Nlog{r}_n)-log{r}_n\to -\infty .\hfill \end{array}$$

 ☐

Remark 7.

It is clear that the maximization of ${\widehat{l}}_1(\rho )$ with respect to β, in the proof of Proposition 4, cannot be done analytically and numerical techniques must be used. The search for the maximum can be reduced to a compact interval $[{\beta }_L,{\beta }_U]$, with ${\beta }_L>0$, as explained below.

Let us write $\rho (\beta )$ instead of just ρ, to make explicit the dependence on β. Then, by Lemma 8 (ii), there exists ${\beta }_L\in (0,1)$ such that ${\widehat{l}}_1(\rho (\beta ))<{\widehat{l}}_1(\rho (1))$, for all $\beta <{\beta }_L$ and hence $arg\underset{\beta }{max}{\widehat{l}}_1(\rho (\beta ))\subset [{\beta }_L,\infty )$. For the upper bound ${\beta }_U$ we observe, from Lemma 10, that a value ${\beta }_U>1$ can be found, such that ${\widehat{l}}_1(\rho (\beta ))<{\widehat{l}}_1(\rho (1))$, for all $\beta >{\beta }_U$. Therefore, $arg\underset{\beta }{max}{\widehat{l}}_1(\rho (\beta ))\subset (-\infty ,{\beta }_U]$ and, since ${\beta }_L<{\beta }_U$, we have $arg\underset{\beta }{max}{\widehat{l}}_1(\rho (\beta ))\subset [{\beta }_L,{\beta }_U]$. Note that, when writing ${\widehat{l}}_1(\rho (1))$, we mean that β is replaced by 1 in the whole expression for ${\widehat{l}}_1$, not only in $\rho (\beta )$.