A Novel Isomap-SVR Soft Sensor Model and Its Application in Rotary Kiln Calcination Zone Temperature Prediction
Abstract
1. Introduction
2. Pellet Production Process and Soft Sensor Model
2.1. Pellet Production Process
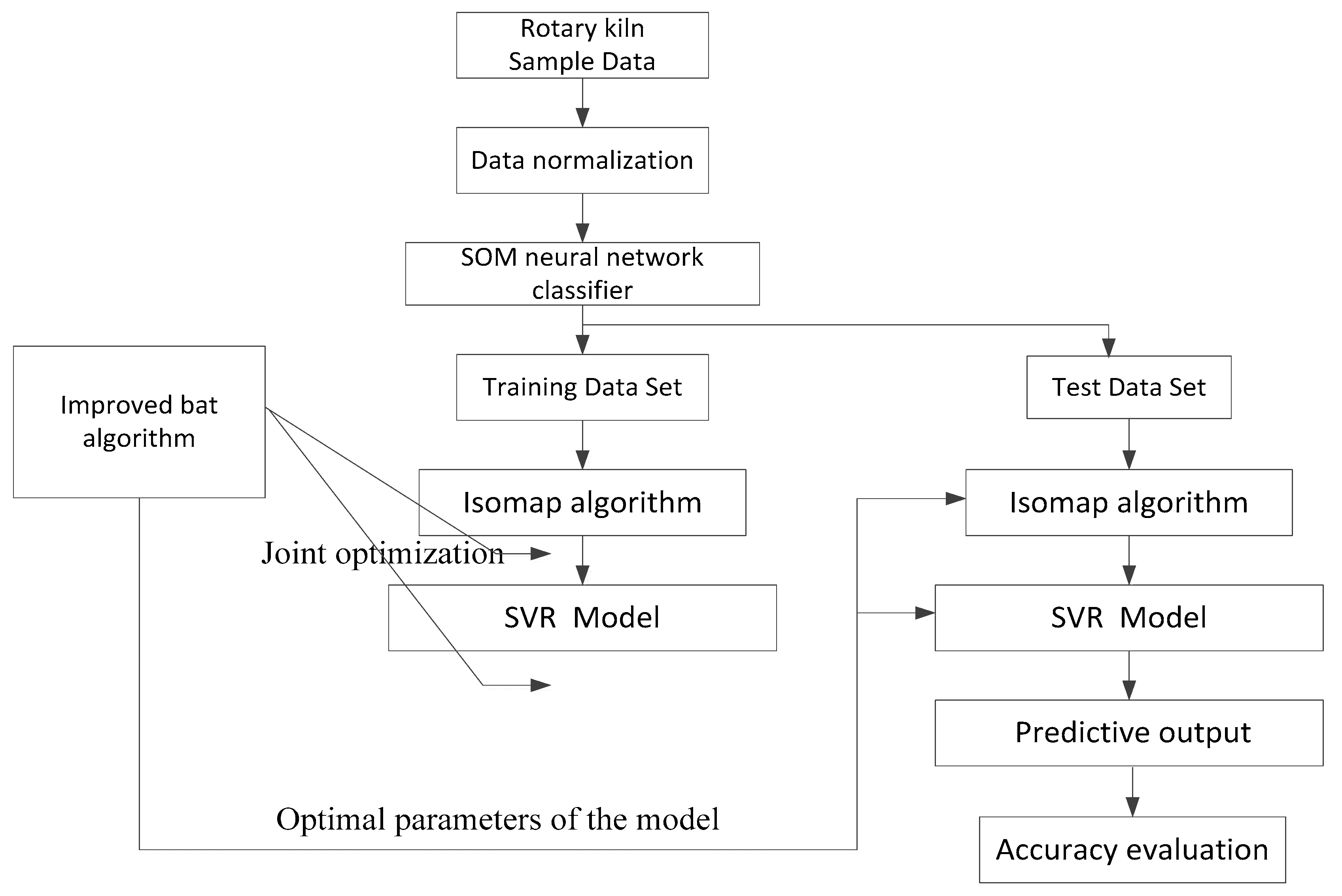
2.2. Soft Sensor Model Structure
3. Data Dimension Reduction Processing Based on Isomap
4. SVR Soft Sensor Modeling Optimized by Improved Bat Algorithm
4.1. SVR Algorithm
4.2. Bat Algorithm and Its Improvement
4.2.1. Bat Algorithm
4.2.2. Lévy Flight Strategy
4.2.3. Cauchy Mutation Strategy
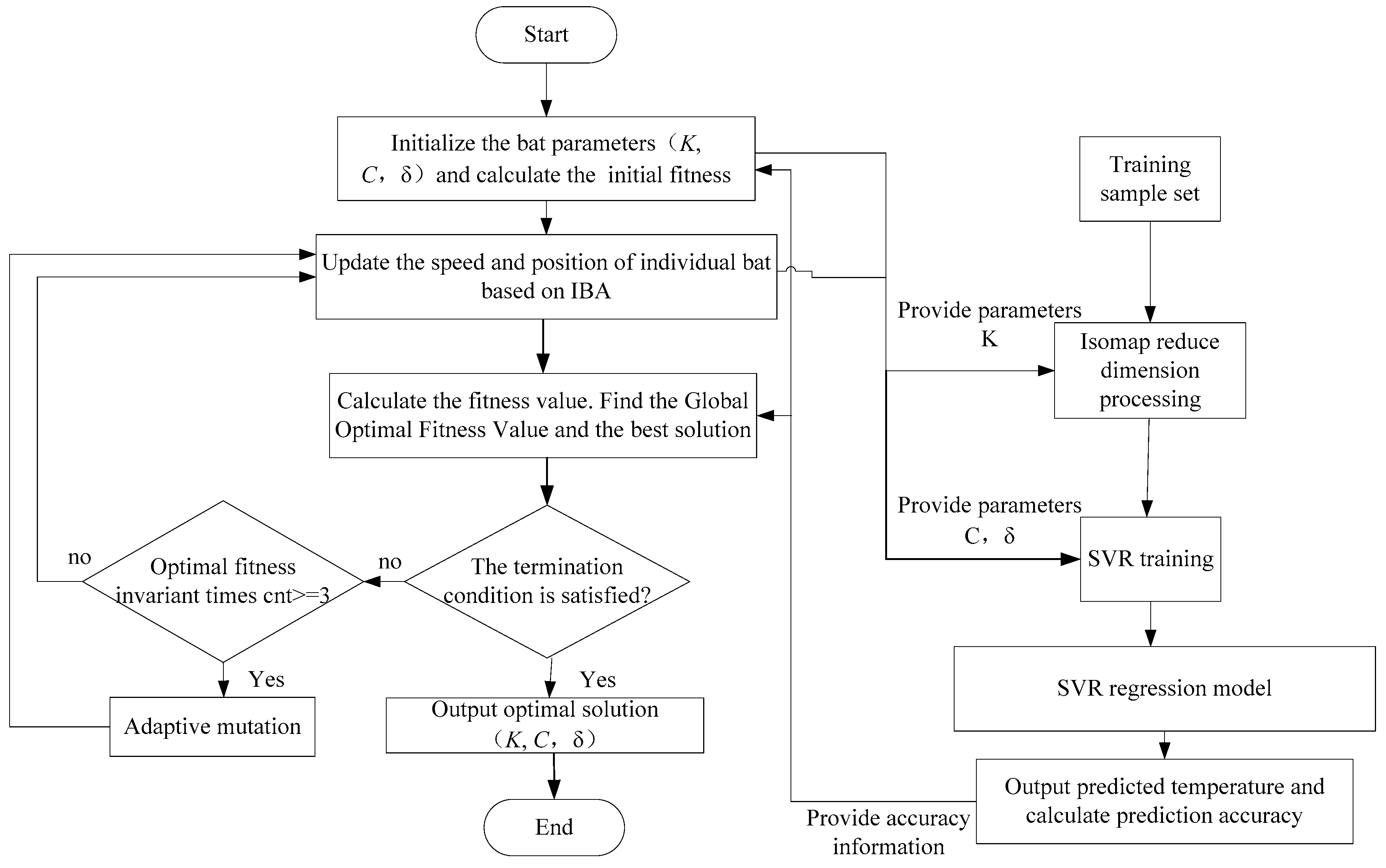
4.3. Soft Sensor Model Optimization Based on IBA Algorithm
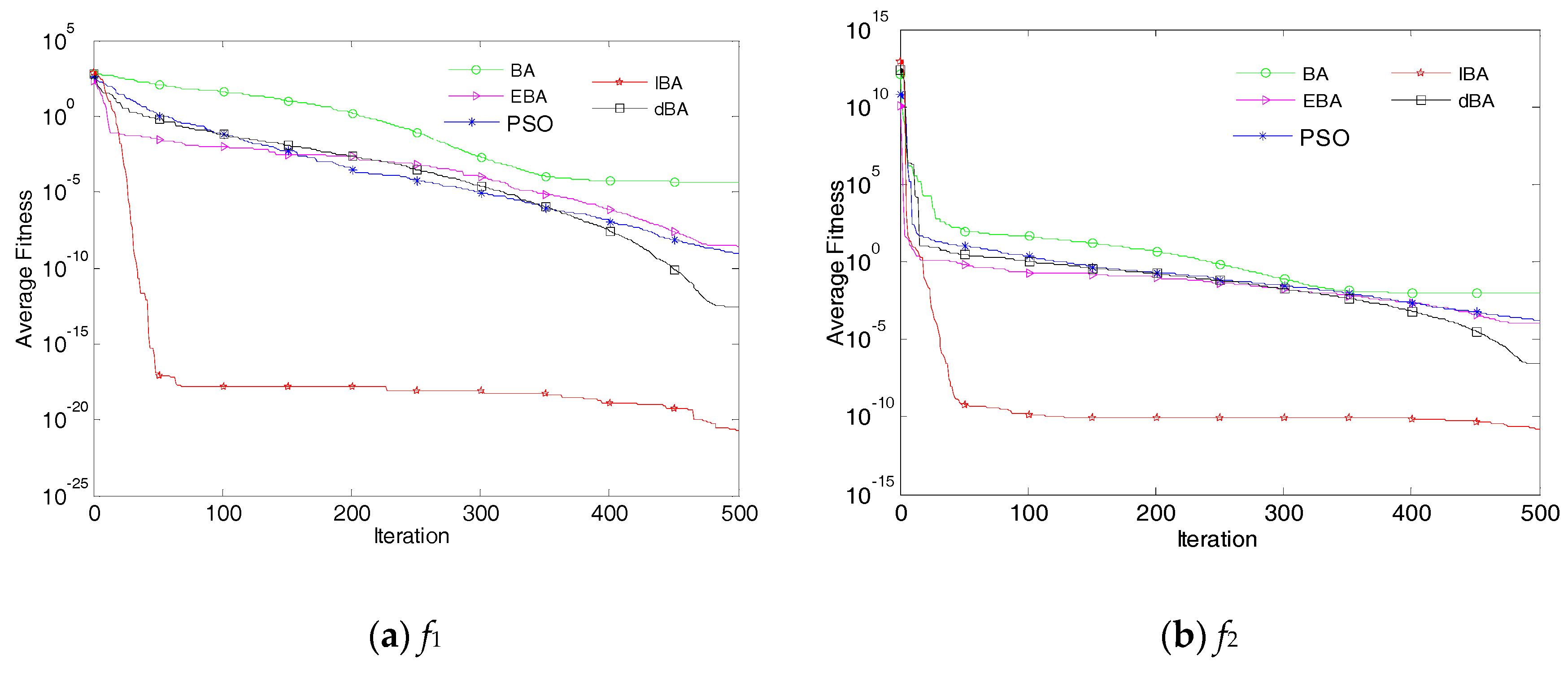
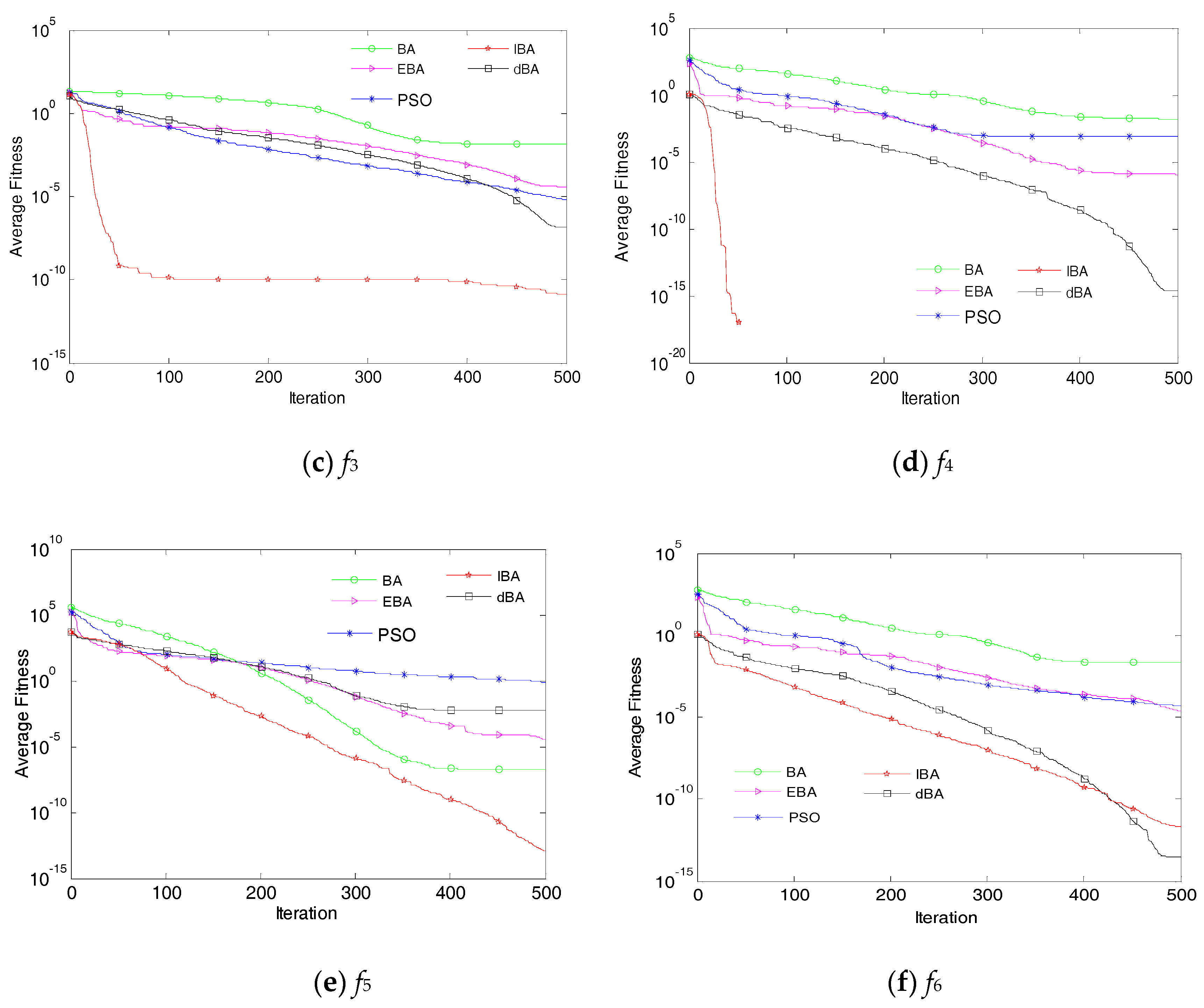
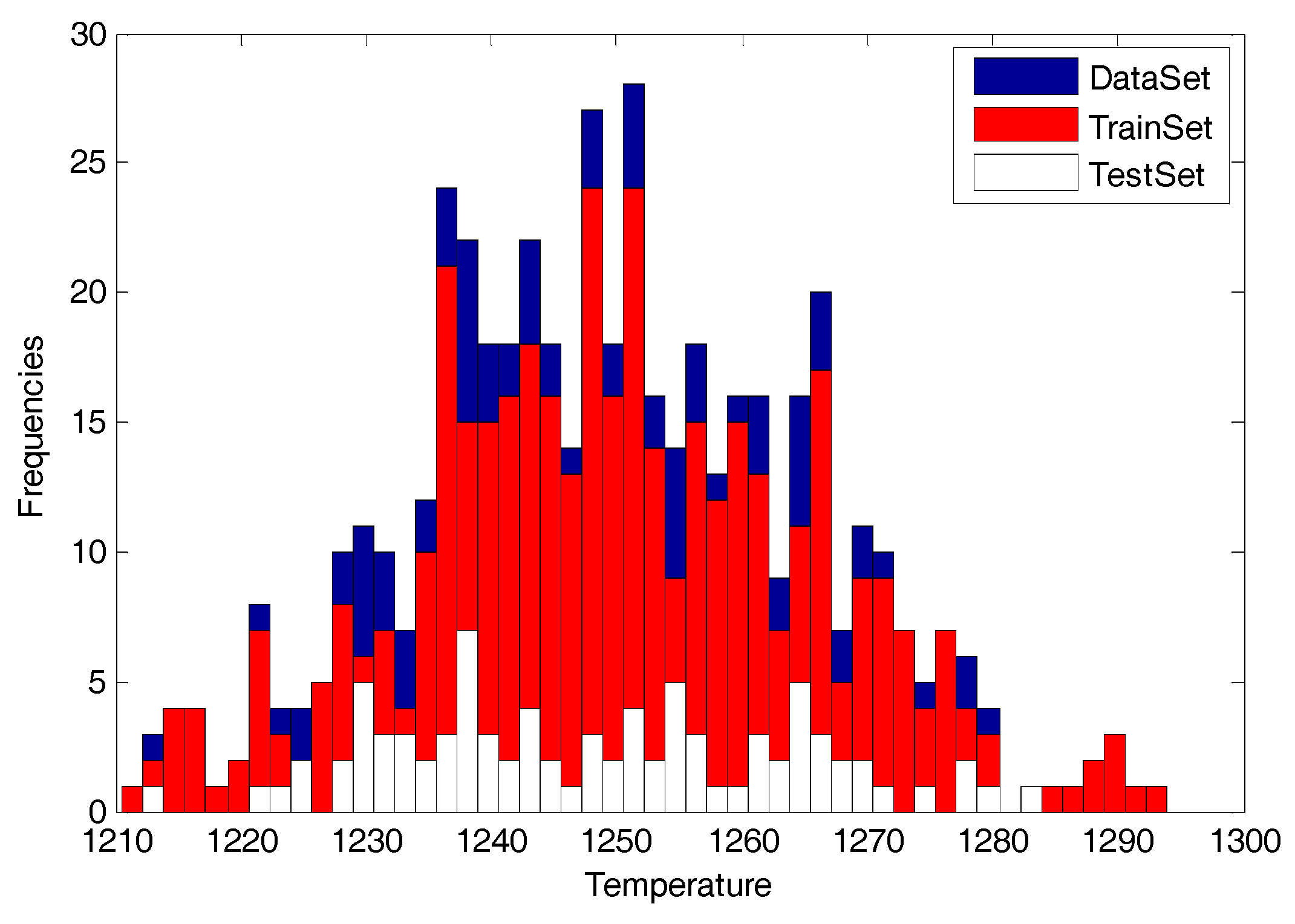
5. Simulation Analysis
- (1)
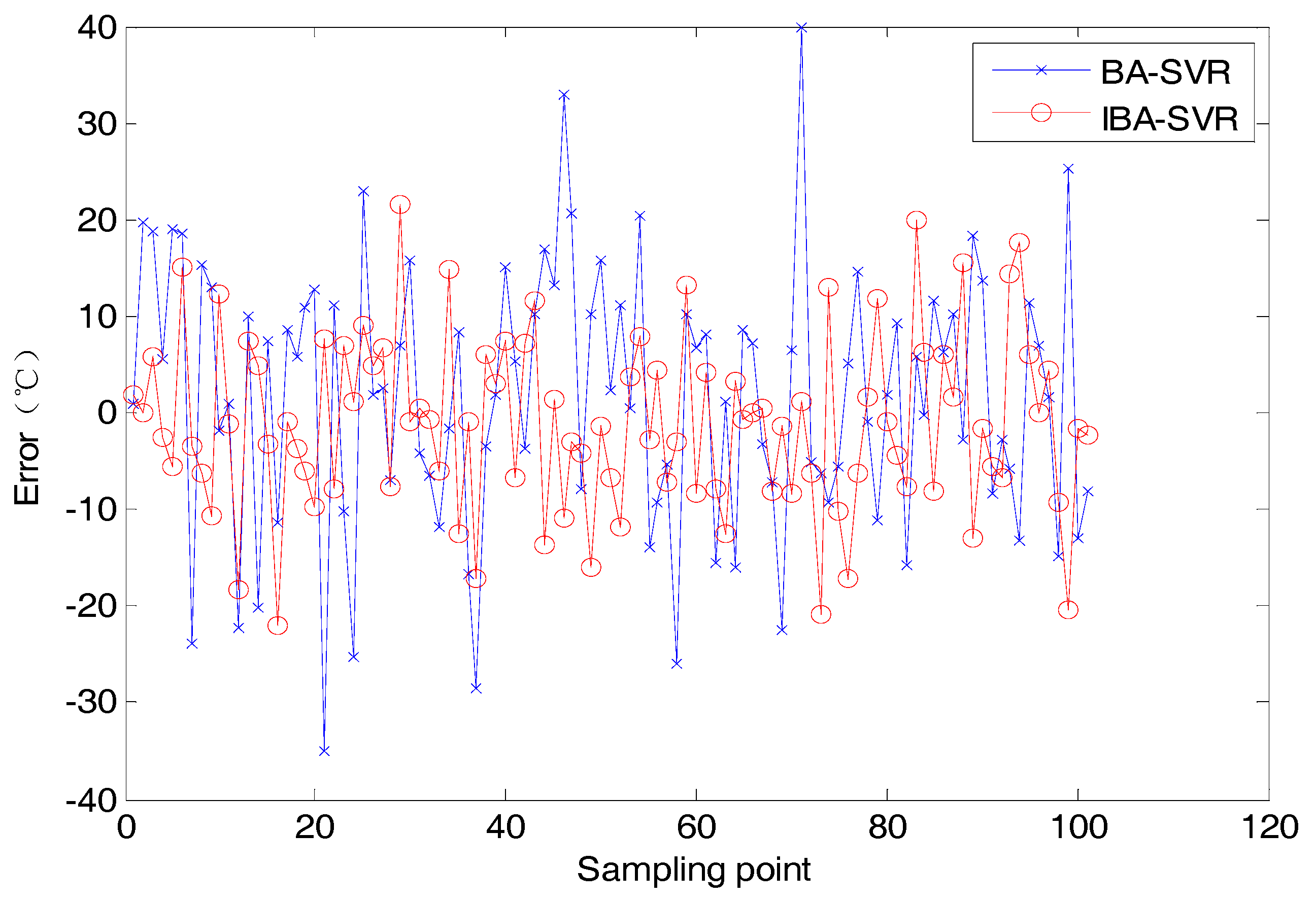
- For Isomap data segmentation method, the value of R2, Q2CV5 and Q2ext of the IBA-SVR algorithm proposed in this paper are better than those of the comparison algorithm. Therefore, the optimization performance of IBA algorithm for SVR model is better than that of other comparison algorithms.
- (2)
- By comparing the dimensionality reduction methods of Isomap and PCA data under IBA-SVR model, we can see that the model performance of dimensionality reduction using Isomap algorithm is better.
- (3)
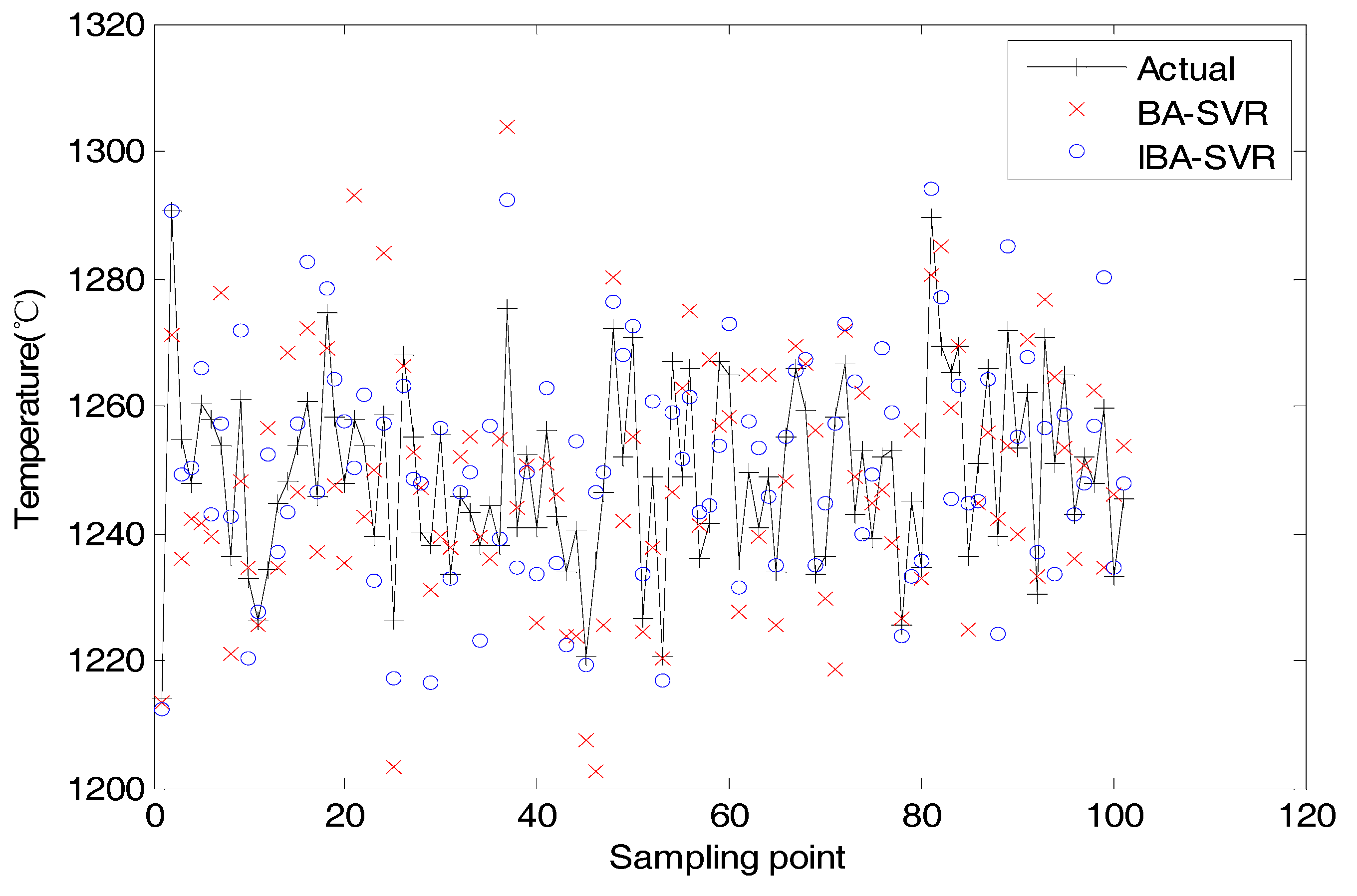
- The joint to optimization of Isomap and SVR model using IBA algorithm effectively improves the prediction accuracy of the model. 98.6% of the prediction results meet the accuracy requirements of level 1.5 instruments, and 97.7% of the prediction results meet the accuracy requirements of level 2.5 instruments.
- (1)
- Considering the fitting ability, different data segmentation methods have little influence on the fitting ability of the model.
- (2)
- Considering the robustness of the model, the model established by the method of randomly segmented data fluctuates more than that established by the method of SOM neural network.
- (3)
- Considering the external prediction ability of the model, the external prediction ability of the model established by the method of SOM neural network segmentation data is more stable.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Boateng, A.A.; Barr, P.V. A Thermal-Model for the Rotary Kiln Including Heat-Transfer within the Bed. Int. J. Heat Mass Transf. 1996, 39, 2131–2147. [Google Scholar] [CrossRef]
- Tian, Z.; Li, S.; Wang, Y.; Wang, X. A multi-model fusion soft sensor modelling method and its application in rotary kiln calcination zone temperature prediction. Trans. Inst. Meas. Control. 2015, 38, 110–124. [Google Scholar]
- Zhang, L.; Gao, X.W.; Wang, J.S.; Zhao, J. Soft-Sensing for Calcining Zone Temperature in Rotary Kiln Based on Model Migration. J. Northeast. Univ. 2011, 32, 175–178. [Google Scholar]
- Li, M.W.; Hong, W.C.; Kang, H.G. Urban traffic flow forecasting using Gauss–SVR with cat mapping, cloud model and PSO hybrid algorithm. Neurocomputing 2013, 99, 230–240. [Google Scholar] [CrossRef]
- Shi, X.; Chi, Q.; Fei, Z.; Liang, J. Soft-Sensing Research on Ethylene Polymerization Based on PCA-SVR Algorithm. Asian J. Chem. 2013, 25, 4957–4961. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Application of online support vector regression for soft sensors. AIChE J. 2014, 60, 600–612. [Google Scholar] [CrossRef]
- Edwin, R.D.J.; Kumanan, S. Evolutionary fuzzy SVR modeling of weld residual stress. Appl. Soft Comput. 2016, 42, 423–430. [Google Scholar] [CrossRef]
- Hou, Y.; Wei, S. Method for Mass Production of Phosphoric Acid with Rotary Kiln. U.S. Patent 10,005,669, 26 June 2018. [Google Scholar]
- Phummiphan, I.; Horpibulsuk, S.; Rachan, R.; Arulrajah, A.; Shen, S.-L.; Chindaprasirt, P. High calcium fly ash geopolymer stabilized lateritic soil and granulated blast furnace slag blends as a pavement base material. J. Hazard. Mater. 2018, 341, 257–267. [Google Scholar] [CrossRef]
- Konrád, K.; Viharos, Z.J.; Németh, G. Evaluation, ranking and positioning of measurement methods for pellet production. Measurement 2018, 124, 568–574. [Google Scholar] [CrossRef]
- Tian, Z.; Li, S.; Wang, Y.; Wang, X. SVM predictive control for calcination zone temperature in lime rotary kiln with improved PSO algorithm. Trans. Inst. Meas. Control. 2017, 40, 3134–3146. [Google Scholar]
- Yin, Q.; Du, W.-J.; Ji, X.-L.; Cheng, L. Optimization design and economic analyses of heat recovery exchangers on rotary kilns. Appl. Energy 2016, 180, 743–756. [Google Scholar] [CrossRef]
- Kim, K.I.; Jung, K.; Kim, H.J. Face recognition using kernel principal component analysis. IEEE Signal Process. Lett. 2002, 9, 40–42. [Google Scholar]
- Bengio, Y.; Paiement, J.; Vincent, P.; Delalleau, O.; Roux, N.; Ouimet, M. Out-of-sample extensions for lle, isomap, mds, eigenmaps, and spectral clustering. In Advances in Neural Information Processing Systems; 2004; pp. 177–184. Available online: https://dl.acm.org/doi/10.5555/2981345.2981368 (accessed on 12 December 2019).
- Hannachi, A.; Turner, A.G. Isomap nonlinear dimensionality reduction and bimodality of Asian monsoon convection. Geophys. Res. Lett. 2013, 40, 1653–1658. [Google Scholar] [CrossRef]
- Hannachi, A.; Turner, A. Monsoon convection dynamics and nonlinear dimensionality reduction vis Isomap. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 22–27 April 2012; EGU General Assembly Conference Abstracts. p. 8534. [Google Scholar]
- Jing, L.; Shao, C. Selection of the Suitable Parameter Value for Isomap. J. Softw. 2011, 6, 1034–1041. [Google Scholar] [CrossRef][Green Version]
- Orsenigo, C.; Vercellis, C. Linear versus nonlinear dimensionality reduction for banks’ credit rating prediction. Knowl. Based Syst. 2013, 47, 14–22. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Sammon, J.W. A nonlinear mapping for data structure analysis. IEEE Trans. Comput. 1969, 100, 401–409. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Golub, G.H.; Welsch, J.H. Calculation of Gauss Quadrature Rules. Math. Comput. 1969, 23, 221–230. [Google Scholar] [CrossRef]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Comput. Knowl. Technol. 2010, 284, 65–74. [Google Scholar]
- Subsequently. A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization. J. Appl. Math. 2013, 2013, 233–256. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2010; pp. 210–214. [Google Scholar]
- Wang, G.-G.; Gandomi, A.H.; Zhao, X.; Chu, H.C.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2014, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, Y.K.; Chen, X.B. Improved multi-area search and asymptotic convergence PSO algorithm with independent local search mechanism. Kongzhi Yu Juece/Control Decis. 2018, 33, 1382–1390. [Google Scholar]
- Ghanem, W.A.H.M.; Jantan, A. An enhanced Bat algorithm with mutation operator for numerical optimization problems. Neural Comput. Appl. 2019, 31, 617–651. [Google Scholar] [CrossRef]
- Chakri, A.; Khelif, R.; Benouaret, M.; Yang, X.-S. New directional bat algorithm for continuous optimization problems. Expert Syst. Appl. 2017, 69, 159–175. [Google Scholar] [CrossRef]
- Shen, X.; Fu, X.; Zhou, C. A combined algorithm for cleaning abnormal data of wind turbine power curve based on change point grouping algorithm and quartile algorithm. IEEE Trans. Sustain. Energy 2018, 10, 46–54. [Google Scholar] [CrossRef]
- Gupta, S.; Perlman, R.M.; Lynch, T.W.; McMinn, B.D. Normalizing Pipelined Floating Point Processing Unit. U.S. Patent 5,058,048, 15 October 1991. [Google Scholar]
- Pedrycz, W. Conditional fuzzy clustering in the design of radial basis function neural networks. IEEE Trans. Neural Netw. 1998, 9, 601–612. [Google Scholar] [CrossRef]

| Name | Function | D | Range | fopt |
|---|---|---|---|---|
| Shpere | 30 | [−10,10]D | 0 | |
| Schwefel 2.22 | 30 | [−10,10]D | 0 | |
| Ackley | 30 | [−32,32]D | 0 | |
| Griewank | 30 | [−600,600]D | 0 | |
| Shifted Sum Square | 30 | [−100,100]D | 0 | |
| Rotated Griewank | 30 | [−600,600]D | 0 |
| Algorithm | Reference | Parameters |
|---|---|---|
| BA | Ref. [23] | , , , |
| PSO | Ref. [27] | , , , |
| EBA | Ref. [28] | , |
| dBA | Ref. [29] | , , , |
| IBA | Present | , , , |
| Dimensionality Reduction Method | Isomap | PCA | |||
|---|---|---|---|---|---|
| Modeling Method | GA-SVR | PSO-SVR | BA-SVR | IBA-SVR | IBA-SVR |
| 95.3% | 95.7% | 96.3% | 98.6% | 96.9% | |
| 98.3% | 98.8% | 98.8% | 99.7% | 99.1% | |
| Min_R2 | 0.794 | 0.822 | 0.816 | 0.841 | 0.842 |
| Max_R2 | 0.911 | 0.921 | 0.891 | 0.922 | 0.921 |
| Mean_R2 | 0.855 | 0.853 | 0.852 | 0.862 | 0.859 |
| Min_Q2CV5 | 0.741 | 0.757 | 0.755 | 0.813 | 0.786 |
| Max_Q2CV5 | 0.866 | 0.839 | 0.821 | 0.871 | 0.857 |
| Mean_Q2CV5 | 0.821 | 0.823 | 0.829 | 0.851 | 0.836 |
| Min_Q2ext | 0.731 | 0.817 | 0.822 | 0.831 | 0.811 |
| Max_Q2ext | 0.832 | 0.855 | 0.869 | 0.874 | 0.862 |
| Mean_Q2ext | 0.811 | 0.831 | 0.847 | 0.851 | 0.836 |
| Method of Data Segmentation | Random | SOM | |
|---|---|---|---|
| Training Data | Min_R2 | 0.835 | 0.841 |
| Max_R2 | 0.912 | 0.922 | |
| Mean_R2 | 0.859 | 0.862 | |
| Min_Q2CV5 | 0.753 | 0.813 | |
| Max_Q2CV5 | 0.891 | 0.871 | |
| Mean_Q2CV5 | 0.821 | 0.851 | |
| Test Data | Min_Q2ext | 0.741 | 0.831 |
| Max_Q2ext | 0.896 | 0.874 | |
| Mean_Q2ext | 0.816 | 0.851 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, Y.; Zhang, Y. A Novel Isomap-SVR Soft Sensor Model and Its Application in Rotary Kiln Calcination Zone Temperature Prediction. Symmetry 2020, 12, 167. https://doi.org/10.3390/sym12010167
Liu J, Wang Y, Zhang Y. A Novel Isomap-SVR Soft Sensor Model and Its Application in Rotary Kiln Calcination Zone Temperature Prediction. Symmetry. 2020; 12(1):167. https://doi.org/10.3390/sym12010167
Chicago/Turabian StyleLiu, Jialun, Yukun Wang, and Yong Zhang. 2020. "A Novel Isomap-SVR Soft Sensor Model and Its Application in Rotary Kiln Calcination Zone Temperature Prediction" Symmetry 12, no. 1: 167. https://doi.org/10.3390/sym12010167
APA StyleLiu, J., Wang, Y., & Zhang, Y. (2020). A Novel Isomap-SVR Soft Sensor Model and Its Application in Rotary Kiln Calcination Zone Temperature Prediction. Symmetry, 12(1), 167. https://doi.org/10.3390/sym12010167





