1. Introduction
The rapid growth of the utilization of mobile and network resources has led to an increase in global network traffic every year. This is one of the most apparent concerns for mobile and network operators. To manage this huge network traffic and slow throughput, several architectures have been proposed to accommodate this rapid growth and its associated problems. One of these proposed architectures is called content centric networking/named data networking (CCN/NDN). CCN/NDN is one of the technologies of the information centric network (ICN) based on 5G network architecture. The main basic features in CCN/NDN architectures are interest-based content retrieval, content-aware naming and routing at the network layer, and in-network caching.
In the CCN/NDN network layer, the sender does not directly send packets (contents) to the receivers and receivers do not access packets (interests) from the data owner. Data owners rather publish content to all networks without necessarily knowing the interested users of the content. These users of the content then request their content without knowing the publisher. Here, the rule for the transaction is evidence of a match between the publisher and subscribers to be followed by the establishment of a delivery path, to enable the delivery of content. The main advantages of this mechanism are, the network nodes cache the content for a fixed period of time and the same content can be requested multiple times, and satisfied from the node without contacting the content owners.
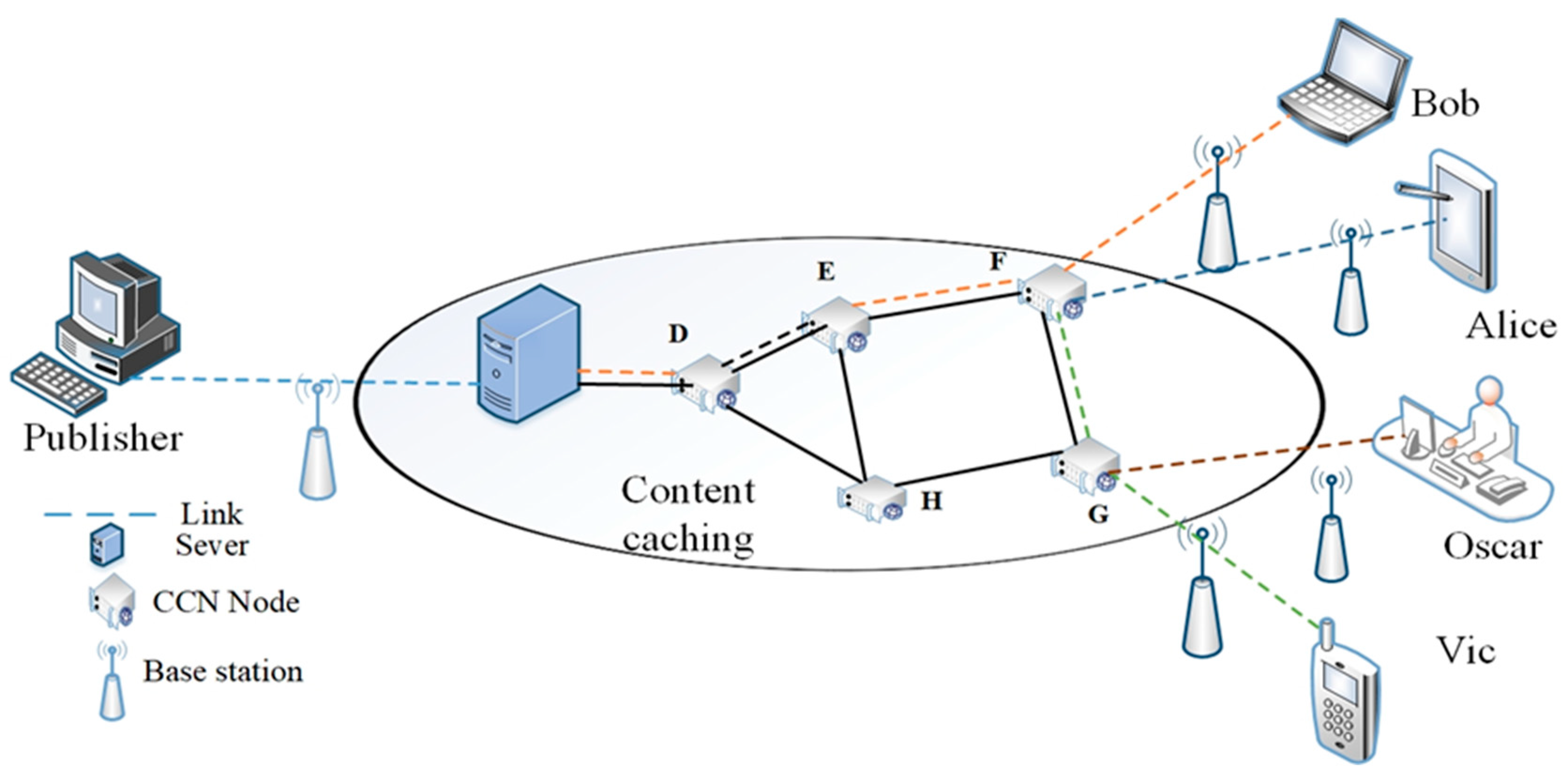
In adopting this phenomenon, we considered a typical internet of things (IoT)-CCN/NDN scenario depicted in
Figure 1. This system consists of publisher, IoT CCN/NDN, and the consumers. The content publishers broadcast content that can be cached in all networks and can be accessed and retrieved from any intermediate node. For example, after Bob retrieves content from the server, the content is cached on each of the intermediate nodes, so Alice and Vic can access the same content from node F, and Oscar can also access the same content from node G.
The CCN/NDN has different techniques with regard to its security model. The security component of CCN/NDN modifies the security approach to secure the cached content, instead of the traditional approach of securing network paths for all the networks. The effective way to achieve a required secured data sharing is to provide more scalable and flexible access control for this pervasive and distributed CCN/NDN environment [
1]. Fortunately, attribute-based encryption (ABE) cryptosystem has been proposed as a fine-grained access control mechanism for CCN/NDN based on the 5G communication network.
The attribute based encryption scheme comes with two main aspects, namely cipher text-policy ABE (CP-ABE) scheme and key-policy ABE (KP-ABE) scheme. With these schemes, users can recover a message if their attributes fulfill the requirement of the access structure. Ciphertext policy ABE (CP-ABE) has some special properties and advantages, over symmetric, asymmetric and KP-ABE. It also has an impressive property of manufacturing and describing access privileges of users in a more intuitive and scalable way. Further, by using this scheme and without prior knowledge of the receivers of information, data could be shared according to the encrypted policy.
Basically, there are two approaches to designing the algorithms of ABE encryption schemes, and these are bilinear map over elliptical curve and the lattice-based approach. However, several gaps and problems exist in the implementation of these algorithms over the years. By and large, these gaps and problems could be mainly categorized into high communication overhead during cipher text uploading and downloading, high computational cost, the problem of quantum and post-quantum attacks and attacks on the plaintext. There are several access control schemes proposed for CNN/NDN. However, most of these exiting proposed access control schemes are based on a bilinear map over the elliptical curve [
2,
3]. Some of these works have large computational overhead during encryption and decryption. They also have a high communication overhead during ciphertext uploading and downloading. These massive storage overheads require additional properties of securing cached contents to authenticate each content consumer. Above all, almost all the proposed schemes for CNN/NDN paradigm are susceptible to quantum attacks. The above-mentioned challenges make most of the existing ABE access control schemes unattractive for CCN/NDN.
Herranz et al. [
4] and Chen et al. [
5] proposed constant ciphertext-policy ABE (CP-ABE) schemes to address the issues of client high computational cost. However, their schemes are inexpressive and based on AND gate and threshold function by the large-scale ciphertext. An outsource computational ABE scheme was proposed by Hohenberger and Waters [
6] and Lai et al. [
7]. These schemes have high communication cost and most of the encryption and decryption computations are outsourced. In order to reduce the policy scale, Zhou and Huang [
8] proposed a minimum sum of product expression and Song et al. [
9] proposed minimum linear code, respectively, to minimize the policy scale. A small-scale policy that has less ciphertext redundancy, the reduction of redundancy is limited and unstable. A compact ciphertext-policy ABE (CP-ABE) scheme was proposed by [
10] to compact the policy scale and reduce ciphertext redundancy. However, the above-mentioned schemes are based on bilinear maps with high computational complexity and could not address the problem of quantum and post-quantum attacks.
To address the problems of quantum attacks, the researchers of [
11] first introduced the idea of the lattice into cryptography. There has been recent progress in the area of quantum cryptography including lattice-based ABE schemes. Zhu et al. [
12] proposed KP-ABE scheme using a threshold access policy for the ideal grid based on the R-LWE problem, which proved to be CPA secured. However, this scheme could not satisfy the attack on plaintext security as claimed by the authors. Instead of adopting the preceding approaches, LSSS CP-ABE access control scheme from the lightweight ideal grid was proposed by Tan et al. [
13], which can resist collision attacks. Yan et al. [
14] used the LSSS access structure to propose the ideal multi-agency CP-ABE scheme. Wang et al. [
15] achieved an effective encryption scheme based on R-LWE with high encryption power. The decryption run time and integrity support features are based on chosen cipher-text security. In 2018, authors of [
16] proposed the attribute-based encryption scheme supporting tree-access structure from ideal lattices. They used an expressive and flexible access policy by Shamir threshold secret sharing technology, including “and”, “or”, and “threshold” operations. In order to construct more efficient lattice-based ABE to resolve inefficient issues in the lattice ABE cryptosystem, the accessed structures and some components such as the trapdoor design and the matrix dimension which play a significant role in the construction of the lattice based ABE scheme need to optimize. Hence, the main contribution of our work is to propose a flexible and efficient CP-ABE access control scheme based on ring learning with error supporting reduced-OBDD for CCN/NDN.
1.1. Clarification of Problem and Contribution
In spite of the enormous benefits of the CCN/NDN technique, security challenges are some of its major concerns. These security challenges consist of the design of secured, efficient, and flexible schemes to secure cached data and also protecting data from illegal data modification, unauthorized access, as well as impersonated data dissemination and retrieval. The CP-ABE scheme is a newly preferable solution identified to achieve access control in CCN/NDN. This security scheme has special properties of encrypting with access policies. It also allows content to be self-protected when they are cached and can be accessed by many users.
However, most of these proposed CP-ABE AC schemes have some loopholes which make them unappealing. Some of these problems which we address in this paper are: (i) They are not flexible, i.e., they cannot support many access policy operations such as AND, OR, NOT, and threshold gates. (ii) They are inefficient, i.e., the computation and communication of secrete keys and ciphertext take a long time. (iii) They vulnerable quantum attacks (i.e., they are based on bilinear maps with pairing and are not quantum secured for polynomial time quantum algorithms.
Above all, most of the proposed secured CCN/NDN information sharing systems cannot secure cached contents from some entities such as trusted service providers and cache routers. Therefore, cache routers can conspire with some users to act maliciously when the contents are cached.
To address the challenges and limitations described above we CP-ABE AC scheme which has the following characteristics:
- (i)
The proposed CP-ABE AC scheme from ideal lattice supports a reduced-OBDD access structure. Reduced-OBDD offers a compact and optimized access structure with fewer nodes and paths. Encryption and decryption are performed by waking on the path instead of using nodes. This means that it has a lower encryption and decryption computational time over rings.
- (ii)
The proposed scheme supports Boolean operations such as AND, OR and threshold gate. Also, it can support multiple subscribers of positive and negative attributes in strategy.
- (iii)
Our scheme is quantum secured for polynomial time quantum algorithms based on the assumption of R-LWE. Due to the algebraic construction from the ideal lattice, it is more effective than schemes based on ring learning LWE.
- (iv)
Our scheme has an improvement over the sample right algorithms with a stronger trapdoor and efficient sampling based on the discrete Gaussian in instead of
Finally, we integrate the proposed reduced-OBDD CP-ABE over ring LWE with CCN/NDN platform and demonstrate how it could be used to provide an access control scheme to enable content to be self-secured against quantum attack.
1.2. Methods
The attribute based encryption scheme represents a promising proposal for content centric network. However, it has some drawbacks such as computational time and flexible access control expression. To deal with these problems and to ensure efficient a secured data sharing over CCN, the following methodologies were used.
1.2.1. Flexible and Expressive Access Policy
Our scheme supports reduced-OBDD: We constructed our access policy from reduced ordered binary decision diagram. This approach is simple but very efficient and expressive. Based on recursive Shannon theorem,
, we constructed a reduced binary decision diagram to represent our access structure. By adopting this approach, a Threshold access structure of five levels with sixty-three (63) nodes can be reduced to six (6) nodes which can perform the same function but in a more efficient way. This structure can support the threshold gate, Boolean operations such as AND, OR, NOT, and also, multiple subscribers of positive and negative attributes in the strategy. To deal with negative attributes, we modified the proposal in [
17] by attaching the negative attributes to a default attribute.
1.2.2. Optimized Algorithms
Compact and optimized access policy: Reduced-OBDD offers a compact and optimized access structure with fewer nodes and links. However, instead of using the number of nodes for our encryption and decryption, we used the links between the nodes which have a direct positive impact on our encryption and decryption algorithms. The terminal nodes with constant meanings were deleted. This means that our scheme has less encryption and decryption computational time over rings.
Optimized sampling algorithm: Instead of using sample left algorithm used by various construction, we combined the theorem of MP12 [
18] to construct an efficient trapdoor. We also design an optimized sampling algorithm to output an invertible matrix
. This is a significant method for delegating trapdoor and sample right algorithm with a trapdoor protocol. The matrix
m is obtained from a discrete Gaussian execution time of
with a trapdoor quality approximately
and matrix
dimension approximately
. Hence, our scheme has an improved storage capacity as compared with other relevant schemes such as [
19]. The performance analysis shows that the size of the master key, secret key, and the ciphertext expansion size is much lower. This is detailed in
Table 1.
1.2.3. Efficient Secured Content Sharing Over CCN/NDN
The ABE scheme has a general computation loophole. To ensure an efficient secured content sharing system, we will adopt a hybrid technique by combining our proposed reduced-OBDD based ABE AC with asymmetric key encryption scheme. An asymmetric encryption scheme known to be efficient is used to encrypt the content needed by the consumer and the proposed reduced-OBDD CP-ABE AC scheme from lattice is used to encrypt the content policy which contains the password or the secret key and other relevant information about the content data to decrypt the content. The content policy is issued with a time value and periodic automatic update properties to ensure the management of our system, and also allows user’s features to be updated individually.
1.3. Organization
The remaining of the paper is organized as follows: In
Section 2, we review some relevant related work. The preliminaries are discussed in
Section 3. We demonstrate our access structure and our scheme in
Section 4. The performance analysis of our scheme is presented in
Section 5. The integration of our proposed scheme into CCN/NDN systems is discussed in
Section 6, and this paper is concluded in
Section 7.
3. Preliminaries
3.1. Lattice
Definition 1. (Lattice [41]) Given as with a linearly independent column vectors The m-dimensional lattice generated by is the set. Now, we consider an integer lattice, where belongs to the set of . We denote the determinant of as .
Definition 2. ([41]): For a prime and define. Note that, if then and therefore, is a shift of .
Definition 3. (An m-dimensional lattice [41]): An m-dimensional lattice is both an additive subgroup: (, and for every, ) and discrete (every has a neighbor in where is the only lattice point). The minimum distance of lattice is the length of a shortest non-zero lattice vector , where denote Euclidian norm. Generally, successive minimum is the smallest such that has linearly independent vectors of the norm at most . Definition 4. (Ideal lattice [41]): A lattice is an ideal lattice if there exists a ring and ideal such that is associated with . Definition 5. (Gram-Schmidt norm of a basis [41]): Given as a finite basis and as Gram-Schmidt orthogonalization. The Gram–Schmidt norm is the value of There are two relevant properties of Gram Schmidt dorm and its bases which are beneficial to the construction lattices. These are: (1) They are quick to compute (The
Gram-Schmidt norm for a general lattice is obtained by conducting the
Gram–Schmidt process to the basis of the lattice and compute the maximum length of the resultant vector). (2) Their size can be small (The size of the lattice which we compute Gaussian sampling and the sample of the private key size should be proportional to
, where
is lattice basis). Therefore, it is significant that
should be small as possible. According to [
18], a full rank set
in a lattice can be converted into T with an equally low Gram–Shmidt norm
of
Lamma 1. ([18], Lemma 7.1): Given as an m-dimensional lattice, there is a deterministic polynomial-time algorithm that gives an arbitrary basis of and a full rank set of in , outputs a basis of T of satisfying and . 3.2. Gaussian Sampling for a Ring
Definition 6. (Gaussian function): Given and as a positive integer greater than zero and dimensional matrix. Let greater than zero and . A Gaussian-shape function on is defined as . For a matrix , we define the discrete of as . The discrete Gaussian distribution over set as and then , the discrete Gaussian distribution over is defined as: 3.3. Some Significant Algorithms
3.3.1. Algorithm Generation of Trapdoor
Theorem 1. . A probabilistic polynomial-time algorithm in an existence accepts inputs of , , parameters ,, where t = . is a polynomial with degree. The algorithm outputs . , statistically close to uniform. , Where , and a small trapdoor bases for lattice which satisfies .
3.3.2. Algorithm for Preimage Sampling
Theorem 2. . A algorithm accepts inputs of as a matrix, where and , as the basis of a trapdoor for , expected image and parameter for Gaussian is and output that satisfies . Based on a new preimage sampling algorithm over rings for is constructed.
). The algorithm takes an input of as a vector, trapdoor of as expected image and a parameter of Gaussian ) and output that satisfies . Here, we have:
3.4. Decision R-LWE Problem
Init: The adversary chooses a specific access structure and sends to the Challenger
Given as security parameter, let and be an integer that depends on . Where and , let . Given a distribution over depending on , the Decision learning with error problem instance consist of access to an unspecified challenge oracle , either a noisy pseudo-random sampler , for random secrete key ; or a truly random sampler . The Decision R-LWE problem is to distinguish the sampling between and , which perform respectively as follows;
Given a uniform distribution constant invariant value across invocation as , a new sample from and a uniform sample . Output a sample of form as .
An exact uniform output sample drawn from .
The aim of the decision ring-LWE problems is to allow repeated quarries to be sent to the challenge oracle . The Attacker’s algorithm decides the decision ring-learning with error problem if is non-negligible random value for . Given defining
3.5. Access Structure
Assuming is a set of parties. Let represent subsets contained in and . The collection of is known as an access structure. The set contains in are called authorize sets and sets are called unauthorized sets. The access is monotone if and then .
3.6. Reduced Ordered Decision Diagram (Reduced-OBDD)
Reduced-OBDD is based on a fixed ordering of variables and has the additional property of being reduced. This means that it is irredundant, unique, and recovers the important canonicity property. Thus, for a fixed variable ordering, each Boolean function has a canonical (unique) representation as a Reduce-OBDD and checking if they are of equal or the same successors. If there are two distinct nodes u and v have the same variable name and low and high successor, i.e., if and implies and no variable node u has identical low and high successor, i.e.,
3.7. Ciphertext-Policy Attribute Base Encryption Model
The CP-ABE basic algorithms include the following four fundamental operations (Setup, Encrypt, KeyGen, Decrypt).
Setup (): This algorithm takes security parameter as input and outputs the public key PK and master key MK.
Encrypt (PK, MK, A): This algorithm takes public parameter PK, plaintext M, and access policy A, to output Ciphertext CT
KeyGen (MK, S): The algorithm takes masters key MK and attribute set S as input and outputs the secret key SK.
Decrypt (PK, CT, SP): This algorithm takes in public parameter PK, ciphertext CT, and a secret key SK as input and outputs the message M
3.8. Selective Set Model
A CP-ABE is secured in a selective -set model if the PP adversary has at most a negligible advantage in the game below.
Initial: The adversary Adv. declares the attribute set which he wants to challenge.
Setup: The setup algorithm is run by the challenger and sends the to the Adv.
Phase 1: The Adv. is allowed to make a private request of its choice as long as
Challenge: The Adv. sends two messages of equal length, and the challenger.
The challenger randomly selects and encrypt using . The ciphertext is sent to the Adv.
Phase 2: Repeat Phase 1.
Guess: Adv. output a guesses of . The advantage in the security game is defined as
4. Our Construction
4.1. Constructing Boolean Function of an Access Policy
We suppose the access policy of a Boolean function is Where and as the whole number of attributes, denotes a sequential predefined access policy number which is represented as . The function is converted between fundamental logical operations such as AND, OR, and NOT.
An operation is considered as threshold gate if and only if attributes of a subset can complete the operation successfully. To be able to decrypt a message in a security system, a user must be able to complete some specific threshold operations. To construct a Boolean function of a given , Where is the attribute set, extract all the subset of with t attributes and separately compute the whole number of subsets by using permutation and combination. This is followed by the construction of a separate set level conjugate for each subset . Finally, obtain the Boolean function of by a disjunctive operation on .
4.2. Reduced- OBDD Access Structure Construction
To construct reduced-OBDD for Boolean function
, we use the recursive algorithm (Algorithms 1 and 2) based on the expansion theorem of Shannon. To obtain a specific and unique reduced-OBDD, the definition of the variable ordering must be specified since different ordering results to different kinds of diagrams. Given a logic function in terms of selected inputs and the required input for logic synthesis using a multiplexer. For any Boolean function
can be expressed as
. The process based on Shannon’s expansion theorem is described as follows: Let
be node numbers where the low terminal node is
and the high terminal node is
. However, the terminal nodes have specific meanings and their attributes may not be considered. The variable ordering
related to
is
. The table,
Table 1 is the inverse of the table
Table 2 which stores the reduced-OBDD. In Algorithm 1,
Table 1 is initialized to be ones (1) and zeros (0) lookup function
Table 1:
maps node
to its attributes
,
and
. To construct an ordered binary decision diagram from the
id,
low, and
high if there must be an existence of the node with variable key
,
, and
. In Algorithm 2,
Table 2 is initialized to be empty and find out if there exist of id, low and high in.
| Algorithm 1 Build Redeuced-OBDD |
| 1: function BUILD [Table 1, Table 2](id, low, high) |
| 2: if low== high then |
| 3: return low |
| 4: end if |
| 5: If element (Table 2, id, low, high) then |
| 6: return lookup(Table 2, id, low, high) |
| 7: end if |
| 8: If low<> high then |
| 9: w=insert(Table 1, ID, low, high) |
| 10: return insert(Table 2, id, low, high) |
| 11: end if |
| 12: end function |
| Algorithm 2 Construct Reduced-OBDD |
| 1: Function CONSTRUCT [Table 1, Table 2](t, i) |
| 2: if i > n then |
| 3: if t== false then |
| 4: return 0 |
| 5: end if |
| 6: if t == true then |
| 7: return 1 |
| 8: end if |
| 9: end if |
| 10: if i ! > n then |
| 11: return q0= CONSTRUCT(t[0/xi], i+1) |
| 12: return q1= CONSTRUCT (t[1/xi], i+1) |
| 13: return BUILD(t, i) |
| 14: end if |
| 15: end function |
Use the lookup function to find
Table 2 (id, low, high) and use insert function to map (id, low, high) to
and assign node serial
with attributes id, high, and low. The algorithm references the attributes of serial
in
Table 1 with in
Table 2 by recalling the BUILD function in Algorithm 1. Let
Table 2:
maps attributes
to
such that for all variables nodes
,
Table 1 if Table 2 (id, low, high)
. After the construction of all nodes
of the reduced-OBDD, the final expression is obtained as
, where
denote all the attributes in the structure and
is the set containing the serial numbers of non-leaf nodes. The final table of
contains the id of the current node
, the
of the attribute in the current node
, the
of the high branch
and the id of the low branch
. Hence, the access structure
4.3. Satisfying Reduced-OBDD Structure
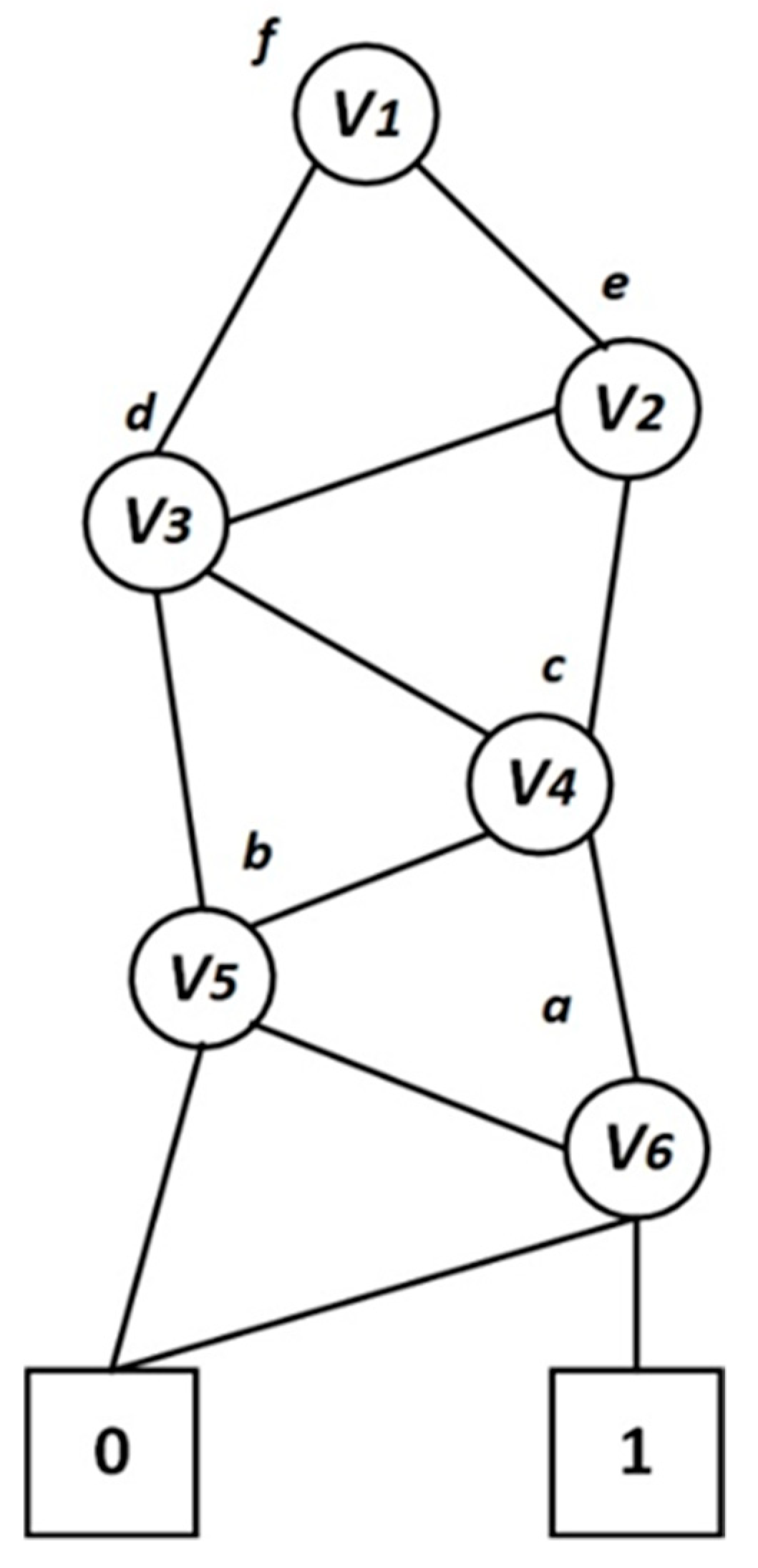
Let
be access structure, attributes set be
and let the valid path be the path from the root node to the terminal
be
as shown in
Figure 2. Based on node values, a recursive comparison is conducted, starting from the root nodes to the leaf nodes. Thus, for a non-leaf node with an attribute of
is 1, send to the high branch node, otherwise send to the low branch node. This process is repeated until it reaches the leaf node. The set
satisfied
if the terminal node is (1). Otherwise, outputs fail. The attributes set
must satisfy the access structure
(i.e.,
) when the leaf node is lastly reached.
4.4. Construction Of Reduced-OBDD ABE AC From Lattice
Our proposed CP-ABE scheme supports positive and negative attributes. In a brief statement, we have where is a default value. Let represent attribute sent with serial numbers, our algorithms are described below.
): The algorithm is given an input of
and
as security parameter and attributes set respectively. Denoting
as a public parameter, let
be matrix. Randomly select
and trapdoor
with a size of less than or equal to
. Execute the
Algorithm to generate a random matrix
, where
is inverse of
. Randomly choose a uniform vector
and finally, output the public parameter and the masters key as:
KeyGen : Given master key MK and the set of users attribute . Set any which doesn’t belong to as a default value and execute the key generation process is as follows:
Define for any ; if and let else, set
Generate and a trapdoor matrix for and a secrete share for each .
Execute to output , where .
The algorithm is given public parameter
, the message
and the access structure
. Let
be a valid and invalid path. Denote the valid paths as
. The information of the attributes in the path
is
and the ciphertext of
is denoted as
. Where
is a random parameter and
is associated with the set of attributes
in
and
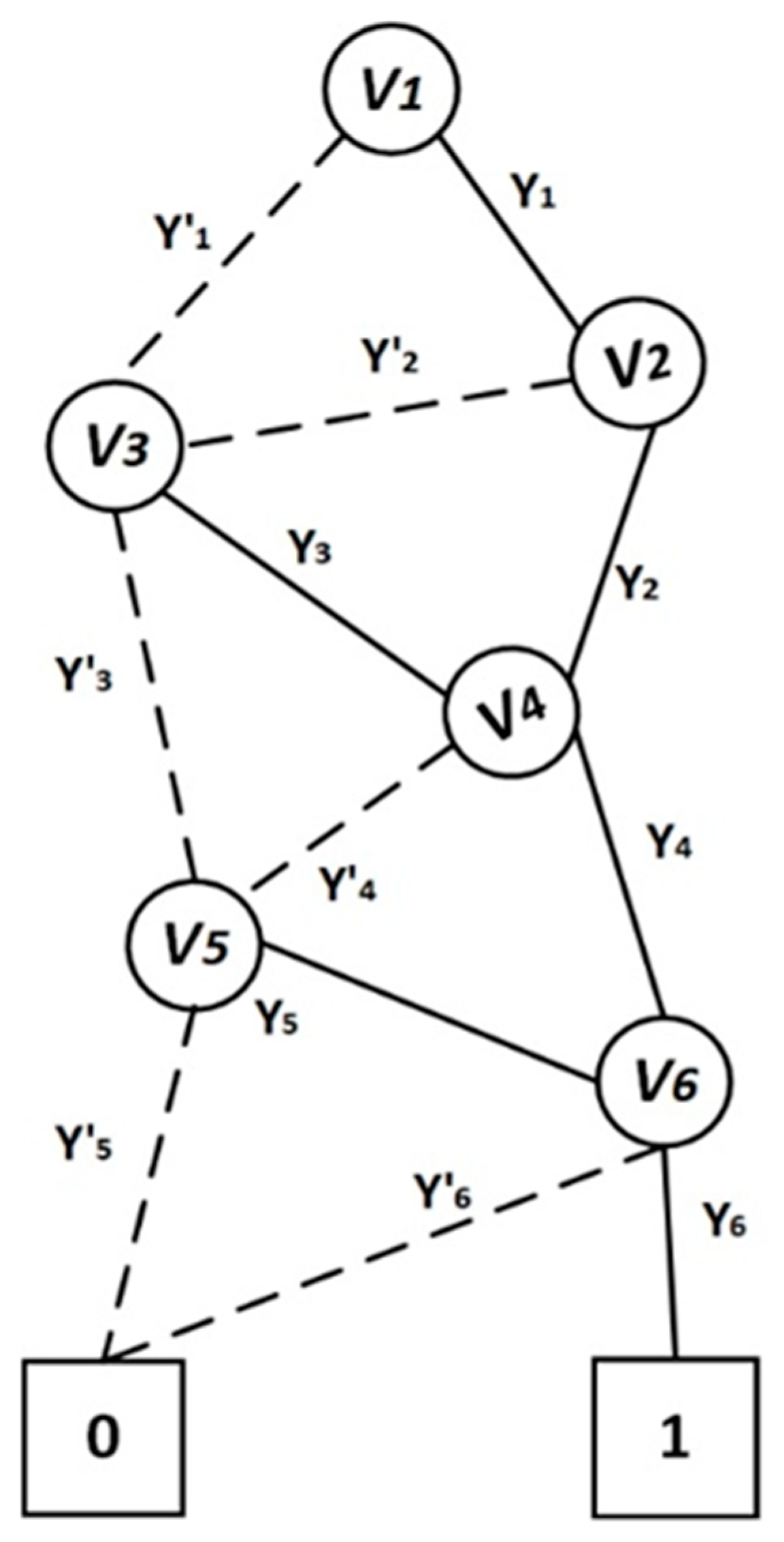
is the secret to be shared. The relationship between
and
is shown in
Figure 3.
Randomly generate parameter and error terms .
The encryption algorithm follows the following steps:
Then, output ciphertext as .
The decryption algorithm takes an input of ciphertext (CT), public parameter (PP), and secret key (SK). Perform recursive Algorithm 3. The algorithm defines the root node as the current node and extracts the current
and the
. The algorithm conducts recursive operations based on a high branch node and the low branch node. If any node is a non-leaf node, the algorithm sets it as a current node. The process continues until it reaches the leaf nodes. Based on the high branch node: if the
, set it as a current node; else if the high branch of the node is the
the algorithm is aborted. Otherwise, the algorithm stores the information in the path next to the leaf
node 1. Based on the low branch node, if the low branch node is a non-leaf node, set it as current node; else if the
the algorithm is aborted; else if the node on the high branch node Based on the high branch node low branch is the high leaf node, the algorithm stores the path to the leaf node (1). Define
as Gaussian parameter and continue with the below computation recursively.
| Algorithm 3 Decryption Process |
| 1: look for the node with serial number 2 |
| 2: Define it as the new node |
| 3: Extract the node details include in the node |
| 4: if then |
| 5: seek the high-branch-node of the new node based on the high order |
| 6: if high-branch -= = 0 then |
| 7: end the process |
| 8: end if |
| 9: if high-branch = = 1 then |
| 10: store the root path |
| 11: end if |
| 12: if high-branch ==non-leaf-node then |
| 13: go to line 2 |
| 14: end if |
| 15: end if |
| 16: if then |
| 17: Seek the low-branch-node of the new node based on the low order |
| 18: if low-branch == 0 then |
| 19 end the process |
| 20: end if |
| 21: if low-branch = =1 then |
| 22: store the root 1 then |
| 23: end if |
| 24: if low-branch = = non-leaf-node then |
| 25: go to line 2 |
| 26: end if |
| 27: end if |
Compute Lagrange coefficients
as
and set
If , the system output 1, else output
4.5. Correctness and Security Proof
In this section, we provide the security proof and the performance achieved by this work.
4.5.1. Correctness
In order to decrypt
we have
where the error term is:
.
It is required to choose the parameters such that considering the overwhelming probability (w.h.p) of
with w.h.p, we have by such that,
is bounded by w.h.p by .
For our trapdoor operation, we choose
to ensure correctness which is less than
w.h.p and set
4.5.2. Security Proof
Theorem 3. If the notion holds, then with a negligible advantage of , there is no polynomial-time adversary . that can selectively win the security game of our system.
Proof : Assuming there is PPT attack on the proposed efficiently secured scheme with an advantage of , then there exists an algorithm that can distinguish problem with an advantage of . The problem of LWE is provided as sample oracle which can be really random or noisy pseudo-random for some secret key . The challenger’s algorithm simulates attack environment and exploits to which oracle is given.
Initialize: Adversary , sends the access structure to the challenger’s Simulator .
Instance:
makes a request to the oracle and the oracle responds by sending new pairs of
, where
to obtain
. Thus
Target: makes an announcement of the set of attributes that it is intended to challenge
Setup: The public parameters are generated by . Let’s denote as .
For , generate
, where and
outputs a matrix for each
where attributes
, by running a trapdoor algorithm to generate a random matrix
and the computes
Using as an input, generates a random matrix and a trapdoor for
Finally, outputs and set to the .
Phase 1: sends a private key request for a set of attributes , where
computes share of for each For any legitimate path, there must exist an attributes satisfying . Generally, attributes satisfy the condition and each attribute is apportioned as follows: ; for .
runs the key generation algorithm to generate and a trapdoor matrix for and invokes function to output and set the private key of as to the
Challenge:
agrees to accept the challenge and submits challenge message
with the attribute set
and flips a coin to generate randomly
.
generates a ciphertext as
to
where:
It is clear that the encrypted message is valid encryption of under the access policy of if . The encrypted message is uniform in and is uniform in .
Phase 2: continues by repeating Phase 1
Decision: outputs a guess for . If = . The challenger considered the samples to be sample, else it guesses them as samples.
Assuming the adversary
can correctly guess
with a probability of at least
Then
can make a decision of the decision ring-LWE problem with an advantage of
5. Performance Analysis
5.1. Complexity Analysis
The complexity analysis of our scheme is based on the performance of the Boolean operations, the factors that affect the communication time and the factors affecting the execution time. The complexity of the Boolean operations depends on the size of the reduced-OBDD. For a Boolean circuit of input bit (OR gates) or input bit (AND gates,) designed as an output gate, the circuit size of the Boolean function is the same as the size of the reduced-OBDD structure. Also, the complexity of the reduced-OBDD Boolean function is equal to the reduced depth of Boolean function . For the function with ordering , the size of the reduced-OBDD is This could either be linear or exponential depending on the variable ordering. The complexity of the Boolean function operations also depends on the number of nodes in the reduced-OBDD. That is to say, for the AND gate, the various operations of our scheme are expressed as threshold while the OR gate and NOT gate are expressed as threshold. The Boolean operation considers all the nodes of the reduced-OBDD with the complexity of where is the number of nodes in the reduced-OBDD. To achieve a better runtime, we deleted the leaf nodes which have specific meanings.
We also improved on the execution and communication time, by reducing some parameters of our scheme such as the size of the trapdoor, the public parameters, the master key size, the secret key size, and the ciphertext. The size of the matrix is reduced to to output a reduced and better trapdoor. This implies a reduction in storage and communication cost. The size of the secret key depends on the end user’s attributes and the size of the matrix column. The size of our public parameter is smaller due to the small lattice size.
Hence, the complexity of our key generation and decryption algorithm is . The execution time of the encryption, decryption, and the resulting ciphertext relates to the number of the legitimate paths in the reduced-OBDD instead of the nodes which directly improve the execution, storage and sharing times
5.2. Discussion of Simulated Result
In this section, we compare our scheme with some relevant existing schemes. The implementation of this work was conducted on an Intel i7-8700 processor at 2.53 GHz and 8GB memory running Windows 10 operating system of 64 bits. Our scheme was simulated with PALISADE library 1.3 on C++ [
42].
The factors considered in the implementation result are execution time and storage capacity of ciphertext, key generation, encryption, and decryption.
Table 1 summarizes the comparison analysis of our proposed scheme with other schemes in terms of key generation, encryption and decryption operation times. The parameters were set as follows: lattice base 1024, 80-bit security, modulus as
the attribute universe,
was set as
, and the sample of attributes used in our encryption was set as
In our scheme, for a ciphertext with
attributes, the key generation, and the encryption and decryption operations were completed at
and
respectively. Although our key generation was a bit slower, the execution time of our scheme had a better performance in encryption and decryption operations than the schemes in [
24,
28,
31].
Table 1.
Comparing the execution time of some related works
Table 1.
Comparing the execution time of some related works
| Scheme | KeyGen
| Encryption
| Decryption
|
|---|
| [28] | (57.6/69.7/78.9/ 91.1/99.8) | (16.13/21.32/27.39/33.91/36.12) | (0.79/0.90/1.38/1.58/1.79) |
| [31] | (73.6/82.5/91.8/102.8/119.8) | (21.78/27.58/33.84/37.12/47.86) | (1.66/1.71/1.98/2.15/2.41) |
| [24] | (65.6/74.1/87.3/101.8/111.9) | (18.98/24.58/29.47/31.22/41.99) | (0.80/1.543/1.69/ 1.81/1.90) |
| ours | (51.6/62.7/ 70.8/82.08/89.8) | (14.51/19.81/24.81/29.99/33.59) | (0.51/0.82/1.11/1.17/1.29) |
The efficiency of our encryption and decryption operations is mainly due to the efficiency of our access structure, the choice of our trapdoor and the discrete Gaussian sampling approach. Our discrete sampling is based on the sample performance in times but not times which applied in most schemes. Also, the trapdoor algorithm used to generate the matrix is efficient which directly improves the system execution time.
Table 2 compares the storage capacity, supported access structures and their operations. The above criteria were used to compare our scheme with three other related schemes in [
24,
28,
31]. Our storage capacity analysis was based on the size of the public parameters
, secrete key size
, and the expansion of the ciphertext.
Table 2.
Relevant related schemes in terms of their access structures, operations and capacity analysis.
Table 2.
Relevant related schemes in terms of their access structures, operations and capacity analysis.
| Scheme | Access
Structures | Operation | PP size | MK Size | SK Size | Ciphertext Size |
|---|
| [28] | LSSS matrix | AND, OR, Threshold | | | | |
| [31] | Threshold gate | Threshold | | | | |
| [24] | Threshold gate | Threshold, AND | | | | |
| ours | Reduce-OBDD | AND, OR, Threshold | | | | |
The following notations were used in this work:
is the initial or universe attributes,
is the number of attributes in the ciphertext,
matrix which relates to
,
secrete share for each
and
is the depth of the attributes. The public parameters
of [
24,
28,
31] are very long as compared to ours of
. The public parameters of the other schemes are not linearly related to the system’s number of attributes. However, they are related to the parameters of the lattice which results in the high storage size. The master key
and the secrete key sizes of [
28,
31] are longer than the other schemes. The schemes in [
28,
31] are based on the sample left approach therefore, their secret keys are related to the number of users’ attributes and the cascaded matrix column. In [
31], the ciphertext and the key size relate to the number of users, matrix column, and the depth of the attribute hierarchy.
In terms of access structures and their operations, the policies of the schemes in [
24,
31] are not flexible and therefore do not support a flexible and fine-grain access policy. They are based on threshold gates. The scheme in [
31] supports only threshold operation, [
24] supports threshold and AND operations whilst the scheme in [
28] supports AND, OR and threshold operation which a bit flexible in terms of an access policy expression. In addition to supporting AND, OR, and threshold operations, our scheme also supports negative and positive attributes making it more flexible as compared to the others. Whilst our scheme is based on a reduced ordered binary decision diagram access structure which gives an efficient access policy expression without redundancy, [
28] is based on the LSSS matrix without a detailed explanation of how the expression of access policy was conducted.
Our scheme is practical with respect to storage capacity, execution time and is secured against quantum attacks due to the choice of an optimized access structure for our access policy expression, lower dimensional size of lattice, and efficient trapdoor approach used.
6. Integrating Lattice Based CP-ABE AC with CCN/NDN
This section entails details of the key exchange and the content sharing protocols. To ensure an efficient content sharing system, a hybrid technique is used. An asymmetric encryption scheme, known to be efficient is used to encrypt the content to be shared whiles the lattice CP-ABE AC scheme is used to encrypt the manifest or policy that contains the password or the key to decrypt the content.
6.1. System Model
The entities of our system and their description are introduced below:
Content Data Publisher (CDP): This can be the owner of the content or a trusted person on behalf of the data owner. He designs access policies, encrypts data and publishes them on the cloud in the ICN approach.
Content Centric Server (CCS): This is the cloud server responsible for content storage and user authentication. The content and the content policy are stored on the CCS in the CCN approach.
Content Data (CD): This is the private information encrypted by the owner and can only be accessed and used by legitimate users. This is stored in the CCN approach and can be accessed by legitimate users from any location
A trusted service provider (TSP): The service provider is a trusted authority responsible for key generation encryption and decryption keys for the publisher and the user. This authority runs two main algorithms:
- (i)
Asymmetric encryption algorithm, which is used for the encryption and the decryption of the content
- (ii)
Lattice CP-ABE AC algorithm, which is used to encrypt the content policy which contains the password used to decrypt the content data
Content users (CU): These are prospective authorized content users who can access content from anywhere.
Content Policy (CP): We describe the data manifest which stores the information about the content as content policy. This stores the decryption key of the content. It is encrypted with the key which is associated with the user’s attribute. The user can obtain the decryption key if his attributes match with the policy enforced on the content.
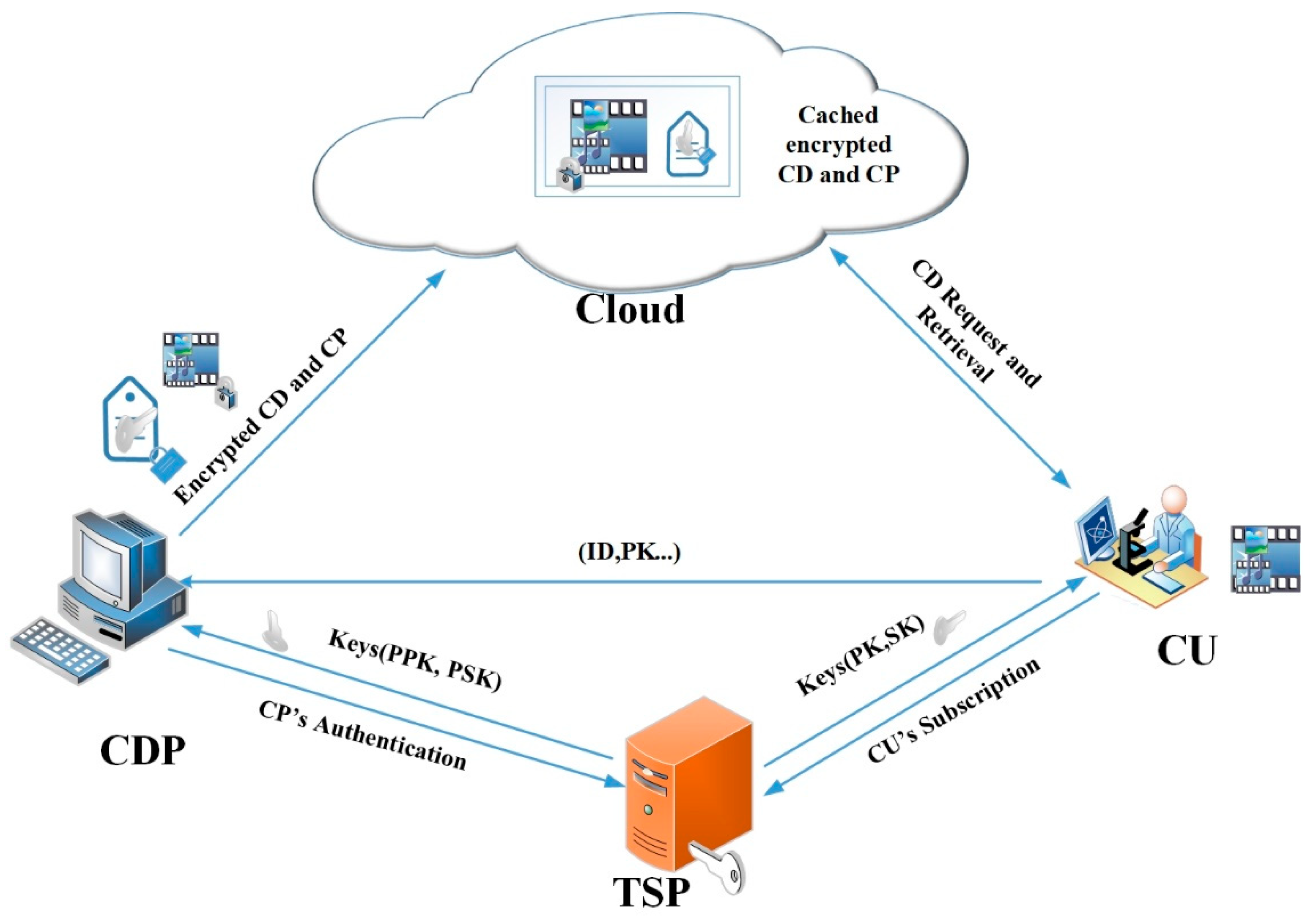
6.2. Our Proposed Secured Information Sharing Scenario
Figure 4 demonstrates a secured information sharing system. In this system, communication is based on one to many information sharing; that is, a publisher and many content users of the same interest and subscription. The main aim of the system is to protect and enforce access control policy on sharing content in the CCN approach so that only users whose properties match with the policy can effectively access and use the content.
TSP generates two pairs of keys to the CU and CDP as follows:
- (i)
The TSP generates a pair of keys
by running
in
Section 4 to the user upon registration. The user installs the secrete key
on his device and sends
to the Publisher.
- (ii)
TSP runs to generate a pair of keys and a hashed code of one of the users } to the . Let be a uniformly random value and be a sample from distribution . The TSP generates and outputs the public key and secret keys as and respectively.The keys generated to users have time validation and automatic key update property, so users will not receive any update once their keys expire or compromised. When the CDP recieves from the TSP and from the CU, he authentics the CU by running a hash function of the ID and compares it with the hash codes, } received from the TSP.
The CP then performs two main encryption processes.
- (i)
CDP selects key pairs, and parameters, He runs the encryption algorithm , where is the encoded CD and set .
- (ii)
The
CDP runs the encryption algorithm
in
Section 4 and the broadcasts
and
to the cloud server. Note that
is the encrypted content data
CD which
CUs are interested and
CT is the encrypted content policy which contains some relevant information about the
CD and secrete key to or password to decrypt
.
The CU on the other side conduct the following processes:
- (i)
The CU runs the decryption
algorithm in
Section 4 to obtain the secret key
To obtain
the user’s attributes
must satisfy
.
- (ii)
The CU runs to output to obtain from .
6.3. Key Exchange Protocol, Encryption and Decryption Model
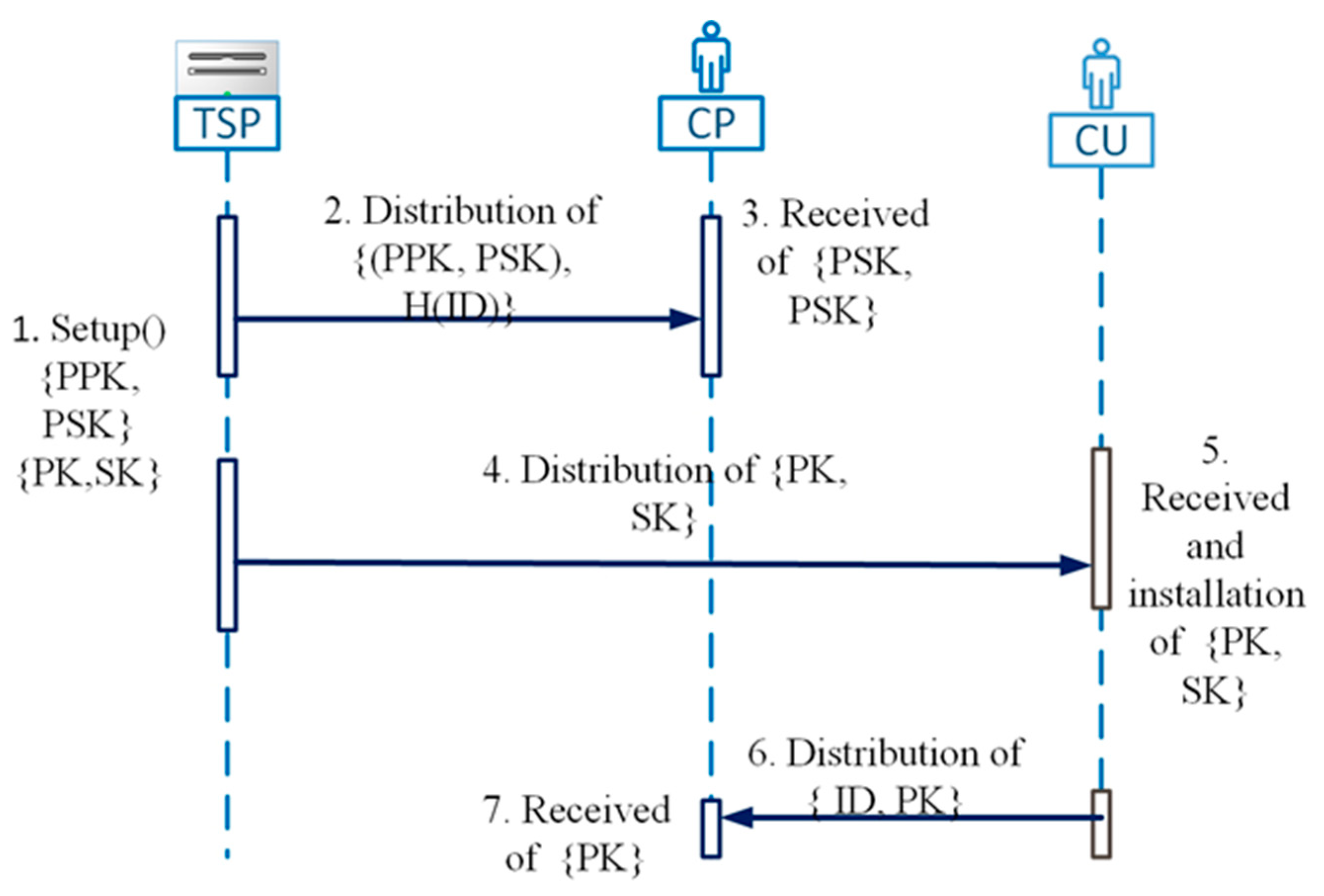
Figure 5 shows the key exchange process of our and
Figure 6 represents content dissemination and retrieval process of our system. In
Figure 5, the TSP generates
based on an asymmetric encryption scheme and sends it to the CDP through a secured key exchange protocol.
To the CU, the generates a pair of keys based on CU’s attributes. When CU receives , he installs on his device and sends to the content data publisher. At the end of the key exchange protocol, the user holds a pair of keys which reflects his attributes and the holds three keys which consist of the public key of users and a pair of asymmetric keys
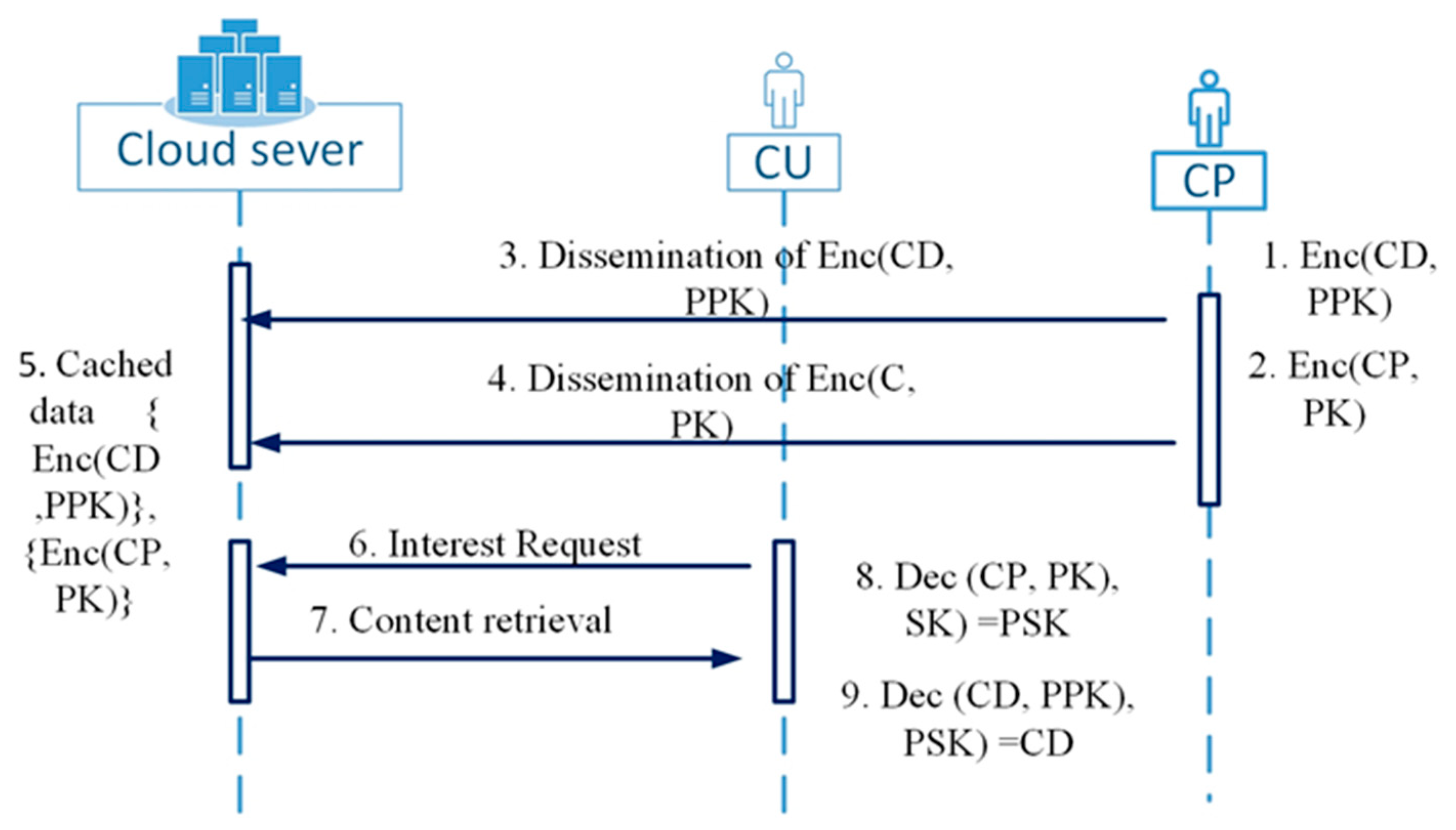
The encryption and decryption process in
Figure 6 consists of the following steps:
The content data publisher firstly selects ) pair of keys and encrypt the content
Secondly, the CDP encrypts the content policy by taking into consideration the attribute set and the updated policy. The content policy contains the secrete key and some information about the content data, including the hash code of the content data. The CDP encrypts content data and content policy and disseminates them unto the cloud server
When the sends for request, the server verifies him and when there is a match between his subscription and the policy, the server replies with the content policy and the content data sequentially. The CU runs two main decryption algorithm which consists of the following.
- (i)
Firstly, the user runs the decryption algorithm
in
Section 4 to extract the secrete kay
using the secret key
associated with his attribute.
- (ii)
Finally, using , the user extracts his interested content data by running the decryption . The user can obtain and utilize the message if and only if his attributes match with the policy enforced on the content policy to obtain the secret key for decryption of the Content data.
6.4. Security Analysis of our System
This section looks at the security analysis of our proposed system. This is based on the privacy of the content and users’ authentication
6.4.1. Privacy
The proposed system consists of four actors,
CU, CP, cloud sever and
TSP. After the
CU receives his pair of keys
from the TSP, he/she sends
and one of his
, to the
CP. The CP authenticates the CU and encrypts the content
with the public key
and then lock up the secret key
with the public key
received from the
CU. The
CP publishes the encrypted content and the encrypted secret key to the cloud server in a content centric approach without leaking any information about the
CD and
Here, the cloud server cannot learn anything about the
CD and except the encrypted content and the encrypted manifest which contains the key
PSK. The
CU also sends the public key to the
CP without disclosing his private keys. So, if the server or any of the users are malicious, none of them can collude to decrypt the content policy to obtain
PSK to decrypt the content. Moreover, an attacker cannot eavesdrop the
CU’s credentials or pretends to be
CP due to the security primitives of the basic scheme described in
Section 4.4. However,
CP conspiring with the
TSP can obtain users’ credentials.
6.4.2. Authentication
The content policy or manifest contains the hash code of the content. This enables the user to verify the authenticity of the message and the CP. Hence, the integrity of the content and the legitimacy of the content publisher is assured.