Particle Methods Simulations by Kinetic Theory Models of Human Crowds Accounting for Stress Conditions

Abstract

This paper tackles the problem of simulating the dynamics of human crowds in high density conditions on venues which include internal obstacles and in the interaction between two crowd streams moving in two opposite directions. The role of stress condition is taken into account as simulations aim at providing a support to crisis managers in charge of reducing the risk of incidents. The rationale of the modeling approach is that kinetic theory approach, where individual interactions, which might be nonlinearly additive, non symmetric, and non nonlocal, lead to collective behaviors to be examined towards safety problems.

1. Plan and Aims of the Paper

This paper tackles the problem of the simulation of crowd dynamics for the case studies briefly described in the abstract. The contents of our paper follows the critical analysis developed in [1] which has suggested to select the kinetic theory approach as the most appropriate to simulate crowd dynamics pedestrians in high density conditions taking into account both the level of stress in the crowd and the specific geometry of the areas, where the crowd moves. An additional feature, which is worth to be considered, is the physical quality of the venue.

The contents of our paper is mainly focused on simulations developed with the aim of enlightening the onset of conditions which may threaten the safety of pedestrians. Motivations to develop this study can be found in the paper [2] which starts by recalling the incident of 24 September 2015, on the Jamarat bridge in Makkah, and subsequently reports about specific features of human crowds to be carefully considered in the modeling. Most of the reasonings in [2] support the aforementioned selection of the mesoscopic scale to represent and model the class of systems under consideration as kinetic theory tools allow to account for the heterogenous behavior within the crowds.

Our paper refers to achievements known in the literature, recently reviewed in [3], to select the model and focuses on the development of simulations to enlighten the following features: the role of obstacles in the generation of overcrowded areas and the dynamics of streams moving towards opposite directions. Both types of simulations are critically analyzed within the general framework of crisis situations. Focusing on empirical data and model validation the following research contributions should be indicated [4,5] referring to the specific features of the velocity and flow diagrams.

Section 2 presents the main achievement of this paper, namely simulations related to two specific case studies. The first one focuses on the dynamics in a venue constituted by parallel walls and which includes internal obstacles in the central part, while the second one focuses on a flow of two streams of crowds moving towards opposite directions in a corridor. The main objective of this type of simulations consists in showing how the dynamics of fragmentation and high density develops depending on the overall density and level of stress and how stress can generate overcrowding areas thus leading to potentially dangerous situations.

The mathematical model selected for the simulations includes, as we shall see, two key parameters, namely a first parameter models the physical quality of the area from a minimal value corresponding to the worst quality conditions which prevent the motion to the highest value which promotes fast motion, where the quality of the venue is induced by lighting, slopes, narrow corridors, stairs etcetera, while a second parameter accounts for the aforementioned level of stress which is also related to local density conditions.

Section 3 shows how the simulations presented in the previous section can be used to support crisis managers. A critical analysis addresses the computational requirements and discusses the possible use of machine learning techniques to enhance the simulation of human crowds. Some research perspectives are proposed in this section.

It is worth stressing that a correct level of the parameter modeling stress, which means a rational choice between the search of the attraction to the stream and the natural search to avoid overcrowded areas, is 0.4. Then, increasing the value from 0.4 to 0.8 increases the attraction to the stream which is a critical situation, while higher values correspond to panic, namely to extreme danger.

2. Selection of a Crowd Model and Simulations

This section includes, as mentioned, the main results of our paper. The presentation is focused on the following four topics: Key requirements of the computational approach, selection of a mathematical model, simulations of a crowd flow on a bridge with internal obstacles, and a simulation of counter-flows. Each of them is treated in the next subsections. These achievements open to a critical analysis proposed in the next section which looks ahead to safety problems.

2.1. Requirements of the Computational Approach

The design of computational codes is related to the scale which has been selected for the modeling approach. In fact, different numerical tools are used for each scale, namely, time integration methods, such as Runge-Kutta methods, for large systems of ordinary differential equations, particle methods in the case of the kinetic theory approach, and finite differences or volumes in the case of the macroscopic approach.

In general, the requirements demanded to simulations essentially are the accuracy in computing local density and velocity and computational times lower or equal to the real time of the crowd. The former is a general requirement to for all types of applications, while the latter applies mainly on crisis management. Therefore, simulations are required to describe the flow patterns focusing both on local density and velocity under the constraint to keep the computational time below a critical time related to the specific dynamics which is investigated. Let us define precisely these two features.

From distribution function to macroscopic variables: The dependent variable of the kinetic theory approach is the probability distribution function over the microscopic state of walkers. As it is known,

Flow patterns: The key derived dependent variable is the density as it needs to be kept below a critical value, for safety reasons. Since dimensionless quantities will be used, the safety level is given by a “reasonable” number of walkers per square meter referred to the maximal “occupancy” number given by 7 walkers in the square meter. Assuming that a safe number is 4, then the safety threshold is $4/7$. In fact, when the dimensionless local density approaches to one, walkers can injury themselves to gain space. Further, increasing density increases the parameter—introduced later—which, in turn, promotes the increasing of density.

Critical time: Each dynamics has a critical time to achieve a certain objective, for instance the exit time increases with the density within the area. An additional effect is that when the density is low, namely the crowd is rarefied, the exit time decreases with the level of stress as the speed increases with this parameter. On the other hand, when the density is high, namely the crowd is dense, the exit time increases with the said × level of stress as even if speed increases with this parameter, walker unconsciously move towards dense areas and subsequently are obliged to decrease the speed. This feature of the dynamics should be put in connection with density patterns. For instance, large times are not acceptable in connection with high densities because of the probability of injuries increases.

2.2. Selection of a Computational Model

Methods of the kinetic theory approach to model human crowds, as reviewed in [1], have been initiated in [6] for crowds in unbounded domains and further developed in [7] to account for the interactions with walls and obstacles as well as for different levels of stress, while propagation of stress by contagion has been studied in [8,9] and [10]. Derivation of models at the macroscopic scale from the microscopic scale can be obtained by development of Hilbert type approaches [11,12,13,14]. The pertinent bibliography on crowd modeling has been already reported in [1] focusing specifically on human crowds. Therefore only the essential references are reported in this present paper. The reader interested to a survey, where crowd dynamics, is related to the modeling of vehicles and swarms, is referred to the recent survey [3] which provides and exhaustive report of the bibliography in the field, where all technical details, which are not repeated here, are available.

The modeling approach is such that walkers, which constitute the sub-system at the microscopic scale, are modeled as active particles. These have the ability of expressing their own heterogeneously distributed walking strategy, called activity, which depends both on the level of the stress and on the physical quality of the venue. Interaction of different groups is considered for a crowd of individuals who share common features and walking strategy. The subdivision of the crowd into groups permits one to model different walking abilities and strategies.

We suppose that the motion is on a plane and that polar coordinates are used for the velocity of walkers, namely the velocity is described by the speed v and by the velocity direction $\phi$. Dimensionless quantities are used for the speed which is divided by a limit velocity expressed by a fast walker in a high quality venue whose geometry is denoted by $\Sigma$. Accordingly, the collective state of each group is described by a distribution function over the microscopic state of walkers:

$$f_i=f_i(t,\mathbf{x},v,\phi ;\alpha ,\beta ),\mathbf{x}\in \Sigma ,v\in [0,1],\phi \in [0,2\pi ),$$

(1)

where the subscript $i=1,\dots ,n$ labels each group of walkers.

Generally, it is convenient referring $f_i$ to the maximum packing density. In practice about seven walkers per square meter. In addition, two dimensionless parameters can be introduced: $\alpha \in [0,1]$ and $\beta \in [0,1]$. Their physical meaning is as follows:

• $\alpha$ models the quality of the venue, where $\alpha =0$ corresponds to worst quality which, in practice, prevents motion, while $\alpha =1$ models high quality which can allows high speeds, however depending on the local density, as increasing density reduces locally the speed.
• $\beta$ models the level of stress, where $\beta =0$ corresponds to absence of concentration, $\beta =0.5$ to a normal level of stress which is needed by a proper self-organization of the motion, and $\beta =1$ models the highest level of stress. The connection between level of stress and local density can be modeled by simple functions which depict how $\beta$ is not a fixed parameter, but it grows with the local density when the said density pass a critical threshold, e.g., ${\rho }_c\ge 0.5$.

Velocity weighted moments of $f_i$ lead, under integrability conditions, to compute macroscopic observable quantities. For instance, the total density is defined as follows:

$$\rho (t,\mathbf{x})=\sum _{i=1}^n{\rho }_i(t,\mathbf{x})=\sum _{i=1}^n{\int }_0^1{\int }_0^{2\pi }{f}_i(t,\mathbf{x},v,\phi ;\alpha ,\beta )vdvd\phi ,$$

(2)

where ${\rho }_i$ is the local density of each functional subsystem, while the flow is computed by

$$\begin{array}{cc}\mathbf{q}(t,\mathbf{x})\hfill & ={\displaystyle \sum _{i=1}^n}{\mathbf{q}}_i(t,\mathbf{x})\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^n}{\int }_0^1{\int }_0^{2\pi }(vcos\phi \mathbf{i}+vsin\phi \mathbf{j})f_i(t,\mathbf{x},v,\phi ;\alpha ,\beta )vdvd\phi ,\hfill \end{array}$$

(3)

where $\mathbf{i}$ and $\mathbf{j}$ are the unit vectors of a plane cartesian frame. Higher order moments provide additional information.

Mathematical models consist in a differential system suitable to describe the dynamics in time and space of the aforementioned probability distribution functions. Kinetic models are obtained referring to the elementary volume in the space of the microscopic states and by equating the variation of particles (walkers) due to transport in the said volume to the inlet-outlet fluxes induced by interactions. As it is known, the key problem consists in the modeling of the interactions which generate the said fluxes.

A possible derivation rationale has been developed in [7]. Our paper reports, without repeating equations, available in [3,7], the key assumptions that lead to the model recalling that both speed and density have been referred to the highest admissible values so that these quantities take value in $[0,1]$. Specifically we look for a minimal model suitable, however, to capture the main features of human crowds.

• Interaction rate: A simple model of the rate of interaction between walkers is obtained by assuming that this rate is constant.
• Walking strategy: Walkers first select the walking direction, which ends up to correspond to the velocity direction, and subsequently adapt the speed to the local density pattern in their visibility zone.
• Selection of the velocity direction: According to [7], the strategy which leads to the velocity direction $\phi$ is a weighted selection out of three directions: (i) towards the trajectory going to the exit, (ii) attraction by the low gradient path, (iii) attraction by the main stream. The selection is driven by the local density $\rho$ and the parameter $\beta$ which models the level of stress. In more detail, attraction (ii) is enhanced by $\rho$, while attraction (iii) is enhanced by $\beta$.
• Perception of the density along the velocity direction: Once a velocity direction has been selected walkers perceive a density different from the real one as follows:

  $$\begin{array}{cc}\hfill & {\partial }_{\phi }\left[\rho \right]\ge 0\Rightarrow {\rho }_{\phi }\left[\rho \right]=\rho +\frac{{\partial }_{\phi }\left[\rho \right]}{\sqrt{1+{\left({\partial }_{\phi }\left[\rho \right]\right)}^2}}(1-\rho ),\hfill \end{array}$$

  (4)

  $$\begin{array}{cc}\hfill & {\partial }_{\phi }\left[\rho \right]<0\Rightarrow {\rho }_{\phi }\left[\rho \right]=\rho +\frac{{\partial }_{\phi }\left[\rho \right]}{\sqrt{1+{\left({\partial }_{\phi }\left[\rho \right]\right)}^2}}\rho ,\hfill \end{array}$$

  (5)

  where ${\partial }_{\phi }$ denotes the derivative along the direction $\phi$. Hence, ${\rho }_{\phi }\left[\rho \right]$ is higher (lower) that the real one in the presence of positive (negative) gradients, by a model which accounts for lower and higher bounds:

  $${\partial }_{\phi }\left[\rho \right]\to \infty \Rightarrow {\rho }_{\phi }\to 1,{\partial }_{\phi }\left[\rho \right]=0\Rightarrow {\rho }_{\phi }=\rho ,{\partial }_{\phi }\left[\rho \right]\to -\infty \Rightarrow {\rho }_{\phi }\to 0.$$
• Adjustment of the speed: Walkers, after perception of the density, adjust their speed to the perceived density conditions. The new speed $v_{\phi }$ can be modeled as follows:

  $$\begin{array}{cc}\hfill & {\partial }_{\phi }\left[\rho \right]\ge 0\Rightarrow v_{\phi }\left[\rho \right]=v-\alpha {\rho }_{\phi }\left[\rho \right]v,\hfill \end{array}$$

  (6)

  $$\begin{array}{cc}\hfill & {\partial }_{\phi }\left[\rho \right]<0\Rightarrow v_{\phi }\left[\rho \right]=v-\alpha {\rho }_{\phi }\left[\rho \right](1-v),\hfill \end{array}$$

  (7)
• Stress-density reciprocal influence: A key feature of the dynamics is the interaction between local density and level of stress as when the local density tends to the maximal value also the local stress tends to limit value $\alpha =1$.
• Boundary conditions: The statement of the mathematical problem requires the implementation of boundary conditions which depend on the distance from the wall measured along the direction of motion. When this distance tends to zero the attraction by the trajectory towards the exit is enhanced with respect to the other directions.

The integro-differential nature of kinetic equations, along with the decision process described above by which pedestrians select their preferred velocity direction and speed, leads to a computational model whose mathematical structure is quite involved. Monte Carlo particle methods are ideally suited for solving such an equation while keeping the computational burden at a reasonable level. The basic idea consists in representing the distribution function by a number of computational particles. These particles move in the computational domain and interact according to stochastic rules derived from the governing kinetic equation. The macroscopic fields are obtained through weighted averages of the particle properties.

Compared to deterministic methods of solution, Monte Carlo simulations shows some important advantages such as computational efficiency and the capability of taking into account sophisticated individual decision processes. This statement refers to kinetic type models only, where the implementation of deterministic methods involves well known technical difficulties.

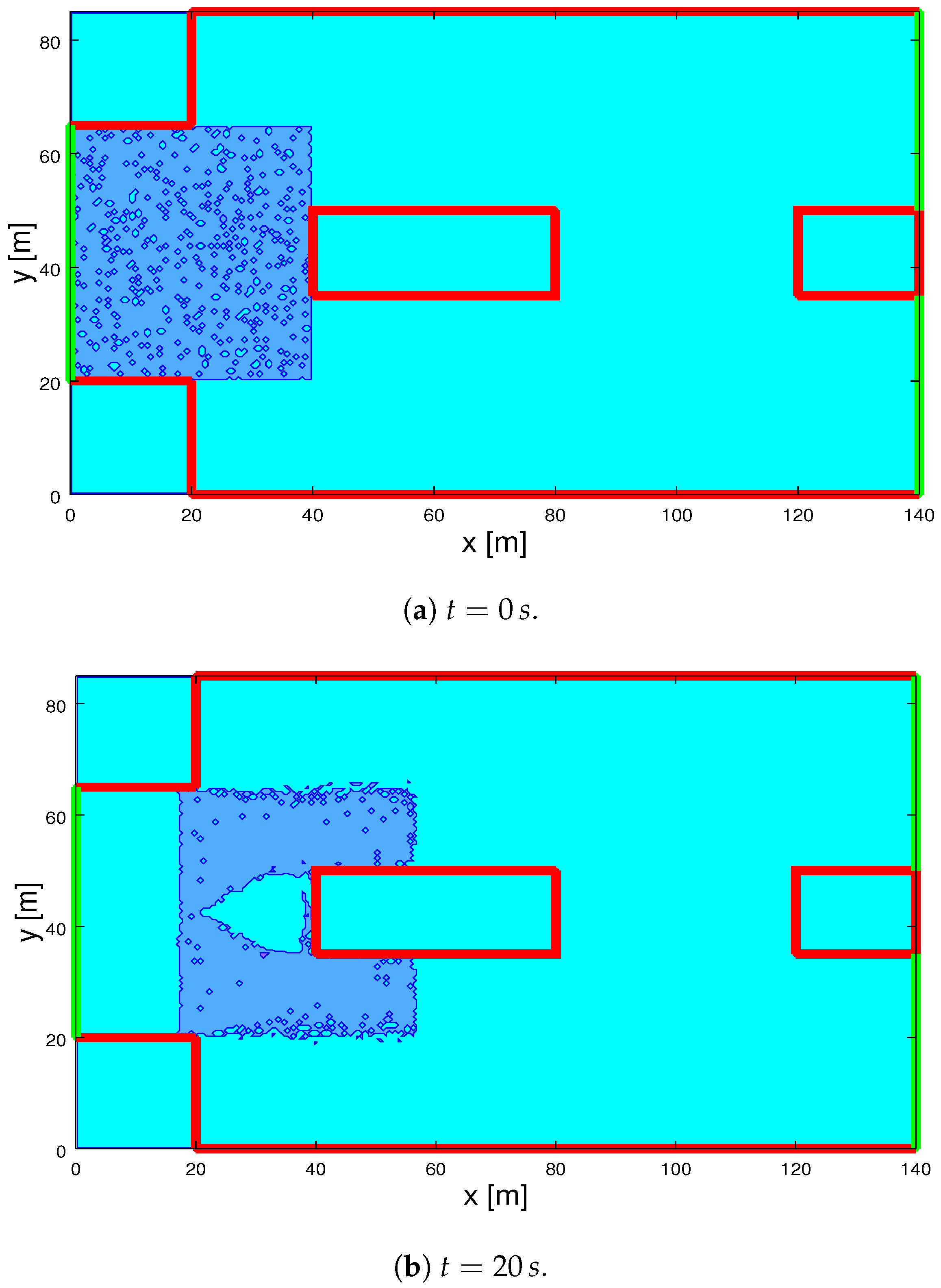
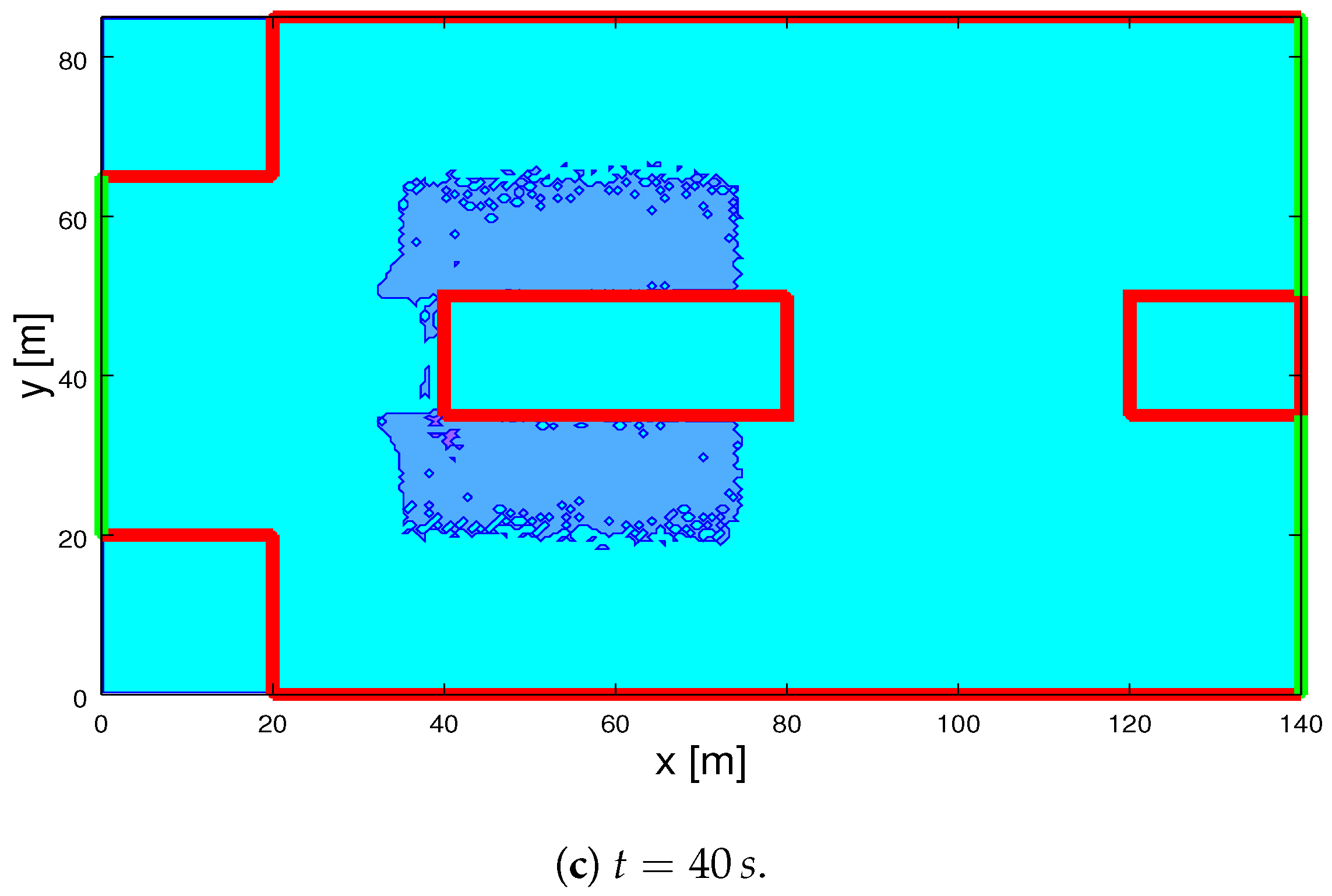
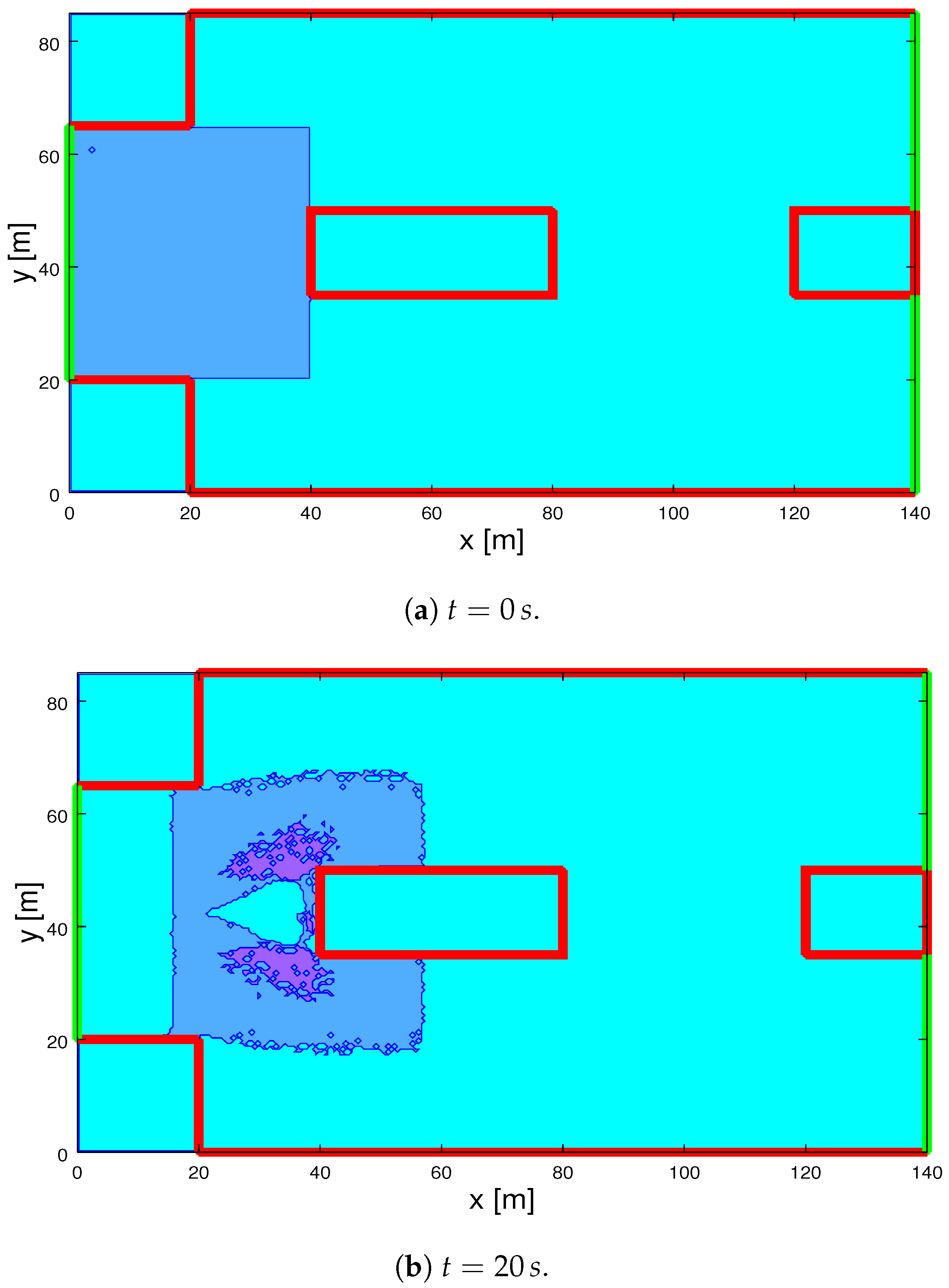
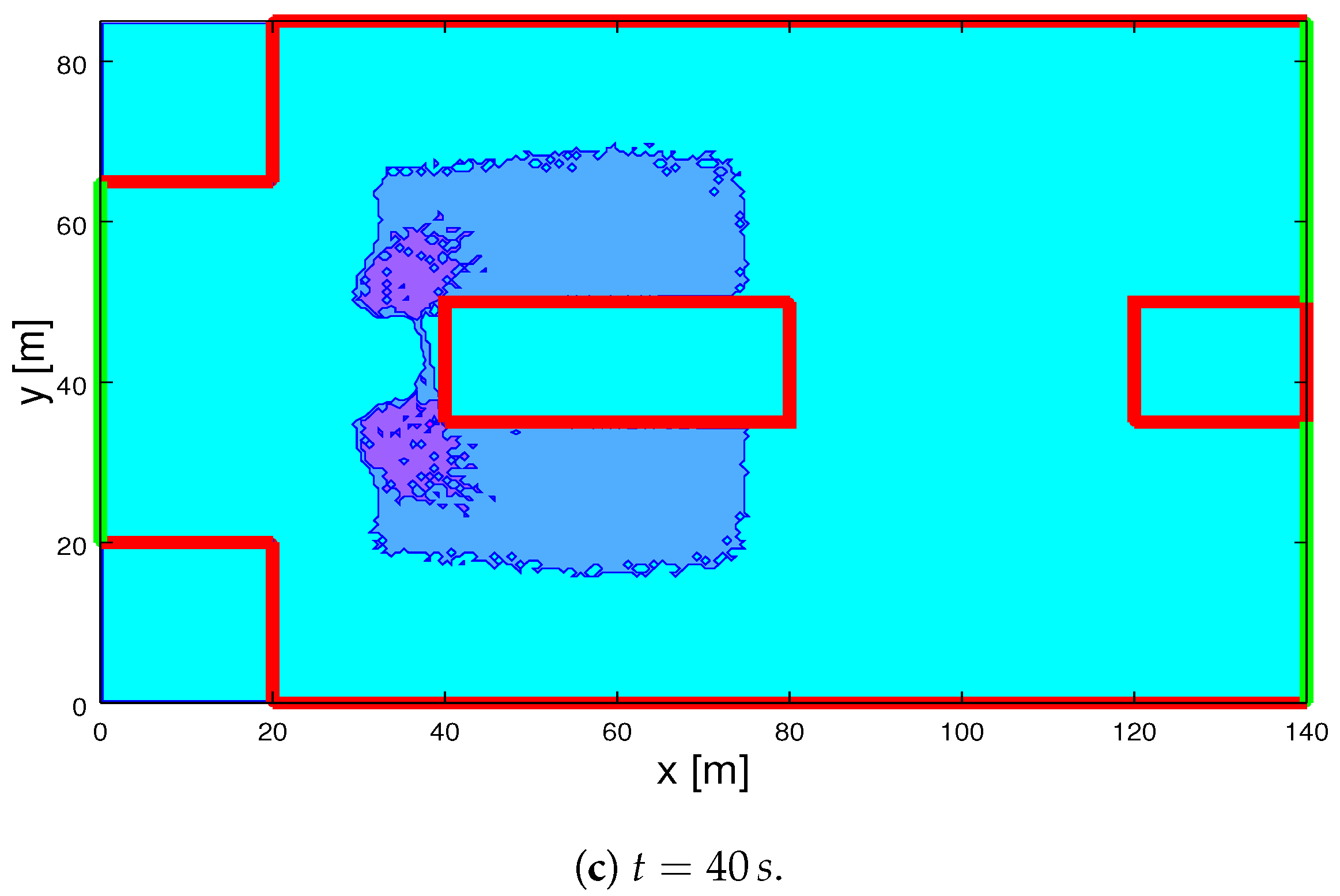
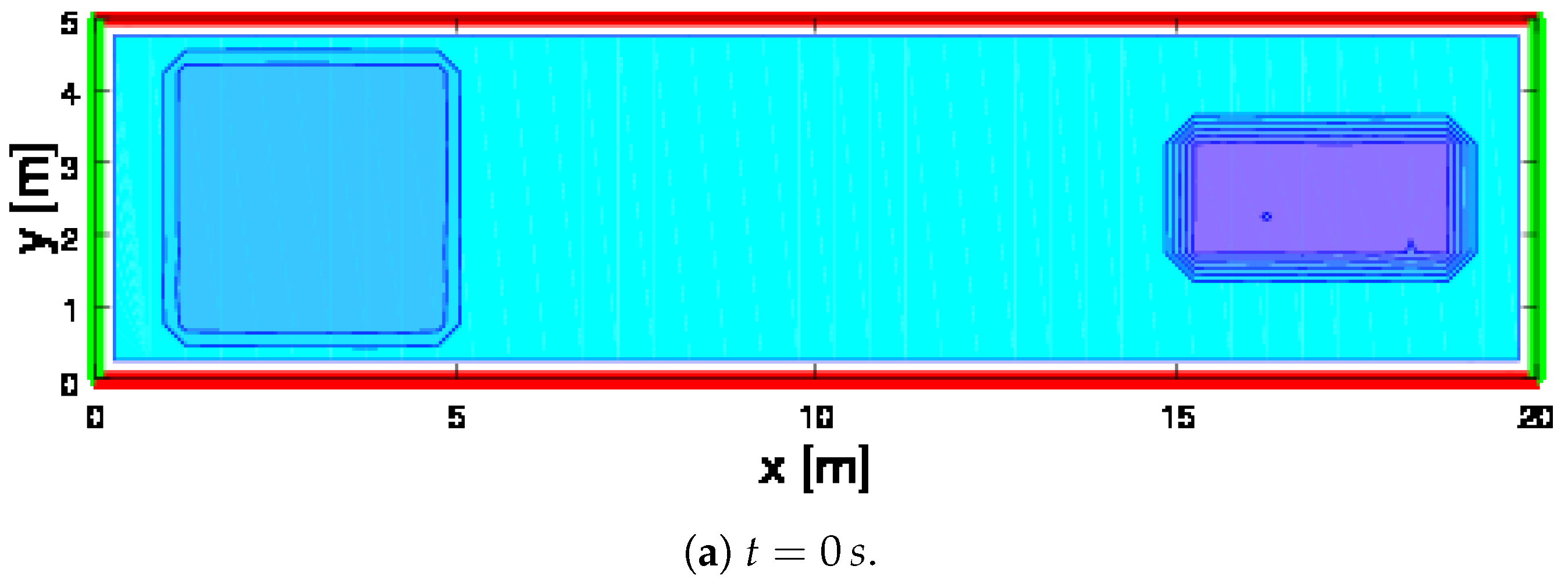
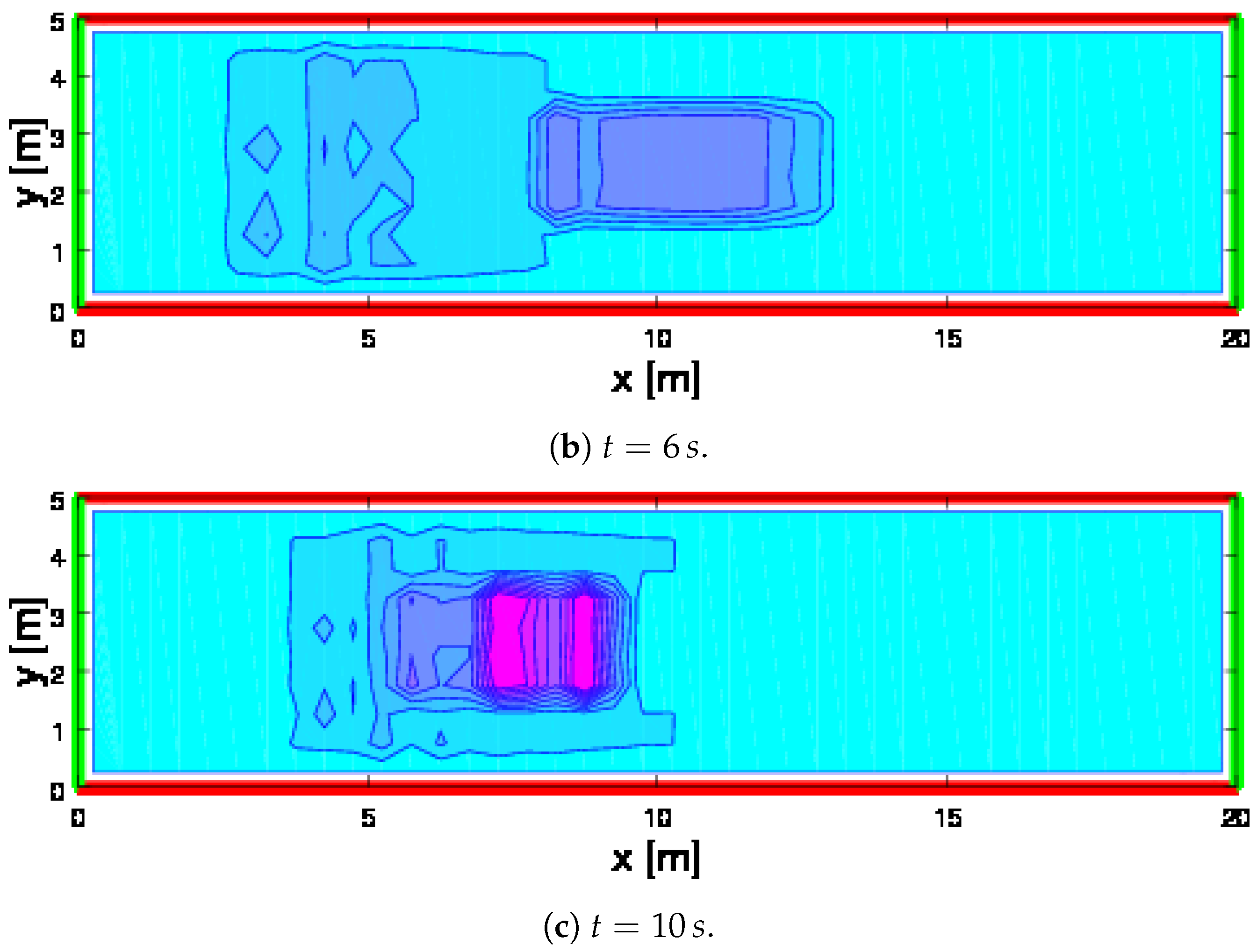
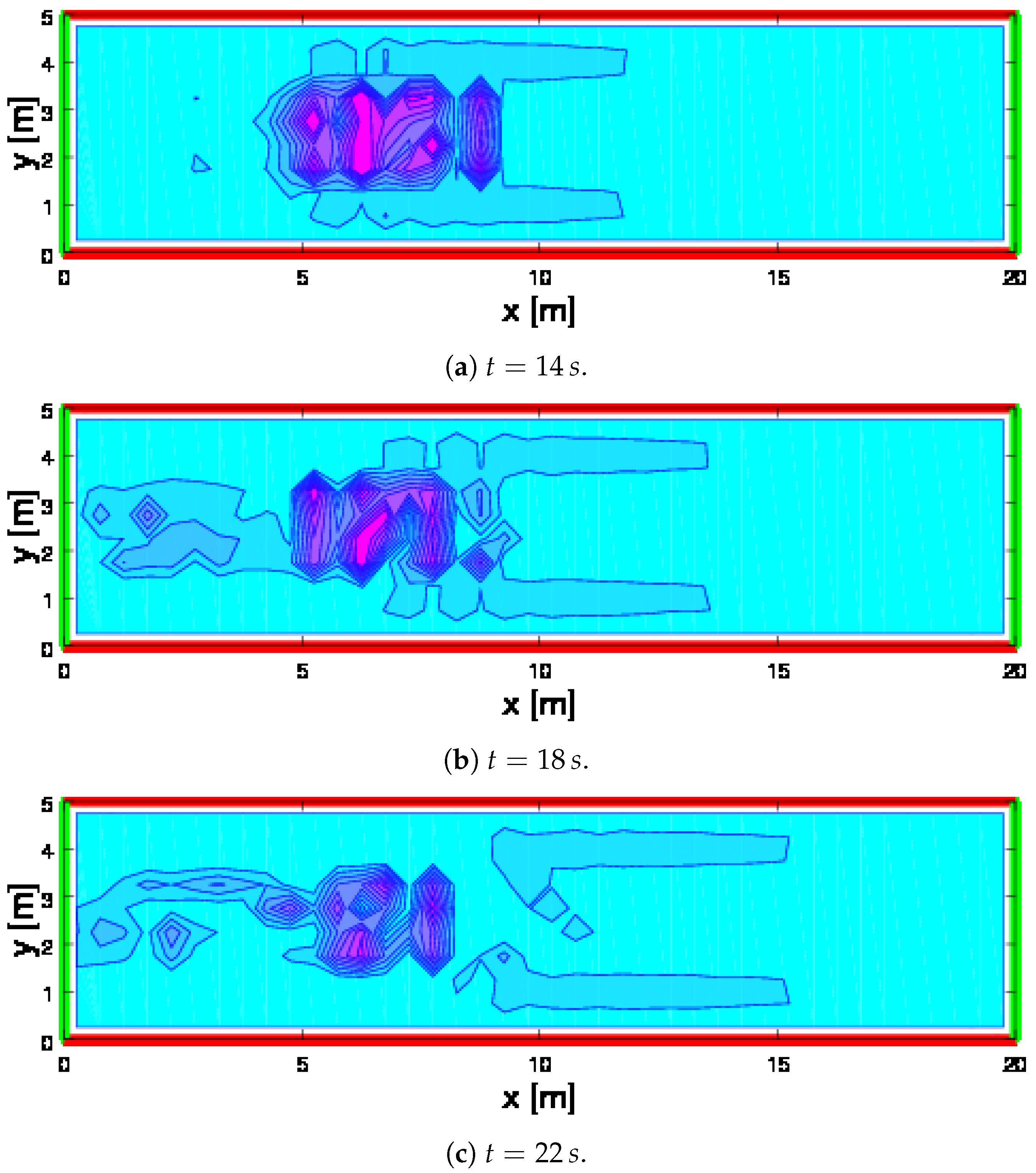
2.3. Simulations of Crowds over a Bridge with Internal Obstacles

This subsection shows how the mathematical and computational tools presented in Section 2.2, can be applied to reproduce the flow of human crowds venues which show geometrical features analogous to that of the Jamarat bridge. Special focus is on the role of columns placed in the middle of the way as these columns might become a source of incidents. As we shall see, useful insights can be obtained which can provide suggestions on how the geometric design of the venue might be revised for optimizing the pedestrian flow and how crisis managers can use the output of simulations to improve safety conditions. It is worth stressing that our paper does not aim at a simulation specifically focused on the aforementioned venue, but at developing mathematical tools which can be specifically addressed to such objective which would require specific data and commitments.

The pioneer approach to safety problems belongs to Helbing and coworkers [15,16,17], while several developments have been recently developed as reported in the bibliography of [8]. A recent research work [18] shows how a systems approach to safety problems can be developed, where a key feature consists in accounting for the connection between local density and stress. Indeed, this is one of the key feature of our paper.

The development of the computational approach first accounts for the requirements presented in the previous section, namely dealing with a crowd with large size, high performance computing suitable to keep the computational time lower that the real simulated time, and accounting for the level of stress in the crowd. Some interesting results have been proposed in the literature concerning simulations of kinetic type models [19,20]. Our computational experiments have suggested the use of Monte Carlo particle methods introduced by Bird [21], within the general framework of computational methods for Boltzmann type equations [22], and subsequently extended by various authors by modifying the method depending on the specific system under consideration, for instance [23,24], see also Section 6 of [3] which is specifically focused on crowd and swarm dynamics, while the survey [25] exhaustively covers this challenging field of scientific computing.

It is worth enlightening some conceptual differences with respect to the recently published paper [20], where some interesting simulations have been developed concerning evacuation dynamics and counter-flows. These differences allow to make more precise the contribution of our paper.

• The number of pedestrians in the simulations is of a higher order, namely of the order f ${10}^3$ instead of ${10}^2$.
• The velocity is continuous rather than discrete in a fixed number of directions, while the speed is not related to the velocity diagram, but it accounts for local gradients.
• The individual decision processes which leads to the selection of the velocity direction account for the presence of obstacles.
• The dynamics accounts for the different level of stress and of their relation to local density.
• A stochastic computational method has been developed to take into account all specific features indicated in the above items.

However, an extensive simulation campaign is, however, beyond the scope of this paper and only sample simulation results are briefly discussed in the following with the aim of validating the computational code.

Figure 1 and Figure 2 show the behavior of a crowd composed of 1000 people and 2000 people for different times, respectively. Pedestrians are initially uniformly distributed in the entrance ramp with a level of stressful conditions of $\beta =0.6$. As the simulation starts, the crowd splits into two groups which follow the shortest path to avoid the obstacle. In the attempt to keep constant their walking speed, however, a few pedestrians move away from the more congested areas and head for the empty region between the two groups.

It is apparent that in the higher density case potentially dangerous conditions occur near the corners where the sudden change in geometry leads to very high congestion levels. Additional simulations have shown that increasing the number of individuals in the crowd enhances the onset of high density zones. Analogous effect appears for increasing values of the parameter modeling the level of stress, simulations are not reported to avoid redundancy of similar simulations.

2.4. Flows of Crowds Moving to Opposite Directions

A different type of simulation is considered in this subsection once again having in mind safety problems. Namely we consider a crowd moving along a corridor being contrasted by a another crowd suddenly moving against. The level of stress in the first group is moderate, say normal, while the level of stress in the second group if high. Therefore, the second group forces against the first group.

This physical situation can appear if the second group has met a dangerous situation, for instance caused by an incident, and consequently a group has decided to invert the direction of motion to escape danger. The main interest of the simulations consists in showing if the dynamics exhibits fragmentation and subsequent localization of high levels of density-stress.

The flow patterns related to this type of dynamics are shown in Figure 3 and Figure 4 which show how the flow pattern at $t=0$ is modified by the interactions between the two streams as well as by the interactions within walkers moving along the same direction.

Simulations show in Figure 3 the progressive formation of high concentration of density-stress patterns, while Figure 4 shows the persistence of high level of concentration even when the two groups have completely gone across each other. In more detail on the density patterns, both groups have an initial density of 3 persons per square meter, that can be considered a high density, but not yet critical. On the other hand, the interaction between these two groups generates concentration approaching 7 persons per square meter, namely a highly critical density as far as safety is concerned.

The sample simulations presented above provide a detailed description of the local density and velocity pattern in each point of the area where the crowd moves by means of the visualization of high concentration zones. In addition, simulations also show how the localization of high concentration zones evolves in time and space.

3. Critical Analysis towards Safety Problems

As we have seen, advanced mathematical and computational tools have been used. However, we do not naively think that these tools can be simplified, as their use can be planned and optimized within a proper research plan. However, some perspective ideas are proposed in the following items which focus both on safety problems and research perspectives.

Concerning safety problems the following perspective is proposed: A huge number of simulations corresponding the all possible variety of situations can be developed by using the approach proposed in our paper. Then, these simulations can be stored in a database. The subsequent use of the database consists in training crisis managers by identification of a broad variety of the possible actions that can effectively reduce the crisis situation. In addition, the database can be used also to train leaders who in the crowd can contribute, by addressing the walking dynamics, to reduce the risk of safety problems. More in general, simulations can provide a detailed description of the role of the geometry and quality of the venue over the dynamics in space of the aforementioned density patterns.

This effort needs additional work with respect to the development of computational schemes. The systems approach [18], the engineering vision of safety problems [26,27], computer vision and virtual reality [28,29,30], while a deep study of the psychology of crowds [31] can contribute to the assessment of all specific features to be taken into account in the modeling approach and hence in the machine learning design.

Concerning research perspectives we bring the attention of the reader to multiscale problems: A multiscale vision of crowd modeling can be important looking at different aspects of the development of computational modeling and of the validation of models. Two key issues have to be taken into account in the development of a multiscale modeling, namely the derivation of models at all scales accounting for the same principles and derivation of models at the higher scale from the underlying description at the lower scale. In principles these two different views can join into a unified multiscale vision. Some work in this direction has been has been developed for crowds in unbounded domains [32].

This perspective appears to be a key requirement in the search of a valid modeling approach. The contributions available in the literature still need additional work which cannot skip over the need of sophisticated analytic tools to achieve this result. A deep analysis of the complex behaviors at the microscopic scale [33,34,35] which can include non symmetrical behaviors [36], can contribute to model the link between individual and collective behaviors.

Development of these two specific perspectives would definitely contribute to design models of crowd dynamics effectively useful to applications.