Fixed Points for Multivalued Weighted Mean Contractions in a Symmetric Generalized Metric Space

Abstract

This paper defines two new concepts: the concept of multivalued left-weighted mean contractions in the generalized sense of Nadler in a symmetric generalized metric space and the concept of multivalued right-weighted mean contractions in the generalized sense of Nadler in a symmetric generalized metric space, and demonstrates fixed-point theorems for them. For these, we demonstrated two fixed-point existence theorems and their corollaries, by using the properties of the regular-global-inf function and the properties of symmetric generalized metric spaces, respectively. Moreover, we demonstrated that the theorems can be applied in particular cases of inclusion systems. This article contains not only an example of application in science, but also an example of application in real life, in biology, in order to find an equilibrium solution to a prey–predator-type problem. The results of this paper extend theorems for multivalued left-weighted mean contractions in the generalized sense of Nadler, demonstrating that some of the results given by Rus (2008), Mureșan (2002), and Nadler (1969) in metric spaces can also be proved in symmetric generalized metric spaces.

1. Introduction

Fixed-point theory has applications in many fields, such as functional and nonlinear analysis in solving partial or random differential equations or in solving problems with the theory of differential and integral equations, in proving differential and integral inclusions, and in demonstrating approximation methods in the study of functional equations, management, economics, finance, computer science, and other fields [1]. There has been extensive research on the topic of fixed points of multivalued operators, using different methods, resulting in an increasing number of papers published on this topic in the past years.

The works of Poincaré, Lefschetz-Hopf, and Leray-Schauder laid the foundation of the field of fixed-point theory. Their theory has also been of high importance for degree theory.

In metric-space theory, the existence and uniqueness of a solution is demonstrated by making successive approximations. One of the most famous and influential mathematicians of the 20th century, Professor Stefan Banach, managed to expand the use of this theory to more than ordinary differential equations and integral equations. One of the theorems that was used to create the fixed-point theory in metric spaces is Banach’s fundamental fixed-point theorem, and it involves contraction mappings that are defined in a complete metric space.

In the year 1965, Browder, Göhde, and Kirk [2,3,4] created the theory of multivalued mappings, with applications in multiple areas: differential inclusions, convex optimization, control theory, economics, management, and finance. Moreover, in 1969, Nadler [5] used Banach’s theory and the concept of Hausdorff metric to prove that the multivalued version of the theory has a fixed point.

In 1996, Angrisani and Clavelli [6] created a new method to prove fixed-point theorems by using the class of regular-global-inf functions. We will apply this method for the study of multivalued left- and right-weighted mean contractions in the generalized sense of Nadler in a symmetric generalized metric space.

In 2004, Ran and Reurings [7] used the Banach contraction principle endowed with a partial order to demonstrate how to solve certain matrix equations. Similarly, in 2007, Nieto and Rodrigues-López [8] solved differential equations by using the extension to the Banach contraction principle. Later, in 2007, Jachymski [9] managed to obtain a more general version of the previous extensions by using graphs instead of the partial order.

Other researchers, such as Espinola and Nicolae [10], Nicolae in 2011 [11], and Leustean [12] used some fixed-point theorems in geodesic metric spaces.

In 2012, Aydi, Abbas, and Vetro [13] extended Nadler’s fixed-point theorem, thus obtaining results for multivalued mappings defined in complete partial metric spaces.

Bucur (2019) [14] and Bucur, Guran, and Petruşel (2009) [15] obtained some results on fixed points of multivalued operators in generalized metric spaces by extending some old fixed-point theorems.

In another paper, published in 2012, Rezapour and Amiri [16] provided different conditions for those theorems [15] published in 2009, thus obtaining new theorems on fixed points for multivalued operators defined in generalized metric spaces.

Alecsa and Petruşel [17] present two results concerning the fixed points of (ϕ−ψ) multivalued operators.

Kikkawa and Suzuki (2008) [18] also obtained results for generalized contractions in complete metric spaces. Later, in the year 2011, Kikkawa’s method was used by Rezapour and Amiri [19] to obtain new theorems on fixed points for multivalued operators defined in generalized metric spaces.

In their paper, Bounegab and Djebali [20] presented new fixed-point theorems for multivalued nonexpansive mappings and obtained some fixed-point results, including existence theorems.

Mukheimer, Vujaković, Hussain et al. (2019) [21] demonstrated a new approach to multivalued nonlinear weakly Picard operators.

Therefore, research has demonstrated that fixed-point theorems of multivalued operators can be applied in different types of spaces. Researchers have obtained results for fixed points in partial metric spaces, b-metric spaces, symmetric metric spaces, etc.

Authors such as Hicks and Rhoades [22] and Joshi, M.C.; Joshi, L.K.; and Dimri [23] studied the existence of fixed points in symmetric spaces, demonstrating that for these theorems it is not necessary to apply all the axioms from the definition of a metric.

This paper is a continuation of my articles “Fixed Points for Multivalued Convex Contractions on Nadler Sense Types in a Geodesic Metric Space” (2019) [14] and “Fixed Point Theorem for Multivalued Operators on a Set Endowed with Vector-Valued Metrics and Applications” (2009) [15].

2. Main Results

For $\left(X,d\right)$ a metric space, we denote by

• $P\left(X\right)$—the set of all subsets of X, which are nonempty;
• $P_c\left(X\right)$—the set of all compact subsets of X, which are nonempty;
• P_cl (X)—the set of all nonempty closed subsets of X.

Using these subsets, we will consider the following operators:

• $D:P\left(X\right)\times P\left(X\right)\to \left[0,\infty \right), D\left(Z,Y\right)≔inf\{d\left(x,y\right):x\in Z, y\in Y\}, Z, Y\in P\left(X\right)$—the gap functional;
• $H:P\left(X\right)\times P\left(X\right)\to \left[0,\infty \right), H\left(Z,Y\right)≔max\{su{p}_{x\in Z}in{f}_{y\in Y}d\left(x,y\right), su{p}_{y\in Y}in{f}_{x\in Z}d\left(x,y\right)\}$—the Pompeiu–Hausdorff functional.

Additionally, for $Z\in P_c\left(X\right)$, we have $diam\left(Z\right)=sup\{d\left(x,y\right):x,y\in Z\}$ and ${\alpha }_K\left(Z\right)=inf\{\epsilon >0:Z={{\displaystyle \cup }}_{i\in I}{Z}_i,diam{Z}_i\le \epsilon \}$, the Kuratowski measure of noncompactness.

Let $F:X\to R$ be a real valued function. For any $p\in R$, we denote $L_p=\{x\in X:F\left(x\right)\le p\}$ as the p-level set and $infF= inf\{F\left(x\right):x\in X\}.$

If $T:X\to P\left(X\right)$ is a multivalued operator, then the fixed point set of T is $Fix\left(T\right)$=$\{x\in X, x\in T\left(x\right)\}$ and $SFix\left(T\right)$ is the strict fixed-point set of T, i.e., $SFix\left(T\right)$=$\{x\in X, x=T\left(x\right)\}$.

Definition 1 

[24]. The functional $F:X\to R$ is known as regular-global-inf (RGI) in $x\in X$ if and only if $F\left(x\right)>infF$ implies that there is a $p>infF$, such that $D\left(x,L_p\right)>0$. The application F is called RGI in X if it is RGI in all $x\in X$.

Proposition 1 

[24].

(i) Let the sets be Z,Y $\in P_c\left(X\right).$ For all $x\in Z$ and $q>1$ exists $y\in Y$, with $d\left(x,y\right)\le qH\left(Z,Y\right)$. (ii) For any $\left(X,d\right)$, a complete metric space, it results that the pair $\left(P_c\left(X\right),H\right)$ is also a complete metric space.

Proposition 2 

[24]. Let $\left(X,d\right)$ be a complete metric space, and $F:X\to \left[0,\infty \right)$ be an RGI function in X. If $\underset{p\downarrow infF}{lim}{\alpha }_K\left(L_p\right)=0$, we obtain that the set of the global minimum points of F is nonempty and compact.

Definition 2 

[15]. Let X be a nonempty set. We consider the vector space of vectors with positive real components $R_{+}^m,$ equipped with the usual component-wise partial order. The operator $d:X\times X\to R_{+}^m$, for which the usual axioms of the metric take place, is called a generalized metric in the sense of Perov.

Let $\left(X,d\right)$ be a generalized metric space in the sense of Perov. In this space, if $v,r\in R^m$ are two vectors: $v≔\left(v_1, v_2, \dots ,v_m\right)$ and $r≔\left(r_1, r_2, \dots ,r_m\right)$, then by $v\le r$ we understand $v_i\le r_i$ for all $i\in \{1,2\dots ,m\}$, while $v<r$ represents $v_i<r_i$ for all $i\in \{1,2\dots ,m\}$. Moreover, $\left|v\right|=\left(\left|v_1\right|, \left|v_2\right|,\dots ,\left|v_m\right|\right)$. Thus, $max\left(v,r\right)≔\left(max\left(v_1,r_1\right), max\left(v_2,r_2\right),\dots ,max\left(v_m,r_m\right)\right)$. In a particular case where $r_i=c\in R$, $i\in \{1,2\dots ,m\}$ and $v\le \left(c, c\dots c\right)$, it implies that $v_i\le c$ for all $i\in \{1,2\dots ,m\}$.

The concepts of convergent sequence, Cauchy sequence, completeness, and open and closed subsets, which are defined in a generalized metric space, are defined similarly to those in a metric space. If $x_0\in X$ and $r\in R_{+}^m$, with $r_i>0$ for all $i\in \{1,2\dots ,m\}$, we will denote by $B\left(x_0,r\right)≔\{x\in X:d\left(x_0,x\right)<r\}$ the open ball centered in $x_0$ with $r$ radius and by $\overline{B}\left(x_0,r\right)≔\{x\in X:d\left(x_0,x\right)\le r\}$ the closed ball centered in $x_0$ with the radius $r$. If $T:X\to P\left(X\right)$ is a multivalued operator, then we denote by Fix(T) the set of fixed points of T. We have $Fix\left(T\right)≔\{x\in X:x\in T\left(x\right)\}$.

We note that a generalized Pompeiu–Hausdorff functional can be applied in the context of a generalized metric space in the sense of Perov. Thus, if $\left(X,d\right)$ is a generalized metric space in the sense of Perov, with $d≔\left(d_1, d_2, \dots ,d_m\right)$, and if H_i denotes the Pompeiu–Hausdorff metric on $P_c\left(X\right)$ generated by d_i, $i\in \{1,2\dots ,m\}$, then we denote by $H:P_c\left(X\right)\times P_c\left(X\right)\to R_{+}^m$, $H≔\left(H_1, H_2, \dots ,H_m\right)$ the vector-valued Pompeiu–Hausdorff metric.

Definition 3 

[25]. A matrix A is convergent to zero if $A^n\to 0$ as $n\to \infty$.

Definition 4 

[15]. Let $A\in M_{m,m}\left(R_{+}\right)$ be a matrix convergent to zero. It is said that any A multivalued operator $T:Y\subset X$→$P_c\left(X\right)$ is a multivalued left A-contraction in the sense of Nadler, if the following inequality takes place:

$$H\left(T\left(x\right), T\left(y\right)\right)\le Ad\left(x,y\right)$$

for all $y\in Y$.

We notice that for m = 1 we obtain a generalization of the contraction mappings defined by S. B. Nadler Jr. (1969).

Based on the previous definition, we can create new definitions.

Definition 5. 

Let $p_1, p_2, \dots , p_n$ be real positive numbers. Let $A_1, A_2,\dots ,A_n\in M_{m,m}\left(R_{+}\right)$ be matrices convergent to zero, and for which

$$\begin{gathered} H\left(T\left(x\right), T\left(y\right)\right)\le \frac{p_1}{p_1+p_2+\cdots +p_n}{A}_{1}d\left(x,y\right)+\frac{p_2}{p_1+p_2+\cdots +p_n}{A}_{2}d\left(x,y\right)+\cdots + \\ \frac{p_n}{p_1+p_2+\cdots +p_n}{A}_{n}d\left(x,y\right), \end{gathered}$$

for all $x,y\in Y$, it is said that any multivalued operator $T:Y\subset X$→$P_c\left(X\right)$ is a multivalued left-weighted mean contraction in the generalized sense of Nadler.

Definition 6. 

Let $p_1, p_2, \dots , p_n$ be real positive numbers. Let $A_1, A_2,\dots ,A_n\in M_{m,m}\left(R_{+}\right)$ be matrices convergent to zero, and for which

$$\begin{gathered} H\left(T\left(x\right), T\left(y\right)\right)\le \frac{p_1}{p_1+p_2+\cdots +p_n}d\left(x,y\right)A_1+\frac{p_2}{p_1+p_2+\cdots +p_n}d\left(x,y\right)A_2+\cdots + \\ \frac{p_n}{p_1+p_2+\cdots +p_n}d\left(x,y\right)A_n, \end{gathered}$$

for all $x,y\in Y$, it is said that any multivalued operator $T:Y\subset X$→$P_c\left(X\right)$ is a multivalued right-weighted mean contraction in the generalized sense of Nadler.

Definition 7. 

Let $\left(X,d\right)$ be a complete metric space, where $d≔\left(d_1, d_2, \dots ,d_m\right)$ is a convex metric. An operator $T: X$→$P_c\left(X\right)$ is said to be a multivalued Lipschitz operator of X into $P_c\left(X\right)$ if and only if the following inequality takes place:

$$H_i\left(\left(1- \alpha \right)T\left(x\right)\oplus \alpha T\left(y\right), T\left(z\right)\right)\le a{d}_i\left(\left(1- \alpha \right)x \oplus \alpha y, z\right),i\in \{1,2\dots ,m\} for all x,y\in X,$$

where $a\ge 0$, $H_i$ denotes the Pompeiu-Hausdorff metric on $P_c\left(X\right)$ generated by $d_i$ for all $i\in \{1,2\dots ,m\}$ and $H:P_c\left(X\right)\times P_c\left(X\right)\to R_{+}^m$, $H≔\left(H_1, H_2, \dots ,H_m\right)$ is the vector-valued Pompeiu-Hausdorff metric on $P_c\left(X\right)$.

In case there is a Lipschitz constant for T, namely, $a<1$, then T is called a multivalued contraction mapping (Nadler, 1969).

Definition 8 

[22]. A symmetry on a set X is a function d: $X\times X\to R_{+}$, such that

(i) 

$d\left(x,y\right)=0$ if and only if $x=y$;

(ii) 

$d\left(x,y\right)=d\left(y,x\right)$.

Starting from definition 8, we can define a symmetric generalized metric; thus,

Definition 9 

[22]. A vector $d≔\left(d_1, d_2, \dots ,d_m\right),$ for which each element $d_i$ is a nonnegative real-valued function on $X\times X$, such that

(i) 

$d_i\left(x,y\right)=0$ if and only if $x=y$ for all $i\in \{1,2\dots ,n\}$;

(ii) 

$d_i\left(x,y\right)=d_i\left(y,x\right)$ for all $i\in \{1,2\dots ,n\}$

is called a symmetric generalized metric on a set X.

A pair $\left(X,d\right)$ will be called a symmetric generalized metric space if subset X is endowed with a symmetric generalized metric $d≔\left(d_1, d_2, \dots ,d_m\right).$

Theorem 1. 

Let $\left(X,d\right)$ be the complete symmetric generalized metric space $d≔\left(d_1, d_2, \dots ,d_m\right).$ Let $T: X$→$P_c\left(X\right)$ be a multivalued left-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric. Additionally, let $p_1, p_2, \dots , p_n$ be real positive numbers. If $A_1, A_2,\dots ,A_n\in M_{m,m}\left(R_{+}\right), A_i=\left(a_{kk}^i\right)\in M_{m,m}\left(R_{+}\right), a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\},i\in \{1,2\dots ,n\}$ are diagonal matrices convergent to zero and the following inequality takes place:

$$H_k\left(\left(1- \alpha \right)T\left(x\right) \oplus \alpha T\left(y\right), T\left(z\right)\right)\le {{\displaystyle \sum }}_{i=1}^n\frac{p_k}{p_1+p_2+\cdots +p_n}{a}_{kk}^i{d}_k\left(\left(1- \alpha \right)x \oplus \alpha y, z\right),$$

where $k\in \{1,2\dots ,m\}$ for all $x,y\in X$, then $Fix\left(T\right)\ne \varnothing$ and is compact.

Proof. 

We will use the following functional:

$$F:X\to \left[0,\infty \right),D\left(x,T\left(x\right)\right)≔in{f}_{k\in \{1,2\dots ,m\}}\{d_k\left(x,\lambda \right):\lambda \in T\left(x\right)\},$$

$$D\left(x, ·\right):P\left(X\right)\to \left[0,\infty \right)$$

and we will demonstrate that that following properties take place:

(i) 

inf F = 0;

(ii) 

$\underset{p\downarrow 0}{\lim }{\alpha }_K\left(L_p\right)=0 ;$

(iii) 

F is RGI in X.

By applying Proposition 2, we obtain the following conclusions:

(i) We use $x_0\in X$ and $x_1\in T{x}_{0 }$.

Let $q_k^i>1$ be such that

$${\beta }_k^i=q_k^i{a}_{kk}^i<1, k\in \{1,2\dots ,m\}, i\in \{1,2\dots ,n\}$$

(1)

from Proposition 2 there will be an $x_2\in T{x}_{1 }$, such that

$$d_k\left(x_1,x_2\right)\le q_k^i{H}_k\left(T(x_0),T\left(x_1\right)\right)\le q_k^i{a}_{kk}^i{d}_k\left(x_0,x_1\right).$$

Therefore, $d_k\left(x_1,x_2\right)\le {\beta }_k^i{d}_k\left(x_0,x_1\right)$.

Thus, the sequence ${\left(x_n\right)}_{n\in N^{*}}$ is obtained, with the following properties:

$$x_n\in T(x_{n-1 })$$

(2)

and

$$d_k\left(x_n,x_{n-1}\right)\le {\beta }_k^i{d}_k\left(x_{n-1},x_n\right),\mathrm{for}n\in N^{*},i\in \{1,2\dots ,n\}.$$

(3)

From (3), $F\left(x_n\right)\le {\displaystyle \sum }_{i=1}^n{d}_k\left(x_0,x_1\right){\left({\beta }_k^i\right)}^n$, which implies that inf F = 0.

(ii) Let $x_0$ be an element from $L_p$ ($D\left(x_0,T\left(x_0\right)\right)\le p$). Due to the fact that $0<{\beta }_k^i<1$, we obtain $x_1\in T\left(x_{0 }\right)$, such that $d_k\left(x_0,x_1\right)\le \frac{p}{{\beta }_k^i}$. For the sequence ${\left(x_n\right)}_{n\in N^{*}}$ we will obtain, from (3), for any $n\in N^{*}$, the following:

$$F\left(x_n\right)\le d_k\left(x_n,x_{n-1}\right)\le p{\left({\beta }_k^i\right)}^n\le p, k\in \{1,2\dots ,m\}, i\in \{1,2\dots ,n\}.$$

Thus, we obtain that $x_n\in L_p$ for all $n\ge 1$.

Due to the fact that $d_k\left(x_0,x_1\right)\le \frac{p}{{\beta }_k^i}$,

$d_k\left(x_0,x_n\right)\le d_k\left(x_0,x_1\right)+ d_k\left(x_1,x_n\right)\le \frac{p}{{\beta }_k^i}+\frac{p}{{\beta }_k^i-1}$ for all $n\ge 1, k\in \{1,2\dots ,m\},i\in \{1,2\dots ,n\},$

$d_k\left(x_n,x_{n-j}\right)\le \frac{p}{{\beta }_k^i-1}$ for all $n\ge 1$ and $j\ge 1$, $i\in \{1,2\dots ,n\},$

we obtain

$${\alpha }_K\left(L_p\right)\le diam\left(x_n\right)\le \frac{p}{{\beta }_k^i}+\frac{p}{{\beta }_k^i-1},$$

which implies that $\underset{p\downarrow 0}{\lim }{\alpha }_K\left(L_p\right)=0$.

(iii) We suppose that F is not RGI in X. Thus, there is an $x\in X$ with the following properties:

$$F\left(x\right)>0\mathrm{and}D\left(x,L_p\right)=0\mathrm{for}\mathrm{any}p>0.$$

(4)

There will be a sequence ${\left(x_n^{\prime }\right)}_{n\in N^{*}}$, such that

$$x_n^{\prime }\in L_{\frac{1}{n}}\mathrm{and}{d}_k\left(x,x_n^{\prime }\right)\le \frac{1}{n}\mathrm{for}\mathrm{all}n\ge 1, k\in \{1,2\dots ,m\}.$$

(5)

Choosing any $x^{″}\in T\left(x\right)$ and $x_n^{″}\in T\left(x_n^{\prime }\right)$, we obtain

$$d_k\left(x,x^{″}\right)\le d_k\left(x,x_n^{\prime }\right)+ d_k\left(x_n^{\prime },x_n^{″}\right)+ d_k\left(x_n^{″},x^{″}\right), k\in \{1,2\dots ,m\}.$$

Using the inequality above and the definitions of gap functional and the Pompeiu-Hausdorff functional

$$D:P\left(X\right)\times P\left(X\right)\to \left[0,\infty \right), D\left(Z,Y\right)≔inf\{d\left(x,y\right):x\in Z, y\in Y\},$$

with Z being part of X, and

$$H:P\left(X\right)\times P\left(X\right)\to \left[0,\infty \right), H\left(Z,Y\right)≔max\{su{p}_{x\in Z}in{f}_{y\in Y}d\left(x,y\right), su{p}_{y\in Y}in{f}_{x\in Z}d\left(x,y\right)\},$$

we have

$$\begin{gathered} d_k\left(x,x^{″}\right)\le \frac{1}{n}+D\left(x_n^{\prime },T(x_n^{\prime })\right)+D\left(T(x_n^{\prime }),x^{″}\right) \\ \le \frac{1}{n}+F\left(x_n^{\prime }\right)+H_k\left(T\left(x_n^{\prime }\right),T\left(x\right)\right) \\ \le \frac{2}{n}+{\displaystyle \sum }_{i=1}^n\frac{p_k}{p_{1+}{p}_2+\cdots +p_n}{a}_{kk}^i d_k\left(x_n^{\prime },x\right)+F\left(x_n^{\prime }\right), \end{gathered}$$

and

$$k\in \{1,2\dots ,m\}.$$

From the sequence (5)$, a_{kk}^i\le 1$, $i\in \{1,2\dots ,m\},$ and $x_n^{\prime }\in L_{\frac{1}{n}}$; thus, we have

$$d_k\left(x,x^{″}\right)\le \frac{1}{n}+{\displaystyle \sum }_{i=1}^n\frac{p_k}{p_1+p_2+\cdots +p_n}\frac{a_{kk}^i}{n}+\frac{1}{n}\le \frac{4}{n}.$$

Then, by applying $in{f}_{x^{″}\in Tx}$ to the last inequality, we obtain that $F\left(x\right)=0$, which is a contradiction with (4). Then, F is RGI in X. □

Similar to Theorem 1, we obtain the following corollary:

Corollary 1. 

Let $\left(X,d\right)$ be the complete symmetric generalized metric space $d≔\left(d_1, d_2, \dots ,d_m\right).$ Let $T: X$→$P_c\left(X\right)$ be a multivalued right-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric. Additionally, let $p_1, p_2, \dots , p_n$ be real positive numbers. If $A_1, A_2,\dots ,A_n\in M_{m,m}\left(R_{+}\right), A_i=\left(a_{kk}^i\right)\in M_{m,m}\left(R_{+}\right), a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\},i\in \{1,2\dots ,n\}$ are diagonal matrices convergent to zero and the following inequality takes place:

$$H_k\left(\left(1- \alpha \right)T\left(x\right) \oplus \alpha T\left(y\right), T\left(z\right)\right)\le {\displaystyle \sum }_{i=1}^n\frac{p_k}{p_1+p_2+\cdots +p_n}{d}_k\left(\left(1- \alpha \right)x \oplus \alpha y, z\right)a_{kk}^i,$$

where $k\in \{1,2\dots ,m\}$ for all $x,y\in X$, then $Fix\left(T\right)\ne \varnothing$ and is compact.

Proof. 

This proof is analogous to the one from Theorem 1. □

We will present two new strict fixed-point results for multivalued left-weighted mean contraction in the generalized sense of Nadler and for multivalued right-weighted mean contraction in the generalized sense of Nadler.

Let $p_1, p_2, \dots , p_n$ be real positive numbers.

Let $A_1, A_2,\dots ,A_n\in M_{m,m}\left(R_{+}\right), A_i=\left(a_{kk}^i\right)\in M_{m,m}\left(R_{+}\right), a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\},i\in \{1,2\dots ,n\}$ be diagonal matrices convergent to zero.

Theorem 2. 

Let $\left(X,d\right)$ be the complete symmetric generalized metric space $d≔\left(d_1, d_2, \dots ,d_m\right).$ Let $T: X$→$P_{cl}\left(X\right)$ be a multivalued left-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric. Supposing that S$Fix\left(T\right)\ne \varnothing$, we obtain that S$Fix\left(T\right)=Fix\left(T\right)=\{x^{*}\}$.

Proof. 

Supposing that $x^{*}\in SFix\left(T\right)$, we obtain $T\left(x^{*}\right)=\{x^{*}\}$. We will demonstrate that $Fix\left(T\right)$ is included in $SFix\left(T\right)$. Thus, if $y\in Fix\left(T\right)$, then, by the contradiction condition, we obtain that

$$\begin{gathered} d\left(y,x^{*}\right)\le \frac{p_1}{p_1+p_2+\cdots +p_n}{A}_{1}d\left(y,x^{*}\right)+\frac{p_2}{p_1+p_2+\cdots +p_n}{A}_{2}d\left(y,x^{*}\right)+\cdots \\ +\frac{p_n}{p_1+p_2+\cdots +p_n}{A}_{n}d\left(y,x^{*}\right). \end{gathered}$$

Therefore,

$$\begin{gathered} \frac{p_1}{p_1+p_2+\cdots +p_n}(I-A_s)d\left(y,x^{*}\right)\le \frac{p_1}{p_1+p_2+\cdots +p_n}(I-A_1)d\left(y,x^{*}\right)+ \\ \frac{p_2}{p_1+p_2+\cdots +p_n}(I-A_2)d\left(y,x^{*}\right)+\cdots +\frac{p_n}{p_1+p_2+\cdots +p_n}(I-A_n)d\left(y,x^{*}\right)\le 0, \\ s\in \{1,2,\dots ,n\} \end{gathered}$$

and, by multiplying with ${(I-A_s)}^{-1}$, we get $d\left(y,x^{*}\right)\le 0$. Hence, $d\left(y,x^{*}\right)=0$. □

Corollary 2. 

Let $\left(X,d\right)$ be the complete symmetric generalized metric space $d≔\left(d_1, d_2, \dots ,d_m\right).$ Let $T: X$→$P_{cl}\left(X\right)$ be a multivalued right-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric. Supposing that S$Fix\left(T\right)\ne \varnothing$, we obtain that S$Fix\left(T\right)=Fix\left(T\right)=\{x^{*}\}$.

Proof. 

This proof is analogous to the one from Theorem 2. □

3. Applications to the Inclusion Systems

Many problems in fields such as biology, physics, chemistry, or engineering are mathematically modeled through bidimensional or multidimensional equation systems, with differential or integral inclusions, respectively [26]. These equation systems, and their respective inclusion systems, can be studied as operatorial equations or operatorial inclusions in generalized metric spaces. In order to obtain solutions, useful tools can be found within the fixed point theory.

Let $p_1, p_2,\dots ,p_m$ be the positive real numbers.

Corollary 3. 

Let $\left(X,| |\right)$ be a complete symmetric generalized metric space, and let $T_i:X\to P_{b,cl}\left(X\right)$ for $i\in \{1,2\dots ,m\}$ be a multivalued left-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric $d≔\left(d_1, d_2, \dots ,d_m\right).$

We suppose there exists $0\le a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\}$, such that for each $u≔\left(u_1, u_2, \dots ,u_m\right)$, $v≔\left(v_1, v_2, \dots ,v_m\right)$ $\in X^m$ and each $y_k\in T_k\left(u_1, u_2, \dots ,u_m\right)$, $k\in \{1,2\dots ,m\}$ there exists $z_k\in T_k\left(v_1, v_2, \dots ,v_m\right)$, such that

$$\left|y_k-z_k\right|\le a_{kk}^i\left|u_k-v_k\right|,k\in \{1,2\dots ,m\},i\in \{1,2\dots ,m\}.$$

Then, the inclusion system

$$\{\begin{array}{c}{u}_1\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^1{T}_k\left(u_1,u_2,\dots ,u_m\right)\\ u_2\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^2{T}_k\left(u_1,u_2,\dots ,u_m\right)\\ u_m\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^m{T}_k\left(u_1,u_2,\dots ,u_m\right)\end{array}$$

has at least one solution in $X^m$.

Proof. 

Consider the multivalued operator $T:X^m\to P\left(X^m\right)$ given by $T≔\left(T_1, T_2, \dots ,T_m\right)$. Then, the conditions from the theorem can be represented in the following form: for each $u,v\in X^m$ and each $y\in T\left(u\right)$, there exists z$\in T\left(v\right)$, such that

$$||y-z||\le {\displaystyle \sum }_{i=1}^m\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{A}_i||u-v||,$$

where $A_i=\left(a_{kk}^i\right)$ are diagonal matrices convergent to zero for each $i\in \{1,2\dots ,m\}$.

Hence, Theorem 1 applies with $d\left(u,v\right)≔||u-v||$ and implies that T has at least one fixed point: $u\in T\left(u\right)$. □

Corollary 4. 

Let $\left(X,| |\right)$ be a complete symmetric generalized metric space, and let $T_i:X\to P_{b,cl}\left(X\right)$ for $i\in \{1,2\dots ,m\}$ be a multivalued right-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric $d≔\left(d_1, d_2, \dots ,d_m\right).$

We suppose there exists $0\le a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\},$ such that for each $u≔\left(u_1, u_2, \dots ,u_m\right)$, $v≔\left(v_1, v_2, \dots ,v_m\right)$ $\in X^m$ and each $y_k\in T_k\left(u_1, u_2, \dots ,u_m\right)$, $k\in \{1,2\dots ,m\}$ there exists $z_k\in T_k\left(v_1, v_2, \dots ,v_m\right)$, such that

$$\left|y_k-z_k\right|\le a_{kk}^i\left|u_k-v_k\right|,k\in \{1,2\dots ,m\},i\in \{1,2\dots ,m\}.$$

Then, the inclusion system

$$\{\begin{array}{c}{u}_1\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{T}_k\left(u_1,u_2,\dots ,u_m\right)a_{kk}^1\\ u_2\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{T}_k\left(u_1,u_2,\dots ,u_m\right)a_{kk}^2\\ u_m\in {\displaystyle {\displaystyle \sum }_{k=1}^m}\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{T}_k\left(u_1,u_2,\dots ,u_m\right)a_{kk}^m\end{array}$$

has at least one solution in $X^m$.

Proof. 

The proof is analogous to the proof from Corollary 3. Hence, Corollary 1 applied to $d\left(u,v\right)≔||u-v||$ implies that T has at least one fixed point: $u\in T\left(u\right)$. □

These results can be applied in biology, in the mathematical modeling of interacting populations, such as prey–predator populations [27].

Example 1. 

(real-life example)

We will refer to the mountain river from the valley of the village Sebeşul de Sus (in German, Ober-Schewesch) from Sibiu County, Romania (Figure 1 and Figure 2).

In this river can be found multiple species of animals, such as frogs, European bullheads, and trout (Figure 3).

Starting from this situation, we imagine a predator–prey-type problem for these three species. The volume of the frog population would increase in a logistic equation in the absence of European bullheads. The European bullheads eat frogs, and the trout eat European bullheads. We model these assumptions with the following equations:

$$\{\begin{array}{c}x\in -\frac{dx}{dt}+xy=T_1\left(x,y,z\right)\hfill \\ y\in -\frac{dy}{dt}+3yz-xy=T_2\left(x,y,z\right)\hfill \\ z \in -\frac{dz}{dt}+2z-z^2-yz=T_3\left(x,y,z\right)\hfill \end{array},$$

(6)

where $x=x\left(t\right)$ represents the trout population, $y=y\left(t\right)$ represents the European bullhead population, $z=z\left(t\right)$ represents the frog population, and $t\in \left[0,\infty \right)$ denotes the time. The workspace X is a three-dimensional geometric space, and the distance is Euclidean. Obviously, the derivatives $\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}$ can also be replaced by their approximations, which can be calculated with numerical methods formulas.

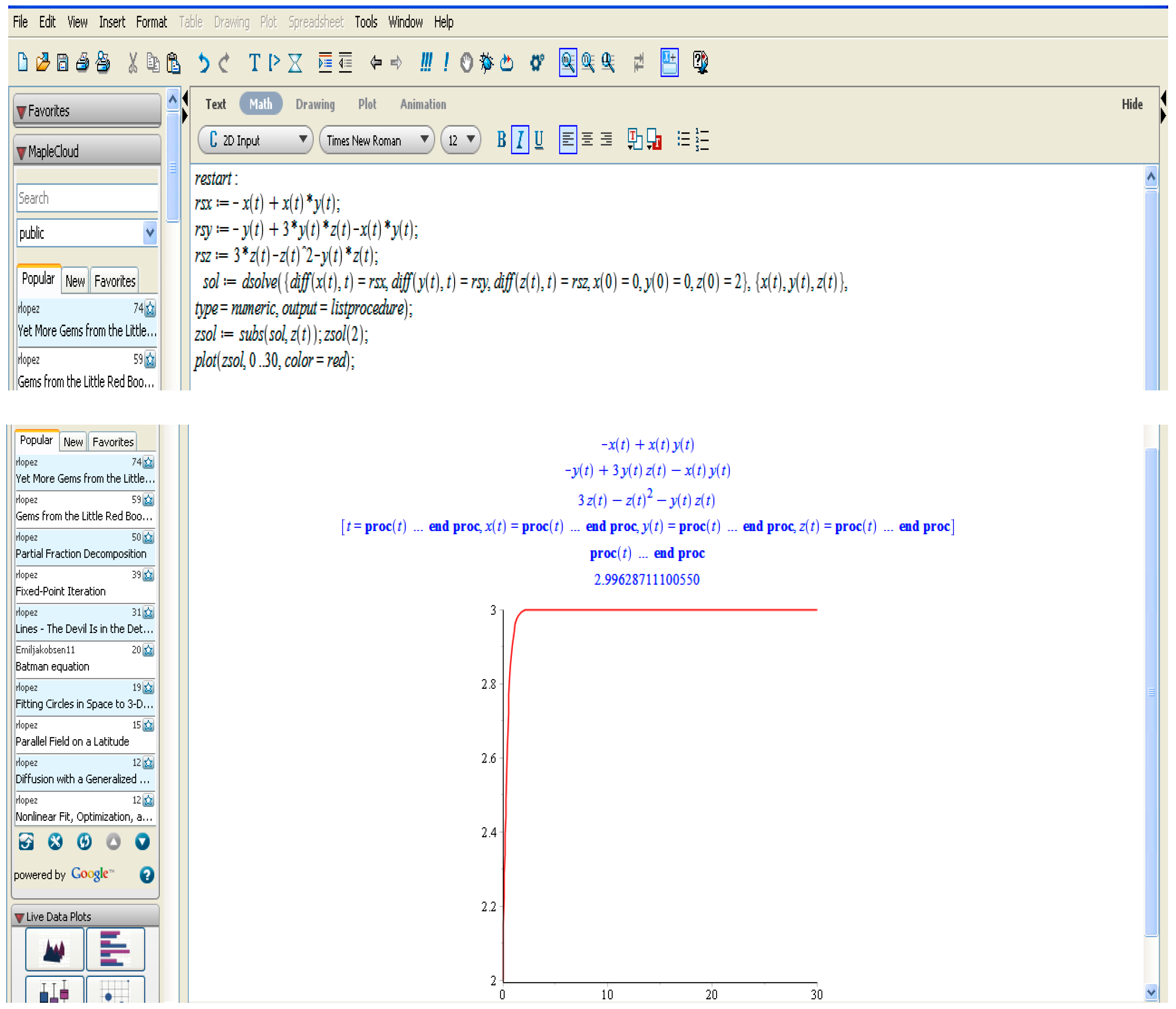
In this case, we can determine the equilibrium state for frogs in the absence of European bullheads and trout, as well as the equilibrium state of the European bullhead population and frog population in the absence or presence of the trout. Moreover, we can verify if the presence of trout brings any benefits to the frog population. Using Maple software, this study can be done as follows:

• restart:
• rsx:=- x(t)+x(t)*y(t);
• rsy:=- y(t)+3*y(t)*z(t)-x(t)*y(t);
• rsz:= 3*z(t)-z(t)ˆ2-y(t)*z(t);

For frogs (Figure 4):

• sol:=dsolve({diff(x(t),t)=rsx,diff(y(t),t)=rsy,diff(z(t),t)=rsz,x(0)=0,y(0)=0,z(0)=2},{x(t),y(t),z(t)},
• type=numeric,output=listprocedure);
• zsol:=subs(sol,z(t)); zsol(2);
• plot(zsol,0..30,color=red);

For frogs and European bullheads (Figure 5):

• sol:=dsolve({diff(x(t),t)=rsx,diff(y(t),t)=rsy,diff(z(t),t)=rsz,x(0)=0,y(0)=1,z(0)=2},{x(t),y(t),z(t)},
• type=numeric,output=listprocedure);
• ysol:=subs(sol,y(t));zsol:=subs(sol,z(t));
• plot([ysol,zsol],0..30,color=[red,blue]);

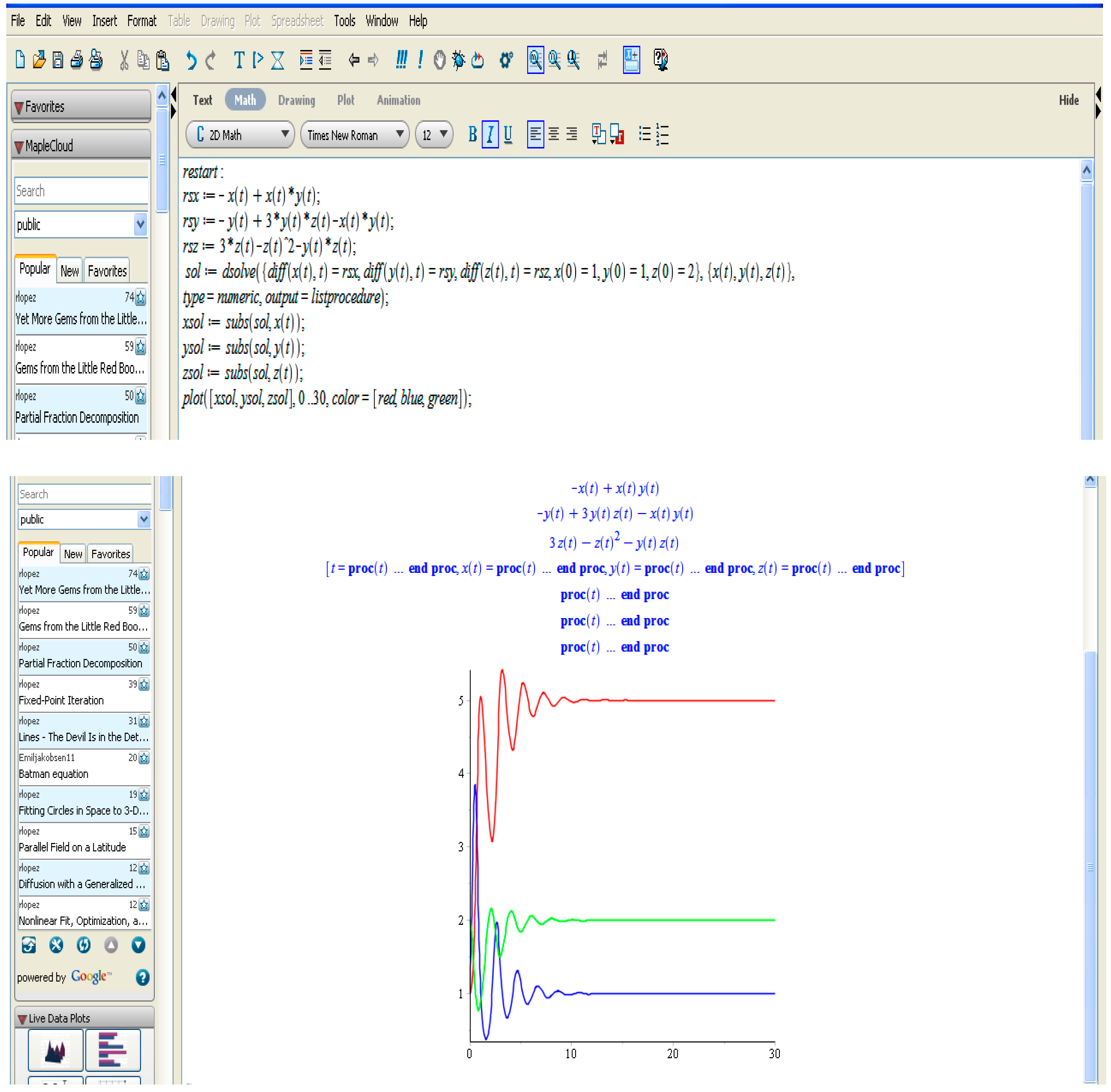
For frogs, European bullheads, and trout (Figure 6):

• sol:=dsolve({diff(x(t),t)=rsx,diff(y(t),t)=rsy,diff(z(t),t)=rsz,x(0)=1,y(0)=1,z(0)=2},{x(t),y(t),z(t)},
• type=numeric,output=listprocedure);
• xsol:=subs(sol,x(t));
• ysol:=subs(sol,y(t));
• zsol:=subs(sol,z(t));
• plot([xsol,ysol,zsol],0..30,color=[red,blue,green]);

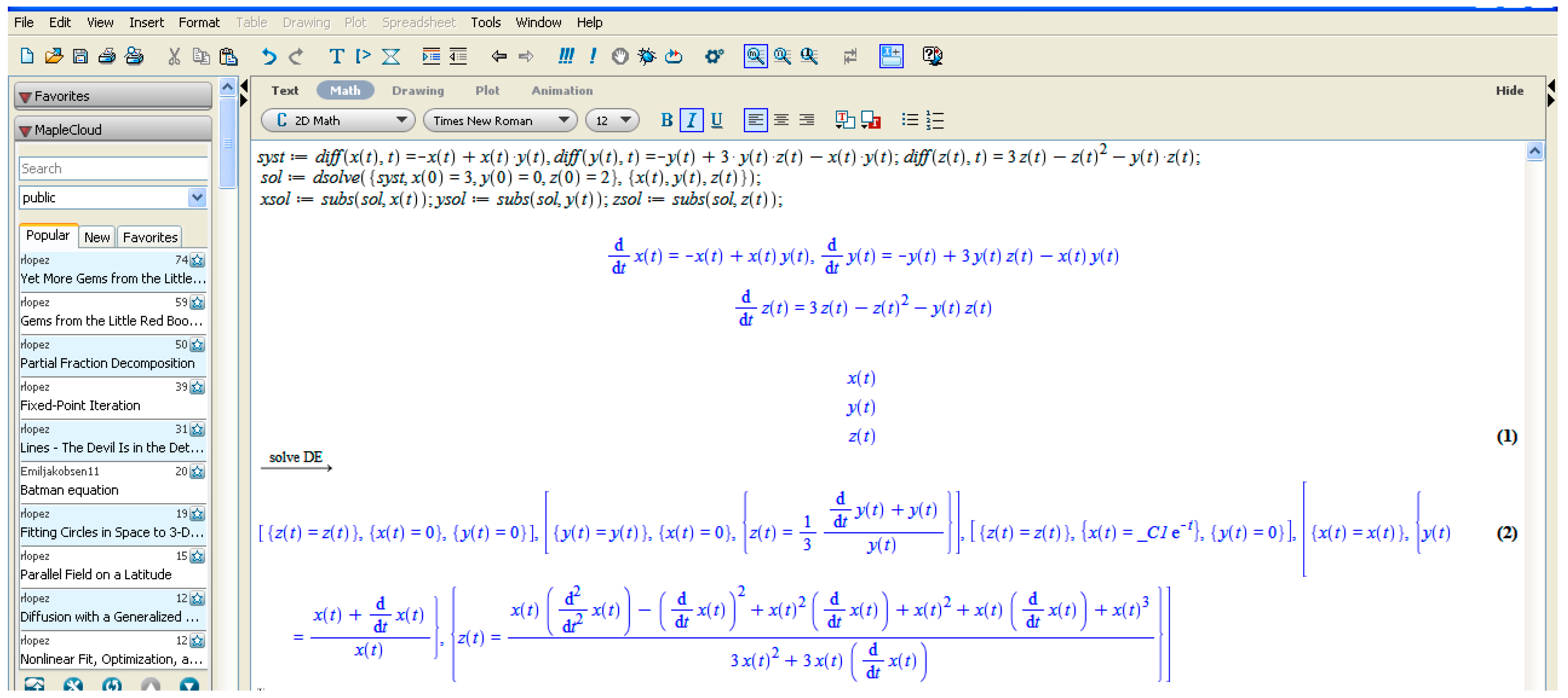
Maple software offers the formula for the system’s solutions (Figure 7).

Thus, the volume of the frog population z(t) is influenced by the volume of the trout population, shown by their relationship in the following form:

$$z\left(t\right)=\frac{1}{3x{\left(t\right)}^2+3x\left(t\right)\frac{dx}{dt}}\left[x\left(t\right)\frac{d^{2}x}{d{t}^2}-{\left(\frac{dx}{dt}\right)}^2+x{\left(t\right)}^2\frac{dx}{dt}+x{\left(t\right)}^2+x\left(t\right)\frac{dx}{dt}+x{\left(t\right)}^3\right]$$

(7)

Particular Case of Corollary 3. 

Let $I= \left[0,\alpha \right]$ be an interval of the set of real numbers and $X=C\left(\left[0,\alpha \right]\right).$ Let $T_i:X\to P_{b,cl}\left(X\right)$ for $i\in \{1,2\dots ,m\}$ be a multivalued left-weighted mean contraction in the generalized sense of Nadler in relation to a symmetric and convex metric $d≔\left(d_1, d_2, \dots ,d_m\right).$

We suppose there exists $0\le a_{kk}^i\le 1$, $k\in \{1,2\dots ,m\}$, such that for each $u\left(t\right)≔\left(u_1\left(t\right), u_2\left(t\right), \dots ,u_m\left(t\right)\right)$, $v≔\left(v_1\left(t\right), v_2\left(t\right), \dots ,v_m\left(t\right)\right)$ $\in X^m$ and each $y_k\in T_k\left(u_1, u_2, \dots ,u_m\right)$, $k\in \{1,2\dots ,m\}$ there exists $z_k\in T_k\left(v_1, v_2, \dots ,v_m\right)$, such that

$$\left|y_k-z_k\right|\le a_{kk}^i\left|u_k-v_k\right|,k\in \{1,2\dots ,m\},i\in \{1,2\dots ,m\}.$$

Then, the inclusion system

$$\{\begin{array}{c}{u}_1\left(t\right)\in {{\displaystyle \sum }}_{k=1}^m\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^1{{\displaystyle \int }}_0^t{F}_k\left(u_1\left(t\right), u_2\left(t\right),\dots , u_n\left(t\right)\right)\\ u_2\left(t\right)\in {{\displaystyle \sum }}_{k=1}^m\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^2{{\displaystyle \int }}_0^t{F}_k\left(u_1\left(t\right), u_2\left(t\right),\dots , u_n\left(t\right)\right)\\ u_m\left(t\right)\in {{\displaystyle \sum }}_{k=1}^m\frac{p_k}{p_{1+}{p}_2+\cdots +p_m}{a}_{kk}^m{{\displaystyle \int }}_0^t{F}_k\left(u_1\left(t\right), u_2\left(t\right),\dots , u_n\left(t\right)\right)\end{array},$$

(8)

where each $F_k:I\times X^m\to X$, $k\in \{1,2\dots ,m\}$ is a multivalued operator, which is bounded measurable and integrable, has at least one solution in $X^m$.

4. Conclusions

Over the years, it has been known that many researchers have written about fixed-point theorems for multivalued left and right contractions in the sense of Nadler, such as Rus (2008) [28]; Nadler (1969) [5]; Mureşan (2002) [24]; Bucur (2019) [14]; Bucur, Guran, and Petruşel (2009) [15]; and Joshi, L.K. and Dimri (2007) [23]. In this paper, we defined two new concepts: the concept of multivalued left-weighted mean contractions in the generalized sense of Nadler in a symmetric generalized metric space and the concept of multivalued right-weighted mean contractions in the generalized sense of Nadler in a symmetric generalized metric space, and demonstrated some fixed point theorems for them. The methods used relied on the properties of the regular-global-inf function and of the symmetric generalized metric spaces. The theorems from this paper can also be used to solve some particular cases of inclusion systems, which are known to be used in the mathematical modeling of some problems, processes, or activities from everyday life, such as the ones from the fields of biology, mathematics, etc. The example presented for applying the results of this article in real life referred to a prey–predator-type problem for three populations that can be found in a river mountain from the valley of a village from Romania. The three species discussed were frogs, European bullheads, and trout. It was found that the presence of the trout influences the presence of the frogs, benefiting their increase in volume and in finding an equilibrium solution for the three interacting species. Mathematical modeling shows that there is an equilibrium solution and indicates the relationships of influence between the volumes of the three types of species. In future research papers, the author plans to find new applications of the theorems from this paper for integro-differential systems.