Abstract
The optimization of the pulsed laser deposition process was attempted here for the generation of hydroxyapatite thin films. The deposition process was monitored with an ICCD (Intensified Coupled Charged Device) fast gated camera and a high-resolution spectrometer. The global dynamics of the laser produced plasma showed a self-structuring into three components with different composition and kinetics. The optical emission spectroscopy revealed the formation of a stoichiometric plasma and proved that the segregation in the kinetic energy of the plasma structure is also reflected by the individual energies of the ejected particles. Atomic Force Microscopy was also implemented to investigate the properties and the quality of the deposited film. The presence of micrometric clusters was seen at a high laser fluence deposition with in-situ ICCD imaging. We developed a fractal model based on Schrödinger type functionalities. The model can cover the distribution of the excited states in the laser produced plasma. Moreover, we proved that SL(2R) invariance can facilitate plasma substructures synchronization through a self-modulation in amplitude.
1. Introduction
In the past few years, hydroxyapatite has drawn significant interest in the research community as well as the medical community for use in synthetic bones substitutes. Although hydroxyapatite (HA) is already used as part of fillers for treating various bone defects, their application can be restricted due to brittle fracturing of ceramic components [1]. Alternatively, due to their better physico-chemical, mechanical, and biological properties, titanium alloy or even titanium are widely used for load bearing applications such as bone plates, screws, and artificial joints. In literature there are reported implementations of a vast range of deposition techniques with the aim to obtain high quality hydroxyapatite coatings [2,3]. The stand out technique which gave the most promising results was proven to be Pulsed Laser Deposition (PLD) [3]. PLD is a multivariable technique which can offer the possibility of tailoring the composition, structure, and properties of the generated film simply by adjusting some of its control parameters (laser pulse geometry, laser fluence, wavelength or repetition frequency, target-substrate distance, substrate temperature, deposition time, etc.) [4]. The PLD technique has been advanced as an alternative to other more established and classical methods, and has an added advantage of enabling complete stoichiometric transfer from the target to the substrate. PLD technique also possesses the ability to form desired film thickness, morphology, and composition by varying the deposition parameters. This method moreover offers a wide range of possibilities in terms of the nature of the irradiated targets and physio-chemical and biological properties single substrates for functional coatings. Some of the most outstanding results of hydroxyapatite (HA) coatings were reported for HA coated Ti, which reduced the fixation period to 3–6 months [3]. Although the advantages of PLD technique are well known, the tailoring of the technique can be time and resource consuming. An alternative approach is envisioned to understand the fundamental kinetics of the ejected particles and their influence over the properties of the thin films. This approach is based on implementation of in situ plasma characterization techniques. The diagnostics techniques have a proven record of showcasing various aspects of the laser produced plasmas with direct implications for pulsed laser deposition technology [5].
In this paper, we report the in-situ investigations of a transient plasma generated on a hydroxyapatite target during the pulsed laser deposition process. ICCD (Intensified Coupled Charged Device) fast camera imaging and optical emission spectroscopy are implemented to showcase different facets of the phenomena. The thin film deposited is investigated by using surface analysis techniques and reveals the best deposition conditions. A fractal model is developed based on Schrodinger type functionalities that can attest to various dynamics seen in HA laser produced plasma.
2. Experimental Set-Up
The experiments were performed using the installation presented in detail in reference [5]. Briefly, plasma was generated by irradiation of the hydroxyapatite target with a pulse generated by an Nd:YAG (10 ns, 10 Hz, 532 nm) laser, with an energy per pulse of 80 mJ and 40 mJ. The target used was a disk-shaped (1 cm in diameter) HA sample and was placed on an XYZ precision displacement system and constantly shifted during irradiation to provide new surfaces for each irradiation occurrence. All the experiments were performed at a background pressure of 10−2 Torr.
The samples of HA deposited by using PLD with thicknesses of 500 nm (P1) and 1000 nm (P2) were analyzed by using atomic force microscopy. The results were obtained on Park NX10 equipment. Two flexion scanning systems for XY and Z axes, respectively, were used that were independent for the sample and for the tip of the probe. These systems involved horizontal and orthogonal XY scanning with a reduced residual arc, movement outside the plane with less than 1 nm over the entire scan range, and the Z linearity deviation of the scanner being less than 0.015% over a full scan range. During the analysis of the surface morphology, experiments were performed using the Pin On module to determine the mechanical properties of the layers. The experiments were performed on the following equipment: Scanning Electron Microscopy (SEM) and Atomic Force Microscopy (AFM) for the analysis of the surface of the thin layers and Energy Dispersive X-Ray Spectroscopy (EDS) for chemical determinations. AFM analyses on EasyScan 2 equipment used a non-contact cantilever. Scans were performed on 12 and 50 µm squares, and the results were obtained in the forms of 2D and 3D, while surface roughness parameters were also provided. The images show a smooth surface with a roughness with nanometric values (around 1 nm), which in some areas show larger particles of material (these are in the order of micrometers according to SEM analyses).
3. Fast ICCD Camera Measurements
To track the global evolutions of the transient plasmas produced by laser ablation on the hydroxyapatite target, the technique of ICCD fast camera imaging was implemented. The role of these investigations was to determine the structure, to study the dynamic collective behavior of the ejected particles, and to understand the effect of the target on the global dynamics of the laser produced plasmas. Figure 1 shows snapshots of the laser produced plasma on a hydroxyapatite target recorded at various moments in time with respect to the laser-target impact moment. It can be observed that, during expansion, the plasma increases its volume and the position of the area with high emissivity (estimated as the center of mass) moves towards higher distances. In this work, the investigations were performed at low pressure and thus according to reference [6], this displacement was defined by a linear function, which translates as an expansion with a constant velocity. The slope of this linear representation defines the global expansion velocity of the plasma. With the increase of the background gas pressure there are reports [7] that show significant changes in the plasma dynamics: increased optical emission coupled with a confinement in the target region with an overall kinetic behavior being described in this case by a “drag” type function [8].

Figure 1.
ICCD fast gated camera snapshots of laser produced plasmas on hydroxyapatite samples (gate width10 ns exposure and a laser fluence of 5 J/cm).
Figure 2 shows an image of the ablation plasma recorded after 350 ns from the interaction of the laser pulse radiation with the target and a cross section on the main expansion axis (where the separation in three structures is highlighted) and on a series of three axes parallel to the target surface (where the symmetry of the plasma with respect to the transverse axis is highlighted). The important feature highlighted by these images is the presence of a plasma separation process in three structures: the first structure (fast structure), the second structure (slow structure), and the existence of a third structure defined by small volume, high emission intensity, and low expansion velocity. The latter structure is usually known in the literature to describe the excitation of heavier and more complex objects ejected from the target such as clusters, molecules, or nanoparticles. This phenomenon was also observed for metals [9] or graphite [10] plasmas and was found numerically in a hydrodynamic fractal model [11]. Various reports from literature show that the observed structures move at constant speeds of the order of 104 m/s for the first structure, 103 m/s for the second structure, and hundreds of m/s for the thirds structure. Here, the experimental results show a good agreement between the obtained values and other reported in the literature [5,6,7,8,9,10]. The generated plasma is characterized by a global expansion speed of 4.5 km/s for the slow structure, 17 km/s for the fast structure, 300 m/s for the cluster structure.
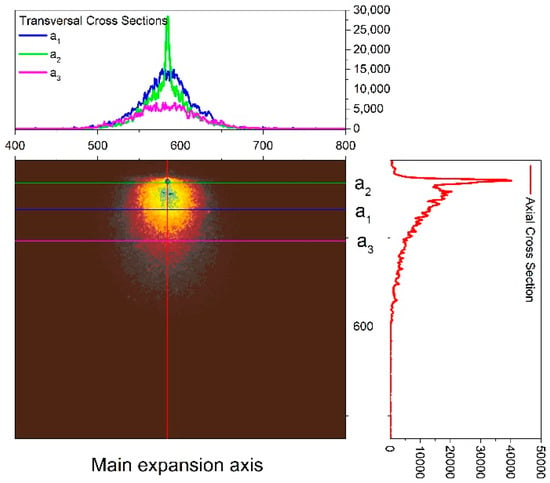
Figure 2.
The image of a hydroxyapatite plasma recorded with the fast-gated camera after 300 ns and the corresponding cross sections.
Let us note that although the exact values are in line with others reported in the literature, it is worth underlining that these values need to be understood on a case to case scenario because the expansion velocities values strongly depend on the experimental conditions, nature of the material, and laser properties. Our group recently shown some dependencies between the expansion velocity and the atomic mass [9]. We also reported on the particle energy distribution in laser produced plasmas on complex targets [6,7] and on the heterogenic energy distribution in ablation plasmas.
The general assumption over the separation of laser produced plasmas into multiple components is that it comes as an effect of the interactions between the plasma particles and those of the background gas [10]. However, given the high vacuum conditions in which our experiments were performed, the plasma separation process may be related to the different ejection mechanisms that are seen in the case on nanosecond laser ablation. Thus, the fast structure is due to the presence of electrostatic mechanisms, such as the Coulomb explosion [9], while the slow structure is due to the presence of thermal mechanisms (such as phase explosions [12]). The results also show the presence of a third component of the plasma (identified in Figure 2 through zone 1). This is present in the vicinity of the target and has expansion speeds of 300 m/s. Figure 2 shows that the structure has a small angular distribution, compared to the classical structures, and is defined by a strong emission. These properties are characteristic, according to the results of the specific literature [13,14], and involve the dynamics of nanoparticle clusters or molecules that can be found in plasma in the Knudsen layer region.
4. Optical Emission Spectroscopy
The recording of the global emission by fast photography only gives a preliminary image of the dynamics of the plasma, and is not able to highlight the individual contributions of each species present in the plasma. For the purpose of separating these contributions, a temporal and spatially resolved spectral study was performed using the optical emission spectroscopy technique. In order to have an overview of the species present in the plasma, a global spectrum was recorded (using a relatively high integration time of ~1 µs). The results are shown in Figure 3. Based on the recorded spectra, the nature of the species present in the plasma can be identified using the authorized databases [15]. In the spectra, we have identified characteristic lines for the atoms and ions of the Ca species. The abundance of lines per each species is not stoichiometric, with the main lines corresponding to the Ca species. This is due to the difference in mass between Ca, O, and P, coupled with strong differences in collision frequency and discrepancies in the energetic levels of each ablated species [13]. This type of experiment manages to highlight very well the complex nature of hydroxyapatite, as shown in Figure 3. In this figure, it can be observed that the global emission spectrum has predominantly characteristic lines Ca, for which we have found correspondences for both atoms and ions.
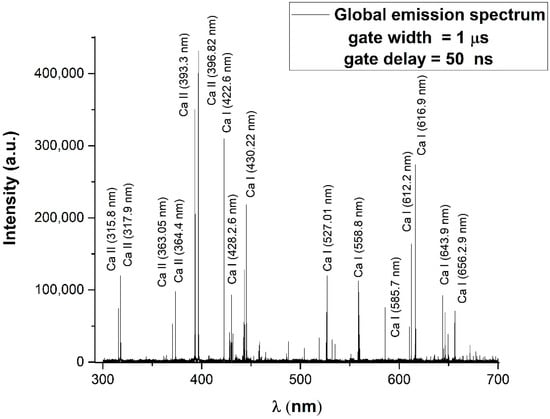
Figure 3.
Global emission spectrum, acquired with a gate width of 1 μs at 50 ns across the main expansion axis.
To determine the excitation temperature of the species present in the plasma, we used the Boltzmann method [11,13]. In Figure 4 it can be seen that the representations for atoms and ions are described by linear decreases over a wide range of energies, which can be attributed to the energetic levels excited in the plasma. The presence of this type of dependence indicates the existence of a local thermodynamic equilibrium. Moreover, we opted to represent the ionic and atomic species separately in order to observe any heterogeneity in the energy of the ejected species. By analyzing the optical emission spectra and implementing the aforementioned Boltzmann plot method, we determined the excitation temperatures for Ca I (~0.3 eV), Ca II (~1.58 eV). Recent studies published by our group relating to laser ablation of metals show an inverse proportionality relationship between the global values of the excitation temperatures and the atomic mass of the elements [9]. Of course, one can comment on the validity of the global value of the excitation temperature in the context of the fast variation of plasma parameters. In literature [6,7,10] it was reported that the space time evolution of the temperature is defined by an increase for small distance and short evolution times followed by a decrease of the excitation temperatures specific to atoms and ions as the plasma expands. This behavior faithfully follows the global emission distribution of plasmas. An important aspect highlighted by our study is the differences found between the excitation temperatures of the atoms and ions in the same plasma. This result can be regarded as an effect of the differential heating by the ns laser pulse.
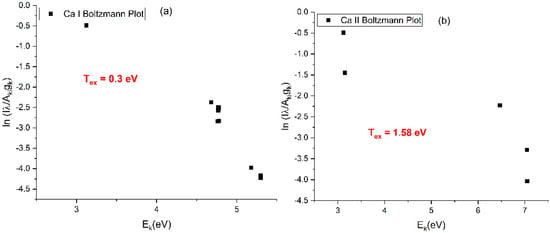
Figure 4.
Boltzmann representation for Ca atoms (a) and ions (b) in HA-plasma. (where λ is the transition wavelength, Aki is he Einstein coefficient of the k-i transition, gk the statistical weight of the upper level).
In order to be able to differentiate between the individual contributions of each species, the space-time evolution of the emission lines characteristic to the plasma atoms and ions was followed. The results of these studies are shown in Figure 5, where the characteristic signals are shown for Ca I (396.15 nm) and Ca II (546 nm). The first emission spectral lines detected after the laser pulse are those of the ions (sign of a high expansion velocity). These are followed by the lines corresponding to the atoms. Such an analysis allows the investigation and separation of the dynamics of the ejected particles after determining their expansion velocity.
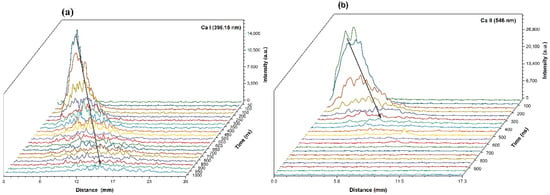
Figure 5.
The comparative spatial-temporal evolution of the emission lines corresponding to Ca I atoms (396.15 nm)—(a) and Ca II ions (546 nm)—(b).
At the same time, we can see that the spatial profiles are structured into two main groups: a fast one, represented by the spectral lines of the ions, and a slower one, due mainly to the contribution of the neutrals. Such behavior may be related to the temporal evolution of the plasma recorded by fast photography with the ICCD camera. The velocity analysis of these groups confirms that the first structure observed by fast photography consists mainly of ionic species, while the second structure consists of neutral atoms.
In order to determine the expansion velocity of the individual species and then to compare with the global speeds presented above, the spatial evolutions of the intensities of the respective species were represented at different time points (Figure 6). It is observed that the emission maximum undergoes a displacement to greater distances with the evolution of the plasma. By representing this spatial-temporal variation and fitting with a linear function (Figure 6b), the expansion velocities of atoms (Ca I—8.7 km/s) and ions (Ca II—16.3 km/s) were determined. The evolution of plasma species velocities highlights a link between the degree of ionization and the expansion velocity. This dependence specifies the influence of the fundamental particle ejection mechanisms. In general, atomic species are removed by thermal mechanisms that impose an inverse proportional time link between the velocity and the square root of the atomic mass. Plasma ions do not have the same type of dependence, most of them being removed by electrostatic mechanisms, which can account for the difference in expansion velocity between the two species.
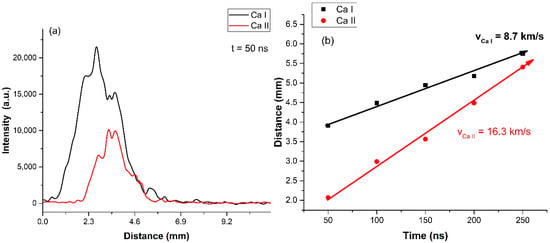
Figure 6.
The comparative spatial distribution of Ca atoms and ions recorded after 50 ns (a) and the dependence of the maximum emission in space-time for the two species (b).
The heterogeneity of the ablated ions and atoms could seen from an energetic perspective, with significant kinetic and thermal energies recorded for the Ca atoms and ions coupled with the structuring in three plasma structure with distinct inner composition. All these factors would effectively affect both the quality and the stoichiometry of the HA film. In the following section (Section 5 and Section 6), we tested this statement by employing surface analysis techniques to characterize the films generated in the conditions discussed in the Section 3 and Section 4.
5. Surface Investigations of Hydroxyapatite Thin Films
Figure 7 shows the results obtained by scanning the surfaces of the two samples: P1 (500 nm) and P2 (1000 nm). Sample P1 was obtained by depositing with a fluency of 2.5 J/cm2, and sample P2 with a fluency of 5 J/cm2, for 10 min. 2D micrographs were made on a surface of 50 × 50 µm2, see Figure 7a for sample P1 and Figure 7c for sample P2. In both scans, a fine surface of the realized layer is observed in a zone covered by droplets of material, with a higher density of drops in the case of sample P2.
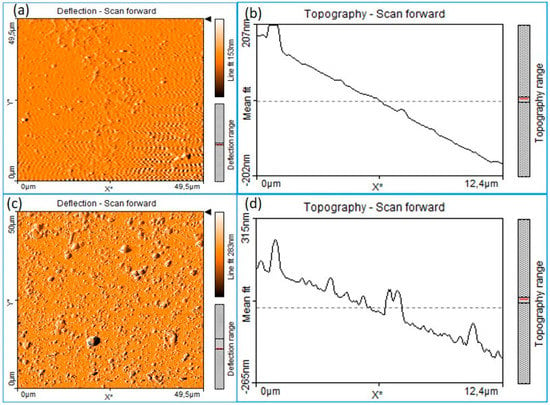
Figure 7.
AFM images of HA thin layers deposited by PLD (a,b) for the sample surface P1 and (c,d) for the sample surface P2.
The 2D images (Figure 7b,d) show the state of the surface of the thin layer and the distribution of the larger particles of distant material on the surface of the thin layer. From what is observed, sample P2 shows more droplets of material on the surface with larger dimensions and a higher roughness (and a value of 30 nm) [16]. These finding are in line with the ICCD fast camera imaging results, where we noticed the presence of a third plasma structure containing clusters and nanoparticles. Even after reducing the fluence, we still noticed a small density of clusters on the films, meaning that the lower density of the sample induces naturally clusters in the laser produced plasmas.
SEM analyses (Figure 8) were performed by using SEM VegaTescan LMH II equipment, as well as a secondary electron (SE) detector and a 30-kV electron cannon supply voltage. The thin films were analyzed in high vacuum using a layered support on carbon-band glass support. In the images, the formation of a layer with a good structural homogeneity and with the appearance of larger particles of material can be observed [17].

Figure 8.
SEM images of the surface of surface layers of HA deposited by PLD for sample P1 (a) and for sample P2 (b).
For sample P2, the droplets of material, generally round in shape, show dimensions from 100 nm to 3 µm. On an area of 200 µm2, an average number of 35 particles, of which only one had a diameter greater than 2 µm, was identified. On sample P1, there were much less particles on the homogeneous surface of the layer, with dimensions also between 100 nm and 2 µm.
EDS analyses were performed on Bruker equipment using the Element List analysis mode. The analysis mainly followed the evolution of the Ca: P ratio obtained on the thin layer compared to the HA target used in the ablation process, with the value of 1.67 [3]. The elements identified on the HA layers, were O, Ca, and P. Table 1 shows the results of the chemical analysis on the two thin films of HA obtained by laser ablation. The results were obtained by mediating 10 chemical compositions taken from 10 different surfaces. Due to the very small dimensions of the layers obtained (<1 µm), the main element obtained is the oxygen that is also part of the target compound HA. The ratios obtained between Ca and P are very good compared to the ratio between them in the HA target. We can thus say that, for a bio-compatible material such as HA, the stoichiometric transfer takes place at low fluences (<2.5 J/cm2), a result confirmed by similar values found in the literature [18]. For high fluency, as mentioned above, the layer has high roughness and has nano- and micro-metric structures. In the case of the higher fluency, a deviation from the target stoichiometry is observed. Based on this in order to obtain stoichiometric transfer on the deposition of thin layers of HA through laser ablation, it is desirable to use a relatively small fluence.

Table 1.
Composition of the component elements of the HA thin layers obtained by laser ablation, for P1 and P2.
6. Mechanical Properties of Thin Layers
6.1. Analysis of the 500 nm HA Layer (P1)
Analysis of the morphology of the deposited layer showed that it is composed of a basic homogeneous layer, but also has some larger formations of materials such as hydroxyapatite (which helps to anchor the layer in contact with the biological material). The formations have heights of up to 100 nm and the deposited layer has surface fluctuations of up to 20 nm.
The mechanical properties (adhesion [nN], deformability [nm], and modulus of elasticity [GPa]) are shown in Figure 9 on the selected surface. The homogeneity of the distribution of adhesion and of the modulus of elasticity shows that a layer with good properties and characteristics close to those of the massive material was obtained. Hydroxyapatite is a ceramic material whose plasticity is recognized [16,19], but in the form of a thin layer, it can borrow from the characteristics of the substrate.
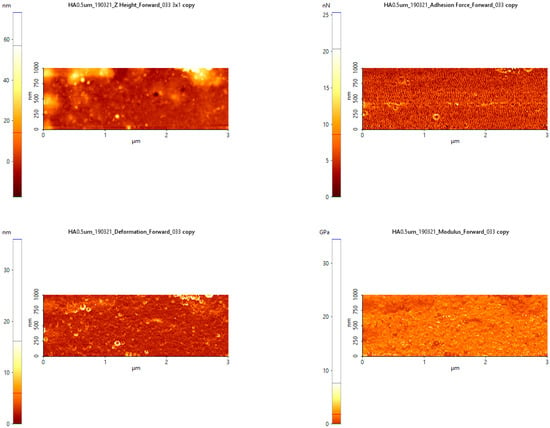
Figure 9.
Analysis of the mechanical properties of the 500 nm HA layer (P1).
6.2. Analysis of the 1000 nm HA Layer (P2)
In the case of the larger 1000 nm layer, here we can find a number of larger HA particles. These can be considered as a separate material because they have different dimensions from the base layer. In height they do not exceed 150 nanometers but are large enough (1–2 µm in diameter) to influence the characteristics of the base layer.
Figure 10 shows an analysis of the mechanical properties of the HA layer (1000 nm). The particles of material increased, rising from 200 nm in height. The adhesion force increased compared to the 500 nm layer shown in Figure 10, reaching values of 40 nN. The drops of HA material do not have an additional adhesive force because they are less attached to the substrate.
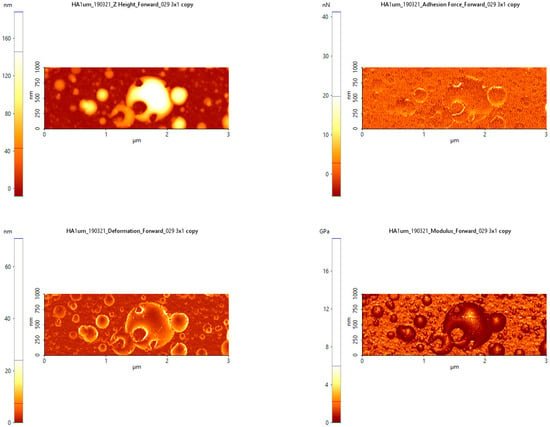
Figure 10.
Analysis of the mechanical properties of the 1000 nm HA layer (P2).
The drops of material that were formed after the base layer had a lower modulus of elasticity (see Figure 10) compared to the base layer, which led to a differentiation of the properties of the ceramic material. The susceptibility to deformation was higher for the droplet material and at higher values for the material with a thickness of 1000 nm, compared to materials with a thickness of 500 nm.
7. Theoretical Model
The merit for the use of a complex theoretical model that can cover a wide range of behavior of transient plasmas has been shown by our group in the past few years in a series of papers that cover: dissipative or dispersive phenomena, particle heterogeneity in laser produced plasma on metallic alloys, oscillatory behavior of charged particles, plasma self-structuring, and stoichiometry issues during the pulsed laser deposition process. The fractal paradigm was proven to be a proper media for the development viable theoretical models used to describe laser produced plasmas complex dynamics. In the following section (Section 7), we focus on studying the dynamics of the laser ablation plasma in a nondifferentiable regime of the Schrodinger type at various resolution scales.
Let us first consider the movement equation (geodesics equation) of the ablation plasma structural units [20]:
where
In relations (1)–(3), xl is the fractal spatial coordinate, t is the nonfractal temporal coordinate with the role of an affine parameter of the movement curve, is the complex velocity, is the scale resolution independent real part of , is the scale resolution (dt) dependent imaginary part of , is the “diffusion coefficient” associated with the fractal nonfractal transition, and DF is the movement curve fractal dimension. For DF we can choose any accepted definition: the Kolmogorov definition, the Haussdorff-Besikovici definition, etc. [21]. However once one definition is accepted, it has to be constant.
Let us consider that the particle ejection as a result of the laser-target interaction is defined through an irrotational movement of the ablation plasma structural units. Then:
where Ψ is the fractal state function, while lnΨ is the scalar potential of the complex velocity field. In these conditions by substituting (3) in (1) and following the procedure from [20], we obtain the Schrödinger equation of fractal type (free of any constraints):
In the case of external constraints given by the scalar potential U, the Schrödinger equation of fractal type becomes:
If we consider a simplified version of this approach by considering the stationary one-dimensional case (i.e., for through the method from reference [20]), restricted by a potential barrier represented in Figure 11, we can find:
where is the fractal stationary state function, E0 is the fractal energy of the ablation plasma structural unit [22] and the m0 is the rest mass of the same structural unit.
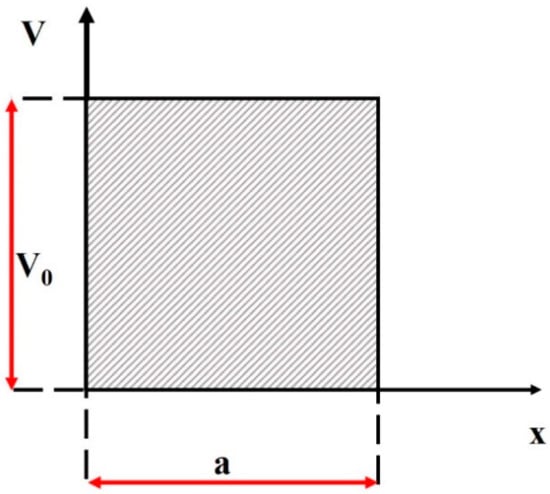
Figure 11.
External scalar potential for the fractal type tunneling effect.
The potential barrier in this case will differentiate between two possible states of the ejected particles in during the expansion (emissive and non-emissive). In this way, we will be able to discriminate between the particles that are recorded using the investigation techniques discussed in the previous sections (Section 3 and Section 4) and those who are not measured explicitly. In such a context, by implementing the method from reference [23], we can find the two coefficients that can be associated with the optical emission process, one describing the excited states of a family of structural units described by the same fractalization degree (I), while the second coefficient defines a different family of states describing the non-excited states of the plasma (N):
with
In Figure 12 we have represented the evolution of the I coefficient for different X-Y fractal coordinates. The Y parameters were used to specify the fractalization of the simulated structural units. We noticed that for various values of the Y (fractalization values attributed to different species in the laser produced plasma), distribution maxima were shifted to higher values of X. This particular behavior was showcased through ICCD fast camera imaging where we saw the global emission spatial distribution presenting multiple maxima characterizing different plasma structures (Figure 2) which were rich in one specific type of particle species (fast structure-ions, slow structure-atoms, last structure- clusters). Each structure, containing different particles, in the fractal paradigm will automatically be defined by a different fractalization degree.
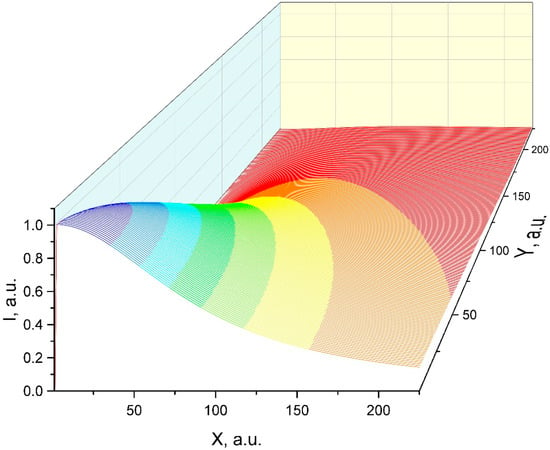
Figure 12.
Modeling of the distribution of the excited states species of the laser produced plasma in the framework of a fractal paradigm.
Therefore, in order to accurately describe the plasma expansion in this representation, we need to account for the functionality of the scale superposition principle. This means that the dynamics of any complex system (here—laser produced plasmas) at a global scale resolution can be identified with the cumulative action of the dynamics at various local scale resolutions. In such a context, we considered the spectral emission representation (I) in a fractal representation for various scale resolutions and fractalization degrees (Figure 13). As a result, we could reconstruct the global distribution by convoluting the three distributions. The cumulative action also implied the interaction between the plasma substructures. Since Equation (7) is invariant with respect to the SL(2R) group [24], the interactions between the plasma substructures (Coulomb substructure, Thermal substructure, and Cluster substructure) were mathematically defined through the Stoka type procedure [25,26]. These procedures specify synchronizations amongst the structure though self-modulation in amplitude according to the results from reference [27]. These phenomena imply Stoler type transformations from a mathematical point of view [28]. These transformations [27,28] led to synchronization between the substructures of the laser ablation plasmas being achieved through charge creation and annihilation mechanisms.
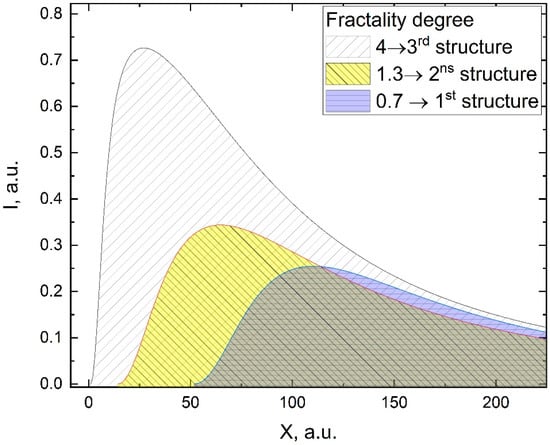
Figure 13.
Selection of laser produced plasma entities spectral emission based on various fractalization degrees.
8. Conclusions
The process of deposition of thin films by laser ablation of hydroxyapatite was studied. Two complementary techniques were implemented: fast camera photography, and both spatially and temporally resolved emission spectroscopy. The fast camera photography allowed the identification of the plasma structures expanding with different velocities and having different geometries. Optical emission spectroscopy allowed the determination of the excitation temperatures of each component of the plasma (Ca, P, and O) and revealed a heterogeneity in the distribution of the internal energy of the plasma. Spatial-temporal evolution of the emission of Ca atoms and ions was also tracked and the expansion velocities of each species were determined.
Two thin layers were deposited under low and high fluency conditions. Complementary surface investigation techniques (SEM, AFM, and EDX) were implemented in order to find the right route for obtaining a thin film with complete stoichiometric transfer. For the high fluency, films with nano- and micrometric-sized structures and a small deviation from the stoichiometry due to these structures were obtained. Therefore the optimum conditions for smoother stoichiometric films were found to be at a fluence of 2.5 J/cm2. We developed a fractal model based on Schrödinger type functionalities. The model can cover the distribution of the excited states in the laser produced plasma. Moreover, we proved that SL(2R) invariance can enable plasma substructure synchronization through self-modulation.
Author Contributions
All authors have read and agreed to the published version of the manuscript. Conceptualization, S.G., M.A. and S.A.I.; methodology S.G., N.C. and M.A.; investigation, S.A.I., N.C. and M.A.; writing—original draft preparation, S.A.I., M.A. and S.G.; writing—review and editing, S.A.I., N.C. and M.A.; visualization, S.A.I.; supervision, M.A. and S.G.
Funding
This work was financially supported by R National Authority for Scientific Research and Innovation in the framework of Nucleus Program–16N/2019.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koch, C.F.; Johnson, S.; Kumar, D.; Jelinek, M.; Chrisey, D.B.; Doraiswamy, A.; Jin, C.; Narayan, R.J.; Mihailescu, I.N. Pulsed laser deposition of hydroxyapatite thin films. Mater. Sci. Eng. 2007, 27, 484–494. [Google Scholar] [CrossRef]
- Fernández-Pradas, J.M.; Clèries, L.; Sardin, G.; Morenza, J.L. Hydroxyapatite coatings grown by pulsed laser deposition with a beam of 355 nm wavelength. J. Mater. Res. 1999, 14, 4715–4719. [Google Scholar] [CrossRef][Green Version]
- Rajesh, P.; Muraleedharan, C.V.; Komath, M.; Varma, H. Pulsed laser deposition of hydroxyapatite on titanium substrate with titania interlayer. J. Mater. Sci. Mater. Med. 2011, 22, 497–505. [Google Scholar] [CrossRef]
- Bulai, G.; Trandafir, V.; Irimiciuc, S.A.; Ursu, L.; Focsa, C.; Gurlui, S. Influence of rare earth addition in cobalt ferrite thin films obtained by pulsed laser deposition. Ceram. Int. 2019, 45, 20165–20171. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Bulai, G.; Agop, M.; Gurlui, S. Influence of laser-produced plasma parameters on the deposition process: In situ space- and time-resolved optical emission spectroscopy and fractal modeling approach. Appl. Phys. A Mater. Sci. Process. 2018, 124, 1–14. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Boidin, R.; Bulai, G.; Gurlui, S.; Nemec, P.; Nazabal, V.; Focsa, C. Laser ablation of (GeSe2)100−x (Sb2Se3)x chalcogenide glasses: Influence of the target composition on the plasma plume dynamics. Appl. Surf. Sci. 2017, 418, 594–600. [Google Scholar] [CrossRef]
- Canulescu, S.; Papadopoulou, E.L.; Anglos, D.; Lippert, T.; Schneider, C.W.; Wokaun, A. Mechanisms of the laser plume expansion during the ablation of LiMn2O4. J. Appl. Phys. 2009, 105, 063107. [Google Scholar] [CrossRef]
- Aké, C.S.; De Castro, R.S.; Sobral, H.; Villagrán-Muniz, M. Plume dynamics of cross-beam pulsed-laser ablation of graphite. J. Appl. Phys. 2006, 100, 053305. [Google Scholar]
- Irimiciuc, S.A.; Nica, P.E.; Agop, M.; Focsa, C. Target properties–plasma dynamics relationship in laser ablation of metals: Common trends for fs, ps and ns irradiation regimes. Appl. Surf. Sci. 2019, 506, 144926. [Google Scholar] [CrossRef]
- Harilal, S.S.; Bindhu, C.V.; Tillack, M.S.; Najmabadi, F.; Gaeris, A.C. Internal structure and expansion dynamics of laser ablation plumes into ambient gases. J. Appl. Phys. 2003, 93, 2380–2388. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Nica, P.; Focsa, C.; Agop, M. A compact non-differential approach for modeling laser ablation plasma dynamics. J. Appl. Phys. 2017, 12, 083301. [Google Scholar] [CrossRef]
- Harilal, S.S.; Bindhu, C.V.; Tillack, M.S.; Najmabadi, F.; Gaeris, A.C. Plume splitting and sharpening in laser-produced aluminium plasma. J. Phys. D Appl. Phys. 2002, 35, 2935–2938. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Agop, M. Particle distribution in transient plasmas generated by ns-laser ablation on ternary metallic alloys. Appl. Phys. B. 2019, 125, 190. [Google Scholar] [CrossRef]
- Milan, M.; Laserna, J.J. Diagnostics of silicon plasmas produced by visible nanosecond laser ablation. Spectrochim. Acta Part B At. Spectrosc. 2001, 56, 275–288. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST ASD Team, NIST Atomic Spectra Database Lines Form, NIST At. Spectra Database (Ver. 5.2). 2014. Available online: http://physics.nist.gov/asd (accessed on 9 October 2018).
- Song, J.; Liu, Y.; Zhang, Y.; Jiao, L. Mechanical properties of hydroxyapatite ceramics sintered form powders with different morphologies. Mater. Sci. Eng. A 2011, 528, 5421–5427. [Google Scholar] [CrossRef]
- Wanga, D.G.; Chena, C.Z.; Yang, X.X.; Ming, X.C.; Zhang, W.L. Effect of bioglass addition on the properties of HA/BG composite films fabricated by pulsed laser deposition. Ceram. Int. 2018, 44, 14528–14533. [Google Scholar] [CrossRef]
- Nishikawa, H.; Umatani, S. Effect of ablation laser pulse repetition rate on the surface protrusion density of hydroxyapatite thin films deposited using pulsed laser deposition. Mater. Lett. 2017, 09, 330–333. [Google Scholar] [CrossRef]
- Cho, M.-Y.; Lee, D.-W.; Kim, I.-S.; Kim, W.-J.; Koo, S.-M.; Lee, D.; Kim, Y.-H.; Oh, J.-M. Evaluation of structural and mechanical properties of aerosol-deposited bioceramic films for orthodontic brackets. Ceram. Int. 2019, l45, 6702–6711. [Google Scholar] [CrossRef]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Singapore, 2016. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; WH Freeman Publisher: New York, NY, USA, 1993. [Google Scholar]
- Enescu, F.; Irimiciuc, S.A.; Cimpoesu, N.; Bedelean, H.; Bulai, G.; Gurlui, S.; Agop, M. Investigations of Laser Produced Plasmas Generated by Laser Ablation on Geomaterials. Experimental and Theoretical Aspects. Symmetry 2019, 11, 1391. [Google Scholar] [CrossRef]
- Bujoreanu, C.; Irimiciuc, S.A.; Benchea, M.; Nedeff, F.; Agop, M. A fractal approach of the sound absorption behaviour of materials. Theoretical and experimental aspects. Int. J. Non-Linear Mech. 2018, 103, 128–137. [Google Scholar] [CrossRef]
- Mihaileanu, M. Differential, Projective and Analytical Geometry; Didactical and Pedagogical Publishing House: Bucuresti, Romania, 1972. [Google Scholar]
- Stoka, M.I. Integral Geometry; Romanian Academy Publishing House: Bucharest, Romania, 1967. [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions—A Great Finishing Touch to a Classical Newtonian Phylosiphy; Nova Publishing: New York, NY, USA, 2012. [Google Scholar]
- Irimiciuc, S.A.; Bulai, G.; Gurlui, S.; Agop, M. On the separation of particle flow during pulse laser deposition of heterogeneous materials—A multi-fractal approach. Powder Technol. 2018, 339, 273–280. [Google Scholar] [CrossRef]
- Stoler, D. Equivalence Classes of Minimum Uncertainty Packets. Phys. Rev. D 1970, 1, 3217. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).