Controller for the Grid-Connected Microinverter Output Current Tracking
Abstract
1. Introduction
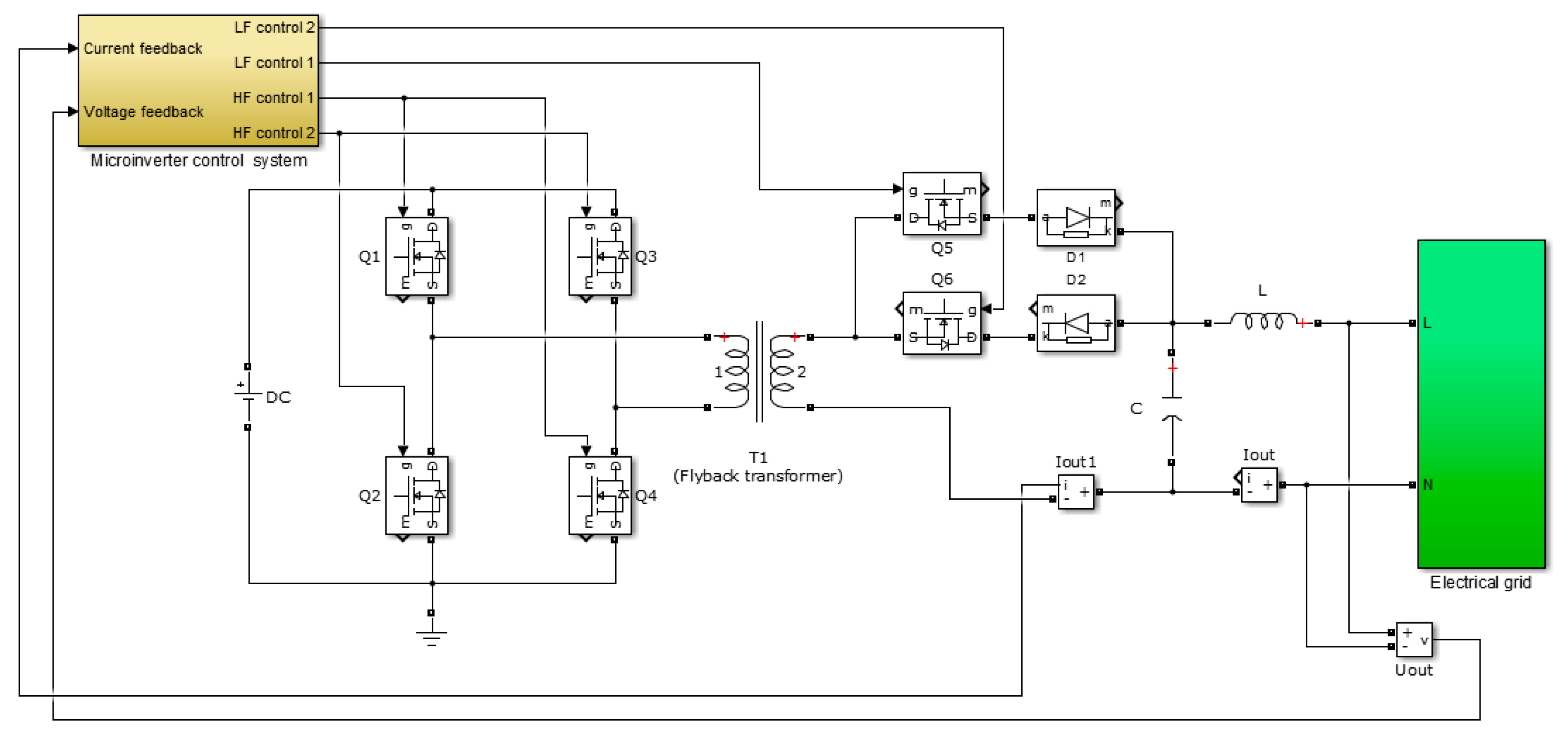
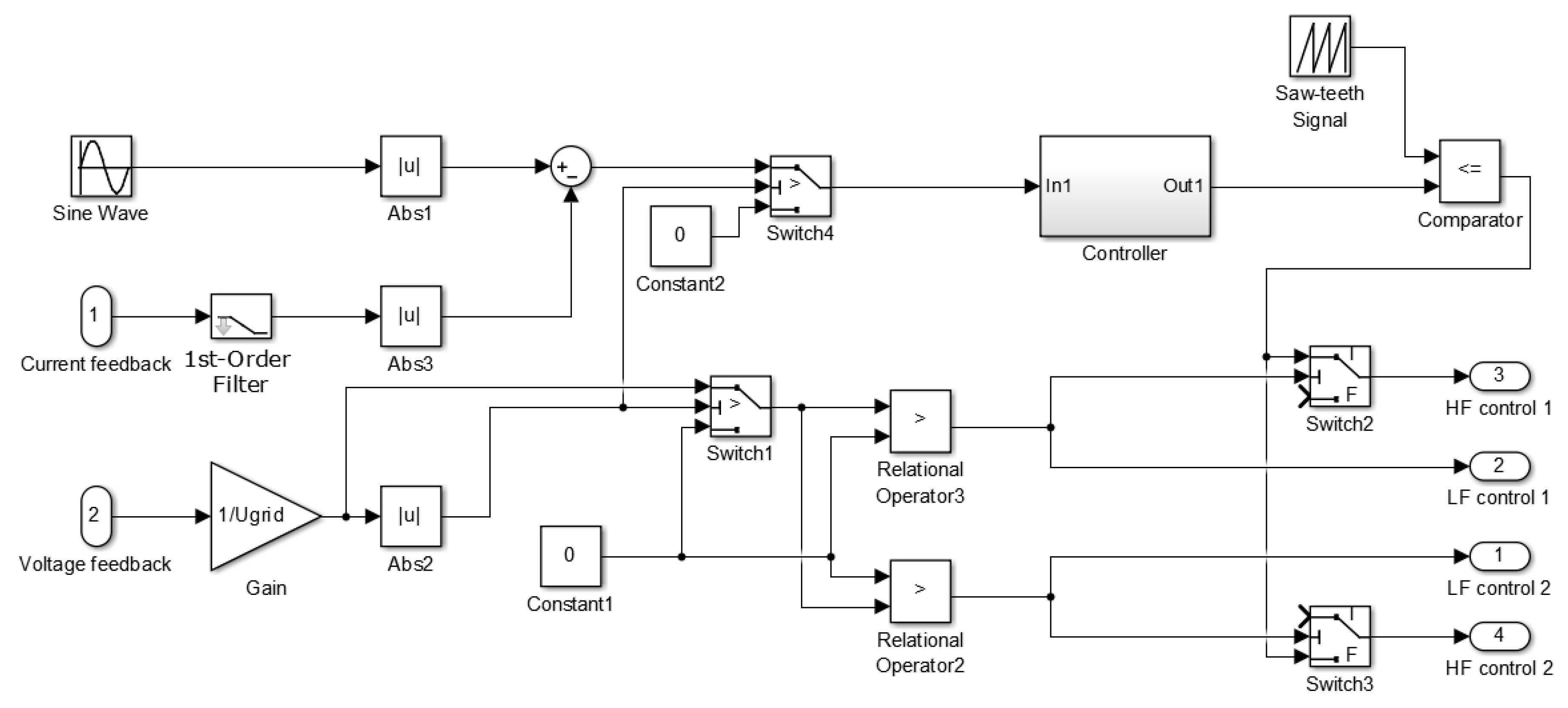
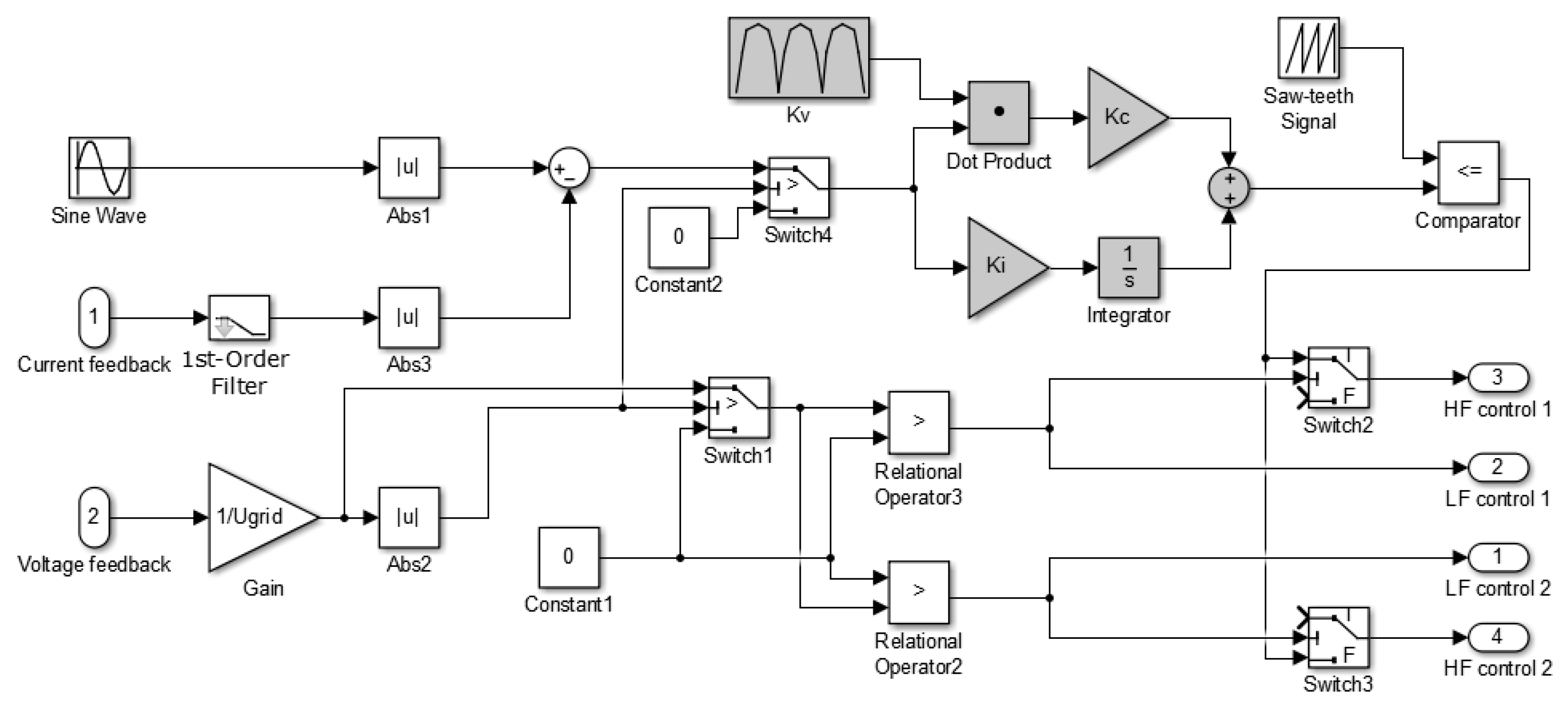
2. Control System for Tracking of the Grid-Connected Microinverter Output Current
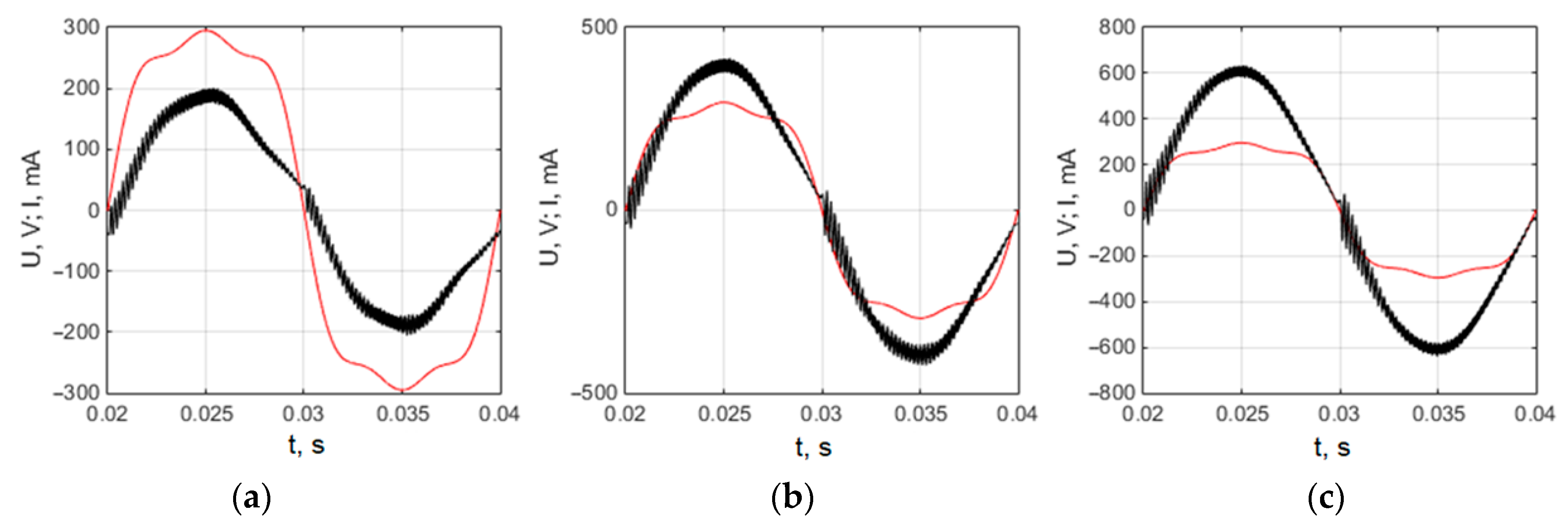
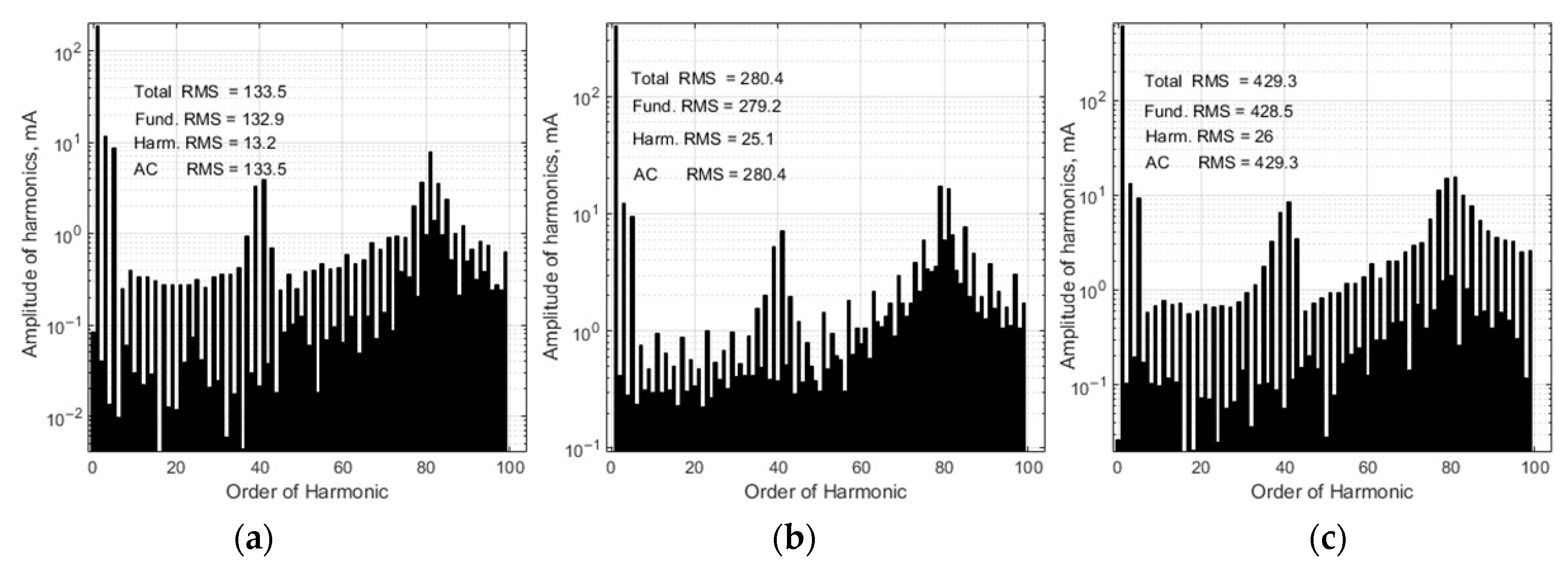
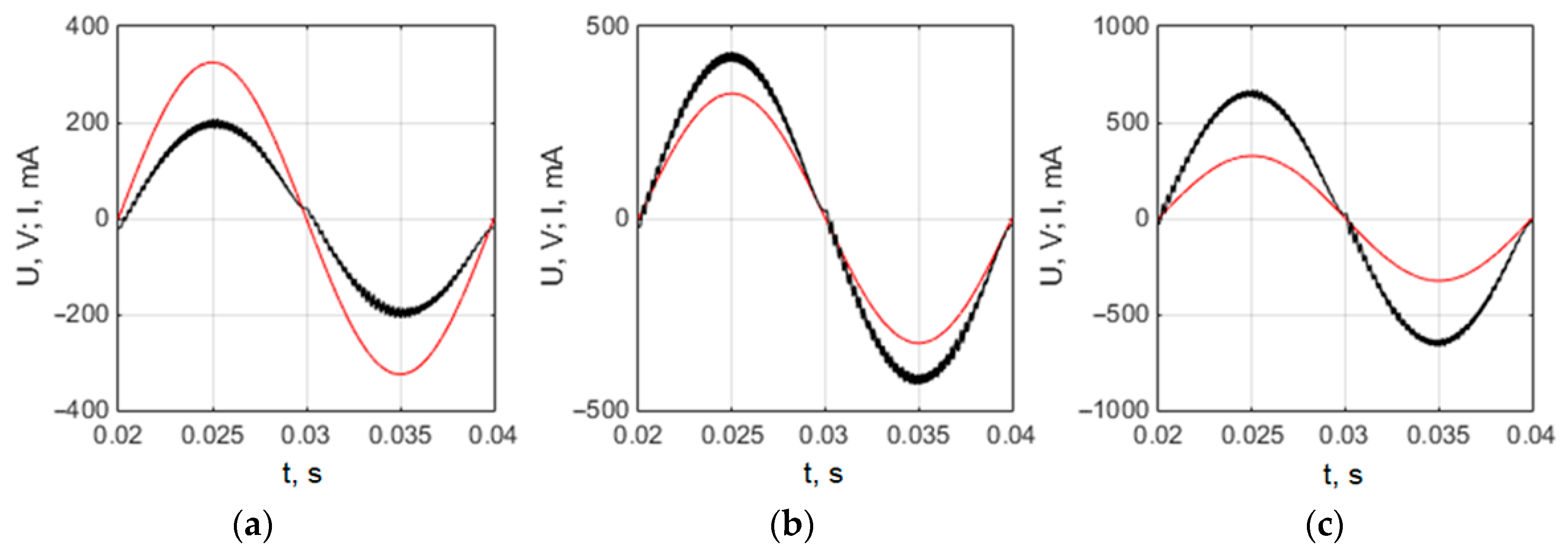
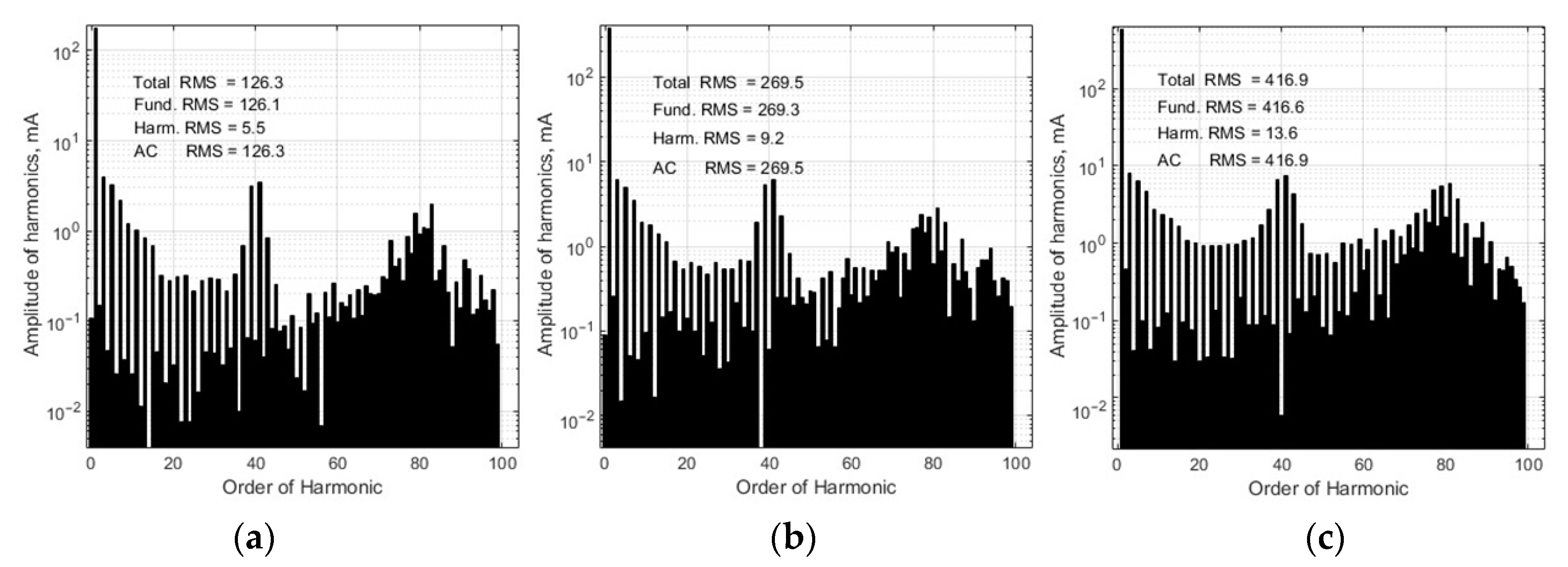
3. Analysis of the Microinverter Control System Based on the PI Controller
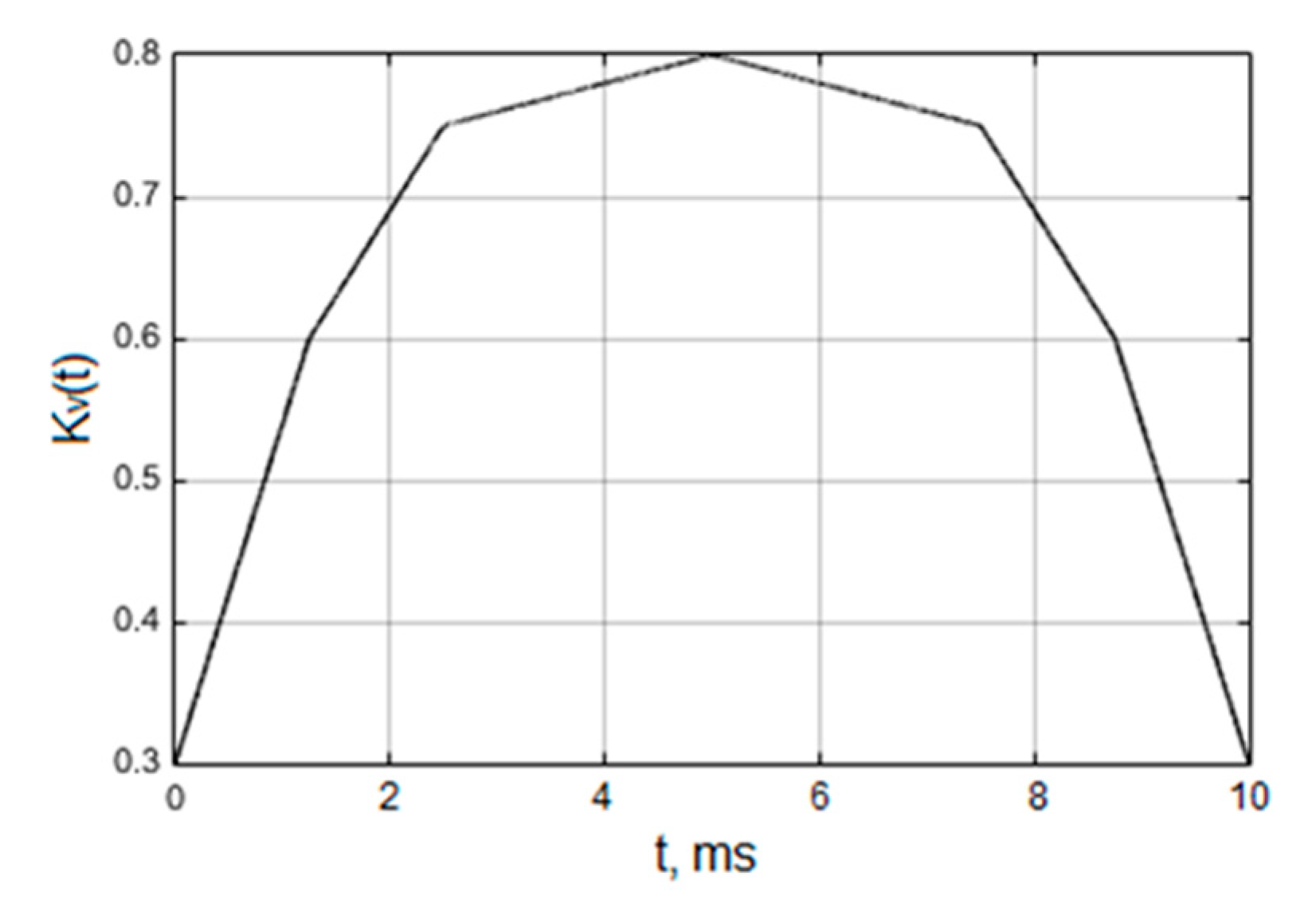
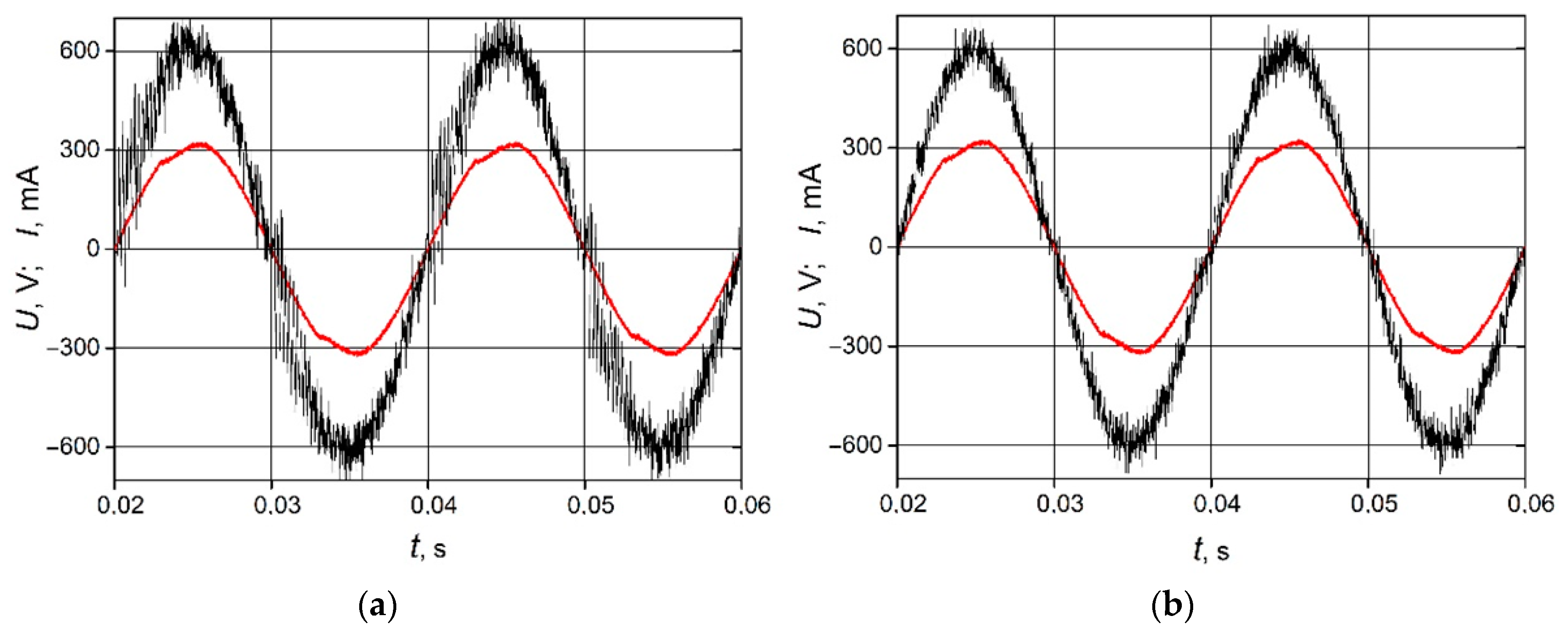
4. PI Controller with the Variable Proportional Constant
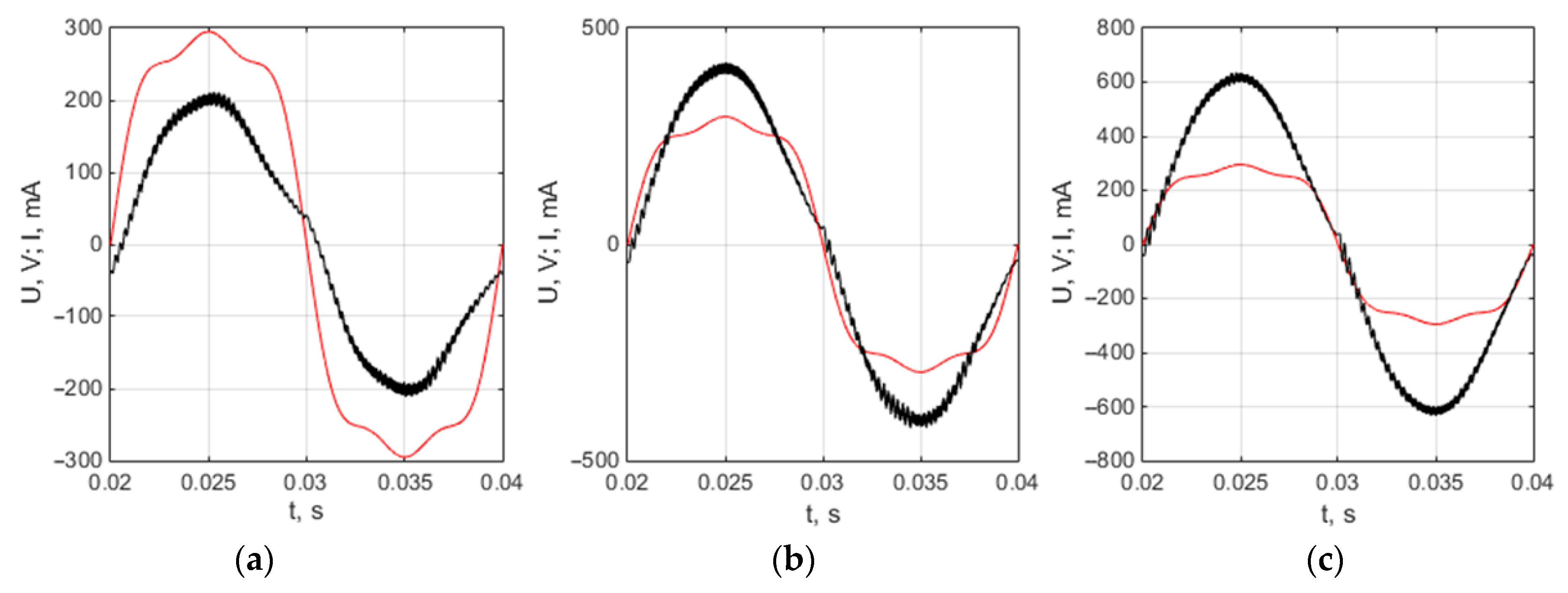
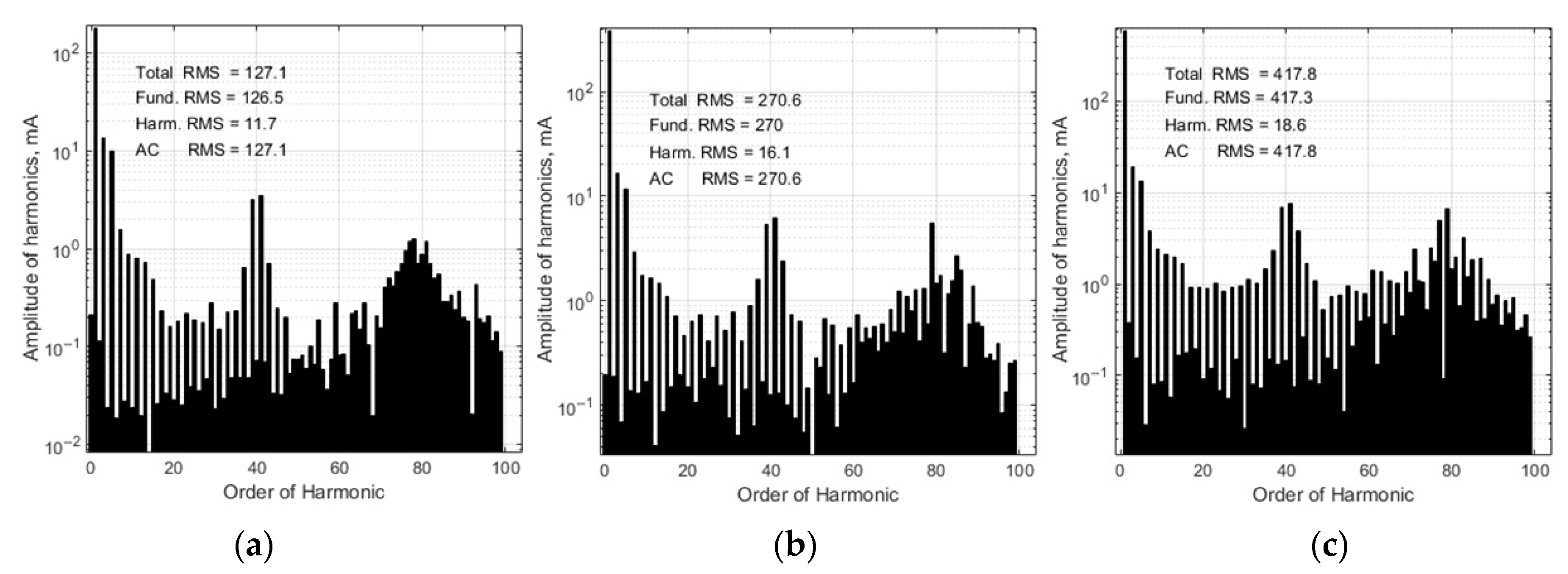
5. Analysis of the Microinverter Control System Based on the PI Controller with the Variable Proportional Constant
6. Conclusions
- The most popular controllers used for tracking of the grid-connected photovoltaic inverter output current in the industrial microinverters are PI and PID controllers.
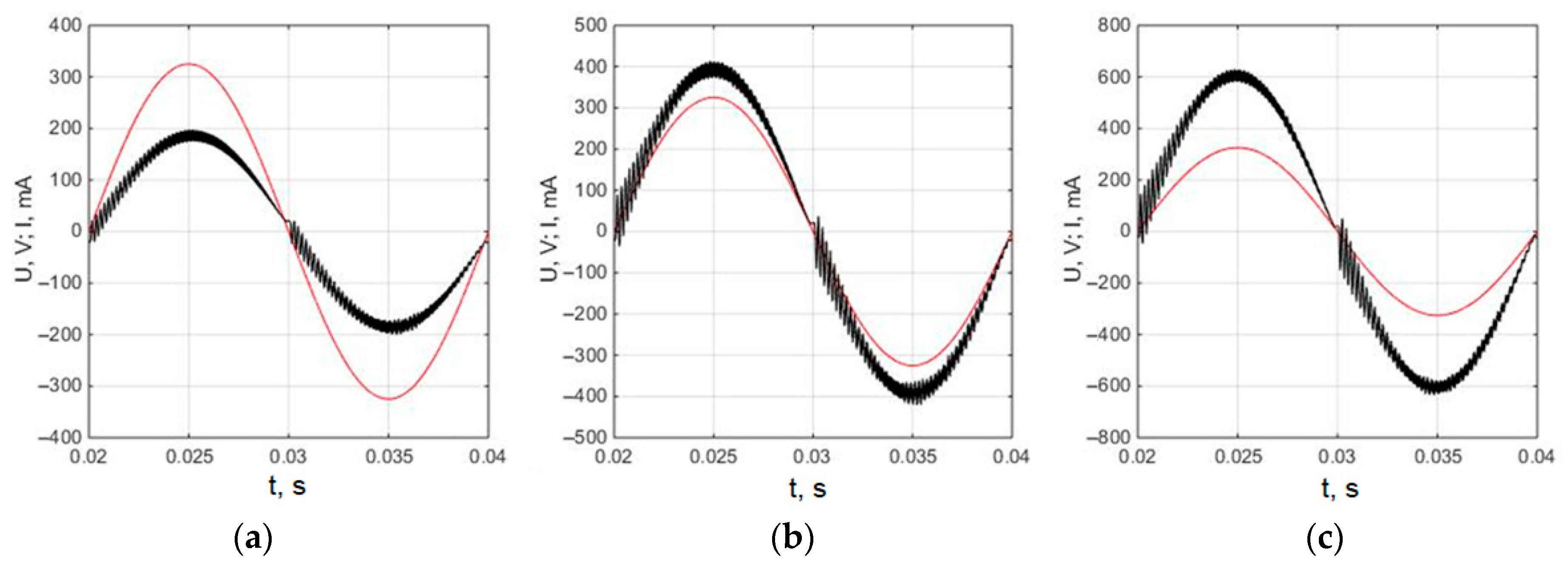
- The distortions of the grid-connected microinverter output current shape can be reduced when the proportional constant of the PI controller during every half period of the current changes in time with the current by the similar law.
- The variation of the proportional constant in the proposed modification of the PI controller is realized by the introduction of the time-varying term, which varies according to the law presented by the piecewise linear approximation of the sinus.
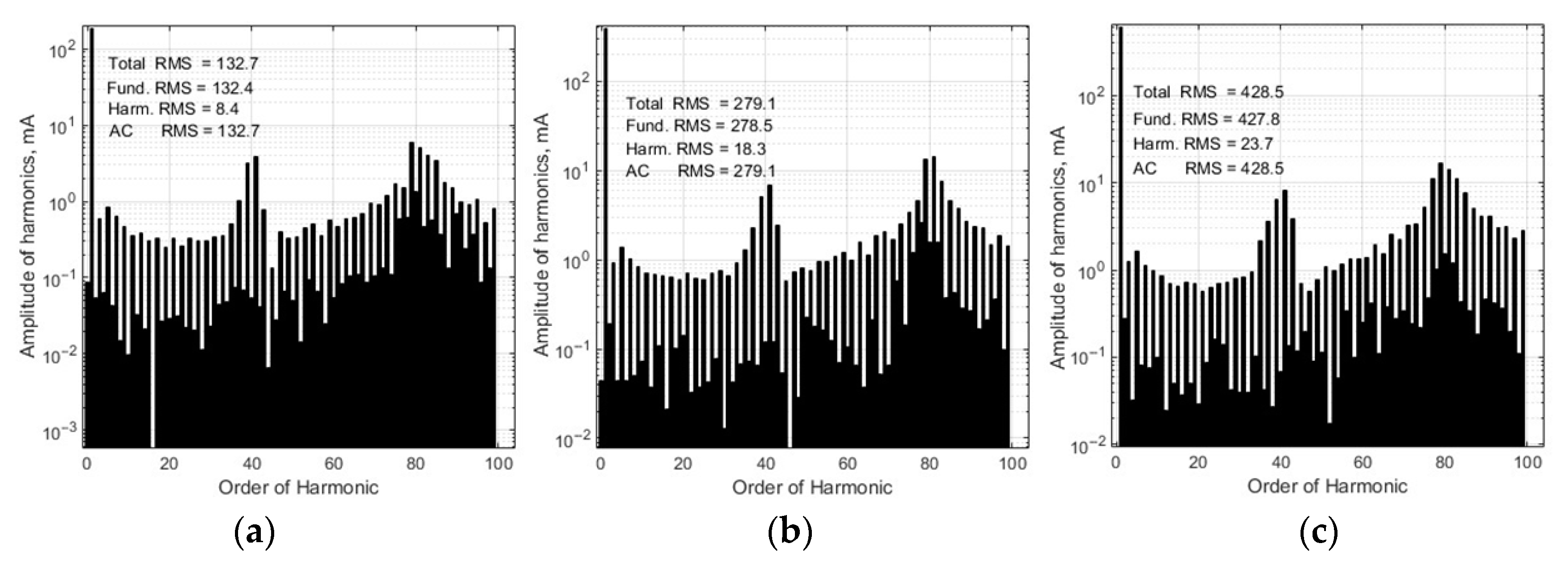
- The employment of the proposed PI controller with the variable proportional constant for tracking of the grid-connected photovoltaic microinverter output current instead of the ordinary PI controller allows us to reduce the THD of the output current by 30% at 32 W, by 48% at 62 W, and by 40% at 97 W load power when the electric grid voltage has a pure sinus shape and by 7% at 32 W, by 33% at 62 W and by 26% at 97 W—in the case when the grid voltage is distorted by the third- and fifth-order harmonics.
- The experimental investigation results prove the superiority of the PI controller with the variable proportional constant over the ordinary PI controller.
- The implementation of the proposed controller is more complicated as compared to the ordinary PI controller because the proportional constant in the proposed controller varies in time according to a certain law.
Author Contributions
Funding
Conflicts of Interest
References
- Meneses, D.; Blaabjerg, F.; García, Ó.; Cobos, J.A. Review and Comparison of Step-Up Transformerless Topologies for Photovoltaic AC-Module Application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef]
- Caiza, D.L.; Kouro, S.; Flores-Bahamonde, F.; Hernandez, R. Unfolding PV Microinverter Current Control: Rectified Sinusoidal vs Sinusoidal Reference Waveform. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018; ISBN 978-1-4799-7312-5. [Google Scholar] [CrossRef]
- Yongjun, L.; Shun, W.; Jing, L.; Chen, C.; Weiliang, L. Grid-connected current control of micro inverter based on ANN inverse model. In Proceedings of the 2017 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; ISBN 978-1-5090-4657-7. [Google Scholar] [CrossRef]
- Kojabadi, H.M.; Yu, B.; Gadoura, I.A.; Chang, L.; Ghribi, M. A novel DSP-based current-controlled PWM strategy for single phase grid connected inverters. IEEE Trans. Power Electron. 2006, 21, 985–993. [Google Scholar] [CrossRef]
- Nan, W.; Shangsheng, L. Current output control strategy based on current reference feed-forward for H-bridge cascaded inverter. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; ISBN 978-1-5386-1127-2. [Google Scholar] [CrossRef]
- Suzuki, K.E.; Wada, K. Current Control using Pulsed Current Sampling Considering Sampling Points and Sensor Positions for Single-Phase Inverter. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; ISBN 978-1-5386-8330-9. [Google Scholar] [CrossRef]
- Xia, Y.; Ayyanar, R. Naturally Adaptive, Low-Loss Zero-Voltage-Transition Circuit for High-Frequency Full-Bridge Inverters with Hybrid PWM Grid-Tied Inverter. IEEE Trans. Power Electron. 2017, 33, 4916–4933. [Google Scholar] [CrossRef]
- Na, T.; Zhang, Q.; Tang, J.; Wang, J. Active power filter for single-phase Quasi-Z-source integrated on-board charger. CPSS Trans. Power Electron. Appl. 2018, 3, 197–201. [Google Scholar] [CrossRef]
- Wang, R.N.; Hu, B.; Sun, S. Linear Active Disturbance Rejection Control for DC Side Voltage of Single-Phase Active Power Filters. IEEE Access 2019, 7, 73095–73105. [Google Scholar] [CrossRef]
- Popescu, M.; Bitoleanu, A.; Preda, A. A New Design Method of an LCL Filter Applied in Active DC-Traction Substations. IEEE Trans. Ind. Appl. 2018, 55, 3497–3507. [Google Scholar] [CrossRef]
- Motta, L.; Faúndes, N. Active/passive harmonic filters: Applications, challenges & trends. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016, ISSN 2164-0610. [Google Scholar] [CrossRef]
- Lee, T.-L.; Hu, S.-H. An Active Filter With Resonant Current Control to Suppress Harmonic Resonance in a Distribution Power System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 198–209. [Google Scholar] [CrossRef]
- Nora, D.; Francisco, G.M.; Najib, A.; Yacine, D. A Hybrid Active Filter Using the Backstepping Controller for Harmonic Current Compensation. Symmetry 2019, 11, 1161. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Rajeev, M.; Agarwal, V. Analysis and Control of a Novel Transformer-Less Microinverter for PV-Grid Interface. IEEE J. Photovolt. 2018, 8, 1110–1118. [Google Scholar] [CrossRef]
- Xin, Z.; Mattavelli, P.; Yao, W. Mitigation of Grid-Current Distortion for LCL-Filtered Voltage-Source Inverter with Inverter-Current Feedback Control. IEEE Trans. Power Electron. 2017, 33, 6248–6261. [Google Scholar] [CrossRef]
- Bayhan, S.; Seyedalipour, S.S.; Komurcugil, H.; Abu-Rub, H. Lyapunov Energy Function Based Control Method for Three-Phase UPS Inverters with Output Voltage Feedback Loops. IEEE Access 2019, 7, 113699–113711. [Google Scholar] [CrossRef]
- Zha, Z.; Yang, J.; Li, S. Continuous Output Feedback TSM Control for Uncertain Systems With a DC–AC Inverter Example. IEEE Trans. Circuits Syst. Express Briefs 2017, 65, 71–75. [Google Scholar] [CrossRef]
- Dash, P.P.; Kazeran, M. Dynamic Modeling and Performance Analysis of a Grid-Connected Current-Source Inverter-Based Photovoltaic System. IEEE Trans. Sustain. Energy 2011, 2, 71–75. [Google Scholar] [CrossRef]
- Kamil, M. Grid-Connected Solar Microinverter Reference Design Using a dsPIC Digital Signal Controller. Available online: http://ww1.microchip.com/downloads/en/appnotes/pv_appnotes.pdf (accessed on 9 December 2019).
- Gazoli1, J.R.; Villalva, M.G.; Ruppert, E. Micro-inverter for integrated grid-tie photovoltaic module using resonant controller. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; ISBN 978-1-4673-2729-9. [Google Scholar] [CrossRef]
- Hlali, M.; Bahri, I.; Belloumi, H.; Kourda, F. Comparative analysis of PI and PR based Current Controllers for Grid Connected Photovoltaic Micro-inverters. In Proceedings of the 2019 10th International Renewable Energy Congress, Sousse, Tunisia, 26–28 March 2019; ISBN 978-1-7281-0140-8. [Google Scholar] [CrossRef]
- Sahu, P.K.; Shaw, P.; Maity, S. Modeling and control of grid-connected DC/AC converters for single-phase micro-inverter application. In Proceedings of the 2015 Annual IEEE India Conference, New Delhi, India, 17–19 December 2015; ISBN 978-1-4673-7399-9. [Google Scholar] [CrossRef]
- Kim, H.; Yu, T.; Choi, S. Indirect Current Control Algorithm for Utility Interactive Inverters in Distributed Generation Systems. IEEE Trans. Power Electron. 2008, 23, 1342–1347. [Google Scholar] [CrossRef]
- Hassan, M.A.; Abido, M.A. Optimal Design of Microgrids in Autonomous and Grid-Connected Modes Using Particle Swarm Optimization. IEEE Trans. Power Electron. 2011, 26, 755–769. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, H.-C. Photovoltaic Grid-connected Micro-inverter Based on Self-tuning Fuzzy-PI Controller. Adv. Mater. Res. 2014, 986, 1098–1102. [Google Scholar] [CrossRef]
- Wang, T.H.; Lo, Y.K. A DSP-based Grid-tied Solar Cascade-micra-inverter. In Proceedings of the 2013 1st International Future Energy Electronics Conference, Tainan, Taiwan, 3–6 November 2013; ISBN 978-1-4799-0073-2. [Google Scholar] [CrossRef]
- Melo, F.O.C.; Garcia, L.S.; De Freitas, L.C.; Coelho, E.A.A. Proposal of a Photovoltaic AC-Module with a Single-Stage Transformerless Grid-Connected Boost Microinverter. IEEE Trans. Ind. Electron. 2017, 65, 2289–2301. [Google Scholar] [CrossRef]
- Rodriguez, C.T.; Fuente, D.V.; Garcera, G. Reconfigurable Control Scheme for a PV Microinverter Working in Both Grid-Connected and Island Modes. IEEE Trans. Ind. Electron. 2011, 60, 1582–1595. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, X.; Zhang, J.; Xu, D. A New Feedback Method for PR Current Control of LCL-Filter-Based Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2010, 57, 2033–2041. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Zhang, N.; Tang, H.; Yao, C. A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters. Energies 2014, 7, 3934–3954. [Google Scholar] [CrossRef]
- Bode, G.H.; Loh, P.C.; Newman, M.J.; Holmes, D.G. An improved robust predictive current regulation algorithm. IEEE Trans. Ind. Appl. 2005, 41, 1720–1733. [Google Scholar] [CrossRef]
- Mario, L.R.; Juan, G.; Francisco, V.M.F. Interactive Tuning Tool of Proportional-Integral Controllers for First Order Plus Time Delay Processes. Symmetry 2018, 10, 569. [Google Scholar] [CrossRef]
- Jayalath, S.; Hanif, M. Controller tuning for a single phase grid-connected current source inverter. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference, Taipei, Taiwan, 1–4 November 2015; ISBN 978-1-4799-7657-7. [Google Scholar] [CrossRef]
- Bielskis, E.; Baskys, A.; Sapurov, M. Single Stage Microinverter Based on Two-Switch DC-DC Flyback Converter. Elektronika ir Elektrotechnika 2017, 23, 29–32. [Google Scholar] [CrossRef][Green Version]
- Bielskis, E.; Baskys, A.; Sapurov, M. Impact of Transformer Design on Flyback Converter Voltage Spikes. Elektronika ir Elektrotechnika 2016, 22, 58–61. [Google Scholar] [CrossRef][Green Version]
- Singh, B.; Joshi, N. Tuning Techniques of PID controller: A review. Int. J. Emerg. Technol. 2017, 8, 481–485. [Google Scholar]
- Al-Saleh, M.A.; Mir, M. A modified univariate search algorithm. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems, Orlando, FL, USA, 30 May–2 June 1999; ISBN 0-7803-5471-0. [Google Scholar] [CrossRef]
- Wilson, P.; Mantooth, H.A. Model-Based Engineering for Complex Electronic Systems; Newnes: Kidlington, UK, 2013; pp. 347–367. [Google Scholar]
| Component | Parameter | Value |
|---|---|---|
| Flyback transformer | Magnetic inductance | 36 µH |
| Primary winding active resistance | 0.01 Ω | |
| Secondary winding active resistance | 0.47 Ω | |
| Transformation ratio | 1:12 | |
| Capacitor of CL filter | Capacitance | 200 nF |
| Inductor of CL filter | Inductance | 330 µH |
| Component | Type | Parameters |
|---|---|---|
| Q1, Q2, Q3, Q4 | IRF3205 | 55 V; 110 A |
| Q5, Q6 | 2SK2717 | 900 V; 5 A |
| D1, D2 | FUF5408 | 1000 V; 3 A |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bielskis, E.; Baskys, A.; Valiulis, G. Controller for the Grid-Connected Microinverter Output Current Tracking. Symmetry 2020, 12, 112. https://doi.org/10.3390/sym12010112
Bielskis E, Baskys A, Valiulis G. Controller for the Grid-Connected Microinverter Output Current Tracking. Symmetry. 2020; 12(1):112. https://doi.org/10.3390/sym12010112
Chicago/Turabian StyleBielskis, Edvardas, Algirdas Baskys, and Gediminas Valiulis. 2020. "Controller for the Grid-Connected Microinverter Output Current Tracking" Symmetry 12, no. 1: 112. https://doi.org/10.3390/sym12010112
APA StyleBielskis, E., Baskys, A., & Valiulis, G. (2020). Controller for the Grid-Connected Microinverter Output Current Tracking. Symmetry, 12(1), 112. https://doi.org/10.3390/sym12010112





