Abstract
We define a new algebraic structure for two-component dichromatic links. This definition extends the notion of a kei (or involutory quandle) from regular links to dichromatic links. We call this structure a dikei that results from the generalized Reidemeister moves representing dichromatic isotopy. We give several examples on dikei and show that the set of colorings by these algebraic structures is an invariant of dichromatic links. As an application, we distinguish several pairs of dichromatic links that are symmetric as monochromatic links.
1. Introduction
A dichromatic link is a two-color link, where the two colors are usually represented by the labels “1” and “2”. Many link invariants have been generalized to dichromatic links. For example, see [1,2,3].
Kei and quandles are used to describe knots and links. They are algebraic structures satisfying a number of axioms resulting from Reidemeister moves. A kei or a quandle for a given knot diagram is presented in terms of generators and relations, where the generators represent arcs, and the relations result from the crossings. See [4,5,6,7,8,9,10,11,12,13,14,15,16] for more information.
In this paper, we introduce an algebraic structure, which we call a dikei. This structure works as an involutory quandle (or a kei) for dichromatic links. This structure distinguishes several pairs of dichromatic links that are symmetric as monochromatic links (symmetric monochromatic links are identical links without colors). The isotopy of the dichromatic links involves a larger number of Reidemeister moves. Therefore, our dikei involves new axioms resulting from the extra Reidemeister moves. We give many examples of algebraic structures satisfying the axioms of a dikei. As a by-product of this structure, we apply the theory to distinguish among dichromatic links which are symmetric without the two colors.
This article is organized as follows. In Section 2, the basic concepts and terminology for kei and quandles are given. We also define dichromatic links and their isotopy invariance. In Section 3, the structure of a dikei is introduced. Many examples of structure satisfying the axioms of dikei are also given. In Section 4, we use dikei on examples of dichromatic links to distinguish them as an application of our new structure.
2. Basic Concepts and Terminology
In [9], most of the basic concepts and terminology on quandles can be found. This section begins with the definition of an involutory quandle (or a kei), and we show how the axioms of a kei are induced by the three Reidemeister moves. In Figure 1, each “color” corresponds to an arc in a diagram, and the operation corresponds to the transformation that, when an arc x passes under another arc y, we get . So, when x crosses under y, is a new arc, but y is unchanged; y is doing something to x. See [9] for reference.
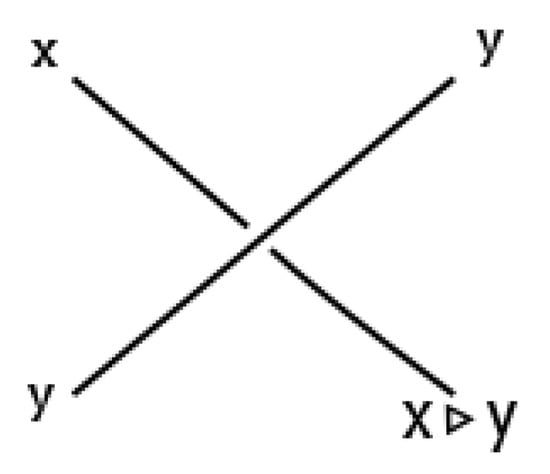
Figure 1.
The coloring of a regular crossing with one operation.
We give the definition of a kei.
Definition 1
([9]). A kei (involutory quandle) is a set X with a binary operation
▹: satisfying the following three axioms:
- 1.
- , for all .
- 2.
- , for all .
- 3.
- , for all .
The axioms of a kei result from the three Reidemeister moves as in the following Figure 2.
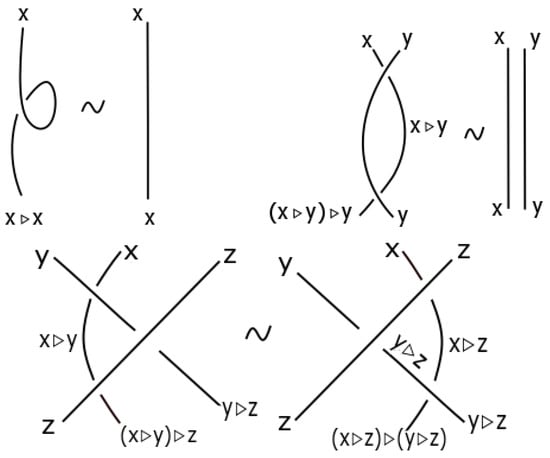
Figure 2.
The coloring of Reidemeister moves RI, RII, and RIII.
Definition 2
([9]). Let X and Y be kei with operations and , respectively. Then, a map is a kei homomorphism if for all x, we have
Definition 3
([9]). A kei isomorphism is a bijective kei homomorphism, and two kei are isomorphic if there is a kei isomorphism between them.
Usual examples of kei include the following:
- Any non-empty set X with operation , for all is a kei. It is called the trivial kei.
- Let be a symmetric bi-linear form on . Let X be the subset of consisting of vectors such that . Then, the operationdefines a kei structure on X. This kei is called a Coxeter kei.
- A set with operation , for all is a kei.
- A group with operation is a kei. It is called the core kei of the group G.
A dichromatic link in is the image of a smooth immersion of a finite number of circles in that have two colors, where the two colors are usually represented by the labels “1” and “2”. For example, see Figure 3.
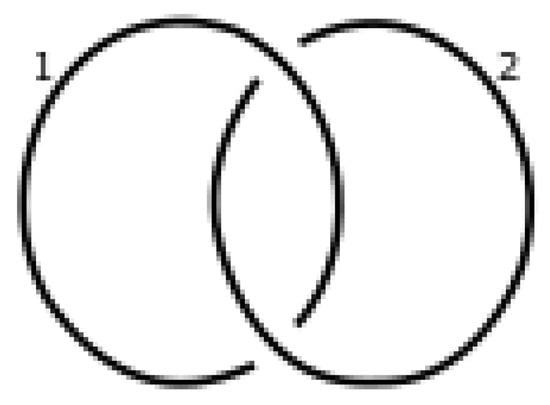
Figure 3.
The dichromatic Hopf link.
Note that the word “color” is sometimes used for the colors of the components, and sometimes the same word is used for the arcs used in constructing a kei. The use of the word “color” in two contexts should not be confusing for the reader.
Two dichromatic links, and , are isotopy equivalent if one of them can be obtained from the other by a finite number of the extended Reidemeister moves, shown below in the Figure 4, which preserves the color of each component.
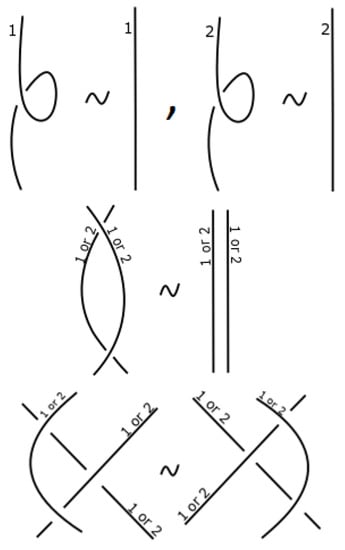
Figure 4.
Reidemeister moves which preserve the color of the component.
Example 1.
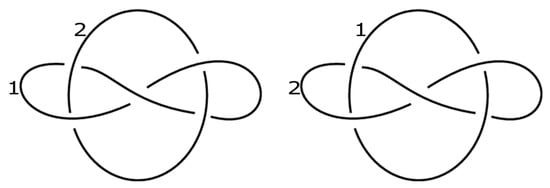
The two dichromatic links in the following Figure 5 are isotopy equivalent.

Figure 5.
The Whitehead dichromatic link diagrams.
3. Construction of Dikei
In this section, we define the notion of a dikei and give solid examples on dikei. We draw the coloring of the regular dichromatic crossings, as in the following Figure 6.
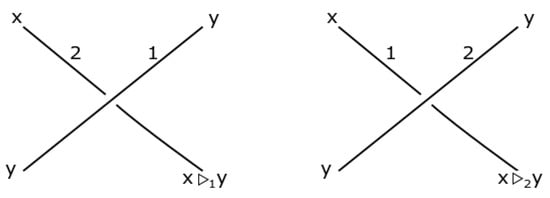
Figure 6.
The coloring of regular dichromatic crossings.
Next, we show how the extended Reidemeister moves induce the relations of a dikei. The following definition comes from the extended Reidemeister moves and the axioms illustrated in Figure 7, Figure 8 and Figure 9.
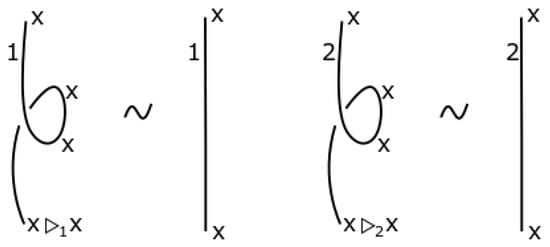
Figure 7.
Reidemeister move RI for dichromatic link.
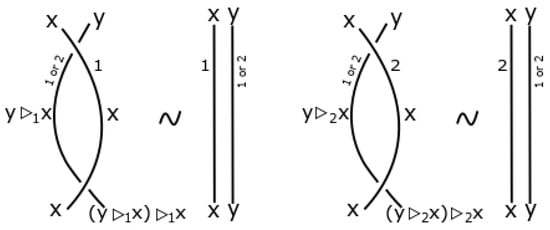
Figure 8.
Reidemeister move RII for dichromatic link.
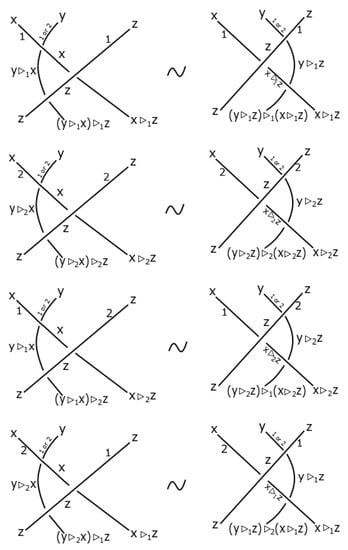
Figure 9.
Reidemeister moves RIII for dichromatic link.
Definition 4.
Let and be two kei. Then, is called a dikei if the following two axioms are satisfied:
The following straightforward lemma makes the set of coloring of a dichromatic link by a dikei an invariant of dichromatic links.
Lemma 1.
The set of coloring of a dichromatic link by a dikei does not change by the Reidemeister moves.
Lemma 2.
Let (X, ⊳) be a kei, and let . Then, is a dikei.
Lemma 3.
Let (X, ⊳) be a kei, and let , and . Then, is a dikei.
Proof.
We show that and satisfy the axiom (1), (2).
So, is a dikei. □
Lemma 4.
Let be the set of integers with and . Then, is a dikei.
Proof.
We show that and satisfy the axiom (1), (2).
So, is a dikei. □
Lemma 5.
Let G be a group with and . Then, is a dikei.
Proof.
We show that and satisfy the axiom (1), (2).
So, is a dikei. □
Theorem 1.
Let be the additive finite cyclic group of order n with the binary operations and . Then, is a dikei.
Proof.
We show that is a kei.
while
So, by Lemma 3, is a dikei. □
Example 2.
Let with and . Then, is a dikei.
Proof.
We show that and satisfy the axiom (1), (2).
So, is a dikei. □
Theorem 2.
Let G be a group, and with a binary operation . Then, is a kei. See [15] for reference.
Proof.
We show that ⊳ satisfies the axioms in Definition 1.
while
So, is a kei. □
Theorem 3.
Let G be a group, and with the operations and . Then, is a dikei.
Proof.
We show that and satisfy the axiom (1), (2).
So, is a dikei. □
4. Applications
Example 3.
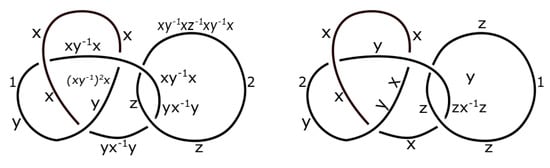
Consider the following two dichromatic links. Let G be a group with the operations and . See Figure 10 for reference, where the numbers 1 and 2 represent the colors of the components in the dichromatic links.

Figure 10.
The dichromatic links A and B in Example 3, respectively.
In Figure 10, the leftt-hand image (A) shows the relations at the crossings resulting from the binary operations, which give , , and . Thus, the set of coloring is
Justification:
In Figure 10, the right-hand image (B) shows the relations at the crossings resulting from the binary operations, which give , , and . Thus, the set of coloring is
Justification:
Therefore, this coloring invariant distinguishes these two dichromatic links. To explain this, let be the additive finite cyclic group of order 3; then, , and . Therefore, , and .
Example 4.
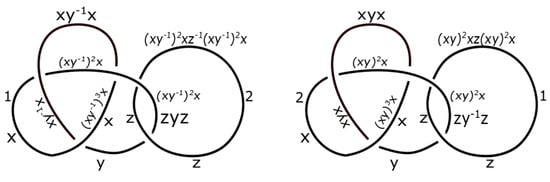
Consider the following two dichromatic links. Let G be a group, and with the operations and . See Figure 11 for reference, where the numbers 1 and 2 represent the colors of the components in the dichromatic links.

Figure 11.
The dichromatic links A and B in Example 4, respectively.
In Figure 11, the left-hand image (A) shows the relations at the crossings resulting from the binary operations, which give , , and . Thus, the set of coloring is
Justification:
In Figure 11, the right-hand image (B) show the relations at the crossings resulting from the binary operations give , , and . Thus, the set of coloring is
Justification:
Therefore, this coloring invariant distinguishes these two dichromatic links. To explain this, let be the additive finite cyclic group of order 4, and ; then, , and . Therefore, , and .
Example 5.
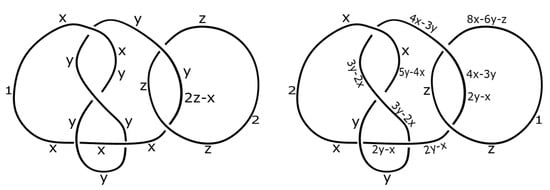
Consider the following two dichromatic links. Let with the operations and . See Figure 12 for reference, where the numbers 1 and 2 represent the colors of the components in the dichromatic links.

Figure 12.
The dichromatic links A and B in Example 5, respectively.
In Figure 12, the leftt-hand image (A) shows the relations at the crossings resulting from the binary operations, which give , and . Thus, the set of coloring is
Justification:
In Figure 12, the right-hand image (B) shows the relations at the crossings resulting from the binary operations, which give , and . Thus, the set of coloring is
Justification:
The solution set is equal for both of the sets of coloring above. Therefore, this coloring invariant does not distinguish these two dichromatic links.
Example 6.
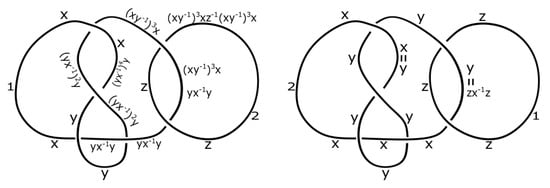
Consider the following two dichromatic links. Let G be a group with the operations and . See Figure 13 for reference, where the numbers 1 and 2 represent the colors of the components in the dichromatic links.

Figure 13.
The dichromatic links A and B in Example 6, respectively.
In Figure 13, the left-hand image (A) shows the relations at the crossings resulting from the binary operations, which give , , and . Thus, the set of coloring is
Justification:
In Figure 13, the right-hand image (B) shows the relations at the crossings resulting from the binary operations, which give , , and . Thus, the set of coloring is
Justification:
Therefore, this coloring invariant distinguishes these two dichromatic links. To explain this, let be the additive finite cyclic group of order 10; then , and . Therefore, , and ; we leave the calculations for the reader.
Example 7.
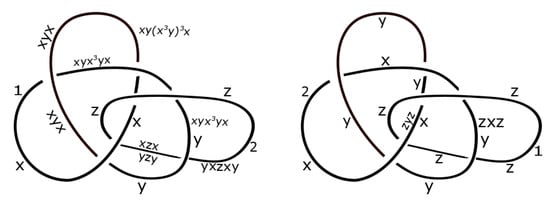
Consider the following two dichromatic links. Let G be a group, and with the operations and . See Figure 14 for reference, where the numbers 1 and 2 represent the colors of the components in the dichromatic links.

Figure 14.
The dichromatic links A and B in Example 7, respectively.
In Figure 14, the left-hand image (A) shows the relations at the crossings resulting from the binary operations, which give , , , and . Thus, the set of coloring is
Justification:
In Figure 14, the right-hand image (B) shows the relations at the crossings resulting from the binary operations, which give , and . Thus, the set of coloring is
Justification:
Therefore, this coloring invariant distinguishes these two dichromatic links. To explain this, let be the additive finite cyclic group of order 4, and , then , and . Therefore, , and .
5. Conclusions
Our idea is that we extend the notion of an involutory quandle (or kei) from regular links to dichromatic links, and define a new algebraic structure for two-component dichromatic links. We call this structure a dikei. It results from the generalized Reidemeister moves representing dichromatic isotopy. We give several examples on dikei, and we could distinguish many two-component dichromatic links that are isotopic as without colors. This evidently provides the power of our structure as it is not affected by the symmetry in the pairs of links in the examples. We failed to distinguish some dichromatic links, as we think that there are other concrete examples satisfying the dikei axioms, and this is definitely to be investigated in future research.
Author Contributions
Both authors equally contributed to the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bataineh, K. On the skein theory of dichromatic links and invariants of finite type. J. Knot Theory Its Ramif. 2017, 26, 1750092. [Google Scholar] [CrossRef]
- Hoste, J.; Kidwell, M.E. Dichromatic link invariants. Trans. Am. Math. Soc. 1990, 321, 197–229. [Google Scholar] [CrossRef]
- Hoste, J.; Przytycki, J.H. An invariant of dichromatic link. Proc. Am. Math. Soc. 1989, 105, 1003–1007. [Google Scholar] [CrossRef]
- Bataineh, K.; Elhamdadi, M.; Hajij, M.; Youmans, W. Generating sets of Reidemeister moves of oriented singular links and quandles. J. Knot Theory Its Ramif. 2018, 27, 1850064. [Google Scholar] [CrossRef]
- Carter, J.S.; Silver, D.S.; Williams, S.G.; Elhamdadi, M.; Saito, M. Virtual knot invariants from group biquandles and their cocycles. J. Knot Theory Its Ramif. 2009, 18, 957–972. [Google Scholar] [CrossRef]
- Chien, J.; Nelson, S. Virtual Links with Finite Medial Bikei. J. Symb. Comput. 2019, 92, 211–221. [Google Scholar] [CrossRef]
- Churchill, I.R.; Elhamdadi, M.; Hajij, M.; Nelson, S. Singular knots and involutive quandles. J. Knot Theory Its Ramif. 2017, 26, 1750099. [Google Scholar] [CrossRef]
- Clark, W.E.; Elhamdadi, M.; Saito, M.; Yeatman, T. Quandle colorings of knots and applications. J. Knot Theory Its Ramif. 2014, 23, 1450035. [Google Scholar] [CrossRef] [PubMed]
- Elhamdadi, M.; Nelson, S. Quandles; American Mathematical Soc.: Providence, RI, USA, 2015; p. 47. [Google Scholar]
- Henrich, A.; Nelson, S. Semiquandles and flat virtual knots. Pac. J. Math. 2010, 248, 155–170. [Google Scholar] [CrossRef][Green Version]
- Joyce, D. A classifying invariant of knots, the knot quandle. J. Pure Appl. Algebra 1982, 23, 37–65. [Google Scholar] [CrossRef]
- Kauffman, L.H. Invariants of graphs in three-space. Trans. Am. Math. Soc. 1989, 311, 697–710. [Google Scholar] [CrossRef]
- Nelson, S.; Rivera, P. Bikei invariants and gauss diagrams for virtual knotted surfaces. J. Knot Theory Its Ramif. 2016, 25, 1640008. [Google Scholar] [CrossRef]
- Przytycki, J. 3-coloring and other elementary invariants of knots. Banach Cent. Publ. 1998, 42, 275–295. [Google Scholar] [CrossRef]
- Stanovský, D. The origins of involutory quandles. arXiv 2015, arXiv:1506.02389. [Google Scholar]
- Wada, M. Group invariants of links. Topology 1992, 31, 399–406. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).