Maximum-Entropy-Model-Enabled Complexity Reduction Algorithm in Modern Video Coding Standards

Abstract

Symmetry considerations play a key role in modern science, and any differentiable symmetry of the action of a physical system has a corresponding conservation law. Symmetry may be regarded as reduction of Entropy. This work focuses on reducing the computational complexity of modern video coding standards by using the maximum entropy principle. The high computational complexity of the coding unit (CU) size decision in modern video coding standards is a critical challenge for real-time applications. This problem is solved in a novel approach considering CU termination, skip, and normal decisions as three-class making problems. The maximum entropy model (MEM) is formulated to the CU size decision problem, which can optimize the conditional entropy; the improved iterative scaling (IIS) algorithm is used to solve this optimization problem. The classification features consist of the spatio-temporal information of the CU, including the rate–distortion (RD) cost, coded block flag (CBF), and depth. For the case analysis, the proposed method is based on High Efficiency Video Coding (H.265/HEVC) standards. The experimental results demonstrate that the proposed method can reduce the computational complexity of the H.265/HEVC encoder significantly. Compared with the H.265/HEVC reference model, the proposed method can reduce the average encoding time by 53.27% and 56.36% under low delay and random access configurations, while Bjontegaard Delta Bit Rates (BD-BRs) are 0.72% and 0.93% on average.

1. Introduction

With the rapid development of the Internet, high-resolution video applications are very broad and a variety of different video applications have emerged. However, modern video coding technologies face great challenges. The modern video coding standards, including H.264/AVC and H.265/HEVC, generally adopt hybrid codec structures. The modern video encoders consist of (1) inter- and intra-frame prediction, (2) transformation, (3) quantization, and (4) entropy coding. Moreover, most video sequences contain huge redundancies that can be divided into two categories: Statistical and visual redundancies. Therefore, this work focuses on reducing the computational complexity of modern video encoders by using statistical redundancies.

In 2013, the Joint Collaborative Team on Video Coding (JCT-VC) organization released the High Efficiency Video Coding standard (HEVC or H.265) [1], which uses hybrid encoding technology. Compared with Advanced Video Coding(AVC, or H.264), the coding block size of H.265/HEVC increases from $16\times 16$ to $64\times 64$, while the average encoding compression ratio is increased by 55–87%. Moreover, the computational complexity of H.265/HEVC increases significantly. With the adoption of mobile and embedded terminals, the H.265/HEVC encoder faces real-time and low-power challenges. In general, the computational complexity of the modern video encoder increases dramatically due to its recursive quad-tree construction. In previous works, the spatial redundancies [2,3], spatio-temporal redundancies [4,5], and visual redundancies [6] were used to reduce the computational complexity of the modern video encoder. However, most of them balance the computational complexity and encoding efficiency unsuccessfully.

In order to achieve the trade-off between the computational complexity and encoding efficiency of the modern video encoder, the maximum-entropy-model-based coding unit (CU) size decision algorithm is proposed to reduce the computational complexity. However, for the H.264/AVC and H.265/HEVC encoders, the maximum CU sizes are different, and the coded block flag (CBF) definitions are different. For the case analysis, the maximum CU size is $64\times 64$. Therefore, in this work, the proposed algorithm is designed to reduce the computational complexity of the H.265/HEVC encoder. Compared to the traditional classifier, the accuracy of the maximum entropy model is higher and constraints can be set flexibly. The key contributions of this work are summarized as follows:

• A fast CU size decision algorithm is proposed to reduce the complexity of the modern video encoder, which consists of CU termination, skip, and normal decisions. The maximum-entropy-model-enabled CU size decision approach is formulated to maximize the condition of entropy. Moreover, the improved iterative scaling (IIS) algorithm is proposed to solve this optimization problem.
• The rate–distortion (RD) cost, coded block flag (CBF), and depth information of neighboring CUs are as featured as parameters which do not bring in additional calculations. Moreover, the online method is proposed to learn the model parameters.
• Based on H.265/HEVC standards, the proposed method reduces the computational complexity significantly. The simulation results demonstrate that the proposed algorithm reduces the average encoding time by 53.27% and 56.36% under low delay and random access configurations, while Bjontegaard Delta Bit Rates (BD-BRs) are 0.72% and 0.93% on average.

The rest of paper is organized as follows. Related work is surveyed in Section 2. The background is reviewed in Section 3. In Section 4, the proposed CU size decision approach is proposed. Experimental results are discussed in Section 5. The conclusion is depicted in Section 6.

2. Related Work

Previous works focus on reducing the computational complexity of H.265/HEVC. There are mainly three methods for reducing coding complexity: Coding unit (CU) size and depth determination, prediction unit (PU) mode determination, transform unit (TU) size determination, and fast motion estimation (FME). For the CU size decision in inter-prediction, state-of-the-art algorithms mainly focus on the middle parameters of CU-based approaches [7,8], classification-model-based approaches [9,10], and parallel-based approaches [11].

Firstly, the authors of [12] present a novel CU termination algorithm, where the average depth of the coding unit is used to predict coding unit size. The work in [13] focuses on the complexity reduction of the H.265/HEVC encoder, and an efficient coding unit partitioning and prediction unit mode decision method is proposed by using a look-ahead stage. Ref. [14] proposes a depth-segmentation-enabled complexity reduction algorithm for 3D-HEVC inter-prediction, where the depth map can be classified as background, mid-ground, and foreground. The work in [15] proposes a new entropy-based coding unit size decision algorithm, and the threshold can be decided by maximum similarity technology. The work in [16] proposes an adaptive CU termination approach by using the middle parameters of CU, and the search range of motion estimation is adjusted to speed up the H.265/HEVC encoder. The advantage of the middle parameters of CU-based method is that the implementation is simple, though it is sensitive to image boundaries.

Secondly, the authors of [17] propose an efficient block partitioning approach for H.265/HEVC by using Bayesian theory. In this context, Gaussian mixture models are used to estimate statistical parameters. The work in [18] presents a support vector machine (SVM)-based CU size decision algorithm, and a radial basis function (RBF) kernel is used to optimize variables. In [19], a neural-networks-based CU depth decision method is proposed to reduce the complexity of the H.265/HEVC encoder. In this context, a database is developed, which includes image values and encoding information. Moreover, a neural network architecture is designed to train model parameters. In [20], CU size decision is modeled as a Markov decision process (MDP), and the end-to-end actor critic (AC) algorithm is used to train the model. The authors of [21] present a Bayesian-classifier-enabled CU size decision algorithm, and the Markov Chain Monte Carlo (MCMC) technology is used to estimate statistical parameters. The advantage of the classification-model-based method is that the algorithm is simple, and the disadvantage is that the robustness is not high.

Moreover, Ref. [22] presents a novel parallelization approach to accelerate the H.265/HEVC encoder. In this context, a content-aware frame partitioning method is used to reduce the parallelization overhead. The authors of [23] focus on improving the parallelization of the H.265/HEVC encoder, and a novel collaborative-scheduling-enabled parallel approach is proposed to accelerate H.265/HEVC encoding. Ref. [24] presents a new CU size decision framework in parallel to reduce the complexity of the H.265/HEVC encoder, and a many-core platform is developed to speed up the coding unit tree decision. The advantage of the parallel-based method is that the complexity can be reduced significantly while the encoding efficiency is decreased.

3. Background

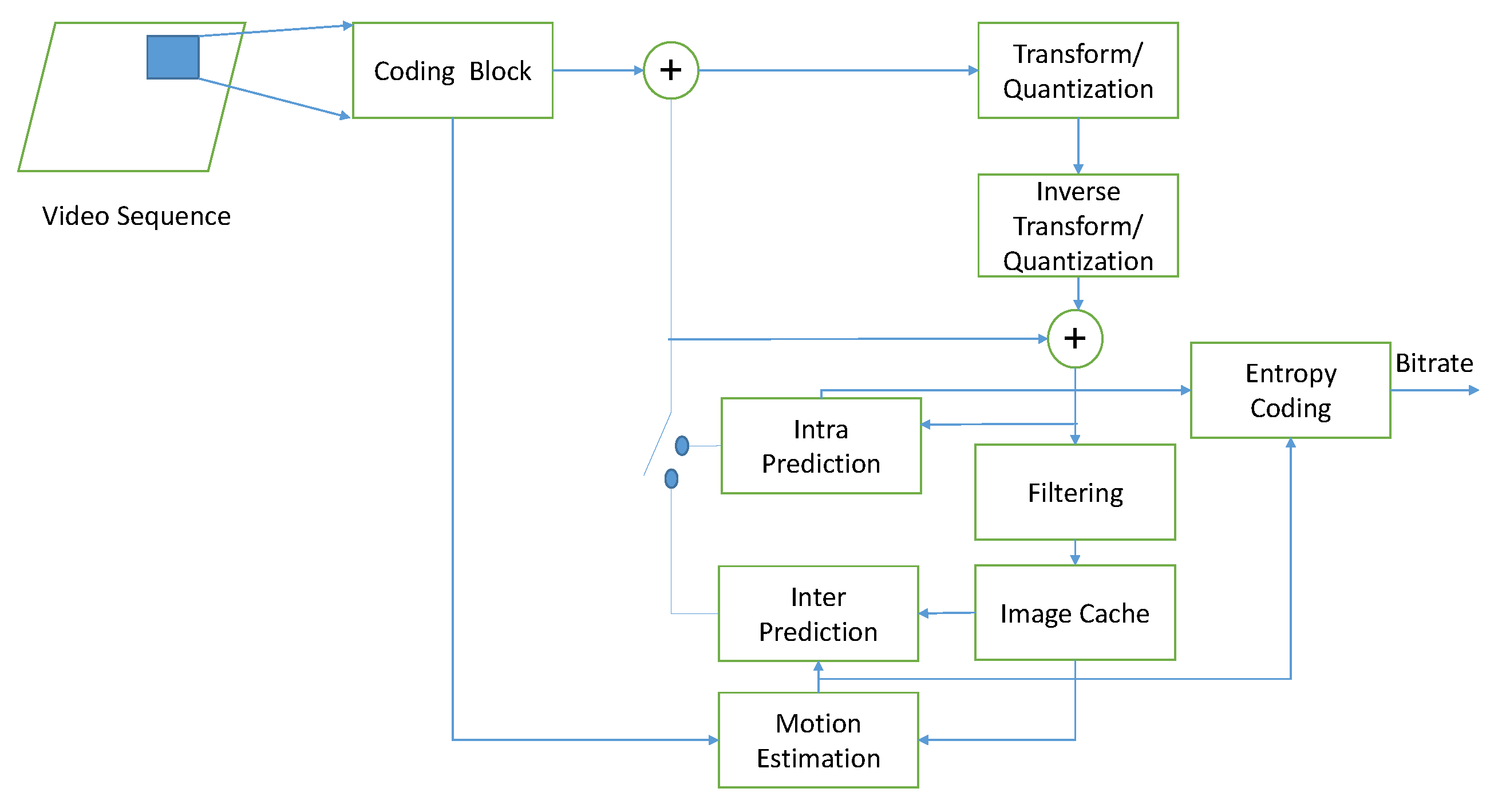
3.1. High-Efficiency Video Coding Standard

The H.265/HEVC coding structure is similar to the previous ITU-T (International Telecommunication Union, Telecommunication Standardization Sector) and ISO/IEC(International Organization for Standardization/International Electrotechnical Commission) MPEG (Moving Picture Experts Group) video compression standards, and it uses a hybrid coding framework. Although its basic coding structure has not changed, its algorithm is more and more flexible, and its coding efficiency is getting higher and higher. The coding framework of H.265/HEVC is shown in Figure 1. The main modules are: Intra-prediction, inter-prediction, transform/quantization, adaptive filtering, and entropy coding.

Figure 1. High Efficiency Video Coding (H.265/HEVC) hybrid coding framework.

In H.265/HEVC, an image is divided into a sequence of coding tree units (CTUs). The concept of the CTU is similar to macro-blocks in the H.264/AVC standard. A CTU contains three sample arrays, which are an N × N luma coding block (CTB) and two corresponding chroma CTBs. In H.265/HEVC, the maximum size of the luminance CTB is 64 × 64. The CTU is the basic processing unit of the decoding process, and the large-size CTU can achieve higher coding efficiency and increase the computational complexity. Therefore, choosing the right CTU size can achieve a balance between the encoding efficiency and computational complexity.

The coding unit (CU) is a square area that is used to represent the leaf nodes of the CTU. It shares the same prediction mode: Intra, inter, and skip. The quad-tree partition structure of the CU allows the parent node to be recursively split into four child nodes of the same size. The size of each CU is from the CTU to 8 × 8 adaptive selection. In the CTU, the split flag (split_cu_flag) is used to indicate whether the current CU block will continue to split into four sub-CUs. When the flag is one yes, the CU splits; for each generated CU block, another flag is transmitted and indicates whether the current block represents one CU or will be further divided into four CU blocks. When the size of the CU block is 8 × 8, no split flag is transmitted during the encoding process. Therefore, the computational complexity of the CU partitioning process is very high. In general, a low complexity encoder will try to choose a larger CU size instead of a small CU size.

The z-scan scan order of the partition and code of the CU is shown in Figure 2. We assume that the size of the coding unit CU${}_t$ is 2N × 2N and the depth is t. When the split flag split_cu_flag is 0, CU${}_t$ does not split; otherwise, CU${}_t$ splits into four CU${}_{t+1}$ of the same size, and CU${}_{t+1}$ is N × N and has a depth of t + 1. Compared with H.264/AVC, the H.265/HEVC CU partitioning method has great advantages:

Figure 2. The diagram of coding unit (CU) partitioning.

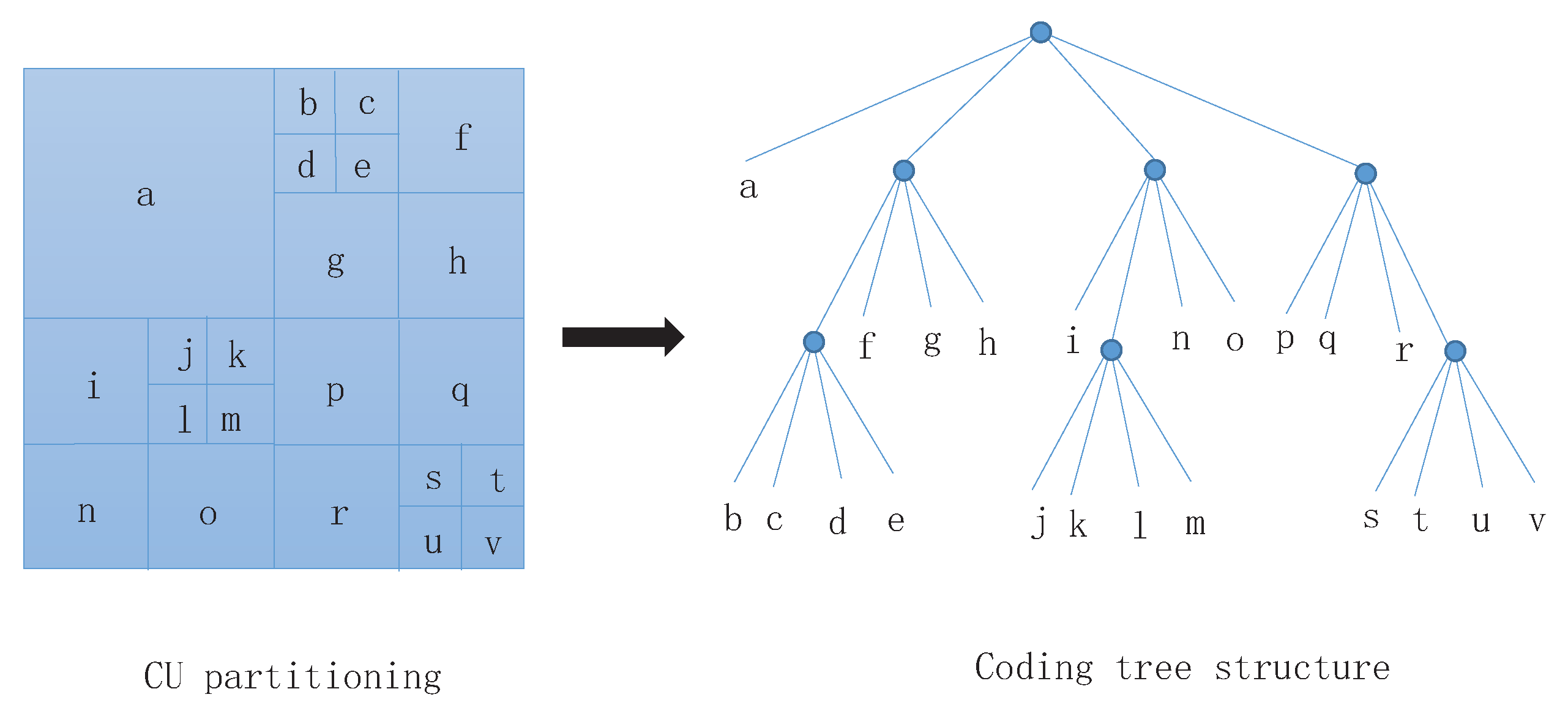
• The size of the CU block in H.265/HEVC is larger than the macroblock size in H.264/AVC. For relatively flat images, a large CU block can be selected, which can save the number of code stream bits and improve coding effectiveness.
• The size and depth of the CU in H.265/HEVC can be selected according to the characteristics of the image, so that the performance of the encoder can be greatly improved.
• There are macroblocks and sub-macroblocks in H.264/AVC. There are only CU blocks in H.265/HEVC, and the structure is simple.

A prediction unit (PU) is an area in which the partitioning structure of the CU is used to define it and share the same prediction information. In general, a PU is not limited to a square shape; it can easily distinguish the true boundary of the image. The PU specifies the prediction mode of the CU, the direction of the intra-prediction, the segmentation mode of the inter-prediction, and the motion vector (MV) information, which are all included in the PU.

The prediction mode of a CU of size 2N × 2N is shown in Figure 3. For intra-prediction, PU has two prediction modes: 2N × 2N and N × N; for inter-prediction, PU has eight prediction modes for four symmetric modes (2N × 2) N, 2N × N, N ×2 N, N × N) and four asymmetric modes (2N × nU, 2N × nD, nL × 2N, nR × 2N). In particular, the SKIP mode is a special case of the inter-prediction mode. When the motion information has only the index of the motion parameter and the residual information is not required, it is in the SKIP mode.

Figure 3. The diagram of prediction unit (PU) modes.

3.2. Maximum Entropy Principle

Entropy is a measure of the uncertainty of a random variable [25]. The greater the uncertainty, the larger the entropy value. If the random variable degenerates to a fixed value, the entropy is zero. Assuming that the probability distribution of the discrete random variable x is $p\left(x\right)$, its entropy is given in [26]:

$$\begin{array}{c}\hfill H\left(X\right)=-\sum _{i=1}^{n}p\left(x_i\right){log}_{2}p\left(x_i\right)=\sum _{i=1}^{n}p\left(x_i\right){log}_2\frac{1}{p\left(x_i\right)}.\end{array}$$

(1)

The joint distribution of X and Y of two random variables can form joint entropy, expressed by $H(X,Y)$, and the conditional entropy $H\left(Y\right|X)$ is expressed in [27]:

$$\begin{array}{c}\hfill H\left(Y\right|X)=H(X,Y)-H\left(X\right)=-\sum _{x,y}^{}p(x,y)logp\left(y\right|x).\end{array}$$

(2)

For a model that is selected from the set of the probability distributions C, when the selecting model satisfies $p^{*}\left(y\right|x)$ ∈ C, the entropy $H\left(Y\right|X)$ is maximum, and the maximum entropy is given in [28]:

$$\begin{array}{c}\hfill p^{*}\left(y\right|x)=argmaxH\left(Y\right|X)\end{array}$$

(3)

The characteristic function $f_i(x,y)$ describes the relationship between the input x and the outputs y. $f_i(x,y)$ is the binary function, which is expressed in [29]:

$$\begin{array}{c}\hfill f_i(x,y)=\left\{\begin{array}{cc}1,\hfill & x=x_i,y=y_i\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right..\end{array}$$

(4)

The expected value of the characteristic function with respect to the empirical distribution $\overline{p}(x,y)$ in the sample is $\overline{E}\left(f_i\right)={\sum }_{x_i,y_i}^{}\overline{p}(x,y)f_i(x,y)$, where $\overline{p}(x,y)=\frac{1}{N}num(x,y)$, N is the size of the training sample, and $num(x,y)$ is the number of simultaneous occurrences of $(x,y)$ in the sample. Moreover, the expected value of the eigenfunction with respect to the model $p\left(y\right|x)$ and the empirical distribution $\overline{p}\left(x\right)$ is $E\left(f_i\right)={\sum }_{x_i,y_i}^{}\overline{p}\left(x\right)p\left(y\right|x)f_i(x,y)$. The complete representation of the maximum entropy model (MEM) is thus obtained as follows:

$$\begin{array}{c}\hfill p^{*}\left(y\right|x)=argmaxH\left(Y\right|X)=argmax\sum _{x,y}^{}\overline{p}\left(x\right)p\left(y\right|x)log\frac{1}{p\left(y\right|x)},\end{array}$$

(5)

where the corresponding constraints are

$$\begin{array}{ll}\mathrm{s}.\mathrm{t}.\hfill & \left(\mathrm{C}1\right):p\left(y\right|x)>=0,\forall x,y,\\ & \left(\mathrm{C}2\right):{\displaystyle \sum _y^{}}p\left(y\right|x)=1,\forall x,\\ & \left(\mathrm{C}3\right):\overline{E}\left(f_i\right)=E\left(f_i\right),i=\{1,2\dots ,n\},\end{array}$$

where n is the number of the characteristic function $f_i(x,y)$. Therefore, this problem is the optimization problem that requires values of several variables (including n, N and num($x,y$)) to maximize the objective function (entropy).

4. The Proposed Approach

In this section, the maximum-entropy-model-based CU size decision approach is proposed to reduce the complexity of inter-prediction in H.265/HEVC.

Firstly, mode selection is based on rate–distortion optimization (RDO) in H.265/HEVC. By using the rate–distortion (RD) cost, H.265/HEVC can make the encoding parameters derivation decision for the quad-tree structure. In addition, the CBF reflects the complexity of the prediction residual under a given quantization parameter (QP).

The H.265/HEVC reference software adopts the algorithm of using CBF as the early termination CU partition. Thus, the RD cost and CBF are closely related to the CU partitioning. The variable $w_{rdc}$ represents the RD cost of the PU with the 2N × 2N mode. The variable $w_{cbf}$ represents the CBF value of the PU with the 2N × 2N mode.

Moreover, the video sequence has a strong spatial and temporal correlation. The context adaptation of context-adaptive binary arithmetic coding (CABAC) fully exploits the context correlation and models the coded symbols. The CU partition depth information is also a very effective feature. Figure 4 shows the neighboring CUs of the current CU; depth information of neighboring CUs is useful for CU size decision. In this work, $w_{dt}$, $w_{dl}$, and $w_{dco}$ represent the depth information of top, left, and co-located CUs of the current CU. Therefore, the feature set w is used to make CU size decision, which consists of

$$\begin{array}{c}\hfill w=\{w_{rdc},w_{cbf},w_{dt},w_{dl},w_{dco}\}.\end{array}$$

(6)

Figure 4. The neighboring CUs of the current CU.

In the H.265/HEVC standard, two fast CU size decision methods are developed to speed up inter-prediction, which includes the CU termination decision and CU skip decision. In the CU termination processing, the splitting of the CU terminates in the current depth. In the CU skip processing, the PU mode is determined at the earliest stage and RDO technology is processed in the next depth. In the CU normal processing, other PU modes are checked in the current depth. Therefore, the CU size decision task (represented by a variable s) consists of CU termination, CU skip, and CU normal decisions, which can be formulated as

$$\begin{array}{c}\hfill s=\left\{\begin{array}{cc}{s}_1,\hfill & CUtermination\hfill \\ s_2,\hfill & CUskip\hfill \\ s_3,\hfill & CUnormal\hfill \end{array}\right..\end{array}$$

(7)

Given the data set $\{{(x_i,s_i)}_i^N\}$ and characteristic function $f_i(w,y)$, the CU size decision problem can be converted into the MEM-based optimization problem to maximize the conditional entropy $H\left(s\right|w)$, which can be formulated as:

$$\begin{array}{c}\hfill \begin{array}{c}maxH\left(s\right|w)=max\sum _{w,s}^{}\overline{p}\left(w\right)p\left(s\right|w)log\frac{1}{p\left(s\right|w)}\hfill \\ \mathrm{s}.\mathrm{t}.\sum _s^{}p\left(s\right|w)=1,\forall w,\hfill \\ \sum _{w,s}^{}\overline{p}\left(w\right)p\left(s\right|w)f_i(w,s)=\sum _{w,s}^{}\overline{p}(w,s)f_i(w,s).\hfill \end{array}\end{array}$$

(8)

In order to solve this optimization problem, the parameter ${\lambda }_i$ is introduced for each $f_i(w,s)$ to obtain the Lagrangian function $L(p,\mathsf{\Lambda },\gamma )$:

$$\begin{array}{c}\hfill \begin{array}{c}L(p,\mathsf{\Lambda },\gamma )=\sum _{w,s}^{}\overline{p}\left(w\right)p\left(s\right|w)log\frac{1}{p\left(s\right|w)}\hfill \\ +\sum _{i=1}^{}{\lambda }_i\sum _{w,s}^{}{f}_i(w,s)[p\left(s\right|w)\overline{p}\left(w\right)-\overline{p}(w,s)]\hfill \\ +\gamma (\sum _s^{}p\left(s\right|w)-1),\hfill \end{array}\end{array}$$

(9)

where the parameter $\mathsf{\Lambda }=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}$. Therefore, the $L(p,\mathsf{\Lambda },\gamma )$ is derived on $p\left(s\right|w)$ as

$$\begin{array}{c}\hfill \frac{\partial L}{\partial p\left(s\right|w)}=\overline{p}\left(w\right)(log\frac{1}{p\left(s\right|w)}-1)+\sum _i^{}{\lambda }_i\overline{p}\left(w\right)f_i(w,s)+\gamma .\end{array}$$

(10)

Let the above Formula (10) equal 0. Therefore, we can obtain the optimal solutions of Equation (8).

$$\begin{array}{c}\hfill p^{*}\left(s\right|w)=\frac{1}{Z\left(w\right)}exp(\sum _{i=1}^{}{\lambda }_i{f}_i(w,s)),\end{array}$$

(11)

where $Z\left(w\right)$ is called the normalization factor and it is equal to

$$\begin{array}{c}\hfill Z\left(w\right)=\sum _{s}exp(\sum _{i=1}^{}{\lambda }_i{f}_i(w,s)),\end{array}$$

(12)

where $p\left(s\right|w)$ and $\gamma$ in the Lagrangian function $L(p,\mathsf{\Lambda },\gamma )$ can be expressed as $\mathsf{\Lambda }$. Therefore, the problem is transformed into the solution parameter $\mathsf{\Lambda }=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}$. To this end, we define the dual function $\psi \left(\mathsf{\Lambda }\right)$ and its optimization problem

$$\begin{array}{c}\hfill \psi \left(\mathsf{\Lambda }\right)=L(p^{*},\mathsf{\Lambda },{\gamma }^{*})\end{array}$$

(13)

$$\begin{array}{c}\hfill find{\mathsf{\Lambda }}^{*}=arg\underset{\mathsf{\Lambda }}{min}\psi \left(\mathsf{\Lambda }\right).\end{array}$$

(14)

According to the Karush–Kuhn–Tucker (KKT) conditions [30], the parameter $\mathsf{\Lambda }$ in the model $p^{*}\left(s\right|w)$ of Equation (11) can be solved by minimizing the dual function $\psi \left(\mathsf{\Lambda }\right)$, as in Equations (13) and (14) shown. In this work, the improved iterative scaling (IIS) algorithm is used to solve the optimization problem corresponding to this maximum entropy model [31].

Moreover, there are two stages for MEM-based CU size decision. The first stage is to extract the features from the sample. The second stage is based on these features to build a model. In this work, the online learning method is used to estimate model parameters $\mathsf{\Lambda }=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}$. Figure 5 shows the online method of updating model parameters. The first frame of each group of pictures (GOP) is used to train the model parameters, which are encoded by the original encoder. When all parameters in $\mathsf{\Lambda }$ have converged, a lookup table (LUT) is used to store optimal parameter values ${\mathsf{\Lambda }}^{*}$ and optimal model $p^{*}$. Then, the other frames of GOP are encoded based on the proposed method.

Figure 5. The online model training method.

Therefore, in order to reduce the encoding complexity for inter-prediction in the H.265/HEVC encoder, the efficient MEM-based CU size decision algorithm is proposed, which consists of CU termination, CU skip, and CU normal decisions. Figure 6 shows the proposed flowchart, which can be described as follows.

Figure 6. The flowchart of the proposed algorithm.

(1)

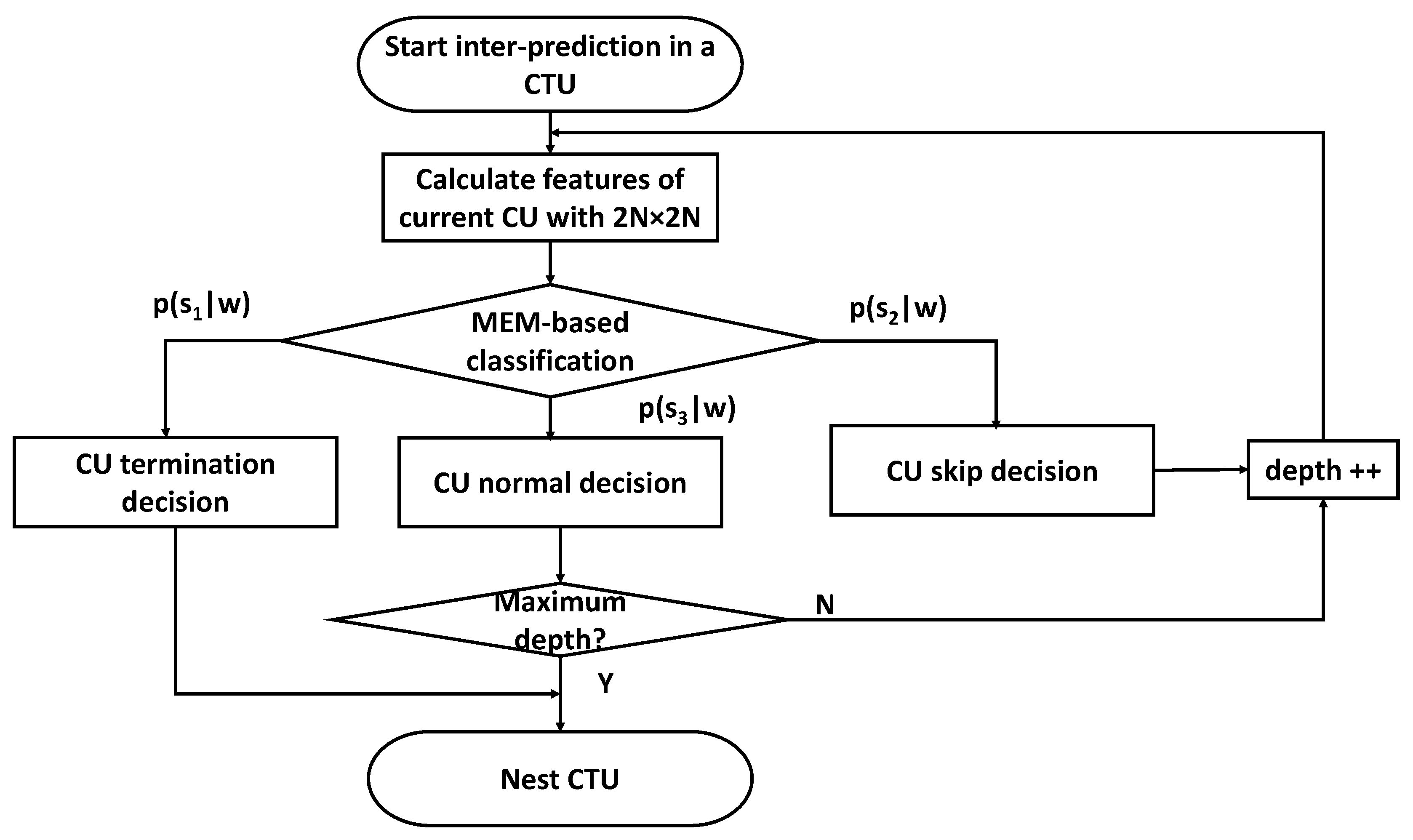
Firstly, model parameter values $\mathsf{\Lambda }=\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\}$ are imported from the LUT. Then, inter-prediction is started in a CTU by using the proposed method.

(2)

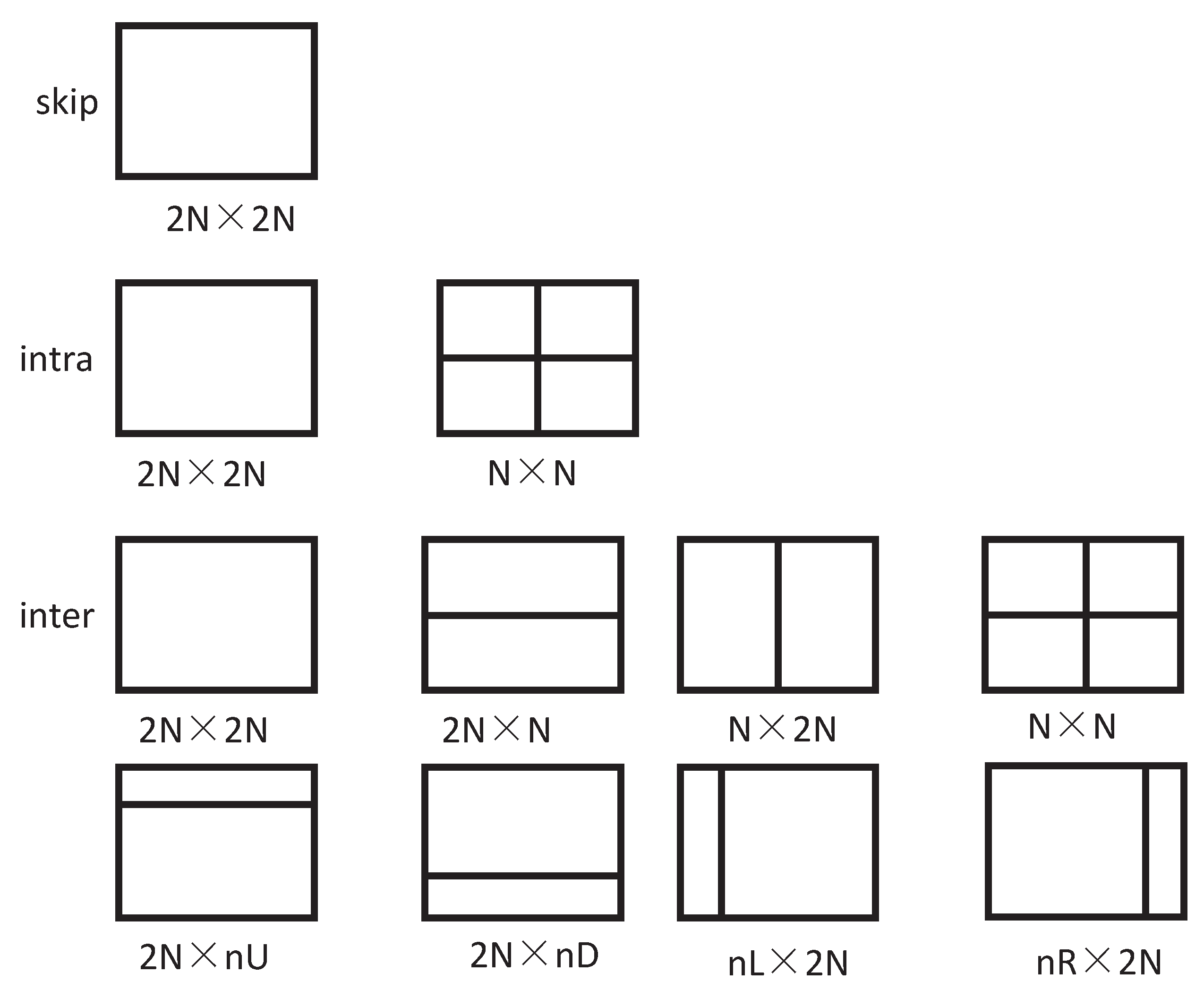
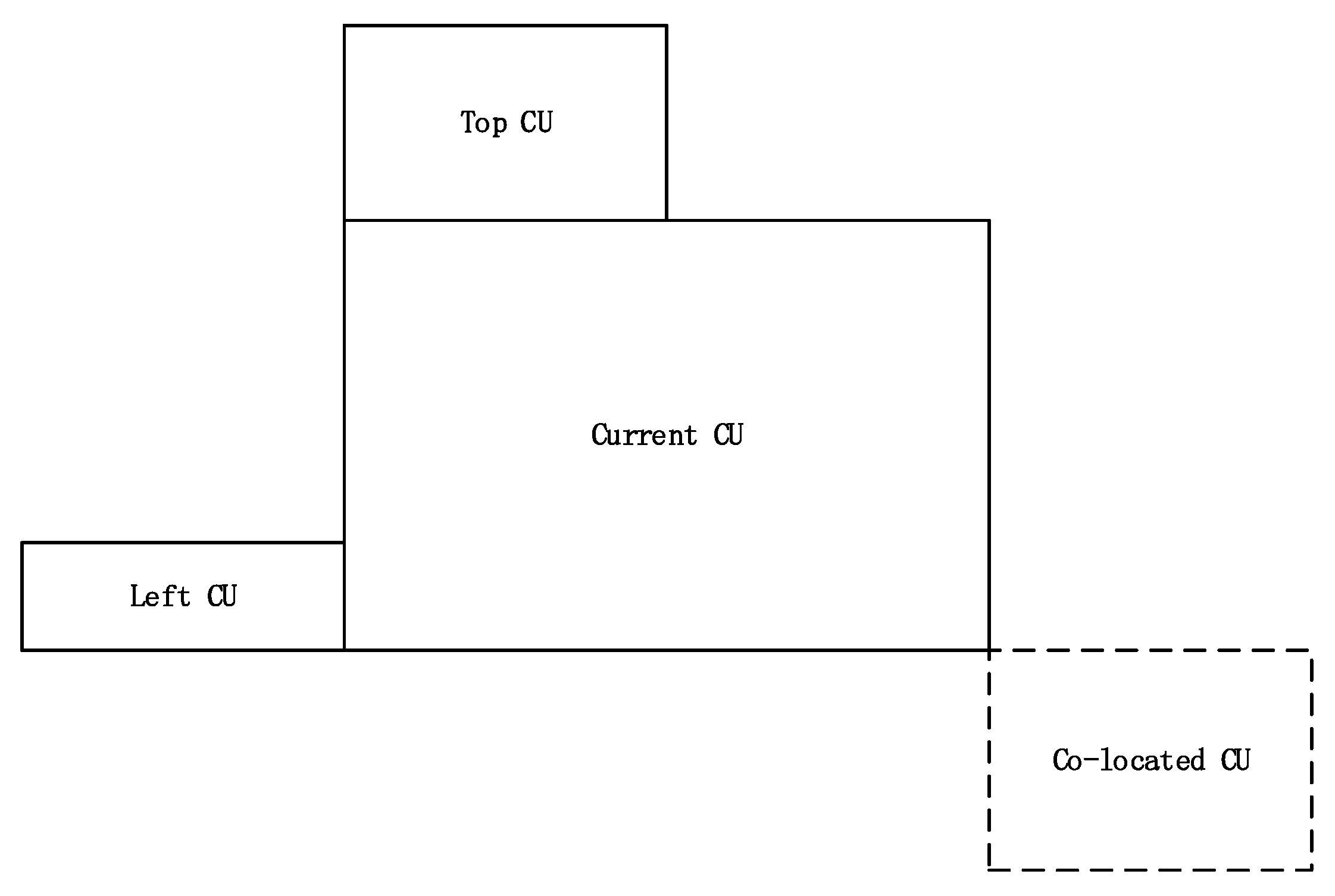
Secondly, spatial and temporal features—including the RD cost, CBF value, depth information of top, left, and co-located CUs of PU with the 2N × 2N mode—are calculated. The feature set is expressed as w.

(3)

Then, based on parameter values ${\mathsf{\Lambda }}^{*}$, the model $p\left(s\right|w)$ is calculated. If $p^{*}=p\left(s_1\right|w)$, the CU termination decision is processed. In this case, the splitting of the CU terminates in the current depth. Otherwise, if $p^{*}=p\left(s_2\right|w)$, the CU skip decision is made. In this case, the PU mode is determined at the earliest stage and RDO technology is processed in the next depth. Otherwise, the CU normal decision is made.

(4)

Finally, when the current depth of CU is less than the maximum depth, the steps (2) and (3) are repeated. Otherwise, the next CTU is checked.

The advantages of the maximum entropy model are: (1) The maximum entropy statistical model obtains the model with the maximum information entropy among all of the models that meet the constraint conditions, and the accuracy is relatively high relative to the classical classification model. (2) By using the maximum entropy principle, we can not only obtain the unique result of a given problem, but also achieve the objective result as far as possible by relying on limited data and overcome the possible deviation. Therefore, the maximum-entropy-model-based classical classification can decide CU partitioning optimally. Moreover, the proposed method can reduce the computational complexity of the modern video codec significantly, while the loss of encoding efficiency is small.

5. Simulation Results

In this section, simulation results have been verified for the performance of the proposed CU size decision algorithm. The simulation platform is based on the H.265/HEVC reference software (HM16.0), and file configurations are based on low delay (LD) and random access (RA) [32]. In the LD configuration file, only the first frame is encoded as an independent decoded frame according to the intra-frame mode, and the subsequent frames are encoded as general P frames and B frames. The LD configuration is designed for real-time video applications. However, the coding structures of the RA configuration consist of hierarchical B frames with clean Random Access frames inserted periodically. This random access method strongly supports channel conversion, search, and dynamic streaming services. Moreover, the depth range of CU is from zero to three, and QP values are set to 22, 27, 32, and 37. The Common Test Conditions (CTC) are provided to conduct experiments. The test sequences in CTC have different spatial and temporal characteristics and frame rates.

The performance of H.265/HEVC is evaluated in terms of the Bjontegaard Delta Bit Rate (BD-BR) and the Bjontegaard Delta Peak Signal to Noise Ratio (BD-PSNR) [33]; an efficient tool is used to compute BD-BR and BD-PSNR in [34]. The average time saving ($\mathsf{\Delta }T$) is formulated as

$$\begin{array}{c}\hfill \mathsf{\Delta }T=\frac{1}{4}\times \sum _{i=1}^4\frac{T_{HM}\left(Q{P}_i\right)-T_{proposed}\left(Q{P}_i\right)}{T_{HM}\left(Q{P}_i\right)}\times 100\end{array}$$

(15)

where $T_{HM}\left(Q{P}_i\right)$ and $T_{proposed}\left(Q{P}_i\right)$ denote the encoding time of using HM16.0 and the proposed algorithm with different QPs.

Table 1 shows experiment results under the LD configuration. With the proposed method, the average encoding time can be saved 53.27%, while BD-BR and BD-PSNR are 0.72% and $-0.027$ dB on average. For the high-resolution sequences (1920 × 1080 and 1280 × 720), the encoding time can be reduced by 57.36% and 64.78%, while the loss of BD-BR is 1.19% and 0.77%. For the low-resolution sequences (832 × 480 and 416 × 240), the encoding time can be reduced by 50.75% and 54.10%, while the loss of BD-BR is 0.83% and 0.87%. Moreover, in the best case, the encoding time of video sequence Vidyo4 can be reduced by 64.89%. In the worse case, the encoding time of video sequence PartyScene can be reduced by 45.57%. Therefore, the proposed method can save more encoding time in the high resolution than in the low resolution. On the contrary, the loss of encoding efficiency is greater in the high resolution than in the low resolution.

Table 1. Performance comparison of different parts of the proposed method (low delay (LD)).

Resolution	Sequence	BD-BR(%)	BD-PSNR(dB)	$\mathsf{\Delta }$T(%)
$1920\times 1080$	Kinomo	1.39	$-0.049$	55.71
	ParkScene	0.84	$-0.028$	54.67
	Cactus	0.84	$-0.021$	50.38
	BQTerrace	0.56	$-0.016$	55.74
	Average	0.91	$-0.029$	54.13
$832\times 480$	BasketballDrill	0.55	$-0.023$	46.26
	BQMall	0.73	$-0.033$	49.71
	PartyScene	0.46	$-0.027$	45.57
	RaceHorses	0.73	$-0.033$	48.93
	Average	0.62	$-0.029$	47.62
$416\times 240$	BasketballPass	0.58	$-0.031$	52.05
	BQSquare	0.06	$-0.004$	49.52
	BlowingBubbles	1.19	$-0.052$	48.52
	Average	0.61	$-0.029$	49.94
$1280\times 720$	Vidyo1	0.77	$-0.026$	62.65
	Vidyo3	0.93	$-0.030$	61.44
	Vidyo4	0.50	$-0.011$	64.89
	Average	0.73	$-0.022$	62.99
Average		0.72	$-0.027$	53.27

Table 2 shows the experiment results under the RA configuration. It is seen that the proposed method can save about 56.36% encoding time on average, while the BD-BR and BD-PSNR are 0.93% and $-0.036$ dB. For the high-resolution sequences (1920 × 1080 and 1280 × 720), the encoding time can be reduced by 54.13% and 62.99%, while the loss of BD-BR is 0.91% and 0.73%. For the low-resolution sequences (832 × 480 and 416 × 240), the encoding time can be reduced by 47.62% and 49.94%, while the loss of BD-BR is 0.62% and 0.61%. Furthermore, in the best case, the encoding time of video sequence Vidyo4 can be reduced by 66.16%. In the worse case, the encoding time of video sequence PartyScene can be reduced by 48.71%. The proposed approach can save more encoding time in the high resolution than in the low resolution. All in all, the proposed method can reduce the computational complexity of the H.265/HEVC encoder significantly, while the loss of the encoding efficiency is small.

Table 2. Performance comparison of different parts of the proposed method (random access(RA)).

Resolution	Sequence	BD-BR(%)	BD-PSNR(dB)	$\mathsf{\Delta }$T(%)
$1920\times 1080$	Kinomo	1.70	$-0.059$	56.72
	ParkScene	1.02	$-0.034$	60.89
	Cactus	1.18	$-0.029$	54.27
	BQTerrace	0.84	$-0.022$	57.54
	Average	1.19	$-0.036$	57.36
$832\times 480$	BasketballDrill	0.54	$-0.023$	49.51
	BQMall	0.96	$-0.046$	54.52
	PartyScene	0.61	$-0.035$	48.71
	RaceHorses	1.23	$-0.054$	50.26
	Average	0.83	$-0.040$	50.75
$416\times 240$	BasketballPass	0.89	$-0.047$	55.32
	BQSquare	0.50	$-0.028$	54.46
	BlowingBubbles	1.21	$-0.053$	52.53
	Average	0.87	$-0.043$	54.10
$1280\times 720$	Vidyo1	1.00	$-0.035$	65.51
	Vidyo3	0.57	$-0.019$	62.66
	Vidyo4	0.74	$-0.025$	66.16
	Average	0.77	$-0.026$	64.78
Average		0.93	$-0.036$	56.36

Figure 7 shows the rate–distortion curve comparison between the proposed algorithm and the reference method under LD and RA configurations for the typical Vidyo4 and PartyScene sequences. As shown in the figure, no matter in the high bitrate interval or in the low bitrate interval, the proposed method can achieve almost the same rate–distortion curves as those of the reference model. Furthermore, the time savings under different QPs and configurations for Vidyo4 and PartyScene sequences are shown in Figure 8. It is seen that when the QP value is 37, the average time saving is highest. As the value of QP decreases, the average time saving decreases. In summary, the proposed method can significantly reduce the computational complexity under the LD and RA configurations.

Figure 7. Rate–distortion (RD) curve of the proposed algorithm for sequences Vidyo4 and PartyScene.

Figure 8. Time savings of the proposed algorithm for sequences Vidyo4 and PartyScene.

Table 3 shows the BD-BR, BD-PSNR, and time saving performance in comparison with those of previous works in [16,18,19]. The authors of [16] propose an efficient complexity reduction method that takes early CU split, CU termination, and search range adjustment into account. The work in [18] presents a fast CU size decision method which is based on SVM with off-line learning. In [19], a neural-network-based CU partitioning method is proposed. However, the proposed method is based on the maximum entropy model. For the low-delay configuration, the average BD-BR, BD-PSNR, and time saving are (0.72%, $-0.027$ dB, and 53.27%) for the proposed method. Compared with Tai’s work, Grellert’s work, and Kim’s work, the proposed method achieves maximum time saving. Although the loss of encoding efficiency of Grellert’s work is less than the loss of encoding efficiency of the proposed work, the time saving of Grellert’s work is only 41.10%. For the random access configuration, the average BD-BR, BD-PSNR, and time saving are (0.93%, $-0.036$ dB, and 56.36%) for the proposed method. Compared with the state-of-the-art, the proposed method achieves maximum time saving. Although the loss of encoding efficiency of Grellert’s work is less than the loss of encoding efficiency of the proposed work, the time saving of Grellert’s work is only 48.00%. Therefore, our work shows a higher performance improvement than the state-of-the-art approaches. Furthermore, the proposed algorithm achieves a better trade-off between the computational complexity and the encoding efficiency.

Table 3. Bjontegaard Delta Bit Rate (BD-BR), Bjontegaard Delta Peak Signal to Noise Ratio (BD-PSNR), and time saving performance comparison with previous works.

Configuration	Approach	(BD-BR, BD-PSNR, $\mathsf{\Delta }$T)
Low Delay	Our work	(0.72, $-0.027$, 53.27)
	Tai et al. [16]	(0.75, $-0.051$ 37.90)
	Grellert et al. [18]	(0.60, $-0.046$, 41.10 )
	Kim et al. [19]	(1.31, $-0.050$, 47.08)
Random Access	Our work	(0.93,$-0.036$, 56.36)
	Tai et al. [16]	(1.41, $-0.054$, 45.70)
	Grellert et al. [18]	(0.48, $-0.048$, 48.00)
	Kim et al. [19]	(1.51, $-0.052$, 47.32)

6. Conclusions

In this work, a novel maximum-entropy-model-based CU size algorithm is proposed to reduce the computational complexity in H.265/HEVC inter-prediction. The RD cost, CBF, and depth information of the relative CUs are used as classifier features, and the on-line learning method is used to estimate model parameters. Moreover, the fast algorithm consists of the CU termination, CU skip, and CU normal decisions. The simulation results show our work saves about 53.27–56.36% of the encoding time on average, while the average loss of encoding efficiency is only 0.72–0.93%.