Hybrid Multi-Domain Analytical and Data-Driven Modeling for Feed Systems in Machine Tools
Abstract
:1. Introduction
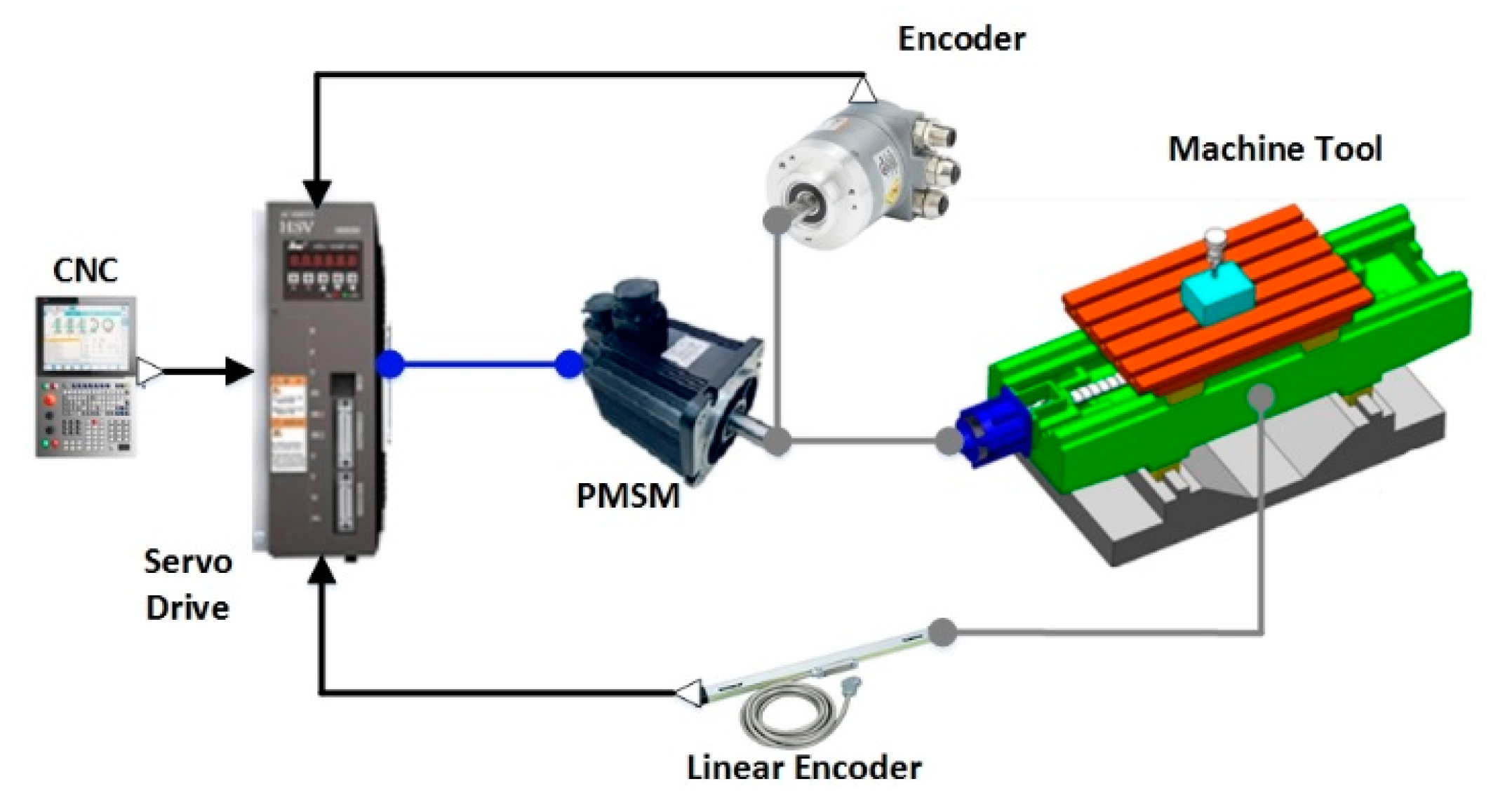
2. Multi-Domain Analytical Model of the Ball Screw Feed System
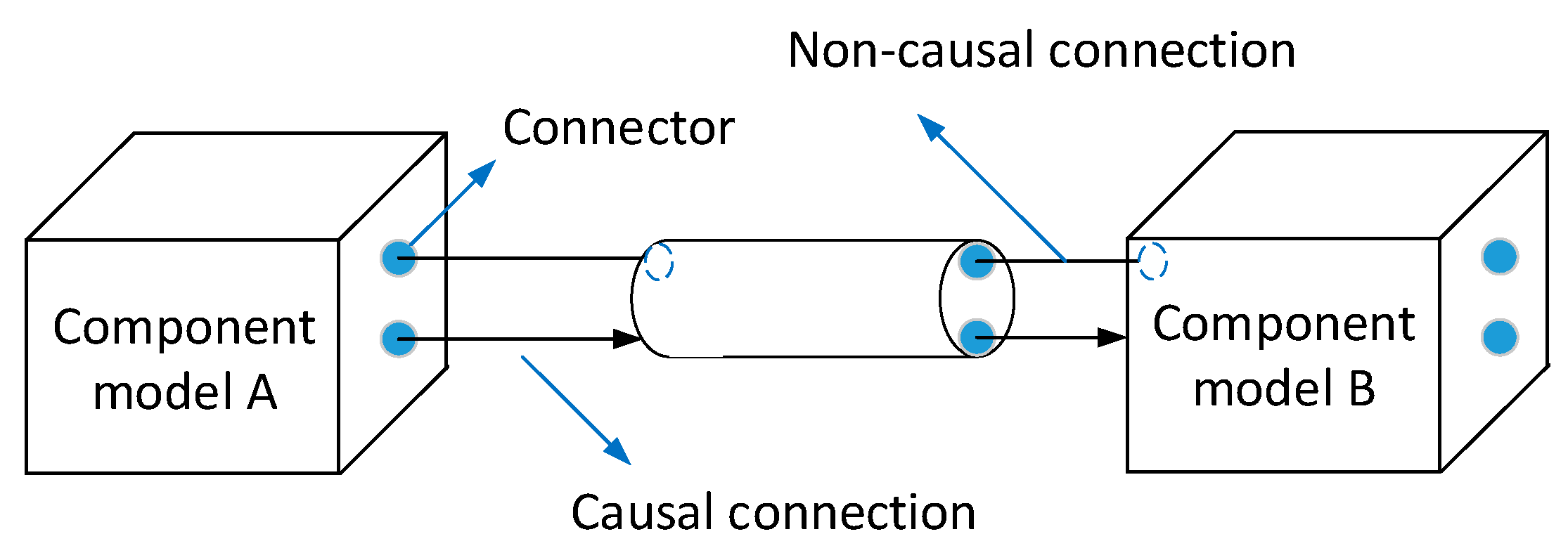
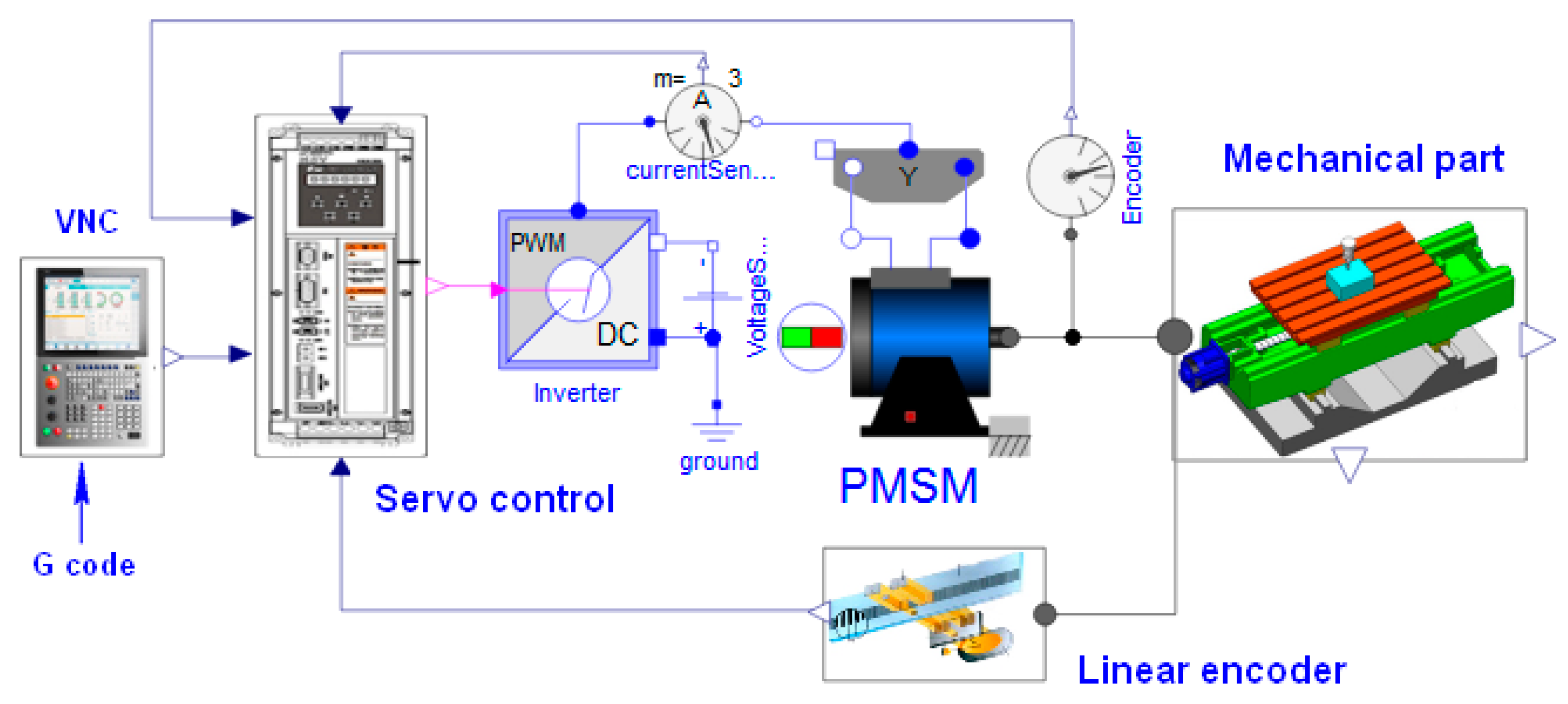
2.1. Multi-Domain Modeling Method for the Ball Screw Feed System
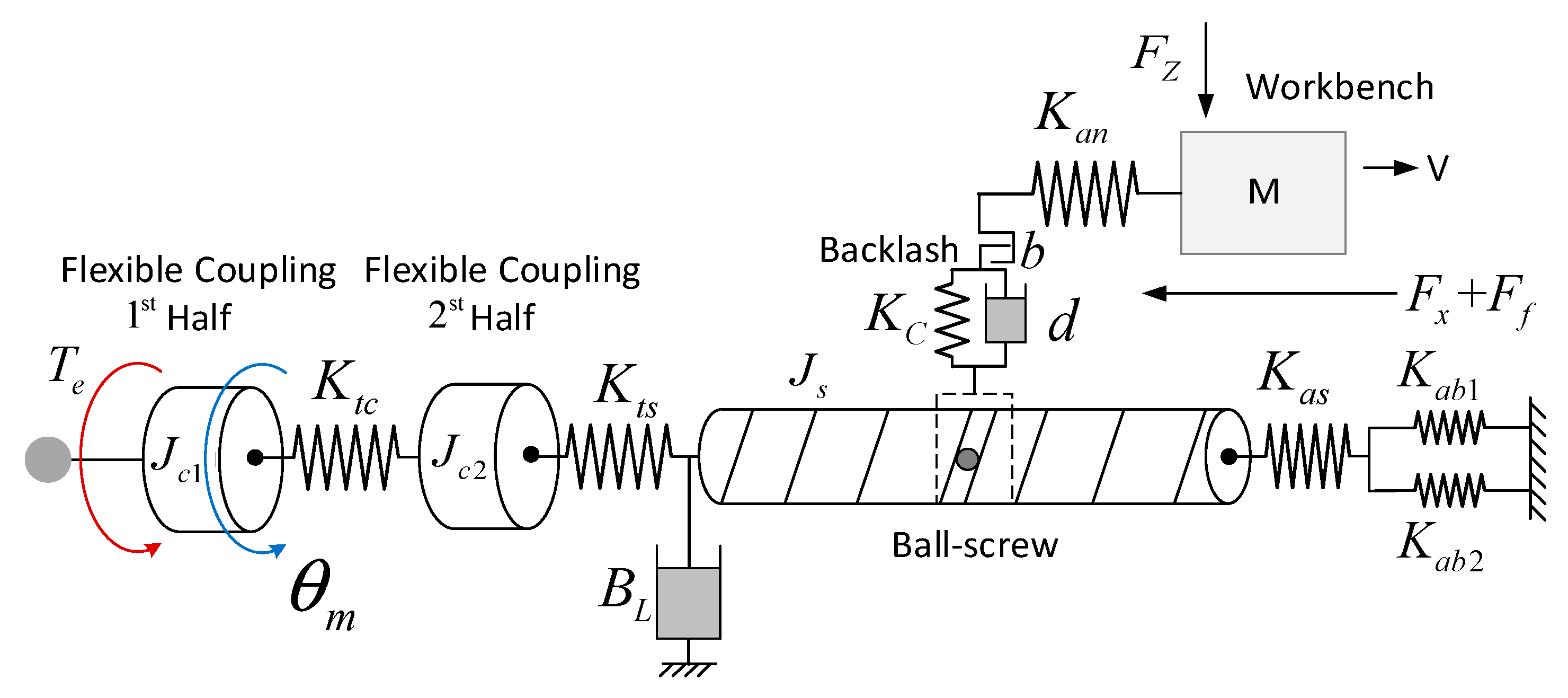
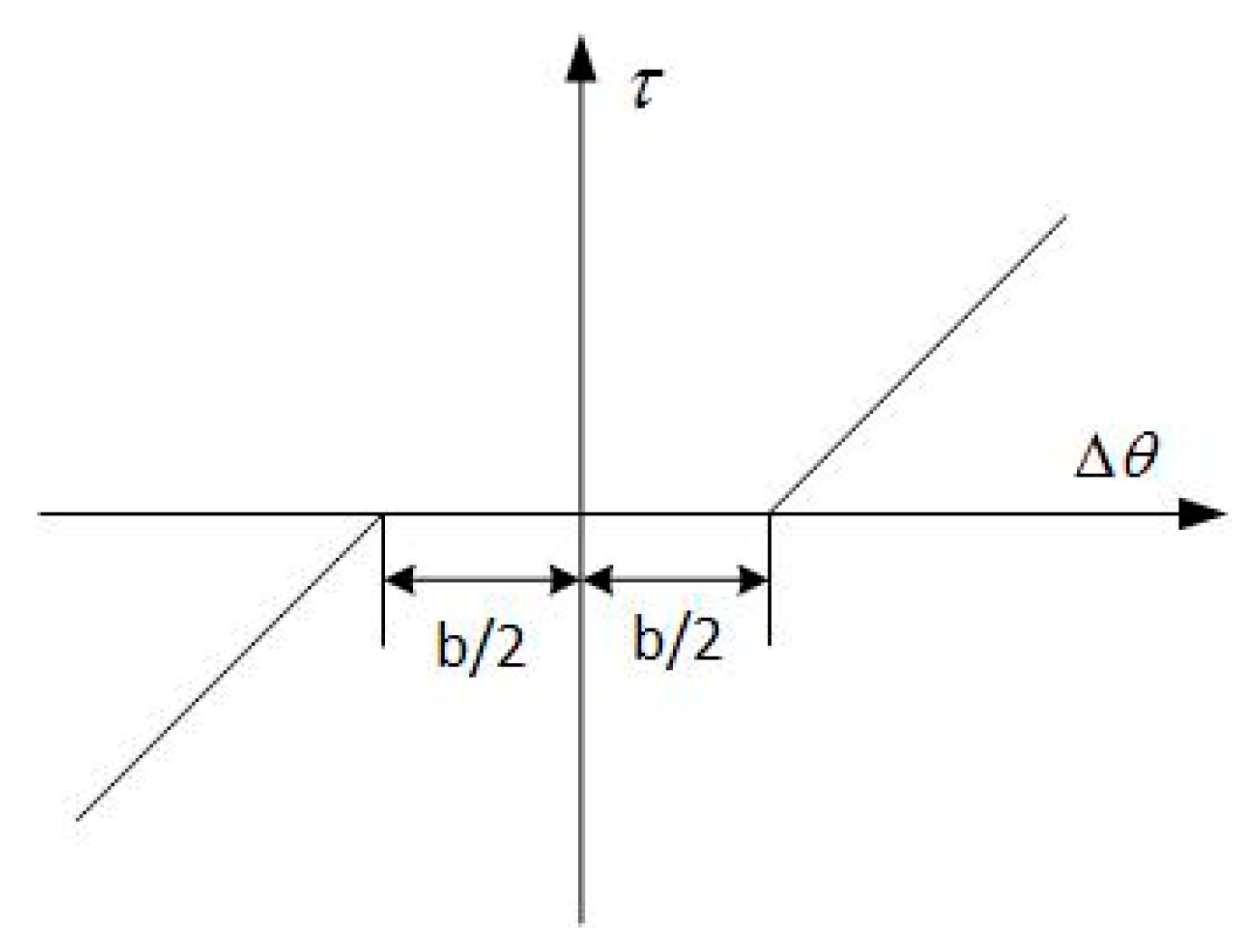
2.2. Modeling and Analysis of the Mechanical Subsystem
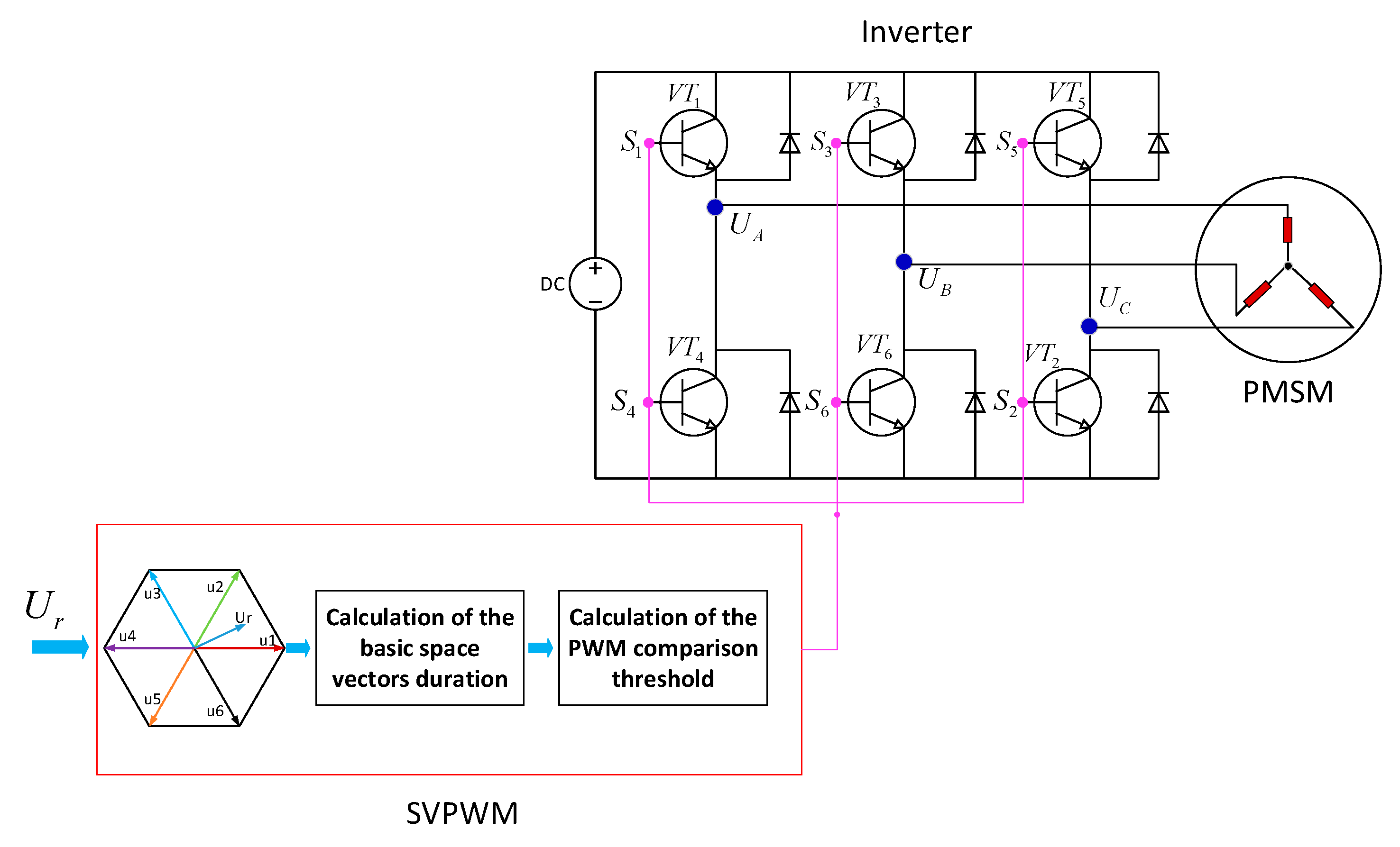
2.3. Modeling of the Servo Drive System
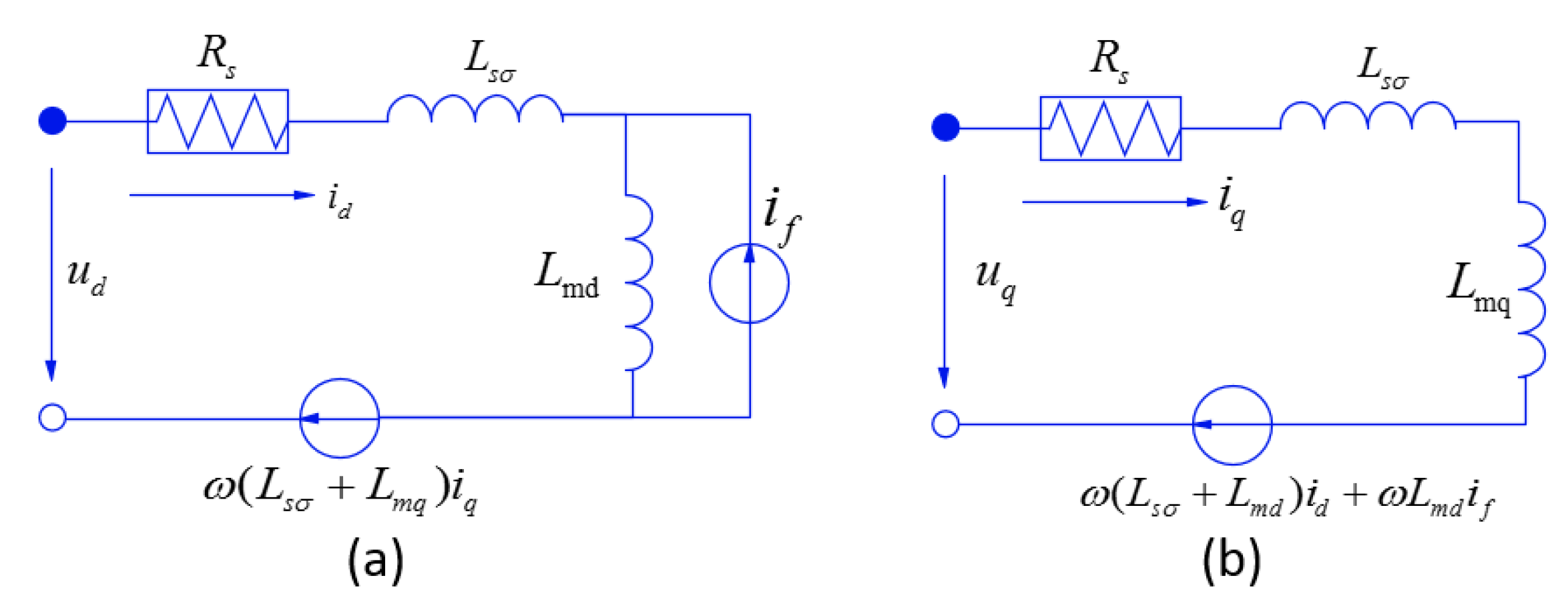
2.4. Modeling of the Permanent Magnet Synchronous Motor
- (1)
- The conductivity of permanent magnet material is zero;
- (2)
- There is no damping winding on the rotor;
- (3)
- Stator winding current produces only sine distribution of magnetic potential in the air gap, ignoring the high-order harmonic of magnetic field;
- (4)
- During the steady-state operation, the waveform of induction electromotive force in phase winding is sinusoidal.
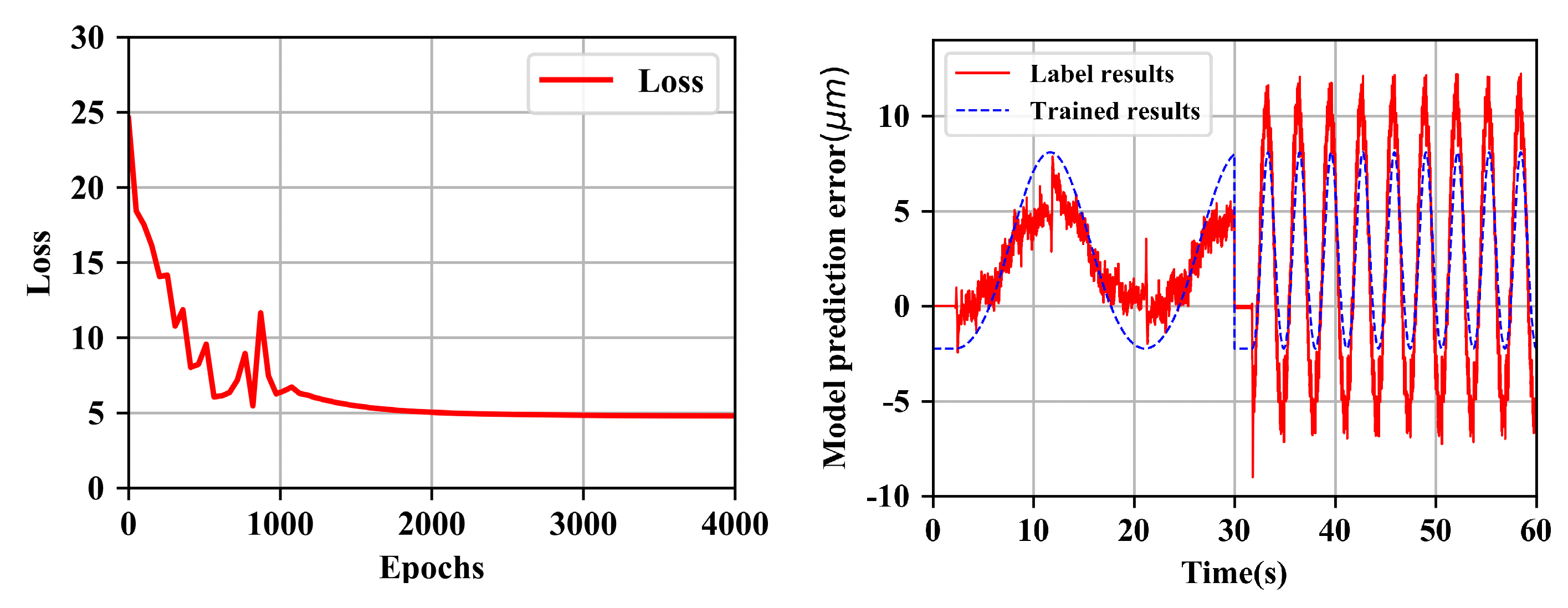
3. The Learned Data-Driven Model
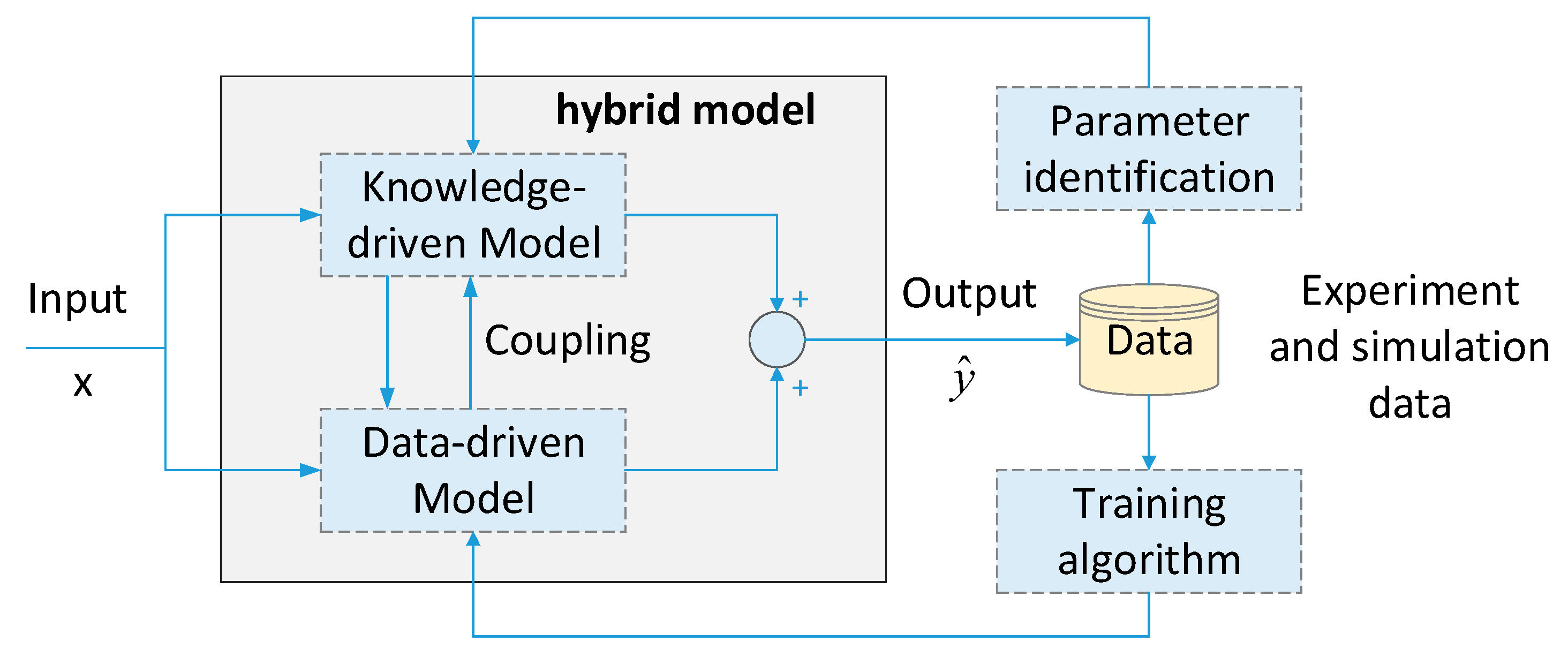
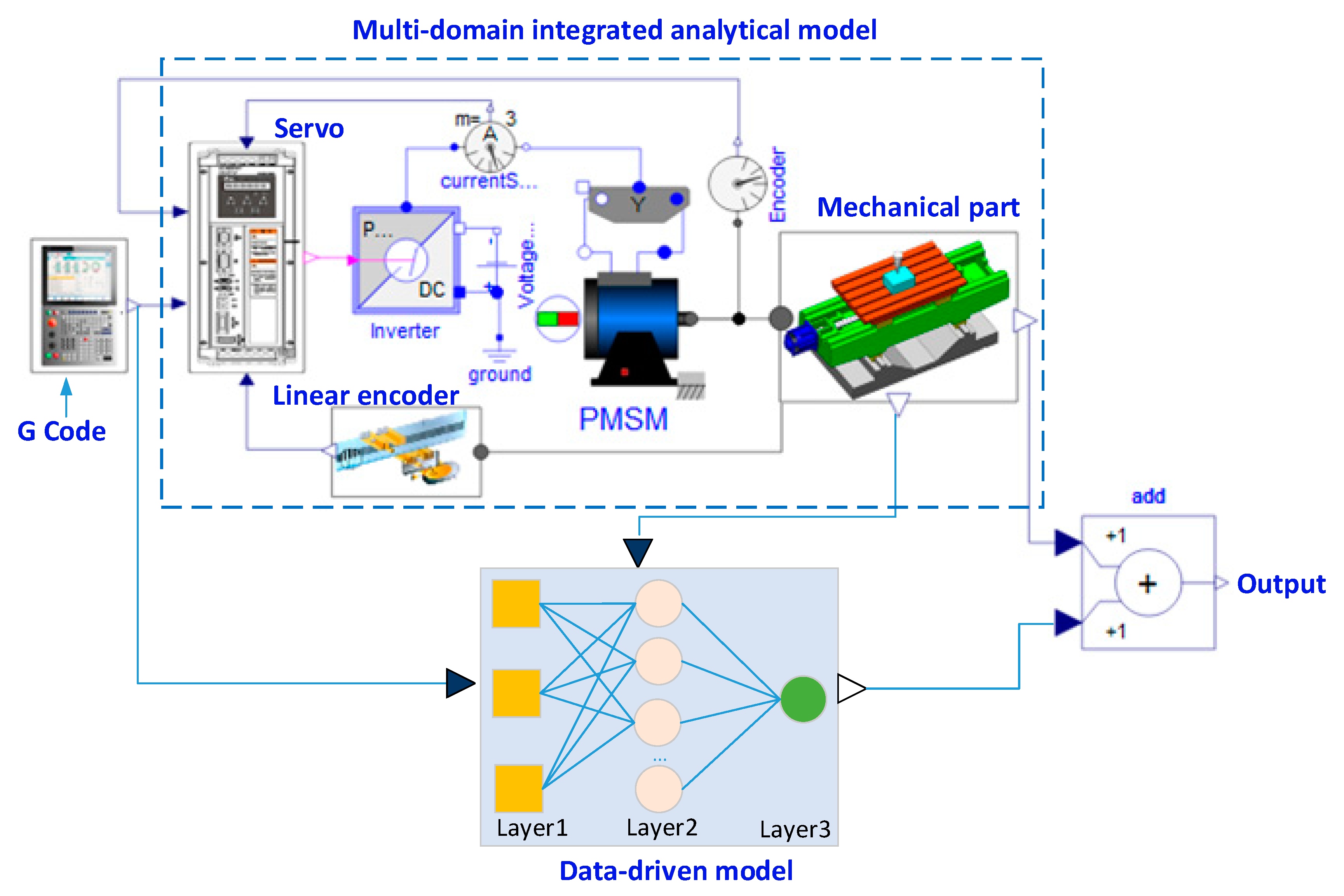
4. Hybrid Model of the Ball Screw Feed System
5. Simulation and Experiments
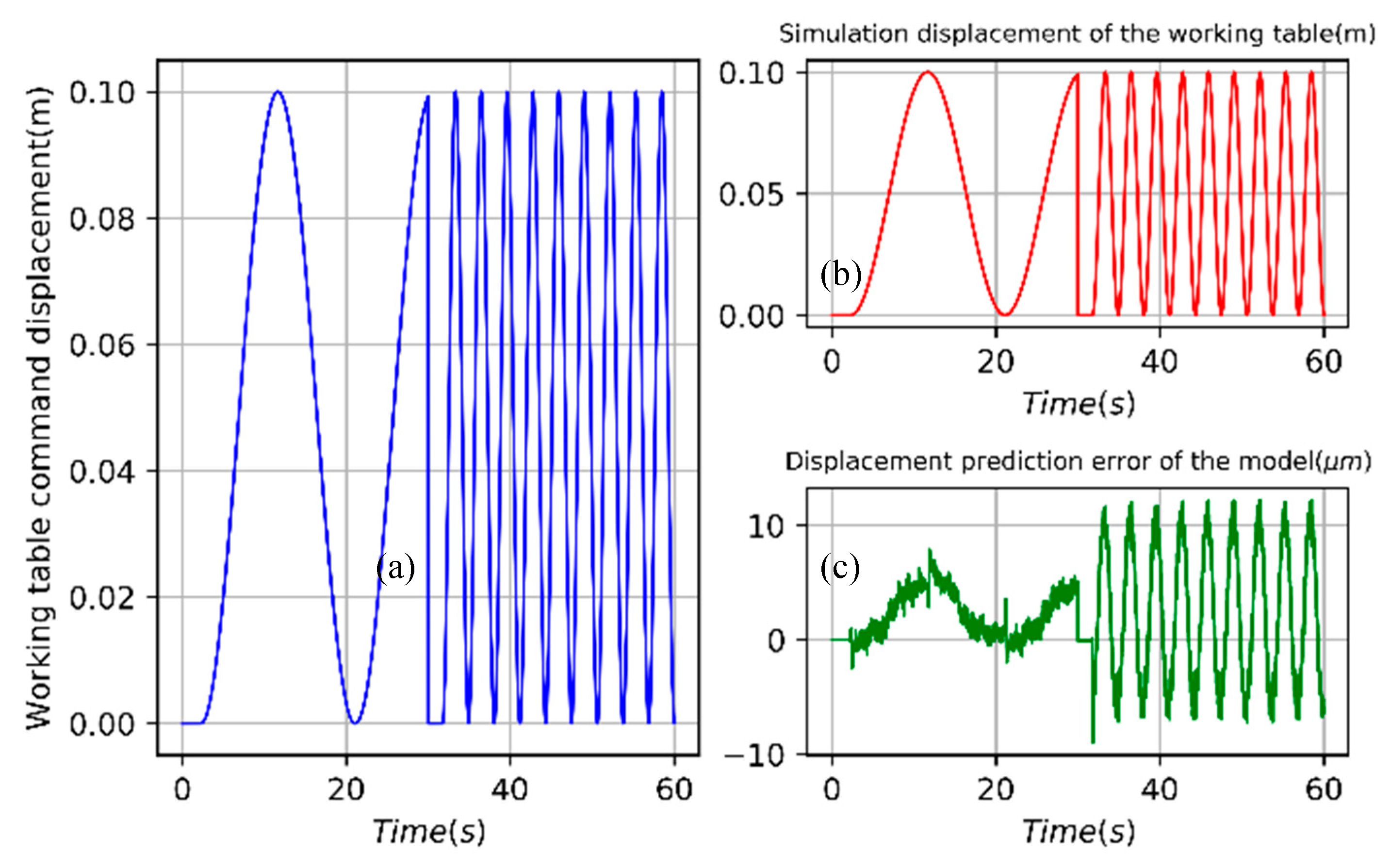
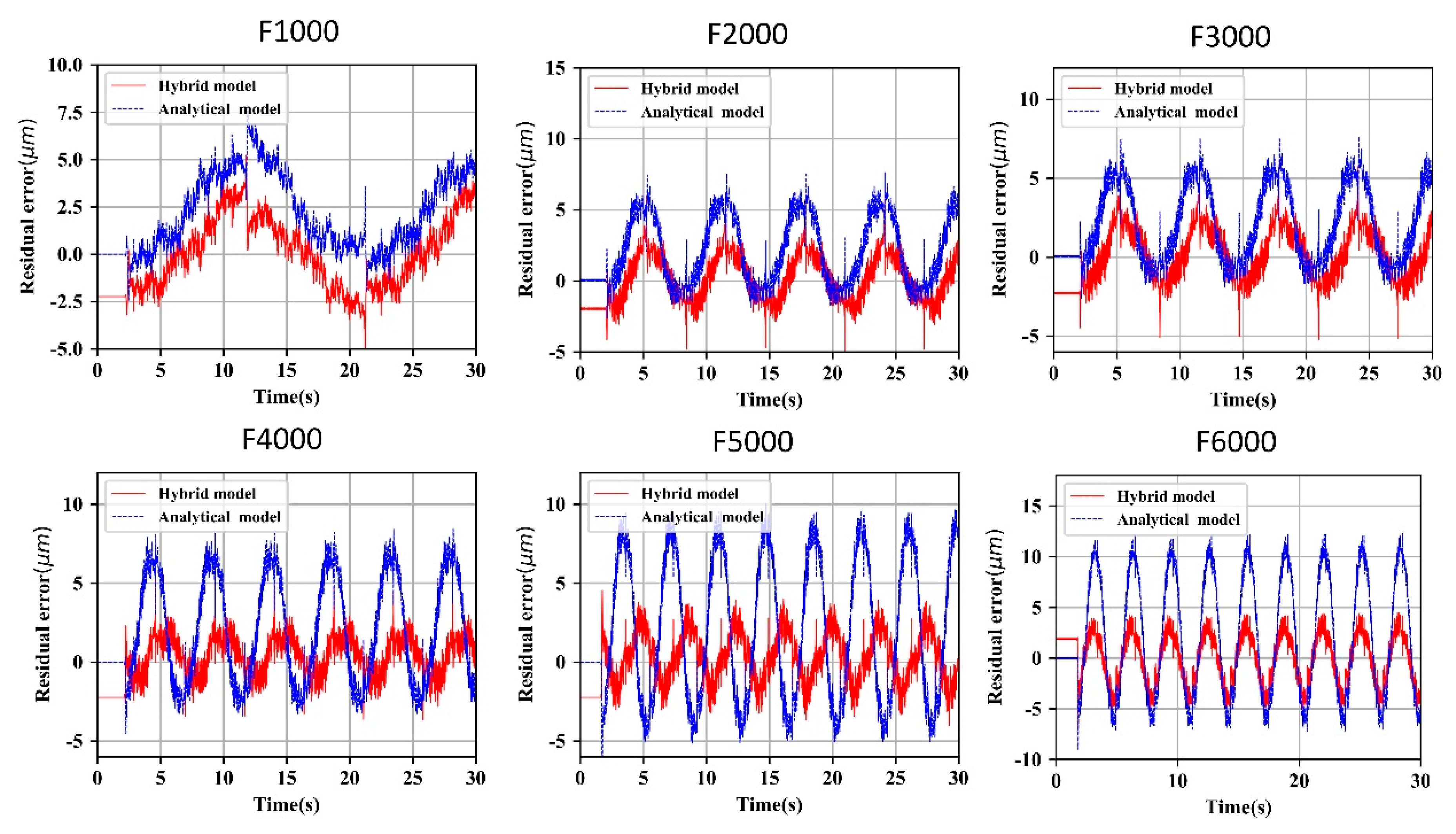
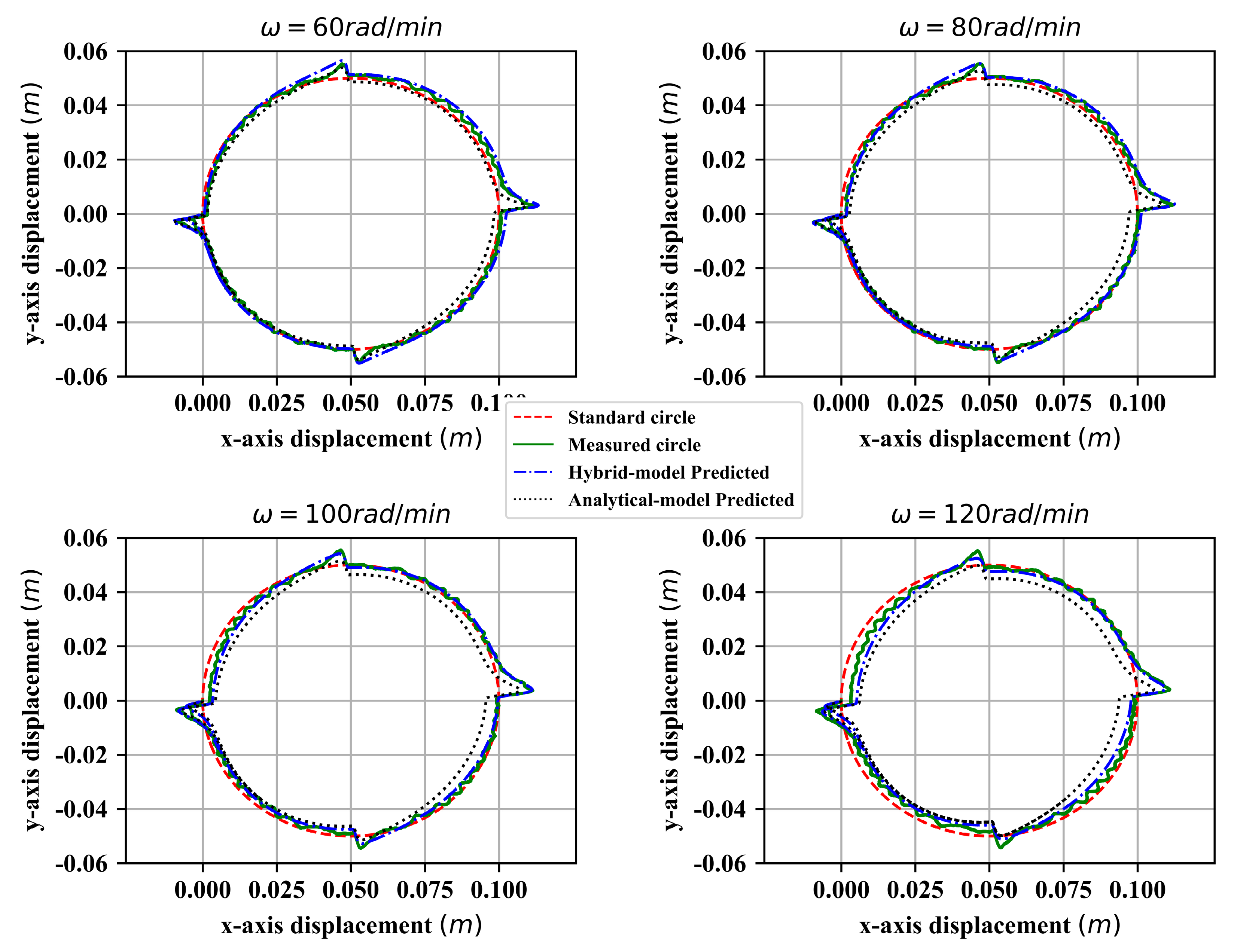
5.1. Single Axis Ball Screw Feed System Hybrid Model
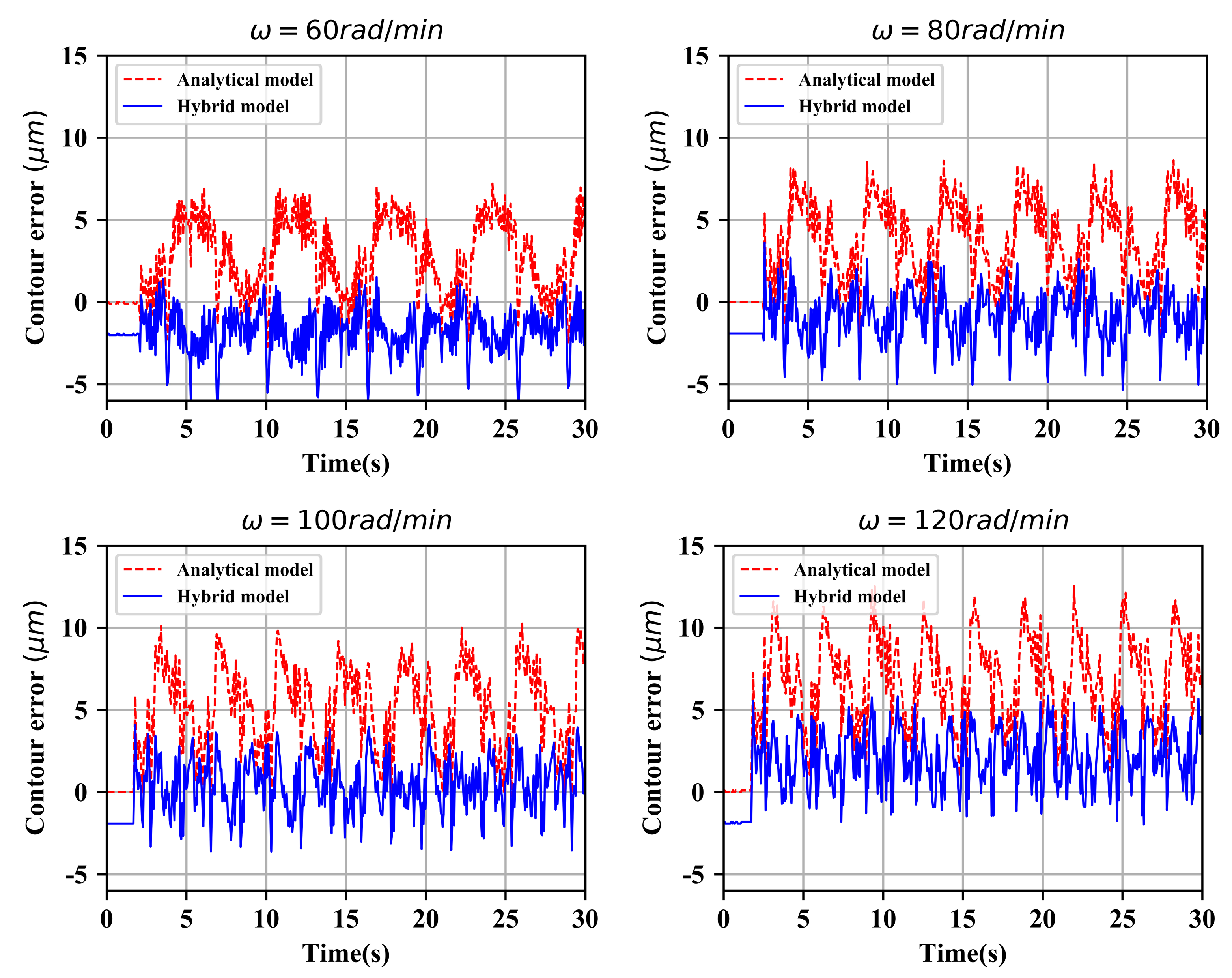
5.2. Double Axis Ball Screw Feed System Hybrid Model
6. Conclusions
- A hybrid multi-domain analytical and data-driven modeling method was proposed in this paper and a hybrid model of a ball screw feed drive system was established accurately using the hybrid modeling method.
- In contrast to the traditional causal modeling method based on signal flow, the multi-domain integrated analytical model of the ball screw feed system was established using the non-causal modeling method based on energy flow. The analytical model of a feed system developed in this paper realized seamless integrated modeling of a complicated multi-domain system.
- A data-driven error model based on a BP neural network was established and the model was trained using experimental data. Then the learned data-driven error model was coupled with the analytical model of the ball screw feed system and the hybrid model was obtained.
- The hybrid model was validated using experimental data at different speeds, and the results show that, whether for the tracking error of a single-axis feeding system or the contour error of a double-axis feeding system, the prediction effect of the hybrid model is better than that of a pure analytical model, and the prediction accuracy of the hybrid model reaches a higher level.
Author Contributions
Funding
Conflicts of Interest
References
- Altintas, Y. Machine tool feed drives. CIRP Ann. 2011, 60, 779–796. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Liu, H.; Liang, T.; Zhao, W. Dynamic modeling and analysis of the high-speed ball screw feed system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 870–877. [Google Scholar] [CrossRef]
- Erkorkmaz, K.; Kamalzadeh, A. High bandwidth control of ball screw drives. CIRP Ann. 2006, 55, 393–398. [Google Scholar] [CrossRef]
- Tsai, P.C.; Cheng, C.C.; Hwang, Y.C. Ball screw preload loss detection using ball pass frequency. Mech. Syst. Signal Process. 2014, 48, 77–91. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Chen, Y.L. Tracking control of ball screw drives using ADRC and equivalent-error-model-based feedforward control. IEEE Trans. Ind. Electron. 2016, 63, 7682–7692. [Google Scholar] [CrossRef]
- Sepasi, D.; Nagamune, R. Tracking control of flexible ball screw drives with runout effect and mass variation. IEEE Trans. Ind. Electron. 2012, 59, 1248–1256. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; DeWit, C.C. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Min, B.K.; Cho, D.W.; Lee, S.J. Motor current prediction of a machine tool feed drive using a component-based simulation model. Int. J. Precis. Eng. Manuf. 2010, 11, 597–606. [Google Scholar] [CrossRef]
- Karnopp, D. Computer simulation of stick-slip friction in mechanical dynamic systems. ASME J. Dyn. Syst. Meas. Control 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Duan, M. Dynamic Modeling and Experiment Research on Twin Ball Screw Feed System Considering the Joint Stiffness. Symmetry 2018, 10, 686. [Google Scholar] [CrossRef]
- Johanastrom, K.; Canudas-de-Wit, C. Revisiting the LuGre friction model. IEEE Control Syst. Mag. 2008, 28, 101–114. [Google Scholar] [CrossRef] [Green Version]
- Grundelius, M.; Angeli, D. Adaptive control of systems with back-lash acting on the input. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; pp. 4689–4694. [Google Scholar]
- Tao, G.; Ma, X.; Ling, Y. Optimal and nonlinear decoupling control of systems with sandwiched backlash. Automatica 2001, 37, 165–176. [Google Scholar] [CrossRef]
- Mata-Jimenez, M.T.; Brogliato, B.; Goswami, A. On the control of mechanical systems with dynamic backlash. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; pp. 1990–1995. [Google Scholar]
- Kamalzadeh, A.; Erkorkmaz, K. Compensation of axial vibrations in ball screw. CIRP Ann. Manuf. Technol. 2007, 56, 373–378. [Google Scholar] [CrossRef]
- Tsai, M.S.; Huang, Y.C.; Lin, M.T.; Wu, S.K. Integration of input shaping technique with interpolation for vibration suppression of servo-feed drive system. J. Chin. Inst. Eng. 2017, 40, 284–295. [Google Scholar] [CrossRef]
- Huang, H.W.; Tsai, M.S.; Huang, Y.C. Modeling and elastic deformation compensation of flexural feed drive system. Int. J. Mach. Tools Manuf. 2018, 132, 96–112. [Google Scholar] [CrossRef]
- Li, F.; Jiang, Y.; Li, T. An improved dynamic model of preloaded ball screw drives considering torque transmission and its application to frequency analysis. Adv. Mech. Eng. 2017, 9, 1687814017710580. [Google Scholar] [CrossRef]
- Xu, Z.Z.; Choi, C.; Liang, L. Study on a novel thermal error compensation system for high-precision ball screw feed drive (2 nd report: Experimental verification). Int. J. Precis. Eng. Manuf. 2015, 16, 2139–2145. [Google Scholar] [CrossRef]
- Pislaru, C.; Derek, G.F.; Holroyd, G. Hybrid modelling and simulation of a computer numerical control machine tool feed drive. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2004, 218, 111–120. [Google Scholar] [CrossRef]
- Whalley, R.; Ebrahimi, M.; Abdul-Ameer, A.A. Hybrid modelling of machine tool axis drives. Int. J. Mach. Tools Manuf. 2005, 45, 1560–1576. [Google Scholar] [CrossRef]
- Whalley, R.; Abdul-Ameer, A.A.; Ebrahimi, M. Machine tool modelling and profile following performance. Appl. Math. Model. 2008, 32, 2290–2311. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Oertli, T.; Milberg, J. Finite element modelling of ball screw feed drive systems. CIRP Ann. Manuf. Technol. 2004, 53, 289–292. [Google Scholar] [CrossRef]
- Yang, X. Electromechanical integrated modeling and analysis for the direct-driven feed system in machine tools. Int. J. Adv. Manuf. Technol. 2018, 98, 1591–1604. [Google Scholar] [CrossRef]
- Zhang, X. Integrated modeling and analysis of ball screw feed system and milling process with consideration of multi-excitation effect. Mech. Syst. Signal Process. 2018, 98, 484–505. [Google Scholar] [CrossRef]
- Maj, R.; Bianchi, G. Mechatronic analysis of machine tools. In Proceedings of the 9th SAMTECH Users Conference, Paris, France, 2–3 February 2005; pp. 2–3. [Google Scholar]
- Ansoategui, I.; Campa, F.J. Mechatronics of a ball screw drive using an N degrees of freedom dynamic model. Int. J. Adv. Manuf. Technol. 2017, 93, 1307–1318. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.S.; Chung, S.C. A systematic approach to design high-performance feed drive systems. Int. J. Mach. Tools Manuf. 2005, 45, 1421–1435. [Google Scholar] [CrossRef]
- Herfs, W. Design of Feed Drives with Object-Oriented Behavior Models. IFAC-PapersOnLine 2015, 48, 268–273. [Google Scholar] [CrossRef]
- Luo, W. Digital twin for CNC machine tool: modeling and using strategy. J. Ambient Intell. Humaniz. Comput. 2019, 10, 1129–1140. [Google Scholar] [CrossRef]
- Özdemir, D. Modelica Library for Feed Drive Systems. In Proceedings of the 11th International Modelica Conference, Versailles, France, 21–23 September 2015; Linköping University Electronic Press: Linköping, Sweden, 2015; pp. 117–125. [Google Scholar]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Wuest, T.; Weimer, D.; Irgens, C. Machine learning in manufacturing: advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, Y.; Wang, K. A data-driven method based on deep belief networks for backlash error prediction in machining centers. J. Intell. Manuf. 2017, 1–13. [Google Scholar] [CrossRef]
- Chiu, H.W.; Lee, C.H. Prediction of machining accuracy and surface quality for CNC machine tools using data driven approach. Adv. Eng. Softw. 2017, 114, 246–257. [Google Scholar] [CrossRef]
- Park, J.; Law, K.H.; Bhinge, R. A generalized data-driven energy prediction model with uncertainty for a milling machine tool using Gaussian Process. In Proceedings of the ASME 2015 International Manufacturing Science and Engineering Conference, Charlotte, NC, USA, 8–12 June 2015. [Google Scholar]
- Ziegert, J.C.; Kalle, P. Error compensation in machine tools: a neural network approach. J. Intell. Manuf. 1994, 5, 143–151. [Google Scholar] [CrossRef]
- Ak, R.; Helu, M.M.; Rachuri, S. Ensemble neural network model for predicting the energy consumption of a milling machine. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015. [Google Scholar]
- Yan, J.; Lee, J. Degradation assessment and fault modes classification using logistic regression. J. Manuf. Sci. Eng. 2005, 127, 912–914. [Google Scholar] [CrossRef]
- Carbonneau, R.; Laframboise, K.; Vahidov, R. Application of machine learning techniques for supply chain demand forecasting. Eur. J. Oper. Res. 2008, 184, 1140–1154. [Google Scholar] [CrossRef]
- Hou, Z.; Gao, H.; Lewis, F.L. Data-Driven Control and Learning Systems. IEEE Trans. Ind. Electron. 2017, 64, 4070–4075. [Google Scholar] [CrossRef]
- Park, J.; Ferguson, M.; Law, K.H. Data Driven Analytics (Machine Learning) for System Characterization, Diagnostics and Control Optimization//Workshop of the European Group for Intelligent Computing in Engineering; Springer: Cham, Switzerland, 2018; pp. 16–36. [Google Scholar]
- Reinhart, R.; Shareef, Z.; Steil, J. Hybrid analytical and data-driven modeling for feed-forward robot control. Sensors 2017, 17, 311. [Google Scholar] [CrossRef]
- Reinhart, R.F.; Steil, J.J. Hybrid mechanical and data-driven modeling improves inverse kinematic control of a soft robot. Procedia Technol. 2016, 26, 12–19. [Google Scholar] [CrossRef]
- Chikh, K.; Saad, A.; Khafallah, M. PMSM vector control performance improvement by using pulse with modulation and anti-windup PI controller. In Proceedings of the 2011 International Conference on Multimedia Computing and Systems, Ouarzazate, Morocco, 7–9 April 2011; pp. 1–7. [Google Scholar]
- Sebastian, T.; Slemon, G.R. Transient modeling and performance of variable-speed permanent-magnet motors. IEEE Trans. Ind. Appl. 1989, 25, 101–106. [Google Scholar] [CrossRef]
- Tu, X.; Zhou, Y.F.; Zhao, P. Modeling the static friction in a robot joint by genetically optimized BP neural network. J. Intell. Robot. Syst. 2019, 94, 29–41. [Google Scholar] [CrossRef]


| Mechanical Connectors | Electrical Connectors | Control Connectors | |||
|---|---|---|---|---|---|
| Icon | ⬤ | Icon | ⬤ | Icon | |
| Flow variable | Torque τ | Flow variable | Current i | Input variable u | ▶ |
| Potential variable | Angle φ | Potential variable | Voltage v | Output variable y | ▷ |
| Name of Parameters | Value |
|---|---|
| Nominal torque of the motor | 18 N m |
| Nominal speed of the motor | 2000 rpm |
| Nominal current of the motor | 12.5 A |
| Nominal power of the power | 3.6 Kw |
| Inertia of the motor rotor | 5.3 |
| Pole-pair number of the motor | 4 |
| Equivalent resistance of phase winding | 0.184 |
| axis inductance of the motor | 2.3 H |
| axis inductance of the motor | 2.3 H |
| Control cycle of position loop | 0.001 s |
| Position loop gain | 120 Hz |
| Control cycle of velocity loop | 0.125 ms |
| Velocity loop gain | 800 Hz |
| Integral time constant of velocity loop | 40 ms |
| Control cycle of current loop | 31.25 us |
| Current loop gain | 5000 Hz |
| Integral time constant of current loop | 9.8 ms |
| DC-side voltage of inverter | 560 V |
| Pitch of the ball screw | 16 mm |
| backlash | 17 um |
| Feed Rate (mm/min) | F1000 | F2000 | F3000 | F4000 | F5000 | F6000 | |
|---|---|---|---|---|---|---|---|
| Hybrid model | (MAE)/ | 5.22 | 5.16 | 5.98 | 5.27 | 4.55 | 6.79 |
| (RMSE)/ | 1.87 | 2.33 | 1.72 | 1.41 | 1.64 | 2.63 | |
| (RE) | 2.7% | 2.0% | 1.1% | 0.7% | 0.5% | 0.6% | |
| Analytical model | (MAE)/ | 7.99 | 7.52 | 7.70 | 8.51 | 10.2 | 12.38 |
| (RMSE)/ | 2.91 | 2.83 | 3.15 | 3.84 | 4.89 | 6.21 | |
| (RE) | 4.2% | 4.0% | 1.4% | 1.1% | 1.1% | 1.2% | |
| 60 | 80 | 100 | 120 | |
|---|---|---|---|---|
| Max Error (Analytical model predicted)/ | 7.19 | 8.62 | 10.26 | 12.54 |
| Max Error (Hybrid model predicted)/ | 6.57 | 5.34 | 4.10 | 6.95 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Z.; Ding, J.; Chen, L.; Pi, T.; Mei, Z. Hybrid Multi-Domain Analytical and Data-Driven Modeling for Feed Systems in Machine Tools. Symmetry 2019, 11, 1156. https://doi.org/10.3390/sym11091156
Mei Z, Ding J, Chen L, Pi T, Mei Z. Hybrid Multi-Domain Analytical and Data-Driven Modeling for Feed Systems in Machine Tools. Symmetry. 2019; 11(9):1156. https://doi.org/10.3390/sym11091156
Chicago/Turabian StyleMei, Zaiwu, Jianwan Ding, Liping Chen, Ting Pi, and Zaidao Mei. 2019. "Hybrid Multi-Domain Analytical and Data-Driven Modeling for Feed Systems in Machine Tools" Symmetry 11, no. 9: 1156. https://doi.org/10.3390/sym11091156
APA StyleMei, Z., Ding, J., Chen, L., Pi, T., & Mei, Z. (2019). Hybrid Multi-Domain Analytical and Data-Driven Modeling for Feed Systems in Machine Tools. Symmetry, 11(9), 1156. https://doi.org/10.3390/sym11091156




