Visual Analysis of the Newton’s Method with Fractional Order Derivatives
Abstract
:1. Introduction
2. Fractional Derivatives
- ,
- ,
- for ,
- .
2.1. The Riemann–Liouville Derivative
2.2. The Caputo Derivative
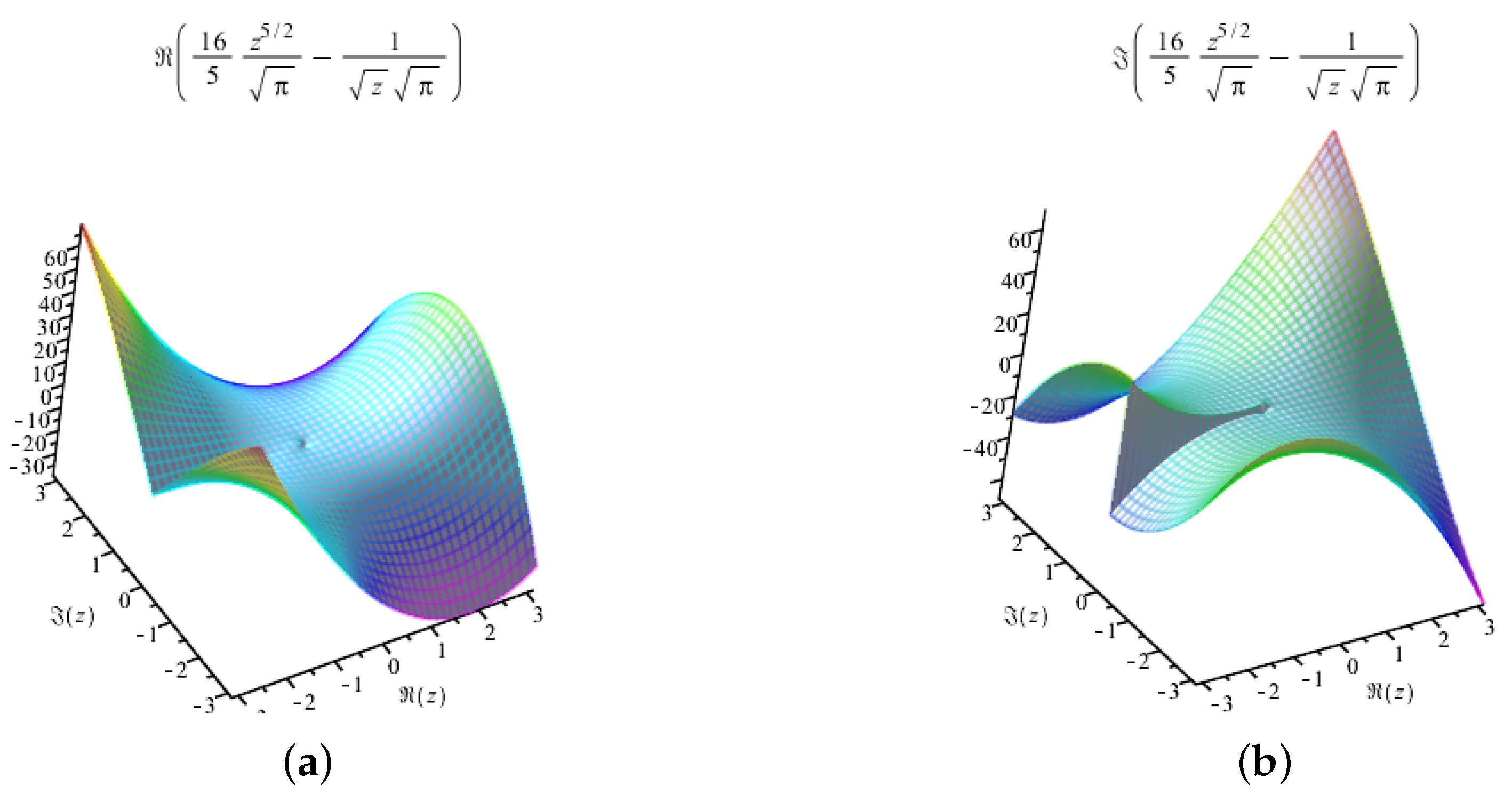
2.3. Complex Plane Derivatives
3. The Newton Method with Fractional Derivatives
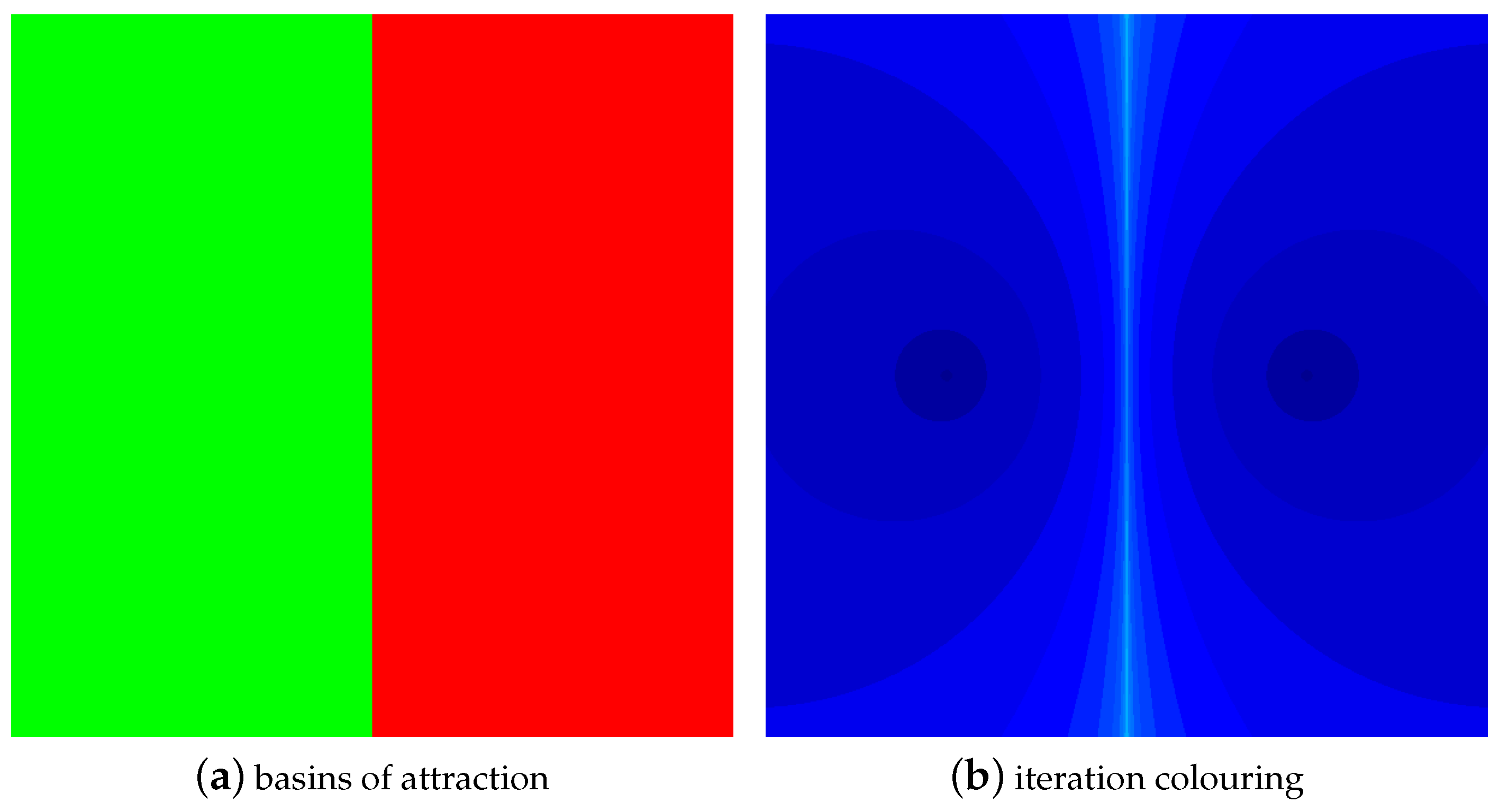
4. Numerical Experiments
| Algorithm 1: Polynomiograph generation. |
 |
- for ,
- for ,
- for ,
- for .
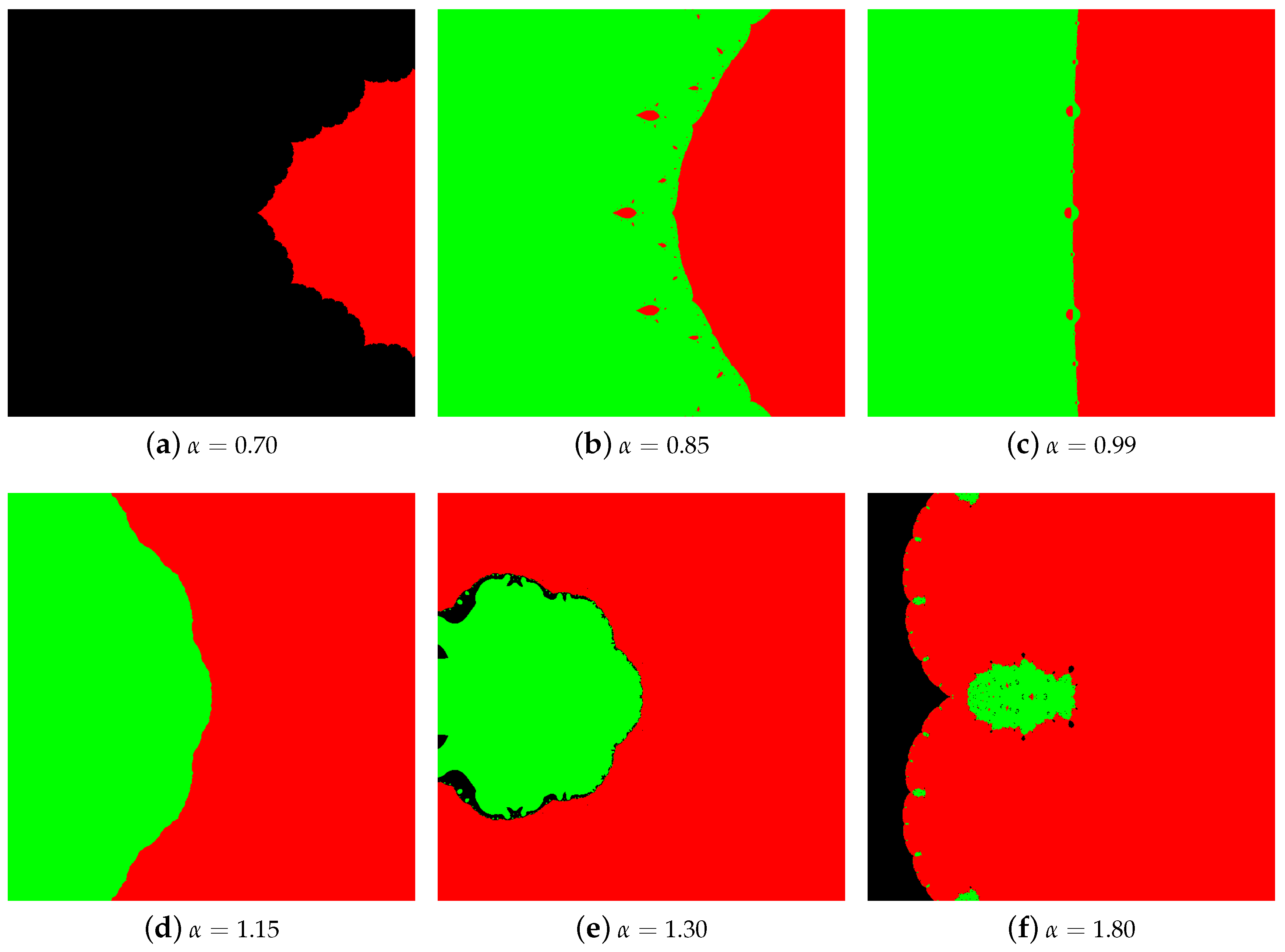
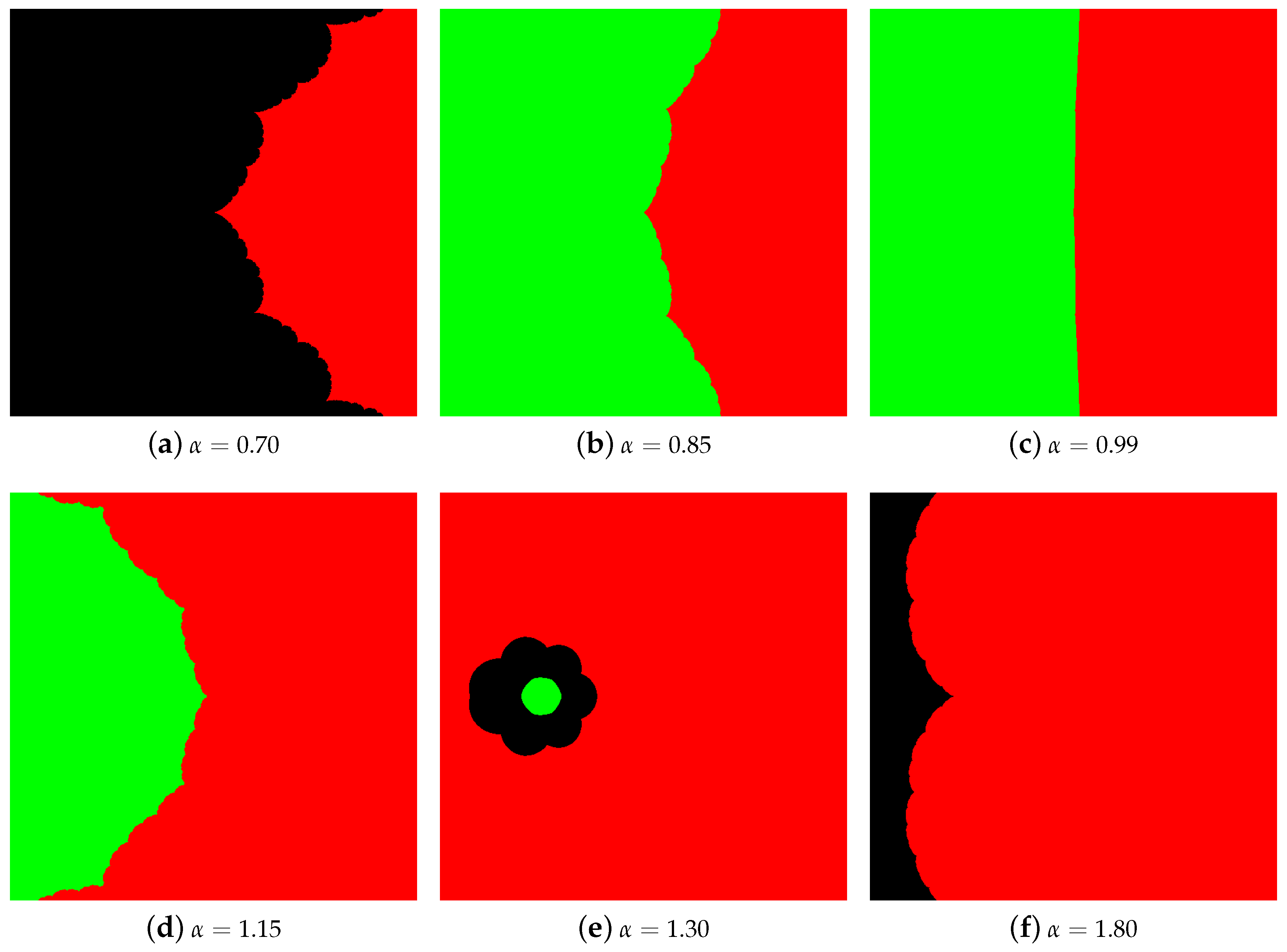
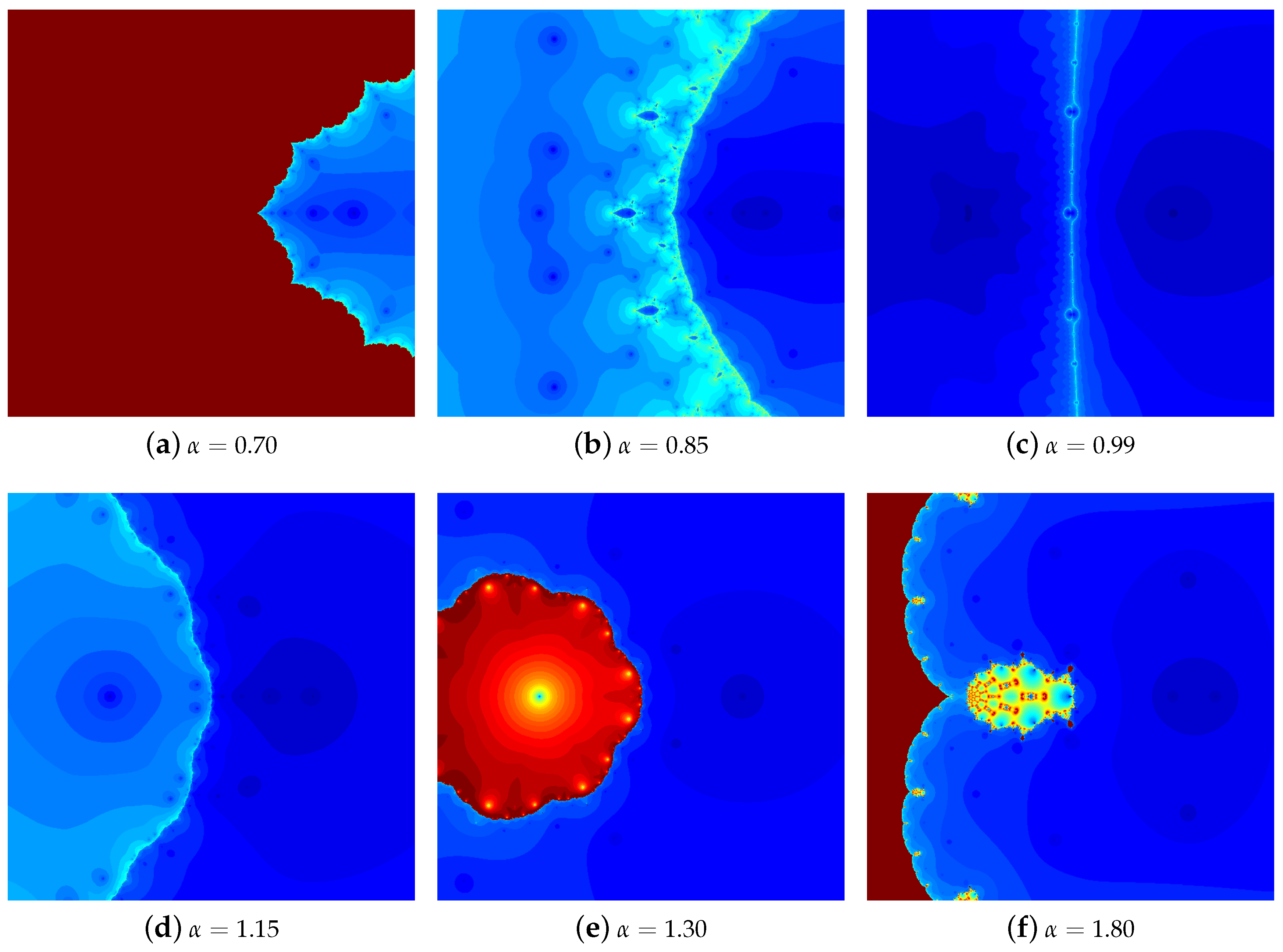
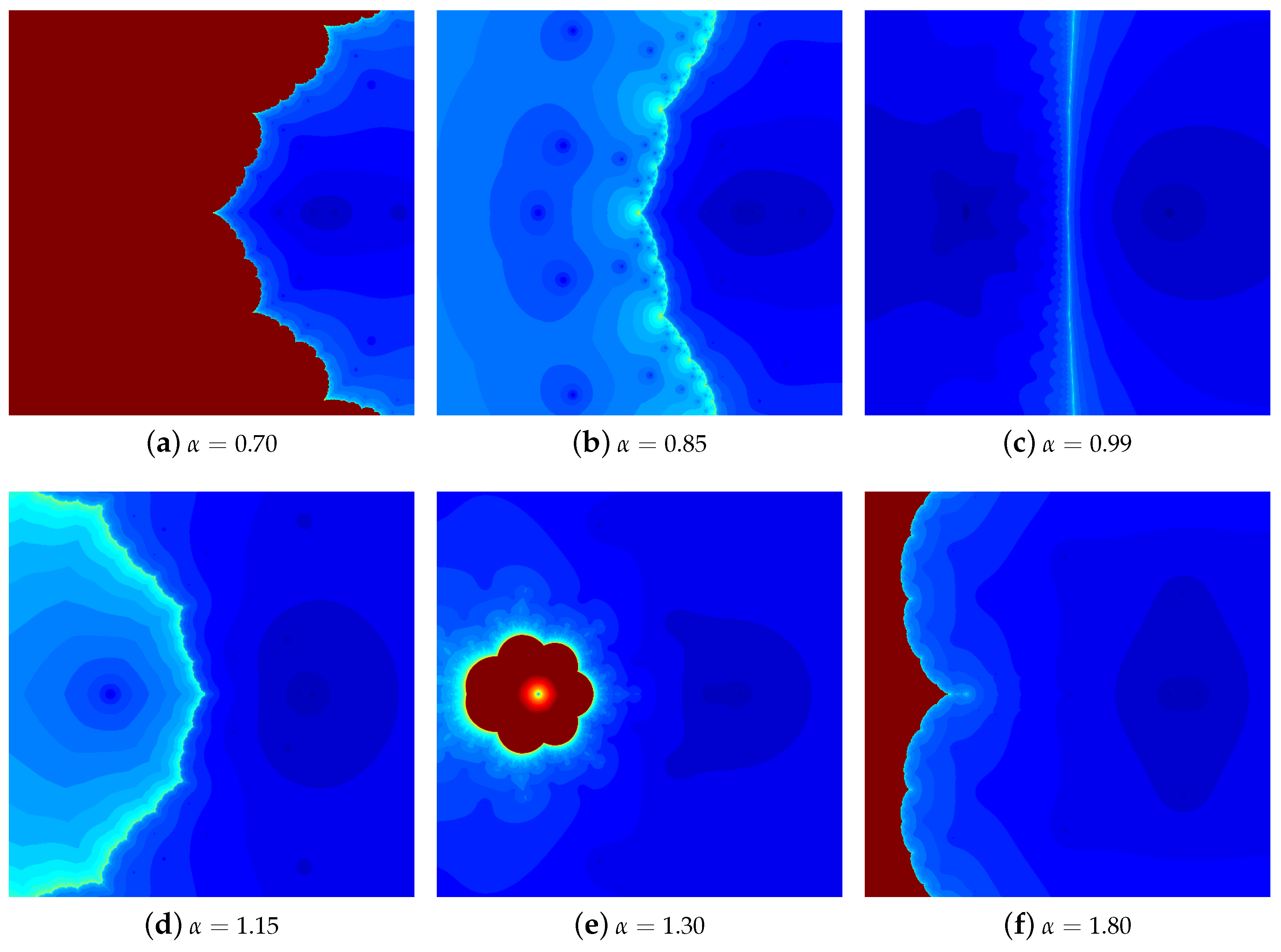
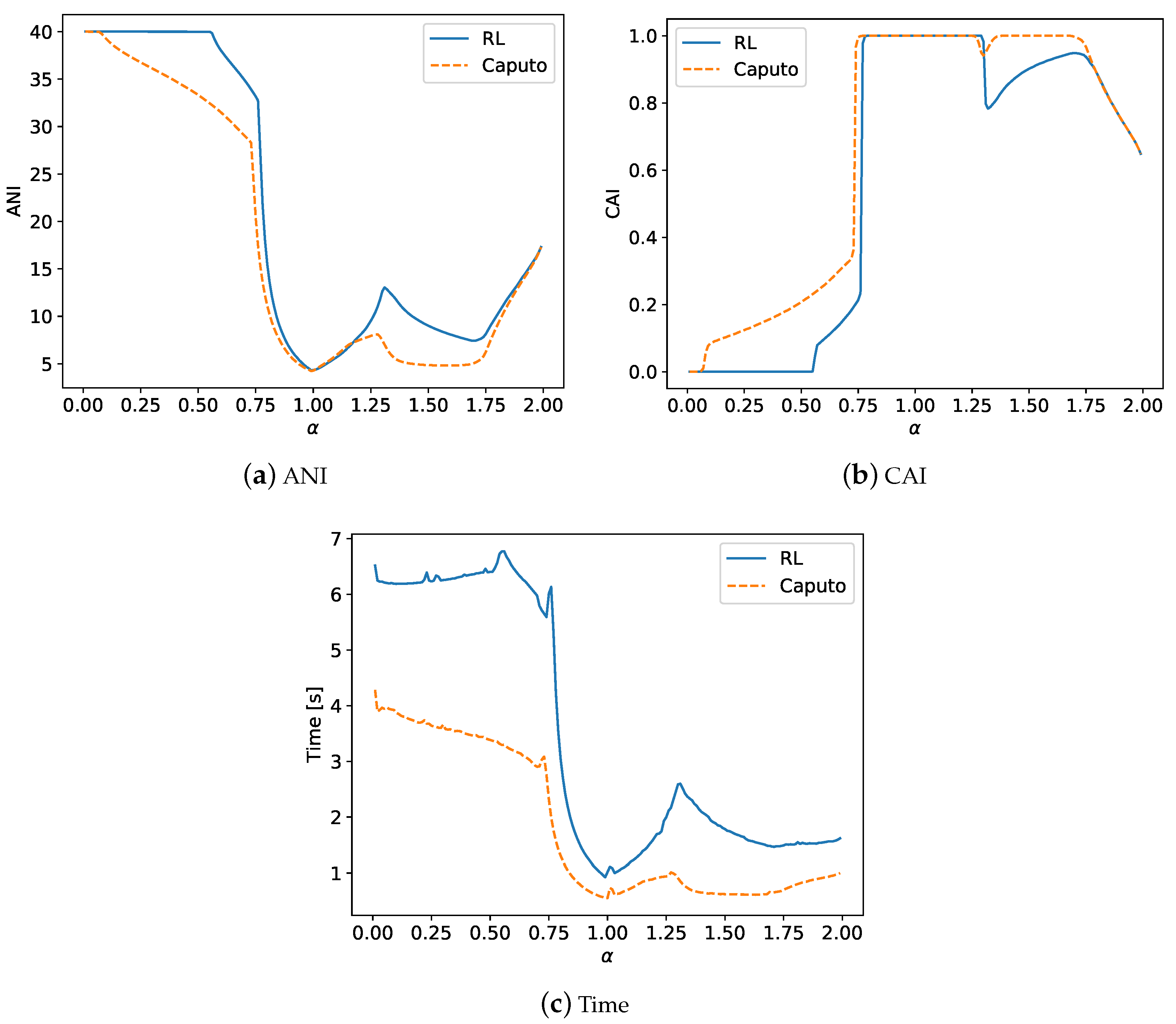
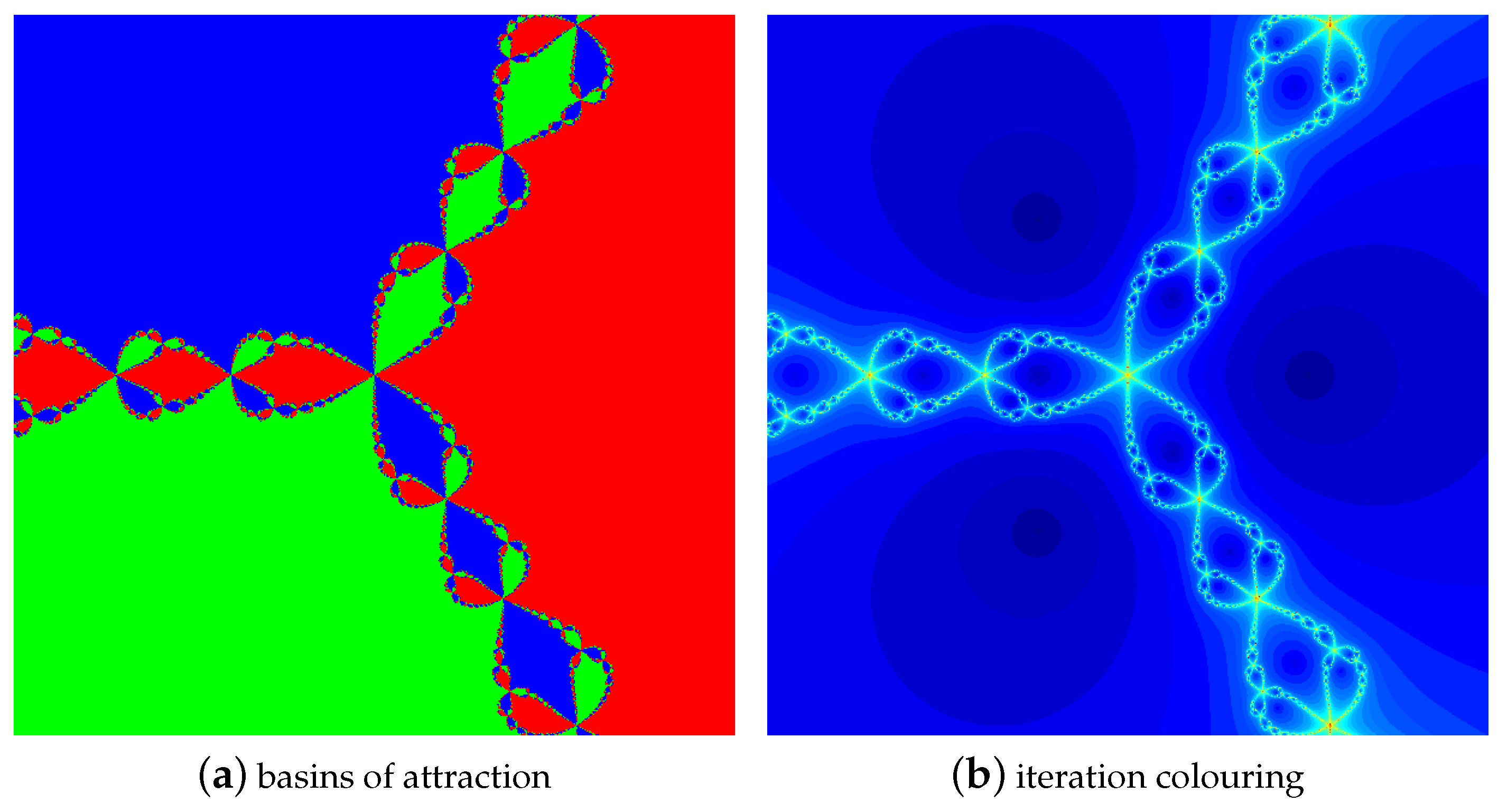
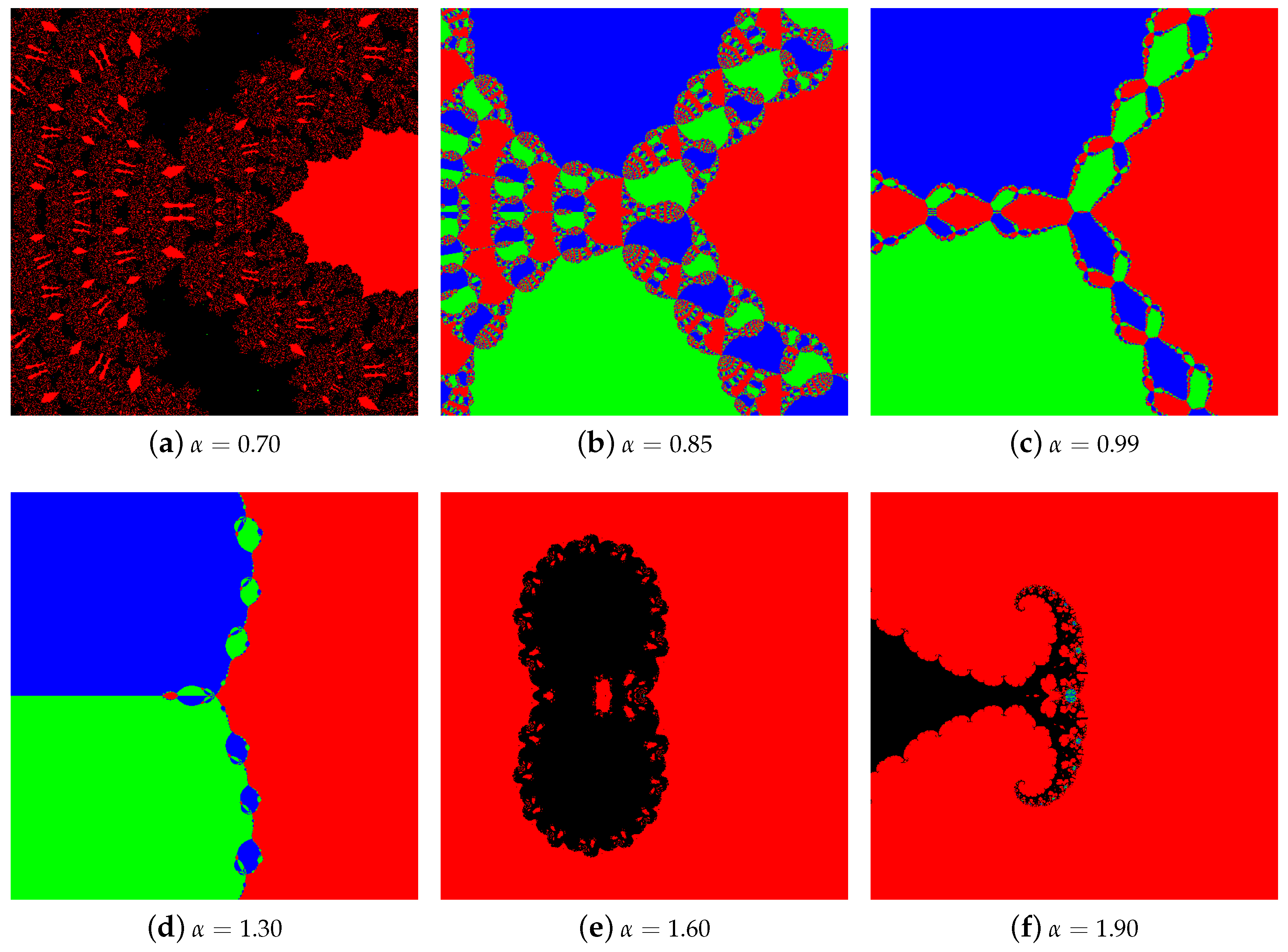
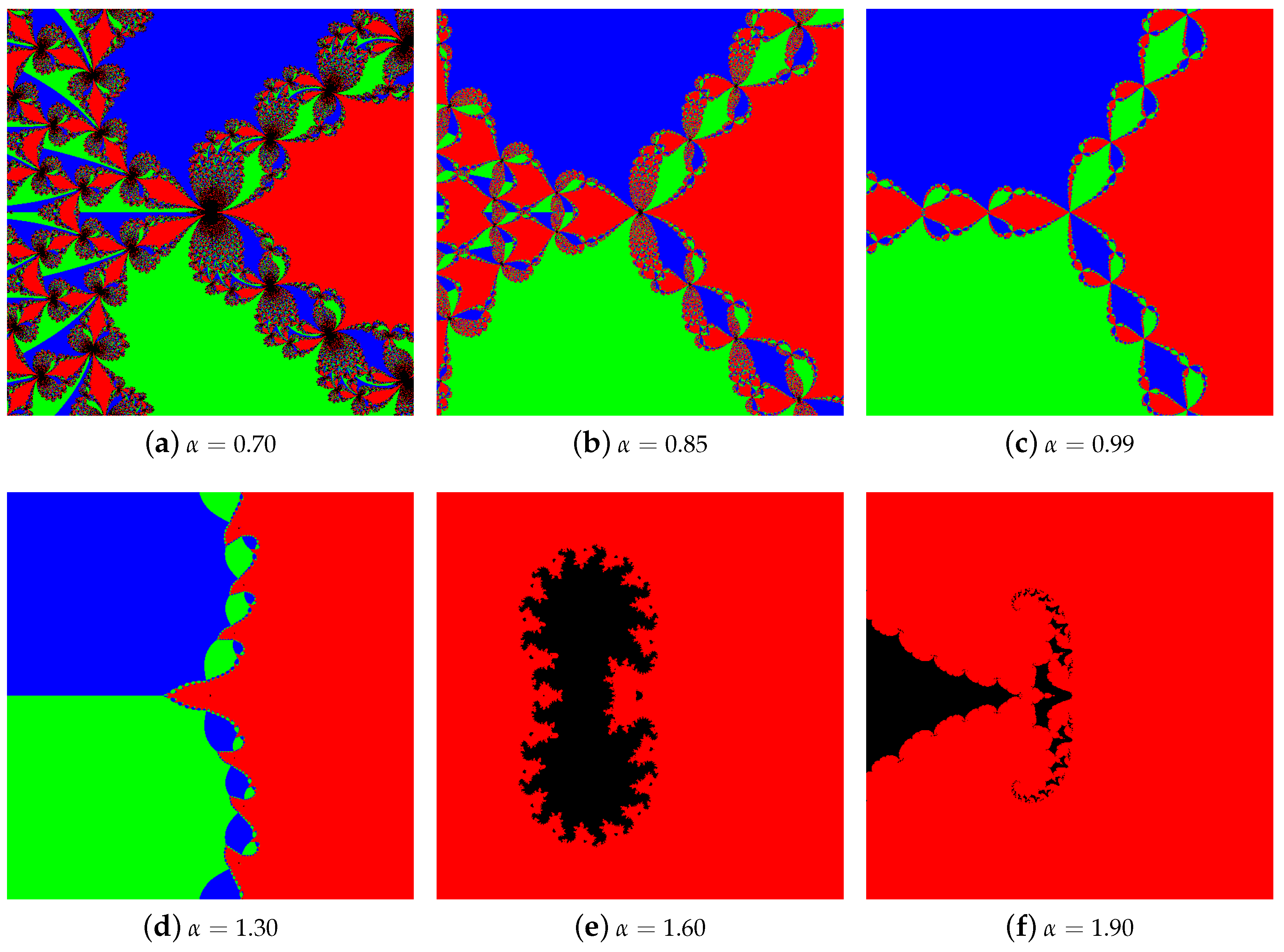
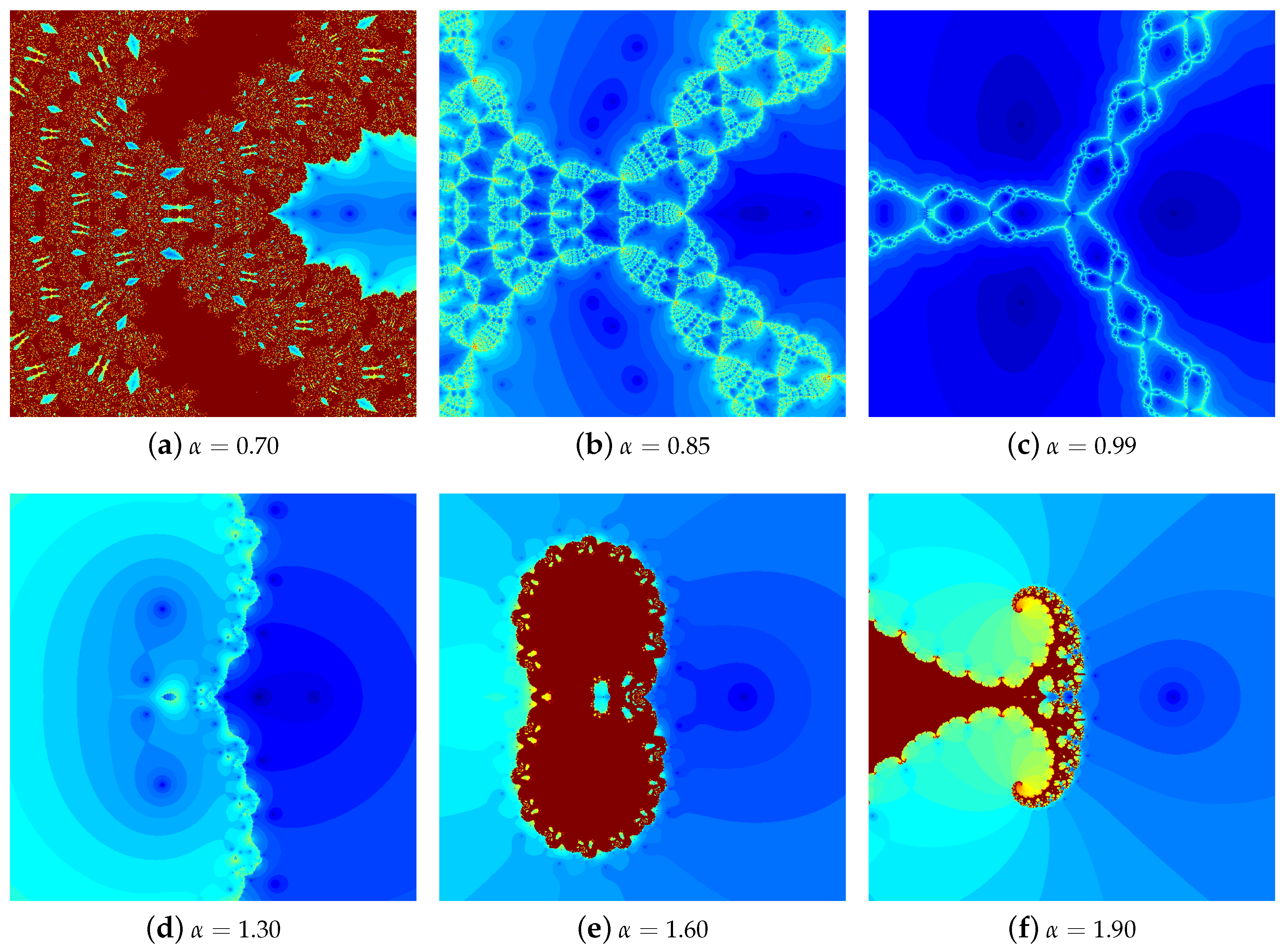
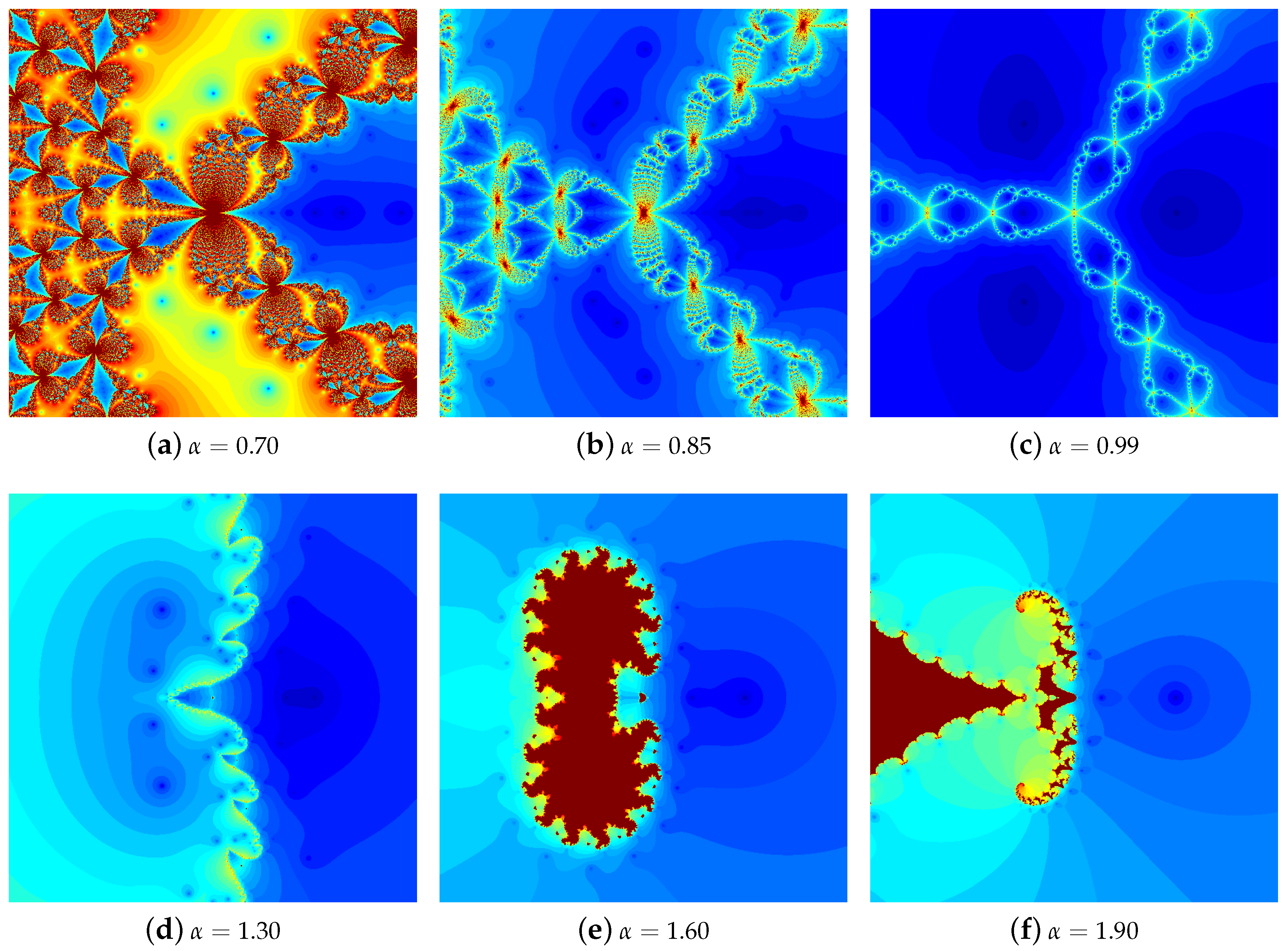
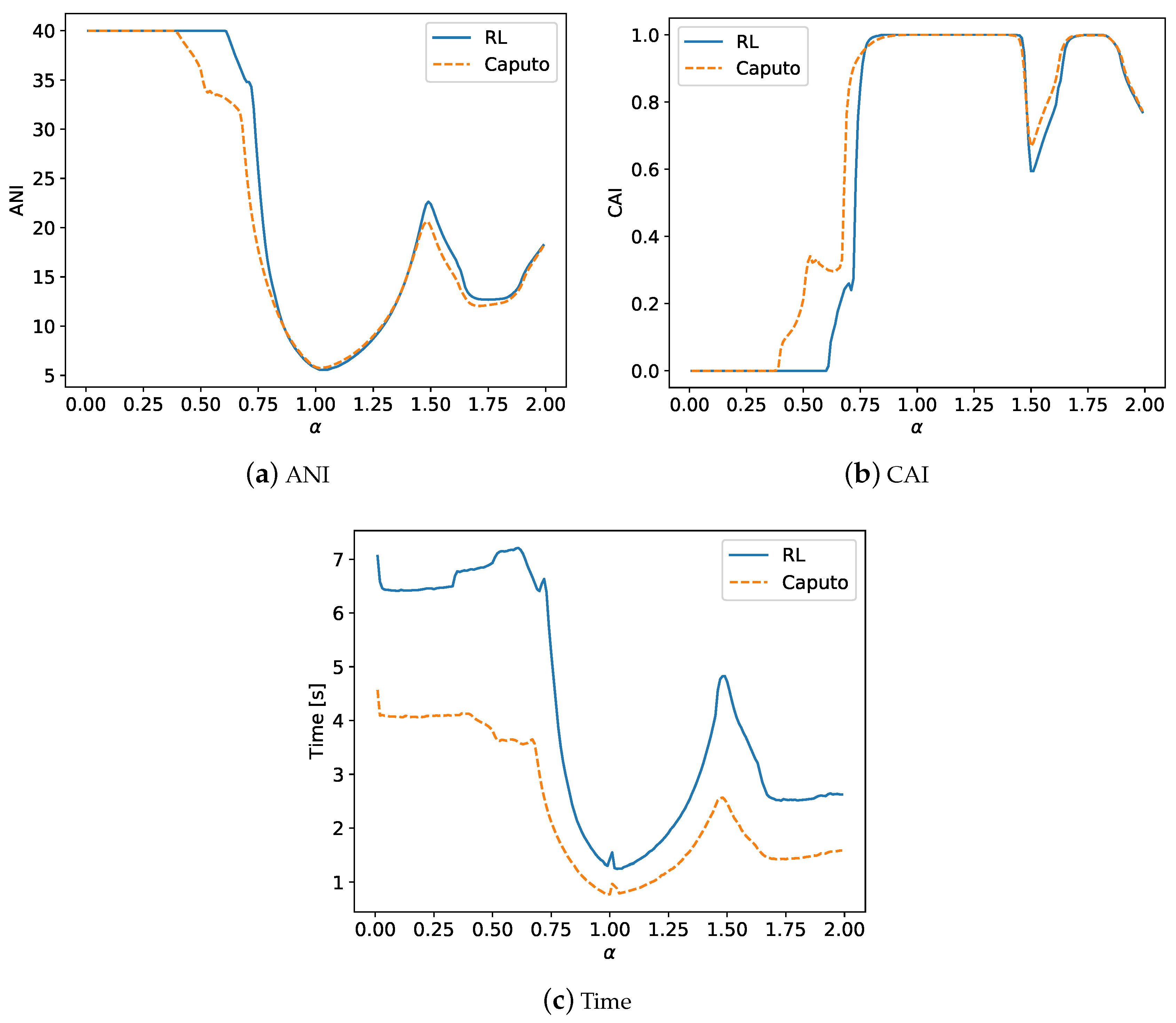
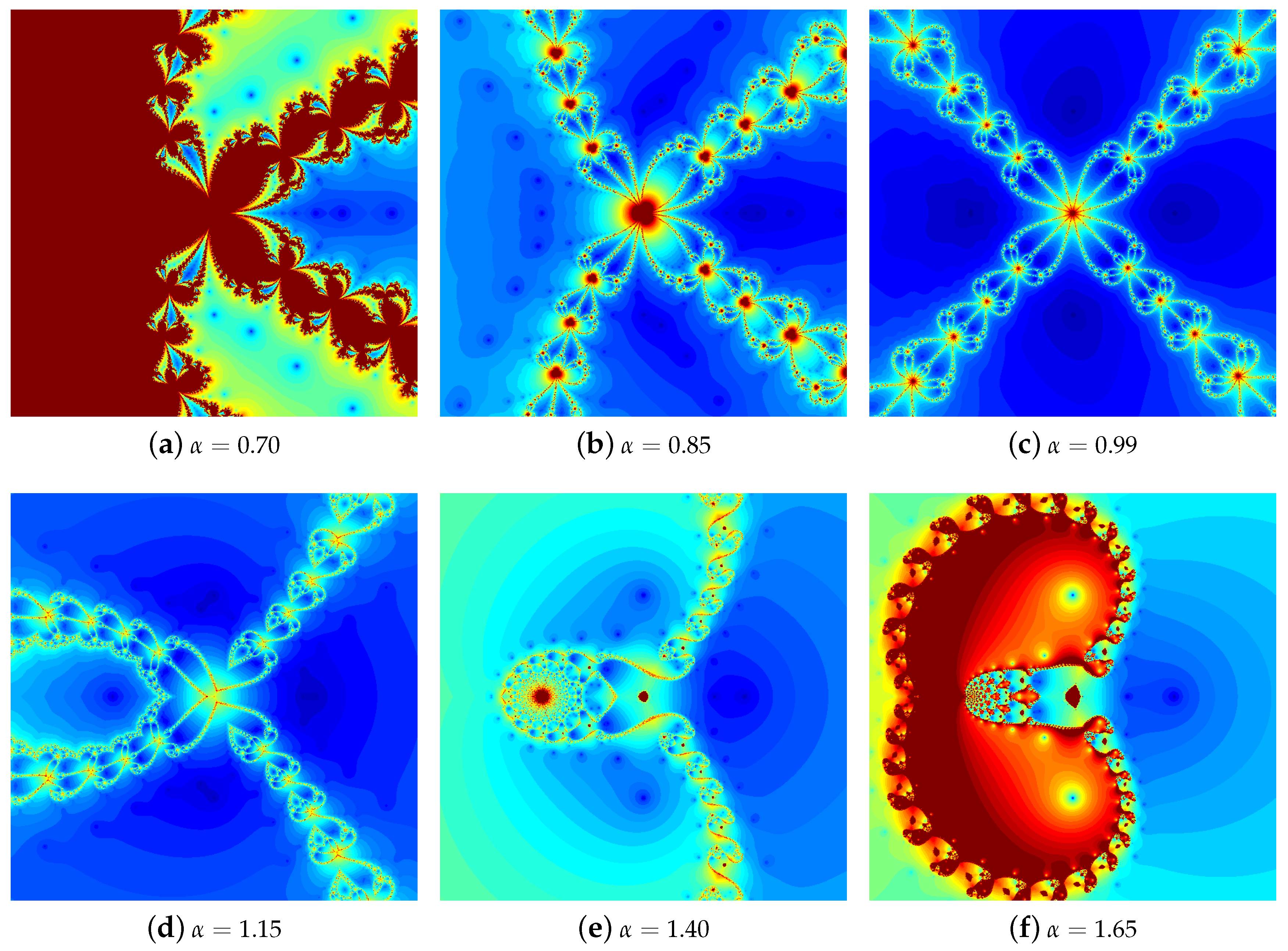
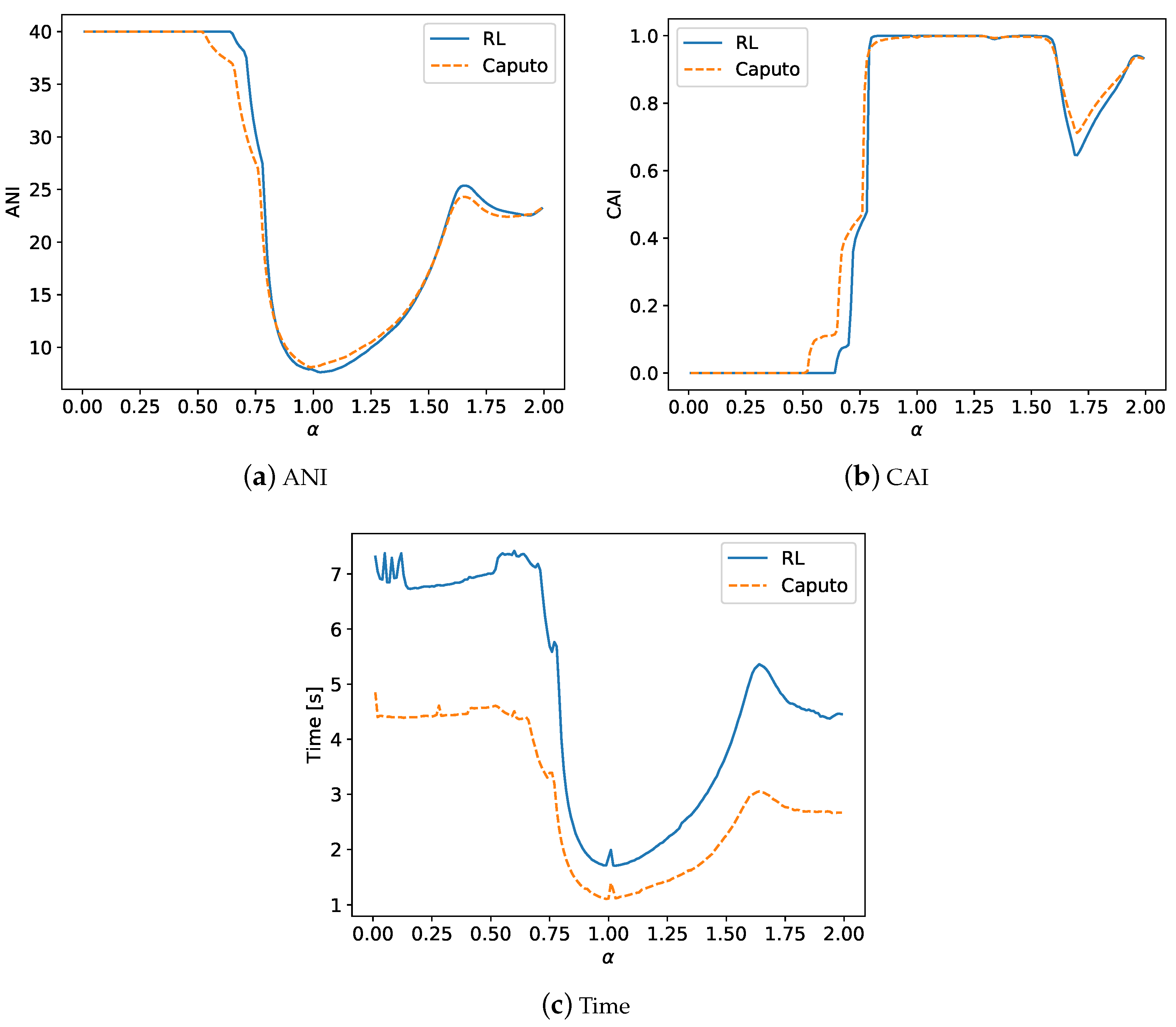
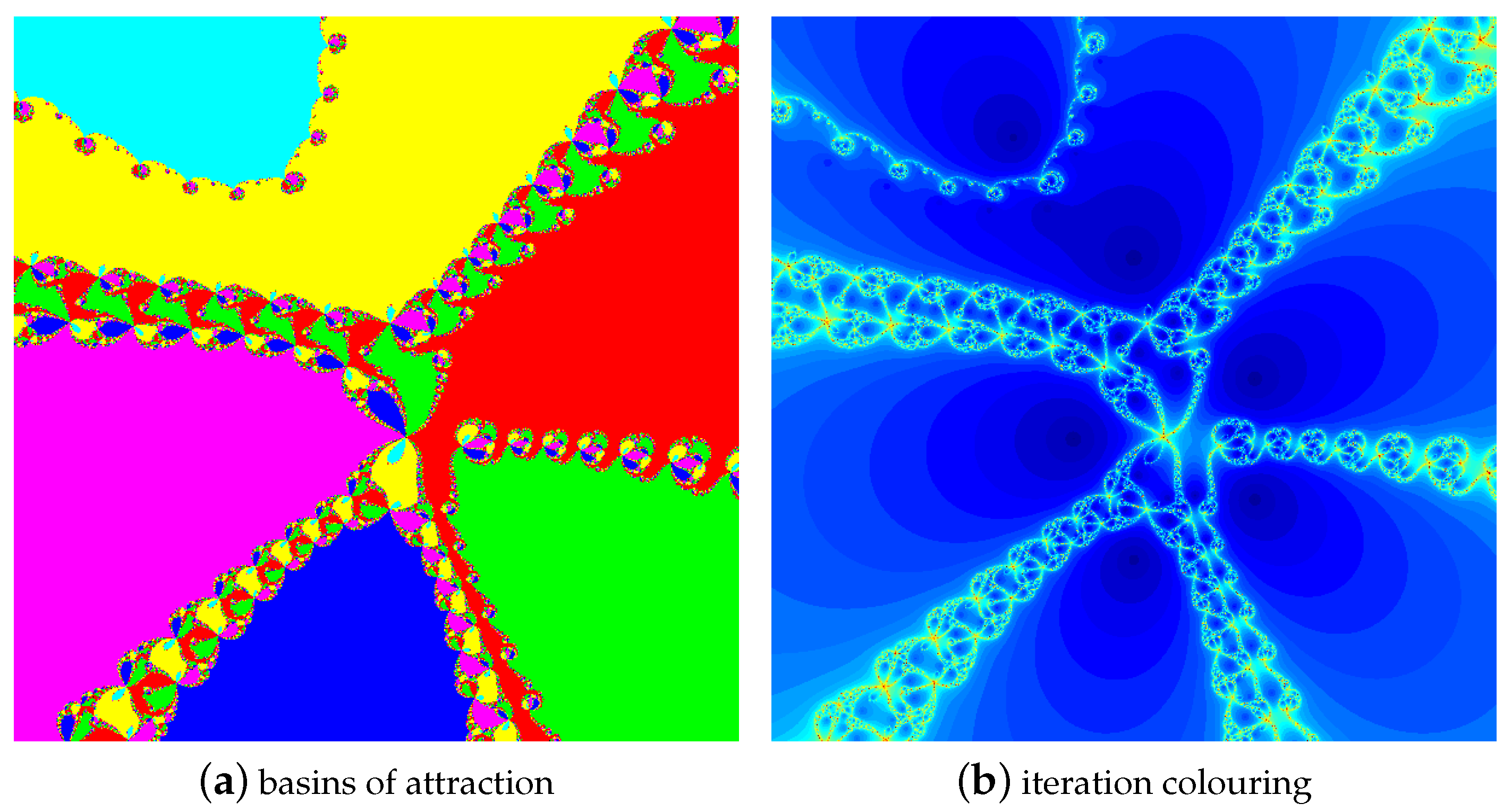
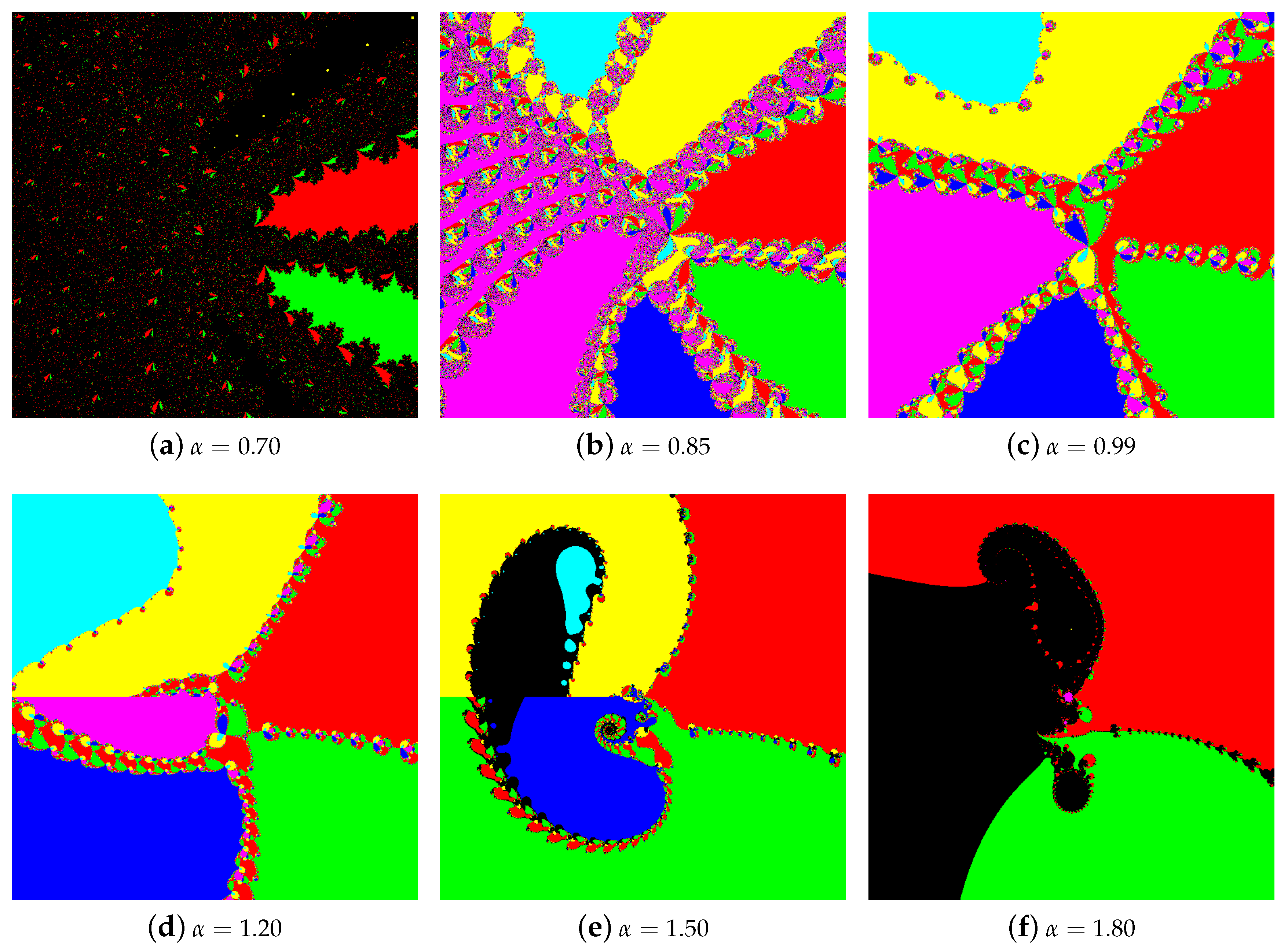
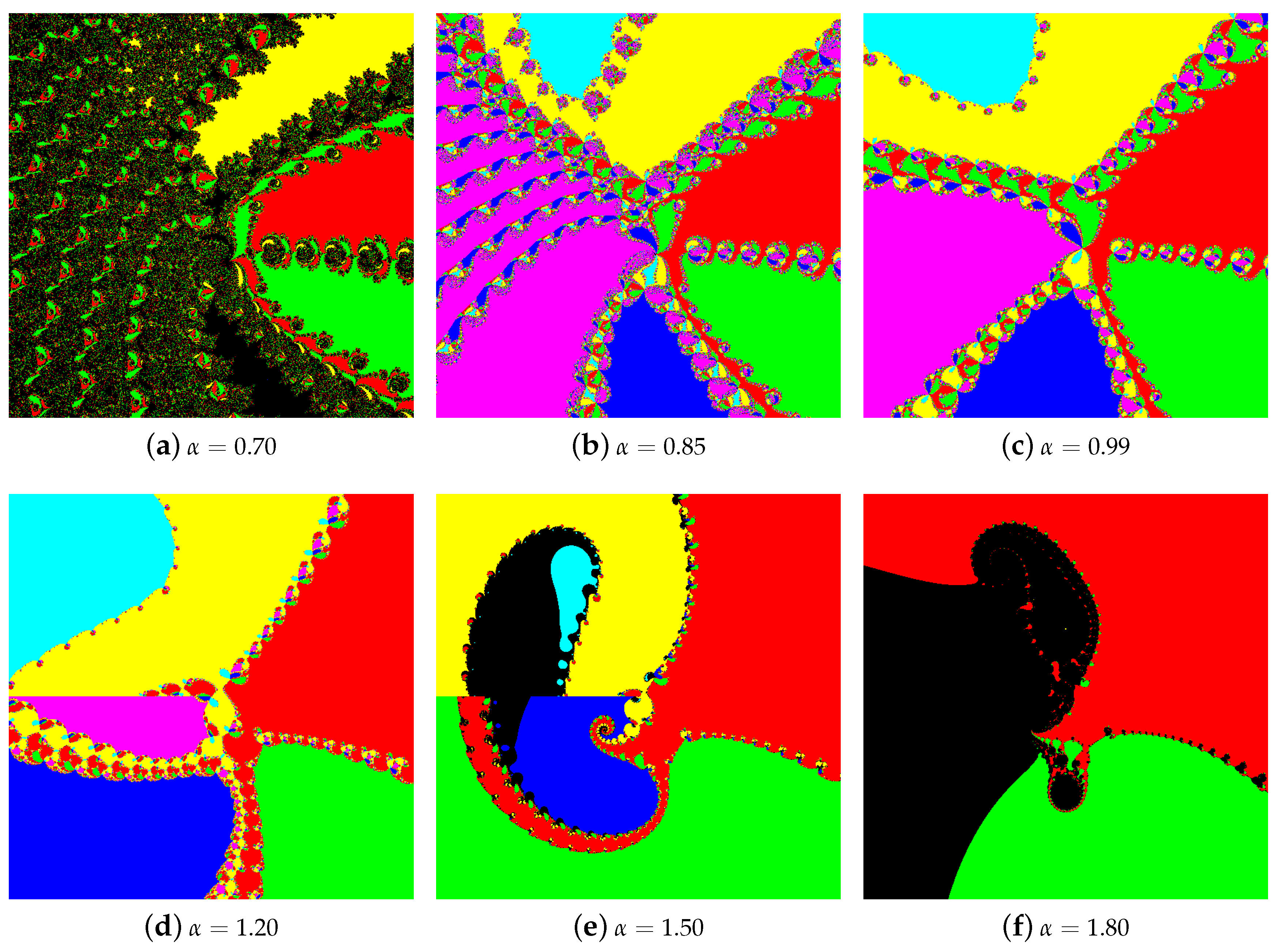
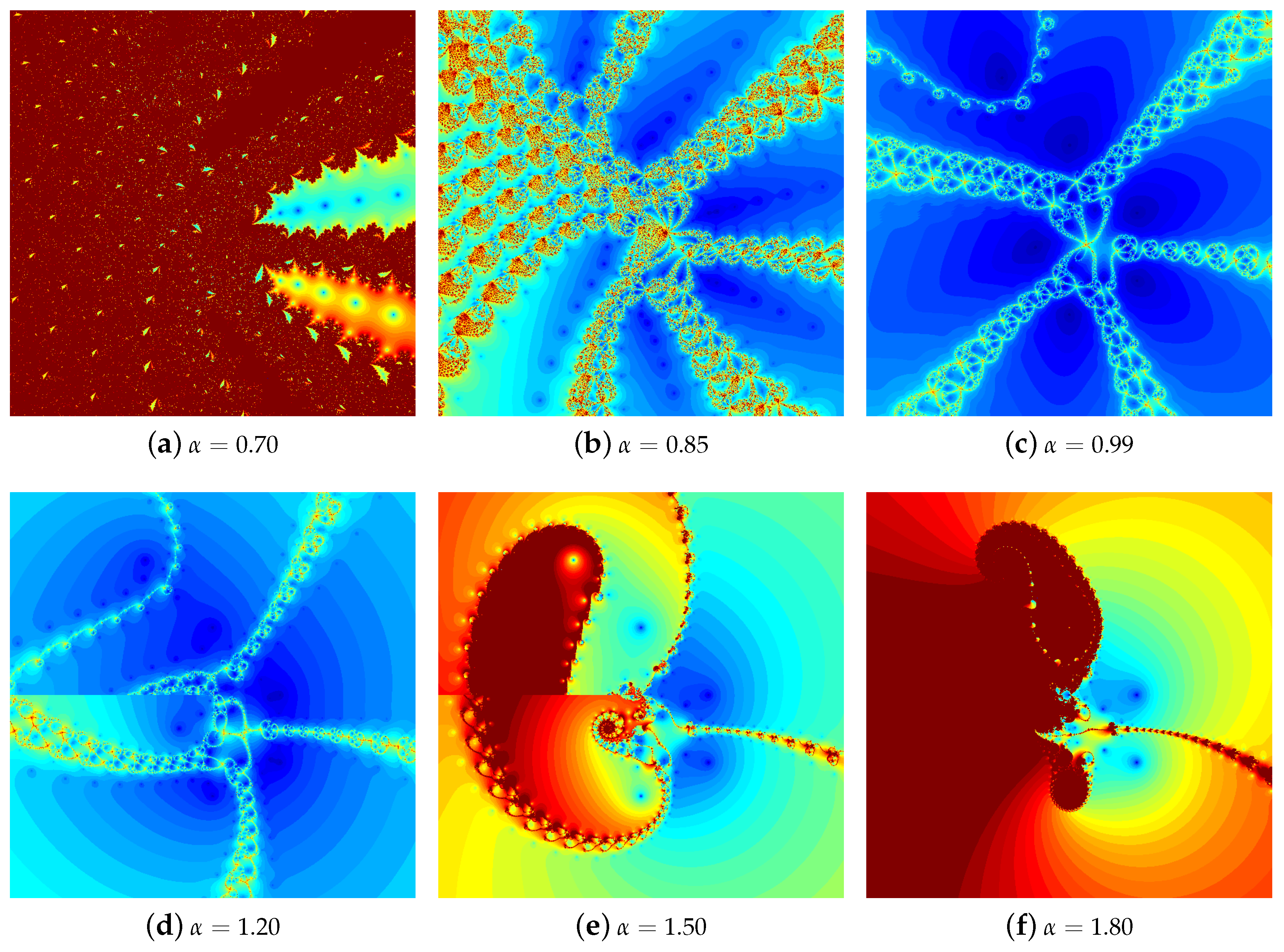
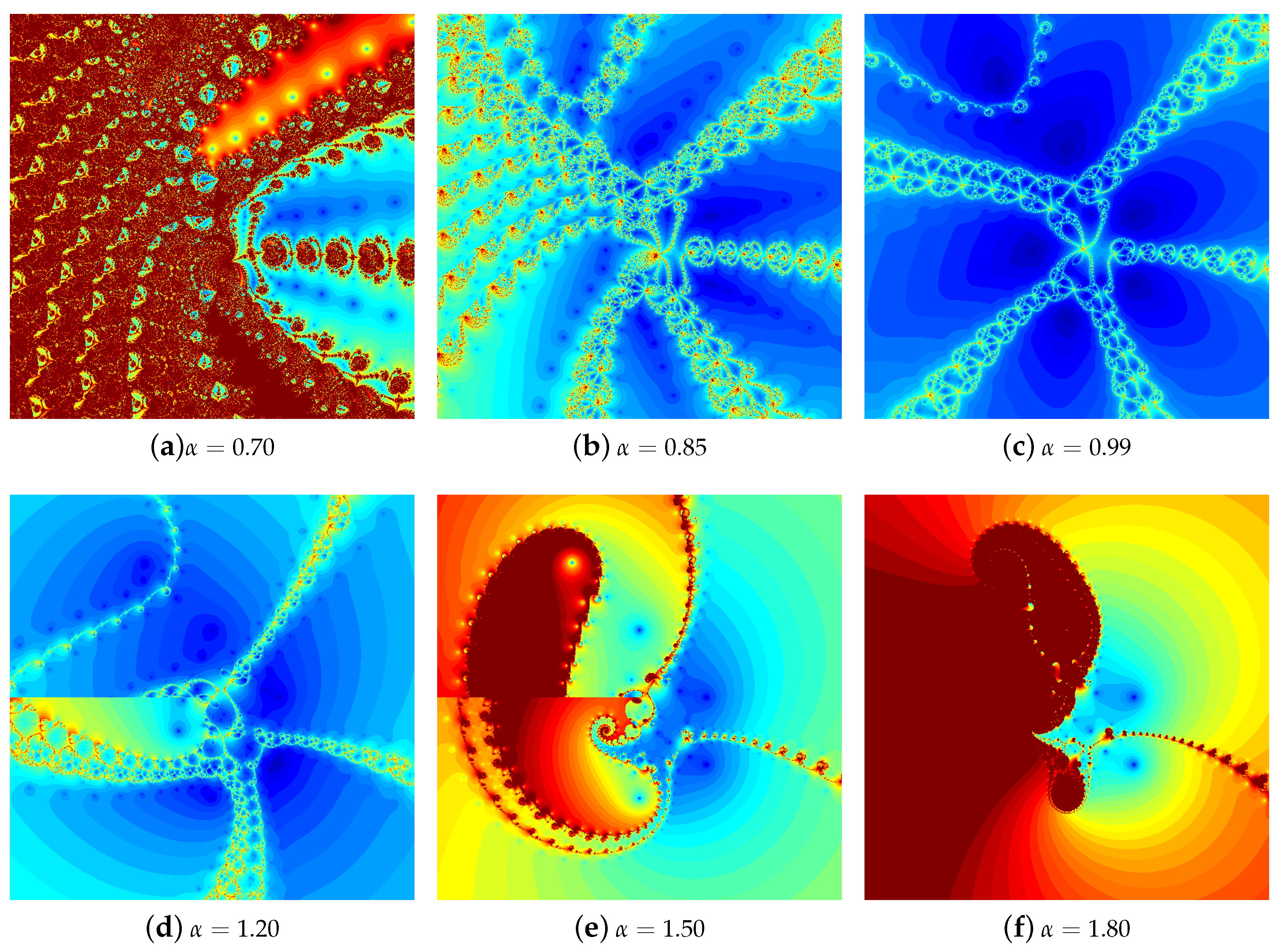
4.1. The Results of Experiments
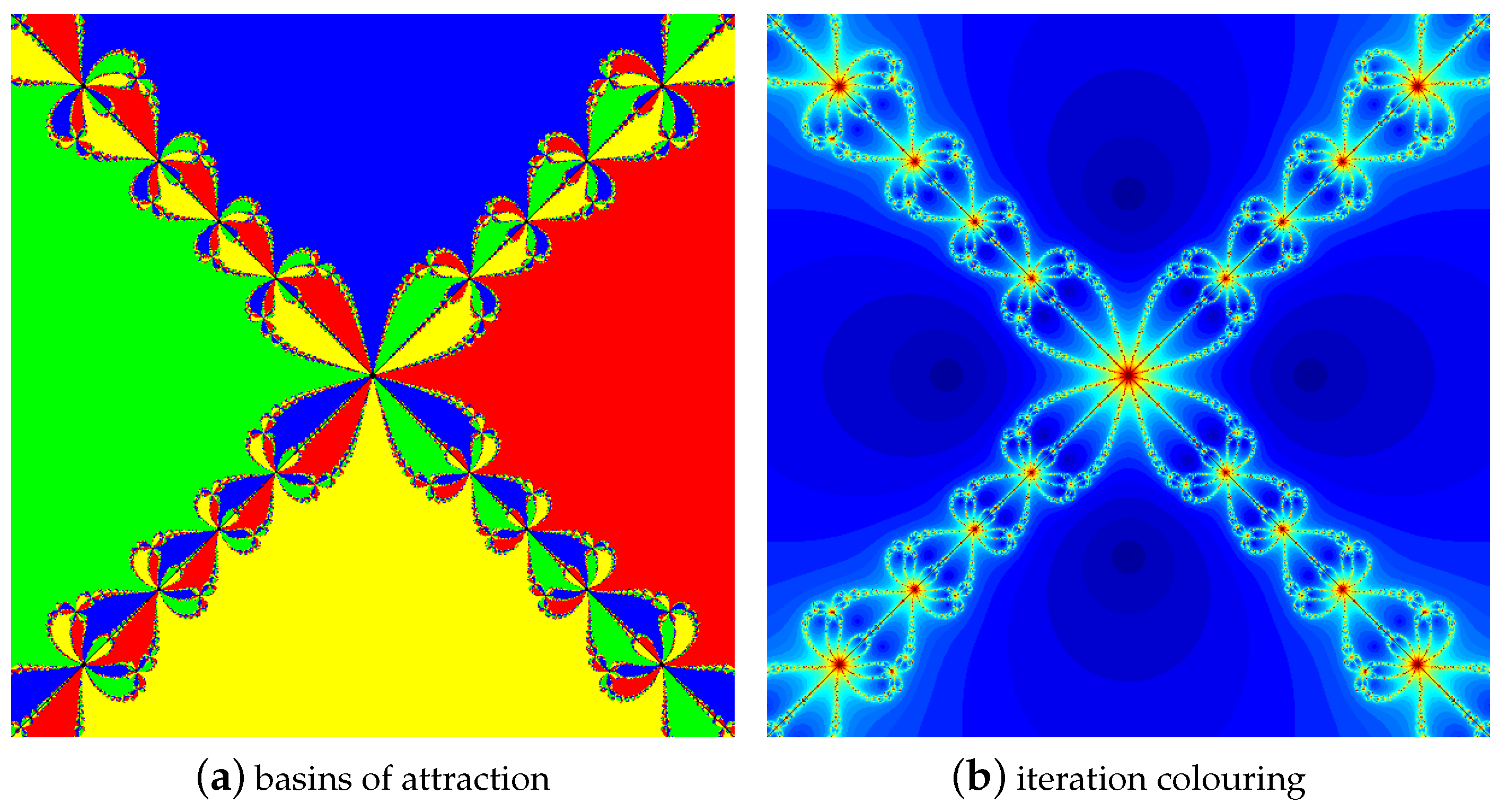
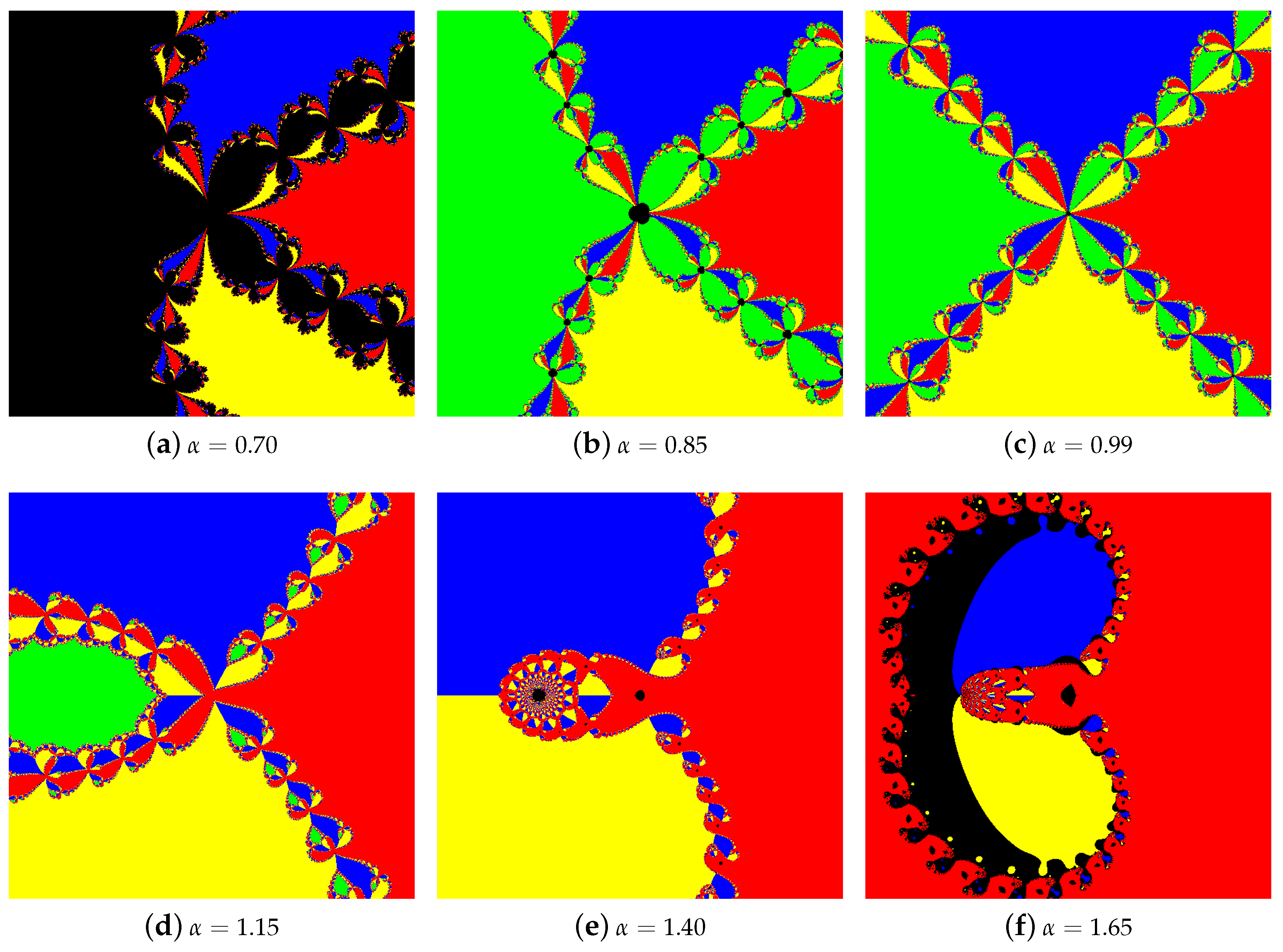
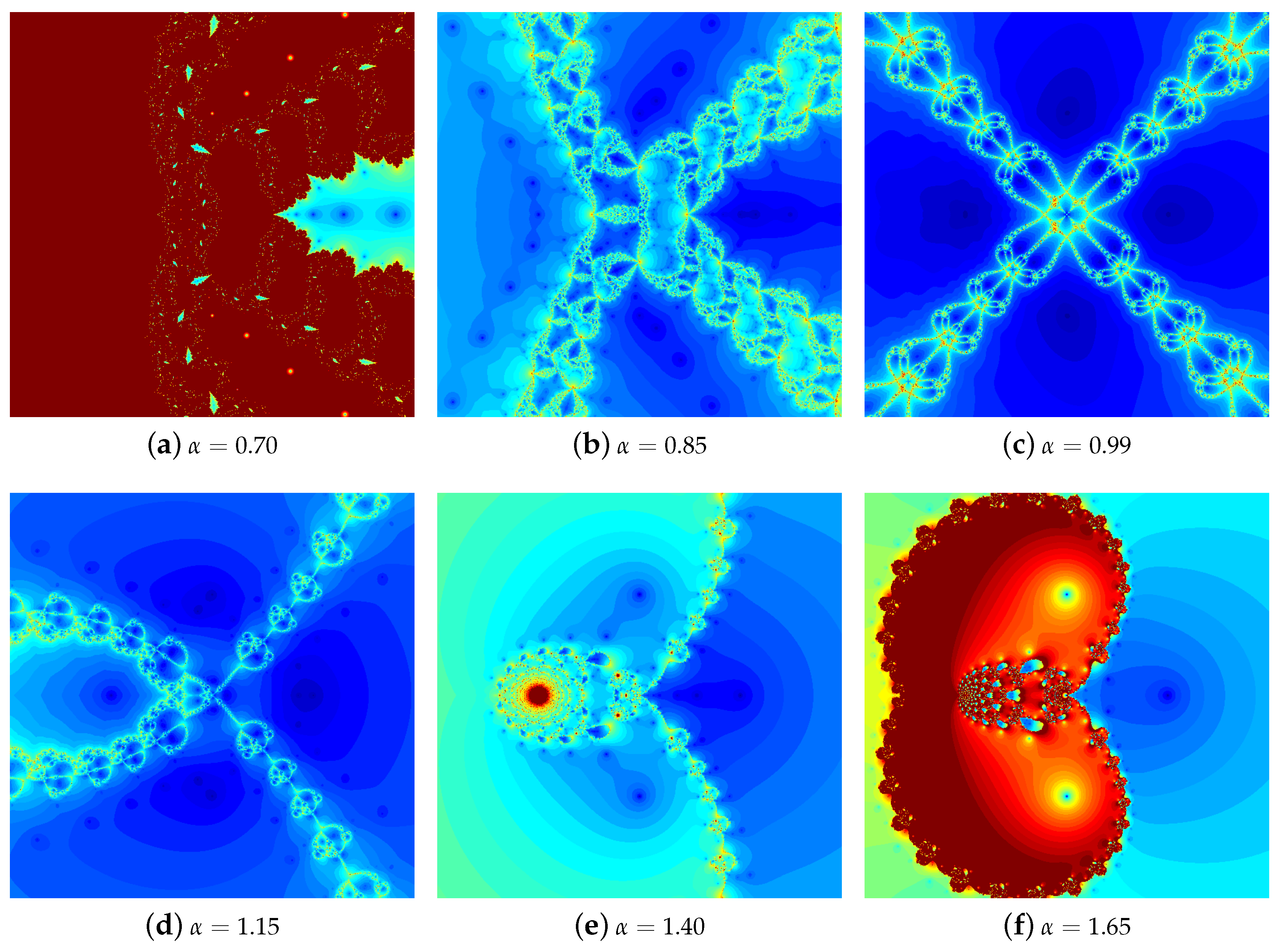
4.1.1. Polynomial
4.1.2. Polynomial
4.1.3. Polynomial
4.1.4. Polynomial
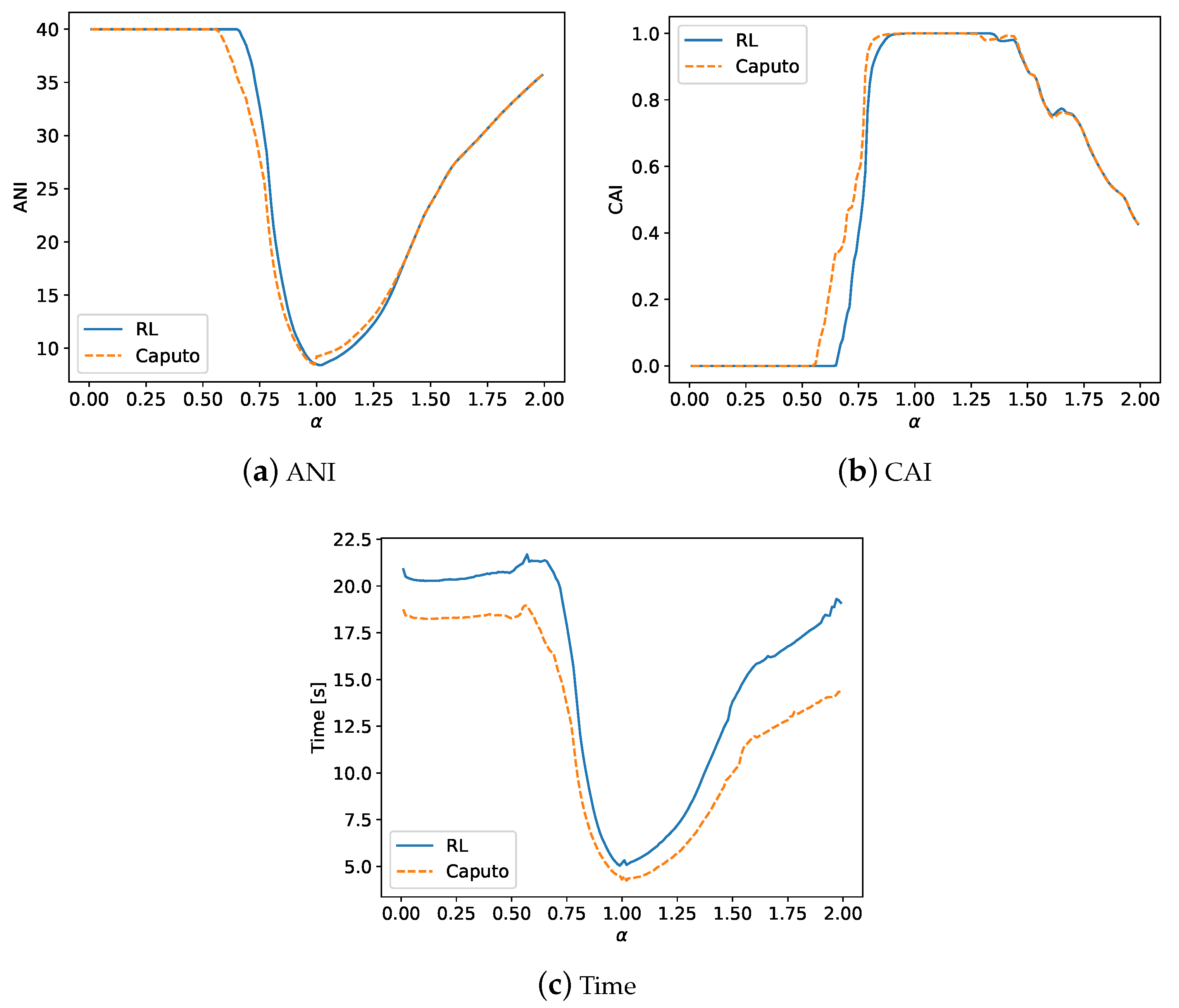
4.2. Summary of the Experiments
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Kalantari, B. Polynomial Root-Finding and Polynomiography; World Scientific: Singapore, 2009. [Google Scholar] [CrossRef]
- Kalantari, B. Polynomiography: From the Fundamental Theorem of Algebra to Art. Leonardo 2005, 38, 233–238. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W. Polynomiography for the Polynomial Infinity Norm via Kalantari’s Formula and Nonstandard Iterations. Appl. Math. Comput. 2017, 307, 17–30. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Polynomiography Based on the Non-standard Newton-like Root Finding Methods. Abstr. Appl. Anal. 2015, 2015, 797594. [Google Scholar] [CrossRef]
- Ardelean, G.; Cosma, O.; Balog, L. A Comparison of Some Fixed Point Iteration Procedures by using the Basins of Attraction. Carpath. J. Math. 2016, 32, 277–284. [Google Scholar]
- Chun, C.; Neta, B. Comparison of Several Families of Optimal Eighth Order Methods. Appl. Math. Comput. 2016, 274, 762–773. [Google Scholar] [CrossRef]
- Chun, C.; Neta, B. On the New Family of Optimal Eighth Order Methods Developed by Lotfi et al. Numer. Algorithms 2016, 72, 636–637. [Google Scholar] [CrossRef]
- Ardelean, G.; Balog, L. A Qualitative Study of Agarwal et al. Iteration Procedure for Fixed Points Approximation. Creat. Math. Inform. 2016, 25, 135–139. [Google Scholar]
- Gdawiec, K. Fractal Patterns from the Dynamics of Combined Polynomial Root Finding Methods. Nonlinear Dyn. 2017, 90, 2457–2479. [Google Scholar] [CrossRef]
- Brambila-Paz, F.; Torres-Hernandez, A. Fractional Newton–Raphson Method. 2017. Available online: https://arxiv.org/abs/1710.07634 (accessed on 28 July 2019).
- Brambila-Paz, F.; Torres-Hernandez, A.; Iturrarán-Viveros, U.; Caballero-Cruz, R. Fractional Newton-Raphson Method Accelerated with Aitken’s Method. 2018. Available online: https://arxiv.org/abs/1804.08445 (accessed on 28 July 2019).
- Abel, N. Opløsning af et Par Opgaver ved Hjælp af bestemte Integraler. Mag. Naturvidensk. 1823, 2, 205–215. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A New Collection of Real World Applications of Fractional Calculus in Science and Engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1974; Volume 111. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Wheeler, N. Construction and Physical Application of the Fractional Calculus. 1997. Available online: https://www.reed.edu/physics/faculty/wheeler/documents/Miscellaneous%20Math/Fractional%20Calculus/A.%20Fractional%20Calculus.pdf (accessed on 28 July 2019).
- Ishteva, M. Properties and Applications of the Fractional Caputo Operator. Master’s Thesis, Department of Mathematics, Universität Karlsruhe, Karlsruhe, Germany, 2005. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Vance, D. Fractional Derivatives and Fractional Mechanics. 2014. Available online: https://sites.math.washington.edu/~morrow/336_14/papers/danny.pdf (accessed on 28 July 2019).
- Chong, Y. Branch Points and Branch Cuts. 2016. Available online: http://www1.spms.ntu.edu.sg/~ydchong/teaching/07_branch_cuts.pdf (accessed on 28 July 2019).
- Le Bourdais, F. Understanding Branch Cuts in the Complex Plane. 2016. Available online: http://flothesof.github.io/branch-cuts-with-square-roots.html (accessed on 28 July 2019).
- Kahan, W. Branch Cuts for Complex Elementary Functions or Much Ado About Nothing’s Sign Bit. In Proceedings of the Joint IMA/SIAM Conference on the State of the Art in Numerical Analysis; Iserles, A., Powell, M., Eds.; Clarendon Press: New York, NY, USA, 1987; pp. 165–211. [Google Scholar]
- England, M.; Cheb-Terrab, E.; Bradford, R.; Davenport, J.; Wilson, D. Branch Cuts in Maple 17. ACM Commun. Comput. Algebra 2014, 48, 24–27. [Google Scholar] [CrossRef]
- Munkhammar, J. Fractional Calculus and the Taylor-Riemann Series. Rose Hulman Undergrad. Math. J. 2005, 6, 6. [Google Scholar]
- Ortigueira, M.; Rodríguez-Germá, L.; Trujillo, J. Complex Grünwald-Letnikov, Liouville, Riemann-Liouville, and Caputo Derivatives for Analytic Functions. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4174–4182. [Google Scholar] [CrossRef]
- Li, C.; Daoa, X.; Guoa, P. Fractional Derivatives in Complex Planes. Nonlinear Anal. 2009, 71, 1857–1869. [Google Scholar] [CrossRef]
- Ortigueira, M.D. A Coherent Approach to Non-integer Order Derivatives. Signal Process. 2006, 86, 2505–2515. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gdawiec, K.; Kotarski, W.; Lisowska, A. Visual Analysis of the Newton’s Method with Fractional Order Derivatives. Symmetry 2019, 11, 1143. https://doi.org/10.3390/sym11091143
Gdawiec K, Kotarski W, Lisowska A. Visual Analysis of the Newton’s Method with Fractional Order Derivatives. Symmetry. 2019; 11(9):1143. https://doi.org/10.3390/sym11091143
Chicago/Turabian StyleGdawiec, Krzysztof, Wiesław Kotarski, and Agnieszka Lisowska. 2019. "Visual Analysis of the Newton’s Method with Fractional Order Derivatives" Symmetry 11, no. 9: 1143. https://doi.org/10.3390/sym11091143
APA StyleGdawiec, K., Kotarski, W., & Lisowska, A. (2019). Visual Analysis of the Newton’s Method with Fractional Order Derivatives. Symmetry, 11(9), 1143. https://doi.org/10.3390/sym11091143




