ExtrIntDetect—A New Universal Method for the Identification of Intelligent Cooperative Multiagent Systems with Extreme Intelligence

Abstract

In this research, we define a specific type of performance of the intelligent agent-based systems (IABSs) in terms of a difficult problem-solving intelligence measure. Many studies present the successful application of intelligent cooperative multiagent systems (ICMASs) for efficient, flexible and robust solving of difficult real-life problems. Based on a comprehensive study of the scientific literature, we conclude that there is no unanimous view in the scientific literature on machine intelligence, or on what an intelligence metric must measure. Metrics presented in the scientific literature are based on diverse paradigms. In our approach, we assume that the measurement of intelligence is based on the ability to solve difficult problems. In our opinion, the measurement of intelligence in this context is important, as it allows the differentiation between ICMASs based on the degree of intelligence in problem-solving. The recent OutIntSys method presented in the scientific literature can identify systems with outlier high and outlier low intelligence from a set of studied ICMASs. In this paper, a novel universal method called ExtrIntDetect, defined on the basis of a specific series of computing processes and analyses, is proposed for the detection of the ICMASs with statistical outlier low and high problem-solving intelligence from a given set of studied ICMASs. ExtrIntDetect eliminates the disadvantage of the OutIntSys method with respect to its limited robustness. The recent symmetric MetrIntSimil metric presented in the literature is capable of measuring and comparing the intelligence of large numbers of ICMASs and based on their respective problem-solving intelligences in order to classify them into intelligence classes. Systems whose intelligence does not statistically differ are classified as belonging to the same class of intelligent systems. Systems classified in the same intelligence class are therefore able to solve difficult problems using similar levels of intelligence. One disadvantage of the symmetric MetrIntSimil lies in the fact that it is not able to detect outlier intelligence. Based on this fact, the ExtrIntDetect method could be used as an extension of the MetrIntSimil metric. To validate and evaluate the ExtrIntDetect method, an experimental evaluation study on six ICMASs is presented and discussed.

1. Introduction

The evaluation of the performance of computing systems includes diverse research topics, including the performance evaluation of cognitive packet networks [1], cognitive packet networks where network worms operate [2], peering-agreements among systems for peer-to-peer traffic that has some kind of autonomy [3], the Internet [4], large-scale SCI multiprocessors [5], algorithms [6], and supply chain management based on Internet of Things technology [7]. Performance evaluation in terms of intelligence is rarely addressed for IABSs, where the property of intelligence requires more complex analysis than that carried out in a usual performance evaluation. IABSs are used for solving a variety of real-life problems: quality measurement of Golden bleached raisins [8], predicting the machining performance parameters of Inconel 690 [9], intelligent diagnosis of certain diseases [10], intelligent support of automatic metrological measurement results [11], intelligent fault diagnosis of wind turbines [12], and the detection and segmentation regions of interest in retinal images [13]. Many IABSs are ICMASs [14]. ICMASs can frequently solve problems with various types of computational complexity. ICMASs are particularly important with respect to the fact that even in CMASs composed of less complex agents, increased intelligence could emerge at a system level [15] as result of flexible, robust and efficient cooperative problem-solving. The cooperative swarms of ground and aerial vehicles with agent properties can be mentioned as examples of developed ICMASs. Kwon and Pack [16] proposed a robust mobile target localization method for cooperative unmanned aerial vehicles. Saska et al. [17] proposed a model for the coordination and navigation of formations of heterogeneous unmanned aerial and ground vehicles (MAV-UGV).

In this research, we consider the expression of a specific type of performance of ICMASs in terms of the intelligence required to solve difficult problems. We carried out long-term study and research into the relevant literature; based on this, we concluded that there is no unanimous definition for, or even a view on, the intelligence of ICMASs. However, even in this situation, machine intelligence can be measured, and its measurement could be effective for the differentiation of ICMASs based on their intelligence. This is somehow similar to human intelligence, for which there is also no unanimous definition. This fact is based on the enormously high complexity of the human brain and human cognition. Many effective intelligence tests for the measurement of human intelligence have been proposed. The most frequently used human IQ tests are carried out using: the Stanford-Binet scale [18,19,20], Raven’s Progressive Matrices [21,22], the Wechsler Adult Intelligence Scale [23,24], and the Kaufman Assessment Battery for Children [25,26,27]. Neisser et al. performed a study [28] that showed that the measurement of intelligence based on IQ test scores without any other considerations ignores many important aspects that are specific to human cognition. It has been proved in some studies that the measurement of human intelligence has applicative effectiveness. According to [29], the human intelligence quotient (IQ) influences, among other things, job and school performance. However, this depends on other factors such as specialty knowledge and, to some degree, commonsense knowledge.

In our approach, it is assumed that the measurement of the machine intelligence of ICMASs is based on some kind of ability to solve difficult problems. The Machine Intelligence Quotient (MIQ), the indicator of the central intelligence tendency of an ICMAS, is obtained by statistical computations after measuring how intelligently a set of difficult problems has been solved. A universal method is effectively being proposed, called the Robust Extreme Intelligence Detection Method (ExtrIntDetect), for the detection of ICMASs with statistically extremely low and high MIQ in solving problems from a set of considered ICMASs. The novelty of the proposal lies in designing a specific series of computing processes and analyses. The usefulness of the method consists in indicating the brilliant systems that are able to most intelligently solve difficult problems and the poor systems that will solve problems with unexpectedly low intelligence. ExtrIntDetect represents an extension of a novel method for detecting outlier intelligence of ICMASs called OutIntSys [30]. The purpose of extending the OutIntSys method was to conserve its properties, while at the same time making it more robust.

The symmetric MetrIntSimil metric [31] is able to compare ICMASs based on the intelligence with which they solve difficult problems and classify them into intelligence classes. Systems that are classified as belonging to the same class are able to solve the given problems with same level of intelligence. One limitation of MetrIntSimil is the fact that it is not able to identify extreme intelligence. The ExtrIntDetect method could be used as an extension of the MetrIntSimil metric in order to detect systems with extremely low and extremely high intelligence.

To evaluate and validate the ExtrIntDetect method, an illustrative experimental case study is presented. We studied six ICMASs, all of which are considered intelligent in the scientific literature based on their efficient and flexible problem-solving, and specialize in solving the class of NP-hard problems.

The rest of this paper is organized as follows: In Section 2, some representative state-of-the-art metrics for the measurement of machine intelligence are presented. Section 3 presents the proposed ExtrIntDetect method. The experimental study for the validation of the ExtrIntDetect method is presented in Section 4. In Section 5, a discussion of the ExtrIntDetect method is presented. Section 6 presents the conclusions of this work.

2. State-of-the-Art Metrics Designed to Measure Machine Intelligence

There are very few developed intelligence metrics that are able to carry out different types of measurement of machine intelligence. In our paper published in 2018 [32], we presented a comprehensive review of recent research directions in measuring the IABSs intelligence. In the following, we present some studies and research focused on metrics/methods for measuring machine intelligence.

According to the well-known work of Alan Turing, as formulated in 1950 [33], a computing system can be considered intelligent if a human judge could not classify it as being artificial or human based on how it responds to questions. Dowe and Hajek in 1998 [34] proposed a specific computational extension of the Turing Test. In 2000, Schreiner [35] analyzed the possibility of creating standard measurements for computing systems that would be able to classify them as intelligent. Park et al., in 2001 [36], studied the measurement of intelligence of human–machine systems, proposing a so-called intelligence task graph as an effective tool for modeling and analysis. In 2003, Sanghi and Dowe [37] presented an advanced computer program that had been successfully evaluated by means of some standard human IQ tests. A measure of performance in difficult and easy environments was defined in 2006 [38]. In 2007 [39], method for measuring intelligence based on the capacity to compare alternatives with different levels of complexity was proposed. In 2010, Hernández-Orallo [40] presented an interesting study related to the Turing Test. A universal anytime intelligence test was proposed by Hernández-Orallo and Dowe in 2010 [41]. The concept of universality was regarded as the advanced ability of a metric to measure artificial and biological intelligence at the same time. In [42], published in 2011, a metric for the measurement of intelligence in consideration of a hierarchy of sets of increasingly difficult environments was proposed. In 2014, Hernández-Orallo et al. [43] studied the development of universal metrics for the measurement of the capabilities of intelligent systems that was inspired by the psychometrics applied for the measurement of human intelligence. In 2015, Besold et al. [44] approached the important research question of whether machine intelligence could be measured using the same methods as human intelligence. In 2016, Chmait et al. [45] elaborated some dynamic intelligence tests for measuring combined intelligence in cooperative systems. In [30], published in 2017, a method called OutIntSys for the identification of ICMASs with extreme intelligence was presented. Liu et al., in 2017 [46], presented a recent complex study related to the analysis of the machine intelligence quotient (MIQ). The recent symmetric MetrIntSimil metric, published in 2018 [31], is able to compare the intelligence of a large number of ICMASs.

As a concluding remark related to state-of-the-art studies and research focusing on the measurement of intelligence, current intelligence metrics are founded on very different principles the measurement of machine intelligence. Based on this consideration, most of them cannot be effectively compared in any way. The main limitation of the designed intelligence metrics and methods presented in the literature consists in the lack of the ability to identify ICMASs with statistically extreme intelligence from a set of studied ICMASs. The maximum or poorest intelligence does not necessarily mean statistically extreme (high/low) intelligence. The expectation of such a method/metric consists in the identification of systems that statistically have a much higher (or lower) problem-solving intelligence than the others. The OutIntSys method is designed with this purpose in mind, but it has limited robustness. The MetrIntSimil metric is appropriate for the measurement and comparison of intelligence, and the classification of intelligence into intelligence classes, but unfortunately it is not able to detect statistical extremes.

3. The Proposed ExtrIntDetect Method

In this section, a novel method called Robust Extreme Intelligence Detection Method (ExtrIntDetect) is proposed for the detection of the ICMASs with extreme intelligence from a set of studied ICMASs, denoted ICM = {ICM₁, ICM₂, …, ICM_z}. Each studied ICMAS comprises a specific number of agents. Each ICMAS can have any number of agents, and could possess any architecture. There are no restrictions related to either the studied systems having an equal number of agents, or to their having the same architectural homogeneity. We will denote with |ICM_r| the cardinality of ICM_r (i.e., the number of its agents).

Human evaluator (He) represents the human specialist (or the groups of human specialists, in the case of extremely complex systems) that performs the measurement of the machine intelligence of the studied ICMASs. A calculated intelligence indicator (IntIndic) gives a quantitative measure of the studied system’s intelligence, which corresponds to an evaluated problem-solving intelligence measure. In the case of a particular set of studied ICMASs, the He must decide on the best-fitting intelligence indicator measure based on the envisioned type of machine intelligence.

Prob = {Prob₁, Prob₂, … Prob_z} denotes the set of problems used for the evaluation of problem-solving intelligence in the studied set of ICMASs. Each system’s problem-solving intelligence is evaluated based on a specific set of problems. We will denote with Prob_k = {Prob_k,₁, Prob_k,₂, …, Prob_k,_m} the set of problems used for the problem-solving intelligence evaluation of ICM_k (ICM_k∈ICM). |Prob_k|, (|Prob_k| = m) represents the cardinality (i.e., the number of problems) used in the experimental intelligence evaluation of ICM_k. There is no requirement for the sets of problems Prob₁, Prob₂, … and Prob_z to be the same. There is no restriction that the cardinalities |Prob₁|, |Prob₂|, … and |Prob_z| of Prob₁, Prob₂, … and Prob_z to be the same. He is responsible in the case of each ICM_k for the establishment of |Prob_k| and Prob_k (as described in the MPSI algorithm). It was determined that the |Prob_k| value should be at least 5 (|Prob_k| ≥ 5) for the calculation of the intelligence quotient of the ICMAS. This minimum permitted value was set in order to allow the application of statistical testing for the verification of the data normality assumption. It is recommended, when possible, that intelligence evaluations be carried out for larger sets, |Prob_k| ≥ 10, or even |Prob_k| ≥ 30.

In the following, Intellig_k = {Intellig_k,1, Intellig_k,2, …, Intellig_k,m} denotes the intelligence indicators obtained as a result of the Prob_k problem-solving intelligence evaluations performed for a specific ICMAS denoted ICM_k.

If necessary, problem-solving intelligence can be calculated as the weighted sum of c types of intelligence components (1). These measure different aspects of the intelligence of the studied ICMASs.

IntIndic = imp₁ × ms₁ + imp₂ × ms₂ + … + imp_c × ms_c.
imp₁ + imp₂ + … + imp_c = 1, imp_i > 0

(1)

where: ms₁, ms₂, …, ms_c represent the considered intelligence components measure at a particular problem-solving intelligence evaluation; imp₁, imp₂, …, imp_c represent the weights associated with the intelligence components. The weight of a component quantifies the importance of that component in the intelligence evaluation measure.

The Scenario of Coalitions of Agent-Based Flying Drones

With to the aim of explaining the previously introduced notions, in the following a scenario is presented. A set of ICMASs is considered that is composed of coalitions of flying agent-based drones denoted ICM₁, ICM₂, …, ICM_n. Each ICMAS is composed of a specific number of agents specialized in the delivery of products to customers. Each ICMAS solves problems in problem-solving cycles. A problem-solving cycle consists of a certain number of deliveries to clients by the drones that compose the respective ICMAS. A problem-solving cycle is finished when all the products have been delivered. A drone could undertake the task of a certain number of product deliveries to one or multiple destinations. Each visited client could be the recipient of one or more products. Each flying drone visits each client only once, at most. After all the deliveries have been completed, the drones should return to their starting locations. To determine the optimal route requirements for delivery, it is necessary that each drone solves a Travelling Salesman Problem.

He decides to evaluate the intelligence of each ICMAS with respect to the intelligence demonstrated in the delivery of the products. The intelligence of a particular flying drone in a flight is calculated based on two intelligence components, with weights imp₁ and imp₂, established by He, based on the intelligence of the delivery. For the delivery of products (one or more) to clients (one or more) at home, a mark between 0 and 7 is given by He. The first intelligent component measure has a weight of 0.65 (ms₁ = 0.65). The second intelligence component measure is established as the mean of the marks with values between 0 and 7 that have been given by clients who have received products in that delivery, with the weight of 0.35 (ms₂ = 0.35). For instance, a scenario involving the delivery of some products to two clients is considered. Each client gives a mark, and the mean of the values is computed. The weight of this mean is marked as 0.35. The reason for choosing these weighting values by He lies in the fact that human assessors have deeper knowledge regarding ICMASs than the clients. The clients are common people who conclude their evaluation mostly based on their satisfaction with the delivery. The reason for the weighting of the evaluation of clients being no less than half of the weighting of the evaluation of the human specialist is that clients’ satisfaction with deliveries is an important factor for the company that owns the drones. The final obtained intelligence indicator value based on the values of the two intelligence components will be a number in the interval [0, 7]. 0 signifies a system with no measurable intelligence. 7 signifies brilliant system (with the utmost possible intelligence).

The intelligence of a CMAS in a problem-solving cycle can be calculated as the average of the marks received by the contributing member agents of the CMAS.

He is in charge of selecting the type of intelligence that is to be measured by the He. This is the first step, and it is executed before the application of the Measuring the Problem-Solving Intelligence (MPSI) algorithm (Algorithm 1) for each studied ICMAS. By applying the MPSI algorithm for each analyzed ICMAS, the problem-solving intelligence indicator is computed for each problem used for the intelligence evaluation.

Algorithm 1 MPSI measurement

Measuring the Problem-Solving Intelligence Algorithm IN: //Given the studied ICMk that have a specific architecture and a specific number of agents. ICMk = {Agent1, Agent2, …, Agentq}; OUT:|Probk|; Probk = {Probk,1, …, Probk,m}; Intelligk = {Intelligk,1, Intelligk,2, …, Intelligk,m}; Begin Step 1. He establishes |Probk| and Probk. |Probk|: = m; Probk = {Probk,1, …, Probk,m} Step 2. Obtaining the intelligence indicators data. //If there are more intelligence components, than each evaluated problem-solving intelligence is calculated according to (1). @Performing the problem-solving intelligence evaluations and calculus; Intelligk = {Intelligk,1, Intelligk,2, …, Intelligk,m}; EndMPSIAlgorithm

|ICM| = z represents the cardinality of the set of studied ICMASs. z sample intelligence indicator datasets are obtained, as the number of studied ICMASs is z. Intellig = {Intellig₁, Intellig₂, …, Intellig_z} denotes the problem-solving intelligence indicators of the studied ICMASs. Intellig₁ represents the problem-solving intelligence obtained by evaluating ICM₁. Intellig₂ represents the problem-solving intelligence obtained by evaluating ICM₂. … Intellig_z represents the problem-solving intelligence obtained by evaluating ICM_z. The MPSI algorithm is applied in order to obtain the intelligence indicators for each ICMAS.

Robust Measurement of the Intelligence Quotient (MMI) algorithm calculates the machine intelligence quotients of ICM₁, ICM₂, …, ICM_z. It describes the calculation of machine intelligence quotients, MIQS = {MIQ₁, MIQ₂, …, MIQ_z} based on the provided intelligence indicator data obtained for ICM₁, ICM₂, …, ICM_z by applying the MPSI algorithm. MIQ_k denotes the machine intelligence quotient of the ICM_k, which indicates its central intelligence tendency. It should be noted that the most suitable indicator of the central intelligence tendency of an ICMAS is the median in cases where the intelligence indicator data does not pass the normality assumption, and the mean in where the data passes the normality assumption. The previous assertion is based on the fact that a very high or a very low value influences the median less than the mean. TypeMIQ, used in the algorithm, is a variable that indicates the calculus of MIQS as mean or median.

For the verification of the data normality assumption of the intelligence indicator, a variety of goodness-of-fit statistical normality tests are available. Among the most frequently used tests, the following must be mentioned [47]: Shapiro-Wilk test (SW test) and Lilliefors test (Lill test). In the MMI algorithm (Algorithm 2), in order to check the normality of the intelligence indicators, the Lill test [47,48,49] and the SW test [47,50] were chosen. In the scientific literature, the usage of the SW test is recommended even in cases with smaller sample sizes. Razali and Wah [47] performed a study that proved that the SW test had the highest power for a given significance when compared to other very frequently used tests, including the Anderson Darling test (AD test), the One-sample Kolmogorov-Smirnov test (KS test), the Lill test, and the SW test. Stephens [51] proved that the SW test was more powerful for testing normality than the KS test and the AD test. In the present study, limitations in cases with many identical values were observed to be a disadvantage of the SW test.

Algorithm 2 MMI measurement method

Robust Measurement of the Intelligence Quotient Algorithm IN:Intellig = {Intellig1, Intellig2, …, Intelligz};//Intelligence indicators sample of the ICM. OUT: TypeMIQ; MIQS; Begin Step 1. Calculus of the MIQS. TypeMIQ: = ”Mean”; For (i: = 1 to z) Do  @Verify if Intelligi passes the normality assumption.  If (Intelligi failed to passes the normality assumption) Then    TypeMIQ: = ”Median”; Exit For;  EndIf EndFor //He can change TypeMIQ based on the problem and domain-specific knowledge. @He makes the final decision on the TypeMIQ calculus as the mean or the median; For (i: = 1 to z) Do  If (TypeMIQ = ”Mean”) then MIQi: = MEAN(Intelligi);     Else MIQi: = MEDIAN(Intelligi);  EndIF EndFor EndMMImeasuring

Visual appreciation is frequently a useful alternative to performing a numerical analysis. One such frequently applied approach is the Quantile-Quantile Plot (QQ plot). The QQ plot [52] is a scatterplot that is appropriate for the visual appreciation of normality. Technically, a QQ plot is created by plotting two sets of quantiles against one another. Visually, it should be interpreted as follows: if both sets of quantiles belong to the same distribution, then the plotted points form a line that is roughly straight. The joint use of the QQ plot with the SW test could be suggested to be a good practice in order to answer the requirement for precise verification of the normality.

There are z sample intelligence indicator datasets, because the number of studied ICMASs is z. All sample intelligence data, Intellig₁, Intellig₂, …, Intellig_z, are initially verified as having passed the normality assumption. According to the algorithm, if one or more ICMASs do not pass the normality assumption, then the automatic decision will be to calculate the MIQ of all ICMASs based on the intelligence indicator medians (TypeMIQ = “Median”). In the contrary case, the automatic decision will be to compute the MIQ of all the ICMASs based on the mean (TypeMIQ = “Mean”). He has the right to make final modifications when choosing the mean or the median if she/he is in possession of domain-specific knowledge.

The ExtrIntDetect algorithm (Algorithm 3) describes the proposed identification of ICMASs with extreme intelligence from among the set ICM of the studied ICMASs. Figure 1 presents the main processing and analysis steps comprising the ExtrIntDetect method. The Detection of ICMASs with Extreme Intelligence algorithm presents the performed processing in depth.

Algorithm 3 ExtrIntDetect method of measurement and detection

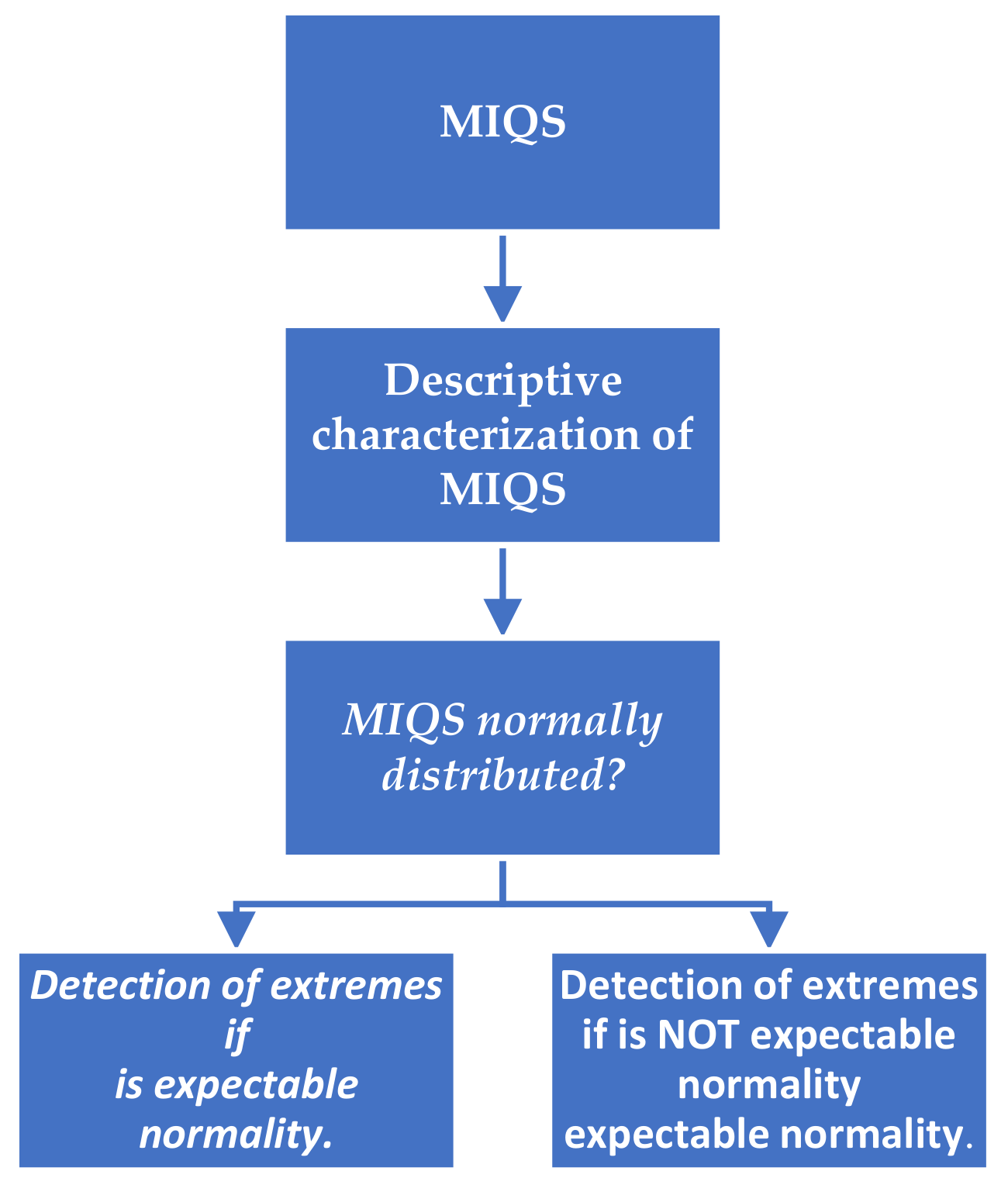
Detection of ICMASs with Extreme Intelligence Algorithm IN:MIQS = {MIQ1, MIQ2, …, MIQz};//Calculated machine intelligence quotients. OUT: //IdOutL, IdOutH, if normality expected. IdOutL;//MIQ of ICMASs with low extreme intelligence. IdOutH;//MIQ of ICMASs with high extreme intelligence. //HExtr, HExtrOut, if normality NOT expected. HExtr;//MIQ of ICMASs with high extreme intelligence. HExtrOut;//MIQ of ICMASs with high outlier extreme intelligence. LExtr;//MIQ of ICMASs with low extreme intelligence. HExtrOut;//MIQ of ICMASs with low outlier extreme intelligence. Begin Step 1. Descriptive characterization of the MIQS data. @Calculates for MIQS the: mean, median, SD, SEM, skew, and kurt. CV: = 100 × (SD/mean); Step 2. Analyze if MIQS data passes the normality assumption. @Apply Lill and SW tests in order to verify MIQS normality. @Constructs the QQ plot for visual analysis of MIQS. @Based on the obtained result of data normality analysis set the value of norm variable; If (norm = ”No”) Then  @He has the right to change norm value to “Yes”. EndIf Step 3. Detection of extremes if normality expected. If (norm = ”Yes”) Then  IdOutL: = ∅;IdOutH: = ∅;  OutFound: = ”Yes”; IdOut: = MIQS;  avg*: = mean(IdOut);  While ((OutFound = ”Yes”) and (|IdOut|≥3)) Do   OutFound: = ”No”; @It is applied the Grubbs test;   If (an outlier denoted OUT was identified) Then    IdOut: = IdOut\{OUT}; OutFound: =”Yes”;    If (OUT < avg*) Then IdOutL: = IdOutL ∪ {OUT};        Else IdOutH: = IdOutH ∪ {OUT};    EndIf  EndIf  avg* = mean(IdOut);  EndWhile EndIF If (|IdOutL| ≥ 2) Then @Order ascending IdOutL. EndIf If (|IdOutH| ≥ 2) Then @Order ascending IdOutH. EndIf Step 4. Detection of extremes if normality is NOT expected. If (Norm = ”No”) Then  HExtr: = ∅; HExtrOut: = ∅; LExtr: = ∅; LExtrOut: = ∅;  @Arrange MIQS = {MIQ1, MIQ2, …, MIQz} in ascending order.  @Calculate Q1 and Q3;//The first and third quartile.  IQR: = Q3−Q1;//Calculates the interquartile range.  @He establishes RangeL and RangeU values.  HLowLim: = Q3 + RangeL × IQR; HUppLim: = Q3 + RangeU × IQR;  LLowLim: = Q1 − RangeU × IQR; LUppLim: = Q1 − RangeL × IQR;  For (i: = 1 to z) Do   If (MIQi ∈ [HLowLim, HUppLim)) Then HExtr: = HExtr ∪ {MIQi};     ElseIf (MIQi ≥ HUppLim) Then HExtrOut: = HExtrOut ∪ {MIQi};   EndIf   If (MIQi ∈ (LLowLim, LUppLim]) Then LExtr: = LExtr ∪ {MIQi};       ElseIf (MIQi ≤ LLowLim) Then LExtrOut: = LExtrOut ∪ {MIQi};   EndIf  EndFor  If (|HExtr| ≥ 2) Then @Order ascending HExtr. EndIf  If (|HExtrOut| ≥ 2) Then @Order ascending HExtrOut. EndIf  If (|LExtr| ≥ 2) Then @Order ascending LExtr. EndIf  If (|LExtrOut| ≥ 2) Then @Order ascending LExtrOut. EndIF End EndExtrIntDetectAlgorithm

The notation “@” used in the algorithm indicates a method that is launched by the algorithm, but that is not described explicitly and in-depth in the algorithm. Step 1 of the ExtrIntDetect method makes a statistical characterization of the MIQS = {MIQ₁, MIQ₂, …, MIQ_z} data. The variable mean represents the calculated mean of MIQS. The variable median represents the calculated median of MIQS. The median is the middle of a sorted list of numbers. If the list has an even number of items, then the median is calculated as the average of the two numbers in the middle. The value Standard deviation (SD) expresses a quantity by the degree to which the members of a dataset differ from the mean of that dataset. SD effectively quantifies the amount of variation/dispersion in a dataset [53]. The standard error (SE) of a specific parameter is effectively the standard deviation of its sampling distribution. When the parameter or the statistic is the mean, then it is referred to as the standard error of the mean (SEM). SEM = SD/sqrt(N), where sqrt denotes the square root. The variable min denotes the lowest value. The variable max denotes the highest value. The variable range = max−min is frequently an important indicator.

Skewness (skew) [54] is a measure of the symmetry of MIQS data. A distribution is called symmetric if it looks the same on both the right and left of the center point. If skew ≥ 1 or skew ≤ −1, the distribution is called highly skewed. If skew ∈ [0.5, 1) or skew ∈ (−1, −0.5], the distribution is called moderately skewed. If skew ∈ (−0.5, 0.5), the distribution is called approximately symmetric.

Kurtosis (kurt) [54] is a measure of whether the MIQS data are heavy-tailed or light-tailed relative to the base normal distribution. Datasets with high kurtosis have heavy tails that could include extreme values. Datasets with low kurtosis tend to have light tails, and do not include extremes. A distribution with zero excess kurtosis is called mesokurtotic. A distribution with positive excess kurtosis is called leptokurtic. A distribution with negative excess kurtosis is called platykurtotic.

The coefficient of variation (CV), CV = (SD/mean) × 100 characterizes the homogeneity–heterogeneity of MIQS. It was viewed that the values of CV_a, CV_b, and CV_c should be set based on the specifics of the studied ICMASs. The dataset exhibits homogeneous variability of intelligence level (hom.) when CV < CV_a; relatively homogeneous variability of intelligence level (rel-hom.) when CV ∈ [CV_a, CV_b); relatively heterogeneous variability of intelligence level (rel-het.) when CV ∈ [CV_b, CV_c); and heterogeneous variability of intelligence level (het.) when CV ≥ CV_c. In most cases, the recommended values for the parameters described above are CV_a = 10, CV_b = 20, and CV_c = 30.

The detection of statistical outliers/extremes is an important subject in statistical data analysis. The detection of outliers/extremes and anomalies has diverse real-life applications, including: detection for plant-wide processes with outlier multisampling rates [55], industrial data stream anomaly detection [56], and sliding nest window control chart in the task of data stream anomaly detection [57].

In experimental studies, outlier values can sometimes influence the numerical results, and even the conclusions derived from them, to a high degree. Many tests for the detection of statistical outlier values have been presented in the scientific literature. These include: Peirce’s criterion [58], the ROUT test [59], the Tietjen-Moore test [60], Chauvenet’s criterion [61], Dixon’s Q test [62] and the Grubbs test [63,64,65,66], just to mention a few.

Step 3 of the algorithm is applied for the recognition of statistical extremes if it is expected that the data will pass the normality assumption. The presented calculus allows the detection of z-3 ICMASs at most with extreme (low or high) intelligence, or an intelligence that is not extreme but is further removed from the rest, from a set of z studied ICMASs.

Step 3 describes a method for the detection of ICMASs with extreme intelligence from among the studied set ICM. MIQ values that are significantly/statistically different from the others are considered to be extremes. IdOut^L is the set of identified ICMASs with low extreme intelligence values. IdOut^H is the set of identified ICMASs with high extreme intelligence values. Depending on the type of studied ICMASs, it could be decided to extend the detection to ICMASs whose intelligence may not be extreme, but which are further removed from the rest. The Grubbs outliers detection test [63,64] is used for the identification of extremes. It is suggested that this test be applied with a significance level αExt = 0.05. This value means that a 5% chance of mistakenly identifying an outlier in the sample is accepted. Other values of significance level could be set, but they are less frequently appropriate. A two-sided test was applied in order to be able to identify both low and high extremes.

This method is able to detect ICMASs with extreme intelligence one-by-one, removing them when the number of remaining ICMASs is greater than or equal to 3. At the first verification, it is able to detect the system (only one system) with the most extreme (low or high) intelligence, if such a system exists. If such an ICMAS is detected, the verification can then be applied once more, to detect the existence of the system with the second most extreme intelligence. For each new application of the method, the ICMASs previously identified as having extreme intelligence are no longer considered. This process is repeated iteratively until no other extremes are identified, or until the condition (≥3) for the number of studied intelligent systems cannot be verified. This method is even capable of detecting systems with intelligence that is not extreme, but which can be considered to be statistically further removed (different) from the rest.

The Tietjen-Moore test [60] proposed in the scientific literature is a generalization of Grubbs’ test. The Tietjen-Moore test can be applied when the number of outliers is known in advance. In the case of a single outlier, the Tietjen-Moore test will give the same results as the Grubbs’ test.

Step 4 of the algorithm describes the process for detecting extremes in cases where normality has not been proven. HExtr denotes the set of identified high extreme intelligence values. HExtrOut denotes the set of identified high outlier extreme intelligence values. LExtr denotes the set of identified low extreme intelligence values. LExtrOut denotes the set of identified low outlier extreme intelligence values.

According to Step 4 of the algorithm, the MIQS dataset is initially arranged in ascending order. Q₁ denotes the first quartile, which represents the median of the lower half of the dataset. About 25% of the elements in the dataset will be positioned below Q₁. Q₃ denotes the third quartile, the median of the upper half of the dataset. About 25% of the numbers will be positioned above Q₃. RangeL and RangeU are parameters whose values must be established by He based on the specific characteristics of the studied set of ICMASs.

Higher machine intelligence quotient values mean higher intelligence. If a system’s intelligence falls within [HLowLim, HUppLim), that ICMAS can be considered to have high extreme intelligence. If a system’s intelligence is higher than HUppLim, the ICMAS can be considered to have high outlier extreme intelligence. HExtr and HExtrOut could even be the empty set. In the final step, if HExtr or HExtrOut include at least 2 values, then they will be ordered in ascending order.

If the intelligence of an ICMAS falls within (LLowLim, LUppLim], that ICMAS can be considered to have low extreme intelligence. If a system’s intelligence is lower than or equal to LLowLim, that ICMAS can be considered to have low outlier extreme intelligence. LExtr and LExtrOut could even be the empty set. In the final step, if LExtr or LExtrOut include at least 2 values, then they will be ordered in ascending order.

4. Experimental Evaluation of the ExtrIntDetect Method

In this section, the results of the experimental evaluation of the ExtrIntDetect method are presented. A set of ICMASs denoted ICM = {ICM₁, ICM₂, ICM₃, ICM₄, ICM₅, ICM₆}, specialized in solving an NP-hard problem, the Symmetric Travelling Salesman Problem (sTSP) [67,68], is considered. The sTSP can be defined by considering a set of cities (nodes of a weighted undirected graph), with the distances between each pair of cities being the same in both directions. The aim is to find the shortest route that visits each city (node) exactly once and then returns to the origin city. A traditional formulation of the sTSP is as an integer linear programming problem [69]. Diverse real-life problems, including vehicle routing, warehouse logistics, circuit board planning, and virtual networking, are modelled as symmetric graphs.

Each studied ICMAS consisted of simple computing agents (artificial ants) that operated by mimicking the search for food of biological ants. Many CMASs mimic the problem-solving that is carried out by biological ants: Merkle and Middendorf [70] proposed a solution to the permutation scheduling problem; Runkler [71] proposed the optimization of clustering models; Crisan, Pintea and Palade [72] proposed emergency management using geographic information systems; and Pholdee and Bureerat [73] proposed the optimization of the constrained mechanical design.

The general operation of the ICMASs presented in [74,75,76] can be explained as follows. Initially, each agent is placed on a randomly chosen node of the graph. An agent_k currently at node i chooses to move to node j by applying the probabilistic transition rule (2). The parameter α denotes the power of the pheromone, and β denotes the relative weight of the heuristic visibility of the pheromone trail. The value d_kh represents the distance between nodes (k and h); η_kh = 1/d_kh is the heuristic visibility of the edge (k, h); and τ_kh(t) represents the pheromone amount deposited on the edge (k, h) at the considered iteration t.

$$p_{ij}^k\left(t\right)=\left\{\begin{array}{cc}\hfill \frac{{[{\tau }_{ij}\left(t\right)]}^{\propto }\times {[{\eta }_{ij}\left(t\right)]}^{\beta }}{{\sum }_{l\in J_k\left(i\right)}{[{\tau }_{il}\left(t\right)]}^{\propto }\times {[{\eta }_{il}\left(t\right)]}^{\beta }},& ifj\in J_k\left(i\right)\hfill \\ \hfill 0,& otherwise\hfill \end{array}\right.$$

(2)

After each agent completes its tour, the pheromone amount on each edge will be adjusted according to (3), (4) and (5). Q is an arbitrary constant. 0 < ρ < 1, is the trail evaporation measure when an agent chooses a node to move to. m is the number of operating agents. L_k is the length of the tour performed by agent_k.

$${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right)\times {\tau }_{ij}\left(t\right)+∆{\tau }_{ij}\left(t\right)$$

(3)

$$∆{\tau }_{ij}\left(t\right)={\displaystyle \sum }_{k=1}^{k=m}∆{\tau }_{ij}^k\left(t\right)$$

(4)

$$∆{\tau }_{ij}^k\left(t\right)=\left\{\begin{array}{l}\frac{Q}{L_k},if\left(i,j\right)\in tour\_performed\_by\_agent\_k\\ 0,otherwise\end{array}\right.$$

(5)

He establishes the type of intelligence sought to be composed of two components, q = 2, which are denoted as ms₁ and ms₂. ms₁ is the global-best solution found during the problem-solving cycle. ms₂ is the number of iterations before the global-best solution is found. The importance of the two components is considered by He as follows, imp₁ = 0.9 and imp₂ = 0.1 (imp₁ + imp₂ = 1). In all cases, the intelligence indicator is calculated on the basis of (1). It should be noted that, based on the specificity of the intelligence indicator, lower values indicate higher intelligence.

ICM₁ is operated as an Ant System (AS) [74,75,76]; ICM₂ is operated as an Elitist Ant System (eAS) [77]; ICM₃ is operated as a Ranked Ant System (rAS) [78]; ICM₄ is operated as a Best-Worst Ant System (bwAS) [79]; ICM₅ is operated as a Min-Max Ant System (mmAS) [80]; ICM₆ is operated as an Ant Colony System (aCS) [75,76,81].

The experimentally determined parameter values were: maps with randomly placed cities on the map, nr = 90; number of agents that formed each studied CMAS, |Probl_i| = 12, ∀ I = 1.6; m = 10; maximal number of iterations, ItNum = 995; α = 1.3; β = 1.35 and ρ = 0.25.

Table 1. Obtained experimental evaluation results of ms₁ and ms₂.

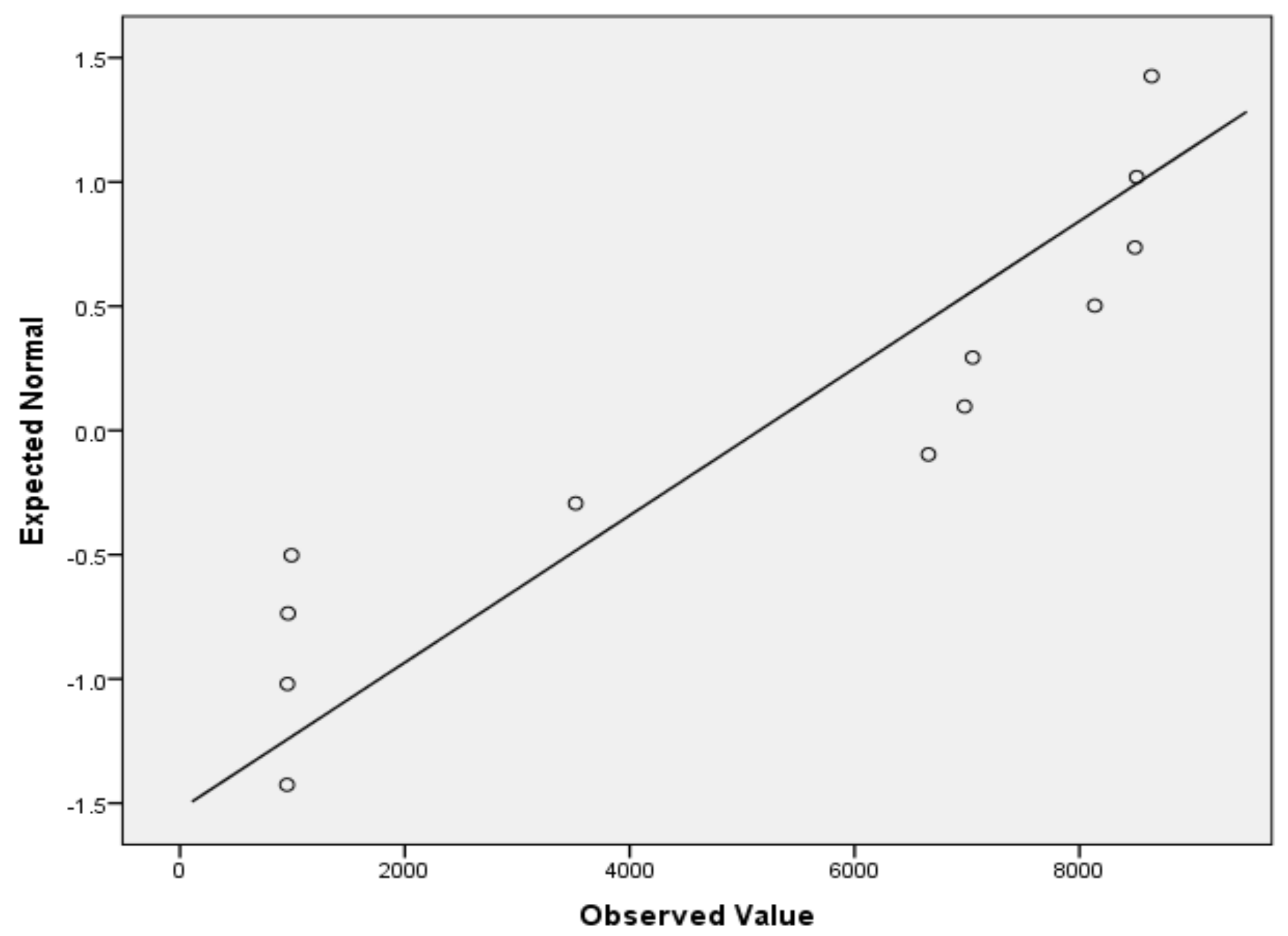
Evaluation Number	ICM1	ICM2	ICM3	ICM4	ICM5	ICM6
	ms1/ms2	ms1/ms2	ms1/ms2	ms1/ms2	ms1/ms2	ms1/ms2
Nr1	1063/104	1050/165	1268/18	1583/22	1488/29	1093/146
Nr2	1073/559	1045/115	1157/32	1709/32	1387/38	1123/226
Nr3	1067/306	1094/70	1255/58	1792/22	1481/19	1184/221
Nr4	1046/92	1048/131	1170/47	1645/21	1380/33	1170/68
Nr5	3698/21	3906/43	7730/53	9518/18	8597/10	3628/67
Nr6	8304/29	7747/64	9484/31	1381/12	1198/38	7935/53
Nr7	7527/16	7384/110	8791/37	1590/27	1090/44	7860/91
Nr8	8291/16	7823/93	9911/16	1423/15	1059/100	8359/87
Nr9	8054/168	8930/991	1023/37	1470/17	1156/39	9123/31
Nr10	9294/181	9598/41	1098/24	1424/28	1205/64	1092/290
Nr11	1015/68	9427/93	1124/48	1664/43	1263/28	1023/174
Nr12	1019/64	9434/182	1182/27	1377/22	1371/19	1024/68

presents the intelligence component results obtained in the experimental problem-solving evaluations.

Table 2. Calculated intelligence evaluation results.

Evaluation Number	Intellig1	Intellig2	Intellig3	Intellig4	Intellig5	Intellig6
Nr1	967.1	961.5	1143.0	1426.9	1342.1	998.3
Nr2	1021.6	952.0	1044.5	1541.3	1252.1	1033.3
Nr3	990.9	991.6	1135.3	1615.0	1334.8	1087.7
Nr4	950.6	956.3	1057.7	1482.6	1245.3	1059.8
Nr5	3330.3	3519.7	6962.3	8568.0	7738.3	3271.9
Nr6	7476.5	6978.7	8538.7	1244.1	1082.0	7146.8
Nr7	6775.9	6656.6	7915.6	1433.7	985.4	7083.1
Nr8	7463.5	7050.0	8921.5	1282.2	963.1	7531.8
Nr9	7265.4	8136.1	924.4	1324.7	1044.3	8213.8
Nr10	8382.7	8642.3	990.6	1284.4	1090.9	1011.8
Nr11	920.3	8493.6	1016.4	1501.9	1139.5	938.1
Nr12	923.5	8508.8	1066.5	1241.5	1235.8	928.4

presents the problem-solving intelligence evaluation results Intellig = {Intellig₁, Intellig₂, …, Intellig₆} calculated according to (1) based on the two measured components, with each component counted based on the established weighting.

Table 3. Characterization of the intelligence of the studied ICMASs.

Calculus	Intellig1	Intellig2	Intellig3	Intellig4	Intellig5	Intellig6
Mean	3872.36	5153.93	3393.04	1995.53	1704.47	3358.73
SD	3265.3	3377.76	3494.04	2073.47	1904.44	3132.09
Median	2175.95	6817.65	1100.9	1430.3	1187.65	1073.75
Kurt	−2.1	−1.9	−1.4	11.9	11.9	−1.6
Skew	0.3	−0.4	0.9	3.4	3.4	0.7
Min	920.3	952	924.4	1241.5	963.1	928.4
Max	8382.7	8642.3	8921.5	8568	7738.3	8213.8
range	7462.4	7690.3	7997.1	7326.5	6775.2	7285.4
CV	84.3	65.5	102	103.9	111.7	93.3
hom.-het.	het.	het.	het.	het.	het.	het.

presents the results of the statistical characterization of intelligence realized based on Intellig = {Intellig₁, Intellig₂, …, Intellig₆}, which allows the formulation of useful conclusions, like the homogeneity–heterogeneity of intelligence indicator data. For the verification of homogeneity–heterogeneity, the following values for the parameters were used: CV_a = 10, CV_b = 20 and CV_c = 30.

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 represent the QQ plots of Intellig₁, Intellig₂, …, Intellig₆. The visual analysis of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 enables the formulation of the conclusion that none of Intellig₁, Intellig₂, …, Intellig₆ fail to pass the normality assumption.

Table 4. Lill and SW normality tests results.

Calculus	Intellig1	Intellig2	Intellig3	Intellig4	Intellig5	Intellig6
Lill Test
Lill statistic	0.309	0.255	0.407	0.489	0.492	0.349
Pnorm (calculated p-value)	0.002	0.03	~0	~0	~0	~0
Normality passed (Pnorm > αNorm)	No	No	No	No	No	No
SW Test
SW statistic	0.753	0.79	0.666	0.381	0.389	0.717
Pnorm (calculated p-value)	0.003	0.007	~0	~0	~0	0.001
Normality passed (Pnorm > αNorm)	No	No	No	No	No	No

presents the results of the Lill and SW normality goodness-of-fit tests applied to Intellig₁, Intellig₂, …, Intellig₆. It was considered that a significance level of αNorm = 0.05 was the most appropriate for the application of both tests. An intelligence indicator dataset fails to pass the normality assumption when Pnorm < αNorm, where Pnorm represents the calculated p-value of an applied normality test. Based on the obtained results, the same conclusion can be formulated with respect to normality as was formulated for the QQ plots.

Based on the fact that none of the intelligence indicator datasets pass the normality assumption, it can be concluded that the most appropriate choice would be to calculate the machine intelligence quotient on the basis of the median. MIQS = {MIQ₁ = 2175.95, MIQ₂ = 6817.65, MIQ₃ = 1100.9, MIQ₄ = 1430.3, MIQ₅ = 1187.65, MIQ₆ = 1073.75}. Figure 8 presents the MIQS data. Based on the specificity of the considered intelligence components and the intelligence indicator, smaller MIQ values indicate higher machine intelligence. For instance, MIQ₂ > MIQ₆ suggests that ICM₆ has a higher intelligence than ICM₂.

Table 5. Descriptive characterization of the MIQS data.

Type of Calculus	Obtained Result
mean/SD/median	2297.7/2252.1/1308.98
Skew/interpretation	2.28/highly skewed
kurt/interpretation	5.28/leptokurtic
CV/hom-het	98/heterogeneous

contains a descriptive statistical characterization of the MIQS.

Table 6. Analysis of normality of the MIQS data.

Performed Calculus	Lill Test	SW Test
Statistic	0.355	0.636
Pnorm (calculated p-value)	0.017	0.001
Normality passed (Pnorm > αNorm)	No	No

presents the results of the Lill and SW tests applied to the MIQS. Both tests were applied with a significance level of αNorm = 0.05. Figure 9 presents the QQ plot constructed based on the MIQS data. All the normality results indicate the failure of the MIQS data to pass the normality assumption.

Based on the fact that the MIQS = {MIQ₁, MIQ₂, MIQ₃, MIQ₄, MIQ₅, MIQ₆} = {2175.95, 6817.65, 1100.9, 1430.3, 1187.65, 1073.75} data does not pass the normality assumption, according to the ExtrIntDetect algorithm, Step 4 is indicated for the identification of extreme intelligence. Acting as He, we decided on RangeL = 1.5 and RangeU = 3. The obtained numerical results were: median = 1308.98, Q₁ = 1094.11, Q₃ = 3336.37, IQR = 5743.9, HLowLim = 11,952.22, HUppLim = 20,568.07, LLowLim = −7521.74, LUppLim = −16,137.6.

The criteria of MIQ_i ∈ (LLowLim, LUppLim] and MIQ_i ≤ LLowLim were not verified. This indicates that there were no ICMASs with high extreme intelligence or high outlier extreme intelligence. Given that lower intelligence values indicate higher intelligence, this is the case for high intelligence.

The condition MIQ_i ≥ HUppLim = 20568.07 was verified for MIQ₁[2175.95] and MIQ₂[6817.65]. In this way, ICM₂ and ICM₁ were identified as having low outlier extreme intelligence, where ICM₂ was less intelligent than ICM₁ (based on the fact that 2175.95 < 6817.65).

The condition of MIQ_i ∈ [HLowLim, HUppLim) = [11952.22, 20568.07) was verified by the value corresponding to MIQ₄[1430.3], identifying ICM₄ in this way as an ICMAS with low extreme intelligence.

The execution of Step 3 of the ExtrIntDetect algorithm is recommended when, after the elimination of extremes, it is expected that the normality assumption will be passed. It was applied for the MIQS = {MIQ₁, MIQ₂, MIQ₃, MIQ₄, MIQ₅, MIQ₆} data. For the identification of the extremes, Grubbs’ test was applied with a significance level of αExt = 0.05. A two-sided test was applied, as both high and low extreme intelligence values were being sought at the same time.

Table 7. The results of the ExtrIntDetect method.

ICMAS	MIQ	Extreme */Furthest #	No.Id @	Type &
ICM1	2175.95	No/Yes	2	Low
ICM2	6817.65	Yes/No	1	Low
ICM3	1100.9	/
ICM4	1430.3	No/Yes	3	Low
ICM5	1187.65	No/Yes	4	Low
ICM6	1073.75	/

* indicates an ICMAS identified as having extreme intelligence; ^# indicates an ICMAS intelligence that is not significantly extreme, but is further removed from the intelligence of the rest of ICMASs; ^@ indicates the application number of the extreme detection test; ^& indicates the type of intelligence “Low” or “High”.

presents the identified extremes.

MIQS* = {MIQ₁, MIQ₂, MIQ₃, MIQ₄, MIQ₅, MIQ₆}, avg* = mean(MIQS*) = 2297.7. With the first application of the identification of extremes based on MIQS* data, ICM₂ was identified as having extreme intelligence, MIQ₂ = 6817.65. ICM₂ has low extreme intelligence based on the fact that MIQ₂ > avg*. MIQS* = MIQS*−{MIQ₂}. With the second application of the identification of extremes based on MIQS* data, no extremes were identified.

With the aim of verifying the correctness of the application of Step 3 of the algorithm (after the elimination of the extremes, a set of normally distributed data was obtained), the data normality of MIQS* was verified using the numerical Lill and SW tests. Both tests were applied at αNorm = 0.05. The Lill test results were: Lill statistics = 0.273, Pnorm = 0.2 (p-value of the Lill test), where Pnorm > αNorm. The SW test results were: SW statistics = 0.273, Pnorm = 0.057 (p-value of the SW test), where Pnorm > αNorm. All of the obtained results confirmed that the normality assumption had been passed at the established αNorm significance level. This proves the correctness of the application of Step 3 of the algorithm, and that by eliminating the extremes, a set of normally distributed data will be obtained.

On the second application of the recognition, only an intelligence indicator value, MIQ₁ = 2175.95, which is far removed from the values, was detected. avg* = mean(MIQS*) = 1393.71; MIQ₁ > avg*, proving that ICM₁ is lower than the rest of the intelligence values. MIQS* = MIQS*−{MIQ₁}, avg* = mean(MIQS*) = 1198. To identify further different intelligence values, the detection of extremes was applied again on the MIQS* data, identifying MIQ₄ = 1430.3 as another value that is not extreme but is far removed from the rest; MIQ₄ > avg* indicates that it was lower than the rest of the intelligence values. avg* = mean(MIQS*) = 1120.77, MIQS* = MIQS*−{MIQ₄}. With a new application, MIQ₅ = 1187.65 was identified as being far removed from the rest (MIQ₅ > avg*). Based on the fact that |MIQS*| = 2, which is not higher than or equal to 3, the detection of other extremes or values far removed from the rest could not be continued.

5. Discussion

5.1. Discussion of the Experimental Results

For the validation of the proposed ExtrIntDetect method, an illustrative experimental case study was performed. In the experimental setup, we used six ICMASs that were specialized in solving a very difficult NP-hard problem. As initial steps, the ExtrIntDetect algorithm performs some initial processing and analyses. According to the algorithm, based on the fact that the MIQS data did not pass the normality assumption, Step 4 of the algorithm was applied.

The results of Step 4 for the set of six studied intelligent systems showed that no ICMAS had high extreme or high outlier extreme intelligence. Two ICMASs were identified, namely ICM_2, and ICM₅, as having low outlier extreme intelligence, and one ICMAS, namely ICM₄, as having low extreme intelligence.

In the presented experimental study, the application of Step 3 was possible even if the MIQS data initially did not pass the normality assumption. The correctness of the application is a result of the elimination of ICMASs, which leads to normally distributed machine intelligence quotient data.

Step 3 identified on ICMAS, namely ICM₂, with low extreme intelligence, and three ICMASs, namely ICM_5, ICM₄ and ICM₁, with low intelligence that was far removed from the rest.

It should be noted that in Step 3, the values of the parameters RangeL and RangeU influenced which ICMASs were identified as extremes or outlier extremes. RangeL and RangeU values must be specified by the He. The most appropriate value in most cases for RangeL is 1.5, and for RangeU, the most appropriate value is a number between 2 and 3. One recommended method for setting these values is to vary the values of RangeL and RangeU, and to analyze the identified ICMASs as extremes and outlier extremes.

5.2. Discussion of the ExtrIntDetect Method

Several intelligence metrics have been presented in the literature, most of which are based on different principles of measuring machine intelligence. In our study, the most appropriate measurement of intelligence is based on difficult problem-solving intelligence, which represents a field of interest for human evaluators specializing in intelligent systems. In the case of each studied ICMAS, evaluations of problem-solving intelligence were performed on several testing problem sets, and the obtained results were used to calculate the MIQ, which is the indicator of the central problem-solving intelligence tendency. This kind of procedure provides universality for the approaches that are based on it. It does not depend on the studied ICMAS architecture. It also does not require the elaboration of definitions of intelligence.

In [30], a method for the identification of ICMASs with extreme intelligence called OutIntSys was presented. One limitation of that method was the fact that its application is based on the assumption that by eliminating the extreme intelligence values, normally distributed intelligence data will be obtained. ExtrIntDetect preserves the properties of the OutIntSys method, while extending it at the same time in order to be more robust. It is applicable even in situations where data normality is not expected. ExtrIntDetect is able to detect extreme (low and high) intelligence and outlier extreme (low and high) intelligence.

The recent symmetric MetrIntSimil metric [31] is able to compare the intelligence of a large number of ICMASs. MetrIntSimil is based on the same principle of considering the difficult problem-solving machine intelligence as the ExtrIntDetect method. MetrIntSimil is able to perform accurate classification of ICMASs that have the same intelligence level, but is not able to detect systems with extreme intelligence. ExtrIntDetect could be used as an extension of the MetrIntSimil metric. First, the MetrIntSimil metric should be applied for a set of ICMASs, measuring their machine intelligence, comparing their intelligence, and classifying them into intelligence classes. After that, the application of the ExtrIntDetect method will be able to detect ICMASs with extreme intelligence.

In [82], an interesting study was presented regarding the effect of motion on the spread of disease in a system composed of random walkers. The presented random walkers could perform long-distance jumps. The main conclusion of the study was that a reduced percentage of jumps in agent motion was sufficient to annihilate local correlations. It also produced a large drop in the epidemic threshold. The studied effect is to a certain degree similar to the crossover existent in the well-known static small-world networks. Furthermore, this can be linked to the structural properties of the dynamic network that defines the interactions between agents. A forthcoming study that we will perform will consist of defining intelligence in networks, the determination of a mathematically grounded method for measuring such intelligence, and finally the identification of extreme (low and high) intelligence.

6. Conclusions

In the research presented in this paper, we defined a specific type of performance of ICMASs in terms of difficult problem-solving intelligence. In this context, the problem of performance measurement was formulated as a problem of the measurement of intelligence. The motivation for the study consists in the fact that an ICMAS with higher intelligence can solve more difficult problems than a system with lower intelligence.

The ExtrIntDetect method proposed in this paper has practical application in identifying ICMASs with extreme (low and high) or outlier extreme (low and high) intelligence for solving difficult problems from among a set of studied ICMASs. For the evaluation and validation of the ExtrIntDetect method, an experimental study was performed, in which the intelligence of six ICMASs was analyzed.

ExtrIntDetect extends another recent method called OutIntSys, which was proposed to identify intelligent systems that had extreme intelligence, retaining its properties, while being more robust. The MetrIntSimil metric proposed in the literature is able, in cases of a larger number of studied intelligent systems, to measure their problem-solving intelligence, compare the systems based on their intelligence, and classify the systems into classes of intelligence. Its main limitation is the fact that it is not able to detect extreme intelligence. ExtrIntDetect can be used in addition after the application of the MetrIntSimil metric in order to detect extreme intelligence.

Although the method was proposed for ICMAS, it could be applied for all intelligent systems, for instance, to agents that need to solve problems in isolation without cooperation with other agents. The method is universal, it is like the black-box method, in that it does not depend on the architecture of the studied ICMASs.

Examples of possible applications include: the identification of swarms of mobile robotic agents with extreme intelligence from a large set of swarms; identification of swarms of agent-based flying drones with extreme intelligence from a large set of swarms.