Next Article in Journal
Visual Lateralization in the Cephalopod Mollusk Octopus vulgaris
Next Article in Special Issue
Localization Properties of Non-Periodic Electrical Transmission Lines
Previous Article in Journal
Double JPEG Compression Detection Based on Noise-Free DCT Coefficients Mixture Histogram Model
Previous Article in Special Issue
The Study of A New Symmetrical Rod Phase in Mg-Zn-Gd Alloys
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 11
Issue 9
10.3390/sym11091120
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices

by
Hao Jing
,
Jie He
,
Ru-Wen Peng
* and
Mu Wang
National Laboratory of Solid State Microstructures, School of Physics, and Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China
*
Author to whom correspondence should be addressed.
Symmetry 2019, 11(9), 1120; https://doi.org/10.3390/sym11091120
Submission received: 3 August 2019 / Revised: 19 August 2019 / Accepted: 20 August 2019 / Published: 4 September 2019
(This article belongs to the Special Issue Symmetry and Asymmetry in Quasicrystals or Amorphous Materials)
Browse Figures
Versions Notes

Abstract

:
Unlike periodic and random structures, many aperiodic structures exhibit unique hierarchical natures. Aperiodic photonic micro/nanostructures usually support optical multimodes due to either the rich variety of unit cells or their hierarchical structure. Mainly based on our recent studies on this topic, here we review some developments of aperiodic-order-induced multimode effects and their applications in optoelectronic devices. It is shown that self-similarity or mirror symmetry in aperiodic micro/nanostructures can lead to optical or plasmonic multimodes in a series of one-dimensional/two-dimensional (1D/2D) photonic or plasmonic systems. These multimode effects have been employed to achieve optical filters for the wavelength division multiplex, open cavities for light–matter strong coupling, multiband waveguides for trapping “rainbow”, high-efficiency plasmonic solar cells, and transmission-enhanced plasmonic arrays, etc. We expect that these investigations will be beneficial to the development of integrated photonic and plasmonic devices for optical communication, energy harvesting, nanoantennas, and photonic chips.

1. Introduction

Motivated by the discovery of quasicrystal [1], much research has been conducted on aperiodic systems in recent years [2,3,4,5,6,7,8,9,10,11]. Aperiodic structures broaden the regime of ordered systems beyond periodic structures, and thereby play a significant role in a wide range of science and engineering disciplines. Unlike periodic and random structures, many aperiodic structures exhibit unique hierarchical natures. For these aperiodic structures, on one hand, the lack of periodicity may create fascinating features on some occasions, such as extraordinary optical transmission and enhanced transmission resonances, etc. On the other hand, aperiodic order can be artificially imposed during sample fabrication and can be precisely controlled. These properties have opened a new avenue for the design of novel devices based on aperiodic structures. Among them, optoelectronic devices based on the multimode effects, which can be induced by aperiodic order, have attracted much attention because of their potential in optical communication [12,13], energy harvesting [14], nanoantennas [15], and so on.
In this review, we mainly summarize the research work in our group concerning the aperiodic-order-induced multimode effects, which have been demonstrated by both theoretical and experimental observations. Moreover, several optoelectronic devices have been designed on the basis of the multimode effects in either one-dimensional (1D) or two-dimensional (2D) aperiodic structures.

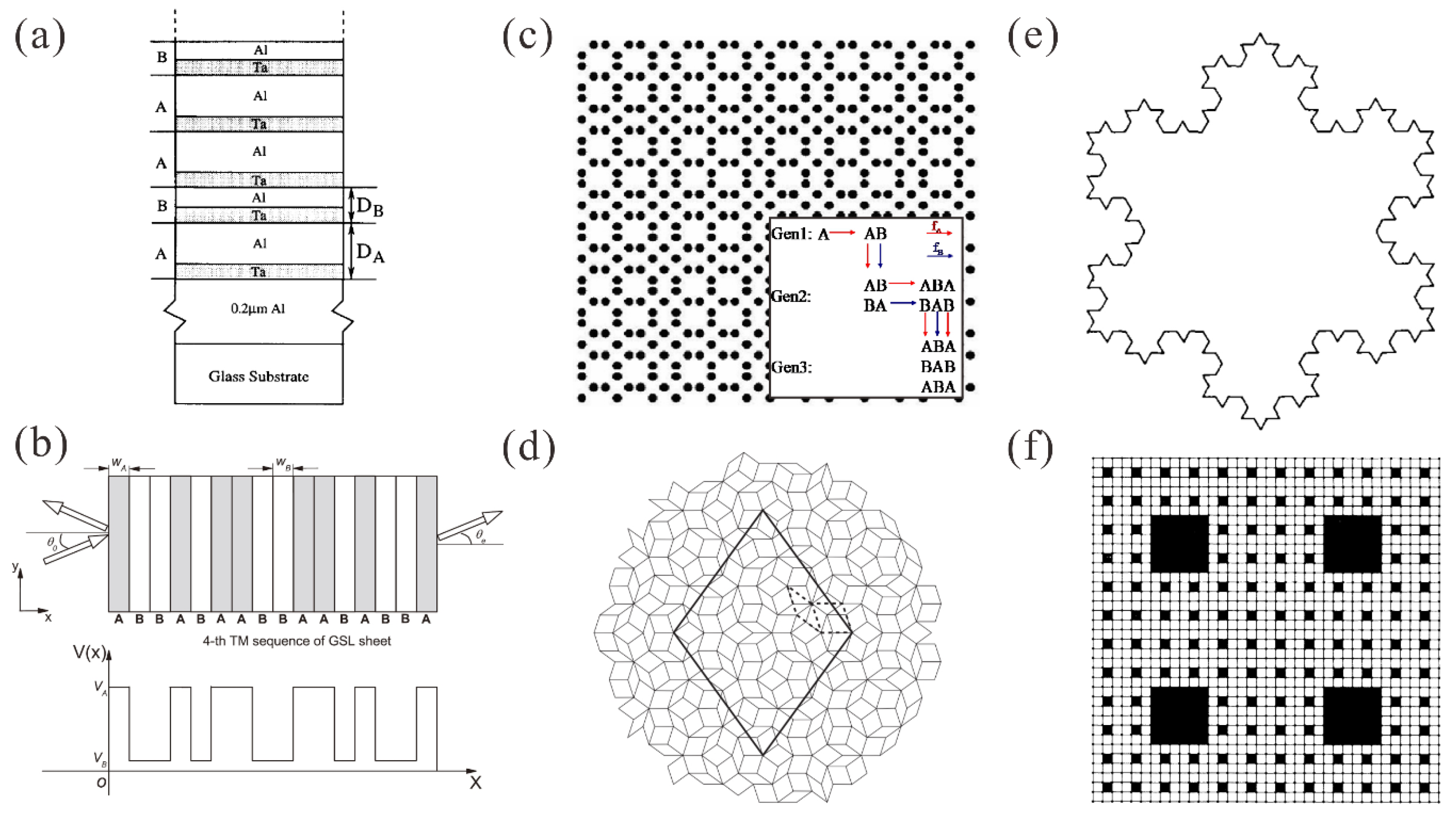
2. Aperiodic Structures

In order to design optoelectronic devices based on aperiodic structures, proper aperiodic lattices should be chosen. These are usually obtained by following the substitution rules. Several typical aperiodic structures are introduced in this section, ranging from one dimension to two dimensions.

2.1. One-Dimensional Aperiodic Structures

A representative example of 1D aperiodic structures is the Fibonacci structure, which follows Fibonacci sequence as shown in Figure 1a [16]. This sequence can be constructed by applying the substitution rule A→AB and B→A repeatedly. By intentionally varying the growth sequence and the number of building blocks, a standard two-component Fibonacci structure can be generalized to a k-component Fibonacci structure [17]. The feature of this k-component Fibonacci structure is related to k, which can show periodic (k = 1), quasiperiodic (k ≤ 5), or only aperiodic ordering (k > 5).
The Thue–Morse sequence is another well-known 1D aperiodic sequence. It can be structured by repeating two building blocks (A and B) applying the substitution rules A→AB and B→BA (Figure 1b) [18]. The initial few generations Sn of the Thue–Morse sequence have the following forms: S0 = {A}, S1 = {AB}, S2 = {ABBA}, S3 = {ABBABAAB}, and so on. The Thue–Morse lattice is not quasiperiodic but deterministically aperiodic, which shows the properties of an intermediate between periodic and quasiperiodic lattices [19,20].
On the basis of various substitution rules, many other 1D aperiodic sequences have been proposed. For example, the Rudin–Shapiro sequence can be produced by repeated application of the substitution rule AA→BBAB and BB→BBBA [21], and the period-doubling sequence can be structured by using the substitution rule A→AB and B→AA [22]. In addition, a kind of quasiperiodic superlattice structures called the precious mean sequences were reported by Birch et al., which can be produced by A→AnB and B→A [23], whereas the metallic mean sequences can be generated by the inflation rule A→ABn and B→A [24].

2.2. Two-Dimensional Aperiodic Structures

Substitution rules used in 1D quasiperiodic structures can be extended to two dimensions. A simple way to obtain a 2D quasiperiodic lattice is to alternate the iterations of 1D inflation rules along different spatial dimensions. For example, as shown in Figure 1c, a 2D Fibonacci quasi-lattice can be structured by using two complementary 1D Fibonacci inflation maps along the horizontal and vertical directions, respectively (fA: A→AB, B→A; fB: A→B, B→BA) [25].
Another way to construct 2D quasiperiodic structures is by employing aperiodic tilings. These tilings are composed of collections of polygons, which could cover a plane without gaps and overlaps with a lack of translational symmetries [26]. Various aperiodic tilings have been proposed before, such as Penrose tiling [27] and square Fibonacci tiling [28], etc. Figure 1d illustrates a Penrose tiling; this tiling is composed of two types of rhombuses. A Penrose construction possesses a long-range quasiperiodic order but lacks translational symmetry. In this case, the notion of repetitiveness mainly shows local isomorphism instead of periodic arrangements [8].

2.3. Fractal Patterns

Fractal patterns exhibit self-similarity, where a structure is repeated over multiple spatial scales. Similar to quasi-crystalline order, certain motifs of the self-similar samples contain the whole structure enfolded within them [29]. A typical fractal design is the Koch snowflake fractal. It can be obtained by repeatedly constructing new triangles based on the middle segments of previous triangles; therefore, fractals can be defined by iteration. A triadic Koch snowflake fractal with an iteration of 3 is shown in Figure 1e [30]. Figure 1f shows another typical fractal pattern, i.e., the Sierpinski carpet pattern. It consists of hierarchically-arranged iteratively-shrinking squares, showing different sizes at different scales [31].

3. Aperiodic-Order-Induced Multimode Effects in Photonic Micro/Nanostructures

Photons in periodic dielectric structures such as photonic crystals can be considered as a counterpart to electrons in solids. As analog of electronic band structures, photonic band structures possess bandgaps in which photons are prohibited from propagating. In view of the fact that numerous photonic devices are required to work at specific wavelengths or photonic modes, the introduction of photonic band structures with multiple modes is desirable for designing these devices. Studies on the multimode effects have been extended to various aperiodic structures including quasiperiodic structures, symmetric self-similar structures, and others. The multimode effects in aperiodic structures offer a new platform for using photons with various frequencies at the same time.

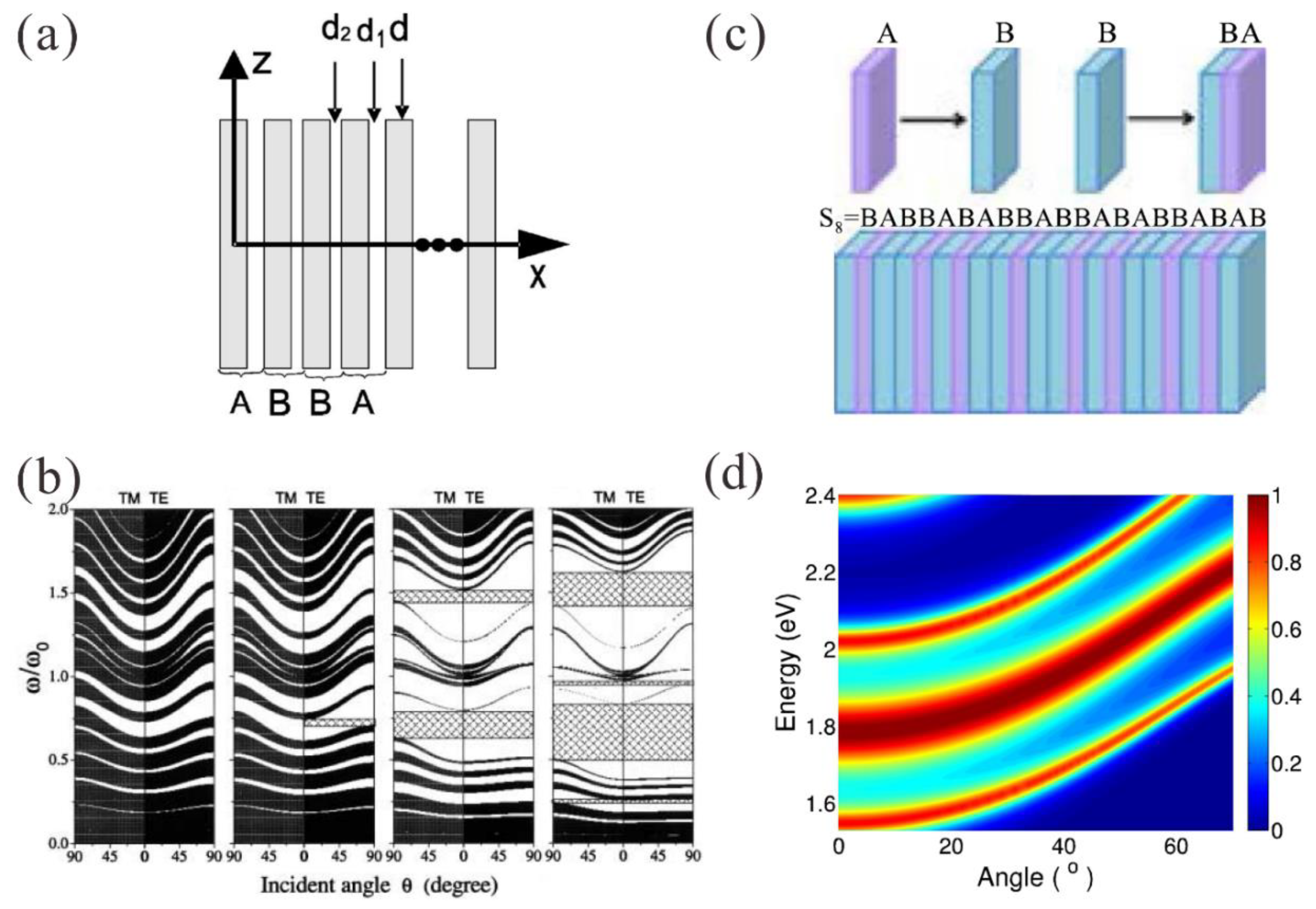
3.1. Multimode Effects Induced by Self-Similarity

Multiple fundamental photonic band gaps (PBGs) can exist in some aperiodic dielectric multilayers. A typical example is in the Thue–Morse structure (Figure 2a) [32], in which the self-similarity of the structure imparts a trifurcation feature on the resonant transmissions around the central frequency. In the Thue–Morse multilayer, the amount of the completely transparent states can be counted [33]. We define Rn as the amount of the resonant transmission mode around the central frequency (where n represents the number of the generation). Then we obtain:
R n + 2 = R n + R n + 1 + R n    ( n ≥ 3 )
considering the initial conditions R3 = 1 and R4 = 3. Finally, we have:
R n = 2 R n − 1 − 1 ± 1 = 1 + 2 n − 1 ± 1 3 ,     w h e r e { +   f o r   e v e n   n −   f o r   o d d   n   , .
which is the number of PBGs around the central frequency ω0. According to Equation (2), the inner feature of the Thue–Morse structure determines the mode amount of resonant transmissions. That is to say, special positional correlation between two blocks in the Thue–Morse structure causes resonant transmission. Multiple PBGs can coexist at the same frequency range in these structures, which is intuitively shown in the photonic band structures in Figure 2b. Moreover, the number of PBGs can be increased by tuning the refractive index contrast. This theoretical analysis was verified by measuring Thue–Morse SiO2/TiO2 multilayers in the range of visible and near-infrared frequencies [34].
Similar to the Thue–Morse structures, photonic quasicrystals can also support multiple modes because of their self-similarity properties [35,36]. For example, a photonic quasicrystal with eighth-generation Fibonacci series made by two blocks of Ta2O5 and SiO2 was constructed (Figure 2c). From the transmission spectra calculated by the transfer matrix method, three photonic modes could be observed in the dispersion map shown in Figure 2d, as demonstrated experimentally [37].

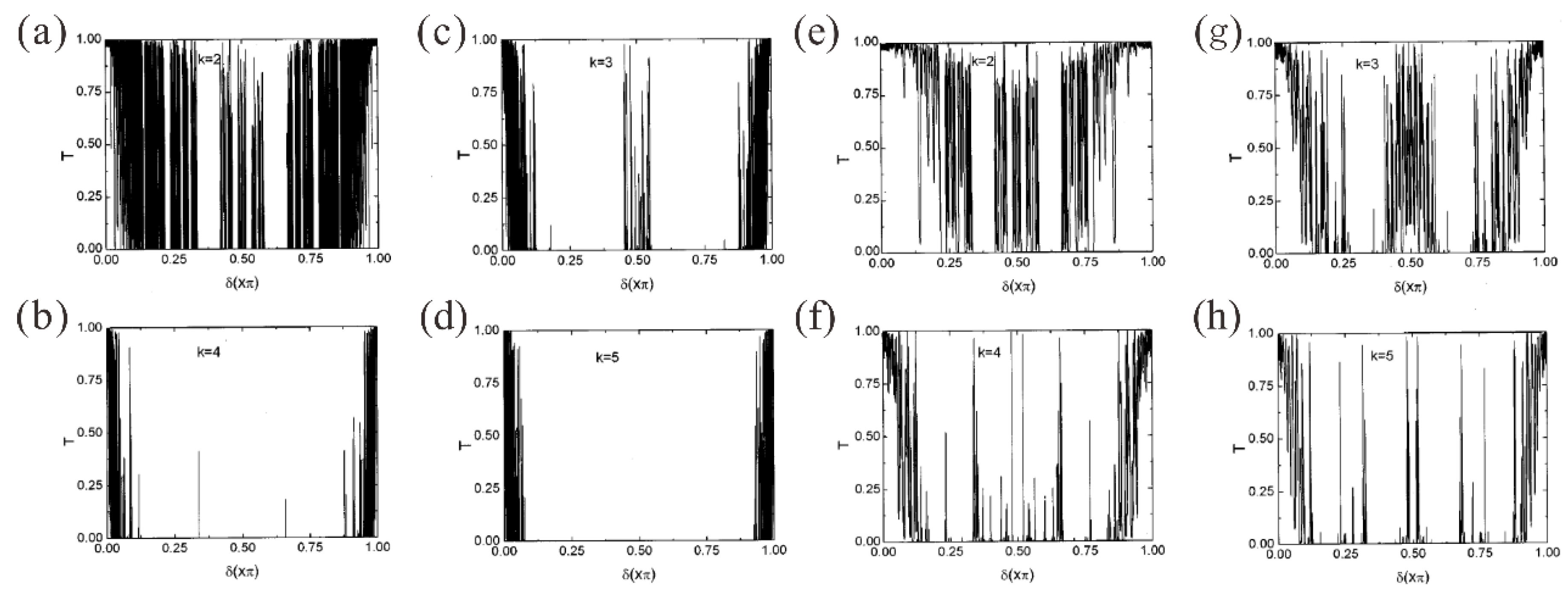
3.2. Multimode Effects in Symmetric Aperiodic Structure

As mentioned previously, multiple modes appearing in photonic quasiperiodic structures have been demonstrated in both calculations and experiments [17,37,38]. However, low transmission coefficients in these work limit their potential applications. A feasible way to realize multiple perfect transmissions is to introduce internal symmetry into a 1D aperiodic dielectric multilayer structure [39,40,41]. For example, a photonic crystal with two types of layers can be arranged in a binary Fibonacci-class (FC(n)) sequence. Then, binary symmetric Fibonacci-class (SFC(n)) can be constructed as shown in Figure 3a. SiO2 and TiO2 were chosen as two elementary layers with the thickness of a quarter wavelength (λ0/4), and the transmission coefficient for the two different systems can be calculated by the transfer matrix method (Figure 3b,c), which shows that the transmission coefficient of the symmetric Fibonacci structure behaves rather differently from that of the Fibonacci structure [39]. As shown in Figure 3, the localization property of optical waves can be influenced by the symmetric internal structure in a quasiperiodic system, which is demonstrated by the sharp transmission peaks with transmission coefficients near unity. That is to say, with the help of symmetric internal structures in the quasiperiodic system, a perfect transmission of the optical wave can replace the initially poor transmission. This improvement is benefited from the positional correlations in the system. Moreover, the resonant transmission can be varied to a certain frequency by tuning the aperiodic structures (Figure 3d). For example, as shown in Figure 3e, the transmission coefficients vary in different symmetric multilayers with defects (SMD) [41].

4. Optoelectronic Devices Based on One-Dimensional Aperiodic Structures

The application diversity of modern optoelectronic and photonic devices requires novel functionalities and the tunability of band structures enabled by a unique alignment of materials. By introducing 1D aperiodic order into multilayer structures, some optical modes can be generated at the desired frequencies, which can be applied in constructing functional components such as optical filters, multiband waveguides, and so on.

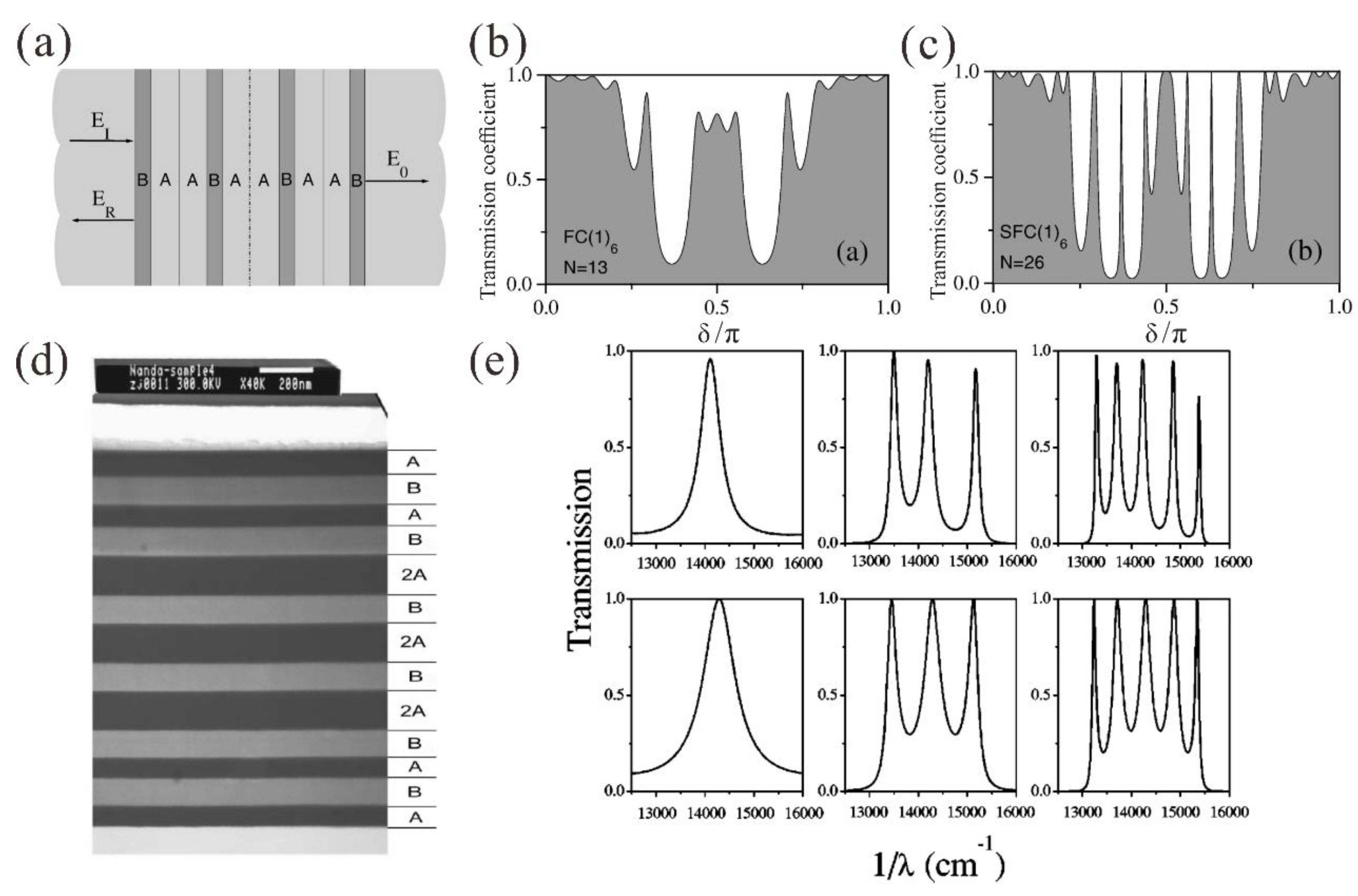
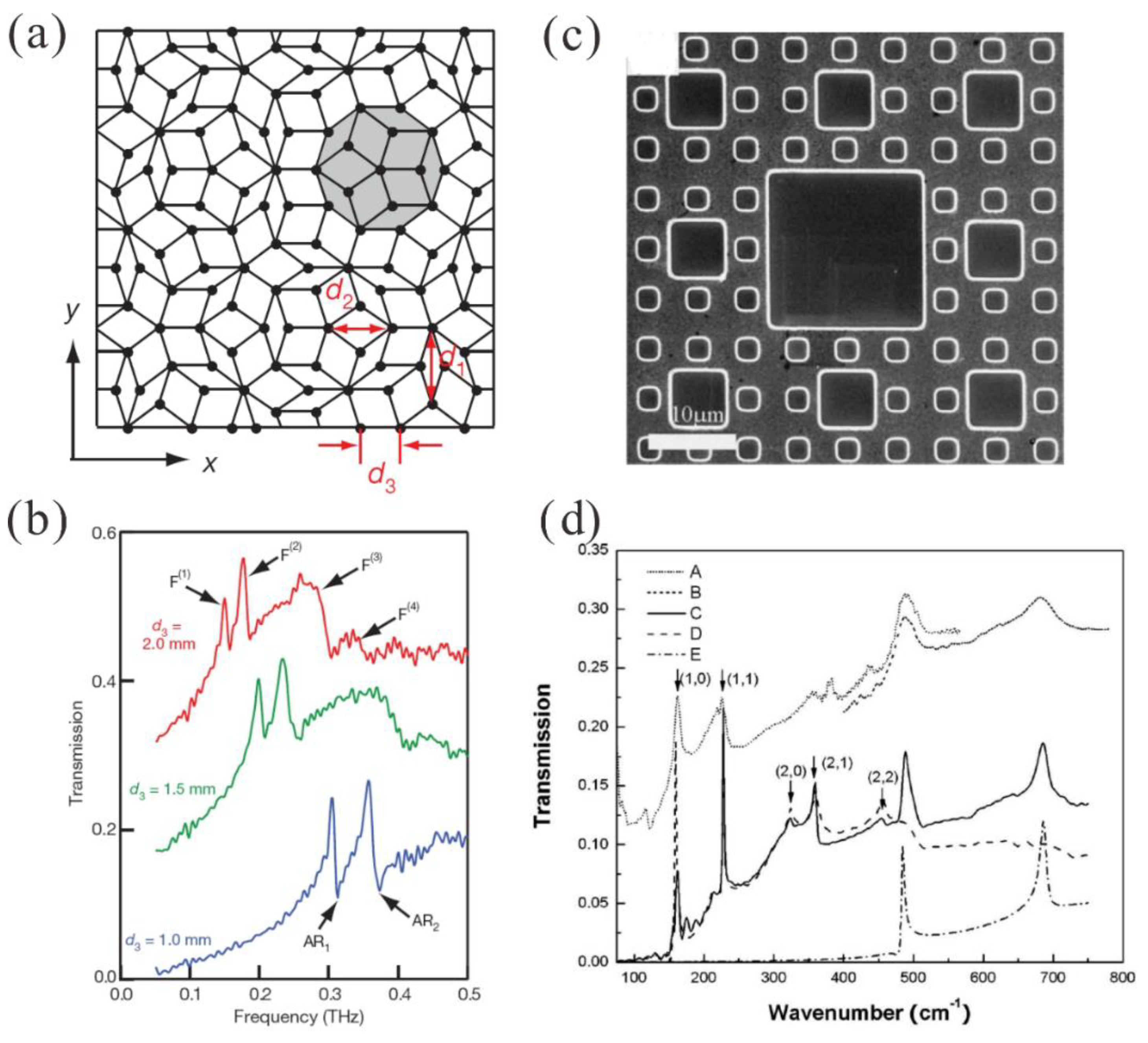
4.1. Optical Filters for the Wavelength Division Multiplexing (WDM) Systems

The propagation of photons with a certain range of energies can be suppressed by PBGs in photonic crystals. Tunable structural parameters are more plentiful in quasiperiodic designs than those in periodic structures, which can be used to control the propagation of light waves with high transmittivity at desired frequencies. Moreover, by combining with mirror symmetry of the structures, resonant transmission will definitely occur, which makes it possible to fabricate multiwavelength narrow band optical filters. For example, an optical filter could be fabricated by following k-component Fibonacci structures. According to the calculated results, the optical transmission coefficient shows a plentiful structure, which depends on the different incommensurate interval sequences k, the layer number N, and the frequency of the light (Figure 4). The transmission coefficient can be tuned by changing the layer number and the number of k; this property makes it useful in the design of high-performance optical filters [40,41,42].

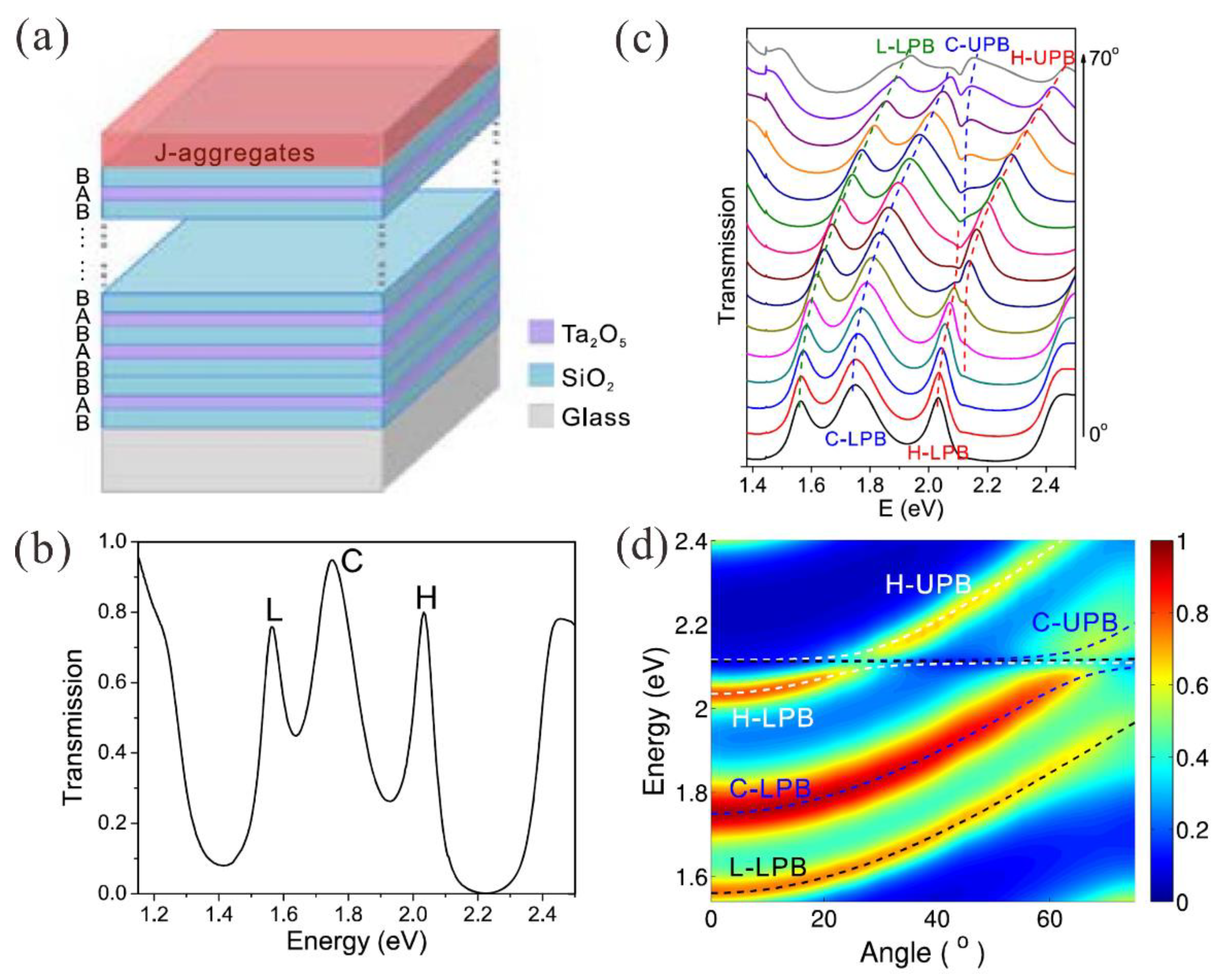
4.2. Open Cavities for the Light–Matter Strong Coupling

Recently intensive studies have been carried out on light–matter interactions, especially their strong coupling. Apart from the studies on interactions between a single excitonic mode with an individual photonic mode, there has been some work on multimode coupling where the excitonic mode couples with multiple photonic modes. Photonic quasicrystals possess multiple optical modes and thus present a platform for showing multimode light–matter interaction. In order to demonstrate it experimentally, a Fibonacci sequence composed of SiO2/Ta2O5 multilayers was chosen and J-aggregates on the top surface of structure offered excitons (Figure 5a) [37]. Figure 5b shows the measured transmission spectrum, where three peaks of different optical modes are recognized. The Rabi splitting and newly generated hybrid polariton bands can be verified from the dispersion map of the hybrid system, clearly showing successive coupling between the modes H, C, and L and the excitons (Figure 5c,d). By varying the substitution rule of the photonic quasicrystal, the open-cavity system can be optimized to provide the various photonic modes in need. By introducing this design, multimode photon–exciton strong couplings can be realized, which may inspire some potential applications, such as optical spectroscopy and multimode sensors.

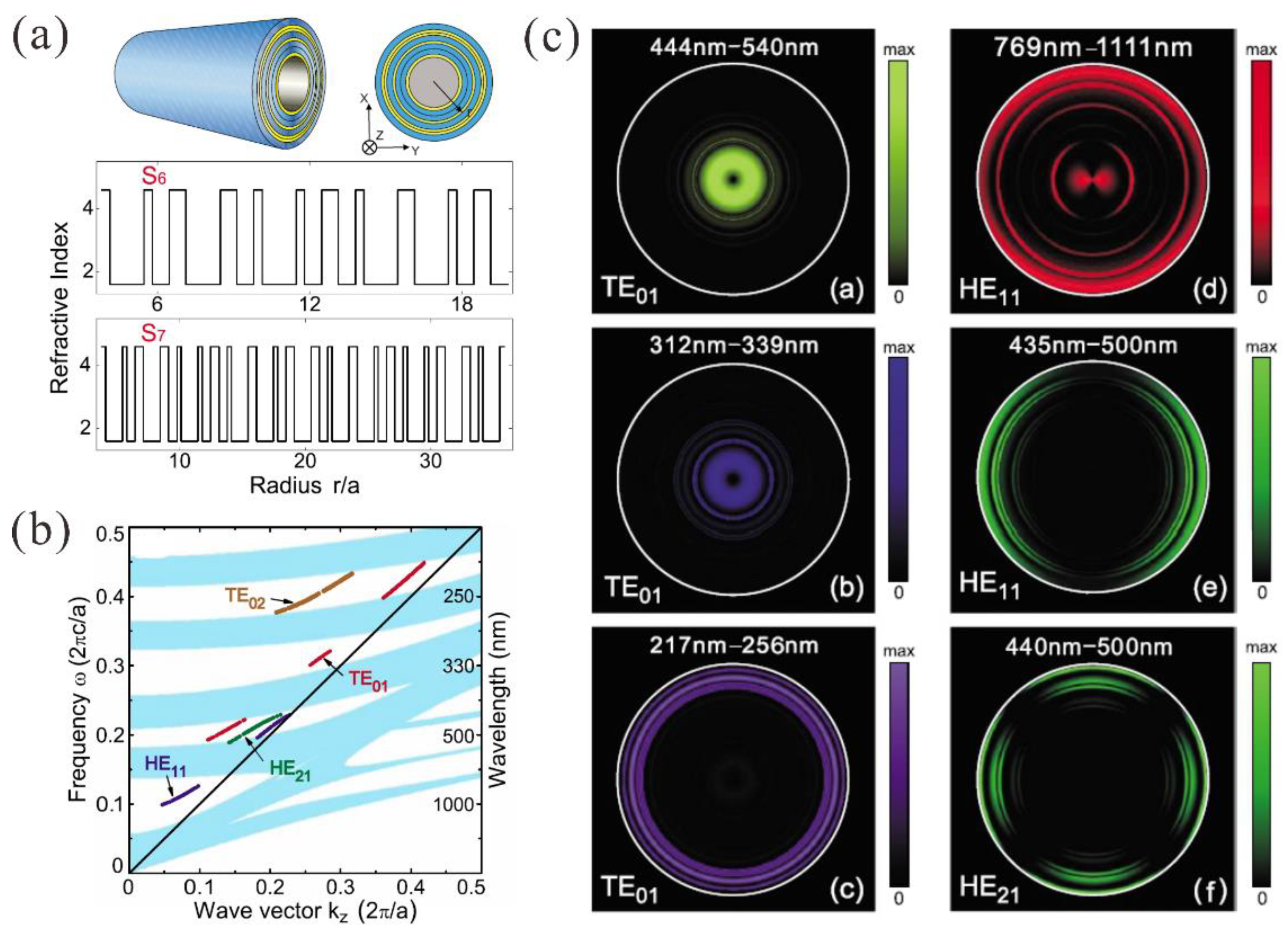
4.3. Multiband Waveguides for Trapping “Rainbow”

In telecommunications and optoelectronics, optical waveguides play a significant role because of their abilities to confine and guide the light waves. However, conventional hollow-core designs have disadvantages such as narrow transmission bands and detrimental dispersive resonances. Introducing a self-similar dielectric waveguide (SDW) is a useful approach to achieve multiband transmission and overcome baneful dispersive resonance, and even to guide the light waves with spatial separation [43]. As shown in Figure 6a, the SDW is designed as a hollow core surrounded by a coaxial Thue–Morse multilayer. In the photonic band structure, multiple transmission bands appear because of the intrinsic self-similar furcation of the structure. In this case, the propagated light with different resonant frequencies are separated in various cladding layers as shown in Figure 6b. Therefore, different modes are separated spatially, forming a “rainbow” trapped in the SDW (Figure 6c). Moreover, both the transmission modes and the photonic bands can be modulated by altering the temperature in an SDW infiltrated by liquid crystal [44]. These designs can be applied to fabricate compact photonic devices, such as integrated spectrographs, color-sorters, and temperature-sensitive optical circuit switches.

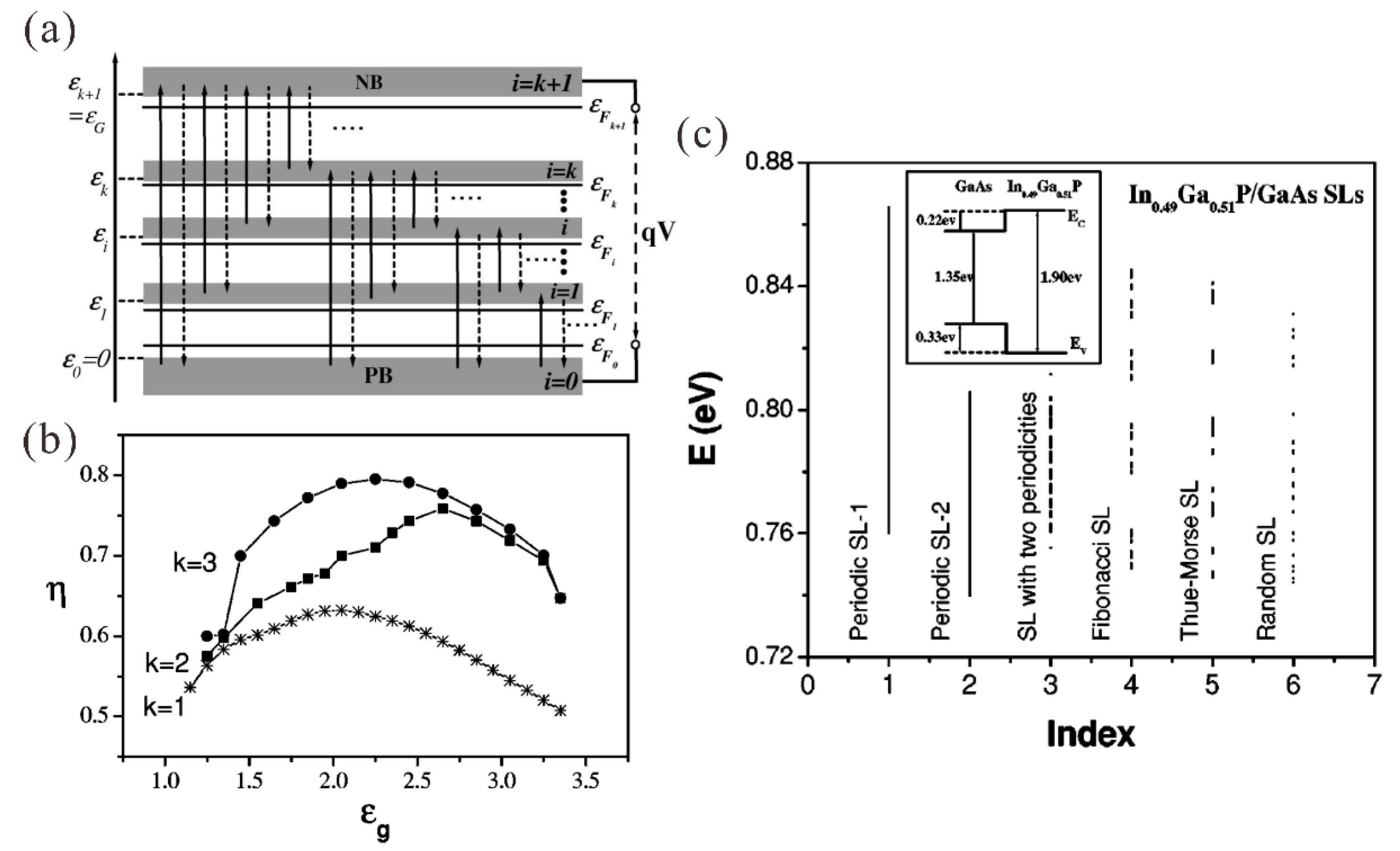
4.4. Solar Cells with Multi-Intermediate Band Structures

Numerous designs have been developed to improve the performance of solar cells. The enhancement of efficiency may originate from additional photon-induced transitions between the designed intermediate levels, as shown in Figure 7a [45]. Therefore, additional photons whose energies are lower than the original band gap in the solar cell can be absorbed, due to the transitions between bands in the multiband structure. In this way, various intermediate band structures can yield different efficiency limits for solar cells as shown in Figure 7b. It is shown that aperiodic semiconductor superlattices can produce these intermediate energy bands. For example, the continuous minibands in the In0.49Ga0.51P/GaAs superlattices can be split by introducing aperiodic order, such as that of the Thue–Morse sequence, the Fibonacci sequence, or even the random case (Figure 7c). This approach by introducing a multi-intermediate band structure may produce low-dimensional high-performance photovoltaic devices based on electronic band gap engineering, and can also be used in other ranges such as optoelectronics.

5. Optoelectronic Devices Based on Two-Dimensional Aperiodic Structures

Combining typical 2D aperiodic structures (such as Penrose tiling or fractal patterns) with optoelectronic devices is a feasible way to achieve resonant transmission or absorption enhancement, which can improve the optical response of devices and pave the way toward the integration of devices on a chip.

5.1. Aperiodic Plasmonic Aperture Arrays with Extraordinary Optical Transmission

As we know, much attention has been paid to the resonant transmission of light through subwavelength apertures for its potential applications in photolithography, displays, and near-field microscopy. The phenomena originate from the effect in which surface plasmon polaritons (SPPs) mediate light transmission through the periodic structure. Actually, resonantly enhanced transmission can be achieved not only in periodic structures but also through 2D quasiperiodic aperture arrays (Figure 8a) [46]. The broad transmission of a single aperture can interact with the discrete resonances caused by diffraction from the array, thus the spectral peaks described by Fano interference at terahertz frequencies occur, as shown in Figure 8b.
In addition to quasiperiodic structures, geometric self-similarity can also be employed to make multiple resonant transmission [47,48]. A Sierpinski carpet fractal-featured metallic thin film was fabricated as shown in Figure 8c. The existence of extraordinarily high transmission at specific wavelengths in infrared frequencies was verified by the transmission spectra. This high transmission was determined by the hierarchy of apertures of various sizes. Therefore, this unique structure may play an important role in the miniaturization and integration of plasmonic circuits.

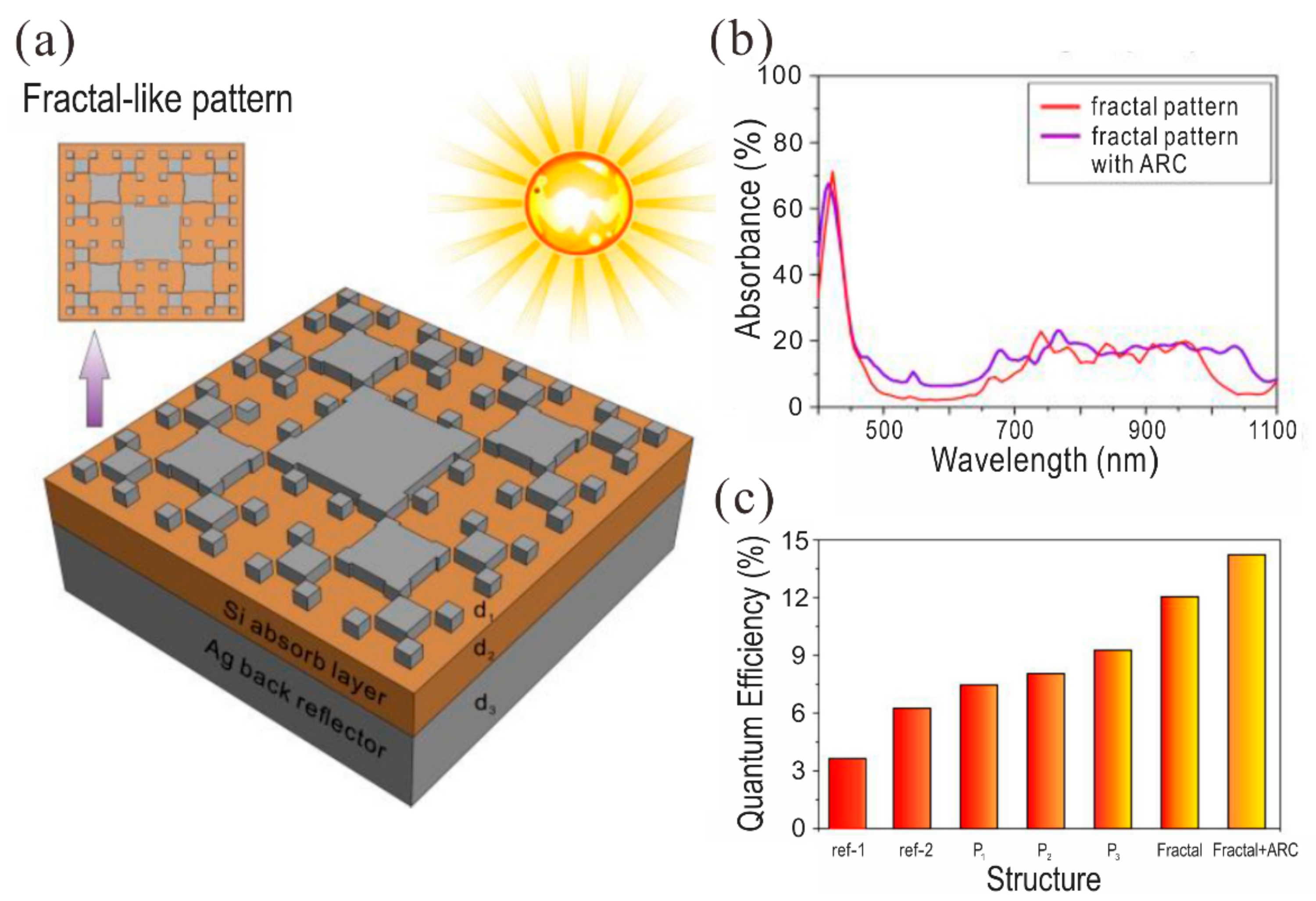
5.2. Solar Cell with a Plasmonic Fractal

The keys to fabricating high-performance solar cells are to extend the absorption of sunlight irradiation to broader bandwidths and increase the power conversion efficiency. A feasible way to enhance broadband absorption is to introduce silver nano cuboids with a fractal-like pattern atop a silicon solar cell, as shown in Figure 9 [49]. The incident light with different wavelengths could couple into various cavity modes and surface plasmon modes in the structure. In this system, the cavity modes originate from Fabry–Perot resonances at the longitudinal and transverse cavities, while the surface plasmon modes exist at the silicon–silver interface. Benefitting from the various feature sizes in the fractal structure, low-index and high-index surface plasmon modes are excited simultaneously. Eventually, broadband absorption can be achieved in this solar cell. By tuning the geometry of the fractal and applying an additional SiO2 antireflection layer, the quantum efficiency of the solar cell could be improved further. Therefore, these kinds of plasmonic fractal structures can be applied to design miniaturized compact photovoltaic devices with high performance.

6. Conclusions

Mainly based on the recent work in our group, we have briefly reviewed the aperiodic-order-induced multimode effects in photonic and plasmonic micro/nanostructures and their applications in optoelectronic devices. We present the multimode effects in a series of 1D/2D photonic or plasmonic aperiodic structures. These multimode effects have been employed to achieve optical filters for the WDM systems, open cavities for light–matter strong coupling, multiband waveguides for trapping “rainbow”, high-efficiency plasmonic solar cells, transmission-enhanced plasmonic arrays, and other devices. The investigations can be applied to the design of integrated photonic and plasmonic devices, which achieve potential applications in areas of optical communication, optical data storage, energy harvesting, nanoantennas, photonic chips, and so on.

Author Contributions

R.W.P., M.W., and H.J. conceived the idea. H.J., J.H., and R.W.P. wrote the paper. R.W.P. and M.W. supervised the research.

Funding

This research was funded by the National Key R&D Program of China (2017YFA0303702) and the National Natural Science Foundation of China (Grants No. 11634005 and No. 11674155).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
  2. Merlin, R.; Bajema, K.; Clarke, R. Quasiperiodic GaAs-AlAs heterostructures. Phys. Rev. Lett. 1985, 55, 1768–1770. [Google Scholar] [CrossRef]
  3. Todd, J.; Merlin, R.; Clarke, R.; Mohanty, K.M.; Axe, J.D. Synchrotron X-ray study of a Fibonacci superlattice. Phys. Rev. Lett. 1986, 57, 1157–1160. [Google Scholar] [CrossRef]
  4. Hu, A.; Tien, C.; Li, X.J.; Wang, Y.H.; Feng, D. X-ray diffraction pattern of quasiperiodic (Fibonacci) Nb-Cu superlattices. Phys. Lett. A 1986, 119, 313–314. [Google Scholar] [CrossRef]
  5. Kohmoto, M.; Sutherland, B.; Iguchi, K. Localization in optics: Quasiperiodic media. Phys. Rev. Lett. 1987, 58, 2436–2438. [Google Scholar] [CrossRef]
  6. Dharma-wardana, M.W.C.; MacDonald, A.H.; Lockwood, D.J.; Baribeau, J.M.; Houghton, D.C. Raman scattering in Fibonacci superlattices. Phys. Rev. Lett. 1987, 58, 1761. [Google Scholar] [CrossRef]
  7. Gellermann, W.; Kohmoto, M.; Sutherland, B.; Taylor, P.C. Localization of light waves in Fibonacci dielectric multilayers. Phys. Rev. Lett. 1994, 72, 633–636. [Google Scholar] [CrossRef]
  8. Maciá, E. Exploiting aperiodic designs in nanophotonic devices. Rep. Prog. Phys. 2012, 75, 036502. [Google Scholar] [CrossRef]
  9. Grimm, U. Aperiodic crystals and beyond. Acta Crystallogr. B 2015, 71, 258–274. [Google Scholar] [CrossRef] [Green Version]
  10. Peng, R.W.; Hu, A.; Jiang, S.S. Study on quasiperiodic Ta/Al multilayer films by x-ray diffraction. Appl. Phys. Lett. 1991, 59, 2512. [Google Scholar] [CrossRef]
  11. Peng, R.W.; Hu, A.; Jiang, S.S.; Zhang, C.S.; Feng, D. Structural characterization of 3-component Fibonacci Ta/Al multilayer films. Phys. Rev. B 1992, 46, 7816. [Google Scholar] [CrossRef] [PubMed]
  12. Chakraborty, S.; Marshall, O.P.; Folland, T.G.; Kim, Y.J.; Grigorenko, A.N.; Novoselov, K.S. Gain modulation by graphene plasmons in aperiodic lattice lasers. Science 2015, 351, 246–248. [Google Scholar] [CrossRef] [PubMed]
  13. Verslegers, L.; Catrysse, P.B.; Yu, Z.; Fan, S. Deep-Subwavelength Focusing and Steering of Light in an Aperiodic MetallicWaveguide Array. Phys. Rev. Lett. 2009, 103, 033902. [Google Scholar] [CrossRef] [PubMed]
  14. Pala, R.A.; Liu, J.S.; Barnard, E.S.; Askarov, D.; Garnett, E.C.; Fan, S.; Brongersma, M.L. Optimization of non-periodic plasmonic light-trapping layers for thin-film solar cells. Nat. Commun. 2013, 4, 2095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Fan, J.A.; Yeo, W.H.; Su, Y.; Hattori, Y.; Lee, W.; Jung, S.Y.; Zhang, Y.; Liu, Z.; Cheng, H.; Falgout, L.; et al. Fractal design concepts for stretchable electronics. Nat. Commun. 2014, 5, 3266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Jiang, S.S.; Hu, A.; Peng, R.W.; Feng, D. Quasiperiodic metallic multilayers. J. Magn. Magn. Mater. 1993, 162, 82–88. [Google Scholar] [CrossRef]
  17. Peng, R.W.; Wang, M.; Hu, A.; Jiang, S.S.; Jin, G.J.; Feng, D. Characterization of the diffraction spectra of one-dimensional k-component Fibonacci structures. Phys. Rev. B 1995, 52, 13310–13316. [Google Scholar] [CrossRef]
  18. Ma, T.; Liang, C.; Wang, L.; Lin, H.Q. Electronic band gaps and transport in aperiodic graphene superlattices of Thue–Morse sequence. Appl. Phys. Lett. 2012, 100, 252402. [Google Scholar] [CrossRef]
  19. Li, Y.; Peng, R.W.; Jin, G.J.; Wang, M.; Huang, X.Q.; Hu, A.; Jiang, S.S. Persistent currents in one-dimensional aperiodic mesoscopic rings. Eur. Phys. J. B 2002, 25, 497–503. [Google Scholar] [CrossRef]
  20. Ryu, C.S.; Oh, G.Y.; Lee, M.H. Extended and critical wave functions in a Thue–Morse chain. Phys. Rev. B 1992, 46, 5162–5168. [Google Scholar] [CrossRef]
  21. Kola, M.; Nori, F. Trace maps of general substitutional sequences. Phys. Rev. B 1990, 42, 1062–1065. [Google Scholar] [CrossRef] [PubMed]
  22. Bellissard, J.; Bovier, A.; Ghez, J.M. Spectral properties of a tight binding Hamiltonian with Period doubling potential. Commun. Math. Phys. 1991, 135, 379–399. [Google Scholar] [CrossRef]
  23. Birch, J.; Severin, M.; Wahlstrom, U.; Yamamoto, Y.; Radnoczi, G.; Riklund, R.; Sundgren, J.; Wallenberg, L.R. Structural characterization of precious-mean quasiperiodic Mo/V single-crystal superlattices grown by dual-target magnetron sputtering. Phys. Rev. B 1990, 41, 10398–10407. [Google Scholar] [CrossRef] [PubMed]
  24. Dotera, T.; Bekku, S.; Ziherl, P. Bronze-mean hexagonal quasicrystal. Nat. Mater. 2017, 16, 987–992. [Google Scholar] [CrossRef] [PubMed]
  25. Dallapiccola, R.; Gopinath, A.; Stellacci, F.; Negro, L.D. Quasi-periodic distribution of plasmon modes in two-dimensional Fibonacci arrays of metal nanoparticles. Opt. Express 2008, 16, 5544–5555. [Google Scholar] [CrossRef] [PubMed]
  26. Pierro, V.; Galdi, V.; Castaldi, G.; Pinto, I.M.; Felsen, L.B. Radiation properties of planar antenna arrays based on certain categories of aperiodic tilings. IEEE Trans. Antennas Propag. 2005, 53, 635–644. [Google Scholar] [CrossRef]
  27. Wang, K. Structural effects on light wave behavior in quasiperiodic regular and decagonal Penrose-tiling dielectric media: A comparative study. Phys. Rev. B 2007, 76, 085107. [Google Scholar] [CrossRef]
  28. Lifshitz, R. The square Fibonacci tiling. J. Alloys Compd. 2002, 342, 186–190. [Google Scholar] [CrossRef] [Green Version]
  29. Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
  30. Uozumi, J.; Kimura, H.; Asakura, T. Fraunhofer Diffraction by Koch Fractals. J. Mod. Opt. 1990, 37, 1011–1031. [Google Scholar] [CrossRef]
  31. Gefen, Y.; Meir, Y.; Mandelbrot, B.B.; Aharony, A. Geometric implementation of hypercubic lattices with noninteger dimensionality by use of low lacunarity fractal lattices. Phys. Rev. Lett. 1983, 50, 145–148. [Google Scholar] [CrossRef]
  32. Zhang, X.F.; Peng, R.W.; Kang, S.S.; Cao, L.S.; Zhang, R.L.; Wang, M.; Hu, A. Tunable High-frequency Magnetostatic Waves in Thue–Morse Antiferromagnetic Multilayers. J. Appl. Phys. 2006, 100, 063911. [Google Scholar] [CrossRef]
  33. Qiu, F.; Peng, R.W.; Huang, X.Q.; Liu, Y.M.; Wang, M.; Hu, A.; Jiang, S.S. Resonant transmission and frequency trifurcation of light waves in Thue–Morse dielectric multilayers. Europhys. Lett. 2003, 63, 853–859. [Google Scholar] [CrossRef]
  34. Qiu, F.; Peng, R.W.; Huang, X.Q.; Hu, X.F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D. Omnidirectional reflection of electromagnetic waves on Thue–Morse dielectric multilayers. Europhys. Lett. 2004, 68, 658–663. [Google Scholar] [CrossRef]
  35. Huang, X.; Wang, Y.; Gong, C. Numerical investigation of light-wave localization in optical Fibonacci superlattices with symmetric internal structure. J. Phys. Condens. Matter 1999, 11, 517–520. [Google Scholar] [CrossRef]
  36. Peng, R.W.; Jin, G.J.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D. Interface optical phonons in k-component Fibonacci dielectric multilayers. Phys. Rev. B 1999, 59, 3599–3605. [Google Scholar] [CrossRef]
  37. Zhang, K.; Xu, Y.; Chen, T.Y.; Jing, H.; Shi, W.B.; Xiong, B.; Peng, R.W.; Wang, M. Multimode photon-exciton coupling in an organic-dye-attached photonic quasicrystal. Opt. Lett. 2016, 41, 5740–5743. [Google Scholar] [CrossRef]
  38. Hu, A.; Wen, Z.X.; Jiang, S.S.; Tong, W.T.; Peng, R.W.; Feng, D. One-dimensional k-component Fibonacci Structures. Phys. Rev. B 1993, 48, 829–835. [Google Scholar] [CrossRef]
  39. Huang, X.Q.; Jiang, S.S.; Peng, R.W.; Hu, A. Perfect transmission and self-similar optical transmission spectra in symmetric Fibonacci-class multilayers. Phys. Rev. B 2001, 63, 245104. [Google Scholar] [CrossRef]
  40. Peng, R.W.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Mazzer, M. Symmetry-induced perfect transmission of light waves in quasiperiodic dielectric multilayers. Appl. Phys. Lett. 2002, 80, 3063–3065. [Google Scholar] [CrossRef]
  41. Peng, R.W.; Liu, Y.M.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D.; Ouyang, L.Z.; Zou, J. Dimerlike positional correlation and resonant transmission of electromagnetic waves in aperiodic dielectric multilayers. Phys. Rev. B 2004, 69, 165109. [Google Scholar] [CrossRef] [Green Version]
  42. Peng, R.W.; Wang, M.; Hu, A.; Jiang, S.S.; Jin, G.J.; Feng, D. Photonic localization in one-dimensional k-component Fibonacci structures. Phys. Rev. B 1998, 57, 1544. [Google Scholar] [CrossRef]
  43. Hu, Q.; Zhao, J.Z.; Peng, R.W.; Gao, F.; Zhang, R.L.; Wang, M. “Rainbow” trapped in a self-similar coaxial optical waveguide. Appl. Phys. Lett. 2010, 96, 161101. [Google Scholar] [CrossRef]
  44. Hu, Q.; Xu, D.H.; Peng, R.W.; Zhou, Y.; Yang, Q.L.; Wang, M. Tune the “rainbow” trapped in a multilayered waveguide. Europhys. Lett. 2012, 99, 57007. [Google Scholar] [CrossRef]
  45. Peng, R.W.; Mazzer, M.; Barnham, K.W.J. Efficiency enhancement of ideal photovoltaic solar cells by photonic excitations in multi-intermediate band structures. Appl. Phys. Lett. 2003, 83, 770–772. [Google Scholar] [CrossRef]
  46. Matsui, T.; Agrawal, A.; Nahata, A.; Vardeny, Z.V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 2007, 446, 517–521. [Google Scholar] [CrossRef]
  47. Bao, Y.J.; Zhang, B.; Wu, Z.; Si, J.W.; Wang, M.; Peng, R.W.; Lu, X.; Li, Z.F.; Hao, X.P.; Ming, N.B. Surface-plasmon-enhanced transmission through metallic film perforated with fractal-featured aperture array. Appl. Phys. Lett. 2007, 90, 251914. [Google Scholar] [CrossRef]
  48. Bao, Y.J.; Li, H.M.; Chen, X.C.; Peng, R.W.; Wang, M.; Lu, X.; Shao, J.; Ming, N.B. Tailoring the resonances of surface plasmas on fractal-featured metal film by adjusting aperture configuration. Appl. Phys. Lett. 2008, 92, 151902. [Google Scholar] [CrossRef]
  49. Zhu, L.H.; Shao, M.R.; Peng, R.W.; Fan, R.H.; Huang, X.R.; Wang, M. Broadband absorption and efficiency enhancement of an ultra-thin silicon solar cell with a plasmonic fractal. Opt. Express 2013, 21, 313–323. [Google Scholar] [CrossRef]
Symmetry 11 01120 g001 550
Figure 1. Schematic description of the typical aperiodic structures. (a) Fibonacci structure [16]. (b) Thue–Morse structure [18]. (c) 2D Fibonacci structure [25]. (Inset: Inflation rules of the first two generations of a 2D Fibonacci sequence). (d) Regular Penrose tiling [27]. (e) Koch snowflake fractal [30]. (f) Sierpinski carpet pattern [31].
Figure 1. Schematic description of the typical aperiodic structures. (a) Fibonacci structure [16]. (b) Thue–Morse structure [18]. (c) 2D Fibonacci structure [25]. (Inset: Inflation rules of the first two generations of a 2D Fibonacci sequence). (d) Regular Penrose tiling [27]. (e) Koch snowflake fractal [30]. (f) Sierpinski carpet pattern [31].
Symmetry 11 01120 g001
Symmetry 11 01120 g002 550
Figure 2. Aperiodic structures and their optical band diagrams: (a,b) Thue–Morse multilayer structure [32,34], and (c,d) Fibonacci multilayer structure [37].
Figure 2. Aperiodic structures and their optical band diagrams: (a,b) Thue–Morse multilayer structure [32,34], and (c,d) Fibonacci multilayer structure [37].
Symmetry 11 01120 g002
Symmetry 11 01120 g003 550
Figure 3. Multimodes in symmetric aperiodic structures. (a) Schematic of the symmetric Fibonacci-class (SFC(1)) multilayer structure. (b) The transmission coefficient of Fibonacci-class (FC(1)) (13 layers) and (c) SFC(1) (26 layers) systems. (d) Symmetrical fifth-generation Fibonacci TiO2/SiO2 multilayer film. (e) The measured (upper row) and calculated (lower row) transmission coefficient T as a function of the wave number for the symmetric TiO2/SiO2 mutilayers with defects in the central gap with different layers (SMD V2, SMD V3, and SMD V4 from left to right). (Adapted from ref. [39] (a–c) and ref. [41] (d,e)).
Figure 3. Multimodes in symmetric aperiodic structures. (a) Schematic of the symmetric Fibonacci-class (SFC(1)) multilayer structure. (b) The transmission coefficient of Fibonacci-class (FC(1)) (13 layers) and (c) SFC(1) (26 layers) systems. (d) Symmetrical fifth-generation Fibonacci TiO2/SiO2 multilayer film. (e) The measured (upper row) and calculated (lower row) transmission coefficient T as a function of the wave number for the symmetric TiO2/SiO2 mutilayers with defects in the central gap with different layers (SMD V2, SMD V3, and SMD V4 from left to right). (Adapted from ref. [39] (a–c) and ref. [41] (d,e)).
Symmetry 11 01120 g003
Symmetry 11 01120 g004 550
Figure 4. Transmission coefficient T as a function of the phase with the different incommensurate intervals k in k-component Fibonacci structures. The number of layers N are as follows: (a) N = 28,657; (b) N = 27,201; (c) N = 31,422; (d) N = 29,244; (e) N = 233; (f) N = 277; (g) N = 250; and (h) N = 245, respectively. (Adapted from ref. [42]).
Figure 4. Transmission coefficient T as a function of the phase with the different incommensurate intervals k in k-component Fibonacci structures. The number of layers N are as follows: (a) N = 28,657; (b) N = 27,201; (c) N = 31,422; (d) N = 29,244; (e) N = 233; (f) N = 277; (g) N = 250; and (h) N = 245, respectively. (Adapted from ref. [42]).
Symmetry 11 01120 g004
Symmetry 11 01120 g005 550
Figure 5. Multimode photon-exciton coupling. (a) Schematic of a Fibonacci photonic quasicrystal with J-aggregates on the top surface. (b) Experimentally measured transmission spectra of the photonic quasicrystal; the modes labeled C, L, and H correspond to three peaks. (c) Transmission spectra of the sample under various incident angles. Polariton bands were traced by dashed lines. (d) Dispersion map of the sample. Calculated dashed lines fit the polariton bands and Rabi splitting. (Adapted from ref. [37]).
Figure 5. Multimode photon-exciton coupling. (a) Schematic of a Fibonacci photonic quasicrystal with J-aggregates on the top surface. (b) Experimentally measured transmission spectra of the photonic quasicrystal; the modes labeled C, L, and H correspond to three peaks. (c) Transmission spectra of the sample under various incident angles. Polariton bands were traced by dashed lines. (d) Dispersion map of the sample. Calculated dashed lines fit the polariton bands and Rabi splitting. (Adapted from ref. [37]).
Symmetry 11 01120 g005
Symmetry 11 01120 g006 550
Figure 6. Multiband waveguide. (a) Structure of a self-similar dielectric waveguide (SDW), where a coaxial Thue–Morse multilayer consisting of two building blocks was employed to cover a hollow core. The lower figure manifests refractive-index distributions in the SDWs. (b) Photonic bands and transmission modes in the SDW. (c) The electric-field time-average energy density distribution in the SDW for different modes. (Adapted from ref. [43]).
Figure 6. Multiband waveguide. (a) Structure of a self-similar dielectric waveguide (SDW), where a coaxial Thue–Morse multilayer consisting of two building blocks was employed to cover a hollow core. The lower figure manifests refractive-index distributions in the SDWs. (b) Photonic bands and transmission modes in the SDW. (c) The electric-field time-average energy density distribution in the SDW for different modes. (Adapted from ref. [43]).
Symmetry 11 01120 g006
Symmetry 11 01120 g007 550
Figure 7. Enhancement of solar cells caused by photon-induced transitions in multi-intermediate band structures. (a) Various radiation transitions between intermediate multiband structures in the designed solar cell. (b) Limiting efficiency η for three model solar cells with diverse intermediate multiband structures (k = 1,2,3). (c) Electronic miniband structures of several periodic and aperiodic In0.49Ga0.51P/GaAs superlattices. The inset shows the band-edge diagram of the In0.49Ga0.51P/GaAs interface (at room temperature). (Adapted from ref. [45]).
Figure 7. Enhancement of solar cells caused by photon-induced transitions in multi-intermediate band structures. (a) Various radiation transitions between intermediate multiband structures in the designed solar cell. (b) Limiting efficiency η for three model solar cells with diverse intermediate multiband structures (k = 1,2,3). (c) Electronic miniband structures of several periodic and aperiodic In0.49Ga0.51P/GaAs superlattices. The inset shows the band-edge diagram of the In0.49Ga0.51P/GaAs interface (at room temperature). (Adapted from ref. [45]).
Symmetry 11 01120 g007
Symmetry 11 01120 g008 550
Figure 8. Transmission through aperiodic aperture arrays. (a) A Penrose quasicrystal constructed of thin and thick rhomb tiles. (b) Transmission of the Penrose-type quasicrystal perforated films with different side lengths. (c) Scanning electron micrograph of an aluminum film perforated with a Sierpinski carpet fractal-featured aperture array. (d) Transmission of the metallic Sierpinski carpet structure. (a,b) are obtained experimentally; (c–e) are simulated results. (Adapted from ref. [46] (a,b) and ref. [47] (c,d)).
Figure 8. Transmission through aperiodic aperture arrays. (a) A Penrose quasicrystal constructed of thin and thick rhomb tiles. (b) Transmission of the Penrose-type quasicrystal perforated films with different side lengths. (c) Scanning electron micrograph of an aluminum film perforated with a Sierpinski carpet fractal-featured aperture array. (d) Transmission of the metallic Sierpinski carpet structure. (a,b) are obtained experimentally; (c–e) are simulated results. (Adapted from ref. [46] (a,b) and ref. [47] (c,d)).
Symmetry 11 01120 g008
Symmetry 11 01120 g009 550
Figure 9. Solar cell with a plasmonic fractal to achieve broadband absorption. (a) Schematic of the solar cell with a plasmonic fractal. Including a Ag fractal-like pattern, a Si absorbent layer, and a silver back reflector. (b) Absorbance spectra of the solar cell with or without the antireflection coating (ARC). (c) Quantum efficiencies of the 50 nm thick silicon solar cells: ref-1 (bare Si film); ref-2 (Si film with Ag back reflector); solar cells with base-periodicity patterns (P1 = 100 nm, P2 = 200 nm, P3 = 400 nm); solar cells with a plasmonic fractal and additional dielectric ARC. (Adapted from ref. [49]).
Figure 9. Solar cell with a plasmonic fractal to achieve broadband absorption. (a) Schematic of the solar cell with a plasmonic fractal. Including a Ag fractal-like pattern, a Si absorbent layer, and a silver back reflector. (b) Absorbance spectra of the solar cell with or without the antireflection coating (ARC). (c) Quantum efficiencies of the 50 nm thick silicon solar cells: ref-1 (bare Si film); ref-2 (Si film with Ag back reflector); solar cells with base-periodicity patterns (P1 = 100 nm, P2 = 200 nm, P3 = 400 nm); solar cells with a plasmonic fractal and additional dielectric ARC. (Adapted from ref. [49]).
Symmetry 11 01120 g009

Share and Cite

MDPI and ACS Style

Jing, H.; He, J.; Peng, R.-W.; Wang, M. Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices. Symmetry 2019, 11, 1120. https://doi.org/10.3390/sym11091120

AMA Style

Jing H, He J, Peng R-W, Wang M. Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices. Symmetry. 2019; 11(9):1120. https://doi.org/10.3390/sym11091120

Chicago/Turabian Style

Jing, Hao, Jie He, Ru-Wen Peng, and Mu Wang. 2019. "Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices" Symmetry 11, no. 9: 1120. https://doi.org/10.3390/sym11091120

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop