Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices
Abstract
1. Introduction
2. Aperiodic Structures
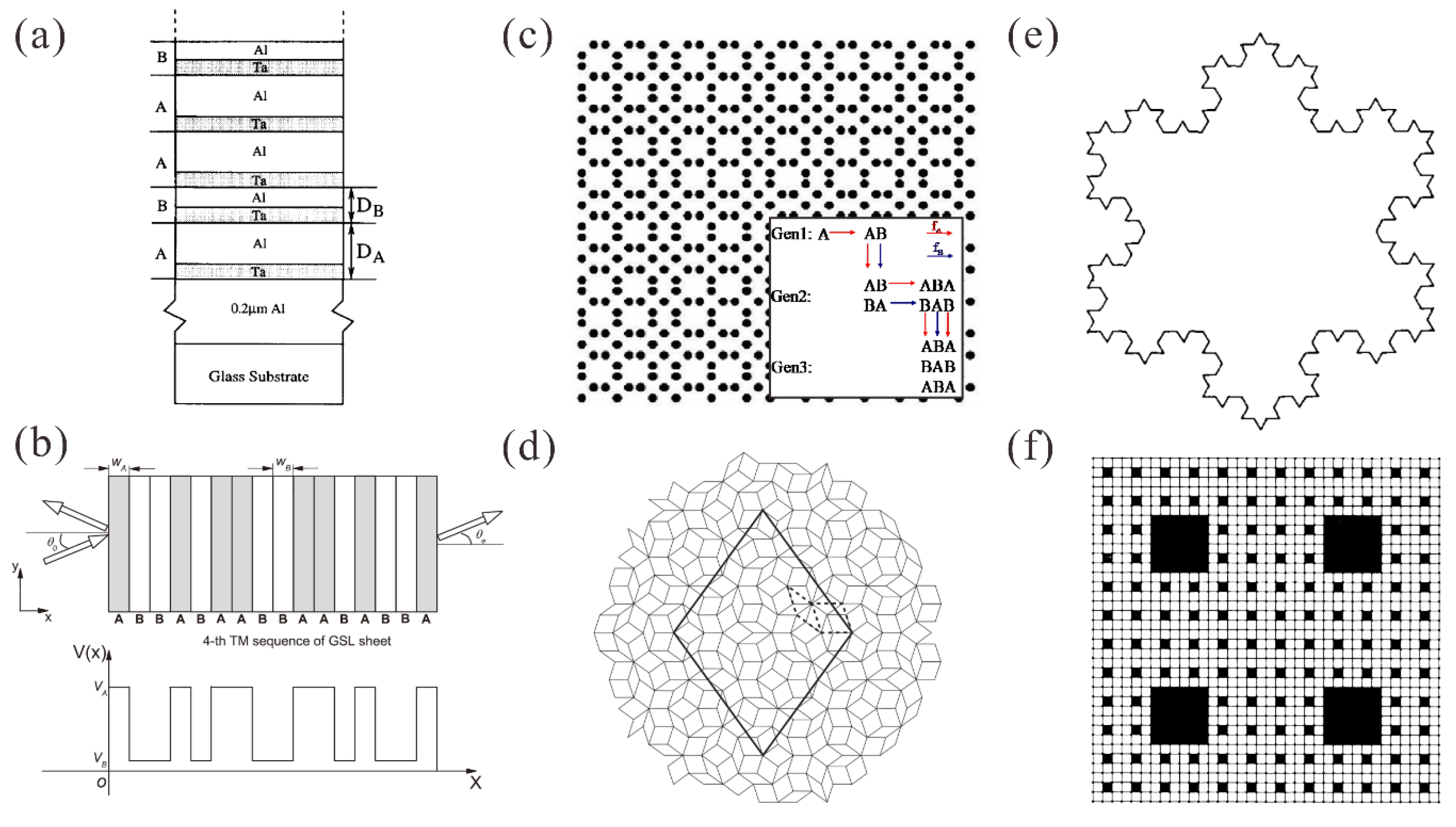
2.1. One-Dimensional Aperiodic Structures
2.2. Two-Dimensional Aperiodic Structures
2.3. Fractal Patterns
3. Aperiodic-Order-Induced Multimode Effects in Photonic Micro/Nanostructures
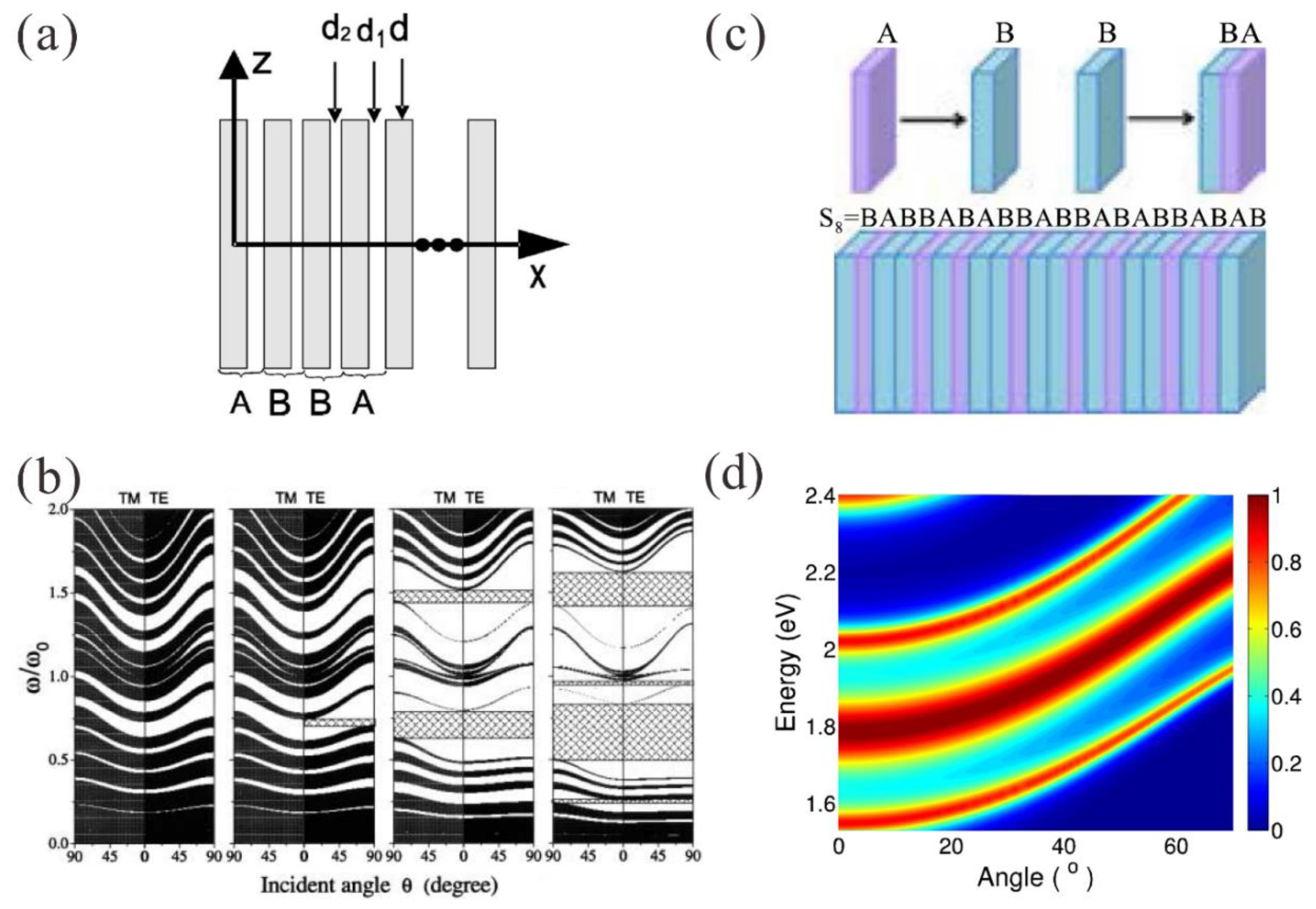
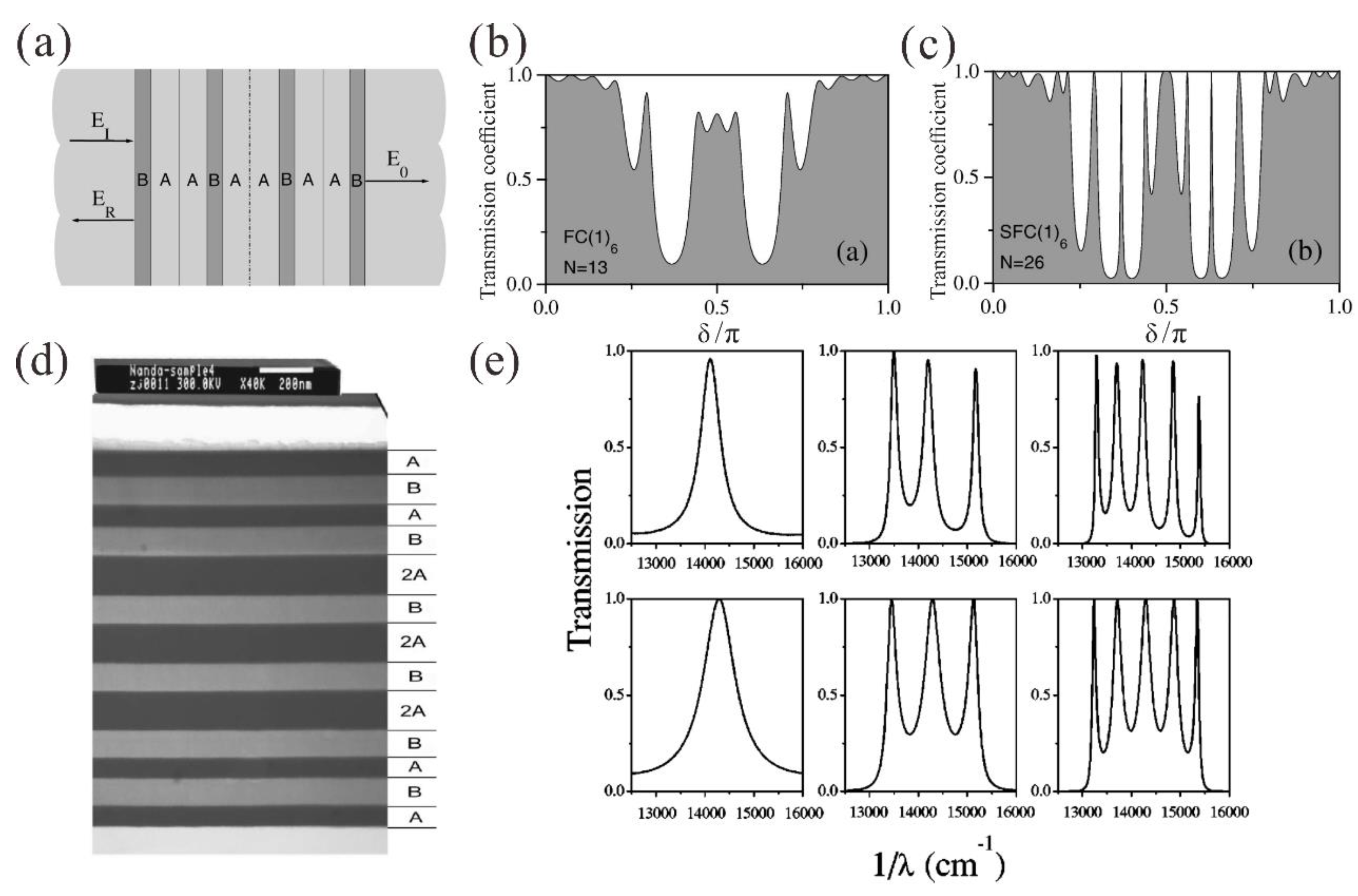
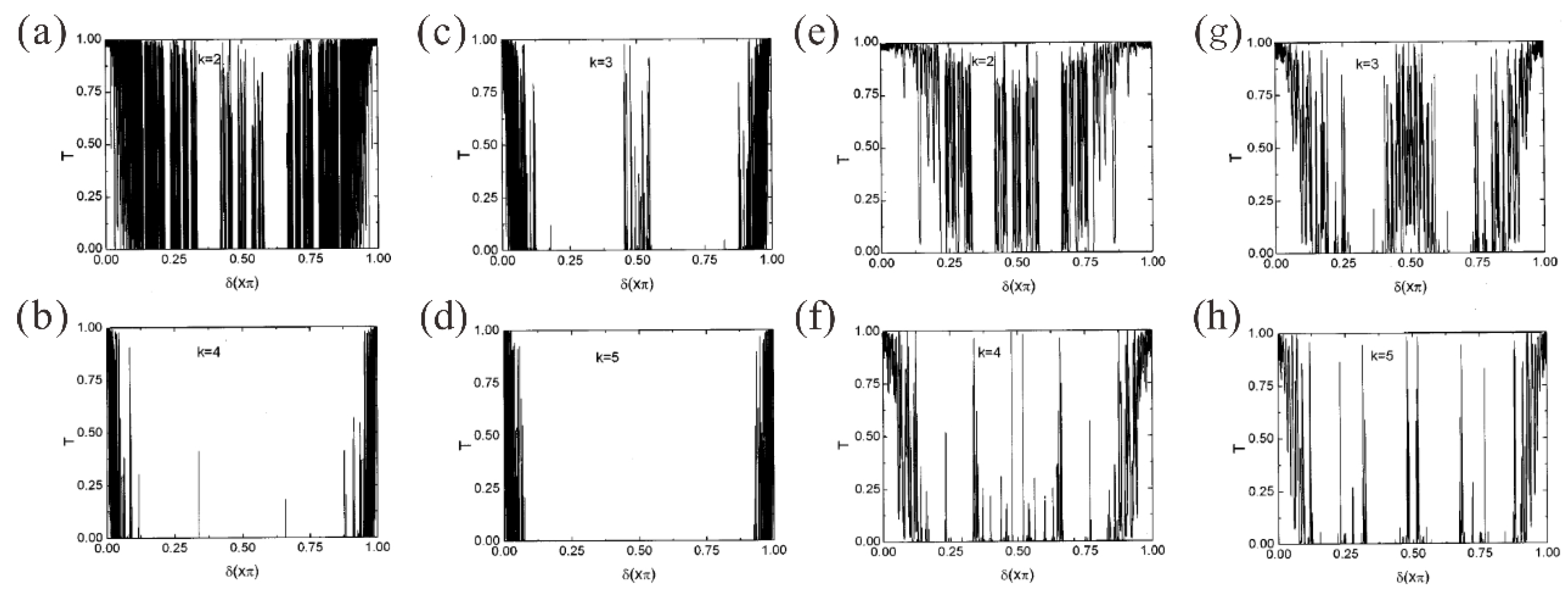
3.1. Multimode Effects Induced by Self-Similarity
3.2. Multimode Effects in Symmetric Aperiodic Structure
4. Optoelectronic Devices Based on One-Dimensional Aperiodic Structures
4.1. Optical Filters for the Wavelength Division Multiplexing (WDM) Systems
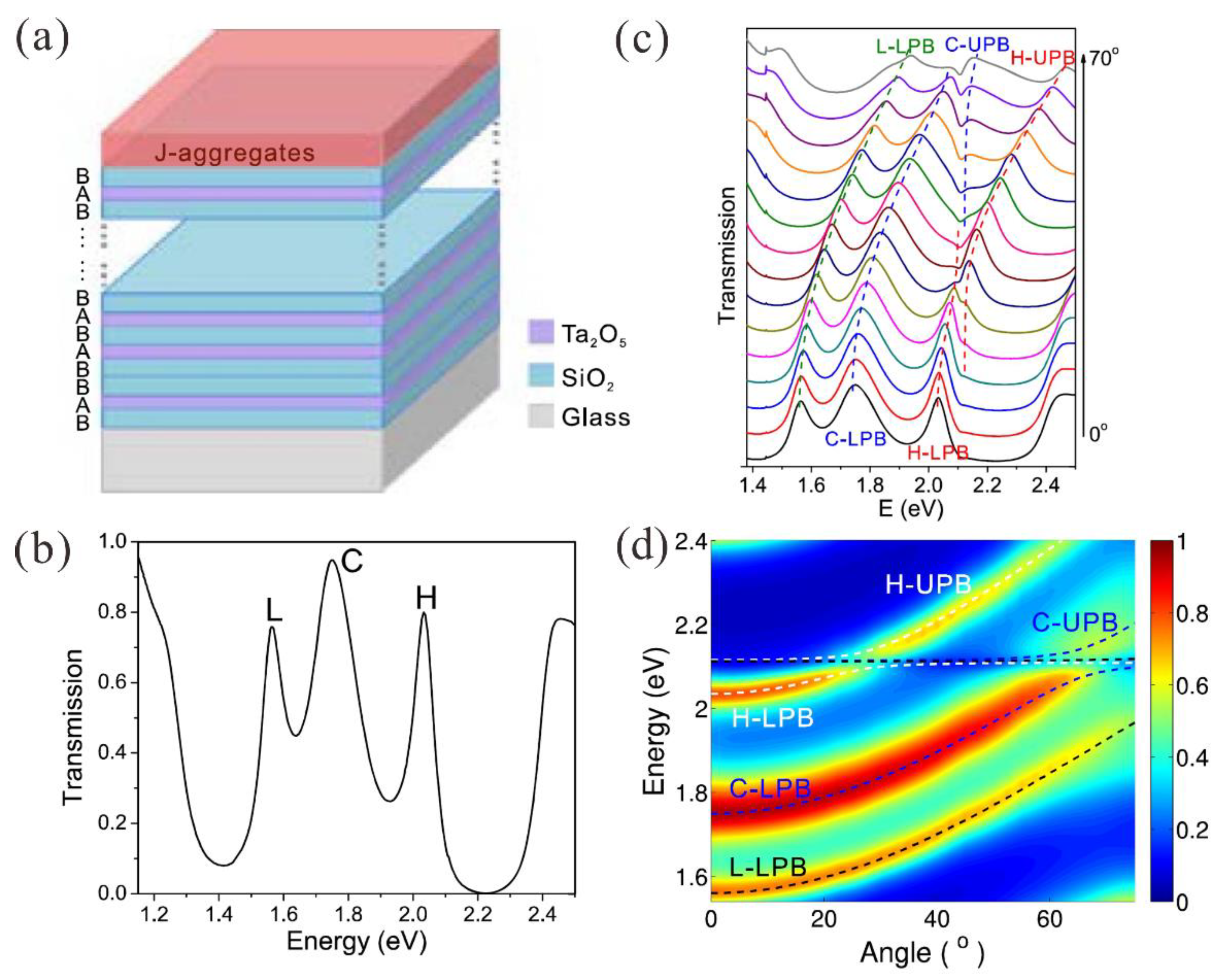
4.2. Open Cavities for the Light–Matter Strong Coupling
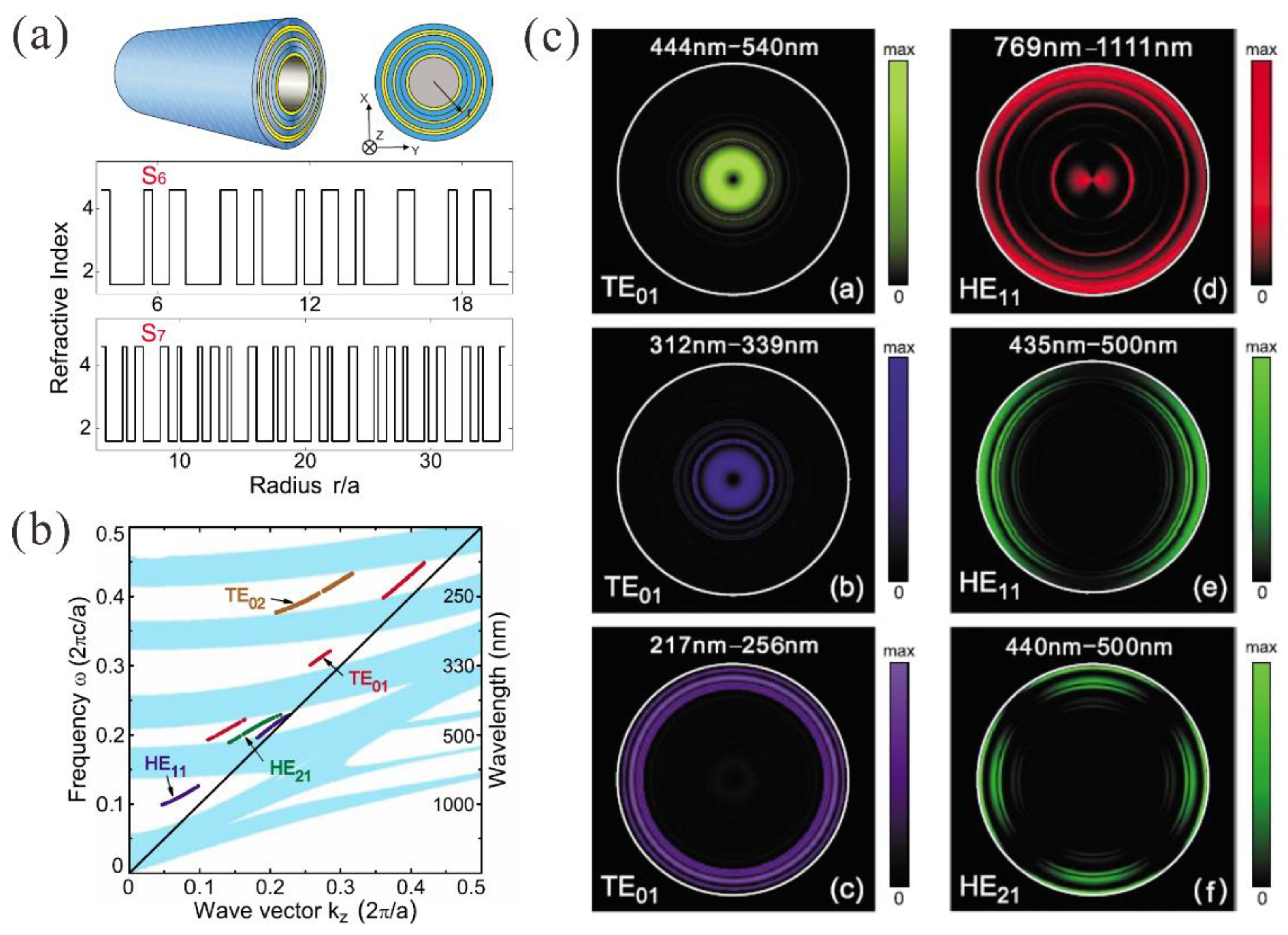
4.3. Multiband Waveguides for Trapping “Rainbow”
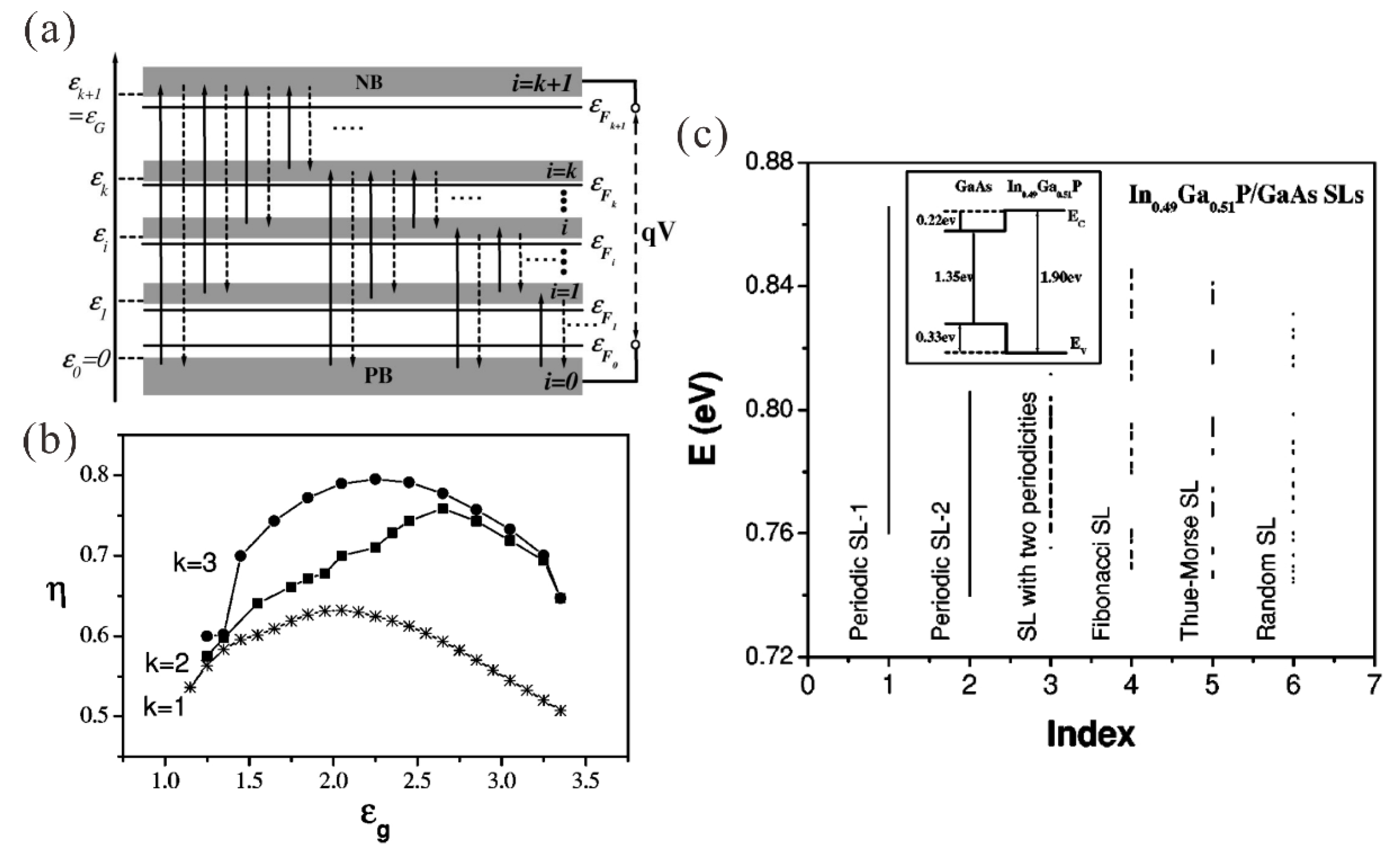
4.4. Solar Cells with Multi-Intermediate Band Structures
5. Optoelectronic Devices Based on Two-Dimensional Aperiodic Structures
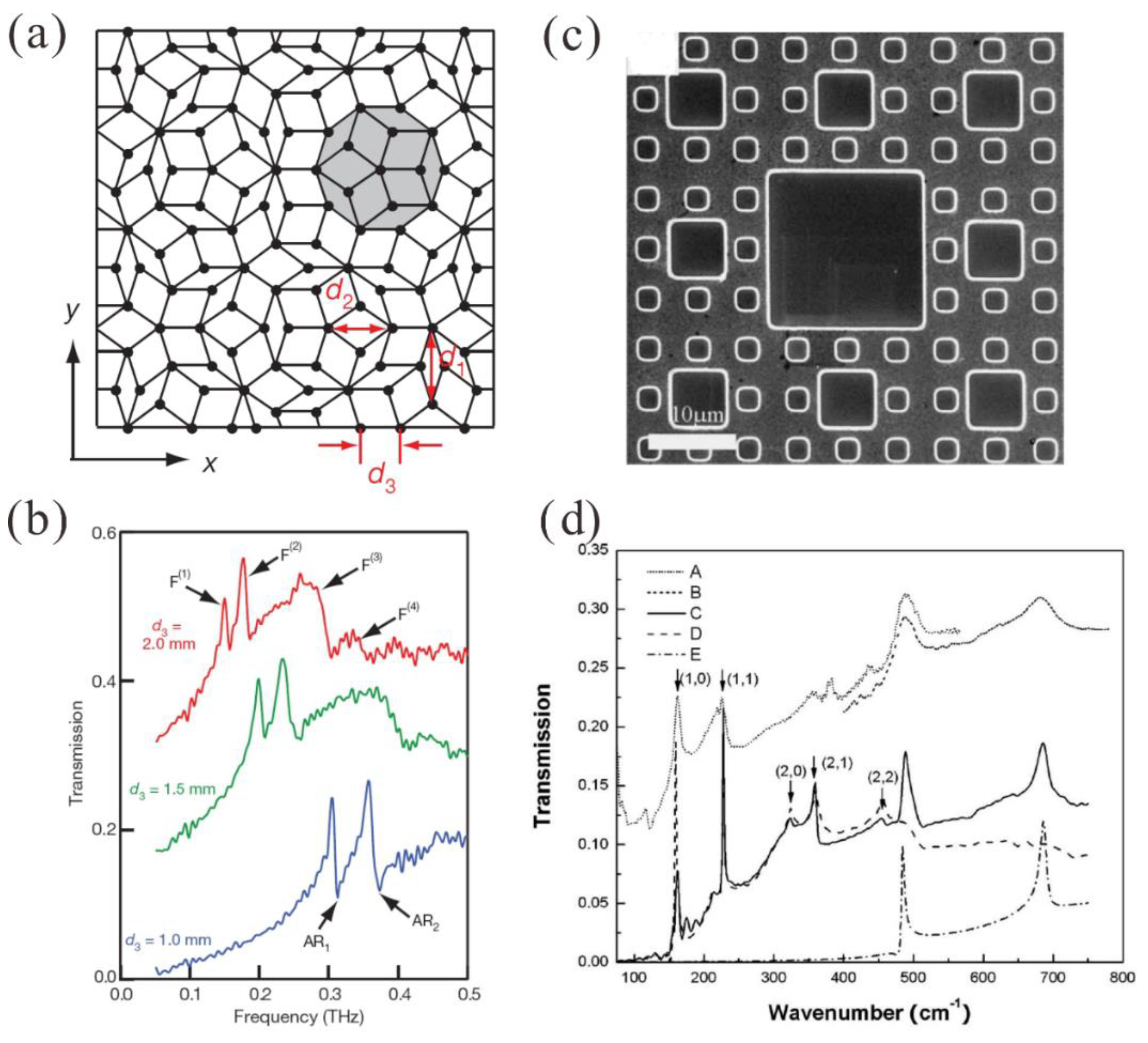
5.1. Aperiodic Plasmonic Aperture Arrays with Extraordinary Optical Transmission
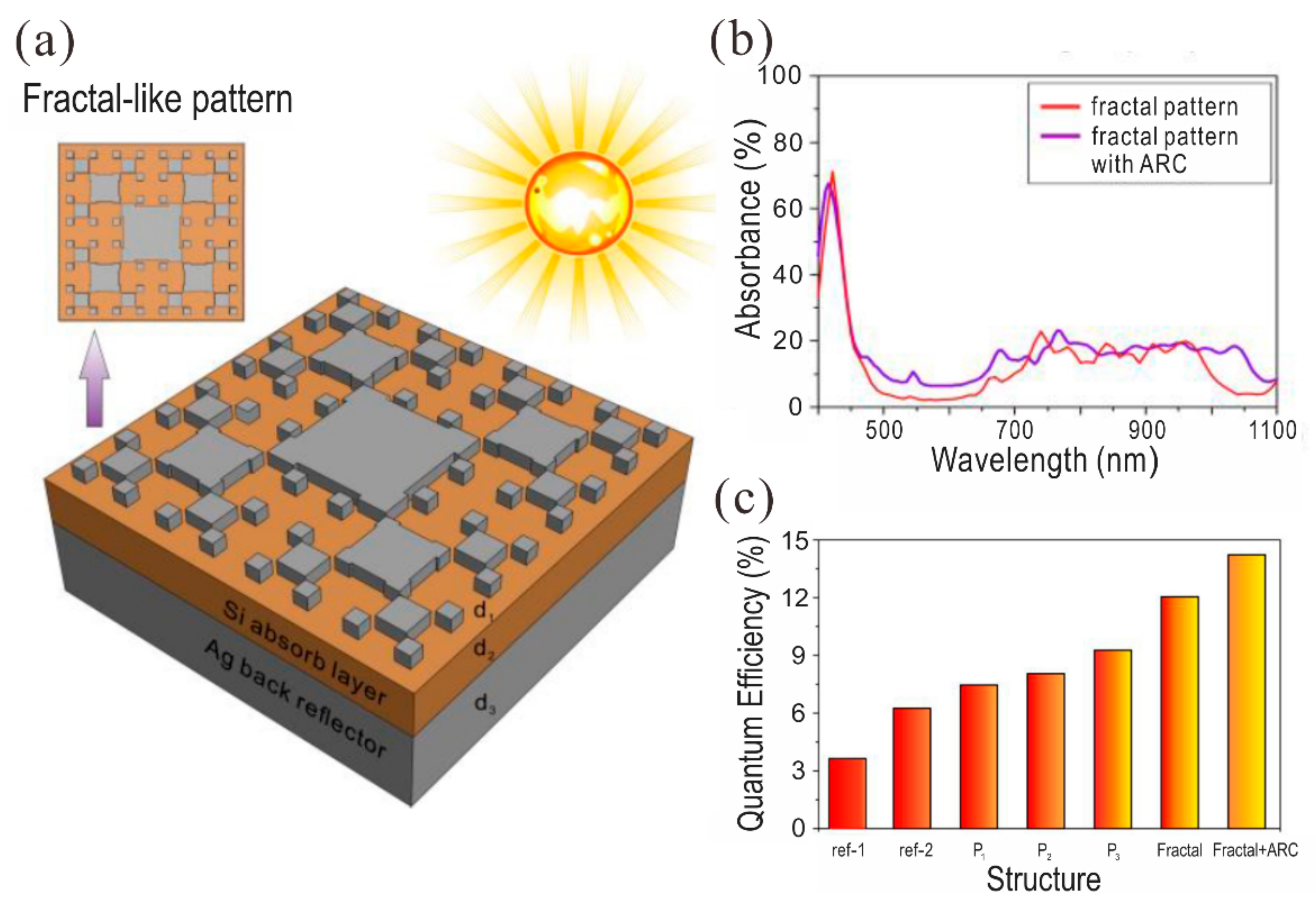
5.2. Solar Cell with a Plasmonic Fractal
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Merlin, R.; Bajema, K.; Clarke, R. Quasiperiodic GaAs-AlAs heterostructures. Phys. Rev. Lett. 1985, 55, 1768–1770. [Google Scholar] [CrossRef]
- Todd, J.; Merlin, R.; Clarke, R.; Mohanty, K.M.; Axe, J.D. Synchrotron X-ray study of a Fibonacci superlattice. Phys. Rev. Lett. 1986, 57, 1157–1160. [Google Scholar] [CrossRef]
- Hu, A.; Tien, C.; Li, X.J.; Wang, Y.H.; Feng, D. X-ray diffraction pattern of quasiperiodic (Fibonacci) Nb-Cu superlattices. Phys. Lett. A 1986, 119, 313–314. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Iguchi, K. Localization in optics: Quasiperiodic media. Phys. Rev. Lett. 1987, 58, 2436–2438. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C.; MacDonald, A.H.; Lockwood, D.J.; Baribeau, J.M.; Houghton, D.C. Raman scattering in Fibonacci superlattices. Phys. Rev. Lett. 1987, 58, 1761. [Google Scholar] [CrossRef]
- Gellermann, W.; Kohmoto, M.; Sutherland, B.; Taylor, P.C. Localization of light waves in Fibonacci dielectric multilayers. Phys. Rev. Lett. 1994, 72, 633–636. [Google Scholar] [CrossRef]
- Maciá, E. Exploiting aperiodic designs in nanophotonic devices. Rep. Prog. Phys. 2012, 75, 036502. [Google Scholar] [CrossRef]
- Grimm, U. Aperiodic crystals and beyond. Acta Crystallogr. B 2015, 71, 258–274. [Google Scholar] [CrossRef]
- Peng, R.W.; Hu, A.; Jiang, S.S. Study on quasiperiodic Ta/Al multilayer films by x-ray diffraction. Appl. Phys. Lett. 1991, 59, 2512. [Google Scholar] [CrossRef]
- Peng, R.W.; Hu, A.; Jiang, S.S.; Zhang, C.S.; Feng, D. Structural characterization of 3-component Fibonacci Ta/Al multilayer films. Phys. Rev. B 1992, 46, 7816. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Marshall, O.P.; Folland, T.G.; Kim, Y.J.; Grigorenko, A.N.; Novoselov, K.S. Gain modulation by graphene plasmons in aperiodic lattice lasers. Science 2015, 351, 246–248. [Google Scholar] [CrossRef] [PubMed]
- Verslegers, L.; Catrysse, P.B.; Yu, Z.; Fan, S. Deep-Subwavelength Focusing and Steering of Light in an Aperiodic MetallicWaveguide Array. Phys. Rev. Lett. 2009, 103, 033902. [Google Scholar] [CrossRef] [PubMed]
- Pala, R.A.; Liu, J.S.; Barnard, E.S.; Askarov, D.; Garnett, E.C.; Fan, S.; Brongersma, M.L. Optimization of non-periodic plasmonic light-trapping layers for thin-film solar cells. Nat. Commun. 2013, 4, 2095. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.A.; Yeo, W.H.; Su, Y.; Hattori, Y.; Lee, W.; Jung, S.Y.; Zhang, Y.; Liu, Z.; Cheng, H.; Falgout, L.; et al. Fractal design concepts for stretchable electronics. Nat. Commun. 2014, 5, 3266. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.S.; Hu, A.; Peng, R.W.; Feng, D. Quasiperiodic metallic multilayers. J. Magn. Magn. Mater. 1993, 162, 82–88. [Google Scholar] [CrossRef]
- Peng, R.W.; Wang, M.; Hu, A.; Jiang, S.S.; Jin, G.J.; Feng, D. Characterization of the diffraction spectra of one-dimensional k-component Fibonacci structures. Phys. Rev. B 1995, 52, 13310–13316. [Google Scholar] [CrossRef]
- Ma, T.; Liang, C.; Wang, L.; Lin, H.Q. Electronic band gaps and transport in aperiodic graphene superlattices of Thue–Morse sequence. Appl. Phys. Lett. 2012, 100, 252402. [Google Scholar] [CrossRef]
- Li, Y.; Peng, R.W.; Jin, G.J.; Wang, M.; Huang, X.Q.; Hu, A.; Jiang, S.S. Persistent currents in one-dimensional aperiodic mesoscopic rings. Eur. Phys. J. B 2002, 25, 497–503. [Google Scholar] [CrossRef]
- Ryu, C.S.; Oh, G.Y.; Lee, M.H. Extended and critical wave functions in a Thue–Morse chain. Phys. Rev. B 1992, 46, 5162–5168. [Google Scholar] [CrossRef]
- Kola, M.; Nori, F. Trace maps of general substitutional sequences. Phys. Rev. B 1990, 42, 1062–1065. [Google Scholar] [CrossRef] [PubMed]
- Bellissard, J.; Bovier, A.; Ghez, J.M. Spectral properties of a tight binding Hamiltonian with Period doubling potential. Commun. Math. Phys. 1991, 135, 379–399. [Google Scholar] [CrossRef]
- Birch, J.; Severin, M.; Wahlstrom, U.; Yamamoto, Y.; Radnoczi, G.; Riklund, R.; Sundgren, J.; Wallenberg, L.R. Structural characterization of precious-mean quasiperiodic Mo/V single-crystal superlattices grown by dual-target magnetron sputtering. Phys. Rev. B 1990, 41, 10398–10407. [Google Scholar] [CrossRef] [PubMed]
- Dotera, T.; Bekku, S.; Ziherl, P. Bronze-mean hexagonal quasicrystal. Nat. Mater. 2017, 16, 987–992. [Google Scholar] [CrossRef] [PubMed]
- Dallapiccola, R.; Gopinath, A.; Stellacci, F.; Negro, L.D. Quasi-periodic distribution of plasmon modes in two-dimensional Fibonacci arrays of metal nanoparticles. Opt. Express 2008, 16, 5544–5555. [Google Scholar] [CrossRef] [PubMed]
- Pierro, V.; Galdi, V.; Castaldi, G.; Pinto, I.M.; Felsen, L.B. Radiation properties of planar antenna arrays based on certain categories of aperiodic tilings. IEEE Trans. Antennas Propag. 2005, 53, 635–644. [Google Scholar] [CrossRef]
- Wang, K. Structural effects on light wave behavior in quasiperiodic regular and decagonal Penrose-tiling dielectric media: A comparative study. Phys. Rev. B 2007, 76, 085107. [Google Scholar] [CrossRef]
- Lifshitz, R. The square Fibonacci tiling. J. Alloys Compd. 2002, 342, 186–190. [Google Scholar] [CrossRef]
- Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
- Uozumi, J.; Kimura, H.; Asakura, T. Fraunhofer Diffraction by Koch Fractals. J. Mod. Opt. 1990, 37, 1011–1031. [Google Scholar] [CrossRef]
- Gefen, Y.; Meir, Y.; Mandelbrot, B.B.; Aharony, A. Geometric implementation of hypercubic lattices with noninteger dimensionality by use of low lacunarity fractal lattices. Phys. Rev. Lett. 1983, 50, 145–148. [Google Scholar] [CrossRef]
- Zhang, X.F.; Peng, R.W.; Kang, S.S.; Cao, L.S.; Zhang, R.L.; Wang, M.; Hu, A. Tunable High-frequency Magnetostatic Waves in Thue–Morse Antiferromagnetic Multilayers. J. Appl. Phys. 2006, 100, 063911. [Google Scholar] [CrossRef]
- Qiu, F.; Peng, R.W.; Huang, X.Q.; Liu, Y.M.; Wang, M.; Hu, A.; Jiang, S.S. Resonant transmission and frequency trifurcation of light waves in Thue–Morse dielectric multilayers. Europhys. Lett. 2003, 63, 853–859. [Google Scholar] [CrossRef][Green Version]
- Qiu, F.; Peng, R.W.; Huang, X.Q.; Hu, X.F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D. Omnidirectional reflection of electromagnetic waves on Thue–Morse dielectric multilayers. Europhys. Lett. 2004, 68, 658–663. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Gong, C. Numerical investigation of light-wave localization in optical Fibonacci superlattices with symmetric internal structure. J. Phys. Condens. Matter 1999, 11, 517–520. [Google Scholar] [CrossRef]
- Peng, R.W.; Jin, G.J.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D. Interface optical phonons in k-component Fibonacci dielectric multilayers. Phys. Rev. B 1999, 59, 3599–3605. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Chen, T.Y.; Jing, H.; Shi, W.B.; Xiong, B.; Peng, R.W.; Wang, M. Multimode photon-exciton coupling in an organic-dye-attached photonic quasicrystal. Opt. Lett. 2016, 41, 5740–5743. [Google Scholar] [CrossRef]
- Hu, A.; Wen, Z.X.; Jiang, S.S.; Tong, W.T.; Peng, R.W.; Feng, D. One-dimensional k-component Fibonacci Structures. Phys. Rev. B 1993, 48, 829–835. [Google Scholar] [CrossRef]
- Huang, X.Q.; Jiang, S.S.; Peng, R.W.; Hu, A. Perfect transmission and self-similar optical transmission spectra in symmetric Fibonacci-class multilayers. Phys. Rev. B 2001, 63, 245104. [Google Scholar] [CrossRef]
- Peng, R.W.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Mazzer, M. Symmetry-induced perfect transmission of light waves in quasiperiodic dielectric multilayers. Appl. Phys. Lett. 2002, 80, 3063–3065. [Google Scholar] [CrossRef]
- Peng, R.W.; Liu, Y.M.; Huang, X.Q.; Qiu, F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D.; Ouyang, L.Z.; Zou, J. Dimerlike positional correlation and resonant transmission of electromagnetic waves in aperiodic dielectric multilayers. Phys. Rev. B 2004, 69, 165109. [Google Scholar] [CrossRef]
- Peng, R.W.; Wang, M.; Hu, A.; Jiang, S.S.; Jin, G.J.; Feng, D. Photonic localization in one-dimensional k-component Fibonacci structures. Phys. Rev. B 1998, 57, 1544. [Google Scholar] [CrossRef]
- Hu, Q.; Zhao, J.Z.; Peng, R.W.; Gao, F.; Zhang, R.L.; Wang, M. “Rainbow” trapped in a self-similar coaxial optical waveguide. Appl. Phys. Lett. 2010, 96, 161101. [Google Scholar] [CrossRef]
- Hu, Q.; Xu, D.H.; Peng, R.W.; Zhou, Y.; Yang, Q.L.; Wang, M. Tune the “rainbow” trapped in a multilayered waveguide. Europhys. Lett. 2012, 99, 57007. [Google Scholar] [CrossRef]
- Peng, R.W.; Mazzer, M.; Barnham, K.W.J. Efficiency enhancement of ideal photovoltaic solar cells by photonic excitations in multi-intermediate band structures. Appl. Phys. Lett. 2003, 83, 770–772. [Google Scholar] [CrossRef]
- Matsui, T.; Agrawal, A.; Nahata, A.; Vardeny, Z.V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 2007, 446, 517–521. [Google Scholar] [CrossRef]
- Bao, Y.J.; Zhang, B.; Wu, Z.; Si, J.W.; Wang, M.; Peng, R.W.; Lu, X.; Li, Z.F.; Hao, X.P.; Ming, N.B. Surface-plasmon-enhanced transmission through metallic film perforated with fractal-featured aperture array. Appl. Phys. Lett. 2007, 90, 251914. [Google Scholar] [CrossRef]
- Bao, Y.J.; Li, H.M.; Chen, X.C.; Peng, R.W.; Wang, M.; Lu, X.; Shao, J.; Ming, N.B. Tailoring the resonances of surface plasmas on fractal-featured metal film by adjusting aperture configuration. Appl. Phys. Lett. 2008, 92, 151902. [Google Scholar] [CrossRef]
- Zhu, L.H.; Shao, M.R.; Peng, R.W.; Fan, R.H.; Huang, X.R.; Wang, M. Broadband absorption and efficiency enhancement of an ultra-thin silicon solar cell with a plasmonic fractal. Opt. Express 2013, 21, 313–323. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, H.; He, J.; Peng, R.-W.; Wang, M. Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices. Symmetry 2019, 11, 1120. https://doi.org/10.3390/sym11091120
Jing H, He J, Peng R-W, Wang M. Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices. Symmetry. 2019; 11(9):1120. https://doi.org/10.3390/sym11091120
Chicago/Turabian StyleJing, Hao, Jie He, Ru-Wen Peng, and Mu Wang. 2019. "Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices" Symmetry 11, no. 9: 1120. https://doi.org/10.3390/sym11091120
APA StyleJing, H., He, J., Peng, R.-W., & Wang, M. (2019). Aperiodic-Order-Induced Multimode Effects and Their Applications in Optoelectronic Devices. Symmetry, 11(9), 1120. https://doi.org/10.3390/sym11091120



