The Entanglement Generation in
Abstract
1. Introduction
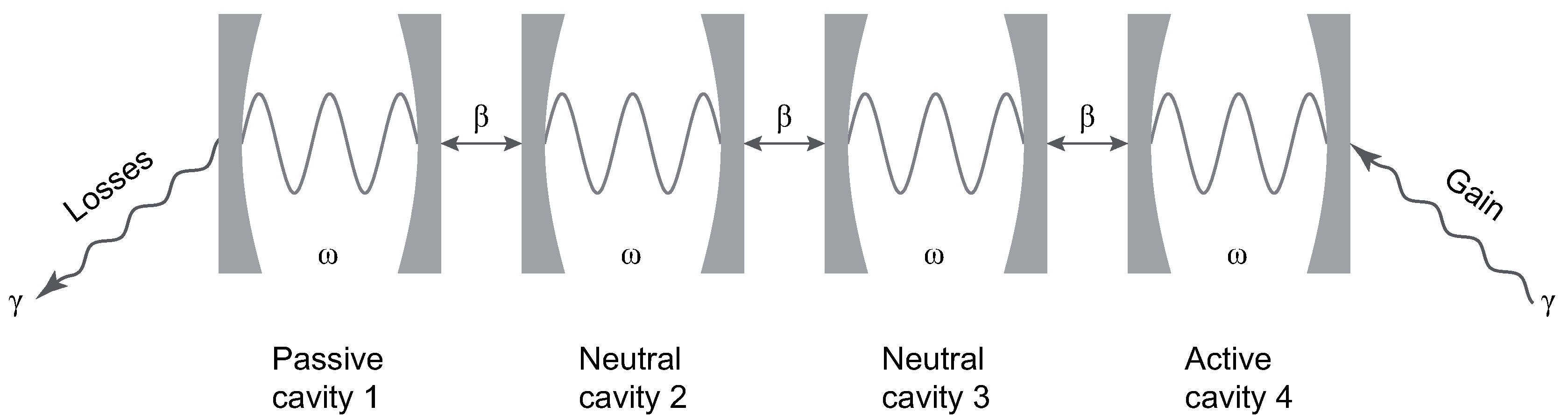
2. The Model
- ;
- ;
- ;
- ,
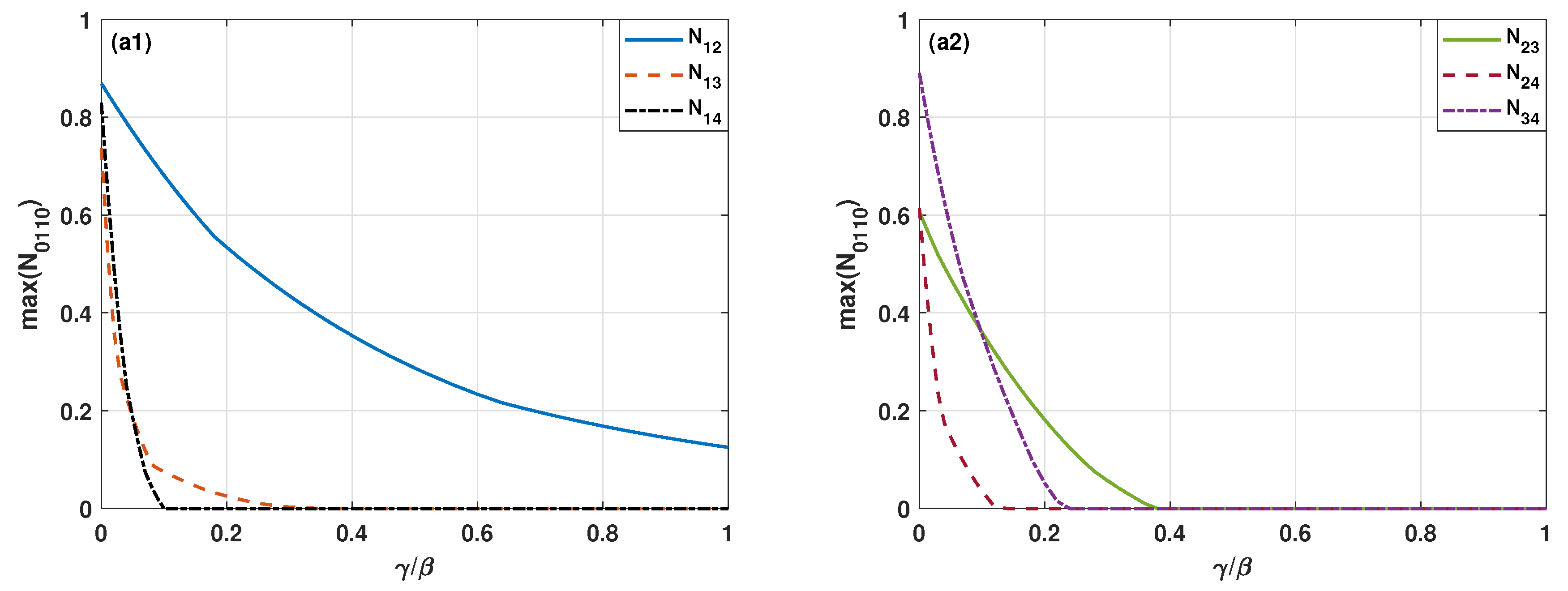
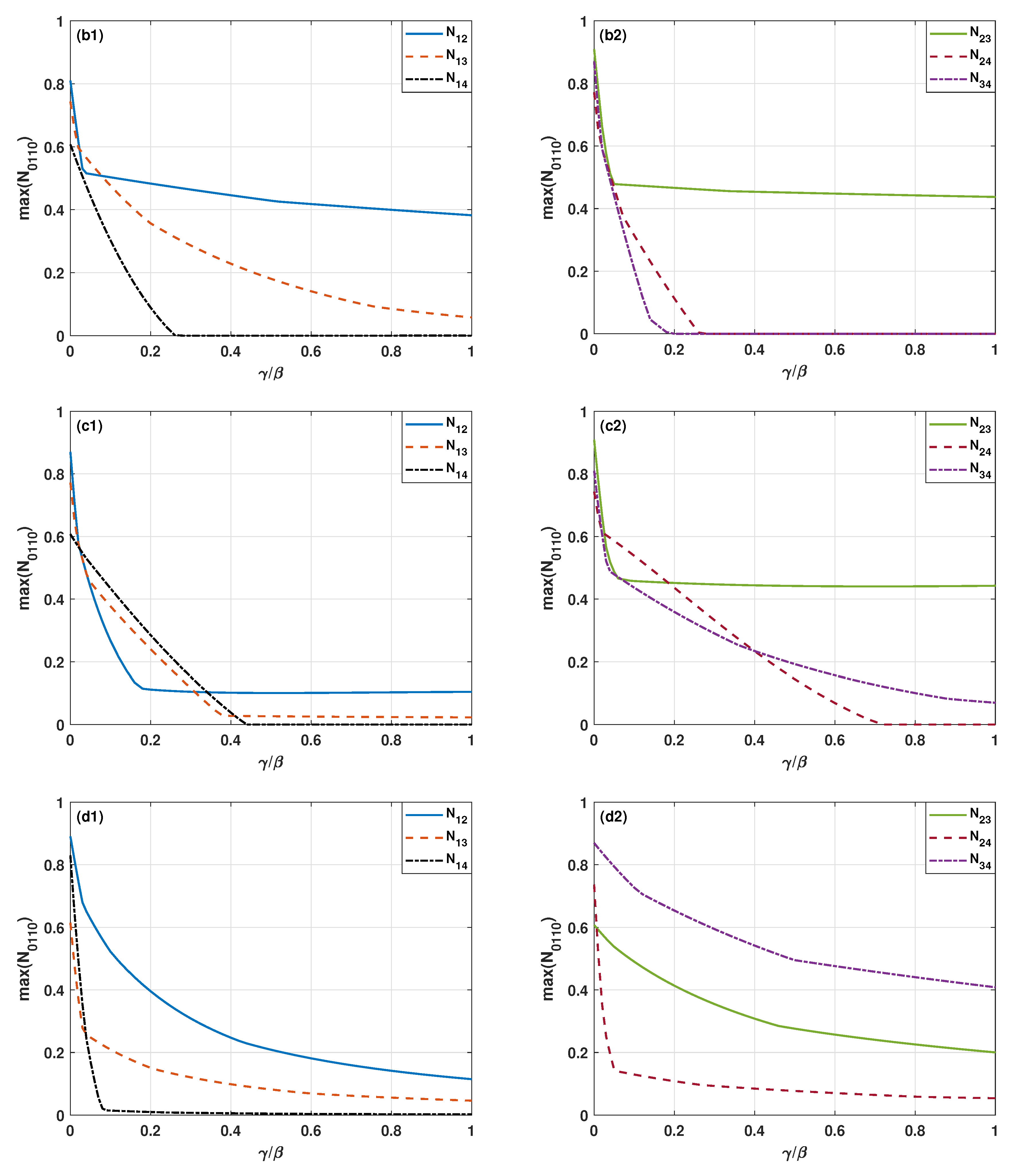
3. The Entanglement Generation
4. Conclusions
Funding
Conflicts of Interest
References
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex Extension of Quantum Mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef] [PubMed]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical -symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef] [PubMed]
- Ramezani, H.; Schindler, J.; Ellis, F.M.; Günther, U.; Kottos, T. Bypassing the bandwidth theorem with symmetry. Phys. Rev. A 2012, 85, 062122. [Google Scholar] [CrossRef]
- Miri, M.A.; Regensburger, A.; Peschel, U.; Christodoulides, D.N. Optical mesh lattices with symmetry. Phys. Rev. A 2012, 86, 023807. [Google Scholar] [CrossRef]
- Graefe, E.M.; Jones, H.F. -symmetric sinusoidal optical lattices at the symmetry-breaking threshold. Phys. Rev. A 2011, 84, 013818. [Google Scholar] [CrossRef]
- Tchodimou, C.; Djorwe, P.; Nana Engo, S.G. Distant entanglement enhanced in -symmetric optomechanics. Phys. Rev. A 2017, 96, 033856. [Google Scholar] [CrossRef]
- Turitsyna, E.G.; Shadrivov, I.V.; Kivshar, Y.S. Guided modes in non-Hermitian optical waveguides. Phys. Rev. A 2017, 96, 033824. [Google Scholar] [CrossRef]
- Zhang, L.L.; Gong, W.J. Transport properties in a non-Hermitian triple-quantum-dot structure. Phys. Rev. A 2017, 95, 062123. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Invisibility and symmetry. Phys. Rev. A 2013, 87, 012103. [Google Scholar] [CrossRef]
- Lü, X.Y.; Jing, H.; Ma, J.Y.; Wu, Y. -Symmetry-Breaking Chaos in Optomechanics. Phys. Rev. Lett. 2015, 114, 253601. [Google Scholar] [CrossRef] [PubMed]
- Mostafazadeh, A. Pseudo-Hermiticity versus symmetry: the necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 2002, 43, 205. [Google Scholar] [CrossRef]
- Bender, C.M.; Gianfreda, M.; Özdemir, C.K.; Peng, B.; Yang, L. Twofold transition in -symmetric coupled oscillators. Phys. Rev. A 2013, 88, 062111. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Khajavikhan, M.; Ge, L. Exceptional points and lasing self-termination in photonic molecules. Phys. Rev. A 2014, 90, 013802. [Google Scholar] [CrossRef]
- Demange, G.; Graefe, E.M. Signatures of three coalescing eigenfunctions. J. Phys. A Math. Theor. 2011, 45, 025303. [Google Scholar] [CrossRef]
- Heiss, W.D.; Cartarius, H.; Wunner, G.; Main, J. Spectral singularities in -symmetric Bose-Einstein condensates. J. Phys. A Math. Theor. 2013, 46, 275307. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Clustering of exceptional points and dynamical phase transitions. Phys. Rev. A 2016, 93, 042116. [Google Scholar] [CrossRef]
- Pick, A.; Lin, Z.; Jin, W.; Rodriguez, A.W. Enhanced nonlinear frequency conversion and Purcell enhancement at exceptional points. Phys. Rev. B 2017, 96, 224303. [Google Scholar] [CrossRef]
- Lin, Z.; Pick, A.; Lončar, M.; Rodriguez, A.W. Enhanced Spontaneous Emission at Third-Order Dirac Exceptional Points in Inverse-Designed Photonic Crystals. Phys. Rev. Lett. 2016, 117, 107402. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Resonances in open quantum systems. Phys. Rev. A 2017, 95, 022117. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Yuan, J.; Kang, M.; Chen, J. High-order exceptional points in non-Hermitian Moiré lattices. Front. Phys. 2019, 14, 53603. [Google Scholar] [CrossRef]
- Pick, A.; Zhen, B.; Miller, O.D.; Hsu, C.W.; Hernandez, F.; Rodriguez, A.W.; Soljačić, M.; Johnson, S.G. General theory of spontaneous emission near exceptional points. Opt. Express 2017, 25, 12325–12348. [Google Scholar] [CrossRef] [PubMed]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, C.K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-induced suppression and revival of lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Helmerson, K.; You, L. Entanglement and spin squeezing of Bose-Einstein-condensed atoms. Phys. Rev. A 2003, 68, 043622. [Google Scholar] [CrossRef]
- Vidal, J.; Palacios, G.; Aslangul, C. Entanglement dynamics in the Lipkin-Meshkov-Glick model. Phys. Rev. A 2004, 70, 062304. [Google Scholar] [CrossRef]
- Mohamed, A.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
- Miranowicz, A.; Özdemir, Ş.K.; Liu, Y.X.; Koashi, M.; Imoto, N.; Hirayama, Y. Generation of maximum spin entanglement induced by a cavity field in quantum-dot systems. Phys. Rev. A 2002, 65, 062321. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P. Quantum Computations with Cold Trapped Ions. Phys. Rev. Lett. 1995, 74, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- Kurpas, M.; Dajka, J.; Zipper, E. Entanglement of qubits via a nonlinear resonator. J. Phys. Condens. Matter 2009, 21, 235602. [Google Scholar] [CrossRef] [PubMed]
- Alexanian, M. Dynamical generation of maximally entangled states in two identical cavities. Phys. Rev. A 2011, 84, 052302. [Google Scholar] [CrossRef]
- Almutairi, K.; Tanaś, R.; Ficek, Z. Generating two-photon entangled states in a driven two-atom system. Phys. Rev. A 2011, 84, 013831. [Google Scholar] [CrossRef]
- Owen, E.T.; Dean, M.C.; Barnes, C.H.W. Generation of entanglement between qubits in a one-dimensional harmonic oscillator. Phys. Rev. A 2012, 85, 022319. [Google Scholar] [CrossRef]
- Brida, G.; Chekhova, M.; Genovese, M.; Krivitsky, L. Generation of different Bell states within the spontaneous parametric down-conversion phase-matching bandwidth. Phys. Rev. A 2007, 76, 053807. [Google Scholar] [CrossRef]
- Coto, R.; Orszag, M.; Eremeev, V. Generation and protection of a maximally entangled state between many modes in an optical network with dissipation. Phys. Rev. A 2016, 93, 062302. [Google Scholar] [CrossRef]
- Ficek, Z.; Tanaś, R. Dark periods and revivals of entanglement in a two-qubit system. Phys. Rev. A 2006, 74, 024304. [Google Scholar] [CrossRef]
- Ficek, Z.; Tanaś, R. Delayed sudden birth of entanglement. Phys. Rev. A 2008, 77, 054301. [Google Scholar] [CrossRef]
- Al-Qasimi, A.; James, D.F.V. Sudden death of entanglement at finite temperature. Phys. Rev. A 2008, 77, 012117. [Google Scholar] [CrossRef]
- López, C.E.; Romero, G.; Lastra, F.; Solano, E.; Retamal, J.C. Sudden Birth versus Sudden Death of Entanglement in Multipartite Systems. Phys. Rev. Lett. 2008, 101, 080503. [Google Scholar] [CrossRef] [PubMed]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413–1415. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalaga, J.K.
The Entanglement Generation in
Kalaga JK.
The Entanglement Generation in
Kalaga, Joanna K.
2019. "The Entanglement Generation in
Kalaga, J. K.
(2019). The Entanglement Generation in




