Abstract
We report a new family of time-dependent single-qubit radiation fields for which the correspondent evolution operator can be disentangled in an exact way via the Wei–Norman formalism. Such fields are characterized in terms of the Mathieu functions. We show that the regions of stability of the Mathieu functions determine the nature of the driving fields: For parameters in the stable region, the fields are oscillating, being able to be periodic under certain conditions. Whereas, for parameters in the instability region, the fields are pulse-like. In addition, in the stability region, this family admits solutions for evolution loops in quantum control. We obtain some prescriptions to reach such a control effect. Geometric phases in the evolution are also analyzed and discussed.
1. Introduction
Exactly solvable models are valuable in quantum mechanics even though the number of cases is very limited. In the case of two-level systems (or qubits), some solutions are well-known and longstanding [1,2,3]. However, the interest in the control of these systems has recently increased due to its potential applications in quantum computation and quantum information [4]. Since the goal is to achieve precise control operations, one should deal with time-dependent driving fields in general. In this context, it is worth mentioning that the design of high-fidelity control operations is required [5,6] and some techniques, such as the adiabatic rapid passage, have been proposed [7]. Nevertheless, the analytical solution for an arbitrary driving field is still an open problem.
The dynamics of a system are determined by the correspondent dynamical law, the interactions to which it is subjected, as well as the initial conditions. However, an alternative approach to obtain exact solutions to such a dynamical law is constituted by the so-called inverse techniques in which some aspects of the dynamics are prescribed and then the interactions are found. This scheme has been widely used to deal with the control of two-level systems through time-dependent radiation fields [8,9,10,11]. Recently, a method to generate new solutions to the one qubit dynamical problem has been proposed within this framework. By requiring that the time-evolution operator be exactly factorized as a product of independent exponential factors involving only one Lie algebra generator, new families of time-dependent driving fields are obtained [12]. The evolution-operator disentangling problem lies in the Wei–Norman theorem context [13]. In the case of the algebra, it is well-known that the direct factorization problem is equivalent to solving a parametric oscillator-like equation whose solutions are known in a limited number of cases [14,15,16,17]. Thus, in the inverse solution proposed in [12], one departs from certain known solutions of such an equation and then the driving fields are determined. Accordingly, the dynamics is sensitive to the nature of such solutions.
The main purpose of the present paper is twofold. First, we obtain new families of analytically solvable driving fields using the formalism presented in [12]. Within this framework we show that the dynamics of one qubit interacting with such a family is closely related to the Mathieu functions properties. Second, we present an analysis on the correspondent dynamics. The interest in Mathieu functions lies in the fact that they are widely used in several branches of physics. They have emerged throughout physics mainly in systems with elliptic symmetry or those involving periodic or oscillating behavior. Initially, they were found by Mathieu in 1868 when he studied the oscillating modes of an elliptical membrane [18]. Since then, extensive theoretical work has been done studying their mathematical properties [19]. This has permitted the application of Mathieu functions to study diverse kinds of systems such as elliptical optical waveguides [20], propagation of invariant optical beams [21], the dynamics of electrons in periodic lattices [22], spectral singularities in symmetric potentials in quantum mechanics [23], and Aharonov–Bohm oscillations [24], among others.
The present work is organized as follows. In Section 2, the method to generate exactly solvable driving fields is revisited. We discuss in Section 3 the dynamics of a two-level system interacting with a family of precessing fields with oscillating amplitude generated using this formalism. When the dynamics is solved, we can request the condition to get a cyclic evolution for any initial state in the form of an evolution loop [25,26]. In Section 4, we get the prescriptions of such effect in terms of the dynamical parameters warranting the cyclic behavior for any initial state under the dynamics. An additional analysis on the geometric phase behavior is then conducted. Finally, conclusions and some perspectives are presented in Section 5.
2. Analytically Solvable Driving Fields
This Section is devoted to presenting the formalism to construct driving fields for which the time-evolution operator is exactly factorized. We first consider the two-level system ruled by the time-dependent Hamiltonian
where and are the three generators of the algebra defined in terms of the three traditional Pauli operators as follows: . Furthermore, the interaction of the qubit with a classical field is described by the complex-valued function V. The correspondent time-evolution operator U is a solution of the equation
As the Hamiltonian (1) is a linear combination of the algebra generators, the Wei–Norman theorem [13] establishes that the time-evolution operator can be written in the form
where the factorization functions , f, and satisfy the following coupled system of non-linear equations:
with the initial conditions . By developing the algebra in the exponential operators, it is an easy task to demonstrate that
where the operator in (5) has linked conditions fulfilled by , and . In fact, the unitary condition on : implies that conditions , and are pure imaginary and fulfill together if at least two of them are requested, which can be proved directly. Analytical solutions of System (4) are found in a limited number of cases [14]. However, in [12], a formalism to generate exact solutions for the disentangling problem has been developed. In such an approach, the radiation field is given by , where the function R reads
here, the real parameter is going to be fixed by the initial conditions and the real-valued function satisfies the Ermakov equation
For reasons to be clarified later, the real number is called the generalized Rabi frequency. Furthermore, the initial conditions are determined by the logarithm derivative of (6) at
where , and without loss of generality we take . Thus, once and are provided as free parameters, the initial conditions are established. Indeed, given such that , it is found that and . It is a well-known fact that a particular solution to Equation (7) is related to the parametric-like equation [27,28]:
where is a real-valued function and the initial conditions read
The former expression is equivalent to the initial condition (see [14] for details). According to Pinney (alternatively Ermakov), if u and v are two linear independent solutions of (9), then
is a solution of (7). Furthermore, , , , , and W stands for the Wronskian of u and v. In addition, note that is also a free parameter to be specified and the function solves the factorization problem [12,14]. Indeed,
The time-evolution of a state can be straightforwardly computed. Because an instance if the qubit’s initial state is , at any time the state of the system reads
An important physical observable is the atomic population inversion defined as . For a general state , the population inversion reads . This quantity is defined on the interval . In fact, for the largest (lowest) possible value of , the state is in the excited (ground) state with certainty. In general, for positive (negative) values of the population inversion the probability of finding the state in the upper (lower) energy state is larger. In the Rabi model, the population inversion is a periodic function of time where field amplitude and detuning (the gap between the field frequency and the spacing level energy of the atom) determine the oscillation period [12,14,29].
We finish this section by summarizing the method: One should start with the second-order differential Equation (9) choosing such that the solutions are known. The function is then obtained via the Ermakov–Pinney solution and so it is possible to generate families of analytically solvable driving fields (6) for which the initial conditions constitute free parameters to control the dynamics. Some examples have been reported in [12]. For instance, if is a negative real constant, the correspondent driving field is a decaying one. However, a precessing field with oscillating amplitude is achieved if is a positive real constant . Such a family of control fields constitutes a generalization of the circularly polarized field, which is obtained as a particular case of this model.
3. Dynamics in a Precessing Field with Oscillating Amplitude
In this section, we report a new family of driving fields for which the time-evolution operator is exactly disentangled. We consider the function in the parametric oscillator-like Equation (9), which can be written as a Mathieu equation [19,30] as follows:
where the identity has been used and
Furthermore, the following initial conditions read , where and . According to (11), the function can be written as
where has been determined considering , . Note that these particular expressions for the initial conditions retrieve the well-known Rabi frequency in the problem of a qubit interacting with a circularly polarized field. Furthermore, it is easy to prove that the Wronskian W does not depend on t.
In most cases, the two linearly independent solutions of the Mathieu Equation (16) can be written in terms of the even and odd Mathieu functions and [19]. As is clarified in the next section, we restrict ourselves to this case.
3.1. The Dynamics of Driving Fields and the Theory of Mathieu Functions
In this section, we study the behavior of the solution (18) of the Ermakov Equation (7) as a function of t, but also as a function of its parameters. The behavior of the driving fields can be very different depending on the values of the frequencies and . Moreover, can be a periodic, non-periodic, oscillating, or pulsed-like function of time. In this respect, the theory of Mathieu functions will be useful.
Given a value of the parameter q of the Mathieu Equation (16), there exist values of a for which the Mathieu functions can be periodic, bounded, or unbounded [19]. When the Mathieu function () is periodic, the values of a are called characteristic values and they are denoted by (), becoming functions of the parameter q
where are given in [19]. The parameter
is called the characteristic exponent and it determines the periodic properties of the Mathieu functions. The even Mathieu function is periodic with period or if the characteristic exponent r can be written as , or , respectively, where . The odd Mathieu function is periodic with period or if r can be written as , or , respectively [19]. When r is an integer , then the Mathieu functions and are not solutions to the same Mathieu equation. On the other hand, when r is not an integer, holds. Then, and are solutions to the same Mathieu equation, and moreover, they are linearly independent [19]. Considering r as a positive rational number, then, it can be written as , where is an integer and , s are relative prime integers. Hence, Mathieu functions and are periodic with period , for . On the other hand, if r is an irrational number, Mathieu functions are not periodic but bounded functions which do not decay to zero as [19].
We define the space as the two dimensional space in which q and a are the abscissa and ordinate, respectively. The behavior of the Mathieu functions is dictated by the region of the space in which the point lies, and so the discussion of the previous paragraph can be summarized into a picture in the space as follows. As mentioned above, the characteristic values are functions of q, therefore in the space, the curves of and lie there as functions of q. Such curves are from now on called the characteristic curves. In Figure 1a, the behavior of the characteristic curves can be observed in the space for different integer values of r, while in Figure 1b, the case is shown with several non-integer values of r. The characteristic curves for all non-integer positive values of r, a case in which , saturate a certain region of the space [19] which is shown shaded in Figure 1b. This region, along with the characteristic curves of integer values of r, is known as the region of stability of the Mathieu functions. A Mathieu function is called stable if it is bounded or tends to zero as , as well as it is called unstable if it diverges as . Therefore, if the point lies inside (outside) the region of stability, the corresponding Mathieu function is a bounded (unbounded) function of t. Regarding Equation (17), it can be observed that can be written as . Taking a as a characteristic value , can be considered as a characteristic frequency (value), in the sense that
in the analog space, since . Figure 2 shows the behavior of the characteristic curves in the space.
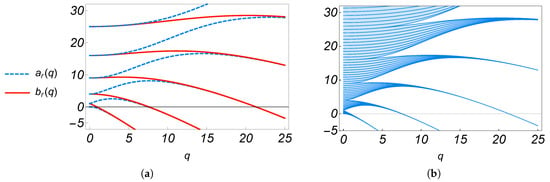
Figure 1.
(a) The characteristic values (blue-dashed curves) for , and (red curves) for , as functions of q, for several values of . Note that . (b) The shaded region is produced by all the characteristic curves with non-integer characteristic values r, case in which .
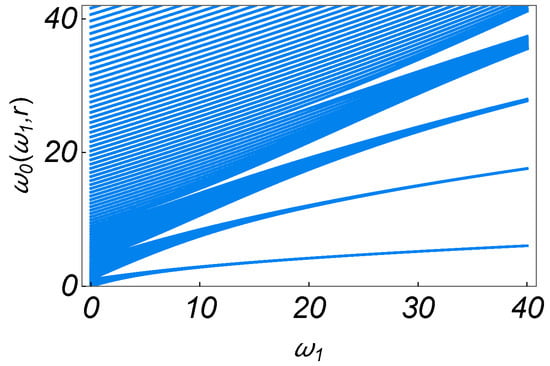
Figure 2.
The characteristic frequency as functions of , for several rational values of r.
Nevertheless, we are interested in the two linearly independent solutions of the Mathieu equation conforming to the Ermakov equation solution . Then, we must separate the space into two regions: the one in which both linearly independent solutions are stable, which will be denoted as ; and the one in which at least one of the two solutions is unstable, represented by . In region , the function is a bounded function of t, while in the region , is unbounded, as can be observed from Equation (18).
As mentioned above, within the stability region, there exist two cases: (i) the characteristic exponent r is not an integer; and () it is an integer. In case (i), both Mathieu functions and are linearly independent stable solutions of
the Mathieu Equation (16). In case (), the second linearly independent solution as well as the second linearly independent are unstable [19]. On the other hand, in the instability region, both linearly independent solutions of the Mathieu equation are unbounded. Therefore, can be described as the region of the space in which the characteristic values r are positive non-integers
(see Figure 2), namely
where is the characteristic value as function of , see Equation (17). Let us denote by the set of points of the characteristic curves for integer values of (denoted in Figure 1a), so the stability region in the space can be written as (note that the set is part of the boundary of (see Figure 1)). Since this is case , one of the solutions to the Mathieu equation is unstable, then . Hence, within , there are two cases: the point belongs to the unstable region or to .
For simplicity, we focus on the case in which can be written in terms of the Mathieu functions and . This case includes the whole region as well as (unstable region case), that is to say, we are excluding the points in . Nevertheless, as the second solutions in are unstable, the asymptotic behavior of for for is similar whether belongs to or not.
Since Equation (16) is invariant under a complex conjugate operation the real or imaginary part of any of its solutions is also a solution and being a real-valued function, it can be written as
where we have defined , , and (the dependence on the frequencies , has been omitted for shortness) in order to satisfy the initial conditions stated in Equation (10) and the ones mentioned after Equation (18). Furthermore, W denotes the Wronskian of two functions. Then, the driving field can be written as
In order to write the factorizing functions, we have to obtain the solution to the parametric oscillator-like Equation (16), satisfying the initial conditions (8), which can be written as
where . The factorizing functions can be written as
where
Now, we are able to calculate the time-evolution of the initial state given in (15). As commented previously, population inversion, is a physical quantity very useful and descriptive for two-level systems with respect to the system dynamics. It depicts, for the quantum state, the dynamical variation between the excited state () and the base state (). Thus, in our case, the population inversion can be written after some algebra as
3.1.1. Driving Fields in the Region
In this case, the solution to Ermakov equation is a time oscillating function that can be periodic if the characteristic exponent r is a rational number. Hence, the driving field , as well as V, is an oscillating function which becomes periodic when the parameters g, , , and the characteristic exponent r satisfy the condition [12]
where p is a natural number and is the period of . Solutions exhibit lots of possibilities due to the set of physical parameters , and (as well as instead of ). They could be selected or highlighted to get several possible control effects: periodicity in the field , the reaching of evolution loops, or simply the control of population inversion. We analyze several of these effects separately in the following sections of the article.
Figure 3 shows three examples of periodic driving fields and their associated population inversion. In these cases, the characteristic exponent r is a rational number, so the associated is periodic and the parameters g and are such that is a periodic function of time. Furthermore, in order to show the time flow correspondence between the left plots with the right ones, a color scale from blue to red has been used. As can be observed from Figure 3b,e, each minimum of the population inversion barely corresponds to a local maximum of the transverse driving field amplitude . Furthermore, the non-negative parameter p is related to the number of “petals” in each flower-like structure of the driving field. In [12], it is shown that our model can describe a two-level system interacting with a magnetic transverse field . It is easy to show that real and imaginary parts of are nothing other than the field components performing a certain rotation. This fact is due to the transverse field causing the state to instantaneously precess around the direction of the entire field, the direction of such precession becomes more horizontal while . Thus, when the relative orientation between the field direction and the state direction on the Bloch sphere becomes more perpendicular, the states rotates more extremely on the sphere, being able to reach a more extreme position there, just as it happens in the case of a circularly polarized field [31]. These rotations becomes more effective the bigger the field is because the instantaneous angular frequency depends on it. When the value of the parameter is changed, with the others held constant, an oscillatory non-periodic driving field is obtained (see the continuous blue curves in Figure 4). In this case, the changes in the amplitude of the driving field are not fast enough for the population inversion to reach its minimum value −1. Now, by only increasing the parameter g and holding the others fixed (the magnitude of is proportional to ), we observe in Figure 4 (red dashed curves) that the changes in the amplitude of the driving field are increased with respect to the previous case, pushing the increment of the range of the peaks of the population inversion towards . The positions of the maxima of the population inversion remain unchanged. We can conclude, in this case, that as the parameter g increases, the peaks of the population inversion are sharpened, presenting a resonant-like behavior. Furthermore, in any of the previous cases, as shown at the end of Section 3.1, the population inversion is periodic.
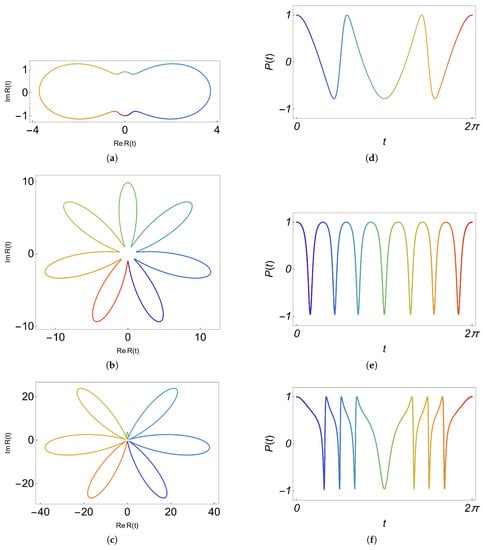
Figure 3.
The driving field (23) in the complex plane for , , (a) , , , , (b) , , , , (c) , , , . In (d–f), the corresponding population inversion is shown. All of the previous values of correspond to characteristic values of the Mathieu functions (16) with rational values of r, that is, . Time flows from blue to red matching the scale between the types of plots.
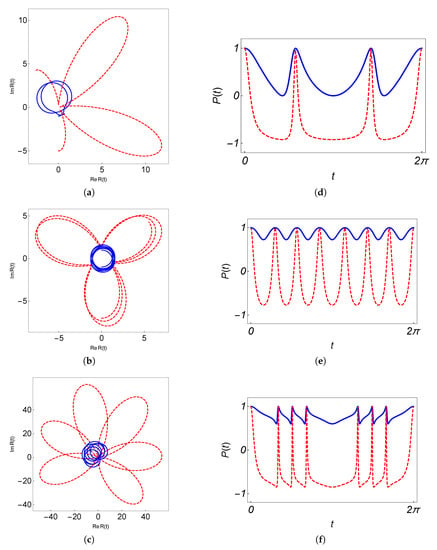
Figure 4.
The driving fields (23) in the complex plane (left column) and the associated population inversion (right column) for the cases of Figure 3, except for the values of g and , which has been increased as follows: (a,d) , (blue), and , (red dashed), (b,e) , (blue), and , (red dashed), (c,f) , (blue), and , (red dashed). The driving field precesses counterclockwise.
3.1.2. Driving Fields in the Region
As mentioned above, at least one of the Mathieu functions, which conform the solution to the Ermakov equation, is an unbounded function diverging as . In this case, we have observed that the zeros of the Mathieu functions and tend to approach each other more and more as t increases, a phenomenon known as condensation of zeros [19]. This gives rise to pulsed-like peaks in the corresponding driving field (), as can be observed in Figure 5a. Therefore, as time passes, the pulses increase their size and become narrower causing a pulsed-like behavior of the population inversion, as can be observed in Figure 5b,c.
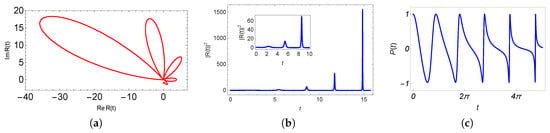
Figure 5.
(a) The driving field (23) in the complex plane. (b) Its square modulus as a function of time. The inset is a zooming of the plot for to show the correspondent local maxima, and (c) the associated population inversion with , , , , where . The driving field precesses counterclockwise.
4. Evolution Loops, Cyclic Evolution and Phases
Evolution loops are a control phenomena present in certain quantum systems admitting dynamic solutions to the restriction for some , which clearly revert the evolution after time . Furthermore, the parameter is the global phase acquired during the process. It is relevant because that reduction becomes independent from the initial states, thus, any initial state evolves after such time. These phenomena boost other intermediate effects which have value in quantum control. In this section, we show that the field being considered admits this kind of effects. In the current case, because if and , then is automatically pure imaginary, then, if in addition, , reduces exactly to . Such is the condition to reach evolution loops for some (otherwise, if only are fulfilled, the evolution reaches the initial state with a non-zero phase). Then, the procedure to find such prescriptions is based in the finding of satisfying , then by using (27), we can adjust the value of to reduce to . This is always possible due to the first two terms on the right side being independent of . Despite this, there are a lot of solutions because there are five free parameters: (otherwise ), .
Figure 6 shows three examples of such an effect from a large variation in the initial state until a smaller one in terms of parameters , and . Those parameters work in a combined way to give dynamical effects, thus, they are not related with the periodicity of , of in an exclusive way. In this sense, examples being considered are only illustrative among a wide variety of possibilities (obtained numerically upon the conditions ), but exhibiting different ranges of variation for . In any case, note that g and play an important role in such variation, as is expected. Plots on the left exhibit the value of while plots on the right show the dynamics represented on the Bloch sphere. Nevertheless, evolution loops are independent from the initial states, examples consider the initial state as the ground state, . The color changes from blue to red in agreement with the value. Note that the intermediate reaching of unitary multiples of with non-zero phases until the zero phase is reached in . The last example in Figure 6c meets the evolution loop under periodic driving field, generating a more regular dynamics around .
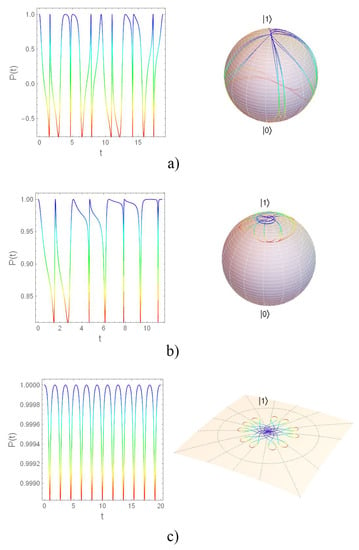
Figure 6.
Population inversion together with the dynamics represented on Bloch spheres for several prescriptions generating evolution loops. In any case, the color depicts the value of in agreement with the left plot. (a) . (b) . (c) depicting a tiny regular evolution loop with a periodic field around of .
Dynamical and Geometric Phases
It is well-known that a geometric phase exists related to a quantum system cyclic evolution governed by a slow change of parameters [32,33]. The relevance of such a phase factor lies in the foundations of quantum theory; however, it has also recently found important applications in quantum information and computation, as a part of the system evolution [34,35].
Consider the dynamic phase , as well as the Aharonov–Anandan geometric phase in evolution loop dynamics [36,37], which depicts the phase when the system returns to its initial physical state at the time (in the current case to the state ):
which even in the simplest case of a time-independent magnetic field, a non-trivial value is obtained: and , where is the relative angle between the magnetic field and the initial Bloch vector. These values are indeed independent of the field amplitude [38]. Conversely, in time-dependent cases, the dynamical trajectory on the Bloch sphere can be manipulated with respect to the field parameters, yielding different values of the geometric phase. Such is our case, as shown in the examples in the Figure 6: (a) , (b) , and (c) . In these examples, the global phase has been selected as the minimum value assuring the positivity for . The present analysis represents a first step in the construction of logical gates for holonomic quantum computation [34,35]. These results will be reported elsewhere.
5. Conclusions
We have presented the study of driving fields generated by the inverse approach given in [12], departing from a sinusoidal parametric oscillator-like equation. Regarding the solution of the associated Ermakov equation, the driving fields and the population inversion can be written in terms of the Mathieu functions. We have shown that the theory of Mathieu functions is determinant in the dynamical analysis of such driving fields, as a clear split in two regions for the space of the frequencies and is acquired. Thus, different dynamical behaviors of the driving fields are shown. In the region , we have shown that the driving fields have an oscillatory nature, but they can still be periodic or non-periodic depending on the value of the parameters g and given by a precise prescription obtained analytically. In this same region, the population inversion is periodic provided that the associated Mathieu functions are also periodic. In the complement of the previous region, for example , the behavior of the driving fields is pulse-like; with the amplitude and sharpness of their peaks increasing in time, yielding a resonant-like behavior for the associated population inversion. We consider that this system presents the advantage of having several kinds of dynamics that can be prescribed on demand by fine tuning the frequencies and (alternatively a or q) of the parametric oscillator-like potential. Together, we showed that evolution loop solutions are numerically achievable and the correspondent geometric phases can be calculated. Our study represents the first stage in the development of technological applications involving single-qubit devices. For instance, in some many-body models, precise selective control operations on single qubits are required, which could be achievable through the driving fields obtained in this work. Such analysis will be reported elsewhere. We hope our results shed some light on the matter.
Author Contributions
Investigation, M.E., A.J.-N. and F.D.; Writing—original draft, M.E., A.J.-N. and F.D.; Writing—review & editing, M.E., A.J.-N. and F.D.
Funding
The support of CONACyT through project A1-S-24569 is acknowledged.
Acknowledgments
M.E. and F.D. would like to acknowledge to School of Engineering and Science of Tecnologico de Monterrey as well as the financial support of Novus Grant with PEP no. PHHT023_17CX00001, TecLabs, Tecnologico de Monterrey, Mexico, in the production of this work. A.J.-N. thanks the support of INAOE and CICESE.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rabi, I. Space quantization in a gyrating magnetic field. Phys. Rev. 1937, 51, 652. [Google Scholar] [CrossRef]
- Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. A 1932, 137, 696–702. [Google Scholar] [CrossRef]
- Schwinger, J. On non-adiabatic processes in inhomogeneous fields. Phys. Rev. 1937, 51, 648. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zeng, J.; Barnes, E. Fastest pulses that implement dynamically corrected single-qubit phase gates. Phys. Rev. A 2018, 98, 012301. [Google Scholar] [CrossRef]
- Motzoi, F.; Wilhelm, F.K. Improving frequency selection of driven pulses using derivative-based transition suppression. Phys. Rev. A 2013, 88, 062318. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Resonant shortcuts for adiabatic rapid passage with only z-field control. Phys. Rev. A 2019, 100, 012111. [Google Scholar] [CrossRef]
- Fernández, D.J.; Rosas-Ortiz, O. Inverse techniques and evolution of spin-1/2. Phys. Lett. A 1997, 236, 275. [Google Scholar] [CrossRef]
- Barnes, E.; Das Sarma, S. Analytically solvable driven time-dependent two-level quantum systems. Phys. Rev. Lett. 2012, 109, 060401. [Google Scholar] [CrossRef]
- Vitanov, N.V. Complete population inversion by a phase jump: An exactly soluble model. New J. Phys. 2007, 9, 58. [Google Scholar] [CrossRef]
- Messina, A.; Nakazato, H. Analytically solvable Hamiltonians for quantum two-level systems and their dynamics. J. Phys. A Math. Theor. 2014, 47, 445302. [Google Scholar] [CrossRef]
- Enríquez, M.; Cruz, S.C.y. Exactly Solvable One-Qubit Driving Fields Generated via Nonlinear Equations. Symmetry 2018, 10, 567. [Google Scholar] [CrossRef]
- Wei, J.; Norman, E. Lie algebraic solution of linear differential equations. J. Math. Phys. 1963, 4, 575–581. [Google Scholar] [CrossRef]
- Enríquez, M.; Cruz, S.C.y. Disentangling the time-evolution operator of a single qubit. J. Phys. Conf. Ser. 2017, 839, 012015. [Google Scholar] [CrossRef]
- Datolli, G.; Solimeno, S.; Torre, A. Algebraic time-ordering technics and harmonic oscillator with time-dependent frequency. Phys. Rev. A 1986, 34, 2646. [Google Scholar] [CrossRef] [PubMed]
- Datolli, G.; Torre, A. SU(2) and SU(1,1) time-ordering theorems and Bloch-type equations. J. Math. Phys. 1987, 28, 618. [Google Scholar] [CrossRef]
- Datolli, G.; Richetta, M.; Torre, A. Evolution of SU(2) and SU(1,1) states: A further mathematical analysis. J. Math. Phys. 1988, 29, 2586. [Google Scholar] [CrossRef]
- Mathieu, É. Le mouvement vibratoire d’une membrane de forme elliptique. J. Math. Pures Appl. 1868, 13, 137–203. [Google Scholar]
- McLachlan, N.W. Theory and Application of Mathieu Functions; Oxford University Press: London, UK, 1951. [Google Scholar]
- Li, S.; Wang, B.S. Field expressions and patterns in elliptical waveguides. IEEE Trans. Microw. Theory Tech. 2000, 48, 864–867. [Google Scholar]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Carver, T.R. Mathieu’s functions and electrons in a periodic lattice. Am. J. Phys. 1971, 39, 1225–1231. [Google Scholar] [CrossRef]
- Sinha, A.; Roychoudhury, R. Spectral singularity in confined symmetric optical potential. J. Math. Phys. 2013, 54, 112106. [Google Scholar] [CrossRef]
- Bruno-Alfonso, A.; Latgé, A. Aharonov-Bohm oscillations in a quantum ring: Eccentricity and electric-field effects. Phys. Rev. B 2005, 71, 125312. [Google Scholar] [CrossRef]
- Mielnik, B. Evolution loops. J. Math. Phys. 1986, 27, 2290–2306. [Google Scholar] [CrossRef]
- Delgado, F.; Mielnik, B. Are there Floquet quanta? Phys. Lett. A 1998, 249, 369–375. [Google Scholar] [CrossRef]
- Pinney, E. The nonlinear differential equation y′′ + p(x)y + cy−3 = 0. Proc. Am. Math. Soc. 1950, 1, 581. [Google Scholar] [CrossRef]
- Ermakov, V.P. Second order differential equations. Conditions to complete integrability. Kiev Univ. Izvestia Ser. III 1880, 9, 125. (In Russian) [Google Scholar] [CrossRef]
- Klimov, A.B.; Chumakov, S.M. A Group-Theoretical Approach to Quantum Optics; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Gutiérrez-Vega, J.C.; Rodríguez-Dagnino, R.M.; Meneses-Nava, M.A.; Chávez-Cerda, S. Mathieu functions, a visual approach. Am. J. Phys. 2003, 71, 233–242. [Google Scholar] [CrossRef]
- Haroche, S.; Raimond, J.M. Exploring the Quantum: Atoms, Cavities, and Photons; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Anandan, J. The geometric phase. Nature 1992, 360, 307–313. [Google Scholar] [CrossRef]
- Cohen, E.; Larocque, H.; Bouchard, F.; Nejadsattari, F.; Gefen, Y.; Karimi, E. Geometric phase from Aharonov-Bohm to Pancharatnam-Berry and beyond. Nat. Rev. Phys. 2019, 1, 437–449. [Google Scholar] [CrossRef]
- Zanardi, P.; Rasetti, M. Holonomic quantum computation. Phys. Lett. A 1999, 264, 94–99. [Google Scholar] [CrossRef]
- Jones, J.A.; Vedral, V.; Ekert, A.; Castagnoli, G. Geometric quantum computation using nuclear magnetic resonance. Nature 2000, 403, 869–871. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 1987, 58, 1593–1596. [Google Scholar] [CrossRef] [PubMed]
- Menda, I.; Buric, N.; Popovic, D.B.; Prvanovic, S.; Radonjic, M. Geometric Phase for Analytically Solvable Driven Time-Dependent Two-Level Quantum Systems. Acta Phys. Polonica 2014, 126, 670–672. [Google Scholar] [CrossRef]
- Chruściński, D.; Jamiołkowski, A. Geometric Phases in Classical and Quantum Mechanics; Birkhäuser: Boston, MA, USA, 2004. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).