Abstract
Symmetrical precoding and algorithms play a vital role in the field of wireless communications and cellular networks. This paper proposed a low-complexity hybrid precoding algorithm for mmWave massive multiple-input multiple-output (MIMO) systems. The traditional orthogonal matching pursuit (OMP) has a large complexity, as it requires matrix inversion and known candidate matrices. Therefore, we propose a bird swarm algorithm (BSA) based matrix-inversion bypass (MIB) OMP (BSAMIBOMP) algorithm which has the feature to quickly search the BSA global optimum value. It only directly finds the array response vector multiplied by the residual inner product, so it does not require the candidate’s matrices. Moreover, it deploys the Banachiewicz–Schur generalized inverse of the partitioned matrix to decompose the high-dimensional matrix into low-dimensional in order to avoid the need for a matrix inversion operation. The simulation results show that the proposed algorithm effectively improves the bit error rate (BER), spectral efficiency (SE), complexity, and energy efficiency of the mmWave massive MIMO system as compared with the existing OMP hybrid and SDRAltMin algorithm without any matrix inversion and known candidate matrix information requirement.
1. Introduction
Symmetry concept is utilized in almost all communications systems and cellular network analyses, which is then transformed into various conclusive outcomes. As the main direction of the development of information, communication in the fifth-generation (5G) will penetrate into various fields of future society. It aims to provide users with higher data rates and multiple connections for many Internet-of-Things (IoT) devices. Compared with fourth-generation (4G), the spectrum efficiency of 5G communication is increased by 5–15 times, and energy efficiency and cost efficiency are improved by a hundred times [1]. Massive multiple-input multiple-output (MIMO) technology and millimeter wave (mmWave) communication technology plays an important role as the key technology of 5G. Massive MIMO technology uses multiple antenna units to transmit and receive transmission signals at both ends of the communication system [2,3,4,5,6]. Through spatial multiplexing, beamforming, precoding, and other technologies, the space resources of the wireless channel are fully utilized to improve the system Stability, reducing the system’s bit error rate, simplifying signal processing and reducing system latency. Currently, 6, 15, 18, 28, 45, 60, and 72 GHz are typical candidate bands for 5G research in the industry. The 6–100 GHz frequency range is a typical millimeter-wave band [7,8]. Communication within this range can provide higher capacity for hotspot users and support user transmission rates above 10 GB/s [9,10,11]. The millimeter-wave mainly propagates in space in the form of direct waves. The beam is narrow and has good directivity, but it is greatly affected by the environment, such as rainfall, sand, dust, etc., and the propagation distance is limited [12,13]. Since the millimeter-wave belongs to a very high frequency, the wavelength is small, and a large number of antennas can be packaged in a limited physical space. The combination of the array antenna and the precoding technology can effectively compensate for the transmission loss of the millimeter-wave, increase the transmission distance, and improve the stability of the system [14].
The use of precoding techniques in massive MIMO systems can improve the spectral efficiency of the system, reduce the bit error rate, and simplify the complexity of the receiver. In the 4G communication system, traditional digital precoding technology has been widely used. In order to achieve the maximum theoretical advantage of massive MIMO technology [15], traditional digital precoding technology needs to equip each transmitting antenna with a separate Radio Frequency (RF) link. However, in a millimeter-wave massive MIMO system, due to a large number of transmit antennas, if the traditional digital precoding technology is still used, then the system hardware cost will be too high and the system power consumption will be too large. Therefore, in millimeter-wave massive MIMO systems, hybrid precoding techniques are generally used, that is, precoding processing is divided into baseband precoding (digital precoding) processing and radio frequency precoding (analog precoding) processing [16]. The solution uses only a small number of RF links to solve the high cost and high-power consumption of traditional digital precoding.
Hybrid precoding is used to process the multiplexed signal through the baseband precoder, send it to the RF precoder through the RF link for constant mode phase shift, and then send it to the transmitting antenna for transmission. The hybrid precoding architecture of the millimeter-wave massive MIMO system can be divided into a shared array architecture and a separate sub-array architecture [17], in which each RF link of the shared array architecture is connected to all the transmit antennas, and the separated sub-arrays for each RF link of the architecture is only connected to a portion of the transmit antenna. The shared array architecture has complex hardware design and high-power consumption compared to the separate sub-array architecture, but it can fully exert the precoding performance and achieve better results. Therefore, the research in this paper is based on a shared array architecture.
In the hybrid precoding study of millimeter-wave massive MIMO systems, the literature [18] uses the transmitter and receiver to jointly design the analog beamforming vectors under the multi-resolution codebook. Literature [19] introduces beam space multiple-input multiple-output, and uses a discrete Fourier transform (DFT) beamforming vector to direct the transmitted signal to a subspace with progressively maximized received signal power. Literature [20] converts the hybrid precoding problem into a sparse reconstruction problem based on the sparsity of the millimeter-wave channel. Under the condition of perfect known channel information, a low complexity hybrid precoding algorithm is proposed by using the concept of orthogonal matching pursuit. However, the design of RF precoding in [20] requires that the candidate matrix be selected from the candidate matrix to multiply the largest product by the inner product of the residual, and the construction of the candidate matrix requires high-precision channel estimation. Upon completion, it is necessary to estimate the signal emission angle and angle of arrival, which will cause system delay and consume system resources. At the same time, the algorithm uses the least-squares method to perform matrix inversion when updating the baseband precoding. The complexity of matrix inversion increases with the number of base vectors. High dimensional matrix inversion will lead to longer calculation delay and higher power consumption. The authors in [21] proposed a semidefinite relaxation algorithm by utilizing the idea of alternating minimization, which can provide substantial performance gains for phase shifters (PSs). However, while the PSs are studied substantially, there still exist an inevitable gap compared with the performance of PSs. The authors in [22] proposed an analog PSs and spatial multiplexing by utilizing multiple RF chains connected to a fixed subset of antenna elements. This algorithm is based on analog beamforming and therefore, it lacks the ability to provide the required precoding performance for mmWave massive MIMO systems. In [23], for single-stream single-user MIMO-OFDM systems, a hybrid precoding is proposed to maximize the received signal strength.
Therefore, in view of the problems in [20,21,22], this proposed an efficient algorithm for effective precoding in mmWave massive MIMO systems.
The novel contributions of this paper are as follows:
- This study deploys bird swarm algorithm (BSA) to eliminate the need for the known candidate matrices in mmWave channel estimation as in the traditional algorithms.
- The proposed algorithm uses the characteristics of BSA with global search optimal (GSO) value to search for the largest array response vector multiplied by the residual matrix, and uses the Banachiewicz–Schur (BS) block matrix generalized inverse to transform the high-dimensional matrix into a low-dimensional matrix, avoiding matrix inversion and reducing the amount of calculation.
- It uses the results of each iteration to avoid matrix inversion and to simplify the computational complexity of the system.
2. System Model
The shared array architecture of the mmWave massive MIMO system is shown in Figure 1. The number of transmitting antennas at the transmitting end is , the number of receiving antennas at the receiving end is , the number of RF links at the transmitting end is , the number of RF links at the receiving end is , and the data streams of the transmitting end and the receiving end are both .
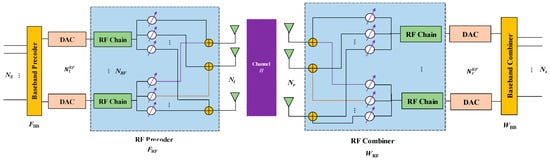
Figure 1.
Proposed array architecture of mmWave massive MIMO systems.
In order to ensure multi-stream transmission, it is necessary to satisfy and . Under this hardware structure, the signal is transmitted to the channel by the processing of the baseband precoder and the RF precoder and the transmitting signal of the transmitting end is:
where is the data stream of the signal, and ; is the transmitting signal for the transmitting end.
The received signal arriving at the receiving end antenna after channel transmission is:
where represents a Gaussian white noise with zero mean and a covariance matrix of , is the signal received by the receiving antenna, is the average received power, is the channel matrix, and .
The received signal is further processed by the RF combiner and the baseband combiner , and the received signal received by the receiver is:
where is the signal received at the receiving end. is implemented using the analog network so that it satisfies the elements , where represent the diagonal element of the matrix. Similarly, . The total power constraint at the transmitting end is .
Considering the high path loss of the mmWave channel, the sparse distribution in space, the close arrangement of the antenna array on the transceiver in the massive MIMO system, and the high correlation of the antenna elements, the traditional fading statistical channel model is not applicable. Therefore, the ray-tracing model is usually used for modeling. If the mmWave channel contains scattering clusters, with each cluster containing strip propagation paths, the channel of the system can be described as:
where represents the gain factor of the propagation path in the scattering cluster that follows a complex Gaussian distribution with zero mean and a variance of , and it satisfies , and must satisfy with as the angle of arrival (AoA). For the scattering cluster, is randomly distributed on with as the angle of departure (AoD), and for the scattering cluster, is randomly distributed on . Generally, we choose the Laplacian distribution as a random distribution; and represent the array response vectors of the transmitter and receiver, respectively.
The types of antenna arrays can be combined into various configurations depending on the arrangement of the antenna in the array. In mmWave massive MIMO systems, a uniform antenna array is generally selected to design the antennas at both ends of the transceiver. Common uniform antenna arrays have a uniform linear array (ULA) and uniform planar array (UPA). In a ULA, either the elevation or the azimuth perspective is considered, since it is a one-dimensional antenna array. The UPA is a two-dimensional antenna array, and this type of antenna arrays is preferable for mmWaves since it can accommodate more antenna elements within a small area at both the user equipment and the base station (BS). It also facilitates beamforming in an extra dimension, which results in the 3D-beamforming. For the convenience of analysis, a ULA is used in this paper. For a ULA, assuming that there are antennas on the y-axis, the array response vector can be expressed as:
where , , is the wavelength of the signal, and is the spacing between antenna elements. In an actual system, channel state information (CSI) can be known by channel estimation. In order to focus only on precoding research, assuming that the transceiver knows the CSI, the spectral efficiency of the system is:
where is the noise covariance matrix processed by the receiver and is the identity matrix of the noise. Reference [9] approximates the spectral efficiency to minimize the Euclidian distance of the hybrid precoding matrix and the all-digital precoding matrix, whereby the precoding design problem can be written as:
where is an all-digital precoding matrix, which is the first column of the right singular matrix of the channel matrix . Then, this precoding design problem can be expressed as finding the projection of on the subspace formed by the hybrid precoder set under the condition of . Similarly, the design method of the combiner at the receiving end is similar.
3. Proposed Algorithm
3.1. BSA-Based Solution
The RF precoder is constructed by the OMP-based hybrid precoding algorithm using the candidate matrix to select the largest multiplication of the inner product of the residual, wherein the candidate matrix is constructed by the antenna array response vector. By observing the structure of the array response vector, we can find that the complete array response vector can be constructed by determining the AOA, so here we use the BSA algorithm to search for the array response vector that multiplies the inner product of the residual by the maximum. BSA is a group of intelligence extracted from the social behavior and social interaction of flocks [24,25]. Birds have three main behaviors: foraging behavior, vigilance, and flight behavior. Each bird searches for food based on his own experience and the experience of the group. Each bird can switch between vigilance and foraging behavior. If a bird’s random number at (0,1) is less than the threshold , the bird will look for food. Otherwise, the bird will remain vigilant. Compared with other swarm intelligence algorithms, the BSA has fewer adjusting parameters, faster convergence speed and stronger robustness. The bird swarm algorithm has been successfully applied to multi-objective optimization of a wireless system, optimal operation of cascade networks, and flexible task scheduling. The global optimal solution for the following objective function is expressed as:
where is the correlation vector, is the residual matrix, and is the antenna array response vector. The motivation of the objective function is to determine the global optimal solution by utilizing the correlation vector, residual matrix and the antenna response vector.
where represents the position of the bird when iterating times, the total number of birds is , , and is the dimension; represents a uniformly distributed random number; and are two positive numbers, called cognitive acceleration factor and social acceleration factor; represents the best position of the bird; and represents the best position for the bird group. Birds will try to move to the center of the flock, and they will inevitably compete with each other. Therefore, each bird does not move directly to the center of the flock. These moves can be expressed as:
Among them:
where is a positive integer, that is, a randomly choose an integer between 1 and ; and are two normally distributed random numbers between [0, 2]; represents the optimal adaptation value of the bird; represents the sum of the best adaptation values of the flock; is a small constant used to avoid the divisor as 0; and represents the average of the -dimensional position of the flock. Birds may fly to another place to cope with prediction threats and foraging. When they arrive at a new location, they will look for food again. Some birds play the role of producers and look for food supplies, while others try to steal food from producers. The behavior of producers and thieves can be described as:
where represents a random number obeying the standard normal distribution, and ; is normally distributed random number between [0, 2].
3.2. The Generalized Inverse of Banachiewicz–Schur Block Matrix Based Solution
For matrix inversion, it is often replaced by the generalized inverse of Banachiewicz–Schur block matrix. It converts the high-dimensional matrix into a low-dimensional matrix and updates it with the result of the previous iteration to avoid matrix inversion and reduce the amount of computation. For convenience, we define as:
where is an matrix whose column consists of the array’s response vector at the transmitting end, and are two arbitrary index sets, and is a sub-array consisting of an index set of . In addition, let , be the index set of the base vector selected in the iteration. Therefore, the least squares solution can be rewritten as:
Applying the Banachiewicz–Schur block matrix generalized inverse to the matrix in Equation (14), the matrix can be written as:
where
where is the index of the currently selected base vector, is the inverse matrix obtained from iterations, is an auxiliary vector of , and is an auxiliary scaler of the generalized inverse of the block matrix. By directly using the previous iteration, , can be reduced to matrix multiplication, matrix addition, and a reciprocal of a real number. Therefore, the calculation of can skip the calculation of with the calculation results of the previous iteration. is defined as the least square’s solution matrix in the iteration, which can be decomposed into:
where is an auxiliary vector of , which is expressed as:
where is the correlation matrix of the base vector and the initial residual matrix . Therefore, Equation (18) can be simplified to:
In summary, , , and can all be updated simultaneously using the auxiliary variables and the calculation results of the previous iteration. This replaces the process of matrix inversion to reduce the amount of computation.
3.3. Algorithm Flow
The proposed Algorithm 1 uses Equation (1) as the fitness function and uses the BSA algorithm to find the global optimal value of Equation (1) in order to transform the high-dimensional matrix into a low-dimensional matrix by using the Banachiewicz–Schur block matrix generalized inverse to avoid matrix inversion.
The specific steps of the proposed bird swarm algorithm (BSA) based matrix-inversion bypass (MIB) orthogonal matching pursuit (BSAMIBOMP) algorithm flow is as follows in Algorithm 1.
| Algorithm 1 BSAMIBOMP Algorithm |
| Input: Optimal unconstrained precoder . |
Output: RF precoder ; baseband precoder .
|
3.4. Computational Complexity Analysis
The complexity of designing a hybrid precoding matrix is discussed in detail and compared with the hybrid precoding method based on the OMP algorithm in [15]. It is mainly divided into two phases: In the first phase, the initial RF precoding matrix is designed, and the complexity is . In the second stage, the initial precoding matrix is updated. Then, the digital precoding matrix design and the residual matrix are designed, which are the same as those in the OMP based algorithm, and the complexity is and respectively. The next step is mainly to process the residual matrix to construct a new RF precoding vector n. Its complexity is . Combining these two phases, the overall complexity of the proposed BSAMIBOMP precoding method is . For the sake of analysis and comparison, it is assumed that the number of elements in the candidate vector set in the OMP algorithm is . In the OMP algorithm, the hybrid precoding method based on the OMP algorithm first uses the calculation of the correlation between the candidate vector matrix and the residual matrix to select the appropriate atom, the complexity and respectively. Then, the digital precoding matrix and the residual matrix are designed, and the complexity has been given. Finally, the residual matrix is normalized and the complexity is . Based on the analysis of each part, the overall complexity of the OMP algorithm in [15] is mainly concentrated on the calculation of the correlation between the candidate vector set matrix and the residual matrix, which is . According to the actual condition, , the algorithm complexity of hybrid precoding design is linear with the number of antennas. Therefore, compared with the hybrid precoding method based on the OMP algorithm, the proposed BSAMIBOMP precoding complexity is lower. Table 1 summarizes the complexity of the algorithms.

Table 1.
Complexity Comparison.
4. Numerical Simulation Analysis
In order to verify the performance of the proposed hybrid precoding Algorithm 1, this section gives the simulation results of full-digital precoding, analog precoding, and OMP-based hybrid precoding, and compares them with the proposed Algorithm 1 in mmWave massive MIMO systems. The simulation parameters are shown in Table 2. We used MATLAB R2017a for simulations, while the results are averaged over 1000 random channel implementations.

Table 2.
Simulation Parameters.
Figure 2 shows the difference in spectral efficiency (SE) with SNR for different precoding algorithms with antennas at the transmitter, antennas at the receiver, and . It can be seen from Figure 2a,b that as the SNR increases, the spectral efficiency of the different precoding algorithms in improved to different degrees, and as the data streams increase, the spectral efficiency of different precoding will be improved to varying degrees. For digital data streams, the full-digital precoding algorithm performs best because it is optimal precoding, and all precoding is aimed at approaching it. The proposed BSAMIBOMP algorithm performs better than the traditional OMP-based hybrid precoding algorithm as it eliminates the matrix inversion operation and candidate matrix requirement. Also, the proposed algorithm outperforms traditional hybrid OMP precoding as it utilizes the BSA algorithm to search for the global optimal solution, while the traditional OMP-based precoding algorithm uses the candidate matrix to select the column with the highest correlation. However, there is an interval between the angles of each column in the candidate matrix, so the selected array response vector is not necessarily the global optimal solution. The analog precoding performance is the worst because the analog precoding is constant modulus; only the phase characteristics are utilized, and the amplitude characteristics are not utilized. Therefore, the proposed algorithm can achieve better results under .
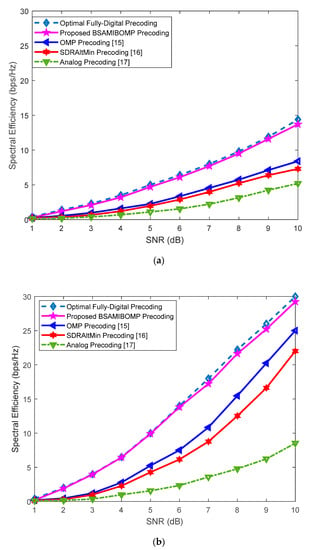
Figure 2.
Comparison of spectral efficiency under different SNR levels of the proposed algorithm with other state-of-the-art algorithms with . (a) ; (b) .
Figure 3a,b shows the spectral efficiency versus SNR for different precoding algorithms with antennas at the transmitter, antennas at the receiver, , and and 4, respectively. As can be seen from Figure 3a,b, as the SNR and data streams increase, the spectral efficiency of different algorithms improves to different degrees. Similarly, for all data streams, the performance of the fully-digital precoding algorithm is the best. The performance of the proposed BSAMIBOMP algorithm is close to the full-digital algorithm and better than the traditional OMP-based hybrid precoding algorithm. The analog precoding performance is the worst of all precoding schemes. Comparing Figure 2 and Figure 3, it can be found that the effect is better when , because in this case, the dimensions of baseband precoding and RF precoding are higher, and the precoding matrix contains more information, so the effect is better. Therefore, the proposed algorithm can achieve better results for .
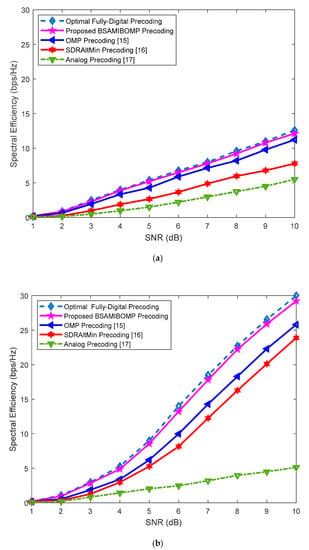
Figure 3.
Comparison of spectral efficiency under different SNR levels of the proposed algorithm with other state-of-the-art algorithms with . (a) ; (b) .
Figure 4a,b shows the spectral efficiency with the number of RF links for different precoding algorithms with antennas at the transmitter, antennas at the receiver, ,3, and . As can be seen from Figure 4a,b, since full-digital precoding is precoded only at the baseband, the analog precoding is precoded only at the radio frequency, so they are not affected by the change in the number of RF links. With the increase of the number of RF links, the proposed algorithm has better spectral efficiency than the traditional OMP-based hybrid precoding scheme. When , the proposed algorithm and the traditional OMP-based hybrid precoding algorithm have approximately similar performances (Figure 4a). When , the proposed algorithm shows a better performance than the traditional OMP-based hybrid precoding algorithm (Figure 4b). Therefore, the proposed algorithm performance gets better when the number of RF links and the number of data streams are relatively large. However, if the difference is too large, then the meaning of hybrid precoding is lost. So, the number of RF links is generally twice that of the data streams for better performance. Therefore, the proposed algorithm can achieve better results for different number of RF link.
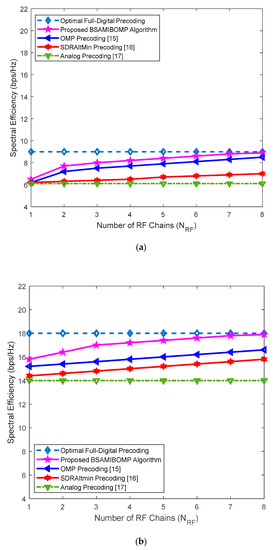
Figure 4.
Comparison of spectral efficiency under different number of RF links with other state-of-the-art algorithms with , and . (a) ; (b) .
Figure 5 and Figure 6 show the different BERs with antennas at the transmitter end, antennas at the receiving end, , and at 1 and 3, respectively. As can be seen from Figure 5 and Figure 6, the BER of the full-digital precoding, the proposed algorithm, and the traditional OMP-based hybrid precoding algorithms decrease with the increase of SNR, while the analog precoding BER remains unchanged. This is because the analog precoder selects the column array response vector with the largest channel gain, and its selection is independent of the SNR. Comparing Figure 5 with Figure 6, it can be found that when , the full-digital precoding algorithm, the proposed BSAMIBOMP, and the traditional OMP-based hybrid precoding algorithm achieved the best BER performance, that is, with no error rate. When , the full-digital precoding algorithm can be optimized at 5 dB, while the OMP-based hybrid precoding and the proposed algorithm tend to be stable after 5 dB SNR, and a closer observation can be found in this paper. The proposed algorithm shows better BER performance than the traditional OMP-based hybrid precoding, and also its performance is closer to the full-digital precoding scheme. We also conclude that the proposed algorithm is especially suitable when there is a difference between the number of RF links and the number of data streams. From the above results, it is clear that the proposed algorithm also shows better performance in terms of BER.
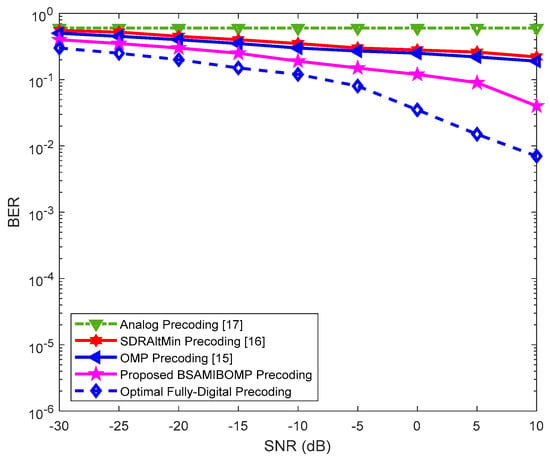
Figure 5.
Comparison of BER under different SNR levels of the proposed algorithm with other state-of-the-art algorithms with and .

Figure 6.
Comparison of BER under different SNR levels of the proposed algorithm with other state-of-the-art algorithms with and .
Figure 7 compares the computational complexity of the proposed BSAMIBOMP algorithm with another existing algorithm under a different number of RF chains. As can be seen from Figure 7, when the number of RF chains increases, the number of multiplications and additions required for all the algorithms increases. It is also shown in the results that the proposed algorithm requires a smaller number of multiplications and additions than the OMP precoding [15] and the SDRAltMin precoding [16] for the same number of RF chains and operating conditions, which makes effective for mmWave systems. This means that the proposed algorithm requires a lesser amount of energy to operate the systems and also results in reduced hardware complexity. On the other hand, the conventional OMP hybrid precoding scheme requires a greater number of complex multiplications and additions, which makes it unsuitable for mmWave communications systems hardware.
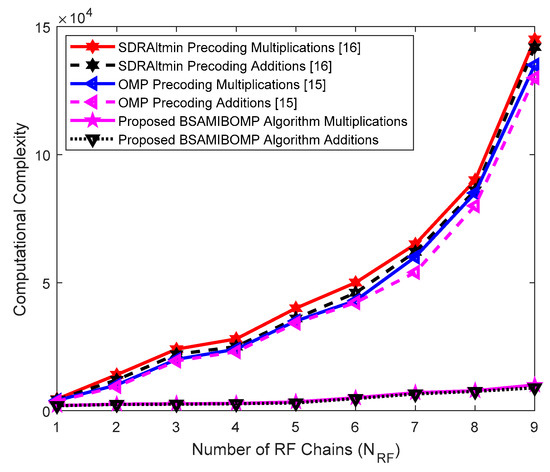
Figure 7.
Computational complexity comparison of the proposed algorithm with existing algorithms.
Figure 8 shows the energy efficiency analysis under different number of RF chains for different precoding schemes. As it can be seen, the energy efficiency of all the precoding schemes decreases with an increasing number of RF chains. Moreover, the proposed BSAMIBOMP precoding algorithm shows better energy efficiency than the existing OMP hybrid precoding [15] and SDRAltMin [16] precoding under the same number of RF chains and operating conditions, which makes it more effective for mmWave systems. Therefore, the proposed algorithm has a close performance to Fully-Digital precoding and an overall better performance than other competing alternatives.
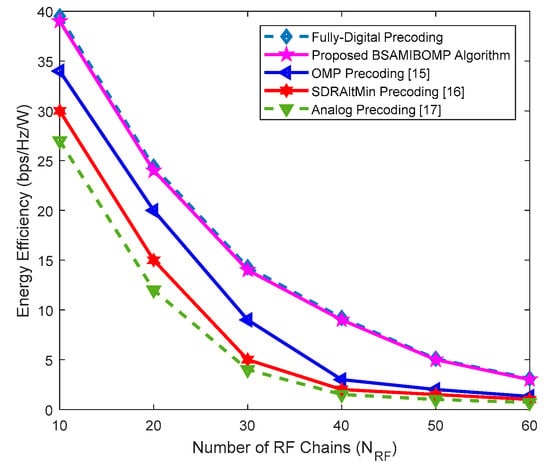
Figure 8.
Energy efficiency comparison of the proposed algorithm with existing algorithms.
5. Conclusions and Future Recommendations
In this paper, we proposed a matrix-inversion bypass (MIB) bird swarm algorithm (BSA) based OMP algorithm (BSAMIBOMP) to eliminate the matrix inversion operation and known candidate matrix requirement so that the number of computations is reduced. The algorithm uses the characteristics of BSA with a global search optimal value to search for the largest array response vector multiplied by the residual matrix and uses the Banachiewicz–Schur block matrix generalized inverse to transform the high-dimensional matrix into a low-dimensional matrix, avoiding matrix inversion and reducing the amount of calculation. Compared with the existing OMP-based hybrid precoding [15], SDRAltMin precoding [16], and analog precoding [17], the proposed algorithm achieves better performance in terms of system spectral efficiency and bit error rate without known candidate matrix and matrix inversion. For future directions, [this study can be further extended by considering the energy efficiency of the proposed algorithm and comparing it with other state-of-the-art algorithms under different important parameters and constraints. Moreover, the future work can also focus on analyzing the hardware impairments versus different parameters for the proposed algorithm and comparing it to existing competing alternatives.
Author Contributions
Conceptualization, I.K., S.H. and N.A.; Data curation, Y.K., M.I.K. and F.A.; Formal analysis, J.R. and A.S.; Funding acquisition I.K. and A.S.; Investigation, I.K. and Y.K.; Methodology, M.I.K., I.K., J.R. and N.A.; Project administration, A.S. and I.K.; Software, S.H., I.K. and N.A.; Writing—original draft, I.K. and S.H.; Writing—review & editing, I.K., S.H. and N.A.
Funding
This work was supported by Universiti Putra Malaysia under the grant NOMA-MIMO: Optimizing 5G Wireless Communication Performance Based on Hybrid NOMA with Partial Feedback for Multiuser MIMO (GP-IPS/2018/9663000, Vot No: 9663000).
Conflicts of Interest
The authors declared that they have no conflict of interest.
References
- Gomez, S.; Roger, S.; Baracca, P.; Martín-Sacristán, D.; Monserrat, J.F.; Braun, V.; Halbauer, H. Performance Evaluation of Analog Beamforming with Hardware Impairments for mmWave Massive MIMO Communication in an Urban Scenario. Sensors 2016, 16, 1555. [Google Scholar]
- Khan, I.; Alsharif, M.H.; Alassafi, M.O.; Ashraf, M.; Huang, Y.; Kim, J.; Kim, J.H. An Efficient Algorithm for mmWave MIMO Systems. Symmetry 2019, 11, 786. [Google Scholar] [CrossRef]
- Parchin, N.O.; Alibakhshikenari, M.; Jahanbakhsh, H.; Abd-Alhameed, R.; Rodriguez, J.; Limiti, E. MM-Wave Phased Array Quasi-Yagi Antenna for the Upcoming 5G Cellular Communications. Appl. Sci. 2019, 9, 978. [Google Scholar] [CrossRef]
- Ge, X.; Sun, Y.; Gharavi, H.; Thompson, J. Joint optimization of computation and communication power in multi-user massive MIMO systems. IEEE Trans. Wirel. Commun. 2018, 17, 4051–4063. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Wang, W.; Meng, H.; So, H.C.; Zhang, H. Efficient beamspace-based algorithm for two-dimensional DOA estimation of incoherently distributed sources in massive MIMO systems. IEEE Trans Veh. Technol. 2018, 67, 11776–11789. [Google Scholar] [CrossRef]
- Gao, X.; Dai, L.; Han, S.; I, C.L.; Heath, R.W. Energy-efficient hybrid analog and digital precoding for mmwave MIMO systems with large antenna arrays. IEEE J. Select. Areas Commun. 2016, 34, 998–1009. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhu, L.; Choi, J.; Xia, P.; Xia, X.-G. Joint Power Allocation and Beamforming for Non-Orthogonal Multiple Access (NOMA) in 5G Millimeter-Wave Communications. IEEE Trans. Wirel. Commun. 2018, 17, 2961–2974. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X.-G. Joint Power Control and Beamforming for Uplink Non-Orthogonal Multiple Access in 5G Millimeter-Wave Communications. IEEE Trans. Wirel. Commun. 2018, 17, 6177–6189. [Google Scholar] [CrossRef]
- Xu, C.; Ye, R.; Huang, Y.; He, S.; Zhang, C. Hybrid Precoding for Broadband Millimeter-Wave Communication Systems with Partial CSI. IEEE Access 2018, 6, 50891–50900. [Google Scholar] [CrossRef]
- Vlachos, E.; Alexandropoulos, G.C.; Thomson, J. Massive MIMO Channel Estimation for Millimeter Wave Systems via Matrix Completion. IEEE Signal Process. Lett. 2018, 25, 1675–1679. [Google Scholar] [CrossRef]
- Yang, B.; Yu, Z.; Lan, J.; Zhang, R.; Zhou, J.; Hong, W. Digital Beamforming-Based Massive MIMO Transceiver for 5G Millimeter-Wave Communications. IEEE Trans. Microw. Theory Tech. 2018, 66, 3403–3418. [Google Scholar] [CrossRef]
- Li, S.; Wu, H.; Jin, L. Codebook-Aided DOA Estimation Algorithms for Massive MIMO System. Electronics 2019, 8, 26. [Google Scholar] [CrossRef]
- Hefnawi, M. Hybrid Beamforming for Millimeter-Wave Heterogeneous Networks. Electronics 2019, 8, 133. [Google Scholar] [CrossRef]
- Sohrabi, F.; Yu, W. Hybrid Digital and Analog Beamforming Design for large-scale antenna arrays. IEEE J. Sel. Top. Signal Process. 2016, 10, 501–513. [Google Scholar] [CrossRef]
- Ayach, O.E.; Rajagopal, S.; Surra, S.A.; Pi, Z.; Heath, R.W. Spatial sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.C.; Zhang, J.; Letaief, K.B. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 485–500. [Google Scholar] [CrossRef]
- Ayach, O.E.; Heath, R.W.; Rajagopal, S.; Pi, Z. Multimode precoding in millimeter wave MIMO transmitters with multiple antenna sub-arrays. In Proceedings of the IEEE Global Communications Conference, Atlanta, GA, USA, 9–13 December 2013; pp. 3476–3480. [Google Scholar]
- Amadori, P.V.; Marouros, C. Low RF-complexity millimeter-wave beamspace-MIMO Systems by beam selection. IEEE Trans. Commun. 2015, 63, 2212–2223. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.H.; Ashraf, M.; Kim, S. Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-Output Systems. Electronics 2018, 7, 382. [Google Scholar] [CrossRef]
- Han, S.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter-wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Hur, S.; Kim, T.; Love, D.J.; Krogmeier, J.V.; Thomas, T.A.; Ghosh, A. Millimeter wave Beamforming for Wireless Backhaul and Access in Small Cell Networks. IEEE Trans. Commun. 2013, 61, 4391–4403. [Google Scholar] [CrossRef]
- Brady, J.; Behdad, N.; Sayeed, A.M. Beamspace MIMO for millimeter-wave communications: System Architecture, modeling, analysis, and measurements. IEEE Trans. Antennas Propag. 2013, 61, 3814–3827. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Huang, G.; Wang, L. High-speed reconstruction with orthogonal matching pursuit via matrix inversion bypass. In Proceedings of the IEEE Workshop on Signal Processing Systems, Quebec City, QC, Canada, 17–19 October 2012; pp. 191–196. [Google Scholar]
- Meng, X.; Gao, X.Z.; Lu, L.; Liu, Y.; Zhang, H. A new bio-inspired optimization algorithm: Bird Swarm Algorithm. J. Exp. Theor. Artif. Intell. 2016, 28, 673–687. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).