ELPKG: A High-Accuracy Link Prediction Approach for Knowledge Graph Completion
Abstract
1. Introduction
- (1)
- We propose a novel model ELPKG that employs both semantic relation and path relation to complete knowledge graphs. Based on entity vectors and path features, ELPKG invents a novel link prediction algorithm to complete knowledge graphs. This algorithm first trains the triple relationship the fact represented with entity vector data, and then it finds the path between nodes through the breadth-first search method. To the best of our knowledge, this is the first attempt to predict link relationship for completing knowledge graphs.
- (2)
- To achieve high accuracy during KGC, ELPKG adopts a reasoning mechanism based on probabilistic soft logic, which effectively solves the problem of non-deterministic knowledge reasoning and improves the effect and efficiency of reasoning on large-scale KG.
- (3)
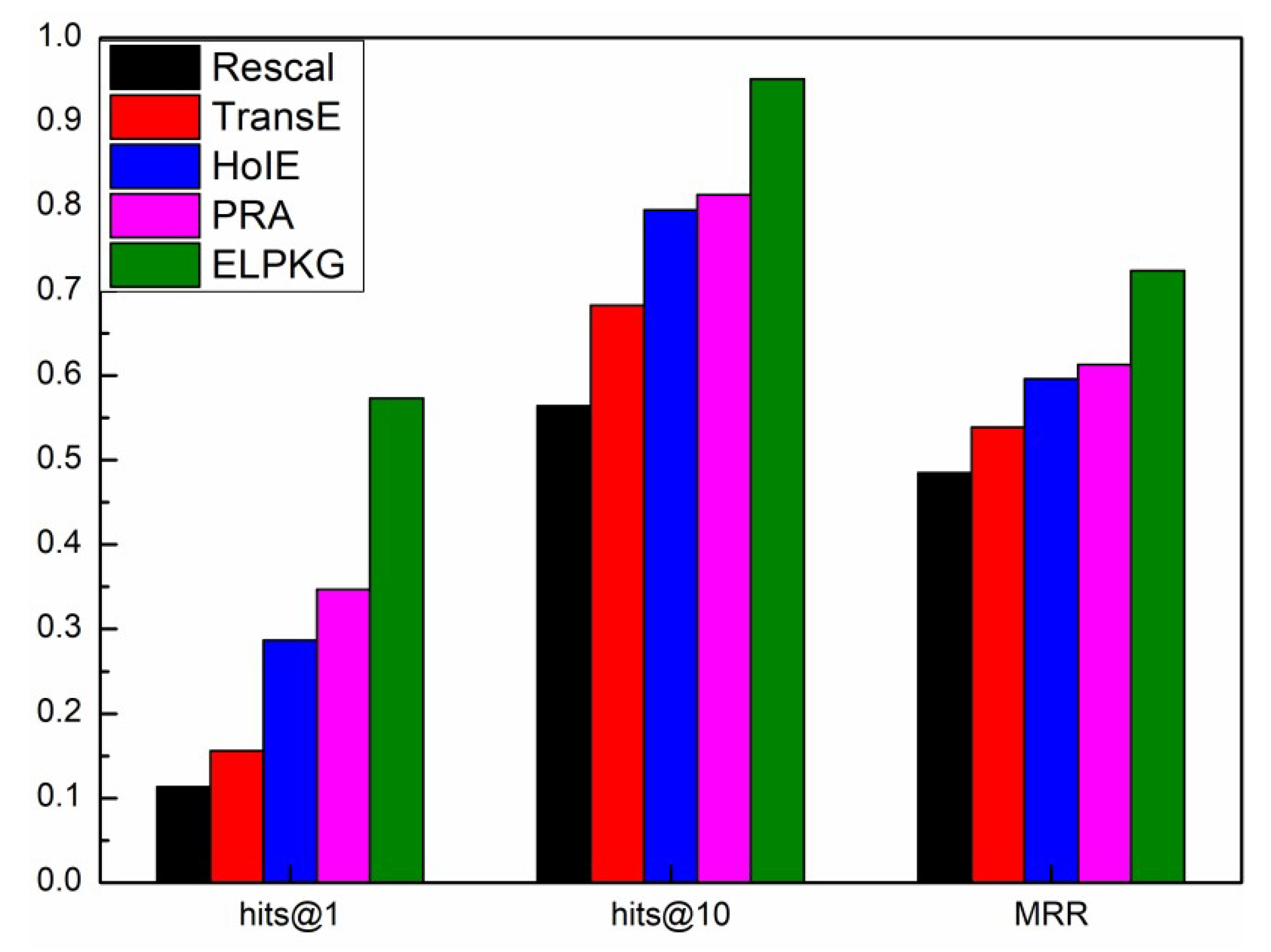
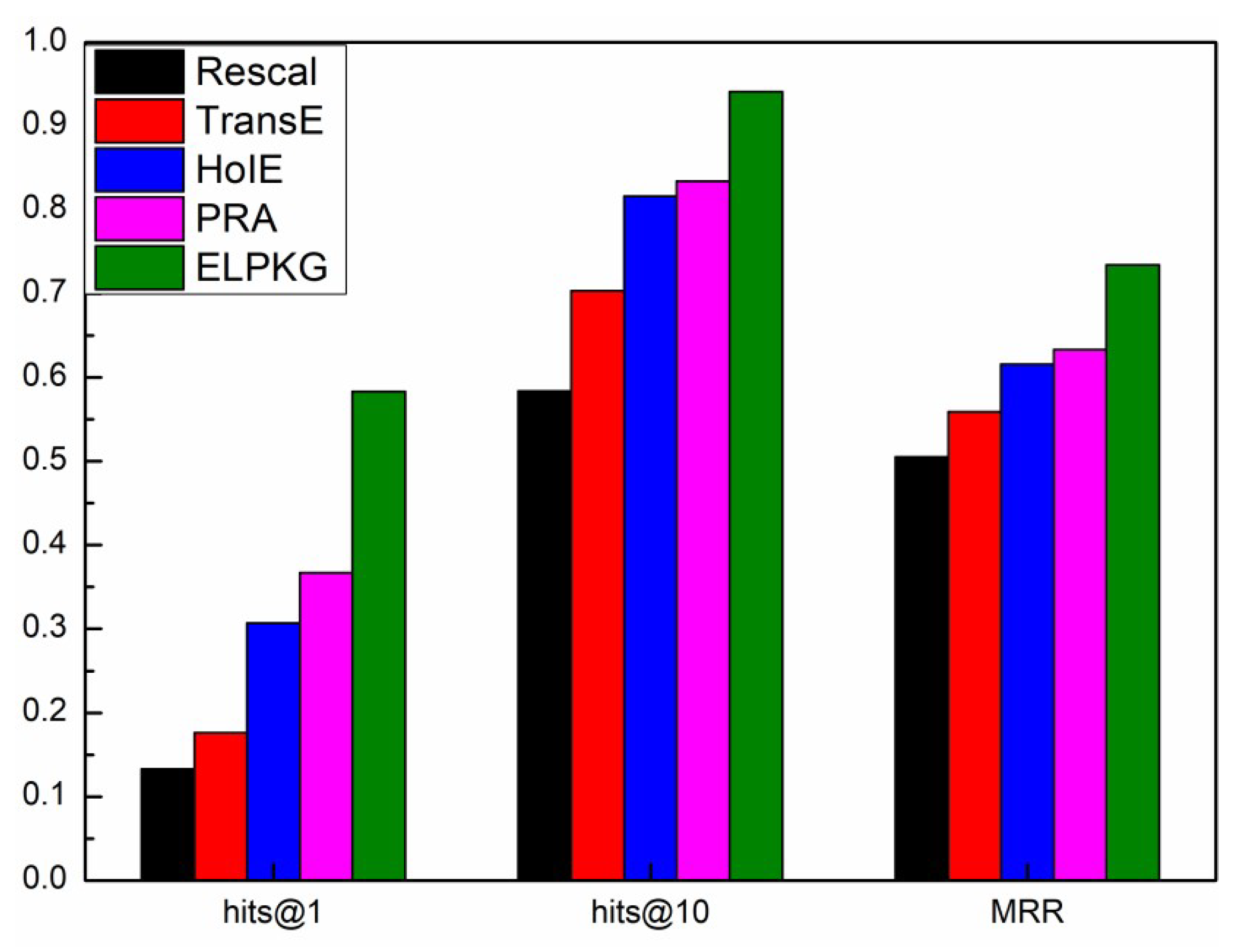
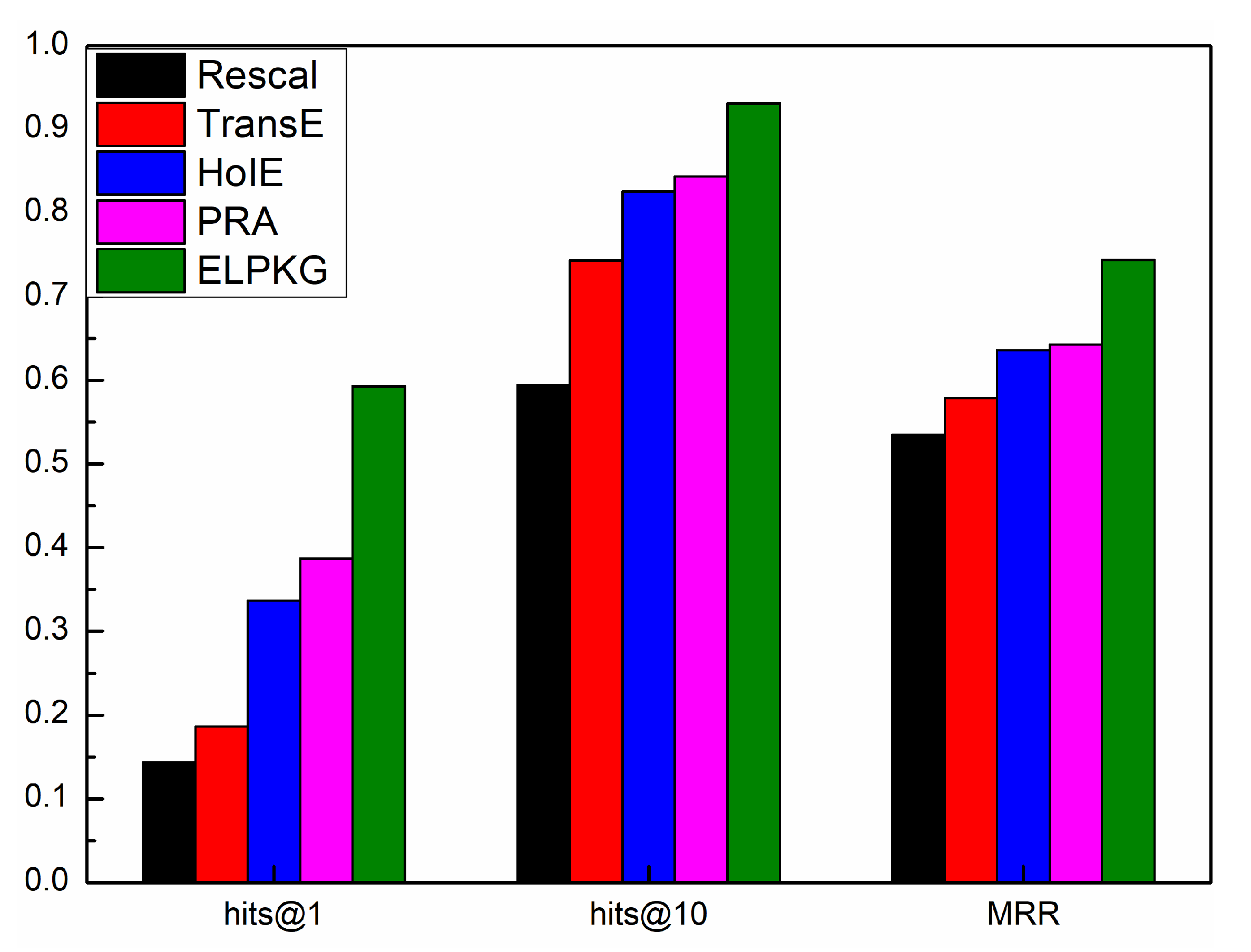
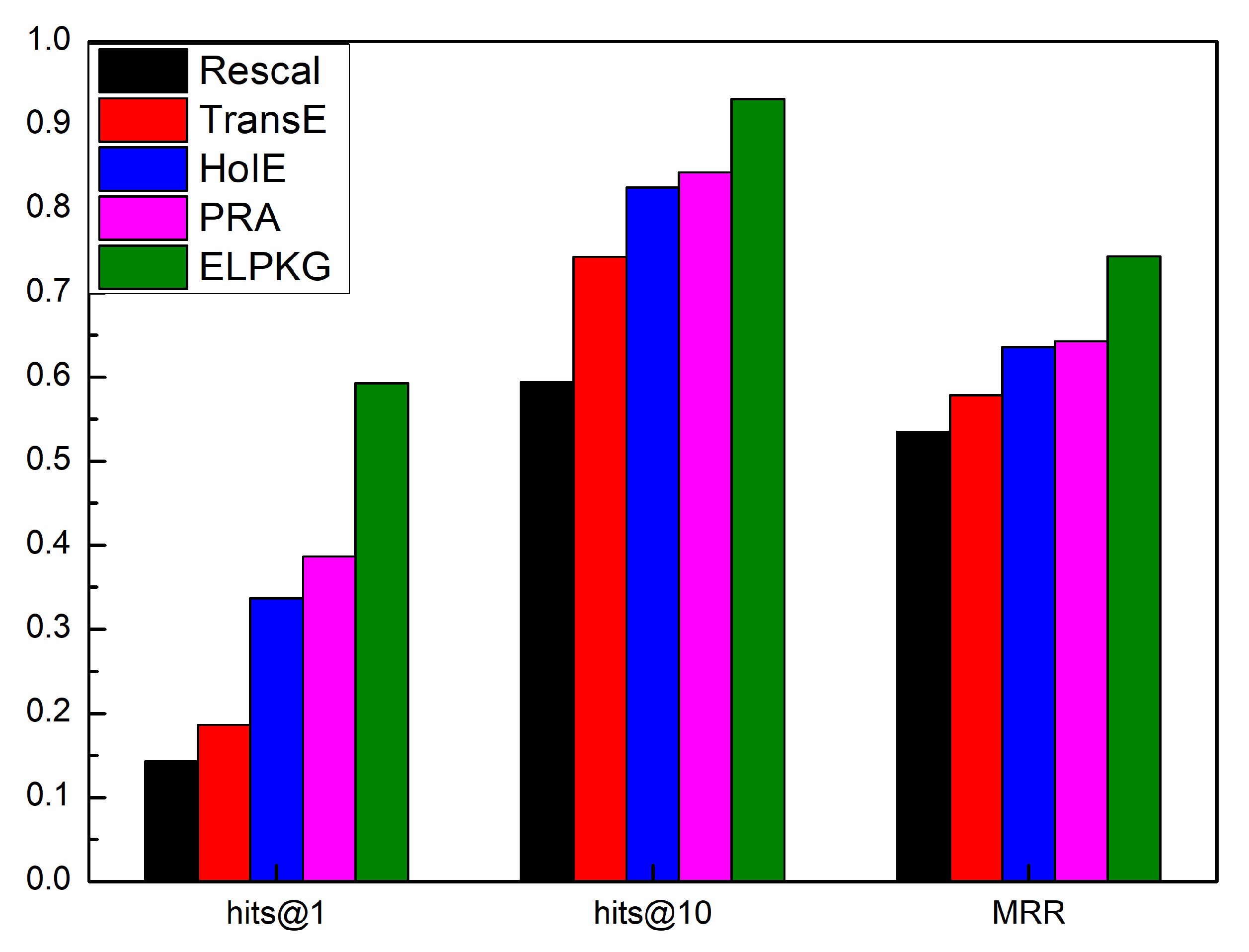
- We conduct a large number of experiments on the real dataset YAGO [20] and NELL [21]. It shows that our approach achieves a significant improvement in prediction accuracy, which are 35%, 24%, and 17% higher than the baseline method on hits@1, hits@10 and MRR on the YAGO dataset, and 34%, 21%, 16% on the NELL dataset, respectively.
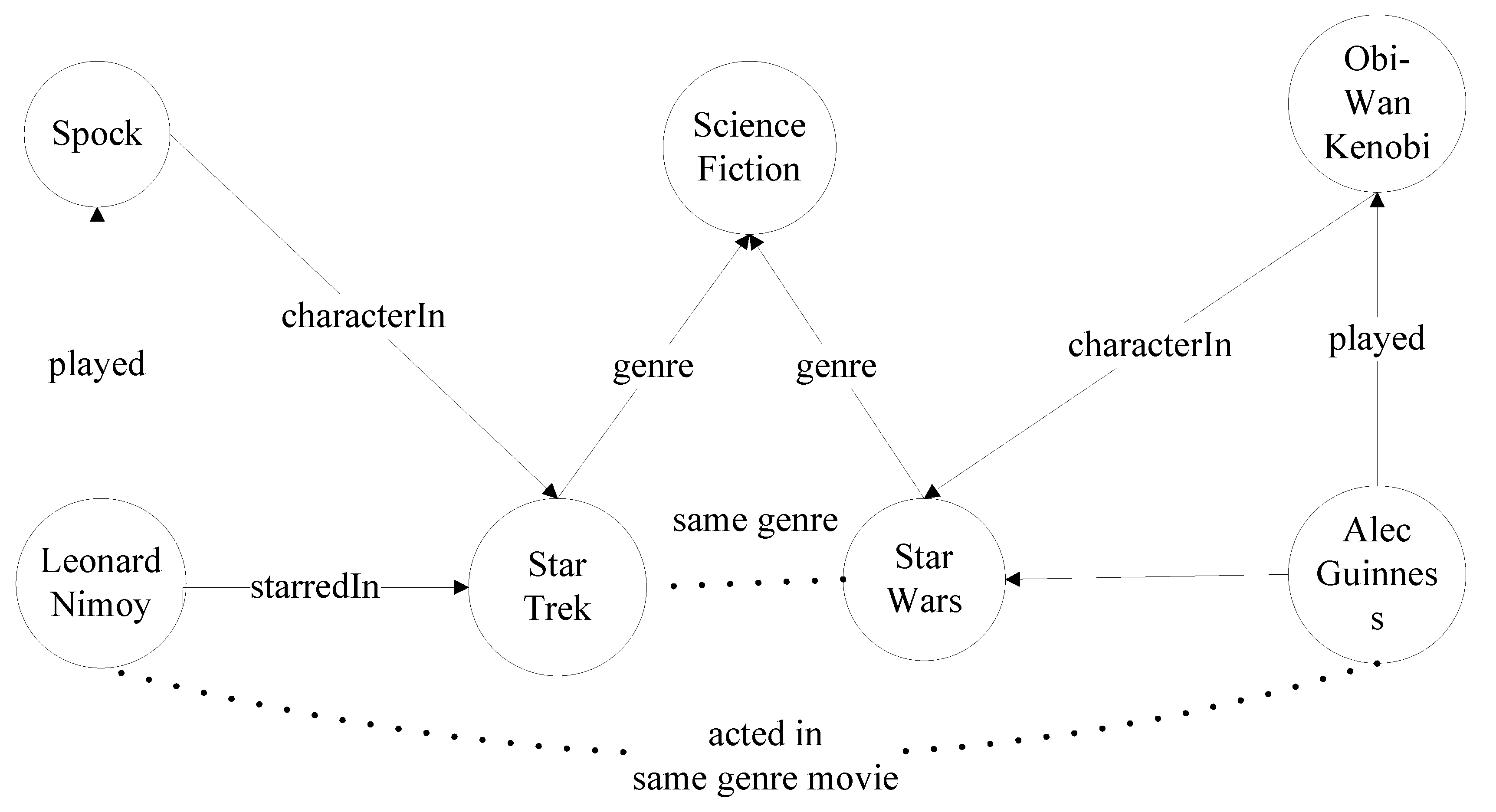
2. Problem Statement
3. Solution Description
3.1. Entity Relation Representation Based on Vector Embedding
3.2. Path-Based Entity Relation Representation
3.3. Probabilistic Soft Logic-Based Reasoning Method
3.4. Entity Linking Prediction Algorithm
| Algorithm 1. Entity Linking Prediction in Knowledge Graph (ELPKG) |
|
|
4. Evaluation
4.1. Dataset
4.2. Evaluation Criteria
4.3. Comparison Methods
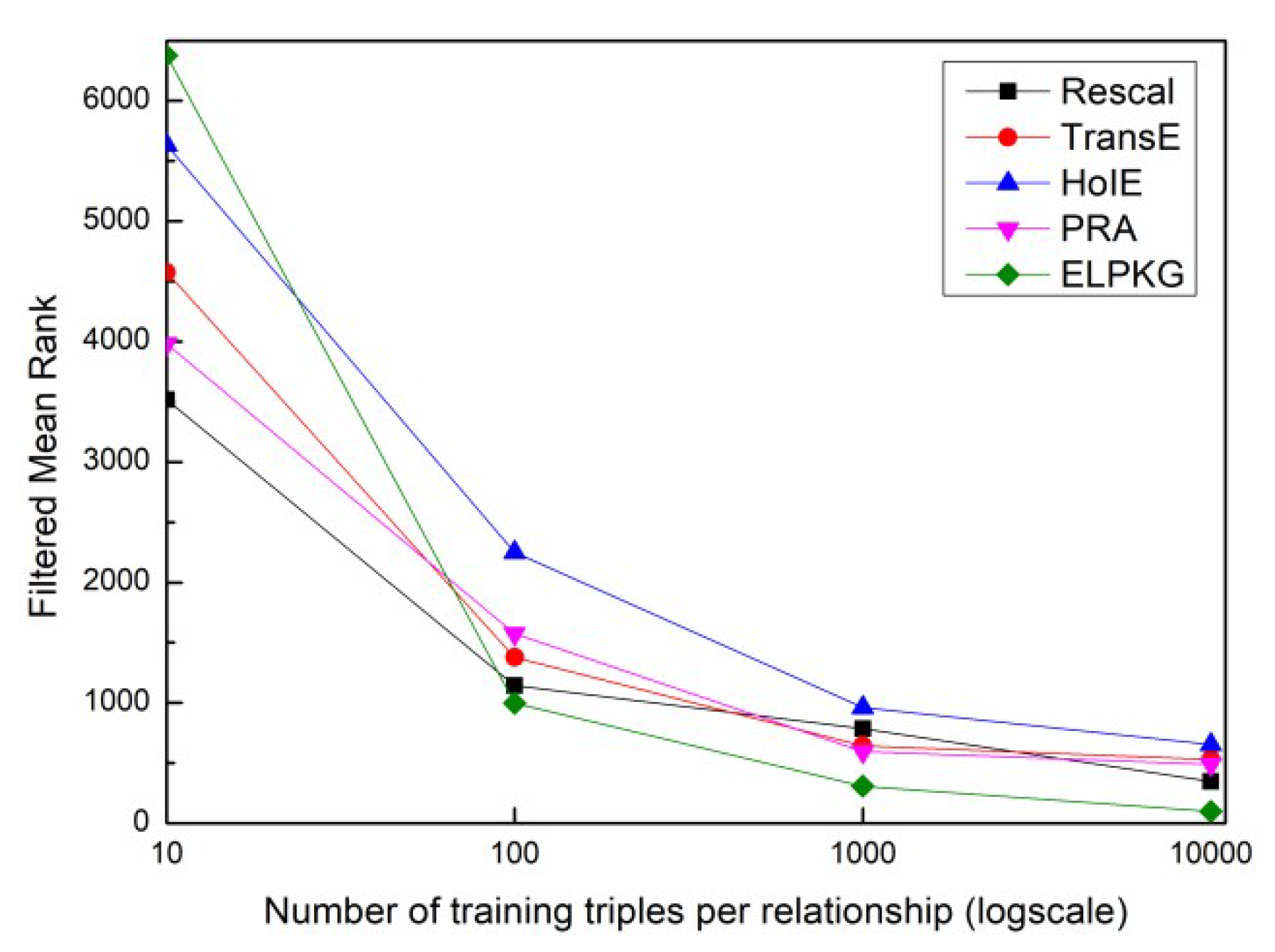
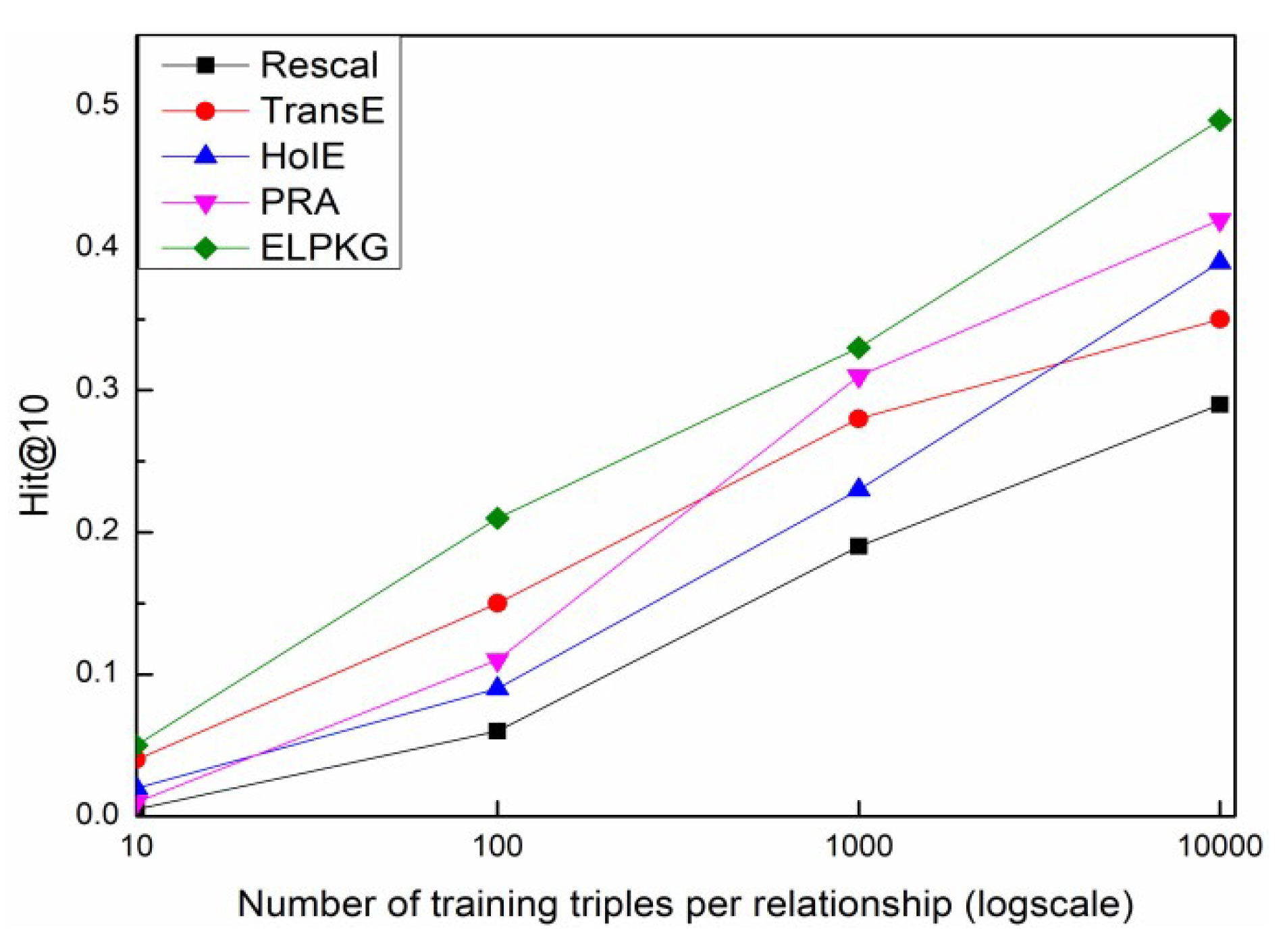
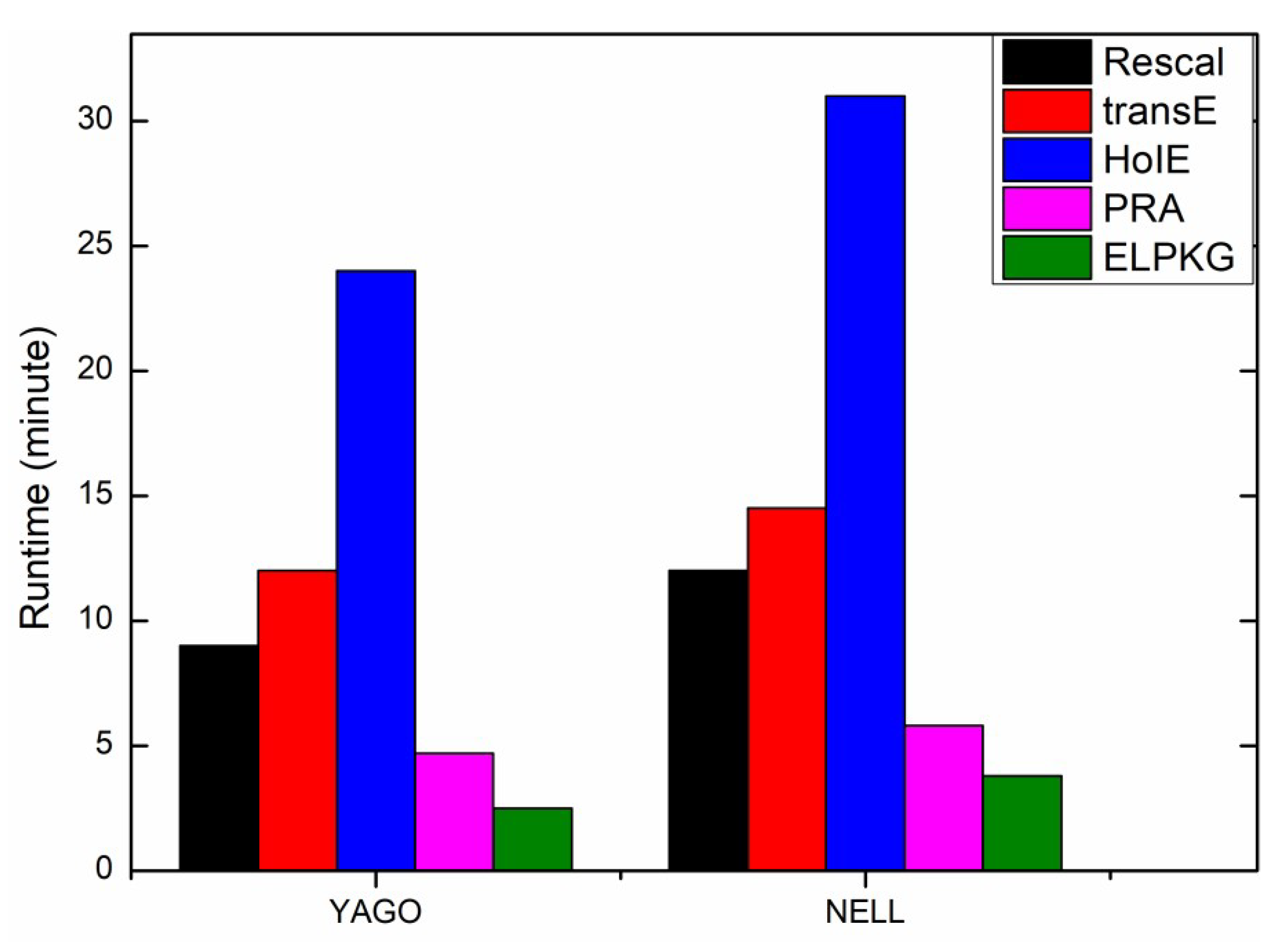
4.4. Experimental Results
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, W.; Yu, J.X.; Zou, L.; Cheng, H. Question Answering Over Knowledge Graphs: Question Understanding Via Template Decomposition. Proc. VLDB Endow. 2018, 11, 1373–1386. [Google Scholar] [CrossRef]
- Ayala-Gómez, F.; Daróczy, B.; Benczúr, A.A.; Mathioudakis, M.; Gionis, A. Global citation recommendation using knowledge graphs. J. Intell. Fuzzy Syst. 2018, 34, 3089–3100. [Google Scholar] [CrossRef]
- Dou, J.; Qin, J.; Jin, Z.; Li, Z. Knowledge graph based on domain ontology and natural language processing technology for Chinese intangible cultural heritage. J. Vis. Lang. Comput. 2018, 48, 19–28. [Google Scholar] [CrossRef]
- Sun, M.; Liu, Z.; Xiong, C.; Liu, Z.-H. Entity-Duet Neural Ranking: Understanding the Role of Knowledge Graph Semantics in Neural Information Retrieval. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; Volume 1, pp. 2395–2405. [Google Scholar]
- Franco-Salvador, M.; Rosso, P.; Montes-y-Gómez, M. A systematic study of knowledge graph analysis for cross-language plagiarism detection. Inf. Process. Manag. 2016, 52, 550–570. [Google Scholar] [CrossRef]
- Dong, X.; Gabrilovich, E.; Heitz, G.; Horn, W.; Lao, N.; Murphy, K.; Strohmann, T.; Sun, S.; Zhang, W. Knowledge Vault: A Web-scale Approach to Probabilistic Knowledge Fusion. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2014; pp. 601–610. [Google Scholar]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A Collaboratively Created Graph Database for Structuring Human Knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; ACM: New York, NY, USA, 2008; pp. 1247–1250. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.-P. A Three-way Model for Collective Learning on Multi-relational Data. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 809–816. [Google Scholar]
- Chang, K.-W.; Yih, S.W.; Yang, B.; Meek, C. Typed Tensor Decomposition of Knowledge Bases for Relation Extraction. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 1568–1579. [Google Scholar]
- Franz, T.; Schultz, A.; Sizov, S.; Staab, S. TripleRank: Ranking Semantic Web Data by Tensor Decomposition. In Proceedings of the Semantic Web—ISWC 2009: 8th International Semantic Web Conference, ISWC 2009, Chantilly, VA, USA, 25–29 October 2009; Bernstein, A., Karger, D.R., Heath, T., Feigenbaum, L., Maynard, D., Motta, E., Thirunarayan, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 213–228. ISBN 978-3-642-04930-9. [Google Scholar]
- Li, X.; Huang, S.; Candan, K.S.; Sapino, M.L. Focusing Decomposition Accuracy by Personalizing Tensor Decomposition (PTD). In Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management; ACM: New York, NY, USA, 2014; pp. 689–698. [Google Scholar]
- Duan, L.; Aggarwal, C.; Ma, S.; Hu, R.; Huai, J. Scaling Up Link Prediction with Ensembles. In Proceedings of the Ninth ACM International Conference on Web Search and Data Mining; ACM: New York, NY, USA, 2016; pp. 367–376. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems 26; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; pp. 2787–2795. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the Twenty-Ninth AAAI conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2181–2187. [Google Scholar]
- Feng, J. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the AAAI, Québec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T. Holographic Embeddings of Knowledge Graphs. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1955–1961. [Google Scholar]
- Socher, R.; Chen, D.; Manning, C.D.; Ng, A. Reasoning with Neural Tensor Networks for Knowledge Base Completion. In Advances in Neural Information Processing Systems 26; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; pp. 926–934. [Google Scholar]
- Lao, N.; Mitchell, T.; Cohen, W.W. Random Walk Inference and Learning in a Large Scale Knowledge Base. In Proceedings of the Conference on Empirical Methods in Natural Language Processing; Association for Computational Linguistics: Stroudsburg, PA, USA, 2011; pp. 529–539. [Google Scholar]
- Das, R.; Neelakantan, A.; Belanger, D.; Mccallum, A. Chains of Reasoning over Entities, Relations, and Text using Recurrent Neural Networks. In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics, Valencia, Spain, 3–7 April 2017; pp. 132–141. [Google Scholar]
- Rebele, T.; Suchanek, F.; Hoffart, J.; Biega, J.; Kuzey, E.; Weikum, G. YAGO: A Multilingual Knowledge Base from Wikipedia, Wordnet, and Geonames. In Proceedings of the Semantic Web—ISWC 2016: 15th International Semantic Web Conference, Kobe, Japan, 17–21 October 2016, Part II; Groth, P., Simperl, E., Gray, A., Sabou, M., Krötzsch, M., Lecue, F., Flöck, F., Gil, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 177–185. ISBN 978-3-319-46547-0. [Google Scholar]
- Mitchell, T.; Cohen, W.; Hruschka, E.; Talukdar, P.; Betteridge, J.; Carlson, A.; Dalvi, B.; Gardner, M.; Kisiel, B.; Krishnamurthy, J.; et al. Never-Ending Learning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI-15), Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Nickel, M.; Murphy, K.; Tresp, V.; Gabrilovich, E. A Review of Relational Machine Learning for Knowledge Graphs. Proc. IEEE 2016, 104, 11–33. [Google Scholar] [CrossRef]
- Bach, S.H.; Broecheler, M.; Huang, B.; Getoor, L. Hinge-Loss Markov Random Fields and Probabilistic Soft Logic. J. Mach. Learn. Res. 2017, 18, 1–67. [Google Scholar]
- Bach, S.H.; Huang, B.; London, B.; Getoor, L. Hinge-loss Markov Random Fields: Convex Inference for Structured Prediction. In Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence, Bellevue, WA, USA, 11–15 August 2013; pp. 32–41. [Google Scholar]
| Dataset | Number of Entities | Number of Relation Type | Number of Tuples |
|---|---|---|---|
| YAGO | 192628 | 51 | 192900 |
| NELL | 2156462 | 50 | 2465372 |
| YAGO-50 | 192628 | 50 | 100774 |
| YAGO-rest | 192628 | 41 | 92126 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Qiao, Y.; Hu, G.; Wang, Y.; Zhang, C.; Huang, Y.; Sangaiah, A.K.; Wu, H.; Zhang, H.; Ren, K. ELPKG: A High-Accuracy Link Prediction Approach for Knowledge Graph Completion. Symmetry 2019, 11, 1096. https://doi.org/10.3390/sym11091096
Ma J, Qiao Y, Hu G, Wang Y, Zhang C, Huang Y, Sangaiah AK, Wu H, Zhang H, Ren K. ELPKG: A High-Accuracy Link Prediction Approach for Knowledge Graph Completion. Symmetry. 2019; 11(9):1096. https://doi.org/10.3390/sym11091096
Chicago/Turabian StyleMa, Jiangtao, Yaqiong Qiao, Guangwu Hu, Yanjun Wang, Chaoqin Zhang, Yongzhong Huang, Arun Kumar Sangaiah, Huaiguang Wu, Hongpo Zhang, and Kai Ren. 2019. "ELPKG: A High-Accuracy Link Prediction Approach for Knowledge Graph Completion" Symmetry 11, no. 9: 1096. https://doi.org/10.3390/sym11091096
APA StyleMa, J., Qiao, Y., Hu, G., Wang, Y., Zhang, C., Huang, Y., Sangaiah, A. K., Wu, H., Zhang, H., & Ren, K. (2019). ELPKG: A High-Accuracy Link Prediction Approach for Knowledge Graph Completion. Symmetry, 11(9), 1096. https://doi.org/10.3390/sym11091096






