An Adaptive Routing-Forwarding Control Scheme Based on an Intelligent Fuzzy Decision-Making System for Opportunistic Social Networks
Abstract
1. Introduction
- A fuzzy inference model is proposed to implement the fusion of multiple social information of mobile users, thereby providing a reliable and stable strategy for opportunistic message routing and forwarding.
- To synthetically evaluate the impact of each social characteristic on the data transmission process in OSNs, we combine the fuzzy inference logic with the analytic hierarchy process, and more importantly, with exploring the data transmission relationships among mobile users.
- On the basis of a feedback mechanism, we are able to build a relatively stable and sustained data transmission connectivity between the source nodes and destinations in opportunistic mobile social network environments.
- Ultimately, simulation results demonstrate that this scheme reduces the network delay and the overhead ratio, and enhances the delivery ratio as compared to several other typical or latest routing protocols in the OSNs.
2. Related Works
2.1. The Proposed Profile-Aware Routing Algorithms for Opportunistic Mobile Social Networks
2.2. The Proposed Profile-Ignorant Routing Algorithms for Opportunistic Mobile Social Networks
3. System Model Design
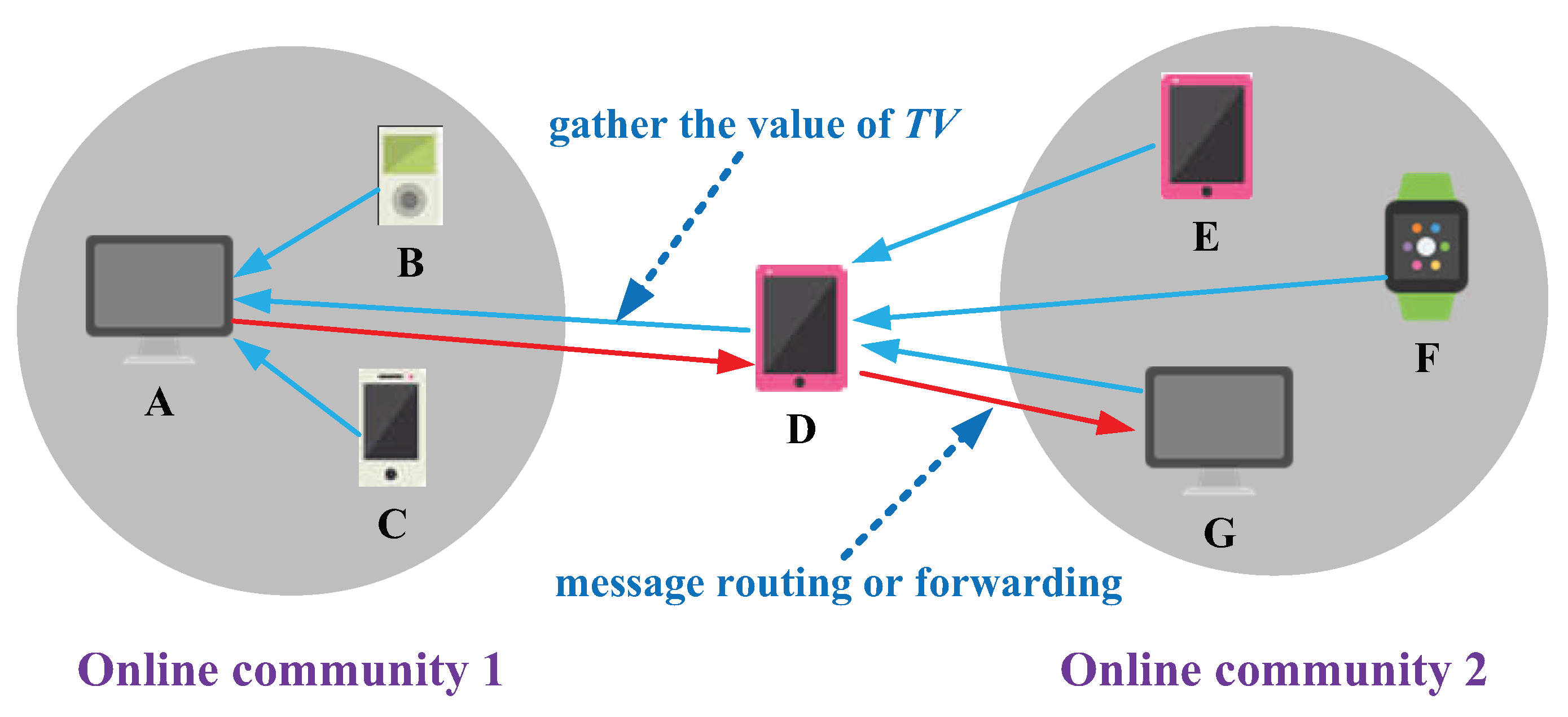
3.1. The Overall Structure of Intelligent Fuzzy Decision-Making System for Opportunistic Mobile Social Networks
3.2. Fuzzy Pattern Recognition Process for Node Classification in Opportunistic Mobile Social Networks
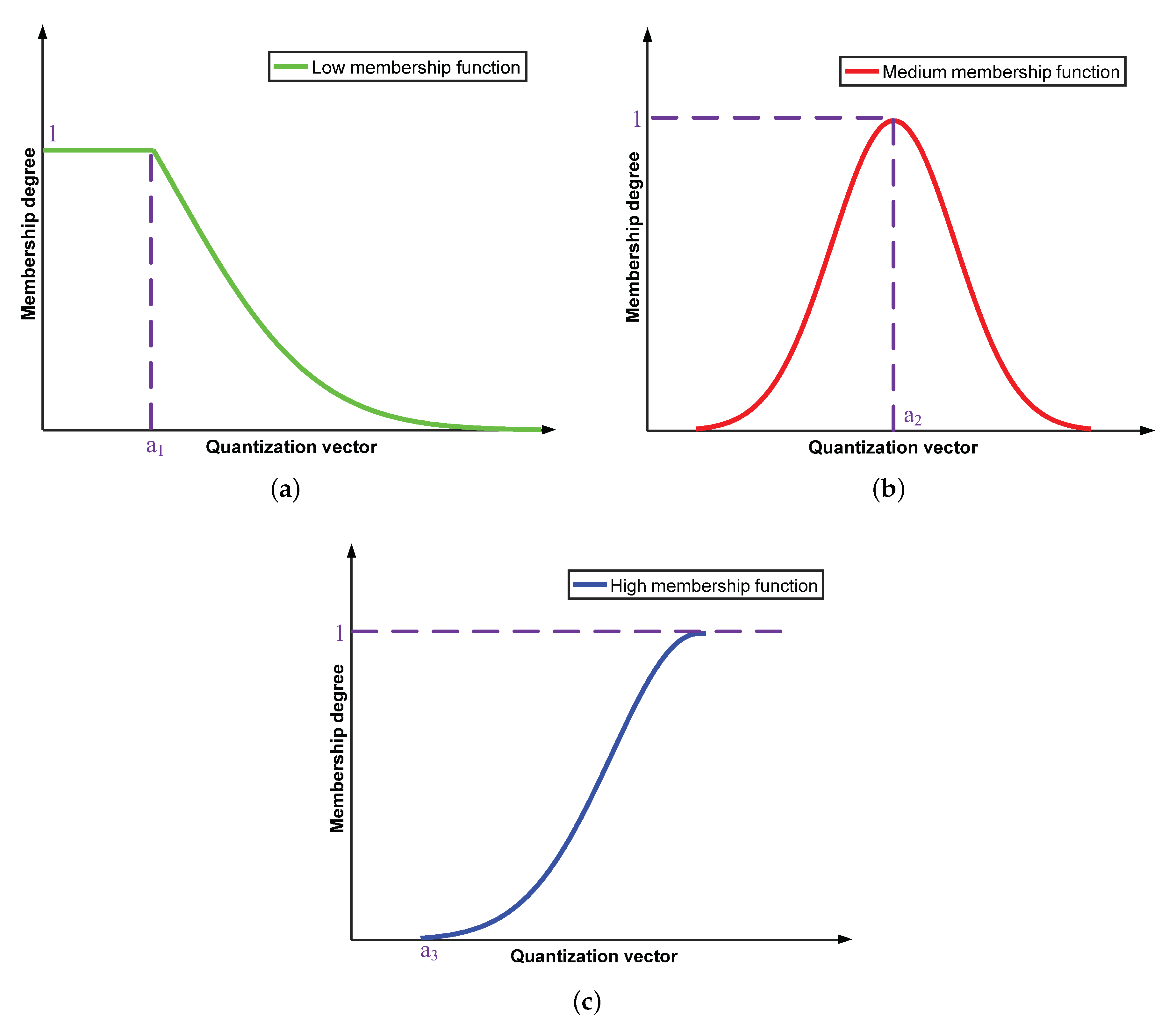
3.2.1. Information Quantification and Determining Membership Degrees for Fuzzy Input
3.2.2. Fuzzy Pattern Recognition for Node Classification in Opportunistic Mobile Social Networks
3.3. Reasonable Weight Allocation and Inference of Fuzzy Relationships Via the Analytic Hierarchy Process
3.4. Information Fusion and Fuzzy Decision-Making for Message Routing-Forwarding in Opportunistic Mobile Social Networks
3.5. Algorithm Complexity Analysis
| Algorithm 1 Fuzzy pattern cognition and decision model |
| Input: social attributes of users Output:
|
4. Simulation And Analysis
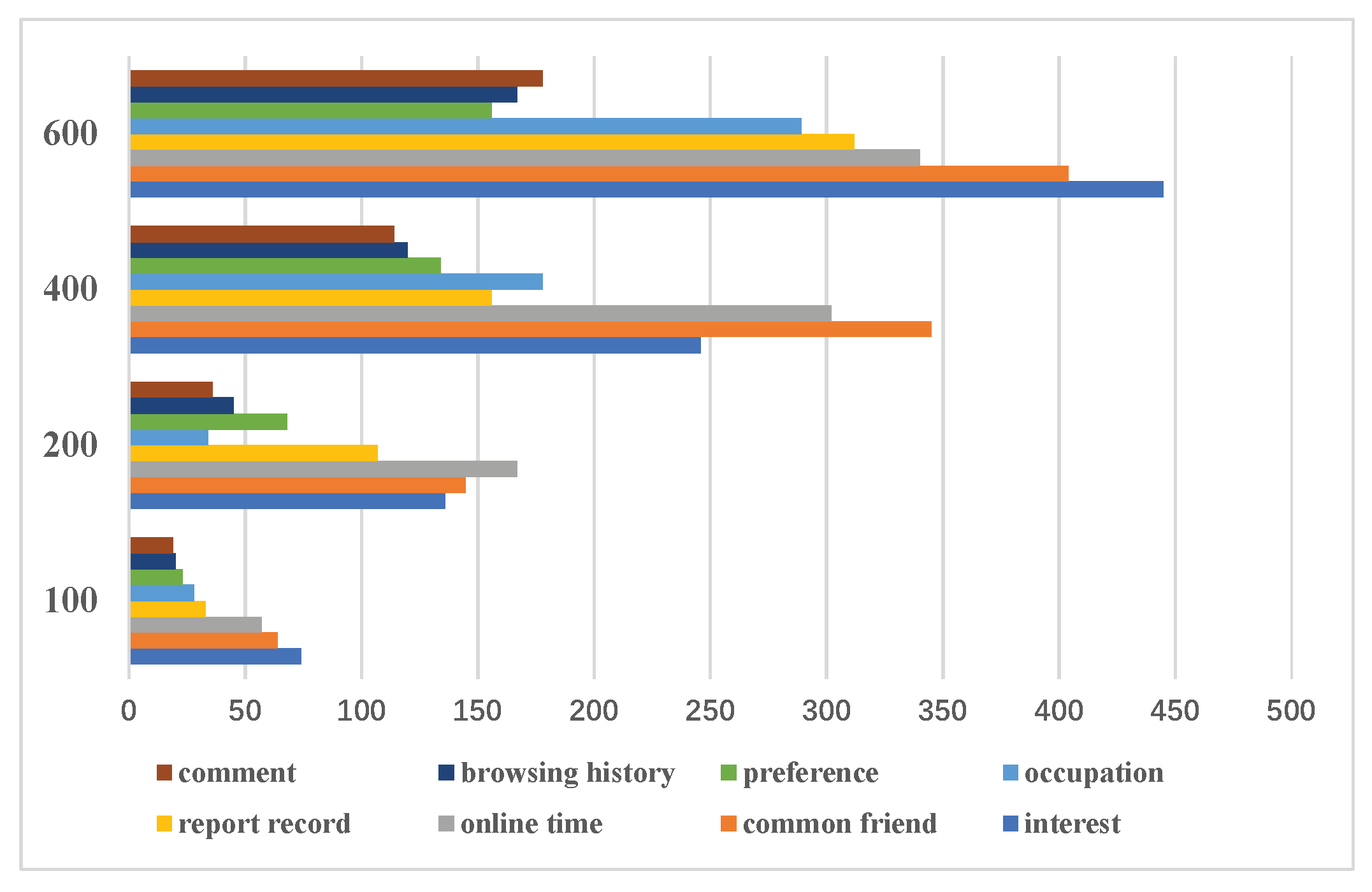
4.1. Setting of Experimental Parameters
4.2. Experimental Measurement Metrics
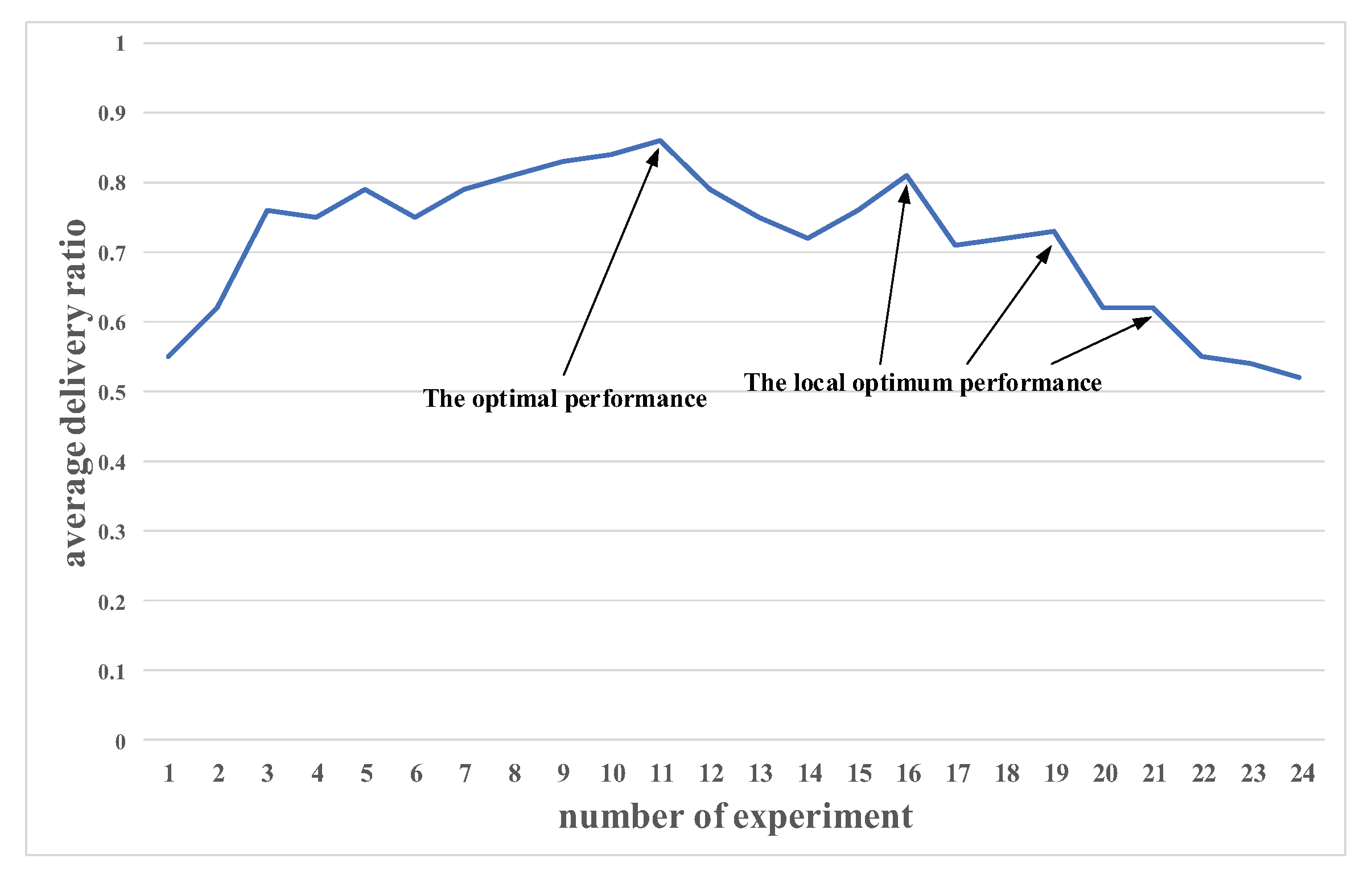
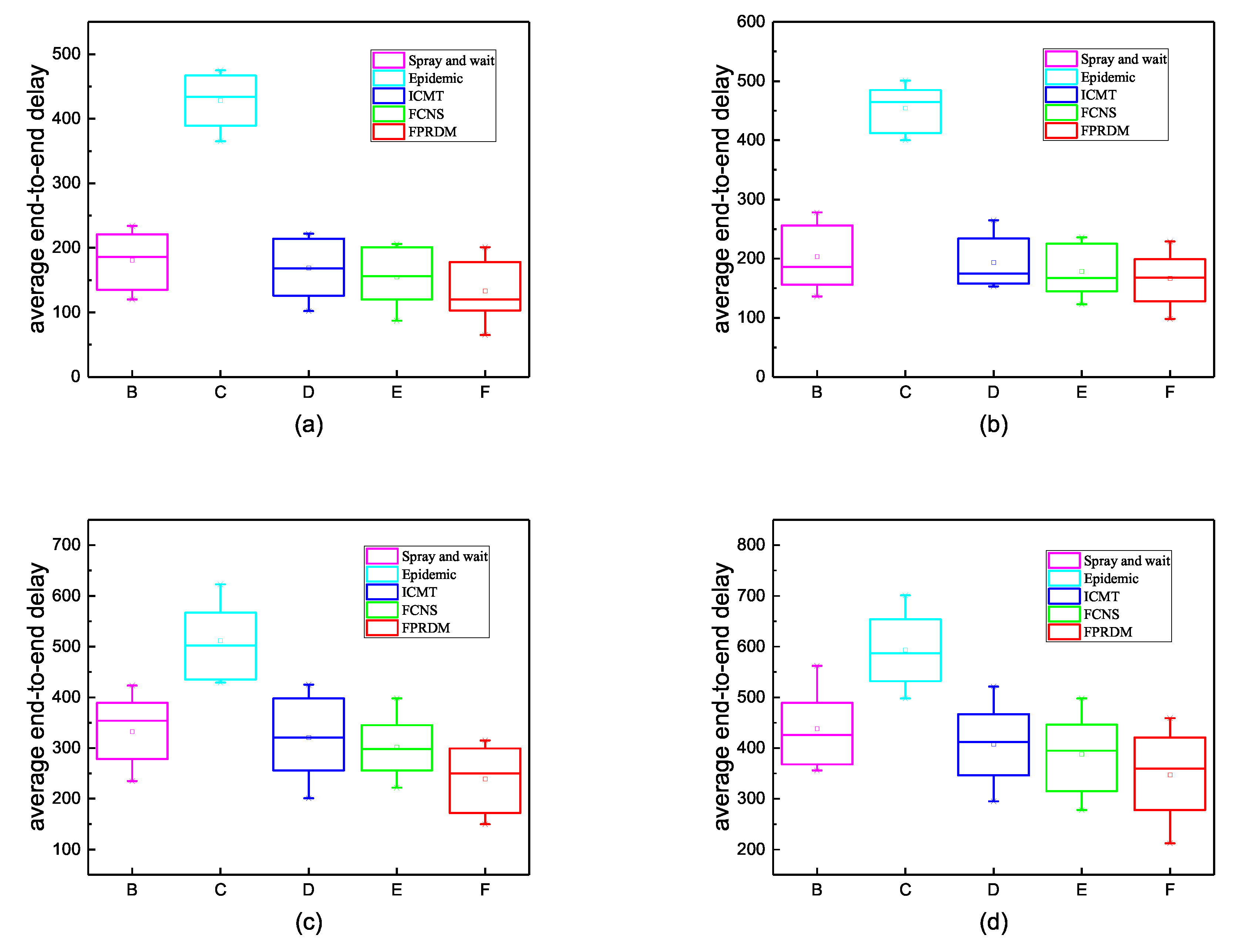
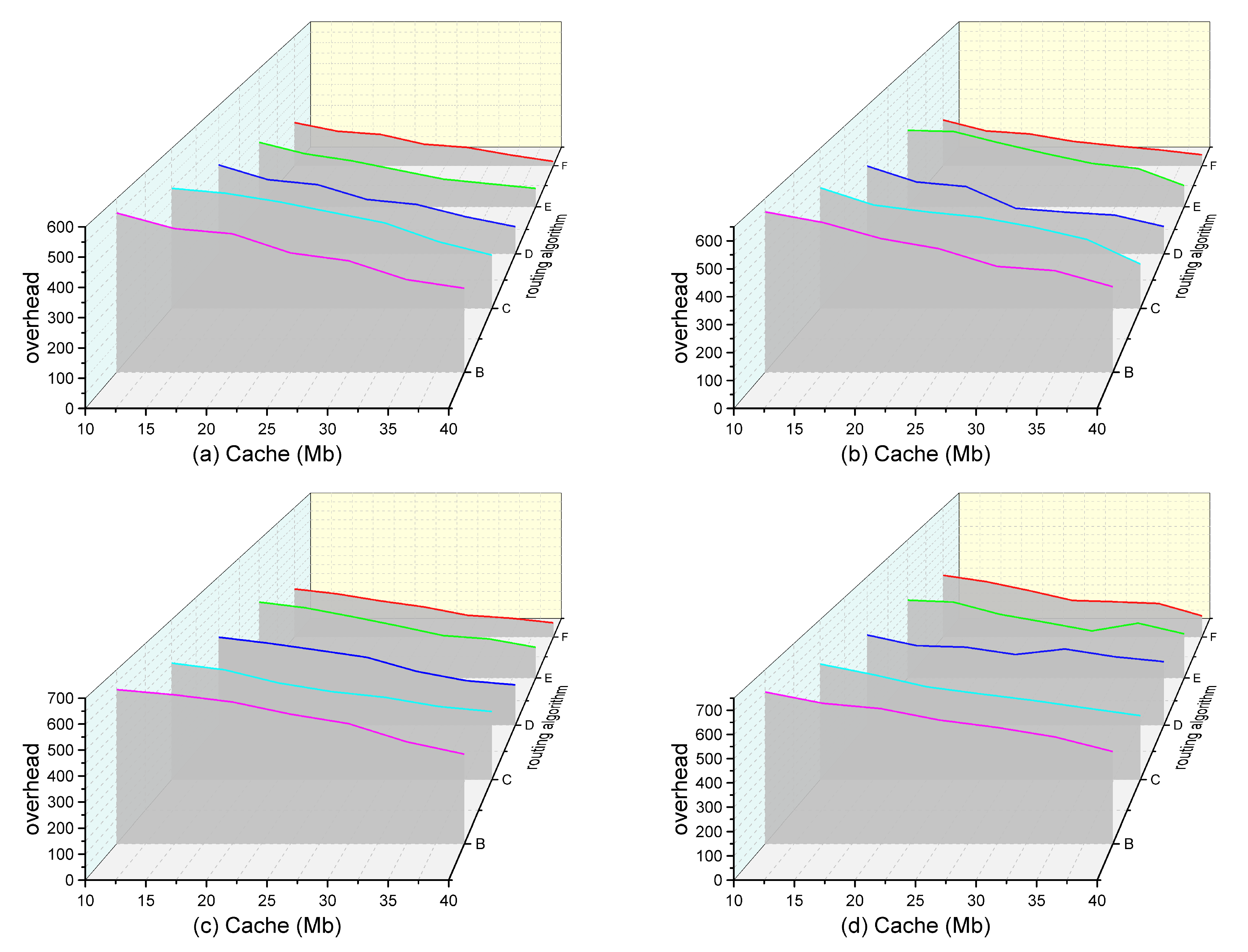
4.3. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| OSNs | opportunistic social networks |
| DTNs | delay tolerant networks |
| SNS | social network service |
| AHP | analytic hierarchy process |
| EpSoc | a flooding-based social-based routing protocol |
| Tanh | tanhyperbolic function |
| Markov | markov Andrey chain |
| CoA | center of area |
| MoM | mean of maximum |
| ONE | opportunistic networking environment |
| FPRDM | an adaptive control scheme based on intelligent fuzzy decision-making system |
| FCNS | fuzzy routing-forwarding algorithm exploiting comprehensive node similarity |
| ICMT | information cache management and data transmission algorithm |
References
- Dede, J.; Forster, A.; Hernandez-Orallo, E.; Herrera-Tapia, J.; Kuladinithi, K.; Kuppusamy, V.; Manzoni, P.; bin Muslim, A.; Udugama, A.; Vatandas, Z. Simulating Opportunistic Networks: Survey and Future Directions. IEEE Commun. Surv. Tutor. 2017, 20, 1547–1573. [Google Scholar] [CrossRef]
- Halikul, L.; Mohamad, A. EpSoc: Social-Based Epidemic-Based Routing Protocol in Opportunistic Mobile Social Network. Mob. Inf. Syst. 2018, 2018, 1–8. [Google Scholar]
- Bulut, E.; Wang, Z.; Szymanski, B.K. Cost-Effective Multiperiod Spraying for Routing in Delay-Tolerant Networks. IEEE/ACM Trans. Netw. 2010, 18, 1530–1543. [Google Scholar] [CrossRef]
- Ali, I.; Chang, R.Y.; Hsu, C.H. SOQAS: Distributively Finding High-Quality Answerers in Dynamic Social Networks. IEEE Access 2018, 6, 55074–55089. [Google Scholar] [CrossRef]
- Pirozmand, P.; Wu, G.; Jedari, B.; Xia, F. Human mobility in opportunistic networks: Characteristics, models and prediction methods. J. Netw. Comput. Appl. 2014, 42, 45–58. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Z.; Wu, J.; Wang, L. FCNS: A fuzzy routing-forwarding algorithm exploiting comprehensive node similarity in opportunistic social networks. Symmetry 2018, 10, 338. [Google Scholar] [CrossRef]
- Ge, X.; Ye, J.; Yang, Y.; Li, Q. User Mobility Evaluation for 5G Small Cell Networks Based on Individual Mobility Model. IEEE J. Sel. Areas Commun. 2016, 34, 528–541. [Google Scholar] [CrossRef]
- Fang, D.; Qian, Y.; Hu, R.Q. Security for 5G Mobile Wireless Network. IEEE Access 2018, 6, 4850–4874. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z.; Zhao, M. Information cache management and data transmission algorithm in opportunistic social networks. Wirel. Netw. 2018, 8, 1–12. [Google Scholar] [CrossRef]
- Mumtaz, S.; Al-Dulaimi, A.; Frascolla, V.; Hassan, S.A.; Dobre, O.A. Guest Editorial Special Issue on 5G and Beyond—Mobile Technologies and Applications for IoT. IEEE Internet Things J. 2019, 6, 203–206. [Google Scholar] [CrossRef]
- Novak, E.; Tang, Z.; Li, Q. Ultrasound Proximity Networking on Smart Mobile Devices for IoT Applications. IEEE Internet Things J. 2019, 6, 399–409. [Google Scholar] [CrossRef]
- Bangerter, B.; Talwar, S.; Arefi, R.; Stewart, K. Networks and devices for the 5G era. IEEE Commun. Mag. 2014, 52, 90–96. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Z.; Wu, J.; Xiao, Y.; Zhang, H. Predict and Forward: An Efficient Routing-Delivery Scheme Based on Node Profile in Opportunistic Networks. Future Internet 2018, 10, 74. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, Z.; Wu, J.; Wang, L.; Liu, K.; Wu, Y. Effective Data Transmission Strategy Based on Node Socialization in Opportunistic Social Networks. IEEE Access 2019, 7, 22144–22160. [Google Scholar] [CrossRef]
- Kafaie, S.; Chen, Y.; Dobre, O.A.; Ahmed, M.H. Joint Inter-Flow Network Coding and Opportunistic Routing in Multi-Hop Wireless Mesh Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2018, 20, 1014–1035. [Google Scholar] [CrossRef]
- Wang, L.L.; Chen, Z.G.; Wu, J. Vehicle trajectory prediction algorithm in vehicular network. Wirel. Netw. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Luo, J.; Hu, J.; Wu, D.; Li, R. Opportunistic Routing Algorithm for Relay Node Selection in Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2015, 11, 112–121. [Google Scholar] [CrossRef]
- Prodhan, A.T.; Das, R.; Kabir, H.; Shoja, G.C. TTL based routing in opportunistic networks. J. Netw. Comput. Appl. 2011, 34, 1660–1670. [Google Scholar] [CrossRef]
- Bapu, B.R.T.; Gowd, L.C.S. Link Quality Based Opportunistic Routing Algorithm for QOS: Aware Wireless Sensor Networks Security. Wirel. Pers. Commun. 2017, 97, 1563–1578. [Google Scholar] [CrossRef]
- Choumas, K.; Syrigos, I.; Korakis, T.; Tassiulas, L. Video aware Multicast Opportunistic Routing over 802.11 two-hop mesh networks. IEEE Trans. Veh. Technol. 2017, 66, 8372–8384. [Google Scholar] [CrossRef]
- Radunovic, B.; Gkantsidis, C.; Key, P.; Rodriguez, P. Toward Practical Opportunistic Routing With Intra-Session Network Coding for Mesh Networks. IEEE/ACM Trans. Netw. 2010, 18, 420–433. [Google Scholar] [CrossRef]
- Borrego, C.; Sánchez-Carmona, A.; Li, Z.; Robles, S. Explore and Wait: A composite routing-delivery scheme for relative Profile-casting in Opportunistic Networks. Comput. Netw. 2017, 123, 51–63. [Google Scholar] [CrossRef]
- Li, N.; Martinez-Ortega, J.F.; Diaz, V.H.; Fernandez, J.A.S. Probability Prediction-Based Reliable and Efficient Opportunistic Routing Algorithm for VANETs. IEEE/ACM Trans. Netw. 2018, 26, 1–15. [Google Scholar] [CrossRef]
- Li, J.; Jia, X.; Lv, X.; Han, Z.; Liu, J.; Hao, J. Opportunistic routing with data fusion for multi-source wireless sensor networks. Wirel. Netw. 2019, 25, 3103–3113. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, G.; Li, K.; Zhou, Y.; Zhou, X.; Li, K. M-Skyline: Taking sunk cost and alternative recommendation in consideration for skyline query on uncertain data. Knowl.-Based Syst. 2019, 163, 204–213. [Google Scholar] [CrossRef]
- Chen, G.; Lu, Y.; Meng, Y.; Li, B.; Tan, K.; Pei, D.; Cheng, P.; Luo, L.; Xiong, Y.; Zhao, Y.; et al. FUSO: Fast Multi-Path Loss Recovery for Data Center Networks. IEEE/ACM Trans. Netw. 2018, 26, 1–14. [Google Scholar] [CrossRef]
- Trifunovic, S.; Kouyoumdjieva, S.T.; Distl, B.; Pajevic, L.; Karlsson, G.; Plattner, B. A Decade of Research in Opportunistic Networks: Challenges, Relevance, and Future Directions. IEEE Commun. Mag. 2017, 55, 168–173. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Zhang, J.; Ye, H.; Tan, Z. Cooperative Store-Carry-Forward Scheme for Intermittently Connected Vehicular Networks. IEEE Trans. Veh. Technol. 2017, 66, 777–784. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Z.; Wu, J.; Tan, Y.; Wang, L.; Yan, Y.; Zhang, H.; Long, J. Big Medical Data Decision-Making Intelligent System Exploiting Fuzzy Inference Logic for Prostate Cancer in Developing Countries. IEEE Access 2019, 7, 2348–2363. [Google Scholar] [CrossRef]
- Nag, K.; Helal, M. Multicriteria Inventory Classification of Diabetes Drugs Using a Comparison of AHP and Fuzzy AHP Models. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 1456–1460. [Google Scholar]
- Conti, M.; Giordano, S.; May, M.; Passarella, A. From opportunistic networks to opportunistic computing. IEEE Commun. Mag. 2010, 48, 126–139. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, H.; Ma, J.; Han, X. Social-aware data dissemination in opportunistic mobile social networks. Int. J. Mod. Phys. C 2017, 28, 1750115. [Google Scholar] [CrossRef]
- Xu, Q.; Su, Z.; Zhang, K.; Ren, P.; Shen, X.S. Epidemic Information Dissemination in Mobile Social Networks With Opportunistic Links. IEEE Trans. Emerg. Top. Comput. 2015, 3, 399–409. [Google Scholar] [CrossRef]
- Li, N.; Martinez-Ortega, J.F.; Díaz, V.H. Cross-layer and Reliable Opportunistic Routing Algorithm for Mobile Ad Hoc Networks. IEEE Sens. J. 2018, 18, 5595–5609. [Google Scholar] [CrossRef]
- Bródka, P.; Kazienko, P. Multilayer Social Networks. In Encyclopedia of Social Network Analysis and Mining; Springer: New York, NY, USA, 2017. [Google Scholar]
- Magnani, M.; Rossi, L. The ML-Model for Multi-layer Social Networks. In Proceedings of the 2011 International Conference on Advances in Social Network Analysis and Mining, Kaohsiung, Taiwan, 25–27 July 2011. [Google Scholar]
- Chen, Q.; Zhang, Q.; Niu, Z. A Graph Theory Based Opportunistic Link Scheduling for Wireless Ad Hoc Networks. IEEE Trans. Wirel. Commun. 2009, 8, 5075–5085. [Google Scholar] [CrossRef]
- Hassan, S.A.; Ingram, M.A. A Quasi-Stationary Markov Chain Model of a Cooperative Multi-Hop Linear Network. IEEE Trans. Wirel. Commun. 2011, 10, 2306–2315. [Google Scholar] [CrossRef]
- Wenli, F.; Zhigang, L.; Ping, H. Identifying node importance based on information entropy in complex networks. Phys. Scr. 2013, 88, 065201. [Google Scholar] [CrossRef]
- Dutu, L.; Mauris, G.; Bolon, P. A Fast and Accurate Rule-Base Generation Method for Mamdani Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 715–733. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Shen, Y.; Wang, Y. Interval Observer Design for Discrete-Time Uncertain Takagi-Sugeno Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 816–823. [Google Scholar] [CrossRef]
- Pak, J.; Song, Y.T. Health Capability Maturity Model: Person-centered approach in Personal Health Record System. In Proceedings of the Americas Conference on Information Systems, San Diego, CA, USA, 11–13 August 2016. [Google Scholar]



| W | ⋯ | |||
|---|---|---|---|---|
| 1 | ⋯ | |||
| 1 | ⋯ | |||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| ⋯ | 1 |
| Dataset | Infocom5 | Infocom6 | Cambridge | Intel |
|---|---|---|---|---|
| Device | iMote | iMote | iMote | iMote |
| Duration (days) | 3.5 | 4 | 11 | 3.5 |
| Number of experimental devices | 41 | 98 | 50 | 8 |
| Number of internal contacts iMote | 2245 | 1706 | 1087 | 1364 |
| Simulation Environment | Description |
|---|---|
| Simulator | Opportunistic Network Environment (ONE) |
| Communication area | 3000 × 3000 |
| Total simulation time (h) | 10–20 |
| Number of nodes N | 100 (initial value), 200, 400, 600 |
| Cache space of a node C (Mb) | 10 (initial value), 15, 20, 25, 30, 35, 40 |
| Speed of a node (m/s) | 1-25 |
| Initial energy for a node (J) | 200 |
| Number of social features | 8 |
| Three location parameters , , | , , |
| Three scale parameters , , |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhang, L.; Shi, H.; Hwang, K.-S.; Shi, X.; Luo, S. An Adaptive Routing-Forwarding Control Scheme Based on an Intelligent Fuzzy Decision-Making System for Opportunistic Social Networks. Symmetry 2019, 11, 1095. https://doi.org/10.3390/sym11091095
Zhu Y, Zhang L, Shi H, Hwang K-S, Shi X, Luo S. An Adaptive Routing-Forwarding Control Scheme Based on an Intelligent Fuzzy Decision-Making System for Opportunistic Social Networks. Symmetry. 2019; 11(9):1095. https://doi.org/10.3390/sym11091095
Chicago/Turabian StyleZhu, Yian, Lin Zhang, Haobin Shi, Kao-Shing Hwang, Xianchen Shi, and Shuyan Luo. 2019. "An Adaptive Routing-Forwarding Control Scheme Based on an Intelligent Fuzzy Decision-Making System for Opportunistic Social Networks" Symmetry 11, no. 9: 1095. https://doi.org/10.3390/sym11091095
APA StyleZhu, Y., Zhang, L., Shi, H., Hwang, K.-S., Shi, X., & Luo, S. (2019). An Adaptive Routing-Forwarding Control Scheme Based on an Intelligent Fuzzy Decision-Making System for Opportunistic Social Networks. Symmetry, 11(9), 1095. https://doi.org/10.3390/sym11091095




