Algorithm for Neutrosophic Soft Sets in Stochastic Multi-Criteria Group Decision Making Based on Prospect Theory

Abstract

To address issues involving inconsistencies, this paper proposes a stochastic multi-criteria group decision making algorithm based on neutrosophic soft sets, which includes a pair of asymmetric functions: Truth-membership and false-membership, and an indeterminacy-membership function. For integrating an inherent stochastic, the algorithm expresses the weights of decision makers and parameter subjective weights by neutrosophic numbers instead of determinate values. Additionally, the algorithm is guided by the prospect theory, which incorporates psychological expectations of decision makers into decision making. To construct the prospect decision matrix, this research establishes a conflict degree measure of neutrosophic numbers and improves it to accommodate the stochastic multi-criteria group decision making. Moreover, we introduce the weighted average aggregation rule and weighted geometric aggregation rule of neutrosophic soft sets. Later, this study presents an algorithm for neutrosophic soft sets in the stochastic multi-criteria group decision making based on the prospect theory. Finally, we perform an illustrative example and a comparative analysis to prove the effectiveness and feasibility of the proposed algorithm.

1. Introduction

Many complex issues in engineering, economics, environmental science and medical science involve uncertainties. In order to address these issues, the theory of possibility, fuzzy set [1], rough set [2], and interval mathematic [3] have been developed successively. However, the above theories have their inherent defects, which are mainly reflected in the inadequacy of parameterization tools [4]. In 1999, Molodtsov [4] initiated the soft set theory for modeling uncertainties from the parameterized point of view.

After Molodtsov, the research interests in the soft set theory have been growing rapidly, such as the algebraic structure [5,6], topology [7,8], normal parameter reduction [9], medical diagnosis [10], game theory [4], and decision making under uncertainties [11,12]. In addition, the study of hybrid models that are developed by combining the soft set theory with other mathematical tools, such as rough sets [13], fuzzy sets [14], and intuitionistic fuzzy sets [15], has also been an important research topic.

Under uncertain environments, a mass of inconsistent information appears due to diversities of source platforms and the differences in the acquisition time. To address issues involving inconsistencies, Smarandache [16] initiated neutrosophic sets from the perspective of philosophy. Subsequently, Maji [17] integrated neutrosophic sets into soft sets to propose neutrosophic soft sets, which retain the characteristics of neutrosophic sets and have adequate parameterization tools. Neutrosophic soft sets are characteristic by three independent functions, including a pair of asymmetric functions: Truth-membership and false-membership, and an indeterminacy-membership function. Among them, the truth-membership and false-membership represent the degree of belongingness and non-belongingness of an element with respect to parameters. The indeterminacy-membership shows the neutrality degree of an element related to parameters.

In recent years, the theory extensions of neutrosophic soft sets have made a rapid progress. Sahin and Küçük [18] constructed generalised neutrosophic soft sets. Deli and Broumi [19] refined the concept and operations of Maji’s neutrosophic soft sets. In addition, they also studied the neutrosophic soft matrix and their operators. Considering that the approximate range is usually used to describe complex situations when there is no sufficient information, Deli [20] expanded the values of the truth-membership, indeterminacy-membership, and false-membership to the form of interval values to construct interval-valued neutrosiphic soft sets. Karaaslan [21] introduced the possibility of neutrosophic soft sets by assigning probability to the three function values and defined related properties and operations. In addition, the concepts of single-valued neutrosophic refined soft sets [22], generalized neutrosophic soft expert sets [23], and neutrosophic soft rough sets [24] were presented successively.

Meanwhile, neutrosophic soft sets are also employed in the fields of clustering, prediction and decision making under uncertainties, among which decision making under uncertainties is the most widely applied. Deli [20] proposed a decision making method of interval-valued neutrosophic soft sets by level soft sets, and illustrated it by an example. Peng and Liu [25] constructed three decision making algorithms of neutrosophic soft sets by evaluation based on the distance from average solution (EDAS), similarity measure, and level soft sets, respectively. Abu Qamar and Hassan [26] presented the similarity, distance, and fuzzy degree measures of Q-neutrosophic soft sets, and put forward the corresponding decision rule. Karaaslan [21] constructed a decision making method for the possibility of neutrosophic soft sets based on the and-product.

However, the existing studies mainly focus on decision making methods under a single decision maker, few scholars have studied group decision making problems by neutrosphic soft sets. At the same time, we also noticed that the existing methods have the following defects. On one hand, the above methods are mainly based on the expected utility theory, which assumes that decision makers are completelyrational. Actually, in decision making processes, decision makers do not make decisions in a complete rational manner, mainly showing that psychological expectations will greatly affect the actual decision making behavior. On the other hand, the parameter subjective weights are directly given determinate values [25], which do not fully reflect the hesitancies of decision makers’ judgments under uncertain environments.

To make up for the gaps of existing researches, this study constructs an algorithm for the stochastic multi-criteria group decision making based on neutrosophic soft sets. Stochastic means that the weights of decision makers and parameters are uncertain or completely unknown under uncertainties. In this paper, neutrosophic numbers rather than determinate values are adopted to express the stochastic of the weights of decision makers and parameters. This method employs the prospect theory [27] rather than the expected utility theory to integrate the hesitancies of alternatives by decision makers’ judgements. The prospect theory, a new theory of bounded rationality, is proposed from the point of view of cognitive psychology. In addition, it integrates the influence of psychological expectations on actual decision making behaviors into the decision making model. Therefore, the prospect theory is more in line with actual decision making behaviors under uncertainties [28]. Then, to establish the prospect decision matrix, we put forward the conflict degree measure of neutrosophic numbers and modify it to adapt group decision making. Moreover, on the purpose of aggregating in group decision making processes, this study proposes the weighted average aggregation rule and weighted geometric aggregation rule of neutrosophic soft sets.

To promote our discussion, some fundamental concepts of neutrosophic sets, soft sets, neutrosophic soft sets, and prospect theory are reviewed in Section 2. In Section 3, we establish the measures of determinacy degree and conflict degree, and construct the weighted average aggregation rule and weighted geometric aggregation rule of a neutrosophic soft set. In Section 4, this paper presents an algorithm for neutrosophic soft sets in the stochastic multi-criteria group decision making based on the prospect theory. In Section 5, to demonstrate the feasibility and effectiveness of the proposed algorithm, we perform an illustrative example and a comparative analysis.

2. Preliminaries

In this section, we briefly recall some basic concepts of neutrosophic sets, soft sets, neutrosophic soft sets, and prospect theory. More detailed conceptual basics can be found in references [4,16,17,27] (pp. 1–2).

2.1. Neutrosophic Soft Sets

Definition 1

[16] (p. 1).Let$U$be the initial universal set, a neutrosophic set$A=\{<u:T_{A(u)},I_{A(u)},F_{A(u)}>,u\in U\}$consists of the truth-membership$T_{A(u)}$, the indeterminacy-membership$I_{A(u)}$, and false-membership$F_{A(u)}$of element$u\in U$to set$A$, where$T,I,F:U\to {]}^{-}0,1^{+}[$. ${]}^{-}0,1^{+}[$ is a non-standard interval, and the left and right borders of it are imprecise. Between them, ${(}^{-}0)=\{0-x:x\in R^{*},x\mathrm{is}\mathrm{infinitesimal}\}$, and $(1^{+})=\{1+x:x\in R^{*},x\mathrm{is}\mathrm{infinitesimal}\}$.

For convenience, we employ $u=<T,I,F>$ to represent the element $u$ in the neutrosophic set $A$, and it can be called a neutrosophic number.

Considering that neutrosophic sets are proposed from the philosophical point of view, it is difficult to apply to practical problems, such as management and engineering problems. Then, Haibin et al. [29] developed single valued neutrosophic sets.

Definition 2

[29].Let$U$be the universal set, a single valued neutrosophic set$A$over$U$can be defined as$A=\{<u:T_{A(u)},I_{A(u)},F_{A(u)}>,u\in U\}$, where$T,I,F:U\to [0,1]$. Similarly, the values of T_A(u), I_A(u) and $F_{A(u)}$ stand for the truth-membership, indeterminacy-membership, and false-membership of $u$ to $A$, respectively.

Definition 3

[30].Let$u=<T,I,F>$be a neutrosophic number, then the score function, accuracy function and certainty function are defined as follows, respectively.

$$s(u)=\frac{2+T-I-F}{3},$$

(1)

$$a(u)=T-F,$$

(2)

$$c\left(u\right)=T,$$

(3)

The score function is an important index for evaluating neutrosophic numbers. For a neutrosophic number $R=<T_r,I_r,F_r>$, the truth-membership $T_r$ is positively correlated with the score function, and the indeterminacy-membership $I_r$ and false-membership $F_r$ are negatively correlated with the score function. In terms of the accuracy function, the greater the difference between the truth-membership $T_r$ and false-membership $F_r$ is, the more affirmative the statement is. Additionally, in regard to the certainty function, it positively depends on the truth-membership $T_r$.

On the basis of Definition 3, the comparison method between two neutrosophic numbers is represented as follows.

Definition 4

[30].Let$u_1=<T_1,I_1,F_1>,u_2=<T_2,I_2,F_2>$be two neutrosophic numbers, the comparison relationships between$u_1$and$u_2$ are as follows:

• If$s(u_1)>s(u_2)$,$u_1$is superior to$u_2$and it can be denoted by$u_1\succ u_2$;
• If$s(u_1)=s(u_2)$,$a(u_1)>a(u_2)$,$u_1$is superior to$u_2$and is denoted by$u_1\succ u_2$;
• If$s(u_1)=s(u_2)$,$a(u_1)=a(u_2)$and$c(u_1)>c(u_2)$,$u_1$is superior to$u_2$and is denoted by$u_1\succ u_2$;
• If$s(u_1)=s(u_2)$,$a(u_1)=a(u_2)$and$c(u_1)=c(u_2)$,$u_1$is equal to$u_2$, denoted by$u_1\succ u_2$.

Example 1.

For two neutrosophic numbers$u_1=<0.8,0.2,0.4>$and$u_2=<0.7,0.4,0.1>$, we can obtain that$s(u_1)=2.2/3$,$s(u_2)=2.2/3$,$a(u_1)=1.2/3$,$a(u_2)=1.8/3$,$c(u_1)=2.4/3$and$c(u_2)=2.1/3$based on Definition 3. Considering Definition 4, we can infer that$u_2$is superior to$u_1$, as denoted by$u_2\succ u_1$.

Definition 5

[31].Let$u_1=<T_1,I_1,F_1>,u_2=<T_2,I_2,F_2>$be two neutrosophic numbers, then the normalized Hamming distance between$u_1$and$u_2$ is defined as follows:

$$D^{△}\left(u_1,u_2\right)=\frac{\left(\left|T_1-T_2|+|I_1-I_2|+|F_1-F_2\right|\right)}{3}.$$

(4)

Definition 6

[4] (p. 1).Let$U$be the set of initial universe,$E$be the parameter set, and$P(U)$be the power set of$U$. Then a pair (F, E)is called a soft set over$U$where$F$is a mapping given by$F:E\to P(U)$.

Remark 1

[32].On account of the single valued neutrosophic set is an instance of the neutrosophic set, it is natural to infer that a single valued neutrosophic soft set is an instance of the neutrosophic soft set. However, Maji only considers neutrosophic soft sets, which take value from the standard subset of$[0,1]$rather than${]}^{-}0,1^{+}[$, so the definition of the single valued neutrosophic soft set is exactly the same as the concept of the neutrosophic soft set defined by Maji.

Definition 7

[17] (p. 1).Let$U$be the initial universal set,$E$be a set of parameters, and$P(U)$be the set of all neutrosophic subsets of$U$. The collection$(F,E)$is regarded as a neutrosophic soft set over$U$, where$F$refers to the mapping$F:E\to P(U)$.

Example 2.

Assume$U=\{u_1,u_2,u_3\}$is a set of three cars under consideration, and$E=\{e_1=\mathrm{cheap},e_2=\mathrm{equipment},e_3=\mathrm{fuel}\mathrm{consumption}\}$be the set of parameters for describing the three. In this case, we can define a function$F:E\to P(U)$as a neutrosophic soft set$(F,E)$, and it is represented as follows:

$$(F,E)=\left\{\begin{array}{c}F(e_1)=\{<u_1,0.8,0.4,0.3>,<u_2,0.5,0.7,0.3>,<u_3,0.2,0.5,0.8>\}\\ F(e_2)=\{<u_1,0.5,0.7,0,4>,<u_2,0.7,0.3,0.2>,<u_3,0.5,0.8,0.5>\}\\ F(e_3)=\{<u_1,0.4,0.6,0.3>,<u_2,0.9,0.3,0.1>,<u_3,0.4,0.7,0.5>\}\end{array}\right\}.$$

2.2. Prospect Theory

The prospect theory [27] (p. 2), proposed by Tversky and Kahneman, is a mainstream theory of behavioral science, and it studies human judgments or decision making behaviors under uncertain environments. The prospect theory mainly considers the value function and decision weight function. It implies three characteristics: Reference dependence, diminishing sensitivity and lose aversion. Reference dependence refers to the change of people’s perception depending on the change of the relative value. Diminishing sensitivity means that utility decreases as income increases. Additionally, loss aversion signifies that people value losses more than gains.

The prospect theory states that decision makers choose the optimal alternative based on the prospect value, which is determined by the value function and decision weight function. The prospect value can be obtained as follows:

$$V={\displaystyle \sum v(x-r)\omega (p_t)}.$$

(5)

$v(x-r)$ is the value function as defined follows:

$$v(x-r)=\{\begin{array}{cc}{(x-r)}^{\alpha },& x\ge r\\ -\lambda {(x-r)}^{\beta },& x<r\end{array},$$

(6)

where $x$ is the evaluation value of an object, $r$ is the reference point, then $(x-r)$ represents losses or gains. $x\ge r$ means gains, and the value function is concave; $x<r$ means losses, and the value function is convex. So $\alpha$, $\beta$ stand for the concave degree and convexity degree of the value function, respectively. $\lambda$ is the risk aversion coefficient, and $\lambda >1$ indicates that decision makers value risk more. By experimental verification, Tversky and Kahneman took the value of parameters as follows: $\alpha =\beta =0.88,\lambda =2.25$.

ω(P_t) is the decision weight function as defined follows:

$$\omega (p_t)=\frac{p_t{}^{\gamma }}{{((p_t{}^{\gamma })+({(1-p_t)}^{\gamma }))}^{\frac{1}{\gamma }}},$$

(7)

where $p_t$ is the objective possibility, and Tversky and Kahneman took the value of parameter $\gamma$ as 0.61.

3. The Measures of Determinacy Degree and Conflict Degree and Neutrosophic Soft Set Aggregation Rules

In this section, we initiate the determinacy degree measure and conflict degree measure of neutrosophic numbers, and then develop two kinds of aggregation rules of a neutrosophic soft set.

3.1. The Measures of Determinacy Degree and Conflict Degree

This paper employs the Hamming distance of information theory, which is a well-known measure designed to provide insights into the similarity of information [33,34] and has been widely employed in distance measures [26,35], to measure the determinacy degree and conflict degree. Before this, we present the concept of a minimum conflict neutrosophic number and maximum conflict neutrosophic number.

Definition 8.

Let$Minc=<1,0,0>$be the minimum conflict neutrosophic number, which means that the belongingness degree of an object is 1, and the non-belongingness degree and the neutrality degree of an object be zero, respectively. That is, the conflict degree of information is the smallest.

Additionally, let$Maxc=<0.5,1,0.5>$be the maximum conflict neutrosophic number. That is, the neutrosophic number, whose neutrality degree is one, and the belongingness degree and non-belongingness degree is 0.5. In order words, the conflict degree of information is the greatest.

Definition 9.

Let$u=<T,I,F>$be a neutrosophic number, the determinacy degree of$u$based on Equation (4) can be defined as follows:

$$d^{\Delta }(u)=\frac{(\left|T-1\right|+I+F)}{3},$$

(8)

which measures the normalized Hamming distance between$u$and the minimum conflict neutrosophic number.

Similarly, the conflict degree of$u$is determined by the normalized Hamming distance between$u$and the maximum conflict neutrosophic number, and defined as follows:

$$c^{\Delta }(u)=\frac{(\left|T-0.5\right|+\left|I-1\right|+\left|F-0.5\right|)}{3}$$

(9)

Example 3.

Considering Example 1, the determinacy degree and conflict degree of$u_1$can be computed as follows:$d^{\Delta }(u_1)=0.8/3$,$c^{\Delta }(u_1)=1.2/3$.

3.2. Aggregation Rules of a Neutrosophic Soft Set

In this subsection, we define two kinds of aggregation rules of a neutrosophic soft set, namely the weighted average aggregation rule and weighted geometric aggregation rule.

Definition 10.

Weighted average aggregation rule. Let$U$be the initial universal set,$E$be the set of parameters,$(F,E)$be a neutrosophic soft set over$U$, as represented by$F(e_j)(x_i)=<F_T(e_j)(x_i),F_I^{}(e_j)(x_i),F_F^{}(e_j)(x_i)>$$(i=1,2,\dots ,m;j=1,2,\dots ,n)$. Then, the weighted average aggregation rule of$(F,E)$can be denoted by${(F,E)}^{\mathsf{\Gamma }}=\{F^{\mathsf{\Gamma }}(x_1),F^{\mathsf{\Gamma }}(x_2),\dots ,F^{\mathsf{\Gamma }}(x_m)\}$, and defined as

$$F^{\mathsf{\Gamma }}(x_i)={\displaystyle \prod _{j=1}^{n}F(e_j)(x_i){\omega }_j}=<1-{{\displaystyle \prod _{j=1}^n(1-F_T(e_j)(x_i))}}^{{\omega }_j},{{\displaystyle \prod _{j=1}^n(F_I^{}(e_j)(x_i))}}^{{\omega }_j},{{\displaystyle \prod _{j=1}^n(F_F^{}(e_j)(x_i))}}^{{\omega }_j}>$$

(10)

where the vector$\omega =\{{\omega }_1,{\omega }_2,\dots ,{\omega }_n\}$stands for the weights of parameters, and${\displaystyle \sum _{j=1}^n{\omega }_j}=1$.

Based on Definition 10, the weighted geometric aggregation rule of a neutrosophic soft set is constructed.

Definition 11.

Weighted geometric aggregation rule. Considering the neutrosophic soft set$(F,E)$in Definition 10, we define the weighted geometric aggregation rule as${(F,E)}^{\mathsf{\Theta }}=\{F^{\mathsf{\Theta }}(x_1),F^{\mathsf{\Theta }}(x_2),\dots ,F^{\mathsf{\Theta }}(x_m)\}$, and

$$F^{\mathsf{\Theta }}(x_i)={\displaystyle \prod _{j=1}^n{(F(e_j)(x_i))}^{{\omega }_j}}=<{{\displaystyle \prod _{j=1}^n(F_T(e_j)(x_i))}}^{{\omega }_j},1-{{\displaystyle \prod _{j=1}^n(1-(F_I(e_j)(x_i)))}}^{{\omega }_j},1-{{\displaystyle \prod _{j=1}^n(1-(F_F(e_j)(x_i)))}}^{{\omega }_j}>$$

(11)

where the vector$\omega =\{{\omega }_1,{\omega }_2,\dots ,{\omega }_n\}$stands for the weights of parameters, and${\displaystyle \sum _{j=1}^n{\omega }_j}=1$.

Example 4.

Consider Example 2. Assume that the weight vector of parameters is$\omega =\{0.4,0.2,0.3\}$, then we can obtain the results of the weighted average aggregation and weighted geometric aggregation as follows, respectively.

$$\begin{gathered} {(F,E)}^{\mathsf{\Gamma }}=\{<u_1,0.6077,0.5537,0.3584>,<u_2,0.7015,0.4749,0.2244>,<u_3,0.3169,0.6512,0.6467>\}. \\ {(F,E)}^{\mathsf{\Theta }}=\{<u_1,0.6049,0.9905,0.9987>,<u_2,0.6837,0.9973,0.9998>,<u_3,0.3474,0.9798,0.9885>\} \end{gathered}$$

4. Algorithm for Neutrosophic Soft Sets in Stochastic Multi-Criteria Group Decision Making Based on Prospect Theory

4.1. Problem Description

In this section, we give a concise description of a stochastic multi-criteria group decision making problem under neutrosophic soft sets. Let $U=\{x_1,x_2,\dots ,x_m\}$ be a set of $m$ alternatives, $E=\{e_1,e_2,\dots ,e_n\}$ be a set of $n$ parameters and $DM=\{Z_1,Z_2,\dots Z_p\}$ be a set of $p$ decision makers. Assume that ${\omega }^{(t)}=<{\omega }_T^{(t)},{\omega }_I^{(t)},{\omega }_F^{(t)}>(t=1,2,\dots ,p)$ is the neutrosophic weight of decision maker $Z_t$, ${\delta }_j^{(t)}=<{\delta }_{Tj}^{(t)},{\delta }_{Ij}^{(t)},{\delta }_{Fj}^{(t)}>$ is the neutrosophic subjective weight assigned for parameter $e_j$ by decision maker $Z_t$, and the evaluation value of alternative $x_i$ related to parameter $e_j$ by decision maker $Z_t$ is expressed as $F^{(t)}(e_j)(x_i)=<F_T^{(t)}(e_j)(x_i),F_I^{(t)}(e_j)(x_i),F_F^{(t)}(e_j)(x_i)>$. Given $p$ neutrosophic soft sets $(F^{(t)},E)$ $(t=1,2,\dots ,p)$ of alternatives evaluated by decision makers, and the tabular representation of $(F^{(t)},E)$ $(t=1,2,\dots ,p)$ is shown in

Table 1. Tabular representation of neutrosophic soft sets $(F^{(t)},E)$ of alternatives.

$\mathbf{(}{\mathbf{F}}^{\mathbf{(}\mathbf{1}\mathbf{)}},\mathbf{E}\mathbf{)}$
	$e_1$	$e_2$	…	$e_n$
$x_1$	$F^{(1)}(e_1)(x_1)$	$F^{(1)}(e_2)(x_1)$	…	$F^{(1)}(e_n)(x_1)$
$x_2$	$F^{(1)}(e_1)(x_2)$	$F^{(1)}(e_2)(x_2)$	…	$F^{(1)}(e_n)(x_2)$
	$⋮$	$⋮$	$\ddots$	$⋮$
$x_m$	$F^{(1)}(e_1)(x_m)$	$F^{(1)}(e_2)(x_m)$	…	$F^{(1)}(e_n)(x_m)$
$\mathbf{(}{\mathbf{F}}^{\mathbf{(}\mathbf{2}\mathbf{)}}\mathbf{,}\mathbf{E}\mathbf{)}$
	$e_1$	$e_2$	…	$e_n$
$x_1$	$F^{(2)}(e_1)(x_1)$	$F^{(2)}(e_2)(x_1)$	…	$F^{(2)}(e_n)(x_1)$
$x_2$	$F^{(2)}(e_1)(x_2)$	$F^{(2)}(e_2)(x_2)$	…	$F^{(2)}(e_n)(x_2)$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
$x_m$	$F^{(2)}(e_1)(x_m)$	$F^{(2)}(e_2)(x_m)$	…	$F^{(2)}(e_n)(x_m)$
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
$\mathbf{(}{\mathbf{F}}^{\mathbf{(}\mathbf{p}\mathbf{)}}\mathbf{,}\mathbf{E}\mathbf{)}$
	$e_1$	$e_2$	…	$e_n$
$x_1$	$F^{(p)}(e_1)(x_1)$	$F^{(p)}(e_2)(x_1)$	…	$F^{(p)}(e_n)(x_1)$
$x_2$	$F^{(p)}(e_1)(x_2)$	$F^{(p)}(e_2)(x_2)$	…	$F^{(p)}(e_n)(x_2)$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
$x_m$	$F^{(p)}(e_1)(x_m)$	$F^{(p)}(e_2)(x_m)$	…	$F^{(p)}(e_n)(x_m)$

.

4.2. Determining the Determinacy Degree of Decision Makers

In stochastic multi-criteria group decision making problems, the weights of decision makers are stochastic and indeterminate. Therefore, how to obtain the weights as determinate values has become an important research topic. In this paper, we express the weights of decision makers as a neutrosophic number, and then compute the determinacy degree of decision makers to replace traditional weights.

Considering Definition 9, let ${\omega }_t=<{\omega }_t^T,{\omega }_t^I,{\omega }_t^F>(t=1,2,\dots ,p)$ be the neutrosophic weight of decision maker $Z_t$, then the determinacy degree of $Z_t$ can be computed as follows by Equation (8):

$$d^{\Delta }(t)=\frac{1-\frac{1}{3}\left(\right|{\omega }_t^T-1|+{\omega }_t^I+{\omega }_t^F)}{{\displaystyle \sum _{t=1}^{p}1-\frac{1}{3}\left(\right|{\omega }_t^T-1|+{\omega }_t^I+{\omega }_t^F)}}(t=1,2,\dots ,p),$$

(12)

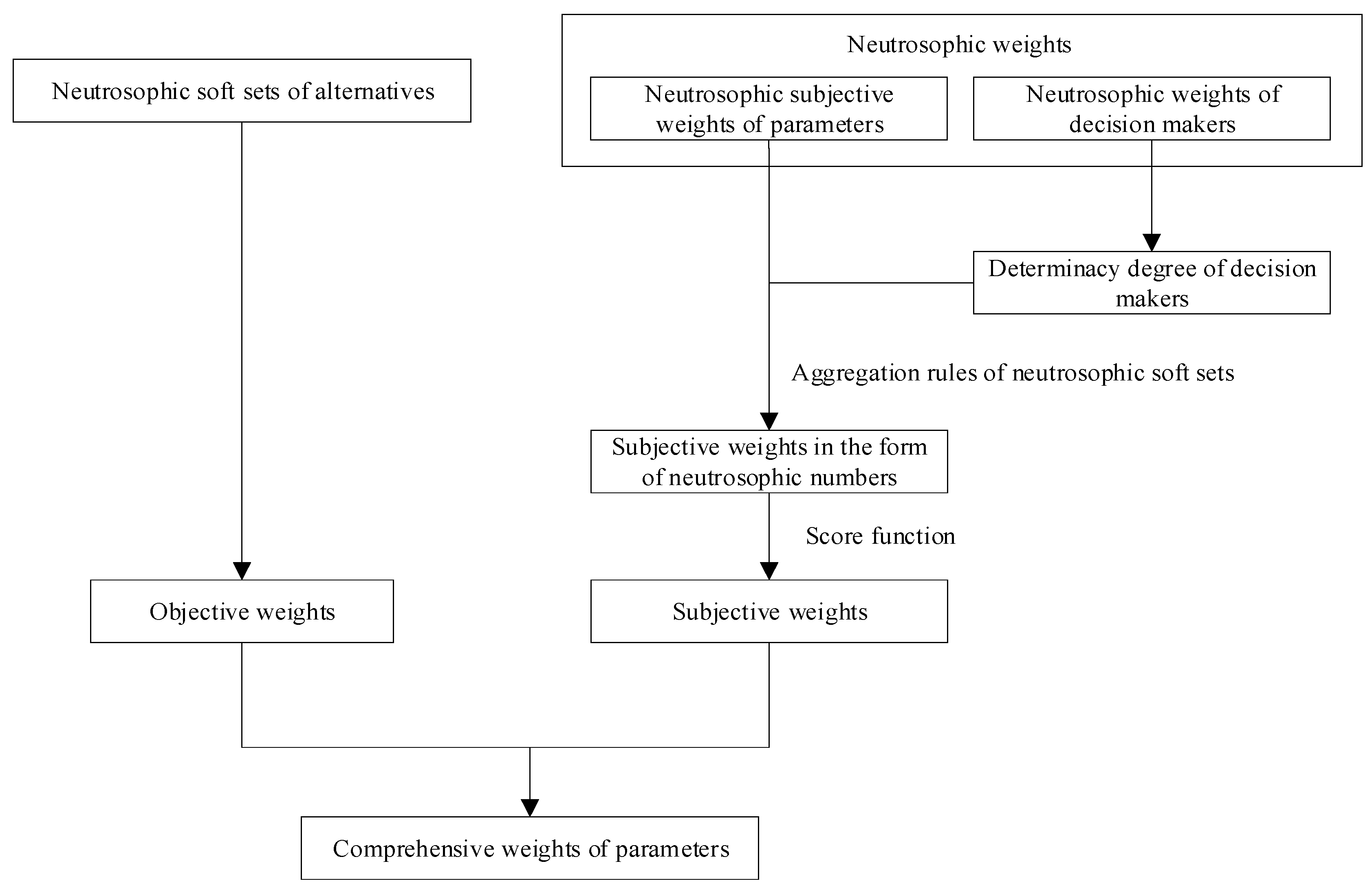
4.3. Calculating the Comprehensive Weights of Parameters

In this paper, the parameter weights are determined by combining subjective weights with objective weights. Among them, subjective weights are obtained by aggregating neutrosophic subjective weights provided by decision makers, which is more accurate than the way directly given by determinate values [25] (p. 2). The objective weights are calculated by the information entropy method [35]. Then, the principle of minimum information entropy [36] is employed to obtain comprehensive weights of parameters by integrating subjective weights and objective weights. The system framework is presented in Figure 1.

4.3.1. Computing the Subjective Weights

Under the stochastic environment, the judgements of decision makers are full of hesitancies. Considering this situation, instead of giving determinate values, this paper firstly aggregates neutrosophic subjective weights of parameters to obtain subjective weights in the form of neutrosophic numbers. Based on this, subjective weights are computed by the score function as Equation (1).

Assume parameter set $E=\{e_1,e_2,\dots ,e_j\}$ is the initial universal set, the set of decision makers $Z=\{z_1,z_2,\dots ,z_t\}$ is the parameter set, and $P(Z)$ is the set of all neutrosophic subsets of $E$. The neutrosophic soft set $(F,Z)$ over $E$ can be integrated by the weighted geometric aggregation rule as ${(F,Z)}^{\mathsf{\Theta }}=\{F^{\mathsf{\Theta }}(e_1),F^{\mathsf{\Theta }}(e_2),\dots ,F^{\mathsf{\Theta }}(e_m)\}$, and

$$F^{\mathsf{\Theta }}(e_j)={{\displaystyle \prod _{t=1}^p\stackrel{}{{\delta }_j^{(t)}}}}^{{\psi }_{{}^t}}=<{{\displaystyle \prod _{t=1}^p{\delta }_{Tj}^{(t)}}}^{{\psi }_t},1-{{\displaystyle \prod _{t=1}^p(1-{\delta }_{Ij}^{(t)})}}^{{\psi }_t},1-{{\displaystyle \prod _{t=1}^p(1-{\delta }_{Fj}^{(t)})}}^{{\psi }_t}>,$$

(13)

where ${\delta }_j^{(t)}=<{\delta }_{jT}^{(t)},{\delta }_{Ij}^{(t)},{\delta }_{Fj}^{(t)}>(j=1,2,\dots ,n)$ is the neutrosophic subjective weight assigned for parameter $e_j$ by $Z_t$, and ${\psi }_{\mathrm{t}}$ is the determinacy degree of $Z_t$.

Then, the subjective weights can be computed by the score function as shown below:

$$S{W}_j=\frac{2+{{\displaystyle \prod _{t=1}^p{\delta }_{Tj}^{(t)}}}^{{\psi }_t}-(1-{{\displaystyle \prod _{t=1}^p(1-{\delta }_{Ij}^{(t)})}}^{{\psi }_t})-(1-{{\displaystyle \prod _{t=1}^p(1-{\delta }_{Fj}^{(t)})}}^{{\psi }_t})}{3}.$$

(14)

4.3.2. Obtaining the Objective Weights: Information Entropy Method

Considering that the computation of objective weights is not the focus of this paper, we obtain objective weights by the information entropy method. The information entropy is used to measure the uncertainty of events. The greater the information entropy is, the greater the uncertainty degree. That is, the smaller the amount of information it carries, the smaller the weight is. Note that the uncertainty of neutrosophic numbers consists of two factors, one is the truth-membership and false-membership, and the other is the indeterminacy-membership.

Based on the information entropy method, we can obtain that the information entropy of parameter $e_j$ given by decision maker $Z_t$ is defined as:

$$E_j^t=1-\frac{1}{m}{{\displaystyle \sum }}_{i=1}^m\left(F_T^{\left(t\right)}\left(e_j\right)\left(x_i\right)+F_F^{\left(t\right)}\left(e_j\right)\left(x_i\right)\right)|F_I^{\left(t\right)}\left(e_j\right)\left(x_i\right)-F_I^{\left(t\right)}{}^c\left(e_j\right)\left(x_i\right)|(j=1,2,\dots ,n).$$

(15)

Then, the comprehensive information entropy of parameter $e_j$ is defined as follows:

$$E_j={\displaystyle \sum _{t=1}^p{\phi }_t}{E}_j^t(j=1,2,\dots ,n)$$

(16)

where ${\phi }_t$ is the determinacy degree of decision maker $Z_t$ computed by Equation (8).

So, the objective weights are obtained as:

$$O{W}_j=\frac{1-E_j}{{\displaystyle \sum _{j=1}^{n}1-E_j}}(j=1,2,\dots ,n).$$

(17)

4.3.3. Calculating the Comprehensive Weights

Based on the principle of the minimum information entropy, the comprehensive weight of parameter ${\varpi }_j$ can be calculated as follows:

$${\varpi }_j=\frac{\sqrt{O{W}_j\cdot S{W}_j}}{{\displaystyle \sum _{j=1}^n\sqrt{O{W}_j\cdot S{W}_j}}},$$

(18)

where $S{W}_j$ and $O{W}_j$ represent the subjective weight and objective weight of parameter $e_j$, respectively.

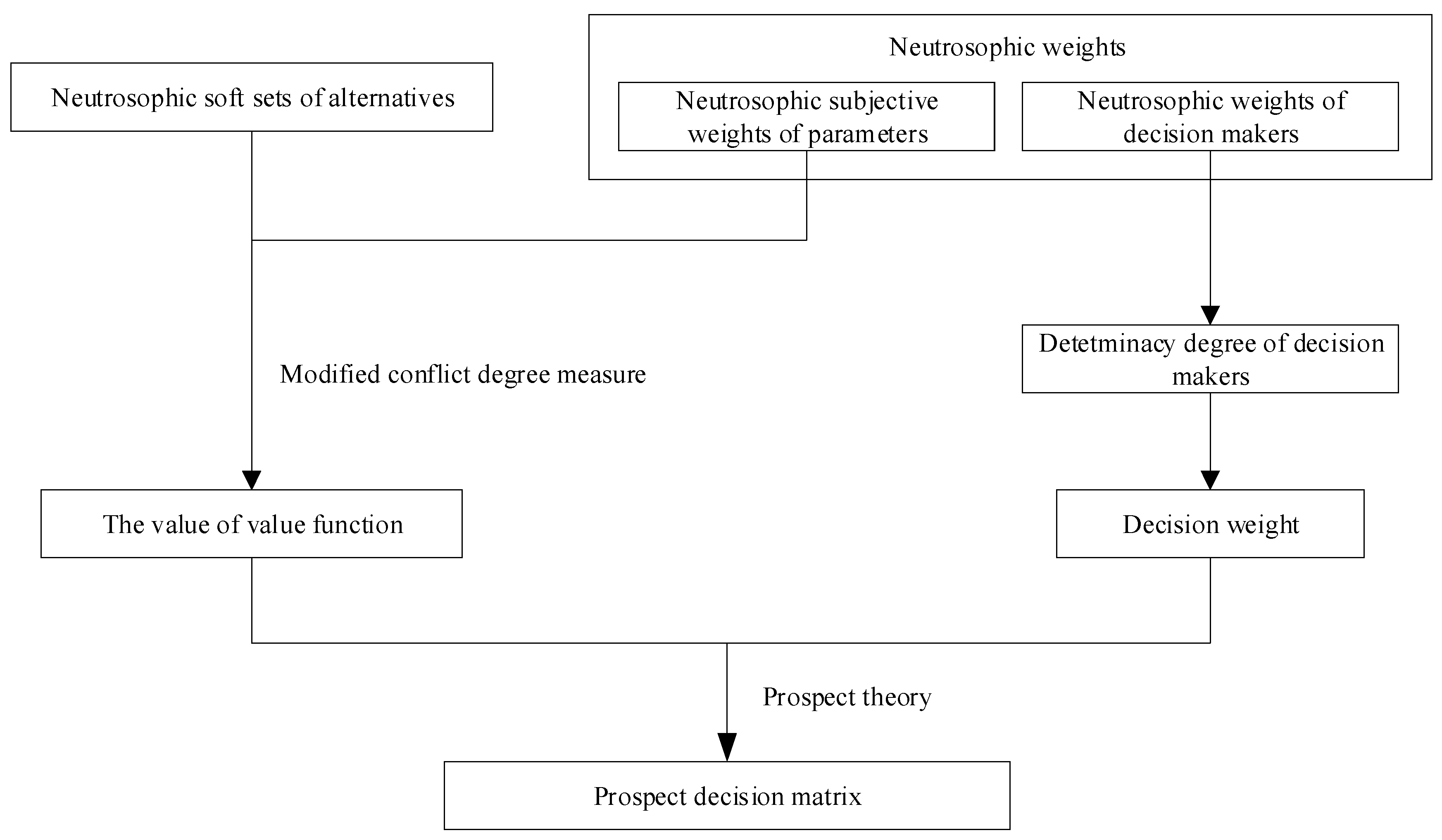
4.4. Computing the Comprehensive Prospect Values

The comprehensive prospect values of alternatives are determined by the prospect decision matrix and the comprehensive weights of parameters. Next, we expound how to generate the prospect decision matrix and obtain comprehensive values of alternatives, respectively.

4.4.1. Constructing the Prospect Decision Matrix

The core of constructing the prospect decision matrix is to compute the value function and decision weight function. In terms of the value function, we need to analyze the distance between the reference point and the actual value. This paper regards the maximum conflict neutrosophic number as the reference point, then the distance can be treated as the conflict degree of the actual value. Additionally, actual values refer to the alternative evaluation values with respect to the parameters. As for the decision weight function, the objective possibility is seen as the determinacy degree of the decision makers. The system framework of constructing the prospect decision matrix is shown in Figure 2.

We assume that the neutrosophic soft sets of alternatives and neutrosophic subjective weights of parameters are both provided by decision makers. So, the conflict degree of the alternative evaluation values with respect to the parameters should take the neutrosophic subjective weights of parameters into account. Based on the conflict degree measure given by Definition 9, we develop a modified conflict degree measure by introducing the neutrosophic subjective weights of parameters.

Assume $F(e_j)(x_i)=<F_T(e_j)(x_i),F_I(e_j)(x_i),F_F(e_j)(x_i)>$ is a neutrosophic number, which represents the value of alternative $x_i$ related to parameter $e_j$, and ${\alpha }_j=<{\alpha }_{jT},{\alpha }_{jI},{\alpha }_{jF}>$ is the neutrosophic subjective weight of parameter $e_j$. Considering the sum of ${\alpha }_{jT},{\alpha }_{jI}\mathrm{and}{\alpha }_{jF}$ may not be one, this paper normalizes them to be more consistent with the reality. Therefore, the measure of the modified conflict degree of $F(e_j)(x_i)$ is defined as follows:

$${mc}^{\Delta }(F(e_j)(x_i))=\frac{{\alpha }_{jT}\cdot \left|F_T(e_j)(x_i)-0.5\right|}{{\alpha }_{jT}+{\alpha }_{jI}+{\alpha }_{jF}}+\frac{{\alpha }_{jI}\cdot \left|F_I(e_j)(x_i)-1\right|}{{\alpha }_{jT}+{\alpha }_{jI}+{\alpha }_{jF}}+\frac{{\alpha }_{jF}\cdot \left|F_F(e_j)(x_i)-0.5\right|}{{\alpha }_{jT}+{\alpha }_{jI}+{\alpha }_{jF}}.$$

(19)

Subsequently, calculate the prospect value of each alternative with respect to the parameters as follows:

$$V_{ij}={\displaystyle \sum _{t=1}^{p}w(z_t)}v(F^{(t)}(e_j)(x_i)-x_0),$$

(20)

where

$$v(F^{(t)}(e_j)(x_i)-x_0)=\{\begin{array}{cc}{(m{c}^{\Delta }(F^{(t)}(e_j)(x_i),x_0))}^{0.88},& F^{(t)}(e_j)(x_i)\ge x_0\\ -2.25{(m{c}^{\Delta }(F^{(t)}(e_j)(x_i),x_0))}^{0.88},& F^{(t)}(e_j)(x_i)<x_0\end{array},$$

(21)

$$\omega (Z_t)=\frac{{({\psi }_t)}^{0.61}}{{({({\psi }_t)}^{0.61}+{(1-{\psi }_t)}^{0.61})}^{\frac{1}{0.61}}}.$$

(22)

Then, we can obtain the prospect decision matrix.

4.4.2. Computing the Comprehensive Prospect Values

Based on comprehensive weights of parameters and the prospect decision matrix, we can compute the comprehensive prospect values for alternatives as follows:

$$V_i={\displaystyle \sum _{j=1}^n{\varpi }_j{V}_{ij}}.$$

(23)

The system framework of computing the comprehensive prospect values is shown in Figure 3.

4.5. Algorithm for Neutrosophic Soft Sets in Stochastic Multi-Criteria Group Decision Making Based on Prospect Theory

In this section, a novel algorithm for neutrosophic soft sets in stochastic multi-criteria group decision making based on the prospect theory is proposed. The detailed operation steps of Algorithm 1 are presented below.

Algorithm 1: Neutrosophic soft sets in stochastic multi-criteria group decision making based on the prospect theory

Step 1: Input a neutrosophic set, which represents neutrosophic weights of decision makers and two neutrosophic soft sets, including alternatives description as shown in Table 1 and neutrosophic subjective weights of parameters evaluated by decision makers. Step 2: Normalize the neutrosophic soft sets of alternatives as follows: $$(\stackrel{△}{F^{(t)}},E)=\{\begin{array}{cc}(F_T^{(t)}(e_j)(x_i),F_I^{(t)}(e_j)(x_i),F_F^{(t)}(e_j)(x_i)),& e_j\mathrm{is}\mathrm{a}\mathrm{benefit}\mathrm{parameter}\\ (F_F^{(t)}(e_j)(x_i),1-F_I^{(t)}(e_j)(x_i),F_T^{(t)}(e_j)(x_i)),& e_j\mathrm{is}\mathrm{a}\cos \mathrm{t}\mathrm{parameter}\end{array}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(24)$$ Step 3: Compute the determinacy degree vector ${\psi }_{\mathrm{t}}=({\psi }_1,{\psi }_2,\dots ,{\psi }_p)$ of decision makers by Equation (8); Step 4: Construct the prospect decision matrix based on Equation (20). Step 5: Obtain the comprehensive weight vector ${\varpi }_j=({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_n)$ by Equation (18); Step 6: Calculate the comprehensive prospect value Vi for each alternative through Equation (23). Step 7: Make a decision by ranking alternatives based on comprehensive prospect values.

5. An Application of the Proposed Algorithm

In order to verify the feasibility of the proposed algorithm, we discuss the investment decision of a finance institution. Meanwhile, the existing five methods [17,25,37] (pp. 1–2) are employed for a comparative analysis to prove the feasibility and superiority of the proposed algorithm.

5.1. Example Analysis

Credit scoring can help financial institutions reduce financial risks and non-performing loans. Generally, financial institutions assess the credit score of borrowers based on basic information, such as age, profession, education, income, capital gains, residence and borrowing frequency. Recently, a financial institution wants to invest an amount of money in borrowers. The institution initially selects five borrowers as candidates. In addition, the institution makes a decision by analyzing the following four parameters: Highly educated, higher borrowing frequency, higher income and higher capital gains. Subsequently, the institution assembles a team composed of three decision makers to make the investment decision. Suppose that $U=\{u_1,u_2,u_3,u_4,u_5\}$ is the set of candidates, $E=\{e_1,e_2,e_3,e_4\}$ is the parameter set, and $DM=\{Z_1,Z_2,Z_3\}$ is the set of decision makers. Let the neutrosophic soft sets $(F^{(t)},E)(t=1,2,3)$ be the alternative evaluation values with respect to the parameters given by decision makers as follows.

$$(F^{(1)},E)=\left\{\begin{array}{c}{F}^{(1)}(e_1)=\{<\frac{u_1}{0.60,0.35,0.80}>,<\frac{u_2}{0.70,0.50,0.60}>,<\frac{u_3}{0.80,0.40,0.70}>,<\frac{u_4}{0.65,0.50,0.50}>,<\frac{u_5}{0.75,0.30,0.60}>\}\hfill \\ F^{(1)}(e_2)=\{<\frac{u_1}{0.50,0.80,0.20}>,<\frac{u_2}{0.60,0.30,0.70}>,<\frac{u_3}{0.70,0.35,0.80}>,<\frac{u_4}{0.80,0.30,0.70}>,<\frac{u_5}{0.80,0.20,0.55}>\}\hfill \\ F^{(1)}{}_1(e_3)=\{<\frac{u_1}{0.60,0.50,0.80}>,<\frac{u_2}{0.70,0.50,0.20}>,<\frac{u_3}{0.80,0.60,0.30}>,<\frac{u_4}{0.70,0.40,0.70}>,<\frac{u_5}{0.85,0.30,0.60}>\}\hfill \\ F^{(1)}(e_4)=\{<\frac{u_1}{0.50,0.80,0.60}>,<\frac{u_2}{0.40,0.70,0.30}>,<\frac{u_3}{0.60,0.40,0.70}>,<\frac{u_4}{0.60,0.35,0.80}>,<\frac{u_5}{0.70,0.30,0.40}>\}\hfill \end{array}\right\}$$

$$(F^{(2)},E)=\left\{\begin{array}{c}{F}^{(2)}(e_1)=\{<\frac{u_1}{0.60,0.35,0.80}>,<\frac{u_2}{0.70,0.50,0.60}>,<\frac{u_3}{0.80,0.40,0.70}>,<\frac{u_4}{0.65,0.50,0.50}>,<\frac{u_5}{0.75,0.30,0.60}>\}\hfill \\ F^{(2)}(e_2)=\{<\frac{u_1}{0.50,0.80,0.20}>,<\frac{u_2}{0.60,0.30,0.70}>,<\frac{u_3}{0.70,0.35,0.80}>,<\frac{u_4}{0.80,0.30,0.70}>,<\frac{u_5}{0.80,0.20,0.55}>\}\hfill \\ F^{(2)}(e_3)=\{<\frac{u_1}{0.60,0.50,0.80}>,<\frac{u_2}{0.70,0.50,0.20}>,<\frac{u_3}{0.80,0.60,0.30}>,<\frac{u_4}{0.70,0.40,0.70}>,<\frac{u_5}{0.85,0.30,0.60}>\}\hfill \\ F^{(2)}(e_4)=\{<\frac{u_1}{0.50,0.80,0.60}>,<\frac{u_2}{0.40,0.70,0.30}>,<\frac{u_3}{0.60,0.40,0.70}>,<\frac{u_4}{0.60,0.35,0.80}>,<\frac{u_5}{0.70,0.30,0.40}>\}\hfill \end{array}\right\}$$

$$(F^{(3)},E)=\left\{\begin{array}{c}{F}^{(3)}(e_1)=\{<\frac{u_1}{0.60,0.35,0.80}>,<\frac{u_2}{0.70,0.50,0.60}>,<\frac{u_3}{0.80,0.40,0.70}>,<\frac{u_4}{0.65,0.50,0.50}>,<\frac{u_5}{0.75,0.30,0.60}>\}\hfill \\ F^{(3)}(e_2)=\{<\frac{u_1}{0.50,0.80,0.20}>,<\frac{u_2}{0.60,0.30,0.70}>,<\frac{u_3}{0.70,0.35,0.80}>,<\frac{u_4}{0.80,0.30,0.70}>,<\frac{u_5}{0.80,0.20,0.55}>\}\hfill \\ F^{(3)}(e_3)=\{<\frac{u_1}{0.60,0.50,0.80}>,<\frac{u_2}{0.70,0.50,0.20}>,<\frac{u_3}{0.80,0.60,0.30}>,<\frac{u_4}{0.70,0.40,0.70}>,<\frac{u_5}{0.85,0.30,0.60}>\}\hfill \\ F^{(3)}(e_4)=\{<\frac{u_1}{0.50,0.80,0.60}>,<\frac{u_2}{0.40,0.70,0.30}>,<\frac{u_3}{0.60,0.40,0.70}>,<\frac{u_4}{0.60,0.35,0.80}>,<\frac{u_5}{0.70,0.30,0.40}>\}\hfill \end{array}\right\}$$

The neutrisophic set $D$ represents the neutrosophic weights of decision makers, and the neutrisophic soft set $(F,Z)$ stands for neutrosophic subjective weights of parameters. They are valued as follows:

$$D=\{<Z_1,0.3,0.5,0.7>,<Z_2,0.1,0.4,0.6>,<Z_3,0.6,0.5,0.2>\}$$

$$(F,Z)=\left\{\begin{array}{c}F(Z_1)=\{<\frac{e_1}{0.40,0.60,0.50}>,<\frac{e_2}{0.35,0.70,0.60}>,<\frac{e_3}{0.40,0.60,0.55}>,<\frac{e_4}{0.40,0.60,0.75}>\}\hfill \\ F(Z_2)=\{<\frac{e_1}{0.70,0.45,0.30}>,<\frac{e_2}{0.50,0.80,0.60}>,<\frac{e_3}{0.70,0.55,0.40}>,<\frac{e_4}{0.70,0.40,0.65}>\}\hfill \\ F(Z_3)=\{<\frac{e_1}{0.65,0.70,0.40}>,<\frac{e_2}{0.60,0.35,0.75}>,<\frac{e_3}{0.40,0.65,0.70}>,<\frac{e_4}{0.35,0.60,0.50}>\}\hfill \end{array}\right\}$$

Step 1: Input the neutrosophic soft sets $(F^{(t)},E)(t=1,2,3)$, $(F,Z)$ and the neutrosophic set $D$.

Step2: There is no need to normalize the neutrosophic soft sets $(F^{(t)},E)(t=1,2,3)$ of alternatives, because the parameters adopted in this study are benefit parameters.

Step 3: Compute the determinacy degree vector of decision makers based on Equation (8) as follows:

$${\psi }_t=\{0.3478,0.4130,0.2391\}$$

Step 4: Construct the prospect decision matrix based on Equation (20).

$$V_{\mathrm{ij}}=\left(\begin{array}{cccc}0.3878& 0.2846& 0.3574& 0.2274\\ 0.3035& 0.3751& 0.3571& 0.2712\\ 0.4536& 0.3834& 0.3226& 0.3180\\ 0.3345& 0.3294& 0.3120& 0.3776\\ 0.3482& 0.4482& 0.4055& 0.3481\end{array}\right).$$

Step 5: Determine the comprehensive weight vector ${\varpi }_j=({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_n)$ for the parameters as Equation (18), and the neutrosophic subjective weights are aggregated by the weighted geometric aggregation rule as Equation (11).

$${\varpi }_j=(0.2991,0.2260,0.2898,0.1851)$$

Step 6: Obtain the comprehensive prospect value $V_i$ by Equation (23).

$$V_1=0.3269,V_2=0.3292,V_3=0.3746,V_4=0.3348,V_5=0.3874.$$

Step 7: Make a decision by ranking the comprehensive prospect value of the five candidates.

$$x_5\succ x_3\succ x_4\succ x_2\succ x_1$$

Therefore, we can see that the optimal candidate is $x_5$. $x_3$, $x_4$ are suboptimal, and $x_2$, $x_1$ are the worst.

Furthermore, we also utilize the weighted average aggregation rule to compute the subjective weights of parameters. In addition, the computational procedure is shown as follows.

Step 1–4: Be consistent with the above steps 1–4.

Step 5: Determine the comprehensive weight vector ${\varpi }_j=({\varpi }_1,{\varpi }_2,\dots ,{\varpi }_n)$ for the parameters as Equation (18), and the neutrosophic subjective weights are aggregated by the weighted average aggregation rule.

$${\varpi }_j=(0.2903,0.2127,0.2523,0.2447).$$

Step 6: Obtain the comprehensive prospect value $V_i$ by Equation (23).

$$V_1=0.3254,V_2=0.3295,V_3=0.3744,V_4=0.3348,V_5=0.3876.$$

Step 7: Make a decision by ranking the five candidates.

$$x_5\succ x_3\succ x_4\succ x_2\succ x_1.$$

So the best optimal is still $x_5$, the following are $x_3$, $x_4$, and the worst are $x_2$, $x_1$.

Obviously, we can see that the ranking orders obtained by two aggregation rules of the neutrosophic soft set are the same.

5.2. Comparative Analysis

A comparative analysis with existing methods is performed to justify the feasibility and superiority of the proposed method. The existing methods include the method proposed by Maji [17] (p. 1), the three methods carried out by Peng and Liu [25] (p. 2) and the aggregated neutrosophic set method [37] (p. 11).

In the decision making method outlined by Maji [17] (p. 1), the final ranking is obtained based on the comparison matrix through briefly comparing with three membership function values. The three neutrosophic soft decision making methods [25] (p. 2) include the non-linear weighted comprehensive method to determine parameter comprehensive weights by combining objective weights and subjective weights. Objective weights are computed by the grey system method, and subjective weights are directly given determinate values. Then, three neutrosophic soft decision making methods are constructed based on EDAS, similarity measure, and the level soft set to rank alternatives in practical problems. Among the three, EDAS and the similarity measure methods obtain the final ranking based on the accurate calculation of alternative evaluation values. In addition, the level soft set method makes a decision by roughly comparing the threshold value with alternative evaluation values. In terms of the aggregated neutrosophic set method [37] (p. 11), alternatives are aggregated using the arithmetic average and sorted by TOPSIS.

Note that there are two crucial issues. On one hand, the above methods all make decisions under a single decision maker. In order to successfully apply them to group decision making, this paper employs the weighted average algorithm to the score of alternatives to all decision makers, based on the decision maker determinacy degree of this study. On the other hand, the method in [17] (p. 1) and [37] (p. 11) does not take parameter weights into consideration. Although the EDAS, similarity measure and level soft set methods [25] (p. 2) comprehensively consider objective weights and subjective weights, the subjective weights are directly given determinate values, which cannot reflect the hesitancies of decision makers under uncertainties. Considering this, the comparative analysis applies the subjective weights obtained from this study to the three methods in [25] (p. 2).

The final ranking of the stochastic multi-criteria group decision making problem mentioned in Section 5.1 are presented in

Table 2. A comparative study with some existing methods.

Method	The Final Ranking	The Optimal Alternative
The proposed method
Weighted geometric neutrosophic rule	$x_5\succ x_3\succ x_4\succ x_2\succ x_1$	$x_5$
Weighted average neutrosophic rule	$x_5\succ x_3\succ x_4\succ x_2\succ x_1$	$x_5$
The determinacy degree of decision makers${\psi }_t=\{0.3913,0.2826,0.3261\}$
Maji [17]	$x_5\succ x_4\succ x_3\succ x_2\succ x_1$	$x_5$
EDAS [25]	$x_5\succ x_3\succ x_4\succ x_2\succ x_1$	$x_5$
Similarity [25]	$x_5\succ x_3\succ x_4\succ x_2\succ x_1$	$x_5$
Level soft set [25]	$x_5\succ x_4\succ x_3\succ x_2\succ x_1$	$x_5$
TOPSIS [37]	$x_5\succ x_3\succ x_4\succ x_2\succ x_1$	$x_5$

, by utilizing the proposed method and the methods in [17,25,37] (pp. 1–2, 11). By comparison, the results of the proposed method are consistent with those of most comparison methods, which prove the effectiveness of the proposed method.

From Table 2, we can find that the final rankings of the proposed algorithm are different from Maji’s method and the level soft set method. The difference can be attributed to two reasons. One is that both methods are approximate comparisons of the alternative evaluation values, and the original evaluation values are not used to the greatest extent. The other is that the threshold value difference of the level soft set method can directly lead to different final rankings. However, decision makers can hardly decide which threshold value to use.

Through comparison, the final rankings of the other three methods are consistent with the proposed method. Among them, EDAS also adopts the aggregation method just as the proposed method. Different from EDAS, the proposed method considers the psychological expectation of decision makers in the borrower selection issue. Thus, in complex group decision making problems, the proposed method can produce more reasonable results than existing methods.

From the above analysis, the main superiorities of the proposed method can be summarized into three aspects. Firstly, this study originally employs neutrosophic soft sets for handling stochastic multi-criteria group decision making problems, which cannot be solved in existing methods. Secondly, the proposed method expresses the weights of subjective weights of parameters by neutrosophic numbers, which can fully reflect the hesitancies of decision makers. Meanwhile, this study presents the weights of decision makers by neutrosophic numbers, which can better incorporate stochastic into the decision making process. Thirdly, the proposed method considers the psychological expectations of decision makers in the borrower selection process. Therefore, it is able to analyze the decision making behavior more objectively.

6. Conclusions

Under uncertain environments, a mass of inconsistent information appears. Neutrosophic soft sets are powerful tools to address these issues involving inconsistent information. Considering this, we develop a generalized stochastic multi-criteria group decision making framework under neutrosophic soft sets, by innovatively integrating the prospect theory and neutrosophic soft sets into our framework. This paper describes the reference point, the psychological expectations of decision makers, in the form of neutrosophic sets. Then, in addition, this study demonstrates how to compute the alternative prospect values as the reference for decision making.

We conduct experiments to test the feasibility and validity of our decision making framework. The main contributions of this paper are fourfold. Firstly, we construct a new algorithm for the stochastic multi-criteria group decision making based on neutrosophic soft sets, which can analyze inconsistent information in decision making effectively. Secondly, the weights of decision makers and parameter subjective weights are both expressed in the form of neutrosophic numbers. Compared with the way directly given determinate values in existing methods [25] (p. 2), the proposed method can embody the stochastic into decision making processes. Thirdly, the research successfully combines the prospect theory with neutrosophic softs sets to construct the stochastic multi-criteria group decision making algorithm. Compared with the existing literatures based on the expected utility theory [16,17,25,26] (pp. 1-2), this research considers the influence of psychological expectations on decision results. Finally, we explore the conflict degree measure of neutrosophic numbers and two aggregation rules of neutrosophic soft sets, and further define the measure of the modified conflict degree to accommodate the multi-criteria group decision making.

The proposed method is not only suitable for credit scoring, but also for decision-making problems in other fields, especially for decisions with inconsistent information. As a suggestion for future researches, we shall integrate more advanced decision theories into neutrosophic soft sets and address stochastic multi-criteria group decision making issues.