Stabilization of Delta Operator Systems with Actuator Saturation via an Anti-Windup Compensator
Abstract
1. Introduction
2. Problem Statement and Preliminaries
3. Main Results
New Model Reformulation
4. Anti-Windup Optimization
- Step 1
- For given , and , fix a sufficiently large such that the constrained minimization (27) is feasible. Then, set . Fix a sufficiently small , and set .
- Step 2
- Solve the following LMI minimization problem:subject to LMIs in (27).
- Step 3
- Substitute the new matrix variables into (27). If the result is feasible, then set and the new solution as , and repeat Step 2; otherwise, is the required estimate: Stop.
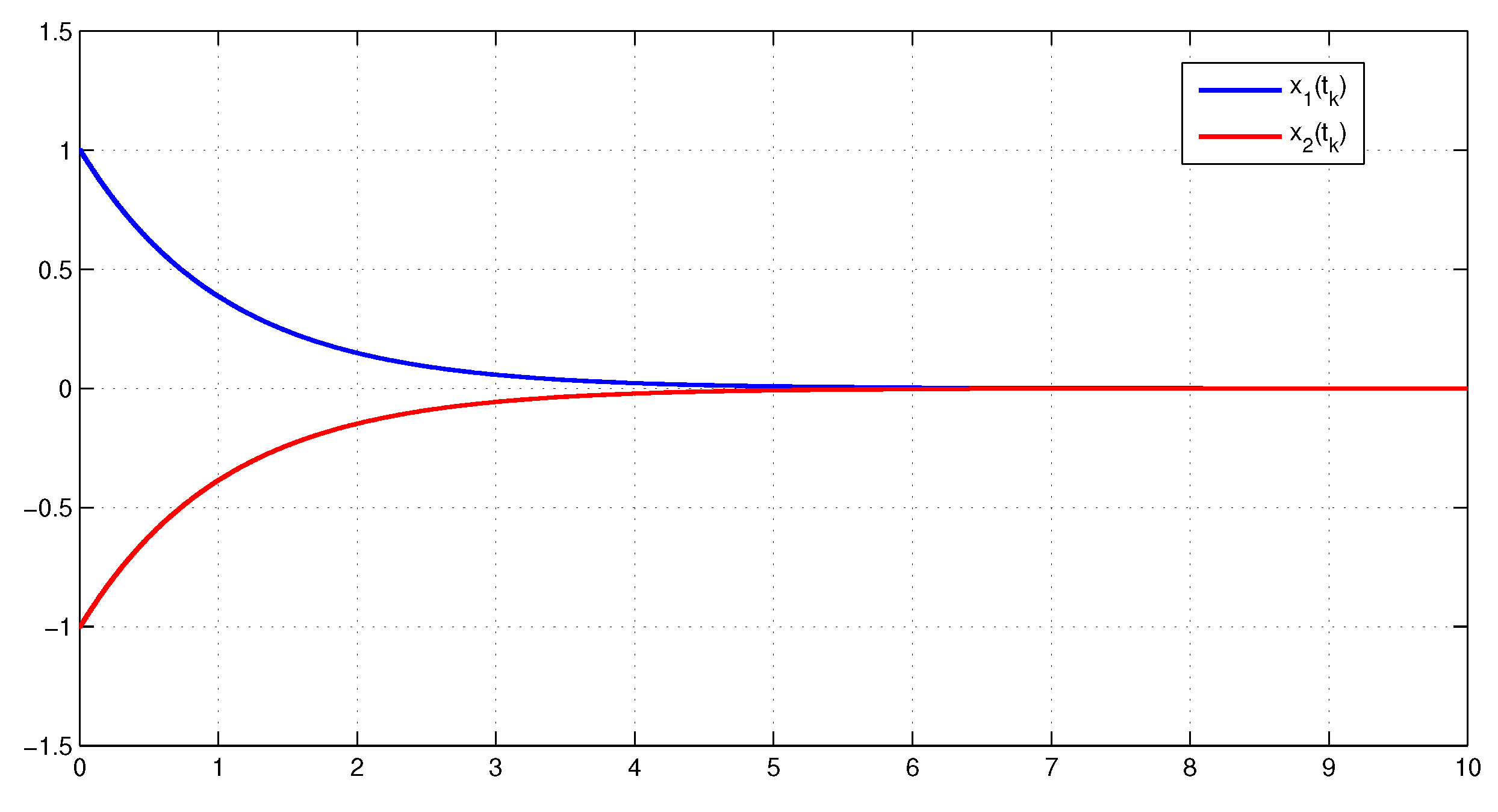
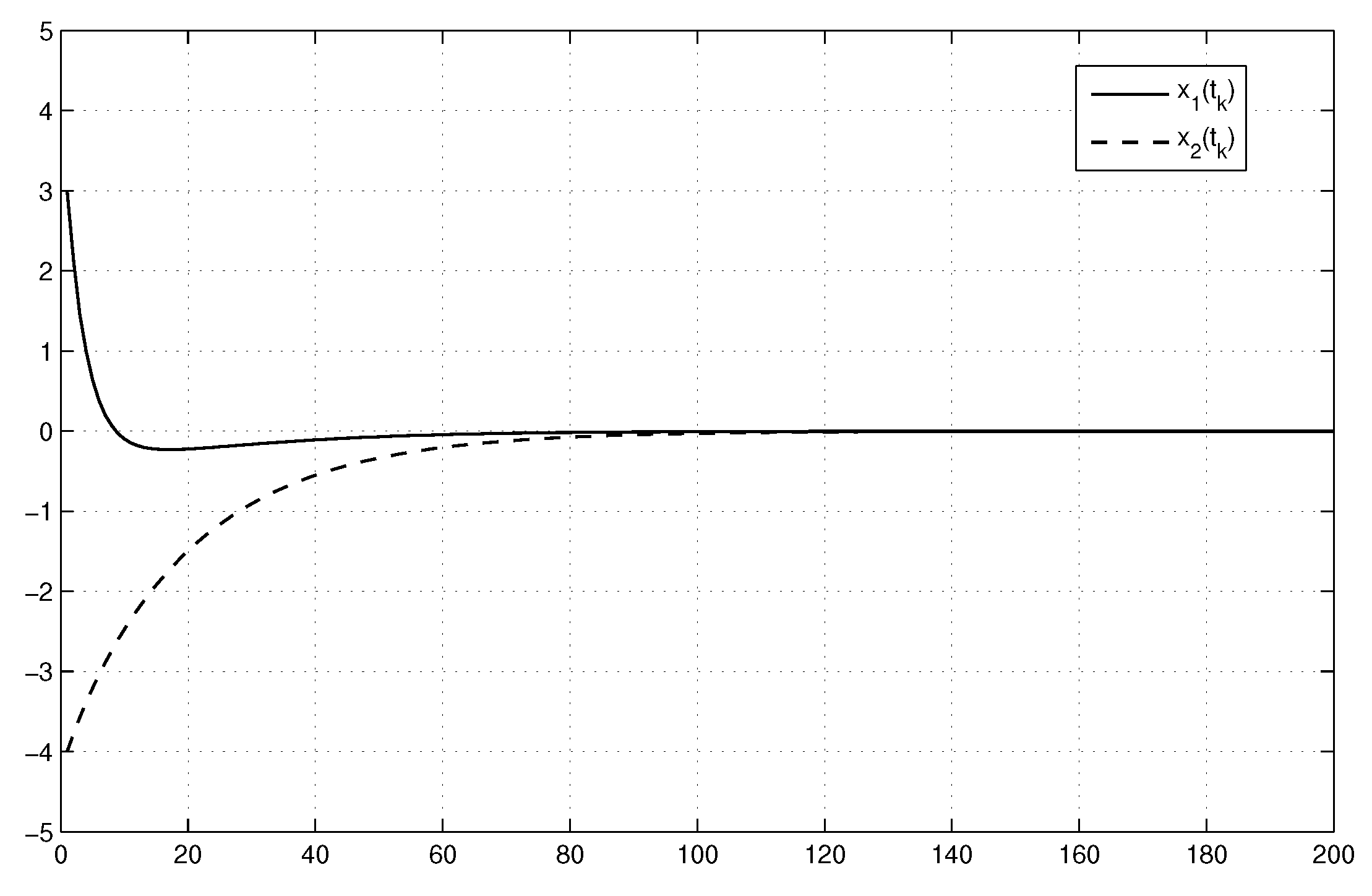
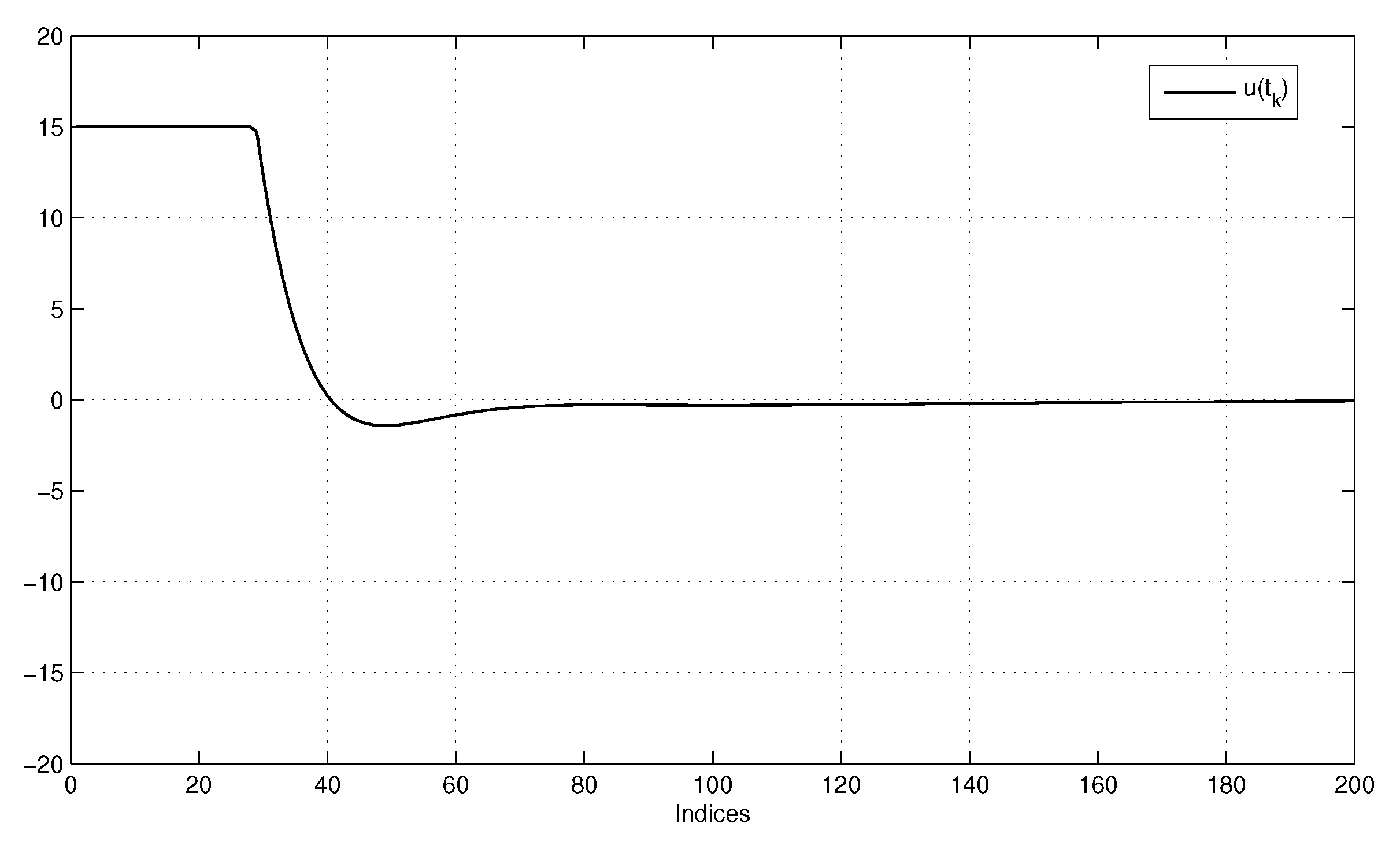
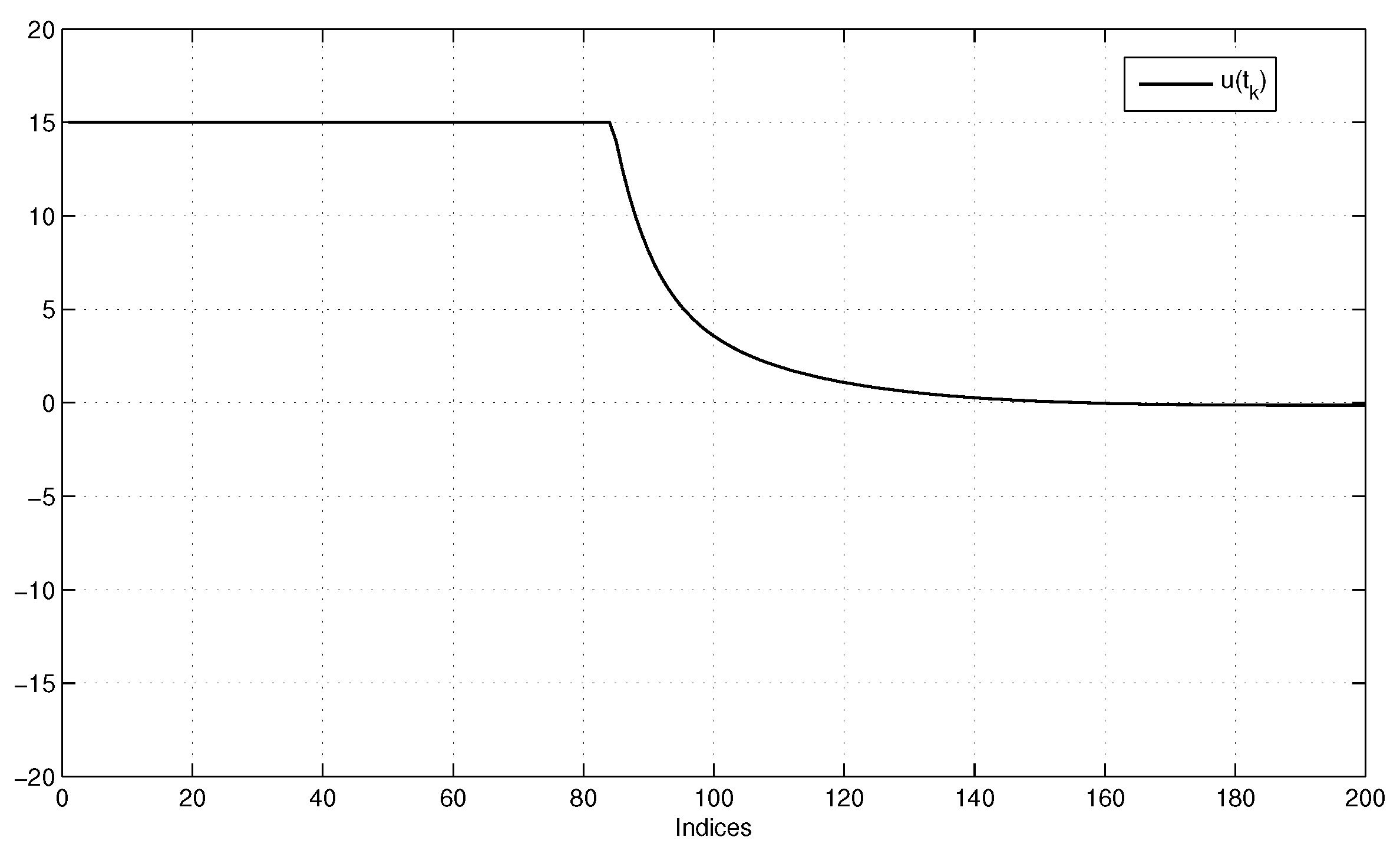
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ech-charqy, A.; Ouahi, M.; Tissir, E.H. Delay-dependent robust stability criteria for singular time-delay systems by delay-partitioning approach. Int. J. Syst. Sci. 2018, 39, 2957–2967. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q.G.; Xie, L.; Lin, C. Further improvement of free weighting matrices technique for systems with time-delay. IEEE Trans. Autom. Control 2007, 52, 293–299. [Google Scholar] [CrossRef]
- Tissir, E.H. Delay-dependent robust stability of linear systems with non-commensurate time varying delays. Int. J. Syst. Sci. 2007, 38, 749–757. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M. Improved robust stabilization method for linear systems with interval time-varying input delays by using wirtinger inequality. ISA Trans. 2015, 56, 111–122. [Google Scholar] [CrossRef]
- Belmfedel Alaoui, S.; Tissir, E.H.; Chaibi, N. Small-Gain Theorem and Finite Frequency Analysis of TCP/AQM System With Time Varing Delay. IET Control Theory Appl. 2019, 13, 1971–1982. [Google Scholar]
- El Aiss, H.; Hmamed, A.; El Hajjaji, A. Improved stability and H∞ performance criteria for linear systems with interval time-varying delays via three terms approximation. Int. J. Syst. Sci. 2017, 48, 3450–3458. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Leal, R.L.; Mayne, D.Q. Rapprochement between continuous and discrete model refrence adaptive control. Automatica 1986, 22, 199–207. [Google Scholar] [CrossRef]
- Mrabti, M.; Hmamed, A. Bounds for the solution of the Lyapunov matrix equation a unified approach. Syst. Control Lett. 1992, 18, 73–81. [Google Scholar] [CrossRef]
- Xie, X.; Yin, S.; Gao, H. Asymptotic stability and stabilization of uncertain delta operator systems with time varying delays. IET Control Theory Appl. 2013, 7, 1071–1078. [Google Scholar] [CrossRef]
- Xu, M. Robust H∞ filtering design for Takagi-Sugeno fuzzy systems with time-varying delay via delta operator approach. Adv. Mech. Eng. 2017, 1–13. [Google Scholar] [CrossRef]
- El Aiss, H.; Rachid, H.; Hmamed, A.; El Hajjaji, A. Approach to delay-dependent robust stability and stabilisation of delta operator systems with time-varying delays. IET Control Theory Appl. 2018, 12, 786–792. [Google Scholar] [CrossRef]
- El Fezazi, N.; Tissir, E.H.; Haoussi, F.E.; Alvarez, T.; Tadeo, F. Control Based on Saturated Time-Delay Systems Theory of Mach Number in Wind Tunnels. Circuits Syst. Signal Process 2017. [Google Scholar] [CrossRef]
- El Fezazi, N.; Haoussi, F.E.; Tissir, E.H.; Alvarez, T.; Tadeo, F. Robust stabilization using a sampled-data strategy of uncertain neutral state-delayed systems subject to input limitations. Circuits Int. J. Appl. Math. Comput. Sci. 2018, 28, 111–122. [Google Scholar] [CrossRef]
- Lamrabet, O.; Ech-charqy, A.; Tissir, E.H.; El Haoussi, F. Sampled data Control for Takagi-Sugeno Fuzzy Systems with Actuator Saturation. Procedia Comput. Sci. 2019, 148, 448–454. [Google Scholar] [CrossRef]
- Lamrabet, O.; Tissir, E.H.; El Haoussi, F. Anti-windup Compensator Synthesis for Sampled-Data Delay Systems. Circuits Syst. Signal Process 2018. [Google Scholar] [CrossRef]
- Lamrabet, O.; El Fezazi, N.; El Haoussi, F.; Tissir, E.H. Using Input Delay Approach for Synthesizing an Anti-windup Compensator to AQM in TCP/IP Networks. In Proceedings of the International Conference on Advanced Technologies, Signal and Image Processing, Fez, Morocco, 22–24 May 2017. [Google Scholar] [CrossRef]
- Yang, H.; Shi, P.; Li, Z.; Hua, C. Analysis and design for delta operator systems with actuator saturation. Int. J. Control. 2014, 87, 987–999. [Google Scholar] [CrossRef]
- Yang, H.; Li, Z.; Hua, C.; Liu, Z. Stability Analysis of Delta Operator Systems with Actuator Saturation by a Saturation-Dependent Lyapunov Function. Circuits Syst. Signal Process 2014. [Google Scholar] [CrossRef]
- Shi, P.; Yang, H.; Zhang, L. Analysis and design of delta operator systems with nested actuator saturation. Int. J. Syst. Sci. 2015, 47, 1–7. [Google Scholar] [CrossRef]
- Middleton, R.H.; Goodwin, G.C. Digital Control and Estimation: A Unified Approach; Prentice Hall: Upper Saddle River, NJ, USA, 1990. [Google Scholar]
- Wang, Y.; Cao, Y.; Sun, Y. Anti-windup compensator gain design for time-delay systems with constraints. Acta Autom. Sin. 2006, 32, 455–470. [Google Scholar]
- Zhang, J.; Peng, C.; Du, D.; Zheng, M. Improved Stability and Stabilization Criteria for Uncertain T-S Fuzzy Systems with Interval Time-Varying Delay via Discrete Wirtinger-Based Inequality. Int. J. Fuzzy Syst. 2015, 18, 784–791. [Google Scholar] [CrossRef]
- Feuer, A.; Goodwin, G.C. Sampling in Digital Signal Processing and Control; Birkhauser: Boston, MA, USA, 1996. [Google Scholar]
- Goodwin, G.C.; Middleton, R.H. High speed digital signal processing and control. Proc. IEEE 1992, 80, 240–259. [Google Scholar] [CrossRef]
- Fridman, E.; Shaked, U. Input-output approach to stability and L2-gain analysis of systems with time-varying delays. Syst. Control Lett. 2007, 55, 1041–1053. [Google Scholar] [CrossRef]
- Kao, C.Y.; Lincoln, B. Simple stability criteria for systems with time-varying delay. Automatica 2004, 40, 1429–1434. [Google Scholar] [CrossRef]
- Gu, K.; Xu, S. Small gain problem in coupled differential-difference equations, time-varying delay, and direct lyapunov method. Int. J. Robust Nonlinear Control 2011, 21, 429–451. [Google Scholar] [CrossRef]
- El Haoussi, F.; Tissir, E.H.; Tadeo, F. Advances in the robust stabilization of neutral systems with saturating actuator. Int. J. Ecol. Dev. 2014, 28, 59–62. [Google Scholar]
- El Fezazi, N.; El Haoussi, F.; Tissir, E.H.; Bender, F.B.; Alvarez, T. Multiclass AQMon a TCP/IP router: A control theory approach. Int. J. Nonlinear Control 2019, 1–15. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Liu, Z.; Zhao, L. Robust fuzzy-scheduling control for nonlinear systems subject to actuator saturation via delta operator approach. Inf. Sci. 2014, 272, 158–172. [Google Scholar] [CrossRef]
- Yang, H.; Xia, Y.; Geng, Q. Analyse and Synthesis of Delta Operator Systems with Actuator Saturation. In Studies in Systems, Decision and Control; Springer: Berlin/Heidelberg, Germany, 2019; Volume 193. [Google Scholar]

| 1 | 21 | |
| 3 | 23 | |
| 5 | 25 | |
| 7 | 27 | |
| 9 | 29 | |
| 11 | 31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rachid, H.; Lamrabet, O.; Tissir, E.H. Stabilization of Delta Operator Systems with Actuator Saturation via an Anti-Windup Compensator. Symmetry 2019, 11, 1084. https://doi.org/10.3390/sym11091084
Rachid H, Lamrabet O, Tissir EH. Stabilization of Delta Operator Systems with Actuator Saturation via an Anti-Windup Compensator. Symmetry. 2019; 11(9):1084. https://doi.org/10.3390/sym11091084
Chicago/Turabian StyleRachid, Hafsaa, Ouarda Lamrabet, and El Houssaine Tissir. 2019. "Stabilization of Delta Operator Systems with Actuator Saturation via an Anti-Windup Compensator" Symmetry 11, no. 9: 1084. https://doi.org/10.3390/sym11091084
APA StyleRachid, H., Lamrabet, O., & Tissir, E. H. (2019). Stabilization of Delta Operator Systems with Actuator Saturation via an Anti-Windup Compensator. Symmetry, 11(9), 1084. https://doi.org/10.3390/sym11091084




