Quadratic Spline Wavelets for Sparse Discretization of Jump–Diffusion Models

Abstract

This paper is concerned with a construction of new quadratic spline wavelets on a bounded interval satisfying homogeneous Dirichlet boundary conditions. The inner wavelets are translations and dilations of four generators. Two of them are symmetrical and two anti-symmetrical. The wavelets have three vanishing moments and the basis is well-conditioned. Furthermore, wavelets at levels i and j where $\left|i-j\right|>2$ are orthogonal. Thus, matrices arising from discretization by the Galerkin method with this basis have $\mathcal{O}\left(1\right)$ nonzero entries in each column for various types of differential equations, which is not the case for most other wavelet bases. To illustrate applicability, the constructed bases are used for option pricing under jump–diffusion models, which are represented by partial integro-differential equations. Due to the orthogonality property and decay of entries of matrices corresponding to the integral term, the Crank–Nicolson method with Richardson extrapolation combined with the wavelet–Galerkin method also leads to matrices that can be approximated by matrices with $\mathcal{O}\left(1\right)$ nonzero entries in each column. Numerical experiments are provided for European options under the Merton model.

1. Introduction

Nowadays, various models and methodologies are available to calculate theoretical values of options, including the famous Black–Scholes model as well as stochastic volatility models such as the Heston or the Stein and Stein models. These models assume that the price of the underlying asset is represented by a continuous function, which is not always consistent with real market prices. This paper focuses on jump–diffusion models originally suggested by Merton [1] and later generalized (e.g., in [2]). These models assume that the spot price S of the underlying asset at time $\tilde{t}$ follows the jump–diffusion process

$$\frac{dS\left(\tilde{t}\right)}{S\left(\tilde{t}-\right)}=\mu d\tilde{t}+\sigma dW\left(\tilde{t}\right)+d\left({\displaystyle \sum _{i=1}^{N\left(\tilde{t}\right)}}\left(V_i-1\right)\right),$$

(1)

where $S\left(\tilde{t}-\right)$ denotes the left-hand limit of S at $\tilde{t}$, $\mu$ is the drift rate, $W\left(\tilde{t}\right)$ is standard Brownian motion and $\sigma$ is the volatility associated with the Brownian component of the process. $N\left(\tilde{t}\right)$ is a Poisson process with intensity $\lambda$ that is independent of $W\left(\tilde{t}\right)$, and $\left\{V_i\right\}$ is a sequence of independent identically distributed nonnegative random variables such that $Y_i=log{V}_i$ has a distribution with the probability density function g. There are several possible choices for the function g. In the Merton model $Y_i$ is normally distributed with the mean ${\mu }_J$ and the standard deviation ${\sigma }_J$ and

$$g\left(x\right)=\frac{1}{\sqrt{2\pi }{\sigma }_J}{e}^{-\frac{{\left(x-{\mu }_J\right)}^2}{2{\sigma }_J^2}}.$$

(2)

For other models and more details, see [1,2,3]. Let the variable $t=T-\tilde{t}$ represent time to maturity and r be a risk-free rate. Using no arbitrage principle and the standard Itô calculus, one can derive that the market price $U\left(S,t\right)$ of the option at time to maturity t is the solution of the equation [1,2,3,4]:

$$\frac{\partial U}{\partial t}-\mathcal{D}\left(U\right)-\mathcal{I}\left(U\right)=0,S>0,t\in \left(0,T\right),$$

(3)

where the operators $\mathcal{D}$ and $\mathcal{I}$ are given by

$$\mathcal{D}\left(U\right)=\frac{{\sigma }^2{S}^2}{2}\frac{{\partial }^{2}U}{\partial S^2}+\left(r-\lambda \kappa \right)S\frac{\partial U}{\partial S}-\left(r+\lambda \right)U$$

(4)

and

$$\mathcal{I}\left(U\right)=\lambda {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}U\left(S{e}^x,t\right)g\left(x\right)dx.$$

(5)

The parameter $\kappa$ represents the expected value $E\left(V_i-1\right)$. The initial and boundary conditions depend on the type of the option.

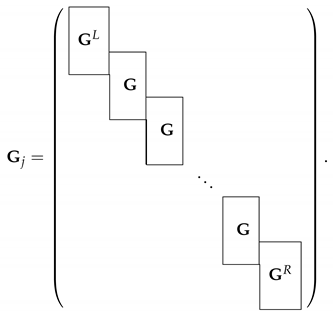
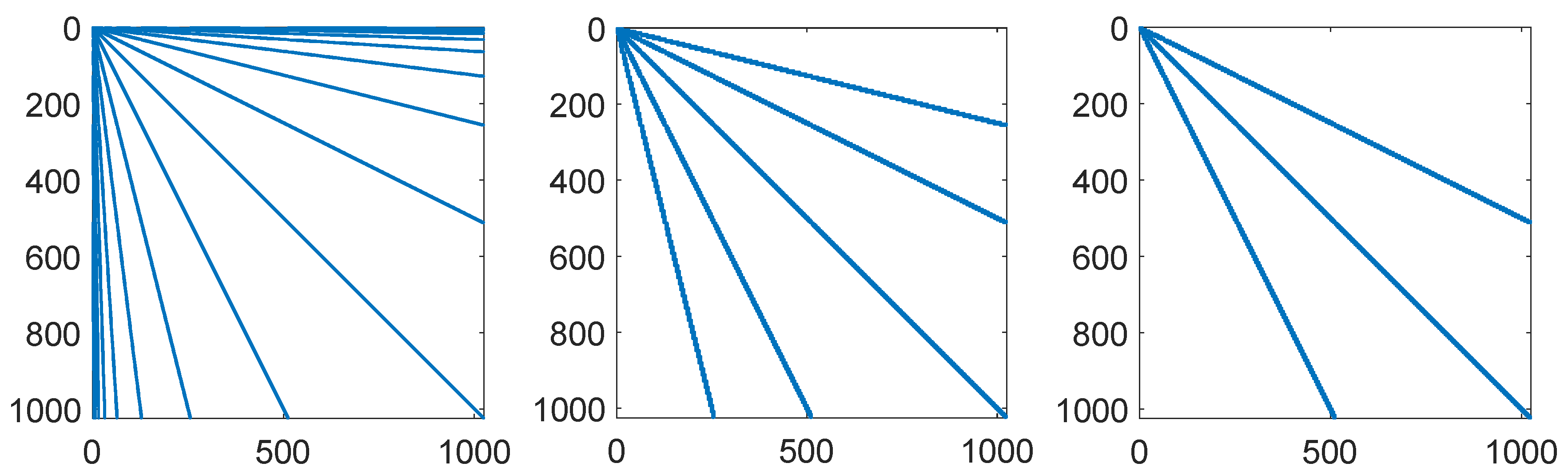
In Section 3, Equation (3) is transformed to logarithmic prices and restricted to a bounded domain. Then, the Galerkin method combined with the Crank–Nicolson scheme is used for its numerical solution. The stability of the scheme and convergence of the method have already been investigated (see [4,5,6] and references therein). This paper focuses on the structure of the discretization matrices. It is known that matrices arising from wavelet discretization of differential operators have a so-called finger pattern (see Figure 1, left). In [7,8,9,10], cubic and quartic wavelet bases were constructed such that the bi-infinite stiffness and mass matrices have a finite number of nonzero entries in each column and have a similar structure, as shown in Figure 1 (left). This simplifies the algorithm and increases the efficiency of wavelet-based methods. However, a construction of quadratic spline wavelets with this property has not yet been proposed, and such a construction is the main aim of this paper. It should also be mentioned that the wavelet bases from [11,12,13], which are semiorthogonal with respect to the $H^1$-seminorm, lead to banded matrices for the one-dimensional Poisson equation, and the $L^2$-orthogonal wavelets from [14,15] lead to diagonal mass matrices.

The differential operator $\mathcal{D}$ is a special case of an operator $\mathcal{A}$ defined by

$$\mathcal{A}u=-{\displaystyle \sum _{k,l=1}^d}\frac{\partial }{\partial x_k}\left(p_{k,l}\frac{\partial u}{\partial x_l}\right)+{\displaystyle \sum _{k=1}^d}{q}_k\frac{\partial u}{\partial x_k}+p_{0}u,$$

(6)

for $d\in \mathbb{N}$. Let $p_{k,l}=p_{l,k}$ and $P={\left(p_{k,l}\right)}_{k,l=1}^d$ be positive definite on $\mathrm{\Omega }$.

$$\mathcal{A}u=f\mathrm{on}\mathrm{\Omega }={\otimes }_{i=1}^d\left(a_i,b_i\right),u=0\mathrm{on}\partial \mathrm{\Omega }$$

(7)

covers the Poisson equation, the Helmholtz equation, the stationary convection diffusion equation and various equations from financial mathematics, such as equations representing the Black–Scholes model and the Heston model semidiscretized in time using the $\theta$-scheme.

For $d=1$, denote $a=a_1$, $b=b_1$, $h=\left(b-a\right)/2^j$, $I_k=\left(\left(k-1\right)h,kh\right)$,

$$P_{m,j}\left(a,b\right)=\left\{v\in L^2\left(a,b\right){:v|}_{I_k}\in {\Pi }_m\left(I_k\right),k=1,\dots ,2^j\right\},$$

(8)

and

$$P_{m,j}^0\left(a,b\right)=P_{m,j}\left(a,b\right)\cap C\left(\left[a,b\right]\right),$$

(9)

where ${\Pi }_m\left(I_k\right)$ represents the set of all polynomials on $I_k$ of degree at most m. The main aim of this paper is to construct a quadratic spline wavelet basis $\mathrm{\Psi }$ on the interval $\left(a,b\right)$ satisfying homogeneous Dirichlet boundary conditions such that the matrix

$$〈\mathcal{A}\mathrm{\Psi },\mathrm{\Psi }〉={\left(〈\mathcal{A}{\psi }_{\lambda },{\psi }_{\mu }〉\right)}_{{\psi }_{\lambda },{\psi }_{\mu }\in \mathrm{\Psi }},$$

(10)

where $〈·,·〉$ is the $L^2$-inner product, has $\mathcal{O}\left(1\right)$ nonzero entries in each column if $p_{1,1}\in P_{2,l}^0\left(a,b\right)$, $q_1\in P_{1,l}^0\left(a,b\right)$, and $p_0\in P_{0,l}\left(a,b\right)$ for some $l\in \mathbb{N}$.

Wavelet bases on product domains can be constructed using an isotropic or anisotropic tensor product approach (see, e.g., [16,17]). The discretization matrices for such multidimensional wavelet bases also have $\mathcal{O}\left(1\right)$ of nonzero entries in each row if

$$p_{k,l}\in {\otimes }_{k=1}^d{P}_{2,l}^0\left(a_k,b_k\right),g_k\in {\otimes }_{k=1}^d{P}_{1,l}^0\left(a_k,b_k\right),p_0\in {\otimes }_{k=1}^d{P}_{0,l}\left(a_k,b_k\right).$$

(11)

Although the property that the matrix has $\mathcal{O}\left(1\right)$ nonzero entries in each column is valid for any $l\in \mathbb{N}$, in most applications l should be small.

Since the differential operator $\mathcal{D}$ is a special case of the operator $\mathcal{A}$, the discretization matrix for this operator is sparse. This paper also aims to derive decay estimates for the entries of matrix arising from discretization of the integral term using the Galerkin method with the proposed wavelet basis and to show that truncated discretization matrices for the problem in Equation (3) are sparse. The sparsity of the discretization matrix has two advantages. First, the multiplication of this matrix with a vector requires $\mathcal{O}\left(N\right)$ floating-point operations, while other quadratic spline wavelet bases require $\mathcal{O}\left(NlogN\right)$ operations and other bases such as quadratic B-spline basis require $\mathcal{O}\left(N^2\right)$ operations because the matrix is typically full. This increases the efficiency of iterative methods for the numerical solution of the resulting discrete system. Second, due to the smaller number of elements, the computation of the discretization matrix is faster for the Galerkin method with the proposed basis than for the Galerkin method with other bases of the same order, e.g., other quadratic spline wavelet bases and quadratic B-spline bases.

In addition to the orthogonality property, it is required that wavelets have vanishing moments and that the wavelet basis is well conditioned. Vanishing wavelet moments determine the decay of entries of discretization matrices. Since the constructed wavelets have three vanishing moments, this decay is fast (see Theorem 5 in Section 3). Furthermore, due to vanishing moments, the basis can be used in adaptive wavelet methods (see [17]). It is important that the basis is well-conditioned because the condition numbers of discretization matrices depend on condition numbers of the basis and small condition numbers of system matrices guarantee the stability of computation and influences the number of iterations of iterative methods used for the numerical solution of the resulting system.

Due to these interesting properties, the wavelet basis proposed in this paper can be used in many applications such as the numerical solution of various types of operator equations using the wavelet-Galerkin method, an adaptive wavelet method or a collocation method. For a survey of such applications, refer to [4,17,18].

The paper is organized as follows. In Section 2, a construction of a wavelet basis satisfying the aforementioned properties is proposed and a rigorous proof of its Riesz basis property is provided. It is shown that the condition numbers of the basis are small with respect to both the $L^2$-norm and the $H^1$-seminorm. In Section 3, the problem in Equation (3) is discretized and the properties of discretization matrices studied. 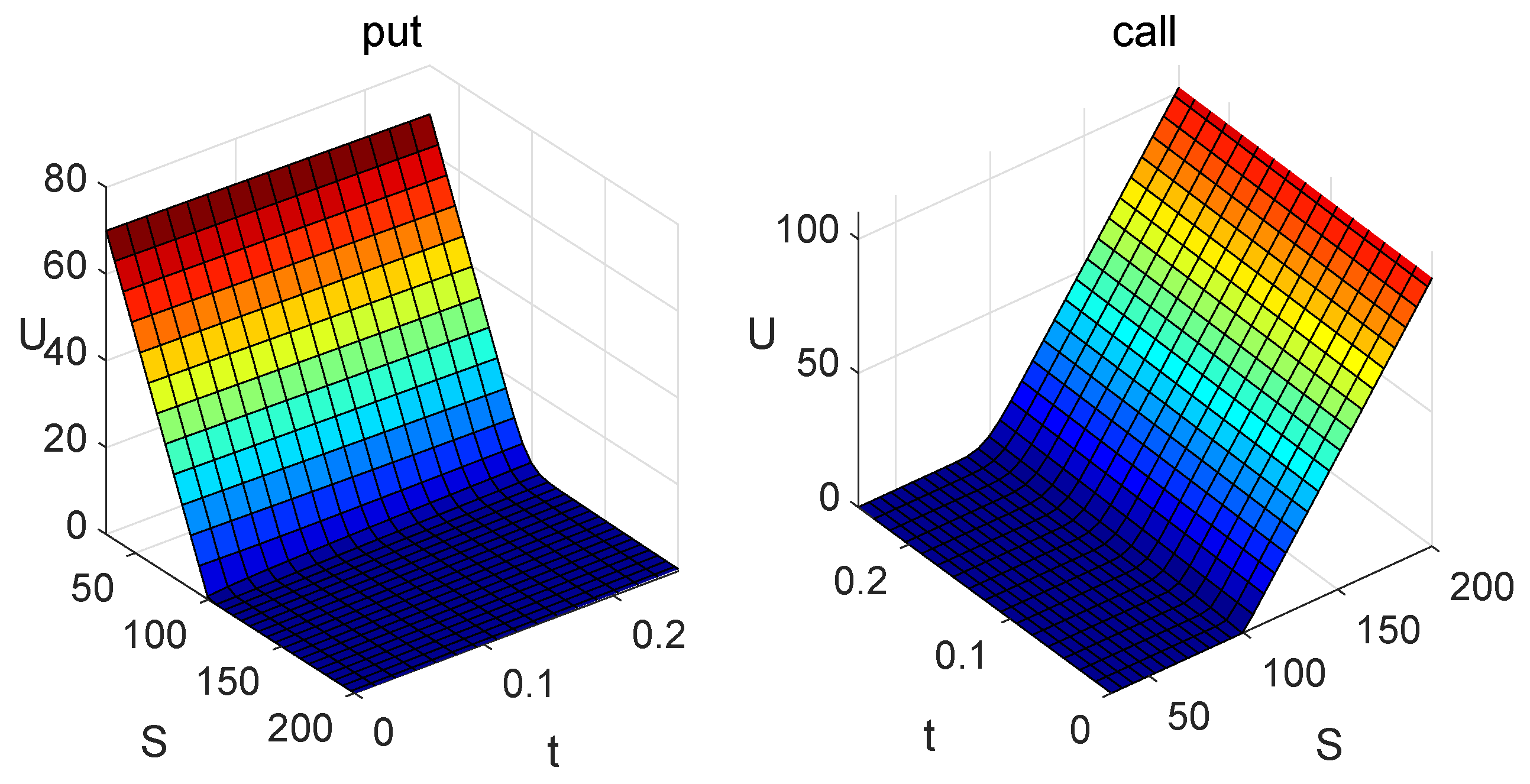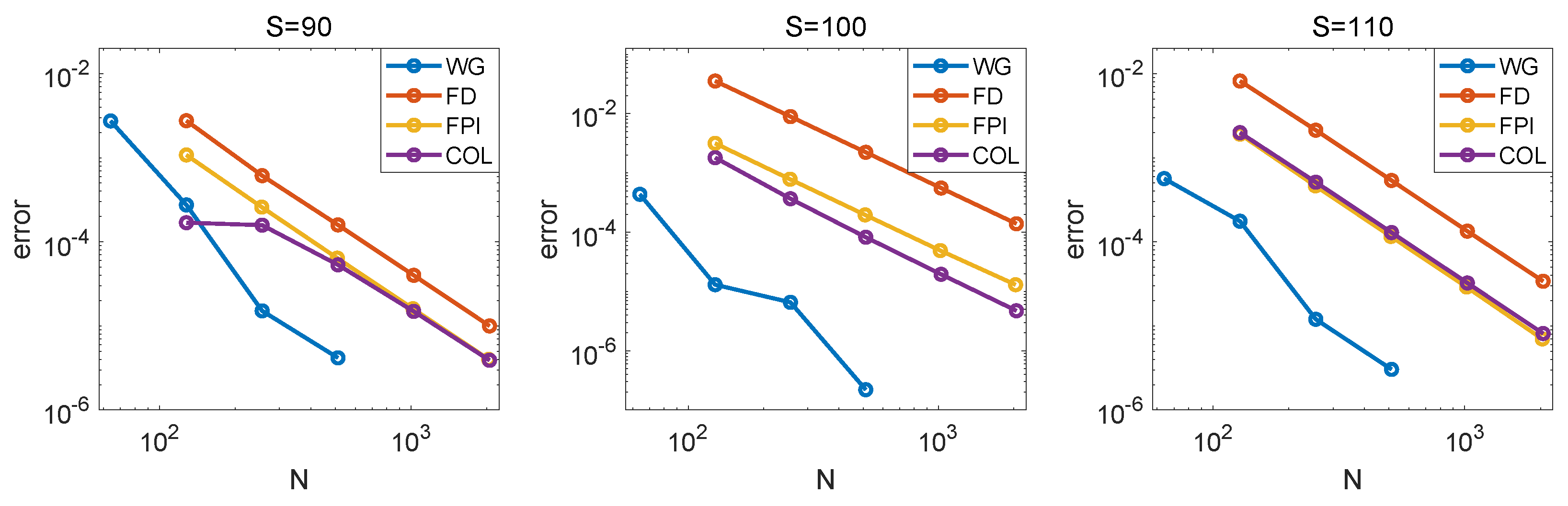Finally, in Section 4, numerical experiments are provided for pricing European options under the Merton model, and it is shown that the proposed method is efficient because it can achieve high-order convergence with respect to both time and spatial variables, the number of iterations is small, and due to sparsity of system matrices one iteration only requires a small number of floating-point operations. Furthermore, in comparison with methods from [19,20,21], the proposed method requires a smaller number of degrees of freedom to obtain a sufficiently accurate solution.

2. Construction of Wavelets

First, briefly recall the concept of a wavelet basis. Let $\mathcal{J}$ be at most a countable index set such that each index $\lambda \in \mathcal{J}$ takes the form $\lambda =\left(j,k\right)$ and denote $\left|\lambda \right|=j\in \mathbb{Z}$. The norm of $\mathbf{v}={\left\{v_{\lambda }\right\}}_{\lambda \in \mathcal{J}}$, $v_{\lambda }\in \mathbb{R}$, is defined by

$$∥\mathbf{v}∥=\sqrt{{\displaystyle {\displaystyle \sum _{\lambda \in \mathcal{J}}}}{v}_{\lambda }^2}.$$

(12)

The space of all sequences $\mathbf{v}$ with finite norm is denoted by

$$l^2\left(\mathcal{J}\right)=\left\{\mathbf{v}:\mathbf{v}={\left\{v_{\lambda }\right\}}_{\lambda \in \mathcal{J}},v_{\lambda }\in \mathbb{R},∥\mathbf{v}∥<\infty \right\}.$$

(13)

The symbol $L^2\left(a,b\right)$ denotes the space of square-integrable functions defined on $\left(a,b\right)$. Let $H\subset L^2\left(a,b\right)$ be a real Hilbert space equipped with the inner product ${〈·,·〉}_H$ and the norm ${∥·∥}_H$, e.g., H is the Sobolev space $H_0^1\left(a,b\right)$ of functions that vanish at boundary points and whose first weak derivatives are in $L^2\left(a,b\right)$. The aim is to construct a wavelet basis for H in the sense of the following definition.

Definition 1.

A family $\mathrm{\Psi }=\left\{{\psi }_{\lambda },\lambda \in \mathcal{J}\right\}$ is called a wavelet basis of H if:

(i) 

Ψ is a Riesz basis for H, i.e., the span of Ψ is dense in H and there exist constants $c,C\in \left(0,\infty \right)$ such that

$$c∥\mathbf{b}∥\le {∥{\displaystyle \sum _{\lambda \in \mathcal{J}}}{b}_{\lambda }{\psi }_{\lambda }∥}_H\le C∥\mathbf{b}∥,$$

(14)

for all $\mathbf{b}={\left\{b_{\lambda }\right\}}_{\lambda \in \mathcal{J}}\in l^2\left(\mathcal{J}\right)$.

(ii) 

The functions are local in the sense that

$$diamsupp{\psi }_{\lambda }\le C{2}^{-\left|\lambda \right|},\lambda \in \mathcal{J},$$

(15)

where the constant C does not depend on λ, and at a given level j the supports of only finitely many wavelets overlap at any point x.

(iii) 

The family Ψ has the hierarchical structure

$$\mathrm{\Psi }={\mathrm{\Phi }}_{j_0}\cup {\displaystyle \bigcup _{j=j_0}^K}{\mathrm{\Psi }}_j$$

(16)

for some $K\in \mathbb{N}\cup \left\{\infty \right\}$.

(iv) 

There exists $L\ge 1$ such that all functions ${\psi }_{\lambda }\in {\mathrm{\Psi }}_j$, $j_0\le j\le K$, have L vanishing moments, i.e.,

$${\displaystyle \underset{a}{\overset{b}{\int }}}{x}^k{\psi }_{\lambda }\left(x\right)=0,k=0,\dots ,L-1.$$

(17)

For the two countable sets of functions $\mathrm{\Gamma },\mathrm{\Theta }\subset L^2\left(\mathrm{\Omega }\right)$, the symbol $〈\mathrm{\Gamma },\mathrm{\Theta }〉$ denotes the matrix

$$〈\mathrm{\Gamma },\mathrm{\Theta }〉={\left\{〈\gamma ,\theta 〉\right\}}_{\gamma \in \mathrm{\Gamma },\theta \in \mathrm{\Theta }}.$$

(18)

The constants

$$c_{\mathrm{\Psi }}=\sup \left\{c:c\mathrm{satisfies}\left(14\right)\right\}\mathrm{and}{C}_{\mathrm{\Psi }}=\inf \left\{C:C\mathrm{satisfies}\left(14\right)\right\}$$

(19)

are called a lower and upper Riesz bound, respectively, and the number $cond\mathrm{\Psi }=C_{\mathrm{\Psi }}/c_{\mathrm{\Psi }}$ is called the condition number of $\mathrm{\Psi }$. In some papers, the squares of norms are used in Equation (14) and the Riesz bounds are defined as $c_{\mathrm{\Psi }}^2$ and $C_{\mathrm{\Psi }}^2$. The Gram matrix $〈\mathrm{\Psi },\mathrm{\Psi }〉$ can be finite or biinfinite and it is known that it represents a linear operator that is continuous, positive definite, and self-adjoint, and that the constants $c_{\mathrm{\Psi }}$ and $C_{\mathrm{\Psi }}$ satisfy

$$c_{\mathrm{\Psi }}=\sqrt{{\lambda }_{min}\left(〈\mathrm{\Psi },\mathrm{\Psi }〉\right)},C_{\mathrm{\Psi }}=\sqrt{{\lambda }_{max}\left(〈\mathrm{\Psi },\mathrm{\Psi }〉\right)}.$$

(20)

If $\mathrm{\Psi }$ satisfies Equation (14) but the span of $\mathrm{\Psi }$ is not necessarily dense in H, then $\mathrm{\Psi }$ is called a Riesz sequence in H.

The definition of a wavelet basis is not unified in the mathematical literature, and Conditions (i)–(iv) from Definition 1 can be generalized. The functions from the set ${\mathrm{\Phi }}_{j_0}$ are called scaling functions and the functions from the set ${\mathrm{\Psi }}_j$, $j\ge j_0$ are called wavelets on the level j. Wavelets in the inner part of the interval are typically translations and dilations of one function $\psi$ or several functions ${\psi }^1,\dots ,{\psi }^p$ also called wavelets, i.e.,

$${\psi }_{j,k}\left(x\right)=2^{j/2}{\psi }^l\left(2^{j}x-m\right),$$

(21)

for some $l\in \left\{1,\dots ,p\right\}$ and some $m\in \mathbb{Z}$, and similarly the wavelets near the boundary are derived from functions called boundary wavelets.

In the following, a construction of a new wavelet basis is proposed. Scaling functions are defined as in [22,23,24]. Let $\varphi$ and ${\varphi }^b$ be quadratic B-splines on knots $[0,1,2,3]$ and $[0,0,1,2]$, respectively. Then, $\varphi$ and ${\varphi }_b$ have the explicit form

$$\varphi \left(x\right)=\left\{\begin{array}{cc}\frac{x^2}{2},& x\in [0,1],\hfill \\ -x^2+3x-\frac{3}{2},& x\in [1,2],\hfill \\ \frac{x^2}{2}-3x+\frac{9}{2},& x\in [2,3],\hfill \\ 0,& \mathrm{otherwise};\hfill \end{array}\right.{\varphi }_b\left(x\right)=\left\{\begin{array}{cc}-\frac{3x^2}{2}+2x,& x\in [0,1],\hfill \\ \frac{x^2}{2}-2x+2,& x\in [1,2],\hfill \\ 0,& \mathrm{otherwise}.\hfill \end{array}\right.$$

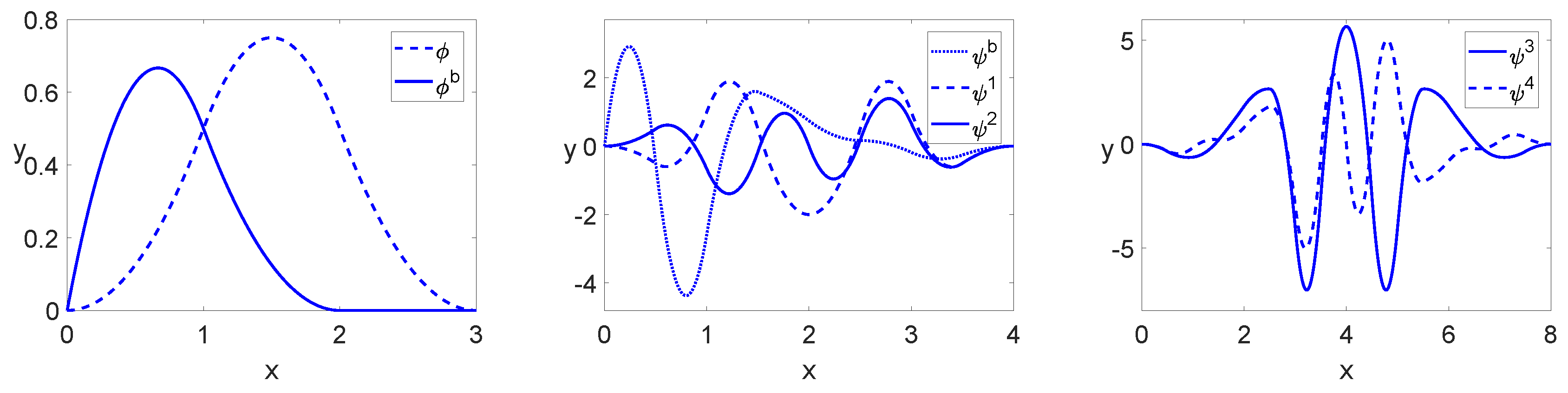
The graphs of the functions ${\varphi }_b$ and $\varphi$ are displayed in Figure 2.

For $j\ge 2$, the functions

$$\begin{array}{ccc}{\varphi }_{j,k}\left(x\right)& =& 2^{j/2}\varphi (2^{j}x-k+2),k=2,\dots ,2^j-1,\hfill \\ {\varphi }_{j,1}\left(x\right)& =& 2^{j/2}{\varphi }^b\left(2^{j}x\right),{\varphi }_{j,2^j}\left(x\right)=2^{j/2}{\varphi }^b\left(2^j(1-x)\right),\hfill \end{array}$$

where $x\in \left[0,1\right]$, form the scaling basis ${\mathrm{\Phi }}_j=\left\{{\varphi }_{j,k},k=1,\dots ,2^j\right\},$ and the spaces $V_j=\mathrm{span}{\mathrm{\Phi }}_j$ form a multiresolution analysis.

For simplicity, denote $P_{m,j}=P_{m,j}\left(0,1\right)$ and $P_{m,j}^0=P_{m,j}^0\left(0,1\right)$. To obtain sparse discretization matrices, dual spaces ${\tilde{V}}_j$ and complement spaces $W_j$ are defined by

$${\tilde{V}}_j=P_{2,j-2}\cup P_{0,j-1},W_j={\tilde{V}}_j^{\perp }\cap V_{j+1},$$

(22)

where ${\tilde{V}}_j^{\perp }$ is the $L^2$-orthogonal complement of ${\tilde{V}}_j$.

Lemma 1.

The functions $g\in W_i$ and $h\in W_j$, $i,j\ge 2$, $\left|i-j\right|>2$, satisfy

$$〈p_{0}g,h〉=0,〈q_1{g}^{\prime },h〉=0,\mathit{and}〈p_{1,1}{g}^{\prime },h^{\prime }〉=0$$

(23)

for $p_{1,1}\in P_{2,l}^0$, $q_1\in P_{1,l}^0$, and $p_0\in P_{0,l}$, $l\le max\left(i,j\right)-2$. Furthermore, the functions $g\in W_i$ and $h\in W_j$, $i,j\ge 2$, $\left|i-j\right|>1$, satisfy $〈g^{\prime },h^{\prime }〉=0$.

Proof. 

Assume that $j>i+2$, $i,j\ge 2$, and $l\le max\left(i,j\right)-2$. Then, $g\in W_i\subset V_{i+1}\subset V_{j-2}\subset {\tilde{V}}_j$, and thus $p_{0}g\in {\tilde{V}}_j$. Since $h\in W_j$ and $W_j$ is orthogonal to ${\tilde{V}}_j$, $〈p_{0}g,h〉=0$ is obtained. Using the similar argument and the relations $〈q_1{g}^{\prime },h〉=-〈g,q_1^{\prime }h+q_1{h}^{\prime }〉$ and $〈p_{1,1}{g}^{\prime },h^{\prime }〉=-〈p_{1,1}^{\prime }{g}^{\prime }+p_{1,1}{g}^{″},h〉$, the remaining part of the lemma is proved. ☐

Therefore, if wavelets are defined as basis functions for the spaces $W_j$, then the matrices in Equation (10) will be sparse. Figure 1 shows the cases $p_{1,1}=1$, $p_0=q_1=0$ and $p_0=1$, $q_1=p_{1,1}=0$. The inner wavelet generators are defined by

$${\psi }^l\left(x\right)={\displaystyle \sum _{k=0}^5}{h}_k^l\varphi \left(2x-k\right),{\psi }^{l+2}={\displaystyle \sum _{k=0}^{13}}{h}_k^{l+2}\varphi \left(2x-k\right),$$

for $l=1,2,$ and the boundary wavelet generator is defined by

$${\psi }^b\left(x\right)=h_{-1}^b{\varphi }_b\left(2x\right)+{\displaystyle \sum _{k=0}^5}{h}_k^b\varphi \left(2x-k\right).$$

The coefficients $h_k^l$ are computed such that ${\psi }^l$ is $L^2$-orthogonal to $p_m\left(x-4k\right)$, $k\in \mathbb{Z}$, where

$$p_i\left(x\right)=\left\{\begin{array}{cc}{\left(x-2\right)}^i,& x\in \left[0,4\right],\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.p_{i+2}\left(x\right)=\left\{\begin{array}{cc}1,& x\in \left[2i-2,2i\right],\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(24)

for $i=1,2$. This leads to systems of linear algebraic equations with infinitely many solutions. Using numerical experiments, the coefficients $h_k^l$ that lead to a well-conditioned wavelet basis were found, namely

$$\begin{array}{ccc}\left[h_0^1,\dots h_5^1\right]& =& \left[1,-3,2,2,-3,1\right],\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\left[h_0^2,\dots h_5^2\right]& =& \left[-1,\frac{7}{3},-2,2,-\frac{7}{3},1\right].\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\left[h_0^3,\dots h_6^3\right]& =& \left[\frac{7}{10},\frac{11}{20},-\frac{24}{25},-\frac{27}{10},-\frac{653}{250},\frac{5343}{500},-\frac{708}{125}\right],\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\left[h_0^4,\dots h_6^4\right]& =& \left[\frac{13}{20},\frac{-8}{25},\frac{-9}{100},\frac{-153}{100},\frac{-423}{200},\frac{4823}{600},\frac{-139}{20}\right],\hfill \end{array}$$

(28)

and $h_k^3=h_{13-k}^3$, $h_k^4=-h_{13-k}^4$, for $k=7,\dots ,13$, and for the boundary wavelet

$$\left[h_{-1}^b,\dots h_5^b\right]=\left[-\frac{121}{20},\frac{841}{120},-\frac{371}{200},-\frac{131}{100},-\frac{17}{100},-\frac{4}{25},\frac{13}{25}\right].$$

(29)

The graphs of constructed wavelets are displayed in Figure 2.

The functions ${\psi }^1$ and ${\psi }^3$ are symmetric; the functions ${\psi }^2$ and ${\psi }^4$ are antisymmetric; $\mathrm{supp}{\psi }^l=\left[0,4\right]$ for $l=b,1,2$; $\mathrm{supp}{\psi }^l=\left[0,8\right]$ for $l=3,4;$ and all the wavelets have three vanishing moments.

For $j\ge 2$, a wavelet basis on the level j

$${\mathrm{\Psi }}_j=\left\{{\psi }_{j,k}/{∥{\psi }_{j,k}∥}_{L^2\left(0,1\right)},k=1,\dots ,2^j\right\},$$

(30)

contains the functions

$$\begin{array}{ccc}{\psi }_{j,1}\left(x\right)& =& 2^{j/2}{\psi }^b\left(2^{j}x\right),{\psi }_{j,2^j}\left(x\right)=2^{j/2}{\psi }^b\left(2^j\left(1-x\right)\right),\hfill \\ {\psi }_{j,4k+l+1}\left(x\right)& =& 2^{j/2}{\psi }^l\left(2^{j}x-4k\right),l=1,\dots 4,1<4k+l+1<2^j,\hfill \end{array}$$

for $x\in \left[0,1\right]$.

For $j\ge j_0$ and $j_0=2$, the sets

$$\mathrm{\Psi }={\mathrm{\Phi }}_{j_0}\cup {\displaystyle \bigcup _{j=j_0}^{\infty }}{\mathrm{\Psi }}_j,{\mathrm{\Psi }}^s={\mathrm{\Phi }}_{j_0}\cup {\displaystyle \bigcup _{j=j_0}^{j_0+s-1}}{\mathrm{\Psi }}_j,$$

(31)

are a wavelet basis in the space $L^2\left(0,1\right)$ and its finite-dimensional subset, respectively. In the following, the proof of the Riesz basis property of $\mathrm{\Psi }$ is provided.

Theorem 1.

The wavelets ${\psi }_{j,k}$ have three vanishing moments, and ${\mathrm{\Psi }}_j$, $j\ge 2$, are Riesz bases of the spaces $W_j$ such that their lower Riesz bounds $c_{{\mathrm{\Psi }}_j}$ and the upper Riesz bounds $C_{{\mathrm{\Psi }}_j}$ are uniformly bounded, i.e., they satisfy $0<c<c_{{\mathrm{\Psi }}_j}\le C_{{\mathrm{\Psi }}_j}<C<\infty$ for some constants c and C independent on j.

Proof. 

It was already mentioned that ${\psi }^l$, $l=1,2,3,4,b$, have three vanishing moments. Indeed, since ${\psi }^l$ are defined to be $L^2$-orthogonal to $p_m\left(x-4k\right)$, $k\in \mathbb{Z}$, and the polynomials $x^i$, $i=0,1,2$, restricted to support of ${\psi }^l$ are linear combinations of $p_m\left(x-4k\right)$, relation $〈{\psi }^l,x^i〉=0$ is obtained, and thus ${\psi }^l$ have three vanishing moments. Therefore, the wavelets ${\psi }_{j,k}$ have three vanishing moments as well.

The $L^2$-orthogonality of ${\psi }^l$ and $p_m\left(x-4k\right)$, $k\in \mathbb{Z}$, implies the $L^2$-orthogonality of ${\psi }_{j,k}$ to the functions $p_m\left(2^{j}x-4l\right)$, $m=1,2,3,4,$$l=0,\dots ,2^{j-2}-1,$ which form the basis of ${\tilde{V}}_j$ and thus ${\psi }_{j,k}\in W_j.$ Since the number of elements in ${\mathrm{\Psi }}_j$ is equal to the dimension of $W_j$, the set ${\mathrm{\Psi }}_j$ is a basis of $W_j$. Every finite dimensional basis is a Riesz basis and thus it remains to be proven that Riesz bounds for ${\mathrm{\Psi }}_j$ are uniformly bounded. Let ${\mathrm{\Gamma }}_j=〈{\mathrm{\Psi }}_j,{\mathrm{\Psi }}_j〉$ and $n=2^j$. The matrix ${\mathrm{\Gamma }}_j$ has similar structure as the matrix ${\mathbf{G}}_j$ in Equation (42), and since its entries are $L^2$-products of piecewise polynomial functions, one is able to compute them precisely or with arbitrary precision. For $j\ge 2$, the Gerschgorin circle theorem from [25] yields

$$\begin{array}{ccc}{c}_{{\mathrm{\Psi }}_j}& =& {\lambda }_{min}\left({\mathrm{\Gamma }}_j\right)\ge {\displaystyle \underset{k=1\dots n}{min}}\left(\left|{\left({\mathrm{\Gamma }}_j\right)}_{k,k}\right|-{\displaystyle \sum _{\begin{array}{c}l=1\\ l\ne k\end{array}}^n}\left|{\left({\mathrm{\Gamma }}_j\right)}_{k,l}\right|\right)\ge 0.3\hfill \end{array}$$

(32)

$$\begin{array}{ccc}{C}_{{\mathrm{\Psi }}_j}& =& {\lambda }_{max}\left({\mathrm{\Gamma }}_j\right)\le {\displaystyle \underset{k=1\dots n}{max}}\left(\left|{\left({\mathrm{\Gamma }}_j\right)}_{k,k}\right|-{\displaystyle \sum _{\begin{array}{c}l=1\\ l\ne k\end{array}}^n}\left|{\left({\mathrm{\Gamma }}_j\right)}_{k,l}\right|\right)\le 1.7,\hfill \end{array}$$

(33)

 ☐

The proof of the Riesz basis property in Equation (14) for $\mathrm{\Psi }$ is based on the following theorem [8,10,26].

Theorem 2.

Let $j_0\in \mathbb{N}$ and, for $j\ge j_0$, let $V_j$ and ${\tilde{V}}_j$ be subspaces of the space $V\subset L^2\left(0,1\right)$, such that $V_j\subset V_{j+1}$, ${\tilde{V}}_j\subset {\tilde{V}}_{j+1}$, $\dim V_j=\dim {\tilde{V}}_j<\infty$. Let ${\mathrm{\Phi }}_j$ be bases of $V_j$, ${\tilde{\mathrm{\Phi }}}_j$ be bases of ${\tilde{V}}_j$, and ${\mathrm{\Psi }}_j$ be bases of ${\tilde{V}}_j^{\perp }\cap V_{j+1}$, such that Riesz bounds with respect to the $L^2$-norm of ${\mathrm{\Phi }}_j$, ${\tilde{\mathrm{\Phi }}}_j$ and ${\mathrm{\Psi }}_j$ are uniformly bounded, and let Ψ be composed of ${\mathrm{\Phi }}_{j_0}$ and ${\mathrm{\Psi }}_j$, $j\ge j_0$, as in Equation (31). Furthermore, assume that

$${\mathbf{G}}_j=〈{\mathrm{\Phi }}_j,{\tilde{\mathrm{\Phi }}}_j〉$$

(34)

is invertible and that the spectral norm of ${\mathbf{G}}_j^{-1}$ is bounded independently on j. In addition, for some positive constants C, γ and d, such that $\gamma <d$, let

$${\displaystyle \underset{v_j\in V_j}{inf}}{∥v-v_j∥}_{L^2\left(0,1\right)}\le C{2}^{-jt}{∥v∥}_{H^t\left(0,1\right)},v\in H^t\left(0,1\right)\cap V,0\le t\le d,$$

(35)

and

$${∥v_j∥}_{H^s\left(0,1\right)}\le C{2}^{js}{∥v_j∥}_{L^2\left(0,1\right)},v_j\in V_j,0\le s<\gamma ,$$

(36)

and similarly let Equations (35) and (36) hold for $\tilde{\gamma }$ and $\tilde{d}$ on the dual side. Then,

$$\left\{{\psi }_{j,k}/{∥{\psi }_{j,k}∥}_{H^s\left(0,1\right)},{\psi }_{j,k}\in \mathrm{\Psi }\right\}$$

(37)

is a Riesz sequence in $H^s\left(0,1\right)$ for $s\in \left(-\tilde{\gamma },\gamma \right)$.

The following theorem shows that the spaces $V_j$ and ${\tilde{V}}_j$ defined above satisfy the assumptions of Theorem 2.

Theorem 3.

There exist uniform Riesz bases ${\tilde{\mathrm{\Phi }}}_j$ of ${\tilde{V}}_j$ such that matrices ${\mathbf{G}}_j$ defined by Equation (34) are invertible and the spectral norms of ${\mathbf{G}}_j^{-1}$ are bounded independently on j.

Proof. 

Let $p_k$ be defined by Equation (24). For $l=1,\dots ,4,$ let

$${\tilde{\varphi }}^l={\displaystyle \sum _{k=1}^4}{c}_k^l{p}_k,$$

(38)

such that

$$〈\varphi \left(·-m\right),{\tilde{\varphi }}^l〉=0,\left|m-l\right|>1,〈\varphi \left(·-l\right),{\tilde{\varphi }}^l〉=1.$$

(39)

Since $\mathrm{supp}\varphi \left(·-m\right)\cap \mathrm{supp}{\tilde{\varphi }}^l=0$ for $m\ne -2,\dots ,4$, the relations in Equation (38) lead to the system of four linear algebraic equations with four unknown coefficients for each function ${\tilde{\varphi }}^l$. The invertibility of all four system matrices was verified using symbolic computations. Thus, the functions ${\tilde{\varphi }}^l$ exist and are unique. Then,

$${\tilde{\mathrm{\Phi }}}_j=\left\{{\tilde{\varphi }}_{j,k},k=1,\dots ,2^j\right\},$$

(40)

where

$${\tilde{\varphi }}_{j,4k+l}\left(x\right)=2^{j/2}{\tilde{\varphi }}^l\left(2^{j}x-4k\right),l=1,2,3,4,k\in \mathbb{Z},$$

(41)

is a basis of ${\tilde{V}}_j$ and the matrix ${\mathbf{G}}_j$ defined by Equation (34) is tridiagonal and has the structure

(42)

Using symbolic computation and rounding the resulting elements of the matrix $\mathbf{G}$ to three decimal digits,

$$\mathbf{G}=\left(\begin{array}{cccc}0.423& 0& 0& 0\\ 1.000& 0.422& 0& 0\\ -0.502& 1.000& 0.167& 0\\ 0& 0.159& 1.000& -0.403\\ 0& 0& 0.417& 1.000\\ 0& 0& 0& 0.406\end{array}\right).$$

(43)

Similarly, the matrices ${\mathbf{G}}^L$ and ${\mathbf{G}}^R$ are given by

$${\mathbf{G}}^L=\left(\begin{array}{cccc}0.577& 0.422& 0& 0\\ -0.502& 1.000& 0.169& 0\\ 0& 0.159& 1.000& -0.403\\ 0& 0& 0.417& 1.000\\ 0& 0& 0& 0.406\end{array}\right)$$

(44)

and

$${\mathbf{G}}^R=\left(\begin{array}{cccc}0.423& 0& 0& 0\\ 1.000& 0.422& 0& 0\\ -0.502& 1.000& 0.169& 0\\ 0& 0.159& 1.000& -0.403\\ 0& 0& 0.417& 0.594\end{array}\right).$$

(45)

Thus, the matrices ${\mathbf{G}}_j$ and ${\mathbf{G}}_j^T$ are diagonally dominant and invertible. Due to the Johnson’s lower bound for the smallest singular value [27],

$$\begin{array}{lll}{\sigma }_{min}\left({\mathbf{G}}_j\right)& \ge & {\displaystyle \underset{k=1\dots n}{min}}\left(\left|{\left({\mathbf{G}}_j\right)}_{k,k}\right|-\frac{1}{2}{\displaystyle \sum _{\begin{array}{c}l=1\\ l\ne k\end{array}}^n}\left(\left|{\left({\mathbf{G}}_j\right)}_{k,l}\right|+\left|{\left({\mathbf{G}}_j\right)}_{l,k}\right|\right)\right)\\ & \ge & 0.115,\end{array}$$

(46)

where $n=2^j$. Therefore, the spectral norm of the inverse matrix satisfies

$$∥{\mathbf{G}}_j^{-1}∥={\left({\sigma }_{min}\left({\mathbf{G}}_j\right)\right)}^{-1}\le 8.696.$$

(47)

It remains to be proven that ${\tilde{\mathrm{\Phi }}}_j$ are uniform Riesz bases of ${\tilde{V}}_j$. The matrices

$${\tilde{\mathrm{\Gamma }}}_j=〈{\tilde{\mathrm{\Phi }}}_j,{\tilde{\mathrm{\Phi }}}_j〉$$

(48)

are block diagonal matrices with $4\times 4$ boundary blocks ${\tilde{\mathrm{\Gamma }}}^L$ and ${\tilde{\mathrm{\Gamma }}}^R$ and inner blocks $\tilde{\mathrm{\Gamma }}$ that do not depend on j.

The Riesz lower bound $c_{\tilde{\mathrm{\Psi }}}$ and the Riesz upper bound $C_{\tilde{\mathrm{\Psi }}}$ satisfy

$$\begin{array}{ccc}{c}_{\tilde{\mathrm{\Psi }}}& =& {\lambda }_{min}\left({\tilde{\mathrm{\Gamma }}}_j\right)=min\left({\lambda }_{min}\left({\tilde{\mathrm{\Gamma }}}^L\right),{\lambda }_{min}\left({\tilde{\mathrm{\Gamma }}}^R\right),{\lambda }_{min}\left(\tilde{\mathrm{\Gamma }}\right)\right)\ge 1.60,\hfill \\ C_{\tilde{\mathrm{\Psi }}}& =& {\lambda }_{max}\left({\tilde{\mathrm{\Gamma }}}_j\right)=max\left({\lambda }_{max}\left({\tilde{\mathrm{\Gamma }}}^L\right),{\lambda }_{max}\left({\tilde{\mathrm{\Gamma }}}^R\right),{\lambda }_{max}\left(\tilde{\mathrm{\Gamma }}\right)\right)\le 7.74.\hfill \end{array}$$

(49)

 ☐

Theorem 4.

The set Ψ satisfies Equation (14) for $H=H^s\left(0,1\right)$, $s\in \left(-0.5,1.5\right)$; especially, Ψ is a Riesz basis of the space $L^2\left(0,1\right)$ and Ψ normalized in the $H^1$-norm or in the $H^1$-seminorm is a Riesz basis of the space $H_0^1\left(0,1\right)$.

Proof. 

Using the Gershgorin circle theorem similarly to in the proof of Theorem 1, estimates $c_{{\mathrm{\Phi }}_j}\ge 0.1$ and $C_{{\mathrm{\Phi }}_j}\le 1$ for the Riesz lower and upper bounds of ${\mathrm{\Phi }}_j$, respectively, are obtained. The estimates in Equations (35) and (36) are satisfied for $d=3$, $\tilde{d}=3$, $\gamma =1.5$, and $\tilde{\gamma }=0.5$. These parameters depend on the polynomial exactness and smoothness of the primal and dual spaces (see [26]). Due to these facts, as well as Theorems 2 and 3, the proof is complete. ☐

Table 1. The condition numbers of the wavelet bases ${\mathrm{\Psi }}^s$ with respect to the $L^2$-norm and the $H^1$-seminorm. s is the number of wavelet levels and N is the number of basis functions.

s	N	${\mathit{\lambda }}_{\mathit{min}}$	${\mathit{\lambda }}_{\mathit{max}}$	${\mathit{\kappa }}_{{\mathit{L}}^2}$	${\mathit{\lambda }}_{\mathit{min}}$	${\mathit{\lambda }}_{\mathit{max}}$	${\mathit{\kappa }}_{{\mathit{H}}^1}$
1	8	0.22	1.77	8.06	0.50	1.53	3.05
2	16	0.18	1.87	10.23	0.50	1.67	3.34
3	32	0.16	1.96	12.21	0.50	1.72	3.45
4	64	0.15	2.01	13.70	0.50	1.74	3.49
5	128	0.14	2.04	14.86	0.50	1.75	3.51
6	256	0.13	2.06	15.79	0.50	1.76	3.52
7	512	0.13	2.08	16.59	0.50	1.76	3.53
8	1024	0.12	2.10	17.28	0.50	1.77	3.53
9	2048	0.12	2.11	17.86	0.50	1.77	3.54
10	4096	0.12	2.12	18.35	0.50	1.77	3.54

presents the minimal and maximal eigenvalues and the condition numbers (cond) of diagonally preconditioned stiffness and mass matrices, i.e.,

$${\kappa }_{L^2}=\mathrm{cond}〈\frac{{\mathrm{\Psi }}^s}{{∥{\mathrm{\Psi }}^s∥}_{L^2\left(0,1\right)}},\frac{{\mathrm{\Psi }}^s}{{∥{\mathrm{\Psi }}^s∥}_{L^2\left(0,1\right)}}〉$$

(50)

and

$${\kappa }_{H^1}=\mathrm{cond}〈\frac{{\left({\mathrm{\Psi }}^s\right)}^{\prime }}{{\left|{\mathrm{\Psi }}^s\right|}_{H^1\left(0,1\right)}},\frac{{\left({\mathrm{\Psi }}^s\right)}^{\prime }}{{\left|{\mathrm{\Psi }}^s\right|}_{H^1\left(0,1\right)}},〉$$

(51)

where ${\left({\mathrm{\Psi }}^s\right)}^{\prime }=\left\{{\psi }_{\lambda }^{\prime }:{\psi }_{\lambda }\in {\mathrm{\Psi }}^s\right\}$.

These values correspond to the lower and upper Riesz bounds and the condition numbers of normalized wavelet bases with respect to the $L^2$-norm and to the $H^1$-seminorm ${\left|·\right|}_{H^1\left(0,1\right)}$. Although the aim is to construct a quadratic spline wavelet basis that leads to sparse discretization matrices rather than the optimization of the condition number, the resulting basis is better conditioned than many other quadratic spline wavelet bases (see comparison of quadratic spline wavelet bases in [16]).

A wavelet basis on a bounded interval $\left[a,b\right]$ can be constructed from the proposed wavelet basis on the unit interval using the simple linear transform $y=a+\left(b-a\right)x$, $x\in \left[0,1\right]$. Wavelet bases on the hypercube that are constructed using an isotropic, anisotropic, or sparse tensor product approach (see, e.g., [4,16,17]) preserve the properties of the wavelet basis on the interval such as the Riesz basis property, vanishing moments, and the sparse structure of the discretization matrices.

3. Discretization of the Jump–Diffusion Option Pricing Models

In this section, the Galerkin method with the constructed wavelet basis is used for valuation of options under jump–diffusion models. The choice of the method is motivated by the fact that the Galerkin method using a wavelet basis, also called the wavelet-Galerkin method, has several advantages for equations containing an integral term. As mentioned above, the discretization matrices for the wavelet-Galerkin method are sparse or quasi-sparse, while most of the standard methods suffer from the fact that the discretization matrices are full. Furthermore, the wavelet-Galerkin method is higher-order accurate if higher-order bases are used and the solution is sufficiently smooth. For many types of equations, the discretization matrices are well-conditioned, which results in a small number of iterations when using iterative methods for solving the resulting discrete system. For details on the methods for the numerical solution of integral equations and operator equations containing the integral term, see [4,18].

Recall that the jump–diffusion models are represented by the partial integro-differential Equation (3). The initial and boundary conditions depend on the type of the option. Here, the method is presented for a European put option. The value of a European call option can be computed using the put–call parity [3]. The initial condition for a vanilla European put option is $U\left(S,0\right)=max\left(K-S,0\right),$ where K is the strike price, and the boundary conditions have the form $U\left(0,t\right)=K{e}^{-rt}$, $U\left(S,t\right)\approx 0$ for $S\to \infty .$

The minimal value $S^{min}>0$ and the maximal value $S^{max}$ are chosen such that a domain $\mathrm{\Omega }=\left(S^{min},S^{max}\right)$ approximates the unbounded domain $\left(0,\infty \right)$. Since $U\left(S,t\right)\approx K{e}^{-rt}-S$ for small S, the boundary conditions at $S^{min}$ have the form

$$U\left(S^{min},t\right)=K{e}^{-rt}-S^{min},U\left(S^{max},t\right)=0.$$

(52)

It is convenient to transform Equation (3) to logarithmic prices $x=logS$ because the transformed differential operator

$$\widehat{\mathcal{D}}\left(\widehat{U}\right)=\frac{{\sigma }^2}{2}\frac{{\partial }^2\widehat{U}}{\partial x^2}+\left(r-\lambda \kappa -\frac{{\sigma }^2}{2}\right)\frac{\partial \widehat{U}}{\partial x}-\left(r+\lambda \right)\widehat{U}$$

(53)

has constant coefficients.

The transformed equation is given by

$$\frac{\partial \widehat{U}}{\partial t}-\widehat{\mathcal{D}}\left(\widehat{U}\right)-\widehat{\mathcal{I}}\left(\widehat{U}\right)=0,x\in X,t\in \left(0,T\right),$$

(54)

where $\widehat{U}\left(x,t\right)=U\left(e^x,t\right)$, $X=\left(x^{min},x^{max}\right)$, $x^{min}=log{S}^{min}$, $x^{max}=log{S}^{max}$, and

$$\widehat{\mathcal{I}}\left(\widehat{U}\right)=\lambda {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\widehat{U}\left(x+y,t\right)g\left(y\right)dy=\lambda {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\widehat{U}\left(y,t\right)g\left(y-x\right)dy.$$

(55)

The error caused by localization, i.e., by solving the Equation (54) on a bounded domain X instead on the whole real line, was studied in [4,28]. Due to decays of a value of a put option and of a probability density function at infinity,

$${\displaystyle \underset{x^{max}}{\overset{\infty }{\int }}}\widehat{U}\left(y,t\right)g\left(y-x\right)dy\approx 0\mathrm{for}{x}^{max}\to \infty .$$

(56)

Furthermore, since $U\left(S,t\right)\approx K{e}^{-rt}-S$ for S close to zero, the integral term $\widehat{\mathcal{I}}$ can be approximated by

$$\widehat{\mathcal{I}}\left(\widehat{U}\right)\approx {\mathcal{I}}_1+{\mathcal{I}}_2\left(\widehat{U}\right),$$

(57)

where

$${\mathcal{I}}_1={\displaystyle \underset{-\infty }{\overset{x^{min}}{\int }}}\left(K{e}^{-rt}-e^x\right)g\left(y-x\right)dy,{\mathcal{I}}_2\left(\widehat{U}\right)={\displaystyle \underset{x^{min}}{\overset{x^{max}}{\int }}}\widehat{U}\left(y,t\right)g\left(y-x\right)dy.$$

(58)

The boundary condition at the point $x^{min}$ is a non-homogeneous Dirichlet boundary condition. Therefore, one can transform Equation (54) into an equation with homogeneous Dirichlet boundary conditions. Let $\tilde{U}=\widehat{U}-W$, where $\widehat{U}$ is the solution of Equation (54) satisfying the initial and boundary conditions defined above and W is a function satisfying boundary conditions that is smooth enough. A possible choice of the function W is

$$W\left(x,t\right)=\left(K{e}^{-rt}-e^{x^{min}}\right)\left(1+x^{min}-x\right)$$

(59)

for $x\in \overline{X}$ and $t\in \left[0,T\right]$. Then, $\tilde{U}$ is the solution of the equation

$$\frac{\partial \tilde{U}}{\partial t}-\widehat{\mathcal{D}}\left(\tilde{U}\right)-{\mathcal{I}}_2\left(\tilde{U}\right)=f\left(W\right),f\left(W\right)=-\frac{\partial W}{\partial t}+\widehat{\mathcal{D}}\left(W\right)+{\mathcal{I}}_2\left(W\right)+{\mathcal{I}}_1$$

(60)

satisfying the initial condition

$$\tilde{U}\left(x,0\right)=U\left(e^x,0\right)-W\left(x,0\right),x\in X,$$

(61)

and boundary conditions

$$\tilde{U}\left(x^{min},t\right)=0,\tilde{U}\left(x^{max},t\right)=0,t\in \left[0,T\right].$$

(62)

The symbol $L^2\left(0,T;B\right)$ denotes the Bochner space of functions f such that $f\left(t\right)=f\left(·,t\right)\in B$ for $t\in \left(0,T\right)$ and

$${∥f∥}_{L^2\left(0,T;X\right)}={\left({\displaystyle \underset{0}{\overset{T}{\int }}}{∥f\left(t\right)∥}_B^{2}dt\right)}^{1/2}<\infty$$

(63)

with ${∥·∥}_B$ being the norm in Banach space B. Let a be a bilinear form defined by

$$a\left(u,v\right)=〈\widehat{\mathcal{D}}\left(u\right),v〉+〈{\mathcal{I}}_2\left(u\right),v〉,$$

(64)

for all $u,v\in H_0^1\left(X\right)$.

Then, the variational formulation of Equation (60) reads as:

Find $\tilde{U}\in H_0^1\left(0,T;H_0^1\left(X\right)\right)$ such that $\frac{\partial \tilde{U}}{\partial t}\in H_0^1\left(0,T;H^{-1}\left(X\right)\right)$ and $\tilde{U}$ satisfies Equation (61) and

$$〈\frac{\partial \tilde{U}}{\partial t},v〉-a\left(u,v\right)=〈f\left(W\right),v〉,v\in H_0^1\left(X\right),$$

(65)

almost everywhere in $\left(0,T\right)$.

It can be shown that the bilinear form a is continuous and satisfies a Gårding inequality, which implies the existence of a unique solution to this problem (see [4]).

The Crank–Nicolson scheme is used for time discretization. Let

$$M\in \mathbb{N},\tau =\frac{T}{M},t_l=l\tau ,l=0,\dots ,M,$$

(66)

and denote

$${\tilde{U}}_l\left(x\right)=\tilde{U}\left(x,t_l\right),f_l\left(x\right)=f\left(W\left(x,t_l\right)\right).$$

(67)

The Crank–Nicolson scheme has the form

$$\frac{〈{\tilde{U}}_{l+1},v〉}{\tau }-\frac{a\left({\tilde{U}}_{l+1},v\right)}{2}=\frac{〈{\tilde{U}}_l,v〉}{\tau }+\frac{a\left({\tilde{U}}_l,v\right)}{2}+〈\frac{f_l+f_{l+1}}{2},v〉$$

(68)

for $l=0,\dots ,M-1$.

Let $\mathrm{\Psi }$ be a wavelet basis for the space $L^2\left(X\right)$ such that $\mathrm{\Psi }$ normalized in the $H^1$-norm is the wavelet basis for the space $H_0^1\left(X\right)$. Let ${\mathrm{\Psi }}^s$ be a finite-dimensional subset of $\mathrm{\Psi }$ with s levels of wavelets, i.e., ${\mathrm{\Psi }}^s$ has the structure in Equation (31), and denote $V^s=\mathrm{span}{\mathrm{\Psi }}^s$. The Galerkin method consists in finding ${\tilde{U}}_{l+1}^s\in V^s$ such that

$$\frac{〈{\tilde{U}}_{l+1}^s,v〉}{\tau }-\frac{a\left({\tilde{U}}_{l+1}^s,v\right)}{2}=\frac{〈{\tilde{U}}_l^s,v〉}{\tau }+\frac{a\left({\tilde{U}}_l^s,v\right)}{2}+〈\frac{f_l+f_{l+1}}{2},v〉$$

(69)

for all $v\in V^s$. Setting $v={\psi }_{\mu }\in {\mathrm{\Psi }}^s$ and expanding ${\tilde{U}}_{l+1}^s$ in a basis ${\mathrm{\Psi }}^s$, i.e.,

$${\tilde{U}}_{l+1}^s={\displaystyle \sum _{{\psi }_{\lambda }\in {\mathrm{\Psi }}^s}}{u}_{\lambda }^s{\psi }_{\lambda },$$

(70)

the vector of coefficients ${\mathbf{u}}^s=\left\{u_{\lambda }^s\right\}$ is the solution of the system of linear algebraic equations ${\mathbf{A}}^s{\mathbf{u}}^s={\mathbf{f}}^s$, where

$${\mathbf{A}}_{\mu ,\lambda }^s=\frac{〈{\psi }_{\lambda },{\psi }_{\mu }〉}{\tau }-\frac{a\left({\psi }_{\lambda },{\psi }_{\mu }\right)}{2}$$

(71)

and

$${\mathbf{f}}_{\mu }^s=\frac{〈{\tilde{U}}_l^s,{\psi }_{\mu }〉}{\tau }+\frac{a\left({\tilde{U}}_l^s,{\psi }_{\mu }\right)}{2}+〈\frac{f_l+f_{l+1}}{2},{\psi }_{\mu }〉.$$

(72)

It is obvious that ${\mathbf{f}}^s$ and ${\mathbf{u}}^s$ depend on the time level $t_l$, but for simplicity the index l is omitted.

The stability of the Crank–Nicolson scheme and error estimates for the Galerkin method combined with the Crank–Nicolson scheme have been already studied (see, e.g., [4,5,6] and references therein). For quadratic spline basis functions and for sufficiently smooth solutions, the $L^2$-norm of the error depends on the error of approximation of function representing the initial condition in the space $V^s$ and the term of order $\mathcal{O}\left({\tau }^2+h^3\right)$, where h represents the spatial step that is in this case for N basis functions given by $h=1/N$.

In the following, the structure of a discretization matrix is studied. Using the Jacobi diagonal preconditioner ${\mathbf{D}}^s$, where the diagonal elements of ${\mathbf{D}}^s$ satisfy

$${\mathbf{D}}_{\lambda ,\lambda }^s=\sqrt{{\mathbf{A}}_{\lambda ,\lambda }^s},$$

(73)

gives the preconditioned system

$${\tilde{\mathbf{A}}}^s{\tilde{\mathbf{u}}}^s={\tilde{\mathbf{f}}}^s$$

(74)

with

$${\tilde{\mathbf{A}}}^s={\left({\mathbf{D}}^s\right)}^{-1}{\mathbf{A}}^s{\left({\mathbf{D}}^s\right)}^{-1},{\tilde{\mathbf{f}}}^s={\left({\mathbf{D}}^s\right)}^{-1}{\mathbf{f}}^s,{\tilde{\mathbf{u}}}^s={\mathbf{D}}^s{\mathbf{u}}^s.$$

(75)

As is already known from the previous section, the matrix arising from discretization of the differential operator $\widehat{\mathcal{D}}$ is sparse and has the structure displayed in Figure 1 (middle). Hence, the main focus is on properties of the matrix ${\mathbf{C}}^s$ corresponding to the integral, i.e., the matrix ${\mathbf{C}}^s$ with entries

$${\mathbf{C}}_{\mu ,\lambda }^s=〈{\mathcal{I}}_2\left({\psi }_{\lambda }\right),{\psi }_{\mu }〉,{\psi }_{\lambda },{\psi }_{\mu }\in {\mathrm{\Psi }}^s.$$

(76)

For the Galerkin method with the standard spline basis, the matrix ${\mathbf{C}}^s$ is full. However, it is known that, for integral operators with some types of kernels and for wavelet bases with vanishing moments, many entries of discretization matrices are small and can be thresholded and the matrices can be approximated with matrices that are sparse or quasi-sparse (see, e.g., [4,18,29,30]). The following theorem provides the decay estimates for the entries of the matrix ${\mathbf{C}}^s$ corresponding to general wavelets with L vanishing moments.

Theorem 5.

Let Ψ be a wavelet basis with L vanishing moments, i.e., Conditions (i)–(iv) from Definition 1 are satisfied. Let ${\psi }_{i,k},{\psi }_{j,l}\in \mathrm{\Psi }$ be wavelets that are generated from wavelets ${\psi }^l$, ${\psi }^m$, respectively, via translations and dilations as in Equation (21). Denote by $C_1$ the maximum of the lengths of the supports of ${\psi }^l$ and ${\psi }^m$ and

$$C_2={\displaystyle \underset{n=l,m}{max}}{\displaystyle \underset{supp{\psi }^n}{\int }}\left|{\psi }^n\left(x\right)\right|dx.$$

(77)

Denote $\left[a_{i,k},b_{i,k}\right]={\mathrm{\Omega }}_{i,k}=supp{\psi }_{i,k}$, $\left[a_{j,l},b_{j,l}\right]={\mathrm{\Omega }}_{j,l}=supp{\psi }_{j,l}$, $I_{i,j,k,l}=\left[a_{j,l}-b_{i,k},b_{j,l}-a_{i,k}\right]$. If $g\in C^{2L}\left(I_{i,j,k,l}\right)$, then

$$\left|〈{\mathcal{I}}_2\left({\psi }_{i,k}\right),{\psi }_{j,l}〉\right|\le C_{i,j,k,l}{2}^{-\left(L+\frac{1}{2}\right)\left(i+j\right)},$$

(78)

with

$$C_{i,j,k,l}=\frac{C_1^{2L}{C}_2^2\lambda }{4^L{\left(L!\right)}^2}{\displaystyle \underset{\left(x,y\right)\in {\mathrm{\Omega }}_{i,j,k,l}}{max}}\left|g^{\left(2L\right)}\left(y-x\right)\right|.$$

(79)

Consequently, if $\mathrm{\Omega }\subset {\left[0,S^{max}\right]}^2$ is a bounded set such that the function

$$K\left(x,y\right)=\lambda g\left(y-x\right)$$

(80)

satisfies $K\in C^{2L}\left(\mathrm{\Omega }\right)$, then there exists a constant C independent of $i,j,k,l$ such that

$$\left|〈{\mathcal{I}}_2\left({\psi }_{i,k}\right),{\psi }_{j,l}〉\right|\le C{2}^{-\left(L+\frac{1}{2}\right)\left(i+j\right)},$$

(81)

for all wavelets ${\psi }_{i,k}$ and ${\psi }_{j,l}$ such that the set ${\mathrm{\Omega }}_{i,j,k,l}={\mathrm{\Omega }}_{i,k}\times {\mathrm{\Omega }}_{j,l}$ satisfies ${\mathrm{\Omega }}_{i,j,k,l}\subset \mathrm{\Omega }$.

Proof. 

The proof is based on Taylor expansion of the kernel in a similar way as in [18,29]. Let the centers of the supports of ${\psi }_{i,k}$ and ${\psi }_{j,l}$ be denoted by $x_{i,k}$ and $y_{j,l}$, respectively. If $g\in C^{2L}\left(I_{i,j,k,l}\right)$, then the function K defined by Equation (80) satisfies $K\in C^{2L}\left({\mathrm{\Omega }}_{i,j,k,l}\right)$. By the Taylor theorem, there exists a function P that is a polynomial of degree at most $L-1$ with respect to x and a function Q that is a polynomial of degree at most $L-1$ with respect to y such that

$$K\left(x,y\right)=P\left(x,y\right)+Q\left(x,y\right)+R\left(x,y\right){\left(x-x_{i,k}\right)}^L{\left(y-y_{j,l}\right)}^L,$$

(82)

where

$$R\left(x,y\right)=\frac{1}{{\left(L!\right)}^2}\frac{{\partial }^{2L}K\left(\xi \left(x,y\right)\right)}{\partial x^L\partial y^L}$$

(83)

and

$$\xi \left(x,y\right)=\left(x_{i,k},y_{j,l}\right)+\alpha \left(\left(x,y\right)-\left(x_{i,k},y_{j,l}\right)\right)$$

(84)

for some $\alpha \in \left[0,1\right]$. Due to L vanishing moments of the wavelets ${\psi }_{i,k}$ and ${\psi }_{j,l}$,

$${\displaystyle \underset{{\mathrm{\Omega }}_{i,j,k,l}}{\int \int }}P\left(x,y\right){\psi }_{i,k}\left(x\right){\psi }_{j,l}\left(y\right)dxdy=0$$

(85)

is obtained and similarly for Q.

Using Property (ii) from Definition 1 gives

$${\left|x-x_{i,k}\right|}^L\le \frac{C_1^L}{2^L}{2}^{-Li},{\left|y-y_{j,l}\right|}^L\le \frac{C_1^L}{2^L}{2}^{-Lj}.$$

(86)

Definition (31) implies

$${\displaystyle \underset{{\mathrm{\Omega }}_{i,k}}{\int }}\left|{\psi }_{i,k}\left(x\right)\right|dx\le C_2{2}^{-i/2}.$$

(87)

Hence,

$$\begin{array}{lll}\left|〈{\mathcal{I}}_2\left({\psi }_{i,k}\right),{\psi }_{j,l}〉\right|& =& \left|{\displaystyle \underset{{\mathrm{\Omega }}_{i,j,k,l}}{\int \int }}K\left(x,y\right){\psi }_{i,k}\left(x\right){\psi }_{j,l}\left(y\right)dxdy\right|\hfill \\ & \le & C{\displaystyle \underset{{\mathrm{\Omega }}_{i,j,k,l}}{\int \int }}{\left|x-x_{i,k}\right|}^L{\left|y-y_{j,l}\right|}^L\left|{\psi }_{i,k}\left(S\right){\psi }_{j,l}\left(y\right)\right|dxdy\hfill \\ & \le & C\frac{C_1^{2L}{C}_2^2}{4^L}{2}^{-Li-Lj-i/2-j/2},\hfill \end{array}$$

(88)

with

$$C=\frac{1}{{\left(L!\right)}^2}{\displaystyle \underset{x,y\in {\mathrm{\Omega }}_{i,j,k,l}}{max}}\left|\frac{{\partial }^{2L}K\left(x,y\right)}{\partial x^L\partial y^L}\right|.$$

(89)

This proves the theorem. ☐

Let

$${\tilde{\mathbf{C}}}^s={\left({\mathbf{D}}^s\right)}^{-1}{\mathbf{C}}^s{\left({\mathbf{D}}^s\right)}^{-1}$$

(90)

with ${\mathbf{D}}^s$ defined by Equation (73). Then, the discretization matrix ${\tilde{\mathbf{A}}}^s$ is the sum of the matrix ${\tilde{\mathbf{C}}}^s$ and the matrix arising from discretization of the differential operator $\widehat{\mathcal{D}}$. Due to Theorem 5, many entries of the matrix ${\tilde{\mathbf{A}}}^s$ are small and can be thresholded, and thus the matrix ${\tilde{\mathbf{A}}}^s$ can be represented by a sparse matrix. 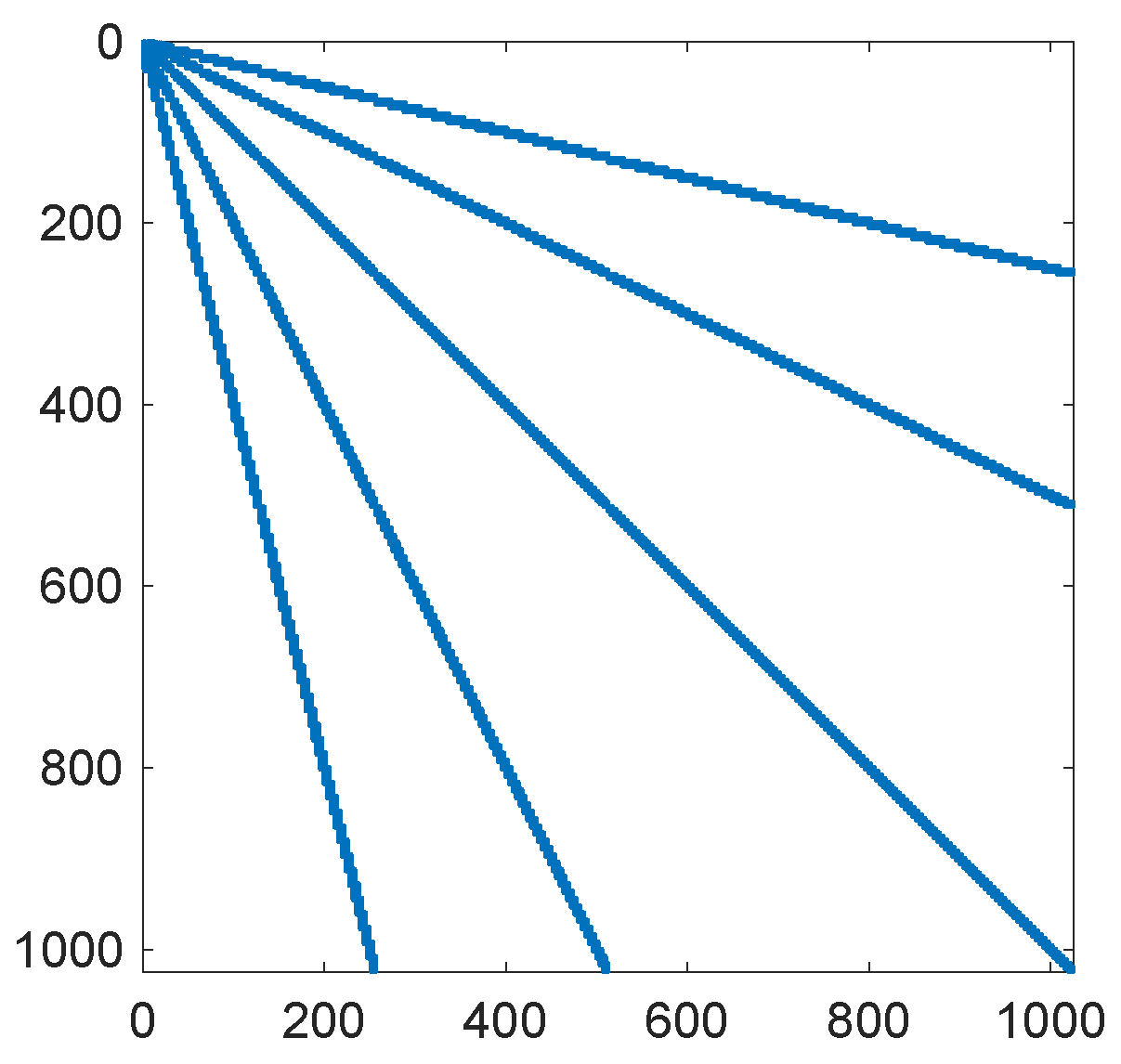The structure of the truncated matrix ${\tilde{\mathbf{A}}}^s$ is presented in Figure 3. This matrix contains only entries larger than ${10}^{-7}$, and it was computed for the option with parameters from Example 1 and the wavelet basis from this paper containing eight levels of wavelets.

In some papers [18,29], decay estimates were derived for integrals with a kernel K that has a singularity or a maximal value on the diagonal $y=x$ and decays with $\left|y-x\right|$. However, in some models such as the Merton model, with the density from Equation (2) that is used in numerical experiments in Section 4, these estimates cannot be used, because the kernel has maximal values for $y=x+{\mu }_J$ and is decaying exponentially with $\left|y-x-{\mu }_J\right|$.

Since the matrix ${\tilde{\mathbf{A}}}^s$ is the same for all time levels, the system matrix can be computed, analyzed and compressed only once as a preprocessing step and then one can work with the compressed matrix. However, since the computation of all integrals in Equation (76) can be time consuming, it is more convenient to use estimates in Equations (78) and (81) to compute only significant entries of the matrix ${\tilde{\mathbf{C}}}^s$. More precisely, the following strategy can be used:

(1)

Choose a tolerance $ϵ$.

(2)

Compute all the entries ${\tilde{\mathbf{C}}}_{\lambda ,\mu }^s$ for indexes $\lambda =\left(i,k\right)$ and $\mu =\left(j,l\right)$ such that $g\notin C^{2L}\left(I_{i,j,k,l}\right)$.

(3)

Based on estimate in Equation (81), set the level $\tilde{L}$ such that ${\tilde{\mathbf{C}}}_{\lambda ,\mu }^s<ϵ$ for any $i+j>\tilde{L}$ and $\lambda ,\mu$ such that $g\in C^{2L}\left(I_{i,j,k,l}\right)$.

(4)

If $i+j\le \tilde{L}$, then use a local estimate in Equation (81) to compute only entries for which it is not guaranteed that ${\tilde{\mathbf{C}}}_{\lambda ,\mu }^s<ϵ$.

Note that Step (4) enables one to obtain the matrix ${\tilde{\mathbf{C}}}^s$ and thus also ${\tilde{\mathbf{A}}}^s$ with more zero elements. To obtain a sparse matrix, it is sufficient to use Steps (1)–(3), i.e., to compute entries for which $i+j\le \tilde{L}$ and entries in regions where $g\left(y-x\right)$ is not smooth, and set to zero any other entries.

The impact of the truncation on the solution of the system in Equation (74) can be described as follows. Let ${\widehat{\mathbf{A}}}^s$ be the truncated matrix and ${\widehat{\mathbf{u}}}^s$ be the solution of the system ${\widehat{\mathbf{A}}}^s{\widehat{\mathbf{u}}}^s={\tilde{\mathbf{f}}}^s$. If

$$C_A=∥{\left({\widehat{\mathbf{A}}}^s\right)}^{-1}·\left({\tilde{\mathbf{A}}}^s-{\widehat{\mathbf{A}}}^s\right)∥<1,$$

(91)

then

$$\frac{∥{\tilde{\mathbf{u}}}^s-{\widehat{\mathbf{u}}}^s∥}{∥{\tilde{\mathbf{u}}}^s∥}\le \frac{\mathrm{cond}{\tilde{\mathbf{A}}}^s}{1-C_A}\frac{∥{\tilde{\mathbf{A}}}^s-{\widehat{\mathbf{A}}}^s∥}{∥{\tilde{\mathbf{A}}}^s∥}$$

(92)

(see [31]). Moreover, the matrices ${\tilde{\mathbf{A}}}^s$ have uniformly bounded condition numbers [4], i.e., $\mathrm{cond}{\tilde{\mathbf{A}}}^s<C$ with C independent on s. Hence, if a threshold is chosen that is small enough, then ${\widehat{\mathbf{u}}}^s$ will be close to ${\tilde{\mathbf{u}}}^s$.

4. Numerical Example

In this section, numerical experiments are provided for a vanilla European option and the Merton model. Since analytic solution is known for this model (see [1]), it is possible to compute the errors for the numerical solution.

Example 1.

The efficiency of the proposed method is illustrated on valuation of vanilla European options under the Merton model [1]. Put and call options with the same parameters as in [19,20,21] are considered, so that one can compare the numerical results for the methods proposed therein. The parameters are the following: option maturity $T=0.25$ year, interest rate $r=0.05$, volatility $\sigma =0.15$, intensity $\lambda =0.1$, and the strike price $K=100$. The probability density function is given by Equation (2) with parameters ${\mu }_J=-0.9$ and ${\sigma }_J=0.45$. The domain of interest is the interval $\left[0,2K\right]$, but because the localization error is the largest near the right endpoint of the interval (see [4,28]), $S_{max}=4K$ is chosen. To obtain $x_{min}\ne -\infty$, one has to choose $S_{min}>0$, thus $S_{min}=30$ is chosen. For the matrix compression, a tolerance $ϵ={10}^{-7}$ is set.

The method proposed in the previous section is used for the computation of the value of the put option and the put–call parity to compute the value of the call option. The resulting functions representing the values of the options are displayed in Figure 4.

In

Table 2. Values of vanilla European put options and pointwise errors.

		Crank–Nicolson			Richardson
S	$\mathit{N}$	$\mathit{M}$	Put	Error	$\mathit{M}$	Put	Error
90	32	6	9.284895	5.23 × ${10}^{-4}$	10	9.287676	2.26 × ${10}^{-3}$
	64	16	9.282265	3.15 × ${10}^{-3}$	16	9.282679	2.74 × ${10}^{-3}$
	128	46	9.285090	3.78 × ${10}^{-4}$	27	9.285143	2.75 × ${10}^{-4}$
	256	128	9.285427	8.69 × ${10}^{-6}$	46	9.285433	1.51 × ${10}^{-5}$
	512	363	9.285413	4.97 × ${10}^{-6}$	77	9.285414	4.17 × ${10}^{-6}$
	1024	1024	9.285417	6.24 × ${10}^{-7}$	128	9.285418	5.39 × ${10}^{-7}$
100	32	6	3.166832	1.78 × ${10}^{-2}$	10	3.165157	1.61 × ${10}^{-2}$
	64	16	3.148937	8.86 × ${10}^{-5}$	16	3.148590	4.36 × ${10}^{-4}$
	128	46	3.149050	2.44 × ${10}^{-5}$	27	3.149012	1.30 × ${10}^{-5}$
	256	128	3.149038	1.20 × ${10}^{-5}$	46	3.149032	6.56 × ${10}^{-6}$
	512	363	3.149027	9.07 × ${10}^{-7}$	77	3.149026	2.20 × ${10}^{-7}$
	1024	1024	3.149026	5.64 × ${10}^{-8}$	128	3.149026	1.76 × ${10}^{-7}$
110	32	6	1.389539	1.16 × ${10}^{-2}$	10	1.389646	1.15 × ${10}^{-2}$
	64	16	1.401664	4.78 × ${10}^{-4}$	16	1.401750	5.65 × ${10}^{-4}$
	128	46	1.401350	1.64 × ${10}^{-4}$	27	1.401362	1.76 × ${10}^{-4}$
	256	128	1.401196	1.06 × ${10}^{-5}$	46	1.401198	1.20 × ${10}^{-5}$
	512	363	1.401183	3.22 × ${10}^{-6}$	77	1.401183	3.04 × ${10}^{-6}$
	1024	1024	1.401186	3.22 × ${10}^{-7}$	128	1.401186	3.00 × ${10}^{-7}$

, the resulting values of the options for the asset prices $S=90$, $S=100$, and $S=110$ are listed. The reference values computed by analytic formula from [1] are $9.28541807$ for $S=90$, $3.14902574$ for $S=100$, and $1.40118588$ for $S=110$, for a put option. Table 2 also presents the pointwise errors, i.e., the differences between the computed values and the reference values.

In this paper, the main focus is on the spatial discretization using the Galerkin method with the proposed basis. However, this method can also be combined with time discretization schemes other than Crank–Nicolson to obtain higher order convergence with respect to time. Here, the order of convergence with respect to τ is improved by simple postprocessing based on Richardson extrapolation, similar to the work in [32,33], i.e., the approximate solution $U_{h,\tau }$ is computed using the spatial step h and the time step τ and the approximate solution $U_{h,\tau /2}$ using the spatial step h and the time step $\tau /2$. Richardson extrapolation consists of computing a new approximate solution

$$U_{h,\tau /2}^R=\frac{4U_{h,\tau /2}-U_{h,\tau }}{3}.$$

(93)

Then, it is possible to compute a sufficiently accurate solution with a significantly smaller number of time steps (see Table 2 and

Table 3. Errors in the $L^{\infty }\left(0,2K\right)$-norm and in the $L^2\left(0,2K\right)$-norm and the corresponding experimental rates of convergence.

	Crank–Nicolson					Richardson
$\mathit{N}$	$\mathit{M}$	${\mathit{L}}^{\infty }$	Rate	${\mathit{L}}^{\mathbf{2}}$	Rate	$\mathit{M}$	${\mathit{L}}^{\infty }$	Rate	${\mathit{L}}^{\mathbf{2}}$	Rate
32	6	3.48 × ${10}^{-2}$	-	9.91 × ${10}^{-2}$	-	10	3.26 × ${10}^{-2}$	-	9.63 × ${10}^{-2}$	-
64	16	3.31 × ${10}^{-3}$	3.39	8.00 × ${10}^{-3}$	3.63	16	2.89 × ${10}^{-3}$	3.49	7.67 × ${10}^{-3}$	3.65
128	46	3.59 × ${10}^{-4}$	3.20	8.80 × ${10}^{-4}$	3.18	27	3.07 × ${10}^{-4}$	3.23	8.55 × ${10}^{-4}$	3.17
256	128	4.24 × ${10}^{-5}$	3.08	1.07 × ${10}^{-4}$	3.04	46	3.78 × ${10}^{-5}$	3.02	1.05 × ${10}^{-4}$	3.03
512	363	5.28 × ${10}^{-6}$	3.01	1.33 × ${10}^{-5}$	3.01	77	4.66 × ${10}^{-6}$	3.02	1.30 × ${10}^{-5}$	3.01
1024	1024	7.35 × ${10}^{-7}$	2.85	1.91 × ${10}^{-6}$	2.80	128	6.52 × ${10}^{-7}$	2.84	1.87 × ${10}^{-6}$	2.80

).

Table 3 lists the errors in the norms of the spaces $L^{\infty }\left(0,2K\right)$ and $L^2\left(0,2K\right)$. The optimal order for the Crank–Nicolson scheme is $\mathcal{O}\left({\tau }^2\right)$, and the optimal order for the quadratic spline approximation is $\mathcal{O}\left(h^3\right)$, where $h=1/N$ represents the spatial step. Thus, in Table 2 and Table 3, if the spatial step is decreased to $h/2$, the time step is decreased to $\tau /⌈\sqrt{8}⌉$, $⌈·⌉$ denoting the upper integer part. Hence, the experimental rate of convergence with respect to spatial step h is computed as

$$rate=\frac{logerror\left(\frac{N}{2},⌈\frac{M}{\sqrt{a}}⌉\right)-logerror\left(N,M\right)}{log2}.$$

(94)

for $a=8$. Experimental rates of convergence for the method with Richardson extrapolation are computed using Equation (94) with $a=2$.

Figure 5 shows the pointwise errors for values of European options corresponding to the Merton model with the same parameters, in dependence on the spatial parameter N. In this figure, WG denotes the wavelet-Galerkin method combined with the Crank–Nicolson scheme with Richardson extrapolation as discussed in this paper, FD denotes the finite difference method from [21], FPI denotes the method from [19], which is based on fixed point iterations and the Crank–Nicolson scheme, and IMEX denotes the explicit–implicit method from [20], which is a combination of the cubic spline collocation method and the backward difference method. The number of time steps is comparable or smaller for the present method than for the other methods (see Table 2 and numerical experiments in [19,20,21]). Other numerical methods for the Merton model can be found in [34,35,36,37,38,39]. In comparison with methods from [19,20,21], the spatial parameter N was significantly smaller for the present method and thus significantly smaller matrices are involved in the computation.

Table 4. The condition numbers (cond) of discretization matrices, and numbers of GMRES iterations (it).

N	M	Cond	It
32	6	11.5	5(1)
64	16	12.9	5(3)
128	46	14.0	5(7)
256	128	14.9	5(10)
512	363	15.7	6(2)
1024	1024	16.3	6(3)

presents the condition numbers (cond) of diagonally preconditioned matrices ${\tilde{\mathbf{A}}}^s$. Furthermore, the table lists the number of outer and the number of inner iterations needed to resolve the resulting system of equations by the generalized minimal residual method (GMRES) with the following input parameters: restart after ten iterations, maximum number of outer iterations is 100 and the iterations stop if the relative residual is less than ${10}^{-12}$.

5. Conclusions

In this paper, the construction of a quadratic spline wavelet basis on the bounded interval is proposed. The basis is adapted to homogeneous Dirichlet boundary conditions, wavelets have three vanishing moments, and the wavelets on the levels i and j are orthogonal both with respect to the $L^2$-norm and with respect to the $H^1$-seminorm if $\left|i-j\right|>2$. A rigorous proof of the Riesz basis property is provided and the condition numbers for the basis are presented. Using the tensor product and appropriate parametric mappings, this basis can be adapted to higher-dimensional bounded domains. Due to properties listed in Equation (23), the matrices arising from discretization using the Galerkin method or adaptive wavelet method are sparse for various types of equations such as Poisson, Helmholtz, Black–Scholes, and convection-diffusion equations.

The applicability of the constructed basis is illustrated on the jump–diffusion option pricing problem that is represented by partial integro-differential equation. The equation is transformed to logarithmic prices, and the Crank–Nicolson scheme is used for time discretization combined with the wavelet-Galerkin method for spatial discretization. Decay estimates are proved for the entries of the resulting matrices arising from discretization and, based on these decays, a strategy for approximation of the system matrix with a sparse matrix is proposed. Then, numerical results are presented for European option pricing under the Merton model. The advantage of the proposed method is the sparse structure of the matrices and, in comparison with methods from [19,20,21], the presented method requires a significantly smaller number of degrees of freedom to compute the solution with desired accuracy. The time step size needed to compute a sufficiently accurate solution is reduced using Richardson extrapolation. Finally, it is shown that the matrices are well-conditioned and that the number of iterations of the GMRES method used for the numerical solution of the resulting system of linear algebraic equations is small.