Abstract
The internet of things (IoT) refers to all the smart objects that are connected to other objects, devices or servers and that are able to collect and share data, in order to “learn” and improve their functionalities. Smart objects suffer from lack of memory and computational power, since they are usually lightweight. Moreover, their security is weakened by the fact that smart objects can be placed in unprotected environments, where adversaries are able to play with the symmetric-key algorithm used and the device on which the cryptographic operations are executed. In this paper, we focus on a family of white-box symmetric ciphers substitution–permutation network (SPN)box, extending and improving our previous paper on the topic presented at WIDECOM2019. We highlight the importance of white-box cryptography in the IoT context, but also the need to have a fast black-box implementation (server-side) of the cipher. We show that, modifying an internal layer of SPNbox, we are able to increase the key length and to improve the performance of the implementation. We measure these improvements (a) on 32/64-bit architectures and (b) in the IoT context by encrypting/decrypting 10,000 payloads of lightweight messaging protocol Message Queuing Telemetry Transport (MQTT).
1. Introduction
The name internet of things (IoT), coined by the MIT researcher Kevin Ashton [1], usually refers to smart objects, connected through the internet to other sensors, devices and servers with which collect and/or share data for improving their functionalities. IoT can also be combined with other technologies, for example with cloud computing [2]. It is possible to create a sustainable smart home aiming to reduce resources’ consumption or develop specific applications in the medical field [3] such as wearable devices which monitor our physical conditions, specific devices used to check patients with chronic illnesses, and so on. Data collected by IoT devices need to be (a) processed to form informations by applying, for example, data mining techniques [4]; (b) evaluated in order to make decision by adopting agent based models [5,6], bayesian decision models [7], fuzzy logic [8] and so on; (c) protected from attacks, failures and leaks during communication [2].
Several issues have to be faced in securing IoT applications. An important example is given by the intrinsic constraints of the devices [9], that usually have a small amount of memory and cannot perform heavy computations. It is very likely to have such devices in non-protected environment, where an adversary can access them and perform attacks. In particular, she/he can perform an analysis of the controlled binary [10] or perform differential fault analysis [11,12]. Moreover, since these devices are connected, compromising one of them can open the way to botnet attacks [2,3]. We can observe that we are exactly in a white-box framework, and white-box cryptography [13] has been first developed to cope with the scenario in which an attacker can physically interact both with the implementation of the used cryptographic algorithm and with the device on which the encryption/decryption operations are executed. The usually studied scenario, namely black-box, in which the execution cannot be observed nor modified by the attacker, is not always suitable for IoT applications [14]. The reader can think about what happens in the context of digital rights management where discovering the key means to have the possibility to spread digital contents to people that have not payed such contents.
The effort of researchers towards white-box cryptographic schemes materialized with [13,15] where white-box versions of AES and DES have been implemented. Nevertheless, it is important to remark that these implementations have been attacked via algebraic attacks [16] (improved by [17]), [18,19,20]. Moreover, also Jacob et al. in [21] can easily break Chow’s implementations.
The need to have white-box algorithms for practical applications leads to develop some specific algorithms. Examples of block ciphers developed to be employed in the framework of white-box cryptography are ASASA [22] and SPACE [23]. However, these ciphers are not free of drawbacks or weaknesses. In particular, decomposition attacks can affect ASASA’s security while SPACE is heavy from a computational point of view [24]. An important step forward for white-box cryptography, was the development of substitution–permutation network (SPN)box [24], another block cipher that relies on internal block ciphers with the aim to reduce the computation time. In [9], the problem of intrinsic constraints on computational power and memory of IoT devices in unprotected environment is addressed. The authors refer to smart objects with limited computational power and memory that may contain sensitive data and can be easily lost or stolen. Differently from AES/DES white-box implementations, the authors do not decline a well-known cipher into the new framework, but they develop a new one, relying on a modification of Lai-Massey structure. The crucial point is that only the encryption is thought to be done on the IoT constrained device, while the decryption phase is supposed to be done on a computer or server and in a black box scenario. In [25] the authors refer to embedded distributed devices which collect and securely send information to centralized servers. Subsequently, these servers decrypt and process all the information. As previously mentioned, the collected information may be sensitive and it is possible for an attacker to get control of the whole device. The scheme proposed in [25] is lightweight and suitable for constrained devices. In particular, such a new design has the following peculiarities:
- the employed operations are very simple; they essentially consist of lookup tables and bit operations;
- the lookup tables and the structure containing sensitive data are small in memory;
- the provided security is medium-level (∼) and protection is ensured for reasonable amount of time;
- it is possible to update the key at small costs.
The scheme is based on a Fesitel structure, but it adds two bijections, as a defence against attacks. Moreover, to cope with structural cryptanalysis [25,26] different size components are used.
This paper improves of a previous work entiteled “White-box Cryptography: A Time-security Trade-off for the SPNbox Family” [27], presented by F.Cioschi, N.Fornari and A.Visconti at the 2nd International Conference on International Conference on Wireless, Intelligent and Distributed Environment for Communication (WIDECOM 2019). In this paper, we (a) introduce the white-box approach in the IoT context, explaining the importance of protecting data in an environment where attackers have full control over the whole system; (b) explain the importance of having a fast black-box implementation of a white-box cipher; (c) summarize our previous idea [27] explaining how to modify the internal block ciphers of the SPNbox family in order to increase the size of the key space; (d) measure the performance of a black-box implementation (server-side) on 32- and 64-bit architectures and by encrypting/decrypting 10,000 payloads of a lightweight messaging protocol—i.e., MQTT—which contains the data sent over the internet.
The remainder of the paper is organized as following. In Section 2, block ciphers are introduced. In Section 3, we present several white-box implementations and related attacks published in literature. In Section 4 and Section 5, we summarize two block ciphers’ families, namely, SPACE and SPNbox, which are white-box friendly by design. In Section 6, we explain the importance of increasing the number of bits of the key used in each round. In Section 7, the testing activities are presented. Finally, Section 8 is devoted to discussion and conclusions.
2. Block Ciphers
There exist two main families of block ciphers: SPN and Feistel network. The main difference between them is that Feistel networks play only with one half of the cipher state in each round.
2.1. Substitution-Permutation Networks
A SPN is a design for block ciphers proposed by Shannon in [28], where he suggested to use multiple mixing layers interleaving substitutions and permutations. Although weak on its own, applying substitutions and then permutations presents good “mixing” properties. Substitutions contribute to local confusion and permutations spread such a local confusion to the more distant subblocks, thus providing diffusion [28]. If a single input bit is flipped, it affects the m output bits of a specific S-box which, subsequently, are sent to different S-boxes by a permutation. Considering the output of such a network, about fifty percent of the bits are affected by this change. Therefore an outcome of a single bit change at the input is difficult to predict, especially if the bit of the secret key are XORed into the block between the encryption layers. In order to get better diffusion properties, several block ciphers adopt linear (as in the case of AES) or affine mappings instead of permutations.
Definition 1.
where by ⊕ we denote the bitwise addition (XOR).
Let with be a block cipher with N rounds. Let be the cipher key and be the round keys generated by k through the key schedule.
Then ϕ is an SPN block cipher if
where and
- is a non linear substitution
- where is the subgroup of the affine transformations of
- is the addition with the round key
2.2. Feistel Networks
A Feistel network is a block cipher introduced by H. Feistel and D. Coppersmith in 1973 [29] which has the advantage of having the encryption and decryption functions almost identical, making the implementation easier and cheaper compared to translation based ciphers.
Let us define the following functions before describing the encryption process.
Definition 2.
Let be a projection, with , defined as:
Considering as a vector of bits, we can use projection to choose the t most significant bits of x.
Definition 3.
Let be a projection, with , defined as:
In the same way, using projection we can choose the t least significant bits of x.
Given (a message) and (a secret key), for some positive integer l, the encryption process works as follows:
- round keys are generated from k by means of the key schedule
- message m is split into a left block and right block, initialized as
- for the round function is applied in the following way:
- final ciphertext c is .
Encryption and decryption only differ in the reverse order of the round keys, as a matter of fact the decryption of ciphertext is accomplished computing for
3. The White-Box Approach
The White-Box approach aims to avoid key recovery attacks by embedding the cryptographic key into a robust representation of the cipher. Consider a block cipher . We compute a map such that, given a key , it holds . If an attacker knows even both and , it should be very hard for him to find out the key.
Example 1.
Let ϕ and ψ be defined as follows:
If , we can consider ψ as a white-box implementation of ϕ, by representing ψ as a lookup table.
The first white-box AES implementation has been proposed by Chow et al. in [13]. The authors suggest that key extraction can be avoided by a careful use of lookup tables. In particular, given a secret key and a block cipher, it is possible to create a lookup table which maps the plaintext in a corresponding ciphertext. In some cases, this lookup table may be huge and unusable due to its dimension. Therefore, a block cipher can be represented as a network of smaller lookup tables (see Figure 1) that have to be read in a particular order [13]. Unfortunately, in the white-box framework an adversary has full access to these tables, exposing the cipher to possible attacks. Since there is no reason to make an attacker’s life easier, tables can be protected by means of internal encodings [13]. This means that a map is composed after table i and its inverse before table , leaving the ciphertext unchanged. However, internal encoding does not protect against code-lifting attacks. Indeed, an attacker may recover the tables of the cipher and understand their concatenation order. Doing so, she/he is able to decrypt messages even though he had not recovered the secret key. Therefore, another protection is required: external encoding. Internal and external encodings are also discussed in [30], while a different approach, based on polynomial algebra techniques [31], gave rise to a perturbated white-box implementation of AES [32], broken by [33] in 2010.
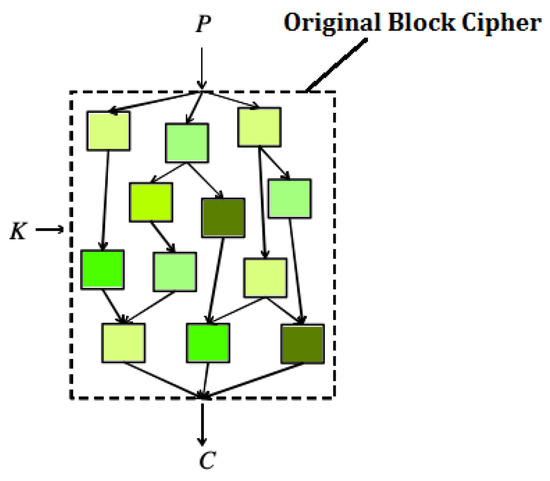
Figure 1.
Table-based white-box implementation: the key k is scrambled by a network of lookup tables.
Chow’s work is a milestone for white-box cryptography and its framework has also been used by some subsequent works such as [34,35]. However, researchers found attacks also for these new approaches:
- White-Box AES Implementation: Chow [13]; Attack: [16]; Work Factor: ;
- White-Box AES Implementation: Karroumi [34]; Attack: [18,20]; Work Factor: ;
- White-Box AES Implementation: Xiao Lai [35]; Attack: [18]; Work Factor: ;
- White-Box AES Implementation: Xiao Lai [35] generic linear version; Attack: [18]; Work Factor: ;
- White-Box AES Implementation: Xiao Lai [35] affine/non-affine version; Attack: [19]; Work Factor: at least .
The attacks listed above may require to know the internal data representation and sometimes this means to produce a significant reverse engineering effort. An improved AES implementation is given in [36]. This implementation is immune to attacks described in [16,18] but it is not to the one presented in [37].
The first paper aiming to break all white-box implementations belonging to the framework introduced in [13] is [19], but it has the weak point to require some additional hypotheses. Differently, Derbez et al. [38] breaks all the papers in Chow’s framework by solving the affine equivalence problem (see [39,40]). Chow’s framework has also been used by [41] and subsequently attacked by [42].
A significant advance from the attacker’s point of view became feasible by shifting the focus from the attacks previously described to side channel attacks [43]. In particular, new approaches to verify the security of a white-box implementation have been proposed in [44] where Bos et al. present differential fault analysis (DFA) and differential computational analysis (DCA) attacks (further information on fault-injection and differential power analysis attacks can be found in [45,46] respectively). In addition, in [47,48] the authors explained more formally why DCA is effective against linear and nibble encoding, Rivain and Wang [43] provide an extensive analysis on the effectiveness of DCA, finally Biryukov and Udovenko [49] give a general protection method for white-box implementations against DCA.
Obfuscation techniques or the randomization of the location of the lookup tables can be used to enhance security of white-box algorithms [50], while [51] examines how these techniques are successful against both DCA and differential power attacks (DPA). The paper [52] exploits noncommutative groups to obfuscate operation that should be made on commutative ones and it is employed in the IoT framework. Finally, an evaluation on software protections to white-box implementations is provided by [51].
Some improvements to DCA have been developed by [43,53]. The first one extends DCA to successfully address implementations using masking and shuffling techniques [53]. The second one provide a DCA-like collision attack with a good complexity [43].
Some paper such as [54,55,56] address the problem of incompressibility or code hardness. The idea is that an attacker in the white-box framework should not be able to rewrite the code of some implementation in order to decrease the code-hardness. In [54] two incompressible white-box schemes called “WhiteKey” and “WhiteBlock” are introduced and one instance for each scheme is provided (called PuppyCipher and CoureurDesBois respectively), [55] describes the concept of code-hardness, time-hardness and memory-hardness, while [56] provides a new incompressible white-box implementation based on the assumption of one-way permutations.
We conclude our extensive analisys of implementations and attacks, citing a white-box signature scheme [57] and the methods [58] used to attack the most resistant implementation submitted to the white-box competition called “CHES 2017 CTF Challenge”.
4. SPACE: A Block Cipher
SPACE is a block cipher developed by Bogdanov and Isobe in [23], that is based on a Feistel network. This cipher is designed so that security against key extraction in the white-box context reduces to the well studied problem of key recovery for block ciphers in the standard black-box setting.
SPACE is a generalized Feistel network [29]. Given a message and a secret key , it encrypts m to a ciphertext . In describing SPACE, three quantities are often employed: . In particular, in [23] , and .
We summarize here the encryption procedure:
- The state at round r can be seen as given by vectors so
- , so it is initialized with the plaintext.
- For the state is updated this way:where is the Feistel function and is the concatenation.
- so we have found the ciphertext.
At each encryption round, the Feistel function takes as input. Then is added to the rest of the state . The first bits of the new state are given by the result of this operation. The last are filled with .
Now, consider be the projection of Definition 2 and the Feistel function used by SPACE, specified in Definition 4.
Definition 4.
Let be a block cipher and r the round number represented in binary with digits (so we see it as an element of ). The Feistel function is defined as
We give a specific notation for the round independent part of .
Definition 5.
The round independent part of the Feistel function is
Notice that, differently from traditional Feistel networks, SPACE does not use round keys. There is one secret key k used by . This secret key cannot be hardcoded, hence is implemented as a look-up table. The reader might ask himself the reason for designing SPACE over another block cipher when could be directly implemented as a look-up table. It turns out that this second possibility cannot be developed. If we were to implement as a look-up table we would need bits of space:
For the construction of such a look-up table is practically impossible. Therefore Bogdanov and Isobe propose to truncate the output of , computed over a smaller domain (see Figure 2):
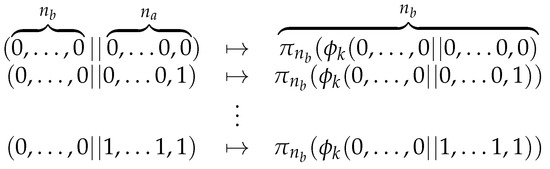
Figure 2.
The value of each image of is saved as a row in a look-up table. Every row is indexed by the value of x, .
Since the first zeros are used as padding in order to form an n-bit input to provide to , it is completely useless to store them, hence the look-up table implementation needs bits. Thus, the size of the tables for different values of —SPACE(, R), where R is the suggested number of rounds—is the following:
- SPACE-(8,300); Table: 3.84 KB
- SPACE-(16,128); Table: 918 KB
- SPACE-(24,128); Table: 218 MB
- SPACE-(32,128); Table: 51.5 GB
Notice that (1) AES white-box implementations of Chow et al. [13] and Xiao Lai [35] has a table of 752 KB and 20.5 MB respectively; (2) not all values are suitable, indeed, for and the size of the table is not good enough to be used in practice. On the contrary, for the table has the same size of that described in [13].
5. The SPNbox Family
The SPACE family of space-hard block ciphers [23] benefits of the Feistel structure from a security point of view and prevents the use of parallel execution (see Section 4). However, as suggested in [24], using an SPN-type design it is possible to satisfy the requirement of parallelism maintaining a suitably high level of space hardness. Thus, Bogdanov et al. described the SPNbox family of space-hard block ciphers [24]. Let us briefly explain their idea.
SPNbox- is a substitution-permutation network (SPN) with a block length of n bits, a k-bit secret key, and based on -bit substitution boxes.
State:
The state of SPNbox- is representable as a vector of elements of bits each:
Key Schedule:
The k-bit master key is expanded, round keys of bits, by means of a Key Derivation Function (KDF)—e.g., PBKDF2 [59,60,61,62], ARGON2 [63], Scrypt [64], and so on:
Round Transformation:
We encrypt a plaintext and we get a ciphertext , by using the following R transformations—e.g., :
The nonlinear layer is a substitution layer where t identical bijective -bit S-boxes depending on the key are applied to the state:
These identical S-boxes are constituted by an internal small block cipher of block length bit.
The linear layer , a diffusion layer, applies a MDS matrix to the state:
The affine layer takes the state and adds round-dependent constants to it:
with for .
The Underlying Small Block Ciphers:
The identical -bit S-boxes in the layer (which depend on the key) are block ciphers. They are based on the round transformation of AES and they are formed by rounds operating on a state of l bytes, where :
where SB, MC and AK indicate the AES transformations SubBytes, MixColumns and AddRoundKey, respectively. Notice that (a) the number of rounds that [24] suggests are = 16, = 20, = 32 and = 64; (b) different matrices are employed in the round transformation. More precisely, for = 32 we use the matrix of AES, while in the other cases a sub-matrix of is used. If = 8, is the identity map’s matrix. Note that, as for the Feistel function in SPACE, in the white-box setting the small block ciphers are implemented as lookup tables.
6. Issues and Possible Solutions
Although the white-box implementation of the cipher is very important, it may have some limitations due to the key embedded into the device. If several devices have to communicate with a server and such devices do not support Transport Layer Security (TLS) protocol due to insufficient resources, the server needs to manage a number of keys (pre-shared or not) in order to decrypt the messages. In a white-box context this means having a number of different implementations that run on our server and this is not a good idea. Therefore, the server will be provided with a fast black-box implementation of the cipher.
Figure 3 helps us to visualize this idea, where a white-box implementation runs on a number of devices and a fast black-box implementation runs on our server.
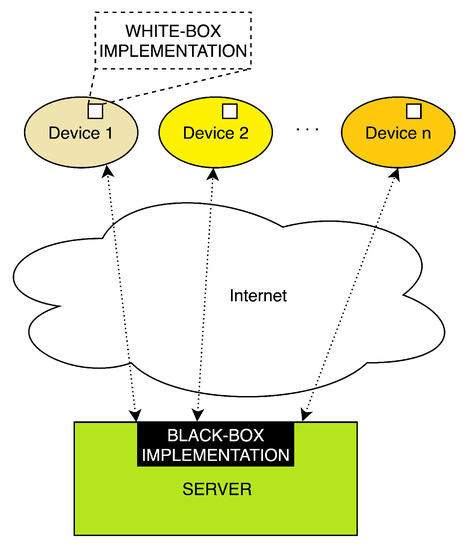
Figure 3.
A black-box implementation (server-side).
In order to design a fast black-box implementation of a white-box cipher, we modify the inner round described in Section 5, increasing the number of bits of the key used in each round. In particular, we replace the AES’ ShiftRow transformation, omitted by [24], with a key-dependent circular bit shift transformation (see Figure 4 and Figure 5).
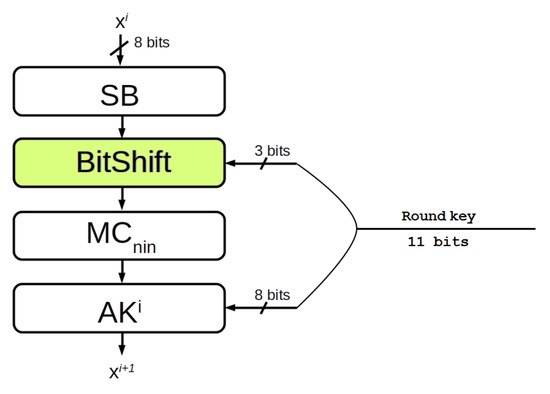
Figure 4.
A BitShift key-dependent: increasing the size of the round key from 8 to 11 bits.
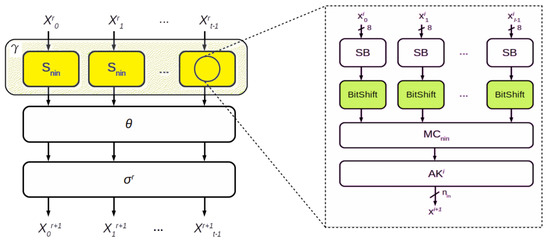
Figure 5.
Substitution–permutation network (SPN)box: a new inner round .
If we are shifting eight bits of the state, i.e., = 8, three bits are required to execute the circular shift. Thus, we use 11 bits of the key in each round i: eight of them for the AK transformation and three for the BitShift transformation. If the state doubled, tripled, or quadrupled, i.e., = 16, 24, 32, the bits of the key used are , and respectively.
Notice that the implementation of [24] employs the AES-NI instructions, while the idea described in this paper does not. In the encryption phase ( = 32, 24, 16), the matrices involved in the computation of the MixColumns transformation (, and for short) are sub-matrices of that used in AES (). On the contrary, in the decryption phase, we need to invert and . Since their inverse matrices are not sub-matrices of and the decryption instruction of AES-NI is based only on , for = 24, 16 we cannot use the AES-NI instructions. Anyway, in IoT context, the impossibility of using AES-NI instructions is not a problem in itself because not all IoT devices support this instruction set.
7. Testing Activities
The testing activity reported is twofold. In the first part, we measure the performance of internal layer (see Algorithm 1)—the external part (layer and ) is exactly the same as in [24], so it would be pointless to evaluate it.
| Algorithm 1: Layer with BitShift transformation. |
 |
We run our code on laptops with different hardware configurations. More precisely, our laptops are equipped with
- Intel® CoreTM i3-330M, 2.13 GHz processor with 3 MB SmartCache, 8 GB RAM and Ubuntu 18.04.1 LTS 64-bit. The source code has been compiled with GCC 7.3.0 with -O3 optimization enabled (see Table 1);
 Table 1. Results of tests on i3-330M with Ubuntu 18.04.1 LTS 64-bit.
Table 1. Results of tests on i3-330M with Ubuntu 18.04.1 LTS 64-bit. - Intel® CoreTM i3-350M, 2.26 GHz processor with 3 MB SmartCache, 8 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see Table 2);
 Table 2. Results of tests on i3-350M with Ubuntu 18.04.2 LTS 64-bit.
Table 2. Results of tests on i3-350M with Ubuntu 18.04.2 LTS 64-bit. - Intel® CoreTM i7-2860QM, 2.50/3.60 GHz processor with 8 MB SmartCache, 16 GB RAM and Kubuntu 18.10 64-bit. The source code has been compiled with GCC 7.3.0 with -O3 optimization enabled (see Table 3);
 Table 3. Results of tests on i7-2860QM with Kubuntu 18.10 64-bit.
Table 3. Results of tests on i7-2860QM with Kubuntu 18.10 64-bit. - Intel® CoreTM i7-5500U, 2.40/3.00 GHz processor with 4 MB Cache, 8 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see Table 4);
 Table 4. Results of tests on i7-5500U with Ubuntu 18.04.2 LTS 64-bit.
Table 4. Results of tests on i7-5500U with Ubuntu 18.04.2 LTS 64-bit. - Intel® CoreTM i7-8550U CPU, 1.80/4.00 GHz processor with 8 MB SmartCache, 32 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see Table 5);
 Table 5. Results of tests on i7-8550U with Ubuntu 18.04.2 LTS 64-bit.
Table 5. Results of tests on i7-8550U with Ubuntu 18.04.2 LTS 64-bit. - Intel® CoreTM i3-350M, 2.26 GHz processor with 3 MB SmartCache, 4 GB RAM and Debian GNU/Linux 9 32-bit. The source code has been compiled with GCC 6.3.0 with -O3 optimization enabled (see Table 6);
 Table 6. Results of tests on i3-350M with Debian GNU/Linux 9 32-bit.
Table 6. Results of tests on i3-350M with Debian GNU/Linux 9 32-bit.
In the second part, as explained in Section 6, we examine the cipher in the IoT context, where black-box and white-box implementations are involved.
7.1. 32/64-Bit Architectures
We compared the performance of internal layer (yellow rectangles of Figure 5) with and without BitShift transformation (green rectangles of Figure 5) for different sizes. We avoid the operations involved in and layers.
Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the time required to encrypt/decrypt one million of different plaintexts (fixed size of 128 bits) using the same key (randomly chosen). Notice that in addition to the key bits needed for the initial AddRoundKey , SPNbox layer uses 512 key bits—i.e., 512 bit = 16 round × 32 bit ( = 32), or 512 bit = 32 round × 16 bit ( = 16), or 512 bit = 64 round × 8 bit ( = 8). Therefore, we set to 512 the minimum amount of key bits to be used in our solution. In particular, we will execute: 12 rounds ( = 12), using 528 key bits ( = 32); 24 rounds ( = 24), using 528 key bits ( = 16); and finally 47 rounds ( = 47), using 517 key bits ( = 8).
Our testing activities show that implementations with BitShift are generally faster than those without it. In particular, several cases show that the improvement in the execution time exceeds 20%. Only in Table 5, = 8, encryption and decryption, we find a different result.
7.2. IoT Environment
The testing activity has been performed using MQTT [65], a lightweight communication protocol designed for small sensors and mobile devices in low bandwidth environments. By default data are sent in clear text over the internet, thus we encrypt data contained in the payload. We measure the performance of layer as described in Algorithm 2. More precisely, we compare the performances with and without BitShift transformation for different —size of 32, 16, and 8 bits—encrypting one million of different plaintexts—size of 16, 64, 256, and 1024 bytes—using the same key. Then, we send one hundred MQTT messages, each of which contains 10,000 encrypted payloads. Finally, adopting the same approach, the server collects and decrypts the same number of MQTT messages with encrypted payloads.
| Algorithm 2: MQTT: testing activity executed for each payload (16, 64, 128, and 1024 bytes). |
 |
Our testing activity has been executed on a machine equipped with an Intel® Core™ i7-6500U CPU @ 2.50 GHz × 4 processor, with 12 GB SDRAM DDR4-2133, Intel® HD Graphics 520 (Skylake GT2) GPU and operating system Ubuntu™ 18.04.2 TLS. We used Eclipse Mosquitto™ [66] version 1.4.15, which implements the MQTT protocol versions 3.1.1. The source code has been compiled with GCC 7.4.0, “-O3” optimization enabled. Table 7 summarizes the results obtained.

Table 7.
Encryption/decryption operations with a black-box implementation (server-side).
In particular, for the encryption phase, we got a highest gain (23.680%) in the case of 128-byte payload and , while the highest loss () in the case of a 64-byte payload and . For the decrypt phase, the highest gain () is obtained with a 16-byte payload and , and the highest loss () with a 128-byte payload and . Notice that the case turned out to be the worst one.
8. Conclusions
In the era of the internet of things, the involved devices are usually lightweight, so they cannot perform heavy computations nor store a huge amount of data. In addition, these data might be sensitive—energy consumptions, medical records, and so on—and could be sent in an unprotected environment. In a white-box scenario, an attacker could easily read these data because she/he has full access to the whole execution platform and white-box cryptography can be used to secure data in this specific context.
Considering the effectiveness of side-channel attacks, new ciphers has been designed with white-box attack model in mind. In this paper, we focused on the SPNbox family [24], suggesting how to increase the number of key bits used in each round and showing that this improvement affects the performance of the cipher. The introduction of a key-dependent circular bit shift transformation helped us to increase the keyspace and to reduce the number of rounds of the cipher, reducing the execution time too.
We described and analyzed the performance of the modified cipher in the IoT context, where both white-box and black-box implementations may be required. In particular, we measured its performance (a) on 32/64-bit architectures and (b) encrypting the payload of an IoT messaging protocol. Our testing activities have been executed on consumer laptops. The results obtained encrypting and decrypting one million of different 128-bit plaintexts on 32/64-bit architectures showed that the execution time for layer is reduced up to 22% while the highest loss is about 8%.
Moreover, the testing activities performed with lightweight protocol MQTT had a gain of about 23% and 22% (encryption and decryption phase, respectively) while a loss of about 9% and 5%. In all our testing activities the case turns out to be the worst one.
Possible future works are try to (a) understand in details why current implementation fails for and (b) implement a communication protocol based on Transport Layer Security pre-shared key ciphersuites (TLS-PSK) in order to compare the performance of white-box implementations with those of lightweight ciphers.
Author Contributions
All the authors contributed equally to the work. D.G.V.A., F.C., and A.S. wrote the code and executed testing activities; M.C., N.F., and A.V. wrote the manuscript; All the authors discussed the results and provided critical comments; A.V. supervised the testing activities.
Funding
This research received no external funding and the APC was funded by Università degli Studi di Milano, Piano di Sostegno alla Ricerca 2018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashton, K. That ‘internet of things’ thing. RFID J. 2009, 22, 97–114. [Google Scholar]
- Harini, S.; Jothika, K.; Jayashree, K. A Survey on Privacy and Security in Internet of Things. Int. J. Innov. Eng. Technol. 2017, 8, 129–134. [Google Scholar]
- Bertino, E. Data Security and Privacy in the IoT. EDBT 2016, 2016, 1–3. [Google Scholar]
- Tsai, C.; Lai, C.F.; Chiang, M.C.; Yang, L.T. Data mining for internet of things: A survey. IEEE Comm. Surv. Tut. 2013, 16, 77–97. [Google Scholar] [CrossRef]
- Schlesinger, M.; Parisi, D. The agent-based approach: A new direction for computational models of development. Dev. Rev. 2001, 21, 121–146. [Google Scholar] [CrossRef][Green Version]
- Visconti, A.; Tahayori, H. Artificial immune system based on interval type-2 fuzzy set paradigm. Appl. Soft Comput. 2011, 11, 4055–4063. [Google Scholar] [CrossRef]
- Lee, S.; Kyon-Mo, Y.; Sung-Bae, C. Integrated modular Bayesian networks with selective inference for context-aware decision making. Neurocomputing 2015, 163, 38–46. [Google Scholar] [CrossRef]
- Visconti, A.; Tahayori, H. Detecting misbehaving nodes in MANET with an artificial immune system based on type-2 fuzzy sets. In Proceedings of the 2009 International Conference for Internet Technology and Secured Transactions, (ICITST), London, UK, 9–13 November 2009. [Google Scholar]
- Shi, Y.; Wei, W.; He, Z.; Fan, H. An ultra-lightweight white-box encryption scheme for securing resource-constrained IoT devices. In Proceedings of the 32nd Annual Conference on Computer Security Applications, Los Angeles, CA, USA, 5–8 December 2016; ACM: New York, NY, USA, 2016. [Google Scholar]
- Shamir, A.; Van Someren, N. Playing “hide and seek” with stored keys. In Proceedings of the Conference Financial Crypto 1999 (FC’99), Anguilla, British West Indies, 22–25 February 1999; Franklin, M., Ed.; Springer: Heidelberg, Germany, 1999; pp. 118–124. [Google Scholar]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the importance of checking cryptographic protocols for faults (extended abstract). In Proceedings of the Conference EUROCRYPT97, Konstanz, Germany, 11–15 May 1997; Fumy, W., Ed.; Springer: Heidelberg, Germany, 1997; pp. 37–51. [Google Scholar]
- Biham, E.; Shamir, A. Differential fault analysis of secret key cryptosystems. In Proceedings of the Conference CRYPTO97, Santa Barbara, CA, USA, 17–21 August 1997; Kaliski, B.S., Ed.; Springer: Heidelberg, Germany, 1997; pp. 513–525. [Google Scholar]
- Chow, S.; Eisen, P.; Johnson, H.; Van Oorschot, P.C. White-box cryptography and an AES implementation. In Proceedings of the International Workshop on Selected Areas in Cryptography 2002, St. John’s, NL, Canada, 15–16 August 2002; Nyberg, K., Heys, H., Eds.; Springer: Berlin, Germany, 2002; pp. 250–270. [Google Scholar]
- Cho, J.; Kyu Young, C.; Dukjae, M. Hybrid WBC: Secure and efficient encryption schemes using the White-Box Cryptography. IACR Cryptol. ePrint Arch. 2015, 2015, 800. [Google Scholar]
- Chow, S.; Eisen, P.; Johnson, H.; Van Oorschot, P.C. A white-box DES implementation for DRM applications. In Proceedings of the ACM Workshop on Digital Rights Management, Washington, DC, USA, 18 November 2002; Feigenbaum, J., Ed.; Springer: Berlin, Germany, 2002; pp. 1–15. [Google Scholar]
- Billet, O.; Henri, G.; Charaf, E. Cryptanalysis of a white box AES implementation. In Proceedings of the International Workshop on Selected Areas in Cryptography, Waterloo, ON, Canada, 9–10 August 2004; Handschuh, H., Hasan, M.A., Eds.; Springer: Berlin, Germany, 2004; pp. 227–240. [Google Scholar]
- De Mulder, Y.; Roelse, P.; Preneel, B. Revisiting the BGE attack on a white-box AES implementation. IACR Cryptol. ePrint Arch. 2013, 2013, 450. [Google Scholar]
- De Mulder, Y.; Roelse, P.; Preneel, B. Cryptanalysis of the Xiao–Lai white-box AES implementation. In Proceedings of the International Conference on Selected Areas in Cryptography 2012, Windsor, ON, Canada, 15–16 August 2012; Knudsen, L.R., Wu, H., Eds.; Springer: Berlin, Germany, 2012; pp. 34–39. [Google Scholar]
- Michiels, W.; Gorissen, P.; Hollmann, H.D.L. Cryptanalysis of a generic class of white-box implementations. In Proceedings of the International Workshop on Selected Areas in Cryptography 2008, Sackville, NB, Canada, 14–15 August 2008; Avanzi, R.M., Keliher, L., Sica, F., Eds.; Springer: Berlin, Germany, 2008; pp. 414–428. [Google Scholar]
- Lepoint, T.; Rivain, M.; De Mulder, Y.; Roelse, P.; Preneel, B. Two attacks on a white-box AES implementation. In Proceedings of the International Conference on Selected Areas in Cryptography 2013, Burnaby, BC, Canada, 14–16 August 2013; Lange, T., Lauter, K., Lisoněk, P., Eds.; Springer: Berlin, Germany, 2013; pp. 265–285. [Google Scholar]
- Jacob, M.; Boneh, D.; Felten, E. Attacking an obfuscated cipher by injecting faults. In Proceedings of the ACM Workshop on Digital Rights Management, 2002, Washington, DC, USA, 18 November 2002; Springer: Berlin, Germany, 2002; pp. 16–31. [Google Scholar]
- Biryukov, A.; Bouillaguet, C.; Khovratovich, D. Cryptographic schemes based on the ASASA structure: Black-box, white-box, and public-key (Extended Abstract). In Advances in Cryptology, Proceedings of the ASIACRYPT 2014, Kaohsiung, Taiwan, 7–11 December 2014; Sarkar, P., Iwata, T., Eds.; Springer: Berlin, Germany, 2014; pp. 63–84. [Google Scholar]
- Bogdanov, A.; Takanori, I. White-box cryptography revisited: Space-hard ciphers. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; ACM: New York, NY, USA, 2015; pp. 1050–1069. [Google Scholar]
- Bogdanov, A.; Takanori, I.; Tischhauser, E. Towards practical whitebox cryptography: Optimizing efficiency and space hardness. In Proceedings of the ASIACRYPT 2016, Hanoi, Vietnam, 4–8 December 2016; Cheon, J.H., Tsuyoshi, T., Eds.; Springer: Berlin, Germany, 2016; pp. 126–158. [Google Scholar]
- Shi, Y.; Wei, W.; Fan, H.; Au, M.H.; Luo, X. A Light-Weight White-Box Encryption Scheme for Securing Distributed Embedded Devices. IEEE Trans. Comput. 2019, in press. [Google Scholar] [CrossRef]
- Biryukov, A.; Shamir, A. Structural cryptanalysis of SASAS. J. Cryptol. 2014, 23, 505–518. [Google Scholar] [CrossRef]
- Cioschi, F.; Fornari, N.; Visconti, A. White-Box Cryptography: A Time-Security Trade-Off for the SPNbox Family. In Proceedings of the 2nd International Conference on Wireless Intelligent and Distributed Environment for Communication (WIDECOM 2019), Milan, Italy, 11–13 February 2019; Woungang, I., Dhurandher, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 153–166. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Feistel, H. Cryptography and computer privacy. Sci. Am. 1973, 228, 15–23. [Google Scholar] [CrossRef]
- Lee, S.; Jho, N.S.; Kim, M. A Key Leakage Preventive White-box Cryptographic Implementation. IACR Cryptol. ePrint Arch. 2018, 2018, 1047. [Google Scholar]
- Bringer, J.; Chabanne, H.; Dottax, E. Perturbing and protecting a traceable block cipher. In Communications and Multimedia Security, Proceedings of the 10th IFIP TC-6 TC-11 International Conference, Heraklion, Greece, 19–21 October 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 109–119. [Google Scholar]
- Bringer, J.; Chabanne, H.; Dottax, E. White box cryptography: Another attempt. IACR Cryptol. ePrint Arch. 2006, 2006, 468. [Google Scholar]
- De Mulder, Y.; Wyseur, B.; Preneel, B. Cryptanalysis of a Perturbated White-Box AES Implementation. In Progress in Cryptology, Proceedings of the Conference INDOCRYPT 2010, Hyderabad, India, 12–15 December 2010; Gong, G., Gupta, K.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 292–310. [Google Scholar]
- Karroumi, M. Protecting white-box AES with dual ciphers. In Proceedings of the International Conference on Information Security and Cryptology 2010, Seoul, Korea, 1–3 December 2010; Rhee, K.H., Nyang, D., Eds.; Springer: Berlin, Germany, 2010; pp. 278–291. [Google Scholar]
- Xiao, Y.; Xuejia, L. A secure implementation of white-box AES. In Proceedings of the 2009 2nd International Conference on Computer Science and Its Applications, Jeju, Korea, 10–12 December 2009; pp. 1–6. [Google Scholar]
- Luo, R.; Lai, X.; You, R. A new attempt of white-box AES implementation. In Proceedings of the International Conference on Security, Pattern Analysis, and Cybernetics, Wuhan, China, 18–19 October 2014; pp. 423–429. [Google Scholar]
- Bai, K.; Wu, C.; Zhang, Z. Protect white-box AES to resist table composition attacks. IET Inf. Secur. 2018, 12, 305–313. [Google Scholar] [CrossRef]
- Derbez, P.; Fouque, P.A.; Lambin, B.; Minaud, B. On Recovering Affine Encodings in White-Box Implementations. In Proceedings of the Conference on Cryptographic Hardware and Embedded Systems 2016 (CHES2016), Santa Barbara, CA, USA, 17–19 August 2016; Gierlichs, B., Poschmann, A.Y., Eds.; Springer: Heidelberg, Germany, 2016; pp. 121–149. [Google Scholar]
- Biryukov, A.; De Cannière, C.; Braeken, A.; Preneel, B. A toolbox for cryptanalysis: Linear and affine equivalence algorithms. In Advances in Cryptology—EUROCRYPT 2003, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 33–50. [Google Scholar]
- Dinu, I. An improved affine equivalence algorithm for random permutations. In Advances in Cryptology, Proceedings of the Conference EUROCRYPT 2018, Tel Aviv, Israel, 29 April–3 May 2018; Springer: Cham, Switzerland, 2018; pp. 413–442. [Google Scholar]
- Xu, T.; Wu, C.; Liu, F.; Zhao, R. Protecting white-box cryptographic implementations with obfuscated round boundaries. Sci. China Inf. Sci. 2017, 61, 039103. [Google Scholar] [CrossRef]
- Yongjin, Y.; Dong-Chan, K.; Hun, B.C.; Junbum, S. Cryptanalysis of the Obfuscated Round Boundary Technique for Whitebox Cryptography. Sci. China Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Rivain, M.; Wang, J. Analysis and Improvement of Differential Computation Attacks against Internally-Encoded White-Box Implementations. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 225–255. [Google Scholar]
- Bos, J.W.; Hubain, C.; Michiels, W.; Teuwen, P. Differential computation analysis: Hiding your white-box designs is not enough. In Proceedings of the Conference on Cryptographic Hardware and Embedded Systems 2016 (CHES2016), Santa Barbara, CA, USA, 17–19 August 2016; Gierlichs, B., Poschmann, A.Y., Eds.; Springer: Heidelberg, Germany, 2016; pp. 215–236. [Google Scholar]
- Dusart, P.; Letourneux, G.; Vivolo, O. Differential fault analysis on AES. In Proceedings of the International Conference on Applied Cryptography and Network Security 2003, Kunming, China, 16–19 October 2003; Zhou, J., Moti, Y., Han, Y., Eds.; Springer: Berlin, Germany, 2003; pp. 293–306. [Google Scholar]
- Kocher, P.; Jaffe, J.; Jun, B.; Rohatgi, P. Introduction to differential power analysis. J. Cryptogr. Eng. 2011, 1, 5–27. [Google Scholar] [CrossRef]
- Alpirez Bock, E.; Bos, J.W.; Brzuska, C.; Hubain, C.; Michiels, W.; Mune, C.; Sanfelix Gonzalez, E.; Teuwen, P.; Treff, A. White-Box Cryptography: Don’t Forget About Grey Box Attacks. IACR Cryptol. ePrint Arch. 2017, 2017, 355. [Google Scholar] [CrossRef]
- Bock, E.A.; Brzuska, C.; Michiels, W.; Treff, A. On the ineffectiveness of internal encodings—Revisiting the DCA attack on white-box cryptography. In Proceedings of the 16th International Conference on Applied Cryptography and Network Security (ACNS2018), Leuven, Belgium, 2–4 July 2018; Preenel, B., Vercauteren, F., Eds.; Springer: Heidelberg, Germany, 2018; pp. 103–120. [Google Scholar]
- Biryukov, A.; Udovenko, A. Attacks and countermeasures for white-box designs. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Springer: Cham, Switzerland, 2019; pp. 373–402. [Google Scholar]
- Lee, S.; Kim, T.; Kang, Y. A masked white-box cryptographic implementation for protecting against differential computation analysis. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2602–2615. [Google Scholar] [CrossRef]
- Banik, S.; Bogdanov, A.; Isobe, T.; Jepsen, M. Analysis of software countermeasures for whitebox encryption. IACR Trans. Symmetric Cryptol. 2017, 2017, 307–328. [Google Scholar]
- Marin, L. White Box Implementations Using Non-Commutative Cryptography. Sensors 2019, 19, 1122. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.; Rivain, M.; Vejre, P.S.; Wang, J. Higher-order DCA against standard side-channel countermeasures. IACR Cryptol. ePrint Arch. 2018, 2018, 869. [Google Scholar]
- Fouque, P.A.; Karpman, P.; Kirchner, P.; Minaud, B. Efficient and provable white-box primitives. In Advances in Cryptology, Proceedings of the ASIACRYPT 2016, Hanoi, Vietnam, 4–8 December 2016; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 159–188. [Google Scholar]
- Biryukov, A.; Perrin, L. Symmetrically and Asymmetrically Hard Cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Springer: Cham, Switzerland, 2017; pp. 417–445. [Google Scholar]
- Bock, E.A.; Amadori, A.; Bos, J.W.; Brzuska, C.; Michiels, W. Doubly half-injective PRGs for incompressible white-box cryptography. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 4–8 March 2019; Springer: Cham, Switzerland, 2019; pp. 189–209. [Google Scholar]
- Feng, Q.; He, D.; Wang, H.; Kumar, N.; Choo, K.K.R. White-Box Implementation of Shamir’s Identity-Based Signature Scheme. IEEE Syst. J. 2019. [Google Scholar] [CrossRef]
- Goubin, L.; Paillier, P.; Rivain, M.; Wang, J. How to reveal the secrets of an obscure white-box implementation. J. Cryptogr. Eng. 2018. [Google Scholar] [CrossRef]
- Moriarty, K.; Kaliski, B.; Rusch, A. PKCS# 5: Password-Based Cryptography Specification Version 2.1. Internet Requests for Comments. RFC 8018 2017. Available online: https://tools.ietf.org/html/rfc8018 (accessed on 3 June 2019).
- Visconti, A.; Bossi, S.; Ragab, H.; Calò, A. On the weaknesses of PBKDF2. In Cryptology and Network Security, Proceedings of the 14th International Conference, CANS 2015, Marrakesh, Morocco, 10–12 December 2015; Reiter, M., Naccache, D., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 119–126. [Google Scholar]
- Visconti, A.; Mosnáček, O.; Brož, M.; Matyáš, V. Examining PBKDF2 security margin—Case study of LUKS. J. Inf. Secur. Appl. 2019, 46, 296–306. [Google Scholar] [CrossRef]
- Visconti, A.; Gorla, F. Exploiting an HMAC-SHA-1 optimization to speed up PBKDF2. IEEE Trans. Dependable Secur. Comput. 2018. [Google Scholar] [CrossRef]
- Biryukov, A.; Dinu, D.; Khovratovich, D. Argon2 (Version 1.2). 2018. Available online: https://password-hashing.net/submissions/specs/Argon-v3.pdf (accessed on 28 May 2019).
- Percival, C.; Josefsson, S. The scrypt Password-Based Key Derivation Function. Internet Requests for Comments. RFC 7914. 2016. Available online: https://tools.ietf.org/html/rfc7914 (accessed on 30 May 2019).
- Banks, A.; Gupta, R. MQTT Version 3.1.1 Plus Errata 01. Available online: http://docs.oasis-open.org/mqtt/mqtt/v3.1.1/mqtt-v3.1.1.html (accessed on 24 May 2019).
- Light, R.A. Mosquitto: Server and client implementation of the MQTT protocol. J. Open Source Softw. 2017, 2, 265. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).