U-Dualities in Type II and M-Theory: A Covariant Approach
Abstract
1. Introduction
1.1. Dualities in String Theory
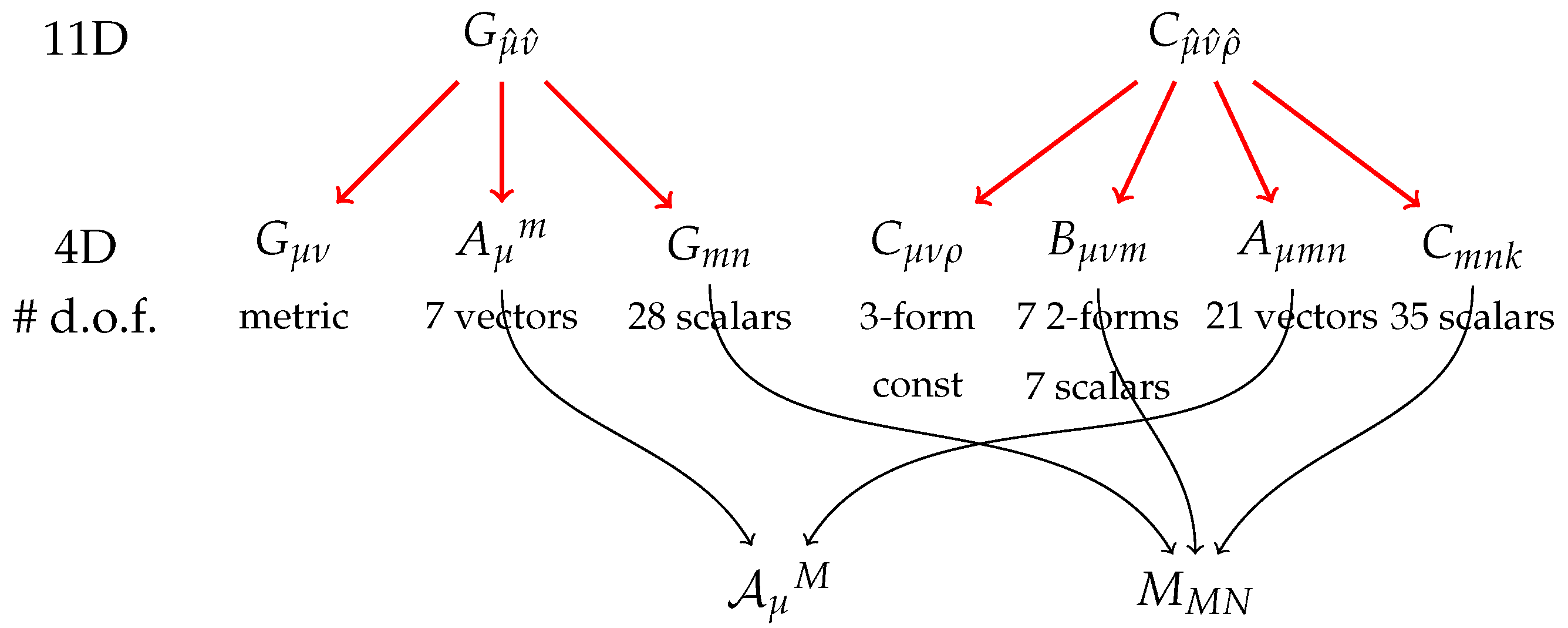
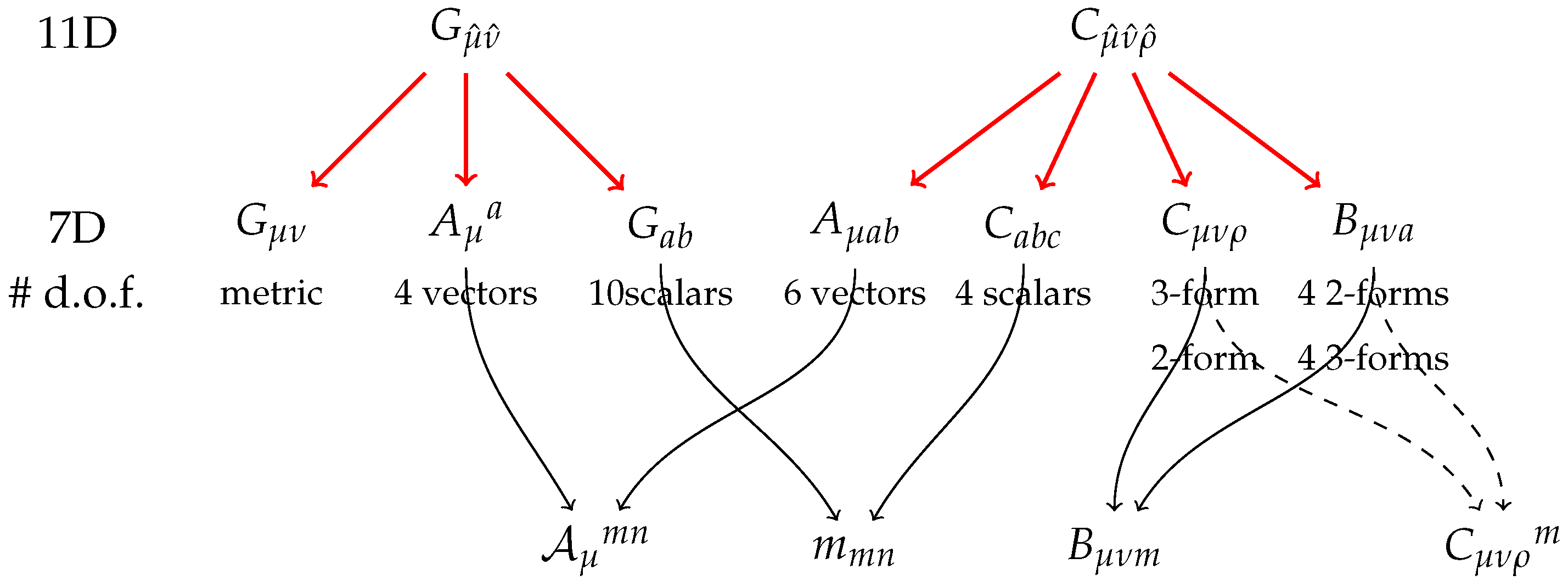
1.2. U-duality in Maximal Supergravity
2. Duality-Covariant Field Theories
2.1. Local Symmetries of Extended Space
2.2. Winding Modes and Exotic Branes
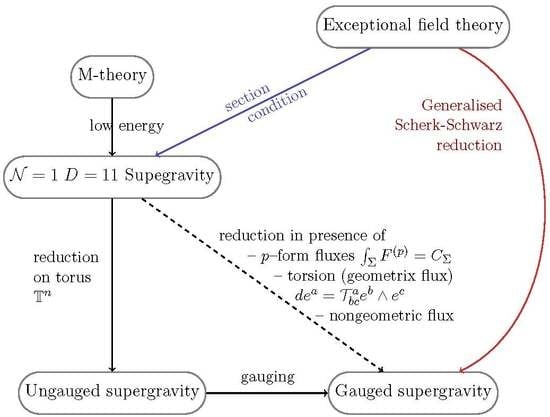
2.3. Exceptional Field Theories
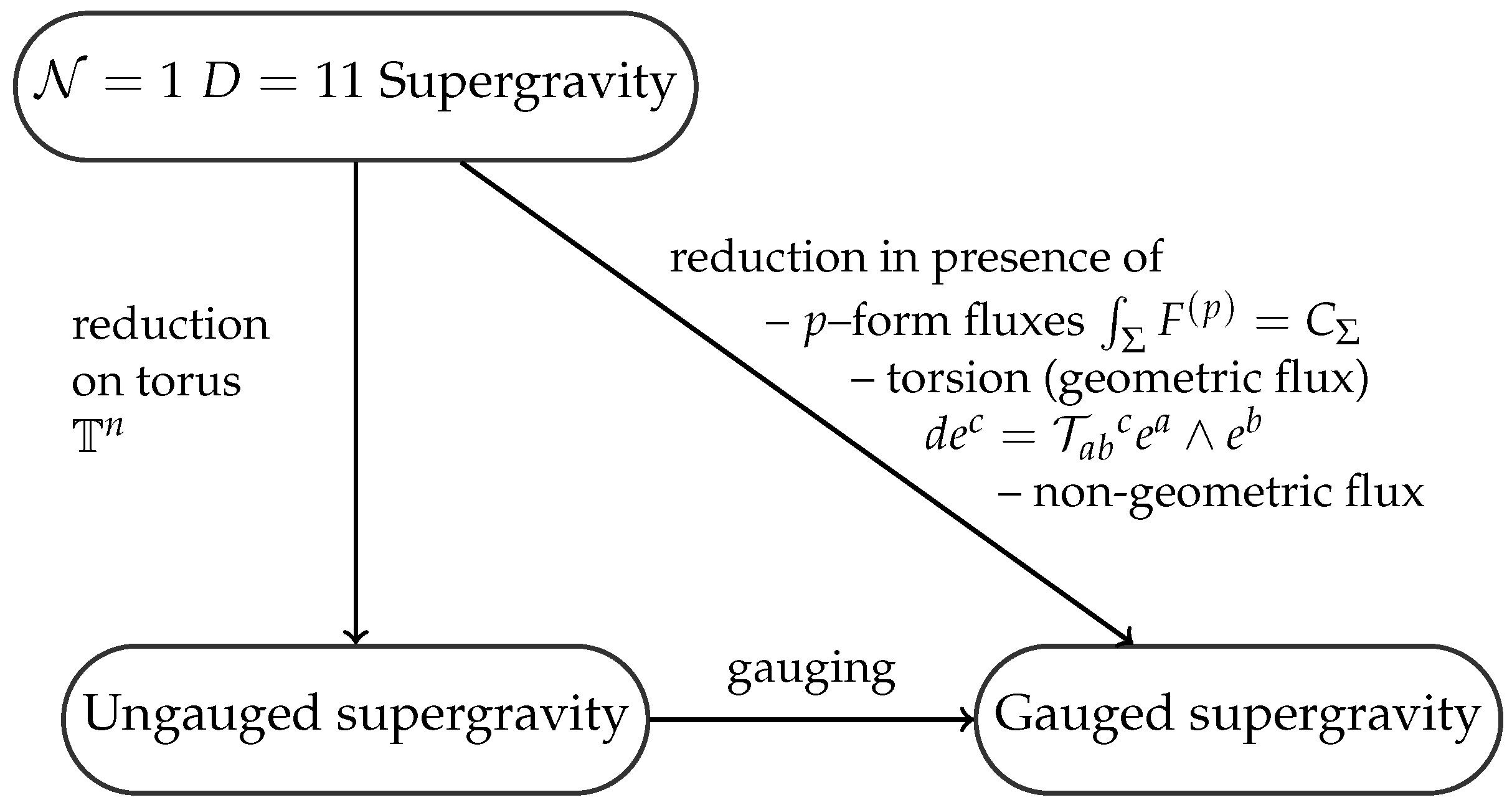
2.4. The Section Constraint
2.5. Double Field Theory
3. Applications
3.1. Non-Geometric Compactifications
3.2. Exotic Brane Backgrounds
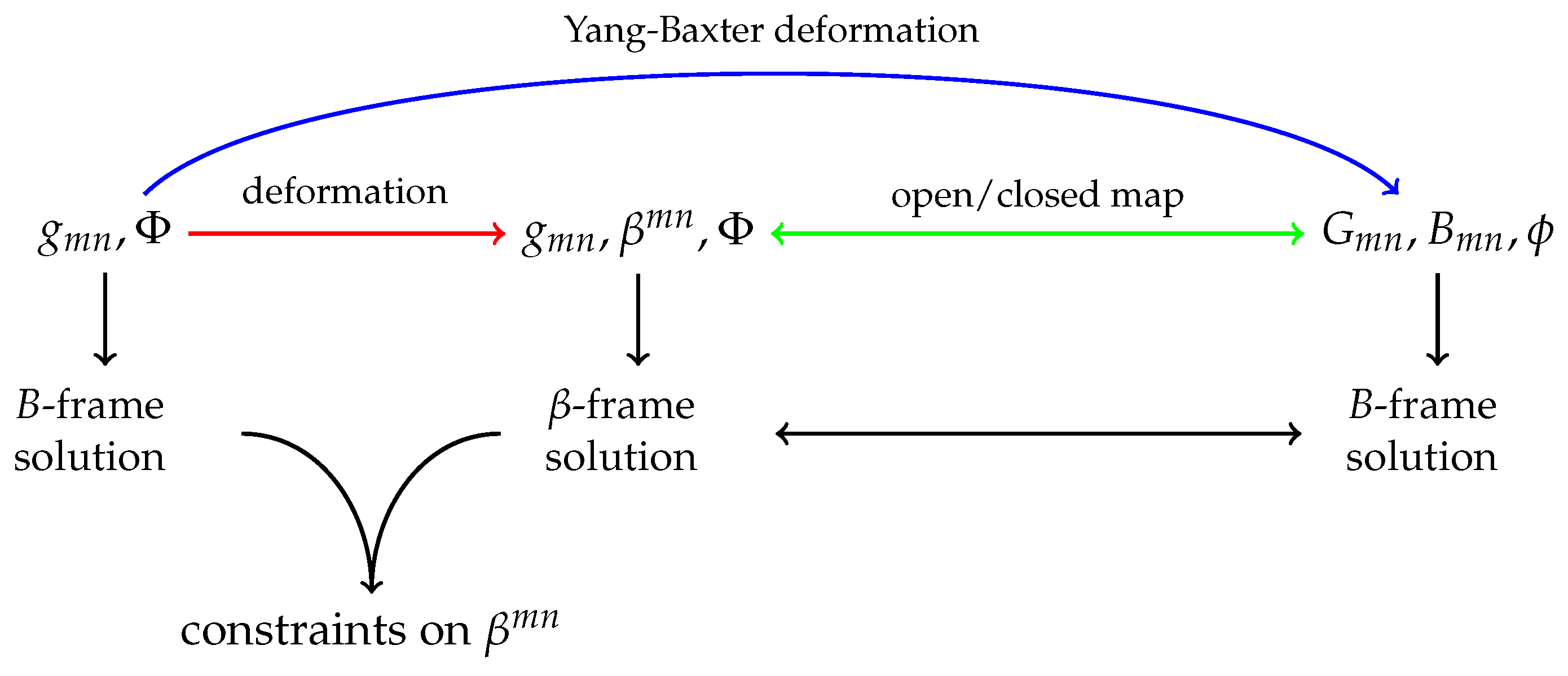
3.3. Deformations of Supergravity Backgrounds
4. Conclusions and Discussion
Funding
Conflicts of Interest
References
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Witten, E. String theory dynamics in various dimensions. Nucl. Phys. 1995, B443, 85–126. [Google Scholar] [CrossRef]
- Obers, N.; Pioline, B. U duality and M theory. Phys. Rept. 1999, 318, 113–225. [Google Scholar] [CrossRef]
- Hull, C. Global aspects of T-duality, gauged sigma models and T-folds. JHEP 2007, 0710, 057. [Google Scholar] [CrossRef]
- Bohm, R.; Gunther, H.; Herrmann, C.; Louis, J. Compactification of type IIB string theory on Calabi-Yau threefolds. Nucl. Phys. 2000, B569, 229–246. [Google Scholar] [CrossRef]
- Morrison, D.R.; Vafa, C. Compactifications of F theory on Calabi-Yau threefolds. 2. Nucl. Phys. 1996, B476, 437–469. [Google Scholar] [CrossRef]
- Sen, A. F theory and orientifolds. Nucl. Phys. 1996, B475, 562–578. [Google Scholar] [CrossRef]
- Musaev, E. U-Dualities in Type II String Theories and M-Theory. Ph.D. Thesis, Queen Mary, University of London, London, UK, 2013. [Google Scholar]
- Duff, M. Duality rotations in string theory. Nucl. Phys. 1990, B335, 610–620. [Google Scholar] [CrossRef]
- Duff, M.; Lu, J. Duality rotations in membrane theory. Nucl. Phys. 1990, B347, 394–419. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B.; Lu, H.; Pope, C. Dualization of dualities. 1. Nucl. Phys. 1998, B523, 73–144. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B.; Lu, H.; Pope, C.N. Dualization of dualities. 2. Twisted self-duality of doubled fields, and superdualities. Nucl. Phys. 1998, B535, 242–292. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. The Maximal D = 4 supergravities. JHEP 2007, 0706, 049. [Google Scholar] [CrossRef]
- Berman, D.S.; Cederwall, M.; Kleinschmidt, A.; Thompson, D.C. The gauge structure of generalised diffeomorphisms. JHEP 2013, 1301, 064. [Google Scholar] [CrossRef]
- Hull, C.M. A Geometry for non-geometric string backgrounds. JHEP 2005, 10, 065. [Google Scholar] [CrossRef]
- Hull, C.M. Doubled geometry and T-folds. JHEP 2007, 0707, 080. [Google Scholar] [CrossRef]
- De Boer, J.; Shigemori, M. Exotic Branes in String Theory. Phys. Rep. 2012, 532, 65–118. [Google Scholar] [CrossRef]
- Shelton, J.; Taylor, W.; Wecht, B. Nongeometric flux compactifications. JHEP 2005, 0510, 085. [Google Scholar] [CrossRef]
- Wecht, B. Lectures on Nongeometric Flux Compactifications. Class. Quant. Grav. 2007, 24, S773–S794. [Google Scholar] [CrossRef]
- Bergshoeff, E.; Kleinschmidt, A.; Musaev, E.T.; Riccioni, F. The different faces of branes in Double Field Theory. arXiv 2019, arXiv:1903.05601. [Google Scholar]
- Hohm, O.; Samtleben, H. Exceptional field theory. III. E8(8). Phys. Rev. 2014, D90, 066002. [Google Scholar] [CrossRef]
- Kleinschmidt, A.; Nicolai, H. Higher spin representations of K(E10). In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; World Scientific: Singapore, 2017; pp. 25–38. [Google Scholar] [CrossRef]
- Bossard, G.; Cederwall, M.; Kleinschmidt, A.; Palmkvist, J.; Samtleben, H. Generalized diffeomorphisms for E9. Phys. Rev. 2017, D96, 106022. [Google Scholar] [CrossRef]
- Bossard, G.; Ciceri, F.; Inverso, G.; Kleinschmidt, A.; Samtleben, H. E9 exceptional field theory. Part I. The potential. JHEP 2019, 03, 089. [Google Scholar] [CrossRef]
- Cederwall, M.; Palmkvist, J. L∞ algebras for extended geometry. J. Phys. Conf. Ser. 2019, 1194, 012021. [Google Scholar] [CrossRef]
- Samtleben, H. Lectures on Gauged Supergravity and Flux Compactifications. Class. Quant. Grav. 2008, 25, 214002. [Google Scholar] [CrossRef]
- Abzalov, A.; Bakhmatov, I.; Musaev, E.T. Exceptional field theory: SO(5,5). JHEP 2015, 06, 088. [Google Scholar] [CrossRef]
- Musaev, E.T. Exceptional field theory: SL(5). JHEP 2016, 02, 012. [Google Scholar] [CrossRef]
- Samtleben, H.; Weidner, M. The Maximal D = 7 supergravities. Nucl. Phys. 2005, B725, 383–419. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. Exceptional Field Theory I: E6(6) covariant Form of M-Theory and Type IIB. Phys. Rev. 2014, D89, 066016. [Google Scholar] [CrossRef]
- Godazgar, H.; Godazgar, M.; Hohm, O.; Nicolai, H.; Samtleben, H. Supersymmetric E7(7) Exceptional Field Theory. JHEP 2014, 1409, 044. [Google Scholar] [CrossRef]
- Musaev, E.; Samtleben, H. Fermions and supersymmetry in E6(6) exceptional field theory. JHEP 2015, 1503, 027. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. Exceptional field theory. II. E7(7). Phys. Rev. 2014, D89, 066017. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J.H. How to Get Masses from Extra Dimensions. Nucl. Phys. 1979, B153, 61–88. [Google Scholar] [CrossRef]
- Graña, M.; Marqués, D. Gauged Double Field Theory. JHEP 2012, 1204, 020. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Thompson, D.C. Duality Invariant M-theory: Gauged supergravities and Scherk-Schwarz reductions. JHEP 2012, 1210, 174. [Google Scholar] [CrossRef]
- Musaev, E.T. Gauged supergravities in 5 and 6 dimensions from generalised Scherk-Schwarz reductions. JHEP 2013, 1305, 161. [Google Scholar] [CrossRef]
- Baron, W.H. Gaugings from E7(7) extended geometries. Phys. Rev. 2015, D91, 024008. [Google Scholar] [CrossRef]
- Hohm, O.; Musaev, E.T.; Samtleben, H. O(d + 1, d + 1) enhanced double field theory. JHEP 2017, 10, 086. [Google Scholar] [CrossRef]
- Nicolai, H.; Samtleben, H. Maximal gauged supergravity in three-dimensions. Phys. Rev. Lett. 2001, 86, 1686–1689. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. On Lagrangians and gaugings of maximal supergravities. Nucl. Phys. 2003, B655, 93–126. [Google Scholar] [CrossRef]
- De Wit, B.; Nicolai, H.; Samtleben, H. Gauged supergravities in three-dimensions: A Panoramic overview. arXiv 2004, arXiv:hep-th/0403014. [Google Scholar]
- Trigiante, M. Gauged Supergravities. Phys. Rept. 2017, 680, 1–175. [Google Scholar] [CrossRef]
- Le Diffon, A.; Samtleben, H. Supergravities without an Action: Gauging the Trombone. Nucl. Phys. 2009, B811, 1–35. [Google Scholar] [CrossRef][Green Version]
- De Wit, B.; Nicolai, H.; Samtleben, H. Gauged Supergravities, Tensor Hierarchies, and M-Theory. JHEP 2008, 0802, 044. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. The Maximal D = 5 supergravities. Nucl. Phys. 2005, B716, 215–247. [Google Scholar] [CrossRef]
- Bergshoeff, E.; Samtleben, H.; Sezgin, E. The Gaugings of Maximal D=6 Supergravity. JHEP 2008, 0803, 068. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B. The SO(8) supergravity. Nucl. Phys. 1979, B159, 141–212. [Google Scholar] [CrossRef]
- De Wit, B.; Nicolai, H. N = 8 Supergravity with Local SO(8) × SU(8) Invariance. Phys. Lett. 1982, B108, 285–290. [Google Scholar] [CrossRef]
- Dibitetto, G.; Fernandez-Melgarejo, J.; Marques, D.; Roest, D. Duality orbits of non-geometric fluxes. Fortsch. Phys. 2012, 60, 1123–1149. [Google Scholar] [CrossRef]
- Danielsson, U.; Dibitetto, G. On the distribution of stable de Sitter vacua. JHEP 2013, 03, 018. [Google Scholar] [CrossRef]
- Damian, C.; Loaiza-Brito, O.; Rey, L.; Sabido, M. Slow-Roll Inflation in Non-geometric Flux Compactification. J. High Energy Phys. 2013, 2013, 109. [Google Scholar] [CrossRef]
- Blabäck, J.; Danielsson, U.; Dibitetto, G. Fully stable dS vacua from generalised fluxes. JHEP 2013, 08, 054. [Google Scholar] [CrossRef]
- Hassler, F.; Lust, D.; Massai, S. On Inflation and de Sitter in Non-Geometric String Backgrounds. arXiv 2014, arXiv:1405.2325. [Google Scholar] [CrossRef]
- Ma, C.T.; Shen, C.M. Cosmological Implications from O(D,D). Fortsch. Phys. 2014, 62, 921–941. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Kors, B.; Lust, D.; Stieberger, S. Four-dimensional String Compactifications with D-Branes, Orientifolds and Fluxes. Phys. Rept. 2007, 445, 1–193. [Google Scholar] [CrossRef]
- Riccioni, F.; West, P.C. E(11)-extended spacetime and gauged supergravities. JHEP 2008, 0802, 039. [Google Scholar] [CrossRef]
- Kleinschmidt, A. Counting supersymmetric branes. JHEP 2011, 10, 144. [Google Scholar] [CrossRef]
- Lombardo, D.M.; Riccioni, F.; Risoli, S. P fluxes and exotic branes. JHEP 2016, 12, 114. [Google Scholar] [CrossRef]
- Gross, D.J.; Perry, M.J. Magnetic Monopoles in Kaluza-Klein Theories. Nucl. Phys. 1983, B226, 29–48. [Google Scholar] [CrossRef]
- Hull, C. Generalised geometry for M-theory. JHEP 2007, 0707, 079. [Google Scholar] [CrossRef]
- Andriot, D.; Hohm, O.; Larfors, M.; Lust, D.; Patalong, P. Non-Geometric Fluxes in Supergravity and Double Field Theory. Fortsch. Phys. 2012, 60, 1150–1186. [Google Scholar] [CrossRef]
- Chatzistavrakidis, A.; Gautason, F.F.; Moutsopoulos, G.; Zagermann, M. Effective actions of nongeometric five-branes. Phys. Rev. 2014, D89, 066004. [Google Scholar] [CrossRef]
- Blair, C.D.A.; Musaev, E.T. Five-brane actions in double field theory. JHEP 2018, 03, 111. [Google Scholar] [CrossRef]
- Andriot, D.; Larfors, M.; Lust, D.; Patalong, P. (Non-)commutative closed string on T-dual toroidal backgrounds. JHEP 2013, 06, 021. [Google Scholar] [CrossRef]
- Blair, C.D.A. Non-commutativity and non-associativity of the doubled string in non-geometric backgrounds. JHEP 2015, 06, 091. [Google Scholar] [CrossRef]
- Berman, D.S.; Rudolph, F.J. Branes are Waves and Monopoles. JHEP 2015, 05, 015. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Kleinschmidt, A.; Musaev, E.T. Non-geometric branes are DFT monopoles. JHEP 2016, 10, 076. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Berman, D.; Kleinschmidt, A.; Musaev, E.; Otsuki, R. Exotic branes in Exceptional Field Theory: The SL(5) duality group. JHEP 2018, 08, 021. [Google Scholar] [CrossRef]
- Fernández-Melgarejo, J.J.; Kimura, T.; Sakatani, Y. Weaving the Exotic Web. JHEP 2018, 09, 072. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Otsuki, R. Exotic Branes in Exceptional Field Theory: E7(7) and Beyond. JHEP 2018, 12, 053. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Otsuki, R. Exotic Branes in M-Theory. In Proceedings of the Dualities and Generalized Geometries, Corfu, Greece, 9–16 September 2018. arXiv 2019, arXiv:hep-th/1903.10247. [Google Scholar]
- Jensen, S. The KK-Monopole/NS5-Brane in Doubled Geometry. JHEP 2011, 1107, 088. [Google Scholar] [CrossRef]
- Gregory, R.; Harvey, J.A.; Moore, G.W. Unwinding strings and t duality of Kaluza-Klein and h monopoles. Adv. Theor. Math. Phys. 1997, 1, 283–297. [Google Scholar] [CrossRef]
- Tong, D. NS5-branes, T duality and world sheet instantons. JHEP 2002, 07, 013. [Google Scholar] [CrossRef]
- Harvey, J.A.; Jensen, S. Worldsheet instanton corrections to the Kaluza-Klein monopole. JHEP 2005, 10, 028. [Google Scholar] [CrossRef]
- Kimura, T.; Sasaki, S. Worldsheet instanton corrections to -brane geometry. JHEP 2013, 08, 126. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Effective Field Theory from Quantized Strings. Phys. Lett. 1985, 158B, 316–322. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Martinec, E.J.; Perry, M.J.; Friedan, D. Strings in Background Fields. Nucl. Phys. 1985, B262, 593–609. [Google Scholar] [CrossRef]
- Hull, C.M.; Townsend, P.K. Finiteness and Conformal Invariance in Nonlinear σ Models. Nucl. Phys. 1986, B274, 349–362. [Google Scholar] [CrossRef]
- Wulff, L.; Tseytlin, A.A. Kappa-symmetry of superstring sigma model and generalized 10d supergravity equations. JHEP 2016, 06, 174. [Google Scholar] [CrossRef]
- Bena, I.; Polchinski, J.; Roiban, R. Hidden symmetries of the AdS(5) x S**5 superstring. Phys. Rev. 2004, D69, 046002. [Google Scholar] [CrossRef]
- Delduc, F.; Magro, M.; Vicedo, B. An integrable deformation of the AdS5xS5 superstring action. Phys. Rev. Lett. 2014, 112, 051601. [Google Scholar] [CrossRef]
- Arutyunov, G.; Borsato, R.; Frolov, S. Puzzles of η-deformed AdS5 × S5. JHEP 2015, 12, 049. [Google Scholar] [CrossRef]
- Arutyunov, G.; Frolov, S.; Hoare, B.; Roiban, R.; Tseytlin, A.A. Scale invariance of the η-deformed AdS5 × S5 superstring, T-duality and modified type II equations. Nucl. Phys. 2016, B903, 262–303. [Google Scholar] [CrossRef]
- Sakamoto, J.i.; Sakatani, Y.; Yoshida, K. Weyl invariance for generalized supergravity backgrounds from the doubled formalism. PTEP 2017, 2017, 053B07. [Google Scholar] [CrossRef]
- Sakatani, Y.; Uehara, S.; Yoshida, K. Generalized gravity from modified DFT. JHEP 2017, 04, 123. [Google Scholar] [CrossRef]
- Baguet, A.; Magro, M.; Samtleben, H. Generalized IIB supergravity from exceptional field theory. JHEP 2017, 03, 100. [Google Scholar] [CrossRef]
- Araujo, T.; Bakhmatov, I.; Colgáin, E.Ó.; Sakamoto, J.I.; Sheikh-Jabbari, M.M.; Yoshida, K. Conformal twists, Yang–Baxter σ-models & holographic noncommutativity. J. Phys. 2018, A51, 235401. [Google Scholar] [CrossRef]
- Araujo, T.; Ó Colgáin, E.; Sakamoto, J.; Sheikh-Jabbari, M.M.; Yoshida, K. I in generalized supergravity. Eur. Phys. J. 2017, C77, 739. [Google Scholar] [CrossRef]
- Sakamoto, J.I.; Sakatani, Y.; Yoshida, K. Homogeneous Yang-Baxter deformations as generalized diffeomorphisms. J. Phys. 2017, A50, 415401. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Ó Colgáin, E.; Sheikh-Jabbari, M.M.; Yavartanoo, H. Yang-Baxter Deformations Beyond Coset Spaces (a slick way to do TsT). JHEP 2018, 06, 161. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Musaev, E.T. Classical Yang-Baxter equation from β-supergravity. JHEP 2019, 01, 140. [Google Scholar] [CrossRef]
- Sakamoto, J.I.; Sakatani, Y. Local β-deformations and Yang-Baxter sigma model. JHEP 2018, 06, 147. [Google Scholar] [CrossRef]
- Andriot, D.; Hohm, O.; Larfors, M.; Lust, D.; Patalong, P. A geometric action for non-geometric fluxes. Phys. Rev. Lett. 2012, 108, 261602. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. JHEP 1999, 9909, 032. [Google Scholar] [CrossRef]
- Andriot, D.; Betz, A. NS-branes, source corrected Bianchi identities, and more on backgrounds with non-geometric fluxes. JHEP 2014, 07, 059. [Google Scholar] [CrossRef]
- Andriot, D.; Betz, A. β-supergravity: A ten-dimensional theory with non-geometric fluxes, and its geometric framework. JHEP 2013, 12, 083. [Google Scholar] [CrossRef]
- Fernández-Melgarejo, J.J.; Sakamoto, J.I.; Sakatani, Y.; Yoshida, K. Weyl Invariance of String Theories in Generalized Supergravity Backgrounds. Phys. Rev. Lett. 2019, 122, 111602. [Google Scholar] [CrossRef]
- Catal-Ozer, A. Non-Abelian T-duality as a Transformation in Double Field Theory. arXiv 2019, arXiv:1904.00362. [Google Scholar]
- Hassler, F. Poisson-Lie T-Duality in Double Field Theory. arXiv 2017, arXiv:707.08624. [Google Scholar]
- Baguet, A.; Hohm, O.; Samtleben, H. Consistent Type IIB Reductions to Maximal 5D Supergravity. Phys. Rev. 2015, D92, 065004. [Google Scholar] [CrossRef]
- Malek, E.; Samtleben, H.; Vall Camell, V. Supersymmetric AdS7 and AdS6 vacua and their minimal consistent truncations from exceptional field theory. Phys. Lett. 2018, B786, 171–179. [Google Scholar] [CrossRef]
- Malek, E.; Samtleben, H.; Vall Camell, V. Supersymmetric AdS7 and AdS6 vacua and their consistent truncations with vector multiplets. JHEP 2019, 04, 088. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. The many facets of exceptional field theory. In Proceedings of the Dualities and Generalized Geometries, Corfu, Greece, 9–16 September 2018. arXiv 2019, arXiv:1905.08312. [Google Scholar]
- Blumenhagen, R.; Font, A.; Plauschinn, E. Relating Double Field Theory to the Scalar Potential of N = 2 Gauged Supergravity. arXiv 2015, arXiv:1507.08059. [Google Scholar] [CrossRef]
- Bosque, P.d.; Hassler, F.; Lust, D. Flux Formulation of DFT on Group Manifolds and Generalized Scherk-Schwarz Compactifications. arXiv 2015, arXiv:1509.04176. [Google Scholar] [CrossRef]

| Duality Group | The Y-Tensor | Dimension of Extended Space |
|---|---|---|
| O(d,d) | ||
| SL(5) | ||
| SO(5,5) | ||
| d | G | P | M2 | M5 | KK6 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | SL(2) | 2 | 1 | - | - | - | - | - | 3 |
| 3 | SL(3)×SL(2) | 3 | 3 | - | - | - | - | - | (3,2) |
| 4 | SL(5) | 4 | 6 | - | - | - | - | - | 10 |
| 5 | SO(5,5) | 5 | 10 | 1 | - | - | - | - | 16s |
| 6 | 6 | 15 | 6 | - | - | - | - | 27 | |
| 7 | 7 | 21 | 21 | 7 | - | - | - | 56 | |
| 8 | 8 | 28 | 56 | 56 | 56 | 28 | 8 | 248 |
| Coordinates | Brane | State |
|---|---|---|
| NS5-brane (H-monopole) | ||
| KK-monopole | ||
| Q-monopole | ||
| R-monopole | ||
| R’-monopole |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musaev, E.T. U-Dualities in Type II and M-Theory: A Covariant Approach. Symmetry 2019, 11, 993. https://doi.org/10.3390/sym11080993
Musaev ET. U-Dualities in Type II and M-Theory: A Covariant Approach. Symmetry. 2019; 11(8):993. https://doi.org/10.3390/sym11080993
Chicago/Turabian StyleMusaev, Edvard T. 2019. "U-Dualities in Type II and M-Theory: A Covariant Approach" Symmetry 11, no. 8: 993. https://doi.org/10.3390/sym11080993
APA StyleMusaev, E. T. (2019). U-Dualities in Type II and M-Theory: A Covariant Approach. Symmetry, 11(8), 993. https://doi.org/10.3390/sym11080993