Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping
Abstract
1. Introduction
2. Basic Motifs
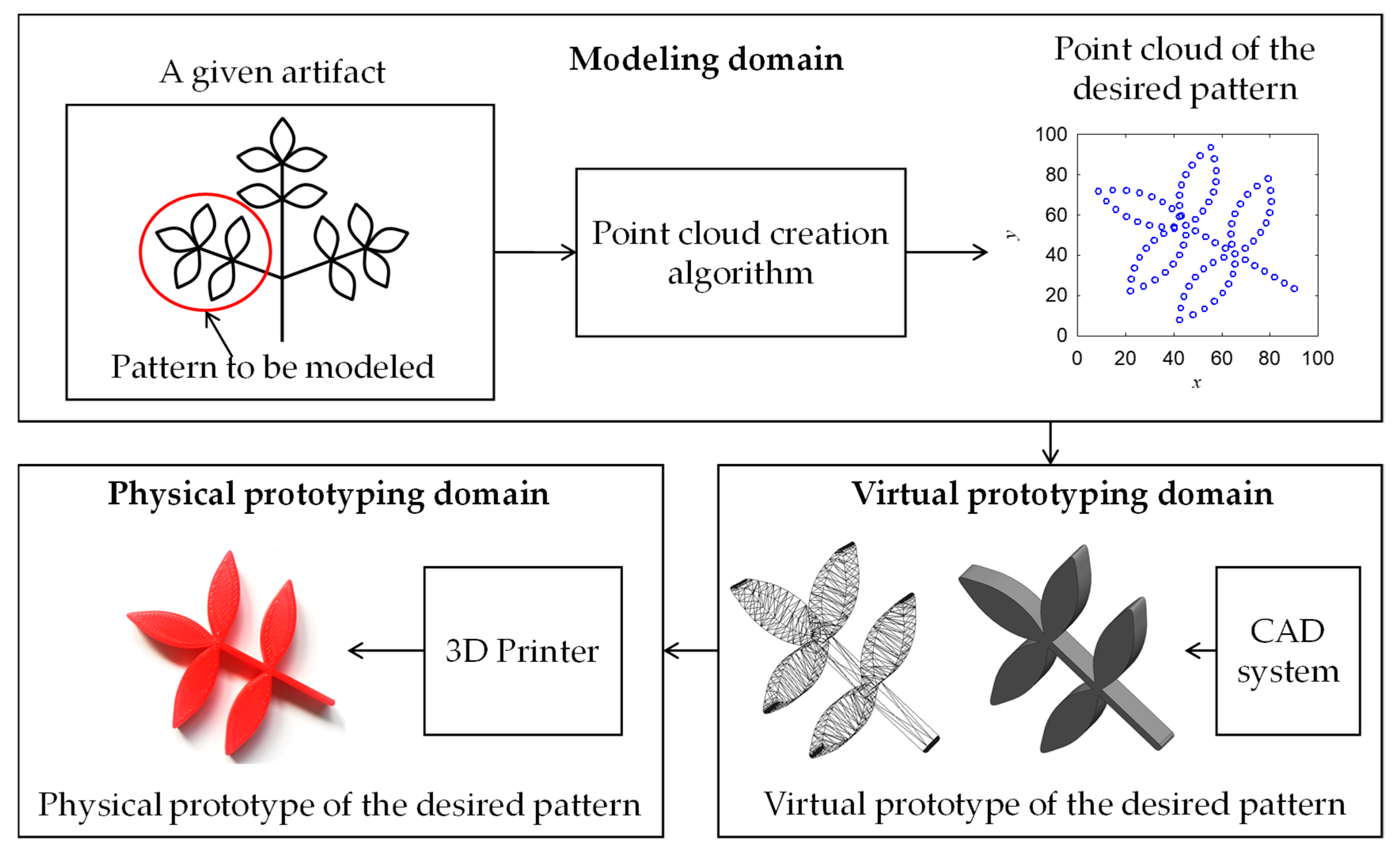
3. Pattern Digitization Methodology
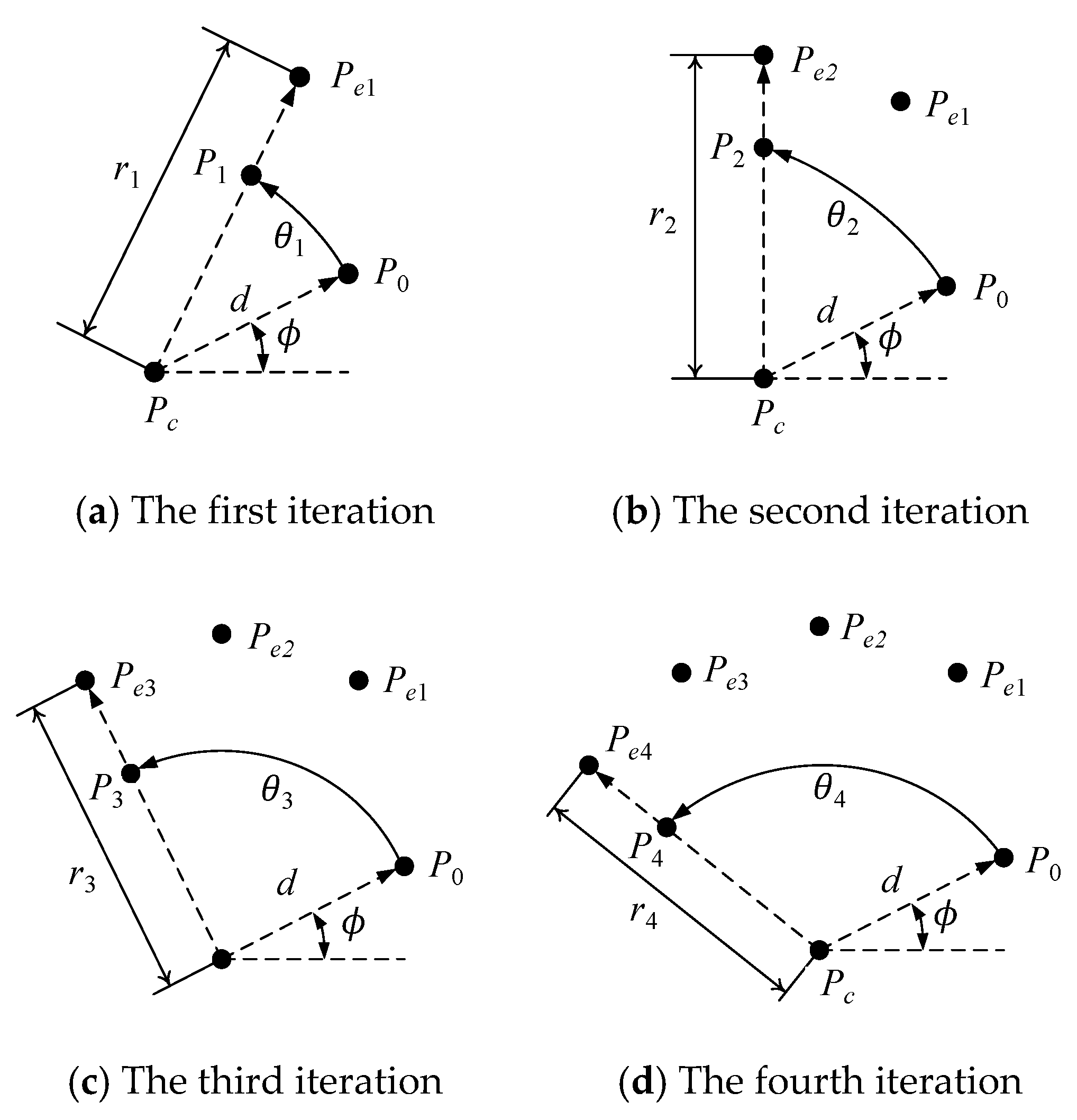
| Algorithm 1 Point Cloud Creation Algorithm | |
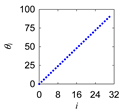
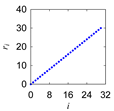
| 1 Define: | Center Point Pc = (Pcx,Pcy) ∈ ℜ2, Initial Length d > 0, Initial Angle ϕ ∈ ℜ Instantaneous Distance (ri ∈ ℜ|i = 0,1,…,n) Instantaneous Rotational Angle (θi ∈ ℜ|i = 0,1,…,n) |
| 2 Calculate: | P0 = (P0x, P0y) so that and |
| 3 Iterate: | For i = 0,1,…,n Rotate P0 by an angle θi around Pc in the counter-clockwise direction to create Pi = (Pix,Piy) so that |
| 4 Output: | PC = (Pei|i = 0,1,…,n) |
4. Digitization of Hokkaido Ainu Motifs
4.1. Point Clouds of the Main Motifs
4.2. Point Cloud of the Synthetic Motifs
4.3. Point Cloud of the Plant Motifs
4.4. Virtual and Physical Prototypes of Ainu Patterns
5. Concluding Remarks
- (a)
- The indigenous people living in the northern part of Japan, known as Ainu, decorate their houses, clothing, ornaments, utensils, and spiritual goods using some unique patterns. Nowadays, goods crafted with Ainu patterns are cherished by many people in Japan and abroad, and different kinds of souvenirs and cultural artifacts carry these patterns, making these significant from both cultural and economic viewpoints.
- (b)
- The fourteen basic motifs underlying the patterns used by the Ainu community living in Hokkaido are elucidated through literature review.
- (c)
- The digital technology that can mimic the Ainu pattern-making craftsmanship is presented. It consists of three domains, namely, modeling domain, virtual prototyping domain, and physical prototyping domain. The modeling domain employs an algorithm. The algorithm recursively creates a point cloud to preserve the shape information of a given pattern. From a point cloud, a representative segment of a pattern can be copied several times, keeping the symmetry of the pattern. The virtual prototyping domain uses CAD systems to produce a solid CAD model of the given pattern directly from its point cloud. The physical prototyping domain uses a 3D printer to produce the physical prototype of the given pattern directly from the triangulation data of the solid CAD model.
- (d)
- Ten basic Hokkaido Ainu motifs and three synthesized motifs were digitized using the presented digital technology. The settings of the parameters to create the respective point clouds are also described elaborately.
- (e)
- The presented methodology helps avoid all sorts of sophisticated transformations and complicated computations that are needed when a scanning- or image-processing-based digitization technique is used.
- (f)
- The outcomes of the study help preserve the cultural heritage as well as the craftsmanship underlying complex patterns not limited to Ainu community.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pintus, R.; Pal, K.; Yang, Y.; Weyrich, T.; Gobbetti, E.; Rushmeier, H. A Survey of Geometric Analysis in Cultural Heritage. Comput. Graph. Forum 2016, 35, 4–31. [Google Scholar] [CrossRef]
- Hann, M. Symbol, Pattern and Symmetry: The Cultural Significance of Structure; Bloomsbury: London, UK, 2013. [Google Scholar]
- Li, X.; Yin, Z.; Wei, L.; Wan, S.; Yu, W.; Li, M. Symmetry and template guided completion of damaged skulls. Comput. Graph. 2011, 35, 885–893. [Google Scholar] [CrossRef]
- Zhou, P.; Shui, W.; Qu, L.; Gao, F.; Wu, Z. Case study: Missing data computation and 3D printing application in symmetrical artifact restoration. In Proceedings of the Symposium on VR Culture and Heritage, Zhuhai, China, 3–4 December 2016; Volume 2, pp. 63–66. [Google Scholar] [CrossRef]
- Fukumoto, I.; Kondo, O. Three-dimensional craniofacial variation and occlusal wear severity among inhabitants of Hokkaido: Comparisons of Okhotsk culture people and the Ainu. Anthr. Sci. 2010, 118, 161–172. [Google Scholar] [CrossRef][Green Version]
- Kura, K.; Armstrong, E.L.; Templer, D.I. Cognitive function among the Ainu people. Intelligence 2014, 44, 149–154. [Google Scholar] [CrossRef][Green Version]
- Nishikiya, T. A Positive Consideration of Ainu pattern. Bull. Jpn. Soc. Sci. Des. 1971, 1971, 49–65. (In Japanese) [Google Scholar] [CrossRef]
- Nishikiya, T. Ainu pattern its origin and composition. Bull. Jpn. Soc. Sci. Des. 1971, 1971, 74–75. (In Japanese) [Google Scholar] [CrossRef]
- Nishikiya, T. Ainu pattern: Its origin and composition. Bull. Jpn. Soc. Sci. Des. 1970, 1970, 8–9. (In Japanese) [Google Scholar] [CrossRef]
- Ogawa, S. Ainu Minzoku Mon’yoshu: Shishu no Sashikata, Tachikata No Sekai, Sapporo-shi: Ainu Bunka Densho no Kai Tezukuri Utara; Hatsubai Karinsha; Sanae Ogawa: Sapporo, Japan, 2010. (In Japanese) [Google Scholar]
- Sugiyama, H. On the composition of Ainu pattern. Bull. Jpn. Soc. Sci. Des. 1968, 1968, 60–61. (In Japanese) [Google Scholar] [CrossRef]
- Tsuda, N. Ainu Shishu Nyumon; Kuruzu: Sapporo, Japan, 2008. (In Japanese) [Google Scholar]
- The Foundation for Ainu Culture. Ainu Living Culture Reproduce Manual. Available online: https://www.ff-ainu.or.jp/ (accessed on 9 April 2019).
- Chiba, T. Problems on Making the Landscape Guideline of Facility Complex in Akan National Park; Summaries of Technical Papers of Annual Meeting of the Architectural Institute of Japan; The Architectural Institute of Japan: Tokyo, Japan, 2013; pp. 397–398. (In Japanese) [Google Scholar]
- City of Sapporo, Ainu-Siriki. Available online: http://www.city.sapporo.jp/shimin/pirka-kotan/jp/kogei/ainu-siriki/index.html (accessed on 9 April 2019).
- Geng, Z.; Bidanda, B. Review of reverse engineering systems—Current state of the art. Virtual Phys. Prototyp. 2017, 13, 1–12. [Google Scholar] [CrossRef]
- Ceccarelli, S.; Guarneri, M.; De Collibus, M.F.; Francucci, M.; Ciaffi, M.; Danielis, A. Laser Scanners for High-Quality 3D and IR Imaging in Cultural Heritage Monitoring and Documentation. J. Imaging 2018, 4, 130. [Google Scholar] [CrossRef]
- Furferi, R.; Governi, L.; Volpe, Y.; Puggelli, L.; Vanni, N.; Carfagni, M. From 2D to 2.5D i.e. from painting to tactile model. Graph. Models 2014, 76, 706–723. [Google Scholar] [CrossRef]
- Hasegawa, K.; Li, L.; Okamoto, N.; Yanai, S.; Yamaguchi, H.; Okamoto, A.; Tanaka, S. Application of Stochastic Point-Based Rendering to Laser-Scanned Point Clouds of Various Cultural Heritage Objects. Int. J. Autom. Technol. 2018, 12, 348–355. [Google Scholar] [CrossRef]
- Jo, Y.H.; Hong, S. Three-Dimensional Digital Documentation of Cultural Heritage Site Based on the Convergence of Terrestrial Laser Scanning and Unmanned Aerial Vehicle Photogrammetry. ISPRS Int. J. Geo-Inf. 2019, 8, 53. [Google Scholar] [CrossRef]
- Neumüller, M.; Reichinger, A.; Rist, F.; Kern, C. 3D printing for cultural heritage: Preservation, accessibility, research and education, 3D Research Challenges in Cultural Heritage. Lect. Notes Comput. Sci. 2014, 8355, 119–134. [Google Scholar] [CrossRef]
- Reichinger, A.; Carrizosa, H.G.; Wood, J.; Schröder, S.; Löw, C.; Luidolt, L.R.; Schimkowitsch, M.; Fuhrmann, A.; Maierhofer, S.; Purgathofer, W. Pictures in your mind: Using interactive gesture-controlled reliefs to explore art. ACM Trans. Access. Comput. 2018, 11, 1–39. [Google Scholar] [CrossRef]
- Scopigno, R.; Cignoni, P.; Pietroni, N.; Callieri, M.; Dellepiane, M. Digital fabrication techniques for cultural heritage: A survey. Comput. Graph. Forum 2017, 36, 6–21. [Google Scholar] [CrossRef]
- Soler, F.; Melero, F.J.; Luzón, M.V.; Rus, F.J.M. A complete 3D information system for cultural heritage documentation. J. Cult. Herit. 2017, 23, 49–57. [Google Scholar] [CrossRef]
- Tashi; Ullah, A.S.; Watanabe, M.; Kubo, A. Analytical Point-Cloud Based Geometric Modeling for Additive Manufacturing and Its Application to Cultural Heritage Preservation. Appl. Sci. 2018, 8, 656. [Google Scholar] [CrossRef]
- James, D.W.; Belblidia, F.; Eckermann, J.E.; Sienz, J. An innovative photogrammetry color segmentation based technique as an alternative approach to 3D scanning for reverse engineering design. Comput. Aided Des. Appl. 2017, 14, 1–16. [Google Scholar] [CrossRef]
- Tamaki, J.; Yanagi, S.; Aoki, Y.; Kubo, A.; Kameda, T.; Ullah, A.M.M.S. 3D Reproduction of a Snow Crystal by Stereolithography. J. Adv. Mech. Des. Syst. Manuf. 2012, 6, 923–935. [Google Scholar] [CrossRef][Green Version]
- Rojas-Sola, J.I.; Galán-Moral, B.; De la Morena-De la Fuente, E. Agustín de Betancourt’s Double-Acting Steam Engine: Geometric Modeling and Virtual Reconstruction. Symmetry 2018, 10, 351. [Google Scholar] [CrossRef]
- Inoguchi, J.; Ziatdinov, R.; Miura, K.T. Generalization of log-aesthetic curves via similarity geometry. Japan J. Ind. Appl. Math. 2019, 36, 239–259. [Google Scholar] [CrossRef]
- Sato, M.; Shimizu, Y. Generalization of log-aesthetic curves by Hamiltonian formalism. JSIAM Lett. 2016, 8, 49–52. [Google Scholar] [CrossRef]
- Okubo, M.; Mizuno, Y. Influence of interactive learning support system using augmented reality on 3D object drawing. J. Adv. Mech. Des. Syst. Manuf. 2018, 12. [Google Scholar] [CrossRef]

| No. | Motif | Name | No. | Motifs | Names |
|---|---|---|---|---|---|
| 1 |  | Ayus | 8 |  | Ski-uren-morew |
| 2 |  | Morew | 8 |  | Morew-etok |
| 3 |  | Arus-morew | 10 |  | Punkar |
| 4 |  | Sikike-nu-morew | 11 |  | Apapo-piras(u) ke |
| 5 |  | Sik | 12 |  | Apapo-epuy |
| 6 | 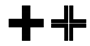 | Utasa | 13 |  | - |
| 7 | 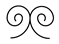 | Uren-morew | 14 |  | - |
| i | Inputs | Outputs (PC) | |
|---|---|---|---|
| ri | θi | ||
| 10 | 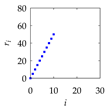 | 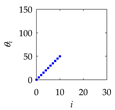 |  |
| 15 | 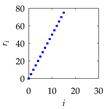 | 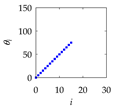 | 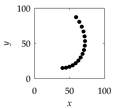 |
| 16 | 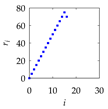 | 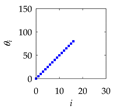 | 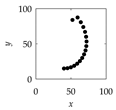 |
| 20 | 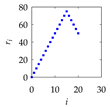 | 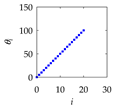 |  |
| 30 |  | 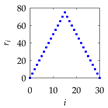 | 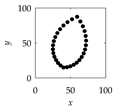 |
| Main Motifs | Instantaneous Rotational Angle | Instantaneous Distance | Segment-Wise Point Clouds (PC) | Integrated Point Cloud |
|---|---|---|---|---|
| Utasa | 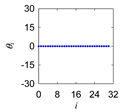 | 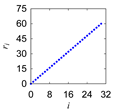 |  |  |
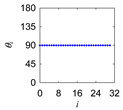 | 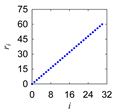 | 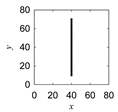 | ||
| Morew | 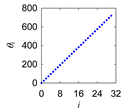 | 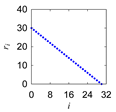 | 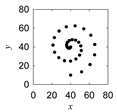 | |
| Sik |  |  | 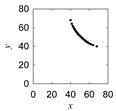 | 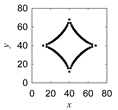 |
| Ayus | 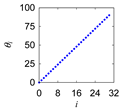 | 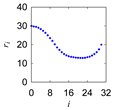 | 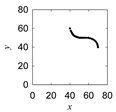 | 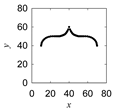 |
| Synthetic Motifs | Point Cloud(s) of Main Motif(s) | Inverted Point Cloud(s) | Integrated Point Clouds |
|---|---|---|---|
| Uren-morew | 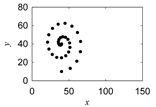 | 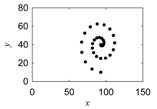 | 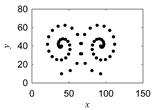 |
| Sik-uren-morew | 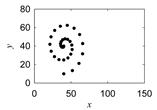 | 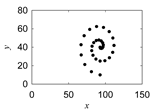 | 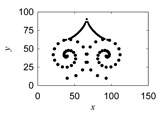 |
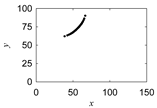 | 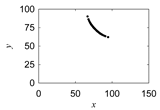 |
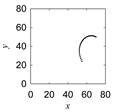
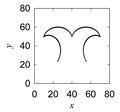
| Motif Name | Instantaneous Rotational Angle | Instantaneous Distance | Segment-Wise Point Cloud (PC) | Integrated Point Cloud |
|---|---|---|---|---|
| Morew-etok | 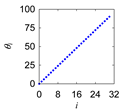 | 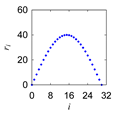 | 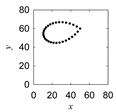 | 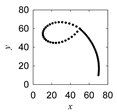 |
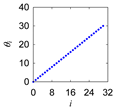 |  |  | ||
| Apapo | 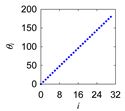 |  | 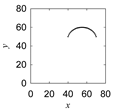 | 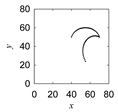 |
 |  |  |  |
| Virtual Models | Physical Models | Virtual Models | Physical Models |
|---|---|---|---|
 |  |  |  |
| Ayus | Sik-uren-morew | ||
 |  |  |  |
| Morew | Morew-etok | ||
 |  |  |  |
| Sik | Punkar | ||
 |  |  |  |
| Utasa | Apapo-piras(u) ke | ||
 |  |  |  |
| Uren-morew | Apapo-epuy | ||
| Model- | Point Clouds | Virtual Prototypes | Physical Prototypes |
|---|---|---|---|
| 1 |  |  |  |
| 2 |  |  |  |
| 3 |  |  |  |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tashi; Ullah, A.S. Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping. Symmetry 2019, 11, 985. https://doi.org/10.3390/sym11080985
Tashi, Ullah AS. Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping. Symmetry. 2019; 11(8):985. https://doi.org/10.3390/sym11080985
Chicago/Turabian StyleTashi, and AMM Sharif Ullah. 2019. "Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping" Symmetry 11, no. 8: 985. https://doi.org/10.3390/sym11080985
APA StyleTashi, & Ullah, A. S. (2019). Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping. Symmetry, 11(8), 985. https://doi.org/10.3390/sym11080985





