Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport

Abstract

This review is devoted to tight-binding (TB) modeling of nucleic acid sequences like DNA and RNA. It addresses how various types of order (periodic, quasiperiodic, fractal) or disorder (diagonal, non-diagonal, random, methylation et cetera) affect charge transport. We include an introduction to TB and a discussion of its various submodels [wire, ladder, extended ladder, fishbone (wire), fishbone ladder] and of the process of renormalization. We proceed to a discussion of aperiodicity, quasicrystals and the mathematics of aperiodic substitutional sequences: primitive substitutions, Perron–Frobenius eigenvalue, induced substitutions, and Pisot property. We discuss the energy structure of nucleic acid wires, the coupling to the leads, the transmission coefficients and the current–voltage curves. We also summarize efforts aiming to examine the potentiality to utilize the charge transport characteristics of nucleic acids as a tool to probe several diseases or disorders.

1. Introduction

Nucleic acids are polymeric macromolecules consisting of units that are called nucleotides. The term nucleic acids is the overall name of deoxyribonucleic acid (DNA) and ribonucleic acid (RNA). DNA’s nucleotide sequence carries the genetic instructions for the development, function, growth and reproduction of living organisms and several viruses. Although RNA’s primary role is to carry out the instructions encoded in DNA for protein synthesis, it also acts like a catalyst of biochemical reactions, while it is the genetic material of many viruses.

For more than sixty years now, the double-stranded structure of DNA has been known [1]. The nucleotides of each strand are composed of one of four planar, aromatic, nitrogenous bases, i.e., guanine (G), cytosine (C), adenine (A) or thymine (T), a pentose sugar (deoxyribose), and a phosphate group. Covalent, phosphodiester bonds between pentoses and phosphate groups of adjacent nucleotides form an alternating sugar-phosphate backbone. The purines (G or A) of a nucleotide belonging to a strand are joined together with the pyrimidines of the other strand (C or T, respectively) via (three or two, respectively) hydrogen bonds, forming the double helix structure. This specificity in the way bases match ensures that G is always bonded with C, and A is always bonded with T. Pairing between non-complementary bases results in mutations that can be detrimental to the development of an organism. In RNA, deoxyribose (whose 2-carbon is bonded with a hydrogen) is replaced by ribose (whose 2-carbon is bonded with a hydroxyl group), and T is replaced by uracil (U). Furthermore, RNA molecules are single-stranded; however, some viruses possess double-stranded RNA (other viruses can contain even single-stranded DNA).

Although the study of nucleic acids is mainly associated with molecular biology and genetics, today, a broad interdisciplinary community is interested in biological systems, such as nucleic acids and analogues. The base-pair stack of nucleic acids creates a nearly one-dimensional $\pi$-stack that allows charge carrier movement, i.e., charge transfer and transport. Let us distinguish between these two terms: transfer means that a carrier, created or injected at a specific nucleotide, moves to a more favorable location, while transport implies the use of electrodes and the application of external voltage between them. Charge transfer is the basis of many biological processes, e.g., in various proteins [2] including metalloproteins [3], and enzymes [4], with medical and bioengineering applications [5,6], while it plays a role in DNA damage and repair [7,8,9]. Charge transport might be an indicator to distinguish pathogenic from non-pathogenic mutations at an early stage [10].

From a physicist’s point of view, the charge transfer and transport properties of nucleic acids are studied in order to obtain a deeper understanding of their biological functions as well as for potential applications, such as nanosensors, nanocircuits or molecular wires, due to their high yield synthesis, near-unity purification, and nanoscale self-organization [11,12,13]. There are many external (aqueousness, presence of counterions, extraction process, electrodes, contacts, purity, substrate), and internal (such as the base-pair sequence and geometry) factors that affect carrier motion along nucleic acids. Both ab initio calculations [14,15,16,17,18,19,20,21,22] and model Hamiltonians [23,24,25,26,27,28,29,30,31,32,33,34] have been used to theoretically explore the variety of experimental results that predict electrical behavior ranging from metallic to insulating, as well as the underlying mechanisms.

It has become evident that the influence of various types of order or disorder plays a central role in the energy structure and the charge transport properties of nucleic acids. This interplay between various types of order or disorder and charge transport is addressed in this brief review. This is done in the context of one of the most widely applied theoretical methods, i.e., with Tight-Binding (TB), because of its simplicity and low computational cost.

The rest of this review is organized as follows. In Section 2, we present the TB formulation and explain some of its most common variations applied in the literature for the study of nucleic acids. In Section 3, we overview several aperiodic substitutional sequences that highlight the influence of disorder in the properties of nucleic acids. In Section 4, we discuss the energy spectra of ordered and disordered nucleic acid sequences. In Section 5, we focus on electron transmission and on the influence of coupling the examined systems with leads. Section 6 is dedicated to the influence of various types of order or disorder on the current–voltage ($I-V$) curves of nucleic acids. Finally, in Section 7, we make some concluding remarks.

2. Tight-Binding and Its Application in Nucleic Acids

TB is an approximate method widely used in condensed matter physics to determine the electronic structure of a solid through the expansion of its wavefunction as a superposition of the wavefunctions corresponding to the isolated moieties located at each lattice site [35]. As the name of the model suggests, the main hypothesis in TB is that the system’s orbitals are tightly bound at the sites at which they belong, so that the overlap with neighboring orbitals is small. Hence, the electronic wavefunction of the moiety that occupies a lattice site is rather similar to the orbital of the free moiety. As a result, the corresponding energy of the electron will be rather close to the (negative) ionization energy of the free moiety due to the weak interaction with its neighbors. This picture is applicable at the bands formed by the core electrons of metals, the valence and conduction bands of insulators and semiconductors, as well as the valence and conduction bands arising from localized d or f states (e.g., in transition metals and rare earths).

Today, several decades after its introduction [36], TB has evolved into a fast and efficient approach, employable to numerous problems regarding the electronic structure and properties of matter, requiring various degrees of accuracy [37,38]. Its main advantages include its intuitive simplicity, the ability it gives to obtain analytic results in several cases, and its low computational cost [39]. The latter makes TB applicable to large systems, currently unreachable by the more sophisticated ab initio methods, such as Density Functional Theory (DFT). In contrast to those methods, TB is semi-empirical, in the sense that an external set of parameters is needed in order to perform calculations. These parameters are (a) the on-site energies that correspond to the energy of the electrons that belong to each lattice site, and (b) the hopping (or transfer) integrals that correspond to the coupling of orbitals which belong to neighboring sites.

Over the last few decades, TB has been widely used to describe, among others, polymers and organic systems. One-dimensional TB models are commonly applied to study the energy structure and thermal, magnetic as well as charge transfer and transport properties of $\pi$-conjugated organic systems that are candidates for molecular wires, such as nucleic acids and analogues. Those models have varying degrees of complexity, and each one of them requires a different number of parameters. As far as nucleic acids are concerned, the models employed include, inter alia, the Wire Model (WM), the Ladder Model (LM), the Extended Ladder Model (ELM), the Fishbone Model (FM) and the Fishbone Ladder Model (FLM). Generally, the studied systems consist of N monomers extended at L chains ($L\ll N$, since nucleic acids are approximately one-dimensional). The problem is reduced to the solution of the so-called system of TB equations, which is a system of coupled stationary, algebraic equations or differential equations of first order, equivalent to a discretized form of the time-independent or time-dependent Schrödinger equation. As far as nucleic acids are concerned, the stationary TB system of equations can be compactly written in the matrix form

$$E{\overrightarrow{\mathbf{\Psi }}}_n={\mathit{\epsilon }}_n{\overrightarrow{\mathbf{\Psi }}}_n+{\mathit{\tau }}_{n-1}^T{\overrightarrow{\mathbf{\Psi }}}_{n-1}+{\mathit{\tau }}_n{\overrightarrow{\mathbf{\Psi }}}_{n+1},$$

(1)

for $n=1,2,\cdots ,N$. ${\overrightarrow{\mathbf{\Psi }}}_n$ is a vector matrix containing the elements of the wavefunction that correspond to monomer n, i.e., ${\overrightarrow{\mathbf{\Psi }}}_n={({\psi }_n^1{\psi }_n^2\cdots {\psi }_n^L)}^T$, ${\mathit{\epsilon }}_n$ is a symmetric $L\times L$ matrix containing the on-site energies of each site, ${ϵ}_n^l$ and the hopping integrals $t_n^{l{l}^{\prime }}$ between the sites of the monomer that belong to different chains, and ${\mathit{\tau }}_n$ is a generally non-symmetric $L\times L$ matrix containing the hopping integrals $t_{n{n}^{\prime }}^{l{l}^{\prime }}$ between each site of a monomer and the neighboring sites of the next monomer. Finally, E is the energy. The situation is schematically presented in Figure 1. From Bloch’s theorem, it holds that ${\overrightarrow{\mathbf{\Psi }}}_{N+n}=z{\overrightarrow{\mathbf{\Psi }}}_n$, where z generally lies in the unit circle ($z=z^{*}=1$, for cyclic boundaries, or $z=z^{*}=0$ for fixed boundaries). Hence, the solution of the system of Equation (1) can be reduced to the diagonalization of the Hamiltonian matrix, written in block form as

$$\mathbf{H}=\left(\begin{array}{ccccc}{\mathit{\epsilon }}_1& {\mathit{\tau }}_1& & & z^{*}{\mathit{\tau }}_0^T\\ {\mathit{\tau }}_1^T& {\mathit{\epsilon }}_2& {\mathit{\tau }}_2& & \\ & & {\mathit{\tau }}_2^T& {\mathit{\epsilon }}_3& {\mathit{\tau }}_3\\ & & \ddots & \ddots & \ddots \\ z{\mathit{\tau }}_N& & & {\mathit{\tau }}_{N-1}^T& {\mathit{\epsilon }}_N\end{array}\right).$$

(2)

Equivalently, Equation (1) can be written in the form

$$\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_{n+1}\\ {\overrightarrow{\mathbf{\Psi }}}_n\end{array}\right)=\left(\begin{array}{cc}{\mathit{\tau }}_n^{-1}(E-{\mathit{\epsilon }}_n)& -{\mathit{\tau }}_n^{-1}{\mathit{\tau }}_{n-1}^T\\ \mathbf{1}& \mathbf{0}\end{array}\right)\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_n\\ {\overrightarrow{\mathbf{\Psi }}}_{n-1}\end{array}\right)={\mathbf{Q}}_n\left(E\right)\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_n\\ {\overrightarrow{\mathbf{\Psi }}}_{n-1}\end{array}\right),$$

(3)

where ${\mathbf{Q}}_n\left(E\right)$ is called the transfer matrix of monomer n, and $\mathbf{1},\mathbf{0}$ are the unit and zero matrix of order L. The product

$${\mathbf{M}}_N\left(E\right)=\prod _{n=N}^1{\mathbf{Q}}_n\left(E\right)$$

(4)

defines the global transfer matrix of the system, which satisfies the relation,

$${\mathbf{M}}_N\left(E\right)\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_1\\ {\overrightarrow{\mathbf{\Psi }}}_0\end{array}\right)=\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_{N+1}\\ {\overrightarrow{\mathbf{\Psi }}}_N\end{array}\right)=z\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_1\\ {\overrightarrow{\mathbf{\Psi }}}_0\end{array}\right),$$

(5)

and contains all the information about its energetics. In fact, since z is an eigenvalue of the global transfer matrix, with eigenvector ${\left(\begin{array}{c}{\overrightarrow{\mathbf{\Psi }}}_1{\overrightarrow{\mathbf{\Psi }}}_0\end{array}\right)}^T$, the whole eigenvector of the Hamiltonian matrix of Equation (2) can be reconstructed via a successive application of Equation (3) [40,41]. Hence, when z is an eigenvalue of ${\mathbf{M}}_N\left(E\right)$, E is an eigenvalue of the system’s Hamiltonian. Thus, both methods can be used to determine the energy structure of the system. The form of the matrices in Equation (1) for various TB models is presented in

Table 1. Form of the matrices ${\overrightarrow{\mathbf{\Psi }}}_n$, ${\mathit{\epsilon }}_n$, ${\mathit{\tau }}_n$ in the TB system of equations (Equation (1)) for several models used to describe nucleic acids and analogues: the Wire Model (WM), the Ladder Model (LM), the Extended Ladder Model (ELM), the Fishbone Model (FM) and the Fishbone Ladder Model (FLM).

Model	L	${\overrightarrow{\mathbf{\Psi }}}_{\mathit{n}}$	${\mathit{\epsilon }}_{\mathit{n}}$	${\mathit{\tau }}_{\mathit{n}}$
WM	1	${\psi }_n$	${ϵ}_n$	$t_{n,n+1}$
LM	2	$\left(\begin{array}{c}{\psi }_n^1\\ {\psi }_n^2\end{array}\right)$	$\left(\begin{array}{cc}{ϵ}_n^1& t_n^{1,2}\\ t_n^{2,1}& {ϵ}_n^2\end{array}\right)$	$\left(\begin{array}{cc}{t}_{n,n+1}^{1,1}& 0\\ 0& t_{n,n+1}^{2,2}\end{array}\right)$
ELM	2	$\left(\begin{array}{c}{\psi }_n^1\\ {\psi }_n^2\end{array}\right)$	$\left(\begin{array}{cc}{ϵ}_n^1& t_n^{1,2}\\ t_n^{2,1}& {ϵ}_n^2\end{array}\right)$	$\left(\begin{array}{cc}{t}_{n,n+1}^{1,1}& t_{n,n+1}^{1,2}\\ t_{n,n+1}^{2,1}& t_{n,n+1}^{2,2}\end{array}\right)$
FM	3	$\left(\begin{array}{c}{\psi }_n^1\\ {\psi }_n^2\\ {\psi }_n^3\end{array}\right)$	$\left(\begin{array}{ccc}{ϵ}_n^1& t_n^{1,2}& 0\\ t_n^{2,1}& {ϵ}_n^2& t_n^{2,3}\\ 0& t_n^{3,2}& {ϵ}_n^3\end{array}\right)$	$\left(\begin{array}{ccc}0& 0& 0\\ 0& t_{n,n+1}^{2,2}& 0\\ 0& 0& 0\end{array}\right)$
FLM	4	$\left(\begin{array}{c}{\psi }_n^1\\ {\psi }_n^2\\ {\psi }_n^3\\ {\psi }_n^4\end{array}\right)$	$\left(\begin{array}{cccc}{ϵ}_n^1& t_n^{1,2}& 0& 0\\ t_n^{2,1}& {ϵ}_n^2& t_n^{2,3}& 0\\ 0& t_n^{3,2}& {ϵ}_n^3& t_n^{3,4}\\ 0& 0& t_n^{4,3}& {ϵ}_n^4\end{array}\right)$	$\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& t_{n,n+1}^{2,2}& 0& 0\\ 0& 0& t_{n,n+1}^{3,3}& 0\\ 0& 0& 0& 0\end{array}\right)$

. Some details on each of these TB models are discussed below.

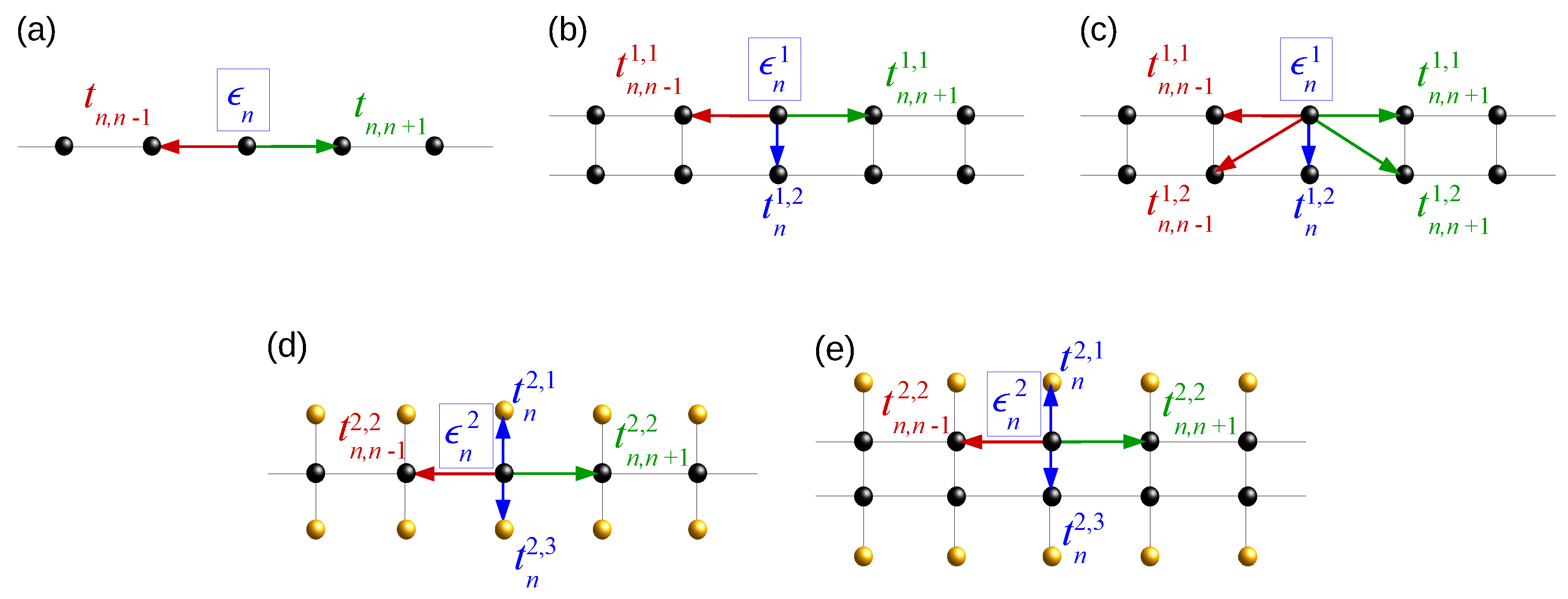
2.1. Wire Model

WM is the simplest TB model to describe nucleic acids and analogues [42,43]. It can be applied to mimic either single-stranded nucleic acids and hairpins at the single-base level [44] or double-stranded ones [45] at the base-pair level. In other words, if the WM refers to a single-stranded nucleic acid, then the on-site energies are related to the energy levels of the four possible bases and the hopping integrals to the interaction between bases, while, if it refers to a double-stranded nucleic acid, then the on-site energies are related to the energy levels of the two possible base-pairs (incorporating the hydrogen bonding) and the hopping integrals to the interaction between base-pairs. It consists of just one chain ($L=1$) and the parameters needed for its employment are the on-site energies of the bases or base pairs, ${ϵ}_n$, and the hopping integrals between successive bases or base pairs, $t_n$. A schematic representation of the WM is shown in Figure 2a.

2.2. Ladder Model

LM is the simplest model that can address the influence of base-pairing in the energetics of nucleic acids [42,46]. It consists of two chains ($L=2$) and the parameters needed for its employment are the on-site energies of the bases, ${ϵ}_n^l$, the inter-strand hopping integrals between successive bases, $t_{n,n\pm 1}^{ll}$, and the intra-base-pair hopping integrals, $t_n^{l{l}^{\prime }}$, due to the hydrogen bonds formed by the complementary bases in a pair. A schematic representation of the LM is shown in Figure 2b.

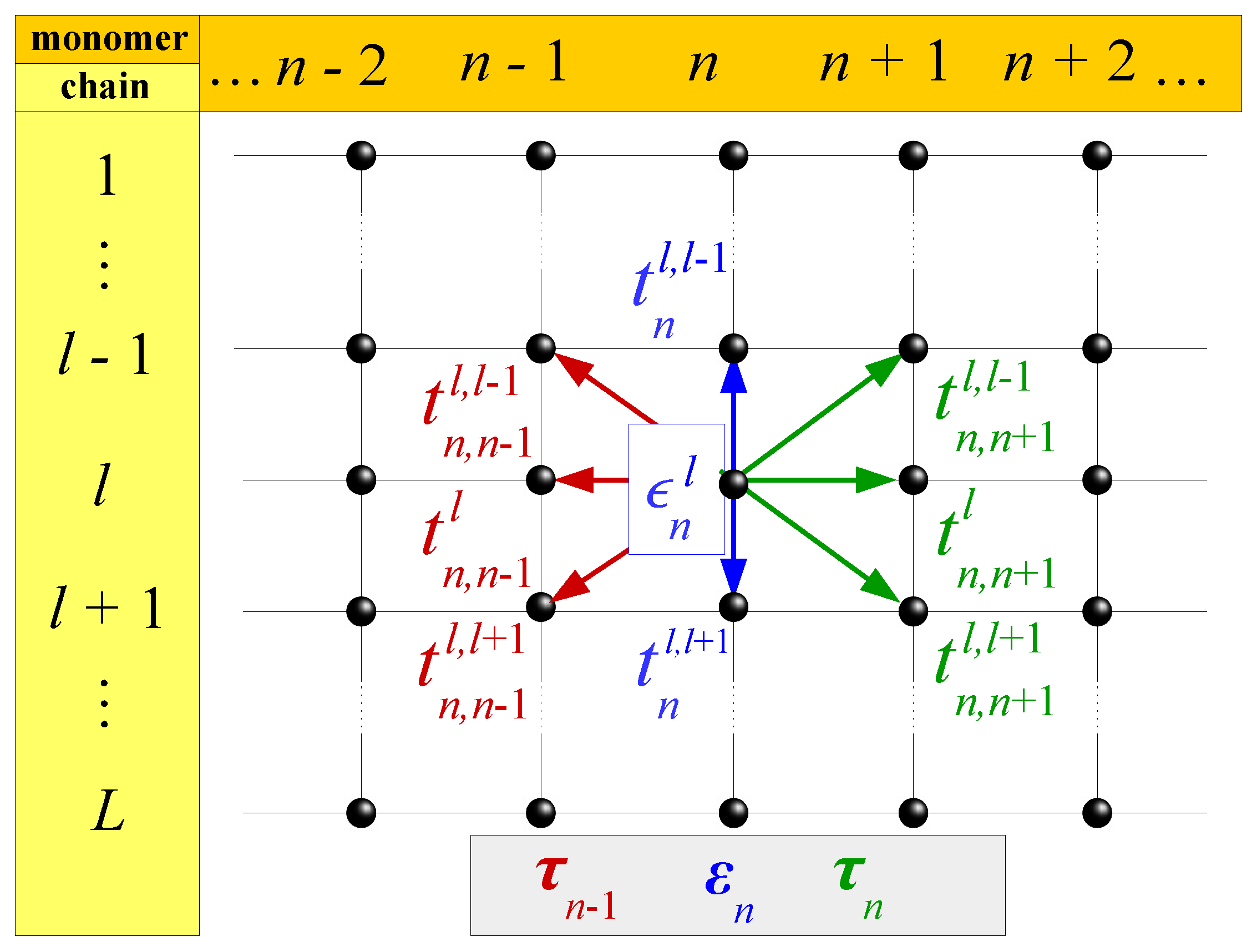
2.3. Extended Ladder Model

ELM is a more detailed version of the LM, including the inter-strand hopping integrals, $t_{n,n\pm 1}^{l{l}^{\prime }}$, between the bases of successive base pairs [46,47]. A schematic representation of the ELM is shown in Figure 2c.

2.4. Fishbone Model

FM is the simplest model that can take into account the effect of the sugar-phosphate backbone [29,42]. It consists of three chains ($L=3$). The central one corresponds to the base pairs, with each one being interconnected with the top and bottom chains, which represent the backbone sites. The latter are not connected with each other, since the insulating sugars are separating phosphate groups from one another [11,48]. Hence, the parameters needed for its employment are the on-site energies, ${ϵ}_n^l$, of the base pairs ($l=2$) and the backbone sites ($l=1,3$), the intra-strand hopping integrals between successive base pairs, $t_{n,n\pm 1}^{2,2}$, and the inter-strand hopping integrals, $t_n^{l{l}^{\prime }}$, between the base pairs and the backbone. A schematic representation of the FM is shown in Figure 2d.

2.5. Fishbone Ladder Model

FLM is a combination of the LM and the FM [29,42]. It thus includes both the effect of base-pairing and the presence of the sugar-phosphate backbone. It consists of four chains ($L=4$). The two central ones ($l=2,3$) correspond to the nitrogenous bases and the edge ones ($l=1,4$) to the backbone sites. Hence, the parameters needed for its employment are the on-site energies, ${ϵ}_n^l$, of the base pairs ($l=2,3$) and the backbone ($l=1,4$), the intra-strand hopping integrals between base pairs, $t_{n,n\pm 1}^{ll}$ ($l=2,3$) and the inter-strand hopping integrals between the bases of a base pair as well as between each base and the backbone, $t_n^{l{l}^{\prime }}$. A schematic representation of the FLM is shown in Figure 2e.

2.6. Additional Remarks

Apart from the models described above, one can introduce several other variants to describe nucleic acids. For example, an obvious extension would be a fishbone extended ladder model. Additionally, several other models have been proposed, including intra-backbone interactions [27,46,49], single-stranded nucleic acids with a backbone [49] and explicit inclusion of helicity [50] strain [51], and spin–orbit coupling [52] effects. We also mention that more complex models can be reduced to simpler ones via a renormalization scheme, which reduces the degrees of freedom of the system. Then, the on-site energies of the renormalized Hamiltonian are energy-dependent. This procedure is important when environmentally induced effects are considered [29]. For example, the FLM can be reduced into an LM via a one-step renormalization procedure [53], or to an even simpler WM via a two-step renormalization procedure [54,55].

Several techniques can be applied to solve the models, depending on what is studied, such as the numerical diagonalization of the Hamiltonian in Equation (2) [47,56,57], the transfer matrix method [58,59,60] outlined above, and the Non-Equilibrium Green’s Function technique [61]. As it is apparent from Equation (3), the transfer matrix method is not applicable if the matrices ${\mathit{\tau }}_n$ are singular. Generally, this is the case, e.g., for the FM and the FLM (cf. Table 1). Then, a renormalization scheme is needed to apply the transfer matrix method.

Relevant parametrizations for nucleic acids have been proposed in many works and used within various TB models. For example, for on-site energies and hopping integrals, cf. Refs. [16,17,20,62,63], for on-site energies, cf. Refs. [64,65,66,67,68,69,70], and for hopping integrals, cf. Refs. [71,72,73]. Such parametrizations allow researchers to go beyond the chemically unrealistic treatments, such as the assumptions that all hopping integrals or on-site energies are equal, i.e., disorder in the Hamiltonian is either purely diagonal or off-diagonal, respectively, and address in more detail the complexity of nucleic acid energy structure.

3. Aperiodic One-Dimensional Wires

The dichotomy between the notions of order and disorder has expanded beyond a simple distinction between periodicity and aperiodicity, since the first observation of icosahedral diffraction patterns in the spectrum of an Al${}_{0.86}$Mn${}_{0.14}$ alloys [74] (2011 Nobel Prize in Chemistry for Prof. Dan Shechtman). The discussion that opened in the scientific community following this and other relevant discoveries led to a change in the very definition of the term crystal by the International Union of Crystallography in 1992, expanding it from referring solely to periodically arranged structures to “any solid having an essentially discrete diffraction diagram” [75]. This extended notion of crystals encompasses a whole family of structures, called quasi-periodic crystals or quasicrystals. Quasicrystals do not possess the translation symmetry that is inherent to classical (periodic) crystals; however, they possess inflation/deflation symmetry which leads to long-range order as well.

The discovery of quasicrystals has turned scientific interest into the study of specific one-dimensional aperiodic lattices, modeled with TB [76], i.e., described by Equation (1). The lattices are typically created using substitutional sequences. Apart from the interest the study of such systems has in itself, it is applicable, among other systems of physical relevance, in nucleic acids, as seen in Section 2. The ability to produce synthetic, de novo, nucleic acid sequences of interest [77], using mainly the phosphoramidite method [78] (although other promising methods have recently been proposed [79]), provides a chance not only to examine theoretical predictions regarding aperiodic structures, but also to create molecular wires with tailored properties. Below, we present some details about substitutional sequences as well as some of the most commonly used ones in the literature of one-dimensional wires generally, and nucleic acids specifically.

3.1. Aperiodic Substitutional Sequences

Aperiodic substitutional sequences are based on an alphabet, e.g., $\mathcal{A}=\{\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D},\cdots \}$ equipped with substitution rules that apply to each of its letters, $s\left(j\right),\forall j\in \mathcal{A}$. In the case of nucleic acids, the alphabet letters correspond to nitrogenous bases, i.e., G, C, A, T, U (for double-stranded chains the complementary strand is implied). The sequences start with a seed, i.e., a letter belonging to the alphabet (0th generation of the sequence). The substitution rules replace each alphabet letter by finite words consisting of alphabet letters, i.e., $s\left(j\right)=j_1^{\prime }{j}_2^{\prime },\cdots j_k^{\prime },\forall j\in \mathcal{A}$. Iterating this procedure g times constructs the gth generation of the sequence.

Substitutional sequences can, in most cases, be described by introducing the substitution matrix, $\mathbf{S}$. It is a square, non-negative matrix of order $card\left(\mathcal{A}\right)$ (the cardinality of a set is the number of elements of the set), and its elements are $S_{ij}=n_i\left[s\left(j\right)\right]$, where $n_i\left[s\left(j\right)\right]$ is the number of times the letter i is present in the substitution rule $s\left(j\right)$. Notice that, by definition, $\mathbf{S}$ does not contain information about the ordering of letters in the sequence, hence more than one substitutions can have the same substitution matrix. However, the substitution matrix reveals much information about the underlying order and other properties of the corresponding sequence at the thermodynamic limit.

3.2. Primitive Substitutions and the Perron–Frobenius Eigenvalue

The matrix $\mathbf{S}$ (and, hence, the substitution) is called primitive if there exists a natural number k such that $S^k$ is a positive matrix. For primitive substitutions, the Perron–Frobenius theorem [80,81] guarantees that $\mathbf{S}$ has a largest, unique, real, positive eigenvalue, ${\lambda }_{PF}$, and its corresponding (left and right) eigenvectors can be chosen to have strictly positive entries. The components of the right eigenvector associated with ${\lambda }_{PF}$, normalized such as their sum is unity, give the asymptotic relative frequencies of the letters in $\mathcal{A}$. Hence, using $\mathbf{S}$, one can determine the occurrence percentage of each nucleotide in a substitutional nucleic acid sequence.

3.3. Induced Substitutions

In addition to the previous discussion, it is also possible to determine the letter frequencies of the legal words of length k in a substitutional sequence with primitive $\mathbf{S}$ (corresponding to nucleotide k-plets). This can be done as follows [82]; let $W=\{w=j_1{j}_2\cdots j_k,\forall j\in \mathcal{A}\}$ be the set of the legal k-letter words in the sequence and $s\left(w\right)=s\left(j_1\right)s\left(j_2\right)\cdots s\left(j_k\right)=j_1^{\prime }{j}_2^{\prime }\cdots j_n^{\prime }$ the word constructed from a letter-by-letter substitution of the word w. Then, the induced substitution of a k-letter word, $s_k\left(w\right)=(j_1^{\prime }{j}_2^{\prime }\cdots j_k^{\prime })(j_2^{\prime }{j}_3^{\prime }\cdots j_{k+1}^{\prime })\cdots (j_l^{\prime }{j}_{l+1}^{\prime }\cdots j_{l+k-1}^{\prime })$, where l is the number of letters in $s\left(j_1\right)$, is also primitive. Hence, an induced primitive substitution matrix ${\mathbf{S}}_k$ can be defined, from which the asymptotic letter frequencies of the legal k-letter words of the sequence can be determined using the Perron–Frobenius theorem. For sequences in which $\mathbf{S}$ is defined via a helping alphabet [83], k-letter word frequencies can be deduced in the same fashion from the legal $2k$-letter words of the helping alphabet.

3.4. The Pisot Property

A real algebraic integer (i.e., a real solution of a monic integer polynomial) is said to be a Pisot–Vijayaraghavan number if its modulus is larger than unity, and all its algebraic conjugates (i.e., the other solutions of the polynomial) have modulus strictly less than unity [84]. A substitution has the Pisot property if the matrix $\mathbf{S}$ has a largest, unique, real, positive eigenvalue which is a Pisot–Vijayaraghavan number, and for all the other eigenvalues, $\lambda$, it holds that $\left|\lambda \right|<1$. If the characteristic polynomial of $\mathbf{S}$ is irreducible over the rationals, the Pisot substitution is called irreducible. Irreducible Pisot substitutions are a subclass of primitive substitutions [85].

Let us remember some definitions. Given n linearly independent vectors ${\mathit{b}}_1,{\mathit{b}}_2,\cdots {\mathit{b}}_n\in {\mathbb{R}}^m$, the lattice generated by them is defined as $\mathcal{L}({\mathit{b}}_1,{\mathit{b}}_2,\cdots {\mathit{b}}_n)={\sum }_i{x}_i{\mathit{b}}_i,x_i\in \mathbb{Z}$. We call the set ${\mathit{b}}_1,{\mathit{b}}_2,\cdots {\mathit{b}}_n$ a basis of the lattice. We say that the rank of the lattice is n and its dimension is m. The Fourier transform of the (direct) lattice is a lattice that is called the reciprocal lattice.

Furthermore, according to the Lebesgue’s decomposition theorem, any measure on $\mathbb{R}$ can be decomposed into three parts: a pure point (or discrete) part, an absolutely continuous part, and singularly continuous part. This theorem helps to categorize the energy or Fourier spectra of aperiodic substitutional sequences.

The first connections between the irreducible Pisot property and the Fourier spectrum of a substitutional sequence were reported in Refs. [86,87], where it was conjectured that if the Perron–Frobenius eigenvalue of a substitutional system is a Pisot–Vijayaraghavan number, then the system is quasiperiodic. Later studies have revealed more details, providing a more sophisticated classification of substitutional systems with respect to the nature of their diffraction spectrum. In the one-dimensional case, sequences produced from irreducible Pisot substitutions have pure point Fourier spectra [88]. (I) The Pisot property, together with (II) the extra condition $\lambda \ne 0$, provide the means to distinguish between:

(1)

strictly quasiperiodic sequences, in which the rank of the reciprocal lattice $n_r$ is finite and larger than the dimension of the physical space of the sequence m, and

(2)

limit-quasiperiodic sequences, in which the rank of reciprocal lattice $n_r$ is countably infinite (in a 1–1 correspondence with the natural numbers or integers).

The distinction criterion between categories (1) and (2) is the value of the determinant of $\mathbf{S}$: unimodular $\mathbf{S}$ implies strict quasiperiodicity, otherwise the structure is limit-quasiperiodic [89,90,91]. Limit-quasiperiodic structures can be interpreted as a superposition of an infinite number of strictly quasiperiodic structures. Examples of strictly quasiperiodic structures are the classical Fibonacci sequence [92] as well as all the precious means sequences [93] and the Fibonacci-class sequences [94] (cf.

Table 2. Substitutional sequences studied in the literature, together with the alphabets through which they are defined, the corresponding substitution rules, and the substitution matrices. In the last row, the subscripts o and e in the substitution rules denote substitutions that are applied on odd and even positions in the sequence, respectively.

Sequence	$\mathcal{A}$	Substitution Rule	S
Fibonacci	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = AB s(B) = A	$\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)$
Precious means	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = A${}^n$B s(B) = A	$\left(\begin{array}{cc}n& 1\\ 1& 0\end{array}\right)$
Fibonacci-class	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = B${}^{n-1}$AB s(B) = B${}^{n-1}$A	$\left(\begin{array}{cc}1& 1\\ n& n-1\end{array}\right)$
Mixed means	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = A${}^n$B${}^m$s(B) = A	$\left(\begin{array}{cc}n& 1\\ m& 0\end{array}\right)$
Metallic means	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = AB${}^n$s(B) = A	$\left(\begin{array}{cc}1& 1\\ n& 0\end{array}\right)$
Period doubling	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = AB s(B) = AA	$\left(\begin{array}{cc}1& 2\\ 1& 0\end{array}\right)$
Thue–Morse	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = AB s(B) = BA	$\left(\begin{array}{cc}1& 2\\ 1& 0\end{array}\right)$
Rudin–Shapiro	$\left\{\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}\right\}$		$\left(\begin{array}{cccc}1& 1& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 1\end{array}\right)$
		s(A) = AB s(B) = AC
		s(C) = DB s(D) = DC
Triadic Cantor set	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = ABA s(B) = BBB	$\left(\begin{array}{cc}2& 0\\ 1& 3\end{array}\right)$
Asymmetric Cantor set	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = ABAA s(B) = BBBB	$\left(\begin{array}{cc}3& 0\\ 1& 4\end{array}\right)$
Generalized Cantor set $(t,d)$	$\left\{\mathrm{A},\mathrm{B}\right\}$	s(A) = A${}^{\frac{t-d}{2}}$B${}^d$A${}^{\frac{t-d}{2}}$s(B) = B${}^t$	$\left(\begin{array}{cc}t-d& 0\\ d& t\end{array}\right)$
Kolakoski $(p=2m,q=2n)$	$\{\mathrm{A}=pp,\mathrm{B}=qq\}$	s(A) = A${}^m$B${}^m$s(B) = A${}^n$B${}^n$	$\left(\begin{array}{cc}m& n\\ m& n\end{array}\right)$
Kolakoski $(p=2m+1,q=2n+1)$			$\left(\begin{array}{ccc}m& m& n\\ 1& 1& 1\\ m& n& n\end{array}\right)$
	$\{\mathrm{A}=pp,\mathrm{B}=pq$,	s(A) = A${}^m$BC${}^m$s(B) = A${}^m$BC${}^n$
	C $=qq\}$	s(C) = A${}^n$BC${}^n$
Kolakoski ($p=2m,q=2m+1$) or	$\{p,q\}$	$s_o\left(q\right)=p^q$$s_o\left(p\right)=p^p$	undefinable
($p=2m+1,q=2m$)		$s_e\left(q\right)=q^q$$s_e\left(p\right)=q^p$

, where several substitutional sequences studied in the literature are listed, together with their substitution rules and matrices). Limit-quasiperiodic structure representatives are the mixed means sequences with $n\ge m$ [95].

For substitutions not satisfying the above-mentioned conditions (I) and (II), the situation is more complex. In such cases, the Fourier spectrum can be:

(3)

limit-periodic, i.e., a superposition of countably infinite periodic structures. Some examples are the period doubling sequence and metallic means sequences with $n=l(l+1)$ [96],

(4)

singular continuous, i.e., non-constant, non-decreasing, continuous and has zero derivative, everywhere that the derivative exists. Examples are the Thue–Morse sequence [97,98,99] and metallic means sequences with $n\ne l(l+1)$ [96], or even

(5)

absolutely continuous, such as the Rudin–Shapiro sequence [100,101].

Apart from the above-mentioned sequences, there are others for which the substitution is not primitive or the matrix $\mathbf{S}$ cannot even be defined at all. Examples of non-primitive substitutions include the sequences inspired by the Cantor set [102], maybe the most well-known deterministic fractal. A sequence for which a substitution matrix cannot be defined is the classical Kolakoski$(1,2)$ sequence [103,104], and generally Kolakoski$(p,q)$ sequences where p is odd and q even or vice versa [105]. The situation is different when p and q are both even or odd; then, a primitive $\mathbf{S}$ can be defined. In the former case, the sequences have been classified as limit-periodic [106]. In the latter case, the irreducible Pisot property holds when $2(p+q)\ge {(p-q)}^2$, and $\mathbf{S}$ is also unimodular when $p=q\pm 2$ [105].

4. Energy Structure of Nucleic Acid Wires

The energy structure of a physical system is closely connected to many of its properties (electrical, magnetic, thermal, optical, et cetera). A useful –and closely related to experimental data—quantity that describes the energy structure of a given system is the density of states (DOS), which shows the number of states that can be occupied by electrons at each energy. It can be formally defined as

$$g\left(E\right)=\sum _k\delta (E-E_k),$$

(6)

where no spin degeneracies are included. The sum runs over all allowed states, each of which has an eigenenergy $E_k$. A closely related quantity is the integrated density of states (IDOS), defined as

$$IDOS\left(E\right)={\int }_{-\infty }^{E}g\left(E^{\prime }\right)d{E}^{\prime },$$

(7)

i.e., it is the number of states that have energy smaller than E. Discontinuities in the IDOS indicate the presence of energy gaps, and the height of an IDOS step gives information about the level population. For periodic systems, the regions of allowed energies lead to smooth parts in DOS or IDOS curves, separated by well defined gaps at specific energies, thus reflecting the continuous electronic band structure of a periodic crystal. On the contrary, the DOS and IDOS of random systems are rough, indicative of the presence of a multitude of gaps between the allowed energy levels. As it has to do with deterministic aperiodic sequences with a substitution rule, which reflects their self-similarity, it has been conjectured (and proven, in several specific cases) that their energy spectrum is singular continuous, i.e., in the thermodynamic limit, it exhibits an infinity of gaps and vanishing bandwidths [107].

Furthermore, for primitive substitutions described by a Hamiltonian corresponding to the WM, the following gap-labeling theorem has been introduced by Bellissard et al. [108]:

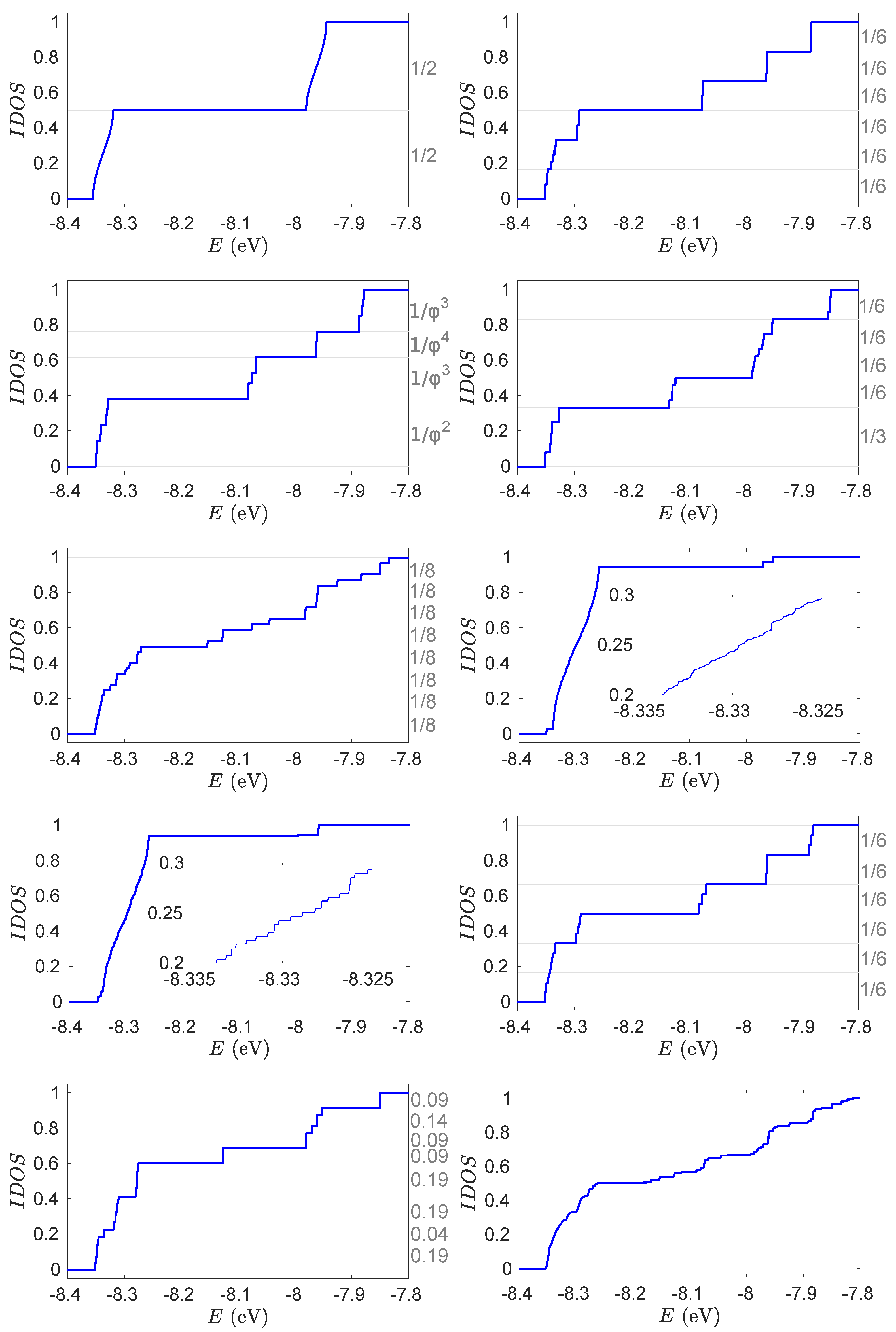
Theorem 5.13 of Ref [108].Let $\widehat{H}$ be a Hamiltionian corresponding to the WM, where the coefficients (i.e., parameters) are determined by a primitive substitution on a finite alphabet. Then, the values of the IDOS of $\widehat{H}$ on the spectral gaps in $[0,1]$ belong to the $\mathbb{Z}\left({\lambda }_{PF}^{-1}\right)$ module generated by the components of the eigenvectors ${\overrightarrow{\mathbf{v}}}_{PF}$ and ${\overrightarrow{\mathbf{v}}}_{PF,2}$ of the substitution matrices $\mathbf{S}$ and ${\mathbf{S}}_2$, respectively.

From the above theorem, it follows that, in order to obtain the position of the gaps in the (normalized) IDOS of a primitive substitutional sequence within the WM, it is sufficient to know the substitution matrices of its legal 1- and 2-letter words (c.f. Section 3.3). Specifically, the gaps can be labeled by the negative powers of ${\lambda }_{PF}$ times integral linear combinations of the components of ${\overrightarrow{\mathbf{v}}}_{PF}$ and ${\overrightarrow{\mathbf{v}}}_{PF,2}$ that lie within the interval $[0,1]$ [108,109]. For example, in the case of Fibonacci sequences, from the diagonalization of $\mathbf{S}$ (cf. Table 2), we get ${\lambda }_{PF}=\varphi$ and ${\overrightarrow{\mathbf{v}}}_{PF}={\left[{\varphi }^{-1}{\varphi }^{-2}\right]}^T$ (where $\varphi$ is the golden ratio). Hence, the sequence consists of ≈61.8% A letters and ≈38.2% B letters. The legal 2-letter words in the Fibonacci sequence are BA, AB, and AA (i.e., BB is forbidden), thus the induced 2-substitution reads (cf. Section 3.3) $s_2$(AA) = (AB)(BA), $s_2$(AB) = (AB)(BA), $s_2$(BA) = (AA), leading to the induced substitution matrix

$${\mathbf{S}}_2=\left(\begin{array}{ccc}0& 0& 1\\ 1& 1& 0\\ 1& 1& 0\end{array}\right).$$

(8)

The Perron–Frobenius eigenvector (cf. Section 3.2) of ${\mathbf{S}}_2$ is ${\overrightarrow{\mathbf{v}}}_{PF,2}={\left[{\varphi }^{-3}{\varphi }^{-2}{\varphi }^{-2}\right]}^T$. Hence, the gaps can be labeled by integer linear combinations of negative powers of $\varphi$. Since every positive power of $\varphi$ can be reduced to a linear expression of the form ${\varphi }^g=N_g\varphi +N_{g-1}$, where $N_g$ is the Fibonacci number of generation g, and it also holds that ${\varphi }^g+{\varphi }^{-g}\in {\mathbb{N}}^{*}$, the situation can be reduced to an integral linear combination of 1 and $\varphi$. Thus, the positions of the gaps in the IDOS of a Fibonacci sequence within the WM can by given by

$$\left\{{\mathcal{G}}_n\right\}=\{n\varphi mod1,\forall n\in \mathbb{Z}\}.$$

(9)

Another interesting remark, arising from the DOS values of a single-stranded Fibonacci DNA sequence consisting of G and C, is that the ratio among the distances between DOS of consecutive generations tends to $\varphi$ [110]. The IDOS of periodic, several aperiodic, and random binary DNA sequences with G and A on the same strand, calculated within the WM, taking into account both diagonal and off-diagonal disorder is presented in Figure 3 [83]. Periodic sequences display two well defined bands, separated by a single energy gap (the largest among all cases). Thue–Morse, Fibonacci, Rudin–Shapiro, and Kolakoski sequences possesss a staircase-like IDOS, while the shape of random sequence IDOS resembles, albeit it is more disrupted, to that of Rudin–Shapiro, and its main energy gap is the smallest among all cases. The fractal, Cantor set based, sequences have a very rough spectrum. For all sequences, the value of the IDOS at the largest energy gap is equal to the occurrence percentage of A. Furthermore, it has been observed that there are steps in the IDOS, the relative value of which is equal to the occurrence percentages of the possible base-pair triplets [83]. This remark holds for all categories of deterministic aperiodic sequences, either generated by a primitive substitution matrix or not, such as Kolakoski (1,2), further connecting the specific base-pair sequence of a DNA segment with its energy structure. The above-mentioned IDOS steps and the corresponding values are marked (where possible) in the left vertical axes of Figure 3.

Apart from the sequential disorder, mentioned above, other disorder types are present or can be induced in nucleic acid sequences. In Ref. [111], the authors study single poly(CG) or poly(CT) DNA strands with diluted base-pairing, i.e., for example, the G sites are randomly attached to their complementary C sites, with a probability p. The C-G base pairs are renormalized onto the first strand, leading to two inter-penetrating lattices: a periodic one containing the G or T sites and a random one containing bare and renormalized C sites. The DOS for three indicative cases, i.e., for $p=0$, $0.5$, and 1, is presented at the top panels of Figure 4. When $p=0$, there are two well defined bands arising from the periodicity of the segment. The band character is maintained for $p=1$, with a smaller gap for poly(CG), while for poly(CT) the number of bands changes to three, reflecting the total number of different sites (since the renormalization procedure takes into account the original structure). When $p=0.5$, for poly(CG), fluctuations of the same magnitude in both allowed energy regions arise and the singularities are rounded off due to the induced disorder. For poly(CT), the bands collapse at a single energy region, stronger fluctuations are present at smaller energies than at larger ones, and there is a persisting van Hove singularity exactly at the on-site energy of T. Hence, in this case, diluted base-pairing produces a gapless structure and keeps a number of states extended (around the on-site energy of T), which is an ideal scenario for charge transport.

Several human diseases are associated with aberrant DNA methylation, which is heritable during cell division but does not alter the DNA sequence. In Ref. [112], a poly(CG) single-stranded segment is considered, with methyl groups randomly connected with the 5-carbon of C bases (forming the so-called 5-methylcytosine), again, with probability p. For completely unmethylated or methylated segments, the DOS consists of two smooth bands, derived by the on-site energy of G and C, for $p=0$, and of G and 5-methylcytosine for $p=1$, respectively; the only difference is in the energy intervals of the allowed states. For $0<p<1$, the smooth profile of the DOS is degraded, since the presence of randomly distributed methyl groups along the chain introduces a small disorder, which in turn leads to an enhancement in the effective resistance that can reach one order of magnitude.

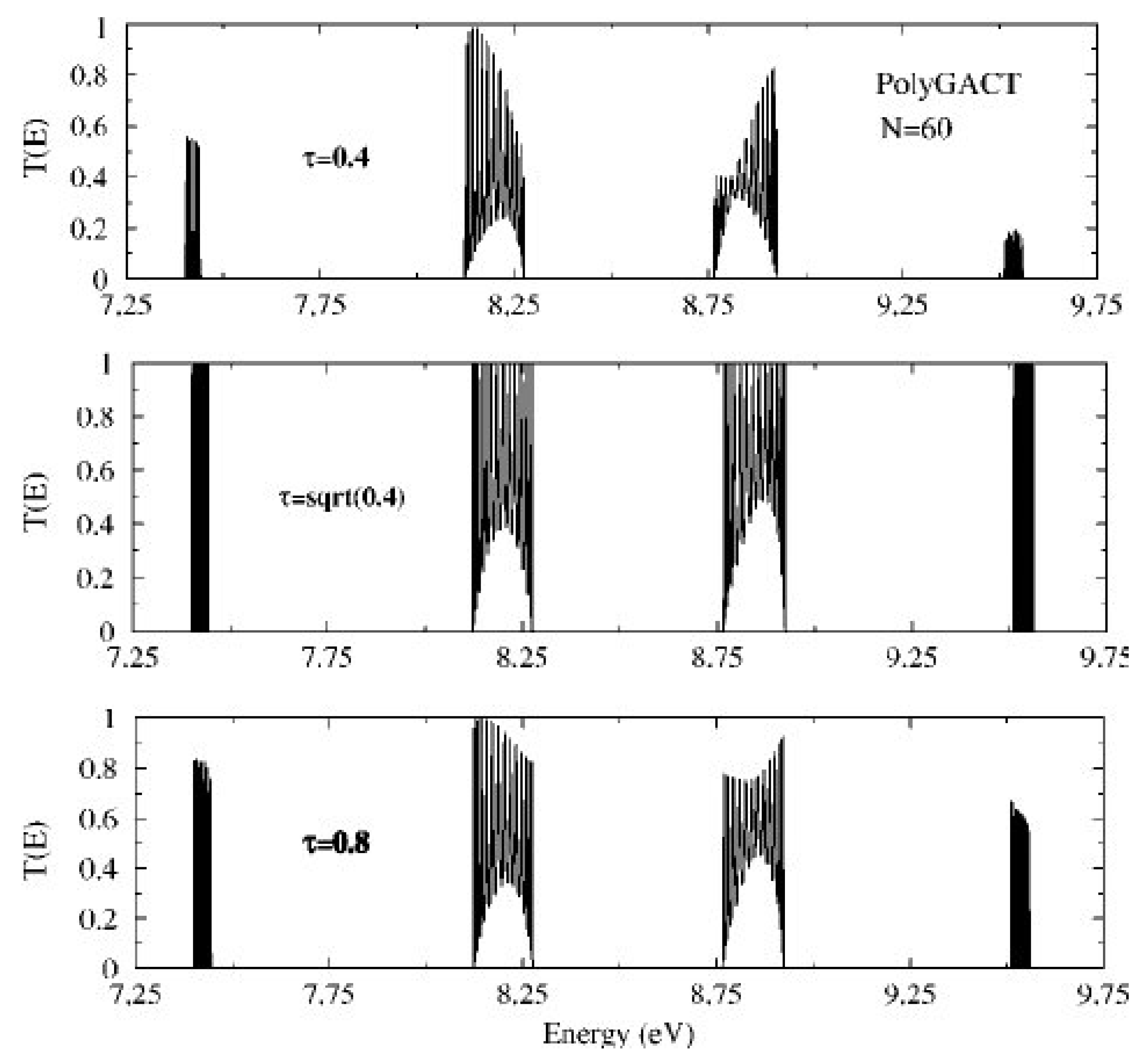
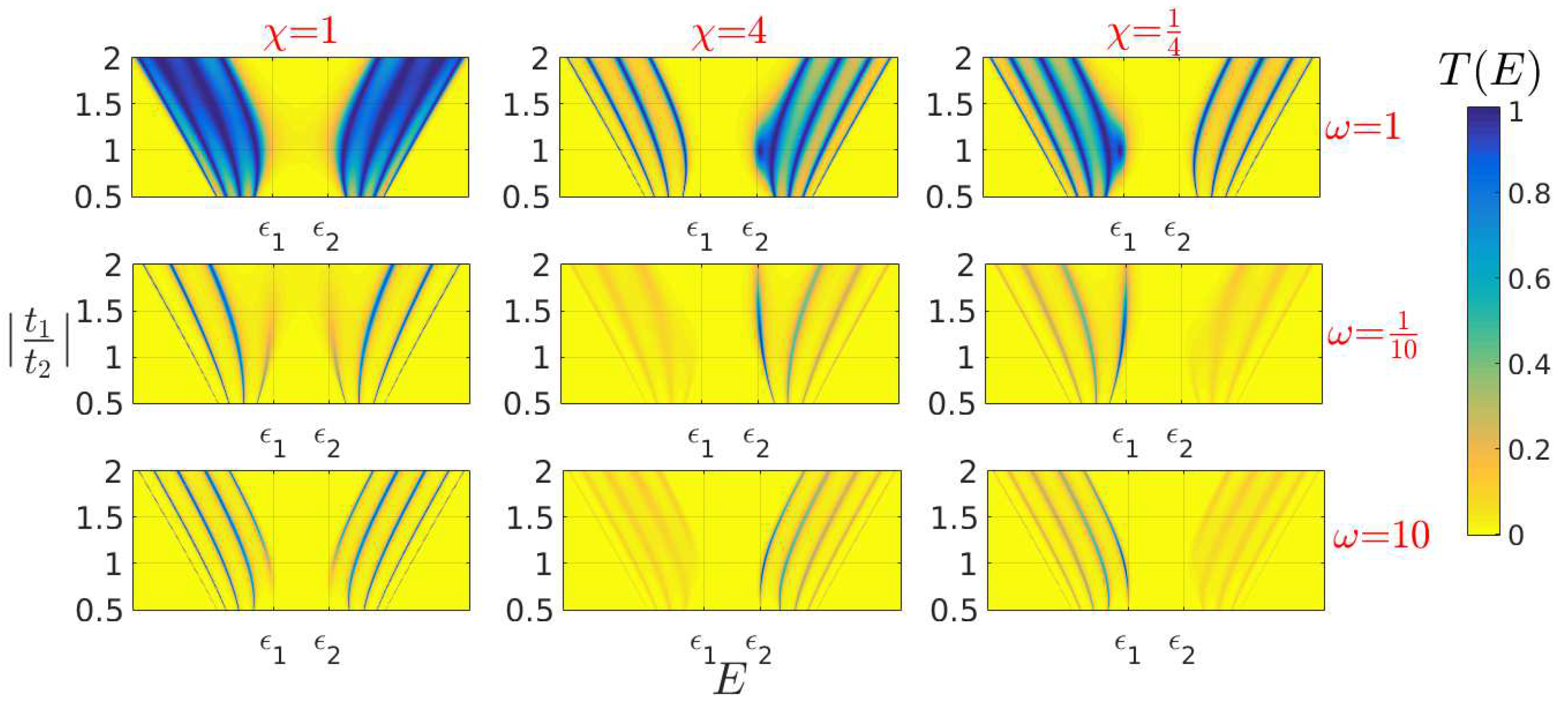
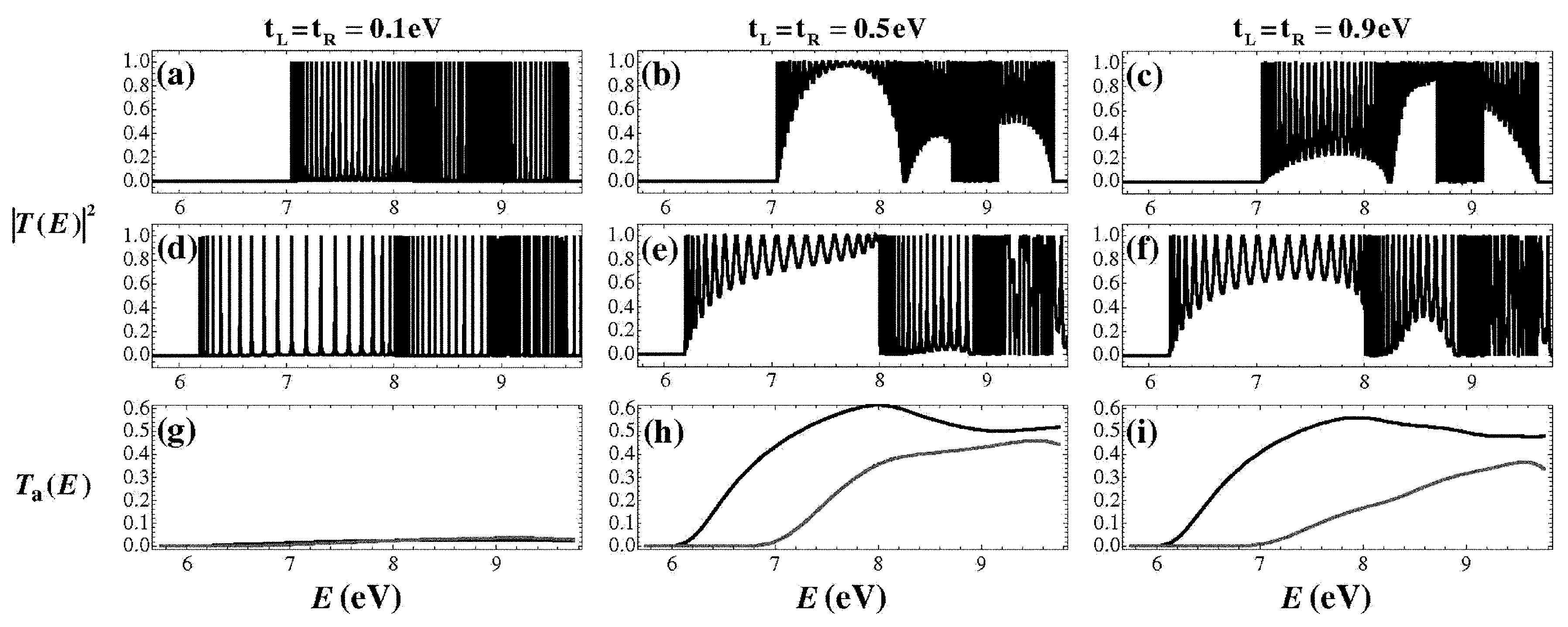
5. Coupling Nucleic Acids with Leads: Transmission Coefficients

In order to study the charge transport properties of nucleic acid nanowires within a TB framework, the system under examination is attached to two semi-infinite homogeneous metallic leads, which play the role of a carrier bath. The leads are characterized by a single on-site energy, ${ϵ}_M$, and a single hopping integral, $t_M$, so that the allowed energy states of the incident and outgoing waves lie in the interval $[{ϵ}_M-2|t_M|,{ϵ}_M+2|t_M\left|\right]$. Since detailed information on the nucleic acid’s chemical bonding at the contacts is not known, one introduces effective parameters dealing with the tunneling probability between the frontier orbitals, roughly encompassing the bonding effects at the interface [113]. These parameters are $t_{R\left(L\right)}$ and couple the left (right) lead with the nucleic acid wire.

A first useful physical quantity to evaluate the charge transport properties of a quantum system is the transmission coefficient, $T\left(E\right)$. It is an energy-dependent quantity that describes the probability that a carrier, incident to a quantum wire, transmits through its eigenstates. Charge transport will experience a sequence-dependent contribution of backscattering, according to the distribution of potential barriers, corresponding to bases or base pairs, over the length scale of the sequence [24].

The coupling between the nucleic acid and the leads plays an important role on the transmission profiles. It has been shown that stronger coupling does not necessarily mean higher transmission. In Ref. [114], the authors studied the transmission profiles of a single-stranded poly(GACT) DNA chain within the WM, with purely diagonal disorder, assuming equal coupling parameters with both leads ($t_R=t_{cL}=\mathit{\tau }$), and arrived at the resonance condition $\mathit{\tau }=\sqrt{t_{M}t}$, where t is the hopping integral between the wire sites. From Figure 5, it is evident that, when the value of the coupling parameter is either smaller or larger than the one fulfilling the resonance condition, quite smaller transmission peaks are obtained. This result properly illustrates the influence of contacts on electrical transport. This extreme sensitivity is due to interference effects between the DNA molecular bands and the electronic structure of the leads at the lead-DNA interface.

The above-mentioned results were generalized in an analytical manner for any periodic WM, through the conditions $\omega =\frac{t_M{t}_u}{t_R{t}_L}=\pm 1$ (ideal coupling condition), where $t_u$ couples the moieties at the end of a unit cell and at the start of the next, and $\chi =\frac{t_L}{t_R}=\pm 1$ (symmetric coupling condition) [60]. The ideal coupling condition, $\omega =\pm 1$, implies that the system and the leads are interconnected as if they were connected to themselves. When this condition is reached, the existence of fully resonant states is guaranteed at specific energies determined by the zeros of Chebyshev polynomials of the second kind [115]. Hence, any periodic sequence can display full transmission, if appropriate couplings are utilized. Deviations from the symmetric coupling condition give rise to secondary peaks. The effect of the coupling strength and the asymmetry factors, together with the internal hoppings, is exemplified in Figure 6, for a generic periodic WM with two sites per unit cell (hence, two hopping integrals $t_1$ and $t_2$ connect the wire sites) and $N=10$. It is evident that the ideal and symmetric coupling conditions lead to the most efficient transmission. For ideal and asymmetric coupling, except for the peaks of magnitude 1, there is one additional peak, which is of significant magnitude only when $|t_1|\approx |t_2|$. In the strong (weak) and symmetric coupling regimes, the peaks that are closer to the band gap vanish (emerge) as $|\frac{t_1}{t_2}|$ increases. When the coupling is asymmetric, transmission is enhanced only in one of the two bands.

Analogous conclusions can be obtained for more complex TB models. In Ref. [31], a poly(G)- poly(C) oligomer ($N=5$) was studied within the FM. The authors report that, for small values of coupling, the transmission shows sharp and narrow unit resonances due to the localization of states, while, as the coupling increases, the well-arranged resonant peaks overlap. An inspection of Figure 7 of Ref. [31] indicates that there are intermediate values of $t_L(=t_R)$ in which the overall transmission is more enhanced compared to smaller and larger values.

In Ref. [116], the authors study a poly(G)-poly(C) chain within an extension of the FLM, which allows hopping between backbone sites as well as all possible diagonal hoppings (between the nitrogenous bases as well as between the bases and the backbone). Each of the two strands containing the DNA bases is connected with each lead with equal coupling parameters. For diagonal hoppings being switched either on or off, it can again be concluded that stronger coupling with the leads does not necessarily lead to enhanced transmission (cf. the panels in the first two rows in Figure 7). This is also evident by comparing the averaged transmission coefficient, which is defined as

$$T_a\left(E\right)=\frac{{\displaystyle {\int }_{E_{\min }}^{E}T\left(e\right)de}}{E-E_{\min }},$$

(10)

cf. the panels in third row of Figure 7. Although $T\left(E\right)$ and $T_a\left(E\right)$ are indeed much smaller for $t_L=t_R=0.1$ eV, an increase from $0.5$ eV to $0.9$ eV does not lead to transmission enhancement. In fact, for diagonal hoppings switched both on and off, $T_a$ reaches larger values for the intermediate coupling $t_L=t_R=0.5$ eV.

The above discussion demonstrates that, apart from the internal degree of disorder of a given sequence, other factors can significantly affect their charge transport properties.

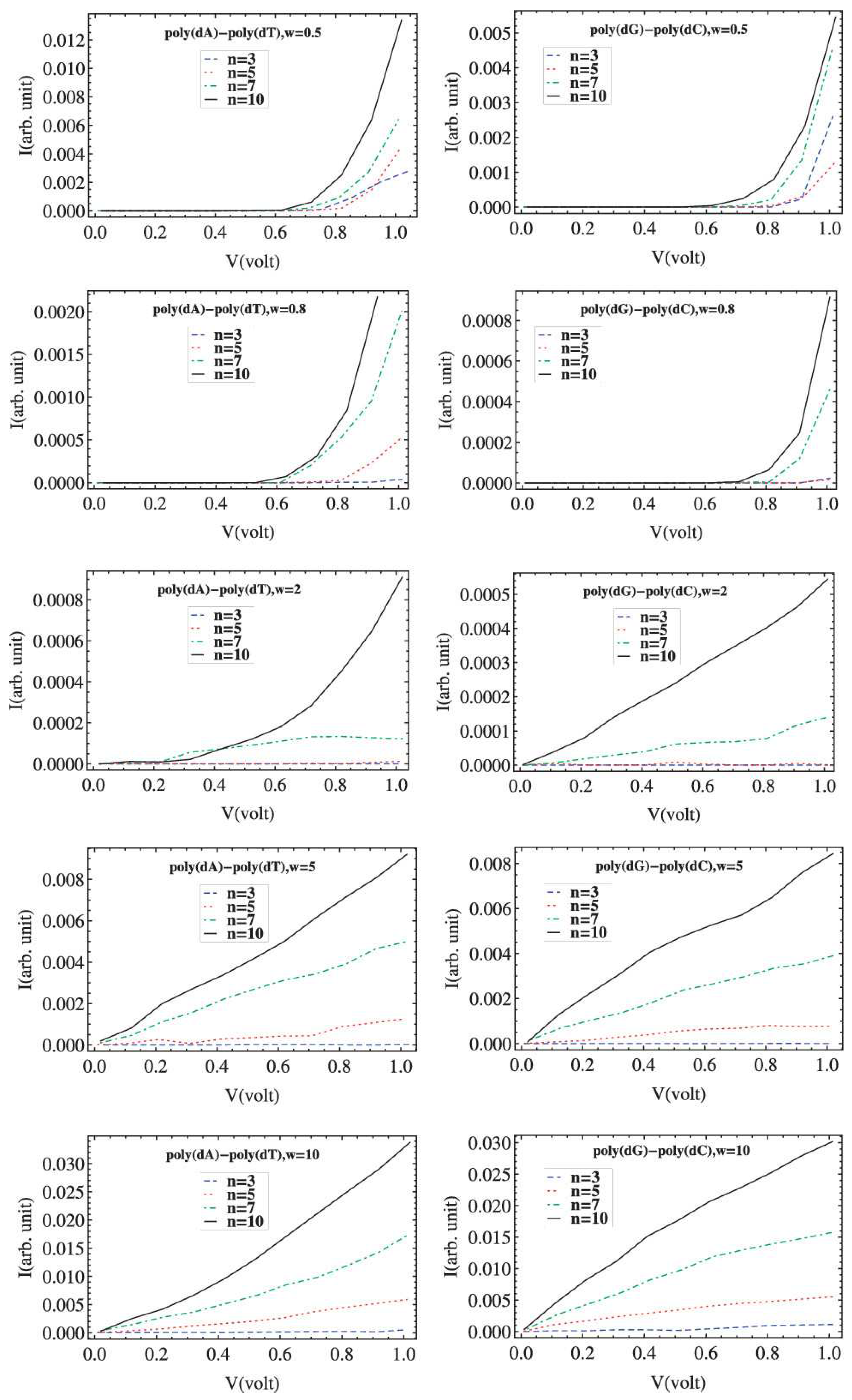
6. Current–Voltage Curves

The situation is more complex as far as the calculation of $I-V$ characteristic curves is concerned. The $I-V$ curve of a given nucleic acid segment can be given, using the Landauer–Büttiker formalism [61,117,118], by the relation

$$I\left(V\right)=\frac{2e}{h}{\int }_{-\infty }^{\infty }T(E,V)[f_L(E-{\mu }_L)-f_R(E-{\mu }_R)]dE,$$

(11)

under the assumption that charge propagates from left to right. ${\mu }_{L\left(R\right)}$ and $f_{L\left(R\right)}\left(E\right)$ are the chemical potential and the Fermi–Dirac distribution at the left (right) lead, respectively. From Equation (11), we deduce that there are several factors, apart from the structure of the sequence under examination that have an effect on the magnitude of currents, the bias regime and the shape of the $I-V$ curves. These factors include:

(a)

The choice of the Fermi level of the leads $E_F$, which coincides with ${ϵ}_M$ if one electron per site is assumed. If $E_F$ is not aligned with an allowed energy region of the segment, then no currents occur in the vicinity of $V=0$, while a metallic behavior is expected otherwise.

(b)

The way the external bias is applied. For example, only one of the leads’ energy bands can be shifted, so that ${\mu }_L=E_F+eV$, and ${\mu }_R=E_F$, or, alternatively, both leads’ bands can be symmetrically shifted so that ${\mu }_{\begin{array}{c}L\\ R\end{array}}=E_F\pm \frac{eV}{2}$. This choice affects both the way the voltage drop is induced in the nucleic acid sequence and the energy limits of the conductance channel. At zero temperature, the Fermi–Dirac distributions become Heaviside step functions and determine the limits of integration. Hence, Equation (11) can be simplified to

$$I\left(V\right)=\frac{2e}{h}{\int }_{{\mu }_R}^{{\mu }_L}T(E,V)dE,$$

(12)

while, at finite temperatures, it can be written in the form

$$I\left(V\right)=\frac{2e}{h}sinh\left(\frac{eV}{2k_{B}T}\right){\int }_{-\infty }^{\infty }\frac{T(E,V)dE}{cosh\left(\frac{E-E_F}{k_{B}T}\right)+cosh\left(\frac{eV}{2k_{B}T}\right)},$$

(13)

i.e., the $I-V$ curve occurs from the modulation of the hyperbolic function $sinh\left(\frac{eV}{2k_{B}T}\right)$ by the integral factor expression [119].

(c)

Whether or not the transmission coefficient is considered as bias-dependent. Although assuming bias-independent transmission coefficient could be a justified choice in the small bias regime, and it is indeed less computationally costly, this assumption cannot lead, under any circumstances, to the occurrence of negative differential resistance, since an increasingly larger part (as V increases) of a nonnegative function is integrated.

There are several works discussing the $I-V$ curves of nucleic acid sequences, considering different types of order or disorder. Regarding sequential order or disorder, in Ref. [83], the $I-V$ curves of periodic, deterministic aperiodic, and random binary DNA segments have been studied within the WM. The curves have been shown to have clearly distinct shapes for different sequence categories. It has also been demonstrated that periodic sequences lead to the most enhanced currents. Additionally, there are several categories deterministic aperiodic sequences (specifically, Fibonacci, Period-doubling, Cantor and generalized Cantor) that can also display significant currents, depending on the Fermi level of the leads. Random sequences represent the least efficient category, since they were found to always display smaller currents than all their deterministic aperiodic counterparts with similar base-pair content.

In Ref. [120], the authors study dry and hydrated DNA sequences with correlated and uncorrelated disorder within a WM, for $N=50$ and at a temperature of 300 K. For different concentrations of G and A sites, the resulting currents are larger for correlated disorder, both for dry and backbone-hydrated sequences. Generally, the authors report a conductor to semiconductor to insulator transition as a function of three effects, i.e., sequence size, disorder, and hydration, suggesting that an appropriate choice of chain size and relative concentration of base pairs can be used to tailor the electrical behavior of DNA strands.

A similar transition has been reported by introducing conformal variation at the helical symmetry as well as backbone disorder into a FLM [121]. Helical symmetry is taken into account via the inclusion of hopping integrals between bases in adjacent pitches (i.e., turns of the helix). The number of base-pairs within a given pitch is denoted by n. Backbone disorder is introduced by a random distribution of backbone on-site energies, characterized by a disorder strength w. The results for poly(G)-poly(C) and poly(A)-poly(T) chains with $N=50$, for different values of n and w are shown in Figure 8. At low disorder, the effect of n is smaller, since, in that case, any path of charge conduction is equivalent, as an electron feels almost no potential variation. As the disorder increases, the effect of n becomes more distinctive, since there is substantial variation of the effective potential at different sites and an increase of n gives an electron more shortcut pathways to move along the DNA chain. The current is enhanced with increasing n, and the effect is more vivid for strong disorder. Furthermore, for weak disorder, a cut-off voltage is observed in the $I-V$ curves, which reduces with increasing n. At strong disorder, the current is enhanced and almost linear response is observed at larger values of n, which indicates a transition from the insulating to the metallic phase.

Thermal structural disorder has been studied in Ref. [122], by introducing a random variation in the hopping integrals of a poly(G)-poly(C) chain with $N=5$, within an FLM allowing inter-backbone hoppings. Comparing the $I-V$ curves of such systems for $T=0$ K and $T=300$ K, the authors report that the voltage threshold for current onset is about the same, indicating that the thermal structural disorder does not affect the voltage gaps. Above that threshold, as the temperature increases, the linear behavior of the current changes to a step-like behavior, and the current is reduced, since the static distortion increases elastic scattering of electrons through the DNA molecule.

The effect of cytosine methylation disorder on the $I-V$ curves of a single stranded GAGCTGACGTTCACGG segment retrieved from the first sequenced human chromosome (chromosome 22) has been studied within the WM in Ref. [123]. The effect of all possible single, double, and triple methylation defects (out of the totally four C sites) is addressed. It is demonstrated that even a single methylated site reduces the currents by one order of magnitude. This reduction is directly associated with the fact that such sites act as additional impurity centers. The observed sensitivity of the saturation current on the position of the methylated cytosine is related to the impact of methylation on the hopping integrals to the neighboring bases. Thus, for a single methylation defect, the saturation current is strongly suppressed when cytosine is connected with guanine; for two defects, this suppression is smaller; for three methylations, the non-methylated base is the one that acts as a defect, hence the suppression of the saturation current will be larger when the cytosine has both hopping amplitudes to the neighboring bases enhanced by methylation. These results suggest the feasibility of using $I-V$ curves to develop biosensors for the purpose of diagnosis.

There also exist efforts aiming to examine the potentiality to utilize the charge transport characteristics of nucleic acids as a tool to probe several diseases or disorders. In Ref. [124], the $I-V$ characteristics of twenty seven single-stranded microRNA chains (with 21 to 23 nucleotides) related to the autism spectrum disorder have been studied. The authors classified the chains into five groups according to their conductivity (from high to negligible), suggesting that a kind of electronic biosensor can be developed to distinguish different profiles of autism disorders.

In Ref. [125], a similar treatment was employed to study DNA sequences related to the Huntington’s Disease. A segment of the human chromosome 4p16.3 was modified by the addition of a variant number of CAG repeats, the number of which determines whether a person does or does not have Huntington’s Disease; repeats smaller than 27 are normal; repeats between 27 and 35 are rarely associated with the disease, but it may expand in paternal transmission; repeats between 36 and 39 are associated with reduced penetration, so individuals may or may not develop the disease; 40 and above are associated with the disease [126]. The increasing presence of periodicity leads to enhanced transmission and thus to more efficient electronic transport. $I-V$ calculations revealed that the above-mentioned groups based on the number of repeats can be characterized by different value ranges for the saturation currents, indicating a promising method for identifying Huntington’s disease.

7. Conclusions

This review was devoted to tight-binding (TB) modeling of nucleic acid sequences like DNA and RNA. We briefly presented the TB approach and discussed its various submodels: wire, ladder, extended ladder, fishbone (wire), and fishbone ladder. We addressed various types of orders (periodic, quasiperiodic, fractal) or disorder (diagonal, non-diagonal, random, methylation) and explained how these various types of order or disorder affect charge transport. We proceeded to a discussion of aperiodicity, quasicrystals and the mathematics of aperiodic substitutional sequences. Specifically, we discussed the notions of primitive substitutions, Perron–Frobenius eigenvalue, induced substitutions, and Pisot property. We explained how the energy structure of nucleic acid wires is affected by order or disorder. We also discussed the corresponding transmission coefficients, focusing on the effects of coupling the nucleic acids to external leads, and demonstrating that, apart from the internal degree of order or disorder of a given sequence, there are several other factors that can significantly affect their charge transport properties. We also discussed the effects that various types of order or disorder induce on the current–voltage curves and presented some efforts aiming to examine the potentiality to utilize the charge transport characteristics of nucleic acids as a tool to probe several diseases or disorders. The sensitivity that the results demonstrate regarding the choice of the nucleic acids sequence, the recruited models and parametrizations, the way the systems are coupled to external leads, the nature of the leads, the environmental conditions, etc, indicate that much work is needed in order to reach a thorough description of the effect the combination such a multitude of factors has on charge transport. Furthermore, other factors, such as the sequence geometry or the use of modified nitrogenous bases could be potentially used to tailor the above-mentioned properties of nucleic acids and analogues.