Abstract
Nowadays, with rapid advancement of both the upcoming 5G architecture construction and emerging Internet of Things (IoT) scenarios, Device-to-Device (D2D) communication provides a novel paradigm for mobile networking. By facilitating continuous and high data rate services between physically proximate devices without interconnection with access points (AP) or service network (SN), spectral efficiency of the 5G network can be drastically increased. However, due to its inherent open wireless communicating features, security issues and privacy risks in D2D communication remain unsolved in spite of its benefits and prosperous future. Hence, proper D2D authentication mechanisms among the D2D entities are of great significance. Moreover, the increasing proliferation of smartphones enables seamlessly biometric sensor data collecting and processing, which highly correspond to the user’s unique behavioral characteristics. For the above consideration, we present a secure certificateless D2D authenticating mechanism intended for extreme scenarios in this paper. In the assumption, the key updating mechanism only requires a small modification in the SN side, while the decryption information of user equipment (UEs) remains constant as soon as the UEs are validated. Note that a symmetric key mechanism is adopted for the further data transmission. Additionally, the user activities data from smartphone sensors are analyzed for continuous authentication, which is periodically conducted after the initial validation. Note that in the assumed scenario, most of the UEs are out of the effective range of cellular networks. In this case, the UEs are capable of conducting data exchange without cellular connection. Security analysis demonstrates that the proposed scheme can provide adequate security properties as well as resistance to various attacks. Furthermore, performance analysis proves that the proposed scheme is efficient compared with state-of-the-art D2D authentication schemes.
1. Introduction
Device-to-Device (D2D) communication is defined as a promising short-distance communicating strategy, which is capable of directly conducting effective data exchange among the proximate entities without involvement of the cellular core network. As for conventional cellular networking services, connectivity between the mobile devices is subjected to the coverage of access point or base stations, where direct communication among mobile devices is not offered [1]. Instead, all the involved traffic floods should be processed through the core cellular network, which severely restrains the large-scale implementation of massive and reliable data exchange between mobile devices. In this case, D2D communication is capable of complementing the traditional cellular network strategy by leveraging the physical proximity of participating devices, which is essential in sparse environments [2].
D2D communication performs as the vital component in the upcoming 5G mobile networks and wireless systems [3,4], which is anticipated to support the deluge of data traffic. Accordingly, the network performance regarding effective coverage, spectrum efficiency, real-time network delay and transmission fairness can be significantly improved. Various emerging D2D applications scenarios regarding social networking and local information aggregating have been widely implemented. Particularly, its combination with Internet of Things (IoT) enables extensive services including vehicle-to-vehicle (V2V) communication, smart grid and early warning systems for natural disasters like hurricanes and earthquakes [5].
Currently, various D2D communicating infrastructures have been designed and investigated by the Third Generation Partnership Project (3GPP), which can be classified into standalone D2D and network-assisted D2D [6]. Standalone D2D communication fully depends on the local hardware capabilities, where the D2D devices organize the interaction themselves. In contrast, the network-assisted D2D network operates with the assistance of certain infrastructure, such as a base station or access point for cellular connection. In typical D2D infrastructure, the user equipment (UE) is considered one of the essential components, which performs as mobile devices operated by terminal users themselves. It can be a portable cellphone or a laptop computer with a wireless broadband adapter.
Due to the open wireless connecting features [7,8,9], D2D data exchange suffers from various security risks and privacy threats, especially in the D2D group communication involving large numbers of participating devices. It is worth emphasizing that the security and privacy requirements vary for different D2D management and application scenarios. In this case, advanced security strategies and privacy preservation techniques are vital for general D2D environments [10]. Effective and efficient authentication mechanism between user equipments (UEs) and the regarding base station (BS) could provide preliminary protection for D2D data exchange, which is particularly essential for group communication. Accordingly, various charted and uncharted secure threats including eavesdropping, impersonation and replaying can be prevented, which is indispensable for the upcoming 5G practical implementation.
Currently, emphasizing the D2D secure authentication issue, lots of research achievements have been made, adopting diverse cryptographic design and verification methods [2]. Note that in some, the key information for individual UEs are fully organized by the key generation center (KGC), resulting in a potential key escrow problem [1,11]. For this consideration, it is of great importance for the UE to independently generate its own partial key information and keep it secret from all other entities including the KGC. For this consideration, the certificateless encryption outperforms other methods by generating the partial secret key from both the KGC and the UE itself. Note that both the KGC and the UE have no access to the partial secret generated by the other party.
Additionally, with multiple advanced features and functionalities, smartphones have played a significant role in our daily lives [12]. Generally, the modern smartphone is equipped with various built-in sensors including an accelerometer and a gyroscope, which are capable of unobtrusively collecting abundant personal biometric data whenever the user conducts daily activities such as sitting, sleeping, running, and walking [13]. Particularly, the gathered personal activity data reflects certain users’ unique characteristics, which can be adopted for continuous authentication.
We assume a particular D2D scenario intended for public safety or field trip applications for extreme environments, where the smartphone acts as the UEs for every terminal user [14]. In most of the isolated nature landscapes including the mountainous regions, desert areas, or tropical rainforests, infrastructures for a cellular network are not always available, especially in the depopulated zones. That is, most of the UEs are not within the cellular coverage. In this assumption, the D2D communication between UEs could provide real time communication for individual users within this area [15,16]. The BS is able to interact with certain UEs and provide cellular connection for all the participating UEs within the D2D network. As for individual users with UE, vital biometric data including accelerometer and gyroscope signals are acquired by the smartphone sensors, revealing personal behavioral features. Subsequently, the user’s behavioral patterns can be adopted for continuous authentication. That is, after the initial authentication operation, the specific verification is conducted periodically for the purpose of guaranteeing secure data transmission throughout the entire process. Therefore, through analysis of a user’s behavioral patterns, continuous authentication can spot vulnerabilities at any point in a session [17]. Note that the above assumption is suitable for both field trip assistance and emergency rescue. The detected anomaly feature demonstrates certain distinctness from existing personal record. That is, the user may encounter unexpected physical danger that causes severe deterioration of health, which is of great significance for real time healthcare monitoring and subsequent emergency aid in complex circumstances [6].
In this paper, a secure certificateless authentication scheme for D2D communication is presented. The nontrivial contributions of this paper can be briefly summarized:
- Secure certificateless authentication scheme: According to our design, a certificateless cryptography mechanism is applied so as to provide improved security assurance. BS and UE itself generate the partial private key respectively so as to prevent the key escrow problem of identity-based encryption. Moreover, conditional privacy-preserving authentication (CPPA) is deployed. That is, the user anonymity is provided through the entire authentication session, preventing illegal tracing towards particular UEs, while the valid identity-related information is recorded in BS side in the preliminary registration phase. Hence the tracking and revocation towards malicious UEs can be conducted by trustworthy authority. Additionally, bilinear pairing is adopted in order for advanced security properties.
- Efficient Group key distribution with updating mechanism: During the authentication process, the allocated group key computed by BS will be delivered to all legitimate UEs through one broadcasting operation, which drastically alleviates the communication cost compared with conventional one-to-one key distribution. Note that only the authentic UEs have the capability of deriving the valid group key. Therefore, the designed key updating mechanism only require small modification in the BS side, while the decrypting information in the UEs side remains constant as soon as the UEs are validated. Similarly, fast UE revocation process can be operated by BS without extensive computation.
- Continuous authentication strategy adopting smartphone sensor behavior analysis: The unique user behavioral data acquired by accelerometer and gyroscope sensors in smart phone (UE) is processed and characterized by time and frequency domain features. Subsequently, appropriate activity recognition implementation is conducted, where the individual behavior profile is evaluated with the pre-defined biometric parameter to reveal the real-time personal activity level. In this case, continuous authentication is performed with the adopted biometric parameter periodically. Security analysis demonstrates that the proposed scheme is able to provide adequate security assurance. Moreover, performance analysis proves that the proposed design is efficient compared with the state-of-the-art authentication schemes. To the best of our knowledge, we are the first to design the D2D authenticating and key distributing method with biometric continuous authentication. Potential scenarios include disaster rescue and medical aid in harsh environment.
The remaining contents of the paper are constructed as follows. Section 2 briefly introduces the corresponding research achievements. Section 3 illustrates the significant preliminaries and the designed system model so that the reader is able to acquire a better understanding. Section 4 introduces the proposed D2D certificateless authentication scheme in detail. Section 5 presents the proposed continuous authentication strategy. Section 6 proves the formal security analysis. Section 7 demonstrates the performance analysis. Finally, the conclusion is drawn in Section 8.
2. Related Works
As the underlay to the upcoming 5G networks, the development of D2D communication has attracted a lot of attention from both academia and industry. Major research regarding radio resource allocation [5], mode selection [1] and interference management [2] have been widely studied, while only a few works have been done emphasizing on the security and privacy protection for D2D communication in both the academic and standardization communities. In 2014, a detailed survey emphasizing on the D2D infrastructure, the major threads and security requirements [3] is presented by Alam et al. After that, Yue et al. initially illustrated the D2D communication into information-theoretic secrecy problem of cellular communication, where the secrecy outage probability is utilized to depict the uncertainty of the eavesdropper [18]. Subsequently, a secure data sharing scheme SeDS is designed for D2D communication in LTE-A network, where the public-key-based digital signature is applied for mutual authentication. Note that the proposed SeDS is capable of detecting free-riding attack and achieving reception nonrepudiation by key hint transmission so as to improve system availability [19]. Similarly, due to the potential threats caused by the open access feature of wireless channel, Shen et al. designed a short authentication-string-based key management scheme for secure D2D communication over WiFi direct [4]. In Reference [20], the spatiotemporal matching is formulated, which is considered to be the crucial primitive for D2D communications. Note that the Bloom filter is adopted during the estimation process as well.
The combination between D2D communication and 5G network enables a new research direction. The structure intended for the LTE-D2D system and its corresponding security threats are discussed in Reference [6] by Zhang et al., where the frameworks for cross-layer D2D security are designed. In 2017, a robust D2D-assisted secure transmission scheme for mobile healthcare system is introduced, where certificateless generalized signcryption (CLGSC) is deployed. Meanwhile, Waqas et al. investigated the physical layer security for secure key generation rate (SKGR) among D2D communication. In order to prevent attack from both the eavesdropper and non-trusted relays, the related privacy protection scheme is conducted [21]. Subsequently, Kim et al. designed a secure link establishing protocol for LoRaWAN D2D communication, where the D2D nodes share cryptographic keys with each other. The proposed scheme is able to guarantee fundamental security requirements with sufficient feasibility [22]. Next, in order for device recognition in D2D communication, the advantage of RF fingerprint of wireless D2D device is taken into consideration in Reference [7]. Note that the support vector machine (SVM) is deployed with the purpose of classifying all the activated devices.
Recently, Wang et al. presented the privacy-preserving authentication and keying schemes PPAKA-HAMC and PPAKA-IBS so as to offer reliable anonymous D2D communications [9]. According to their assumption, the D2D user group members mutually authenticate with each other using the anonymous identity. The group session key for secure D2D communications is built accordingly. For the same purpose, Hsu et al. presented network-absent and network-covered authenticated key exchange schemes, where the authentication process is evaluated under the analytic model, proving that the proposed schemes satisfy proper performance requirements [12]. Moreover, another reliable D2D key distribution protocol is proposed in Reference [10], where the information exchange is conducted through the RF channel and the audio channel.
Furthermore, advancements in human activity recognition regarding smartphone sensors have been presented, which provide a new paradigm for daily health monitoring compared to the initial recognition mechanism with wearable sensors. In 2010, Kwapisz et al. [17] adopted phone-based accelerator data for human activity recognition, where six daily activities from 29 volunteers are involved. Note that the time series data are segmented into examples over 10-s example duration (ED), achieving accuracy over 90% for most activities. Similarly, Sun et al. [23] developed a SVM-based classifier for recognition over seven common physical activities. Both the time- and frequency-domain information are taken into consideration. Subsequently, Shoaib et al. [24] evaluated thoroughly the impacts of various types of sensor data and demonstrated that performance improvement is available by combining individual parameters together.
The health status measurement and prediction can be achieved with the user behavior profiles generated by smartphone sensors. Hence, several existing studies have been conducted, emphasizing practical applications for medical purposes. In Reference [25], the data derived from accelerometer are processed to measure the behavior regarding a patient’s actual stress levels, indicating the generalized and prosperous utilization for healthcare environment with smartphone sensor data analysis. Thereafter, Kelly et al. [14] developed a health status measuring design so as to objectively monitor the real-time physical condition of patients, which provides a unique approach for the clinicians to conduct in-time treatments.
Specifically, the studies on continuous authentication combing user’s behavioral properties have been presented in existing papers. Shen et al. [13] emphasized on the reliability on the usage of motion-sensor behaviors for continuous authentication conducted on smartphones. Subsequently, several human activity recognition for authentication purposes have been proposed [15,26]. Accordingly, continuous authentication towards identification for smartphone users is performed in our authentication scheme, resulting in advanced security properties.
3. Preliminaries and Model Definitions
The necessary preliminaries utilized in this paper are described with the intention of facilitating the reader’s understanding on the proposed method, which includes the definitions of bilinear pairing, the DBDH problem and hash function. Thereafter, the notations, system model and network assumptions are respectively introduced.
3.1. Bilinear Pairing
Let , and be multiplicative cyclic groups with the prime order . A map function is defined as the bilinear pairing if the following three properties is satisfied:
- Bilinearity: , , , there is .
- Non-degeneracy: , , there is .
- Computability: , , there exists an efficient algorithm so that can be calculated.
Definition 1 (Decisional Bilinear Diffie-Hellman (DBDH) Problem).
Given a tuple for , output 1 if and 0 otherwise. is defined as a probabilistic algorithm. Hence the advantage in solving the DBDH problem is defined as:
where and g is a random generator in . If all probabilistic polynomial-time (PPT) algorithms have the negligible advantage in solving the DBDH problem, the DBDH assumption holds in the related bilinear map .
3.2. Hash Function
A secure one-way hash function is defined with the following properties [27]:
- Given a input message x of arbitrary length, the message digest of a fixed length output can be calculated accordingly.
- Given y, it is difficult to calculate the value of .
- Given x, it is computationally infeasible to find such that .
3.3. Notations
The major notations appeared in the proposed scheme are introduced, along with the brief description in Table 1.

Table 1.
Notations.
3.4. System Model
In the assumption, the whole D2D infrastructure is composed of service network (SN) and multiple user entities (UEs). The utilized structure of the proposed D2D authentication architecture is introduced in Figure 1, which is considered as the specific D2D communication scenario devoted to public safety and emergency rescue in the wild. Potential occasions include most of the isolated nature landscapes such as the mountainous regions, desert areas, tropical rainforests or vast oceans [28], which account for comparatively large proportions of the Earth’s surface in total. Most of the regions are depopulated zones. On the other hand, due to the complex and hostile environmental characteristics, it is technically difficult for the involving countries to construct even the basic infrastructure for cellular network coverage in these areas, which requires huge amounts of financial grants. In these regions, few cellular network facilities such as base stations are available, most of the areas are not in the cellular coverage. In this assumption, D2D communication between user entities (UEs) are necessary so as to substitute the cellular connection from the base station. For example, a group of tourists are intended to go hiking in the mountains, where cellular coverage is not available in most of the spots. In this case, interactions between the tourists highly depend on the self-constructed D2D communicating network. It is worth nothing that some UEs are within the effective range of base station. Hence, cellular connections can be achieved for all the participating UEs over the D2D network, even though the UEs are not within the cellular coverage. The corresponding description of service network and the user entities are respectively illustrated below.
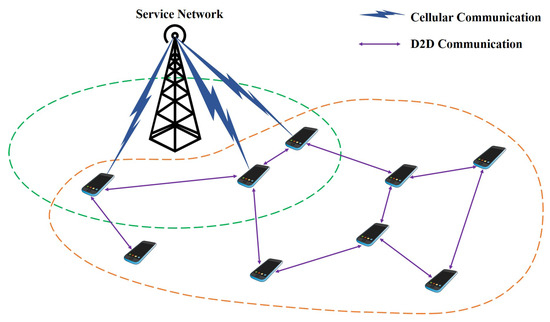
Figure 1.
System Model.
The service network (SN) is assumed to be the powerful controlling center for the whole D2D system. SN takes the responsibility of conducting main operations including system initialization, initial registration, key generation and management, identity verification. In the proposed design, SN is designed to be resistant to all kinds of attacks and remains authentic anytime. In the proposed scheme, as the role of SN are taken by the commercial organizations, it cannot be fully trusted. We consider the SN to be an honest-but-curious authority, where the essential key generation and identification processes are all conducted accordingly. Note that the partial private key is only generated for the registered UEs, while the individual UE is designed to generate the remaining partial secret key itself. The key escrow issue is avoided accordingly. Particularly, SN also offers direct cellular connection for the validated devices within its effective range, while the devices beyond its coverage can acquire cellular access indirectly. In our design, SN can be considered as the combination of cellular base station and validated verifier at the same time.
The user entities (UEs) are designed to be the terminal user of the D2D communication. In the proposed system model, UE refers to the personal smartphone of users. In harsh environment, UEs are involved in the data transmission that is routed over the SN and D2D network structure. That is, the participating UE not only delivers the messages generated by itself, but also forwards the routed information originated from other UEs. As for certain UEs, its interaction with neighboring devices provides high connectivity to all the remaining UEs, even though some devices are out of the SN cellular coverage. It is worth noting that the UEs should be authenticated before accessing the D2D network for security assurance. Besides, the UE (smartphone) is equipped with various behavioral sensors such as the accelerometer and gyroscope. Therefore, vital biometric data can be collected by the smartphone sensors, revealing the personal behavioral features. In our design, the user’s unique behavioral patterns are applied for continuous authentication. That is, after the initial authentication operation, the specific verification is conducted periodically for the purpose of guaranteeing secure data transmission throughout the entire process. To be concluded, the UEs perform as both the D2D terminal device and biometric data collector as well.
3.5. Network Assumptions
As shown in Figure 1, SN is assumed to have full authority to access the entire D2D communication system, where the UEs within its cellular coverage can operate communication directly with SN without additional assistance. Note that these UEs are considered the major devices in the entire D2D network, where both the cellular links and D2D links can be maintained. Moreover, the remaining UEs are beyond the effective range of SN, thus requires the major devices to forward messages to SN. An integrated D2D network is constructed involving all the participating UEs. Communication between the UEs is provided in this way. Additionally, a universal group communication channel is indispensable for message broadcasting to all users.
Due to the inherent wireless characteristic, D2D data exchange suffers from D2D data exchange suffers from various security risks and privacy threats, especially in the D2D group communication involving large numbers of participating devices. The transmitted information may be eavesdropped, impersonated, and even altered illegally. In this case, advanced security strategies and privacy preservation techniques are vital for the proposed D2D scenario. Proper authentication mechanism should be deployed so that the identities of the requesting UEs are verified before accessing the D2D services. Subsequently, the unique group key shared between SN and all legitimate UEs should be generated and allocated, ensuring the secure broadcasting channel for emergency use.
In addition, after being successfully verified, the continuous authentication is of great significance, where periodical validation is activated. In this case, the compromised and disabled UEs can be detected and removed accordingly, offering resistance to various insider attacks. Note that essential behavioral characteristics derived by the user’s smartphone (UE) is adopted in the continuous authentication process.
4. Proposed Secure Certificateless Group Authentication Scheme for D2D Communication
With the purpose of providing an enhanced authentication scheme to D2D communication in specific scenarios, the certificateless group authentication scheme is presented in this paper. For a better description, the proposed scheme is divided into certificateless authentication with group key distribution and the subsequent continuous authentication utilizing smartphone sensor behavioral processing. In this section the former part is illustrated, while the latter part is presented in the following Section.
The certificateless authentication and group key management method is presented, which mainly emphasizes on the verification for participating UEs. Our authentication design can be briefly divided into three different phases including offline registration phase, authentication phase, and group key distribution phase. Initially, the UE registration, along with vital key initialization, is made in the offline registration phase. Consequently, significant authenticating procedures are provided in the authentication phase. Thereafter, the group key is distributed in an efficient and reliable way. Moreover, the strategy for efficient key updating is also introduced, offering dynamic membership management for UEs. Certificateless encryption technique is applied for mutual verification between SN and UEs, where the key escrow issue can be drastically addressed. The proposed certificateless authentication for D2D communication is suitable for practical D2D scenarios in complex environments.
4.1. Offline Registration Phase
The offline registration phase is designed for the D2D initialization, which can be divided into the essential key information management and UE registration.
Initially, on inputting the security parameter , SN first generates a bilinear group , where is defined as a -bit prime, and denote two multiplicative cyclic groups with the prime order . Hence the bilinear map is constructed in the form of . SN selects the generator and randomly chooses as the system master key. Note that is defined as a non-negative integer set less than the prime number .
Subsequently, each UE is a prerequisite to register to SN in offline mode, where the confidential user information including name, address, phone number are correspondingly recorded in SN server securely. Meanwhile, the unique license is assigned to each legitimate UE and stored in the tamper-resistant module constantly during the entire operation. Note that and , where t is defined as the total number of the registered UEs for the D2D network. Hence the D2D device set is defined as . Moreover, the secure cryptographic hash functions , , and are defined.
For each , SN first computes , then randomly chooses and , where . The following computations regarding and are conducted in SN side:
Thereafter, the confidential message is allocated to specific UE with identity . It is worth noting that in our design the delivered for are considered as the partial key generated by SN, while the generated is not revealed to any other entities during the entire authentication process. In this case, for , the key set regrading t participating UEs will be one-to-one corresponded to the concerning , which will be securely recorded in SN side.
In this way, the offline registration for D2D authentication is completed. All the registered UEs store the unique partial secret key , and the intermediate value for following authentication in the next phase.
4.2. Authentication Phase
In this phase, the essential communication rounds between SN and UEs are conducted with the purpose of providing valid D2D verification. The group authentication process is assumed to be initialized with one broadcast conducted by SN. That is, SN computes the public key to be broadcast as:
where is the system master key generated in the previous registration phase. Thereafter, SN broadcast to all entities, where the authentication request, along with the public key is delivered.
After receiving the request, each UE adopts the stored , along with the derived to verify whether the following formula holds:
The correctness of the above equation follows from direct verification of the equalities below:
where the security relies on the DBDH assumption. If the equation does not hold, UE terminates the process and abandons the received message. Otherwise, UE randomly generates its own partial secret key and computes
for subsequent verification. In this case, the full secret key set of UE is denoted as , which are respectively generated by UE and SN. Moreover, the previous calculated authentication result of is stored as . Consequently, the temporary identity of UE is derived as
Additionally, the certificate involving the aforementioned information can be calculated as
which is transmitted to SN in the form of .
It is worth nothing that, due to the broadcasting feature, multiple replying messages are transmitted to SN simultaneously. Hence SN first compares the received with its database in order to search for the matched UE. Note that the corresponding values are computed and stored previously so that repetitive operations are prevented. Thereafter, SN checks the correctness of the received , where can be acquired according to . If it matches, SN computes
which will be used in the subsequent group key distribution phase.
4.3. Group Key Distribution Phase
In our design, a commonly shared secret key is allocated to provide universal group communication channel between SN and all the legitimate UEs. In this way, message broadcasting is available for practical applications such as emergency rescue. Instead of delivering the keying message to individual devices one by one, SN conducts a one-time broadcast to all, offering a more efficient way for key distribution.
It is assumed that t UEs () has passed the previous verification in SN side. Hence the group key should be successfully delivered to all UEs, while the outsiders cannot derive the group key through eavesdropping. Accordingly, for , SN computes
which involves the UE partial secret key and SN information as well. Hence is one-to-one mapped to certain UE with . With the calculated set , SN randomly generates the group key and constructs the following function:
which can then be further illustrated as
where are the coefficients composing the formula. It is worth nothing that for , holds. Subsequently, SN computes
and delivers the following packet to all.
Upon receiving the packet, the correctness of ℘ is validated, as well as the following equation:
At this point, all the UE are able to construct according to the derived coefficient set . In this case, UE computes its corresponding
and adopts into
where the distributed group key is derived in UE side. Note that the coefficient set are distributed in plaintext, indicating that all devices can build the formula . However, only the validated UEs can acquire the correct group key with self-computed . In this way, the group key is preserved.
At this point, the group communication channel is enabled by utilizing the group key . For two strings a and b, let represents the first ℓ bits of a, represents the concatenation of a and b. Hence the following one-time-pad format can be applied for D2D transmission:
where denotes the current timestamp. Moreover, the length of hashed value is defined as ℓ, the length of the transmitted message is defined as with , exclusive disjunction is conducted between message m and the first bits of hashed value, while the remaining bits is used for validation by the receiver. The destination devices can easily decrypt it and derive m, where the hashed value is used as the symmetric key for both encryption and decryption. Hence, the group key is successfully distributed, D2D secure transmission is provided in this way.
4.4. Group Key Updating Strategy
In the proposed centralized scheme, group key updating is provided in an efficient way, which requires comparatively small efforts in the SN side. Note that further communication rounds with the participating devices are not required. Respectively, let denote the UE identity to be revoked, denote the newly joining device identity. The key updating involving multiple UEs can be achieved in the following step:
For device revocation, SN removes the related from the stored set and choose a new group key . Hence the function is built as
In this way, , indicating that the revoked device cannot acquired the updated group key. For , holds. Hence the remaining UEs can directly derive the updated group key with the current . Extra information for key distribution is not required for SN and all the legitimate UEs.
The process for newly joining UE is similar. After successful authentication, SN computes the corresponding related to and adds it to the set , Hence the new function is built as
where denotes the newly generated group key. Obviously, for , holds. All the valid UEs can acquire the update group key in this case.
It is worth nothing that the presented key updating strategy is able to provide efficient group key updating involving multiple UEs simultaneously. That is, SN organizes the newly generated key information with only one broadcasting. The revoked UEs cannot acquire the updated key according to the keying message due to the removal of from function. Similarly, the newly joining UEs can acquire the updated group key using the computed .
5. Proposed Continuous Authentication Method
In the aforementioned section, the certificateless authentication and group key distribution scheme is introduced with the purpose of offering validated D2D communication channel. However, the authentication event is only conducted prior to the entire communication process, while the entire communication process is still vulnerable to all kinds of attacks and security risks. Therefore, the continuous authentication with behavioral biometrics is adopted in our scheme, providing the new perspective to dynamically and periodically detect the anomalies during the entire user session. Intuitively, the regarding steps are conducted as follows.
5.1. Sensor Data Preprocessing
In our design, user’s smartphone is deployed as the terminal device for D2D authentication, as well as the essential entity for continuous authentication. The embedded tri-axial gyroscope and accelerometer of smartphone are capable of capturing massive linear acceleration and angular velocity data, which distinctively reveals the different activities operated by the user.
Subsequently, de-noising on the acquired raw sensor data is enabled. The following cubical smoothing algorithm with five-point approximation is utilized:
where denotes the five adjacent points of data series, are the output of the filtering operation. Note that the computation cost towards the cubical smoothing algorithm is comparatively small, thus it is suitable for the resource-limited smartphone devices. The filtered continuous sensor data are then separated into a number of sliding windows for the further training process. Note that the generated windows are half overlapped in our design. Subsequently, the segmented time window is further divided into action frames regarding to certain motion, where cycle detection is adopted with the purpose of characterizing specific data points in the acceleration sequence of each time windows.
5.2. Feature Extraction
Intuitively, the entire biometric data processing operations are carried out inside the individual smartphone, which is resource and power limited. Hence critical features with less complex computing requirements are adopted. Initially, the acquired three-axis gyroscope and accelerometer data are denoted as and respectively, indicating the measures of angular velocity and acceleration in X-axis, Y-axis and Z-axis. In this case, the magnitude of acceleration and angular velocity signals are respectively calculated as
Accordingly, a set of time and frequency domain sensor data features are calculated:
- and : The maximum and minimum value of input x.
- : The mean value defined as:
- : The overall standard deviation defined as:
- : The skewness of x defined as:
- : The kurtosis of x defined as:
- : The correlation between each pair of axes of the sensor data:
- : Interquartile range of input x.
- : Frequency domain feature of input x.
Thereafter, standard normalization towards the extracted features is conducted before the training process, which is achieved as
where z denotes the normalized output, and are respectively defined as the mean value and standard deviation of specific features.
5.3. Classification and Authentication Design
SVM (Support Vector Machine) is defined as the classifier formally defined by a separating hyperplane. In the supervised learning, with a set of training examples marked as one of the two given categories, SVM algorithm is able to construct the model that assigns new examples to one of the two categories. Based on this, the LibSVM [29] is adopted in our design for multi-class classification, where the radial basis function (RBF) kernel is utilized for core experiments of our study. Intuitively, the entire procedure is conducted independently from others. The personalized classification model is built for each participant. The subsequent evaluation is conducted using the personal testing samples.
At this point, a personalized model for individual participant is constructed locally, where the training data characterize unique behavioral patterns within a relatively long interval. Intuitively, for participants in certain area, similar activities are performed accordingly, indicating unique environmental characteristics. Hence the major performed activities types are denoted as , where . Consequently, the ratio of specific activity among all the detected actions within certain time interval is defined as , which is presented in the form of biometric parameter . Note that for various participants, varies. is then securely transmitted to SN right after the initial successful certificateless authentication process. Subsequently, UE periodically updates its biometric parameter and transmits it to SN. Hence the statistical significance involving the previous data and the fresh data are conducted so as to measure the variation, where the significance level is set to be . If anomalies detected, SN resets the stored keying information of certain UE and requests re-authentication from specific UE. Finally, after each validation, the stored parameter set is updated using newly acquired value so as to timely reveal the recent biometric status of user. It is worth noting that the parameter checking process is performed at set intervals, thus continuous authentication is achieved.
6. Security Analysis
In this section, the security analysis towards the proposed certificateless authentication scheme is presented. The security theorems as well as the corresponding proofs are given below.
6.1. Resistance to Forgery Against Adaptive Chosen Message Attack
Definition 2
(Forking Lemma [30,31]). Let be a probabilistic polynomial time Turing machine, given only the public data as an input. Within a certain time bound , if can produce, with non-negligible probability, a valid signature , where the tuple can be simulated without knowing the secret key. In this case, with an indistinguishable distribution probability, there is another machine which has control over the machine obtained from replacing interaction with the signer by simulation and produces two valid signatures and such that .
Theorem 1.
The proposed certificateless authentication protocol could resist forgery towards adaptive chosen message attack in the assumption of random oracles , , .
Proof of Theorem 1.
The security of unforgeability can be formally defined under the game . Let be a probabilistic polynomial time adversary. In this assumption, is able to break the proposed scheme. In this case, it is claimed that by conducting the following queries from adversary , the challenger is capable of making use of to break the randomness of , , oracles’ outputs. Note that in the constructed game , the used hash functions represent the random oracles. Accordingly, the hash lists are maintained by . We assumed that is able to simulate all the oracles. The following steps to can be operated by :
- Setup Phase. chooses the bilinear group of prime order , as well as the generator . Thereafter, randomly chooses the system master key and computes accordingly. The public parameters are delivered to , where , , and are defined as random oracles controlled by . Similarly, is defined as the anti-collision hash function. Note that the system master key is kept secret from the adversary .
- Query Phase. adaptively issues the following queries:
- -
- hash Query: Assume that does not has the ability to calculate the hash function . The response to hash Query can be simulated by maintaining a list initialized to be empty. When the adversary invokes the hash Query with input values , will then check whether the parameter exists in the hash list . If the tuple has already been stored in , outputs to . Otherwise, chooses random and forwards it to . The new tuple will be subsequently added to .
- -
- hash Query: Assume that does not has the ability to calculate the hash function . The response to hash Query can be simulated by maintaining a list initialized to be empty. When the adversary invokes the hash Query with input values , will then check whether the record exists in the hash list . If the tuple has already been stored in , outputs to . Otherwise, chooses random and forwards it to . The new tuple will be subsequently added to .
- -
- hash Query: Assume that does not has the ability to calculate the hash function . The response to hash Query can be simulated by maintaining a list initialized to be empty. When the adversary invokes the hash Query with input values , will then check whether the record exists in the hash list . If the tuple has already been stored in , outputs to . Otherwise, chooses random and forwards it to . The new tuple will be subsequently added to .
- -
- Extraction Query: Upon the Extract Query with is made to , conducts hash Query on the input and outputs the corresponding tuple . Note that the tuple has already recorded in . randomly selects and computes and adopting the acquired and previously stored . The calculated tuple will be sent to .
Finally, adversary obtains two tuple and after querying , where . Hence, holds. That is, . Due to the assumption that is a random oracle, we can get , which contradicts the aforementioned assumption. Hence the probability that adversary can win the game is , where denote the length of , X and r respectively. Thus, the advantage of winning the game is negligible. Our scheme is resistance to adaptive chosen message attack. □
6.2. Resistance to Replay Attack
In the proposed authentication scheme, the previous collected information cannot pass the current data transmission procedure. As shown in the aforementioned group key distribution phase, the D2D transmission on message m is performed as , where the current time stamp is involved in each transmission process. In this way, the regular data transmission process is resistant to reply attack.
As for the authentication process, the certificate authentication method is adopted, where two partial secret keys are respectively generated by SN and UE itself. Accordingly, the utilized partial secret key is randomly selected after the successful validation of . Note that the partial secret key , as well as the group key , is considered as the randomly generated value in each authenticating session. In this way, the delivered from the previous session cannot pass the current authentication. The replay attack is prevented in this way.
6.3. Provision to Identity Privacy Preserving
In practical D2D communication scenarios, the adversary, including the insider and outsider attacker, is able to perform illegal tracing on particular device. The user privacy is damaged in this way. Therefore, in our design, the original identity of certain UE will not be revealed during the whole communicating phase. Furthermore, for all the participating vehicles, the user unlinkability is also provided. Hence the multiple messages generated by the same vehicle cannot be linked together. The brief description is given as follows.
Theorem 2.
The proposed authentication scheme is resistant to illegal tracing, and provides UE unlinkability. That is, particular UEs can not be traced by extracting the featured information from the delivered messages.
Proof of Theorem 2.
In our assumption, the real identity for certain UE i is hidden all the time. As shown in the aforementioned authentication phase, the one-way hashed function is employed. The newly constructed temporary identity is derived as , which contains the randomly generated value . Note that is previous selected in the SN side. The transmitting message shows no similarity with the subsequent data exchange. In this way, the tracing towards certain device is prevented. □
6.4. Session Key Establishment
In the D2D environment, it is of great significance to generate the shared session key between the SN and all the UEs with the intention to guarantee the data confidentiality and transmission security.
Theorem 3.
Our authentication scheme is able to provide the shared session key between SN and all the validated UEs.
Proof of Theorem 3.
According to our design, the group key generated by SN is finally delivered to valid UEs in a secure way. The is adopted as the group key between SN and all the legitimate devices. Specifically, fast key updating operations can be guaranteed in the corresponding updating process. Within the updating phase, updating the related key for decryption is not necessary for the currently legitimate devices. In other words, the newly distributed key can easily be derived with the formula , where holds for all validated UEs. However, the updated group key does not involve the information of revoked devices. In this way, the revoked device cannot derive the new group key using the expired . The group key can be successfully distributed and updated in our scheme. □
6.5. Certificateless Authentication
The certificateless authentication feature is provided in our scheme, where key escrow issue can be prevented. In this section, the certificateless authentication properties can be analyzed as follows.
Theorem 4.
The proposed protocol can provide certificateless authentication for D2D devices. The malicious entities cannot reveal the confidential key message of particular vehicle. Furthermore, SN cannot impersonate legitimate vehicles with the acquired knowledge.
Proof of Theorem 4.
As illustrated above, during the authentication phase, SN has zero knowledge about the self-generated random partial key from UE side. Moreover, according to DBDH, SN cannot derive the within the received , either. In this way, the impersonation on certain UE cannot be conducted. □
6.6. Continuous Authentication
The continuous authentication strategy is conducted in our scheme, which could periodically detect the anomalies during the entire user session [26]. The analysis about behavioral biometrics is adopted, revealing the real-time human physical status. The personalized model for individual participant is constructed locally, where the training data characterize unique behavioral patterns within a relatively long interval. The biometric parameter is processed for anomalies detection. Additionally, after each validation, the stored parameter set is updated using newly acquired value so as to timely reveal the recent biometric status of user. Noting that the parameter checking process is performed at set intervals, thus continuous authentication is provided in our scheme.
6.7. Comparison on Security Properties
In this section, the comparison in terms of the major security properties for D2D authentication is presented. The proposed protocol is compared with the stat-of-the-art D2D authentication and key agreement schemes including SeDS [19], LRSA [32], GRAAD [12], and PPAKA [9] in order to prove its superiority on security properties. As shown in Table 2, our protocol yields the desirable security properties.

Table 2.
Comparison on Security Properties.
7. Performance Analysis
In this section, the performance analysis towards the proposed D2D authentication protocol is presented.
7.1. Storage Overhead
In our designed D2D communication model, the UEs are resource-limited devices with constrained storing capacity and computing ability. Hence, it is not efficient to store massive key information in the UE storage. Furthermore, additional storage overhead is required for authentication as well. In the contrast, considered as the major component of D2D network, SN is assumed to have adequate storing ability for key information recording and generation towards all the participated devices. Therefore, the analysis here emphasizes on the storage overhead in UE side, while the SN is not included due to the aforementioned design. The state-of-the-art D2D authentication and key agreement schemes including SeDS [19], LRSA [32], GRAAD [12], and PPAKA [9] are compared with the proposed scheme in order to prove its efficiency on storage overhead. Similarly, the storage overhead for D2D device is taken into consideration.
As for the UE in the proposed protocol, the public generators are previously stored in UE side. During the offline registration phase, the confidential key information is stored with its own identity . Accordingly, we define the length of key information including , , and is 160 bits, the identity is 32 bits. At this point, the storage overhead for each UE is bits. Similarly, in the subsequent authentication phase, the length of public key , the validation result , and the self-generated partial secret key are 160 bits each. Hence the storage cost of UE in authentication phase can be calculated as bits. In the following group key distribution phase, the received packet is stored as well, where t denotes the number of participating UEs. The length of the final group key is defined as 32 bits. In this way, the total storage cost can be summarized as bits. Obviously, the storage cost is related to the number of validated UEs. The comparison results on storage overhead with the four existing D2D authentication scheme are illustrated in Table 3. Apparently, minor storage cost is required in our authentication scheme on the resourced-constrained UEs.

Table 3.
Comparison of Storage Overhead.
7.2. Computation Cost
In this section, the computation cost in both the SN and UE side is conducted. and are shortened for symmetric encryption and decryption. Meanwhile, the exponential operation, and the pairing are solely defined as and e. Furthermore, H, M, and D denote the one-way hash function, multiplication operation, and division operation respectively. Finally, the point multiplication operation is denoted as p. The comparison results on computation cost is presented in Table 4, indicating that the relatively smaller computation cost is required for resource-limited UEs in our scheme.

Table 4.
Comparison of Computation Cost.
7.3. Communication Cost
In this section, the required communication rounds for the D2D authentication in SN side is analyzed, where totally t UEs are assumed to be authenticated. In our design, for each UE, only 3 rounds are required for the entire authentication process, where the offline registration phase is not included. Hence, the total communication rounds involving t UEs is in our design, where the authenticating request and the final group key distribution message are through one broadcast operation. Accordingly, the comparison result on communication cost is given in Table 5, demonstrating that less communication rounds are conducted in our scheme comparing with the state-of-the-arts.

Table 5.
Comparison of Communication Cost.
8. Conclusions
In this paper, a secure certificateless group authentication scheme for D2D communication is presented, the user activities data from smartphone sensors are analyzed for continuous authentication as well. The proposed scheme is designed for particular D2D scenario intended for public safety or field trip application for extreme environments, where the smartphone acts as the UEs for every terminal user. Note that most of the user equipments (UEs) are out of the effective range of cellular networks. Consequently, an efficient group key distribution method is constructed, which drastically reduces the communication cost compared with conventional one-to-one key distribution. In this case, the group key updating mechanism only requires a small modification in the SN side, while the decrypting information in the UEs side remains constant as soon as the UEs are validated. Additionally, continuous authentication strategy adopting smartphone sensor behavior analysis is adopted, where the unique user behavioral data acquired by accelerometer and gyroscope sensors in the smart phone (UE) is processed and characterized by time and frequency domain features. Continuous authentication is performed with the adopted biometric parameter periodically. Security and performance analysis demonstrate that the proposed scheme can yield desired security properties towards various attacks. The proposed design is efficient compared with state-of-the-art D2D authentication schemes.
Author Contributions
Conceptualization, H.T. and I.C.; Methodology, H.T.; Formal analysis, H.T.; Investigation, S.X. and S.P.; Writing—Original Draft Preparation, H.T.; Writing—Review and Editing, H.T. and Y.S.; Supervision, I.C.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Korean Government under Grant NRF-2017R1D1A3B03034005 and by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (NRF-2017R1A6A1A03015496).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, X.; Zhang, Y.; Sun, Z.; Hong, Y.; Tao, X. Analytical Modeling of Mode Selection for Moving D2D-Enabled Cellular Networks. IEEE Commun. Lett. 2016, 20, 1203–1206. [Google Scholar] [CrossRef]
- Ma, C.; Liu, J.; Tian, X.; Yu, H.; Cui, Y.; Wang, X. Interference Exploitation in D2D-Enabled Cellular Networks: A Secrecy Perspective. IEEE Trans. Commun. 2015, 63, 229–242. [Google Scholar] [CrossRef]
- Alam, M.; Yang, D.; Rodriguez, J.; Abd-Alhameed, R.A. Secure Device-to-Device Communication in LTE-A. IEEE Commun. Mag. 2014, 52, 66–73. [Google Scholar] [CrossRef]
- Shen, W.; Yin, B.; Cao, X.; Cai, L.X.; Cheng, Y. Secure device-to-device communications over WiFi direct. IEEE Netw. 2016, 30, 4–9. [Google Scholar] [CrossRef]
- Tang, H.; Ding, Z. Mixed Mode Transmission and Resource Allocation for D2D Communication. IEEE Trans. Wirel. Commun. 2016, 15, 162–175. [Google Scholar] [CrossRef]
- Zhang, A.; Lin, X. Security-Aware and Privacy-Preserving D2D Communications in 5G. IEEE Netw. 2017, 31, 70–77. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, X.; Lin, Y. Trust Management Method of D2D Communication Based on RF Fingerprint Identification. IEEE Access 2018, 6, 66082–66087. [Google Scholar] [CrossRef]
- Tan, H.; Choi, D.; Kim, P.; Pan, S.; Chung, I. Secure Certificateless Authentication and Road Message Dissemination Protocol in VANETs. Wirel. Commun. Mobile Comput. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Wang, M.; Yan, Z. Privacy-Preserving Authentication and Key Agreement Protocols for D2D Group Communications. IEEE Trans. Ind. Inform. 2018, 14, 3637–3647. [Google Scholar] [CrossRef]
- Cao, M.; Wang, L.; Xu, H.; Chen, D.; Lou, C.; Zhang, N.; Zhu, Y.; Qin, Z. Sec-D2D: A Secure and Lightweight D2D Communication System With Multiple Sensors. IEEE Access 2019, 7, 33759–33770. [Google Scholar] [CrossRef]
- Tan, H.; Choi, D.; Kim, P.; Pan, S.; Chung, I. Comments on ‘Dual Authentication and Key Management Techniques for Secure Data Transmission in Vehicular Ad Hoc Networks’. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2149–2151. [Google Scholar] [CrossRef]
- Hsu, R.H.; Lee, J.; Quek, T.Q.S.; Chen, J.C. GRAAD: Group Anonymous and Accountable D2D Communication in Mobile Networks. IEEE Trans. Inf. Forensics Secur. 2018, 13, 449–464. [Google Scholar] [CrossRef]
- Shen, C.; Li, Y.; Chen, Y.; Guan, X.; Maxion, R.A. Performance Analysis of Multi-Motion Sensor Behavior for Active Smartphone Authentication. IEEE Trans. Inf. Forensics Secur. 2018, 13, 48–62. [Google Scholar] [CrossRef]
- Kelly, D.; Curran, K.; Caulfield, B. Automatic Prediction of Health Status Using Smartphone-Derived Behavior Profiles. IEEE J. Biomed. Health Inform. 2017, 21, 1750–1760. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Kanhangad, V. Human Activity Classification in Smartphones Using Accelerometer and Gyroscope Sensors. IEEE Sens. J. 2018, 18, 1169–1177. [Google Scholar] [CrossRef]
- Tan, H.; Choi, D.; Kim, P.; Pan, S.; Chung, I. An Efficient Hash-based RFID Grouping Authentication Protocol Providing Missing Tags Detection. J. Internet Technol. 2018, 19, 481–488. [Google Scholar]
- Kwapisz, J.R.; Weiss, G.M.; Moore, S.A. Activity Recognition Using Cell Phone Accelerometers. ACM SIGKDD Explor. Newslett. 2011, 12, 74–82. [Google Scholar] [CrossRef]
- Yue, J.; Ma, C.; Yu, H.; Zhou, W. Secrecy-Based Access Control for Device-to-Device Communication Underlaying Cellular Networks. IEEE Commun. Lett. 2013, 17, 2068–2071. [Google Scholar] [CrossRef]
- Zhang, A.; Chen, J.; Hu, R.Q.; Qian, Y. SeDS: Secure Data Sharing Strategy for D2D Communication in LTE-Advanced Networks. IEEE Trans. Veh. Technol. 2016, 65, 2659–2672. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, R.; Zhang, Y. Privacy-Preserving Spatiotemporal Matching for Secure Device-to-Device Communications. IEEE Internet Things J. 2016, 3, 1048–1060. [Google Scholar] [CrossRef]
- Waqas, M.; Ahmed, M.; Li, Y.; Jin, D.; Chen, S. Social-Aware Secret Key Generation for Secure Device-to-Device Communication via Trusted and Non-Trusted Relays. IEEE Trans. Wirel. Commun. 2018, 17, 3918–3930. [Google Scholar] [CrossRef]
- Kim, J.; Song, J. A Secure Device-to-Device Link Establishment Scheme for LoRaWAN. IEEE Sens. J. 2018, 18, 2153–2160. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, D.; Li, B.; Guo, B.; Li, S. Activity Recognition on an Accelerometer Embedded Mobile Phone with Varying Positions and Orientations. In Ubiquitous Intelligence and Computing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 548–562. [Google Scholar]
- Shoaib, M.; Bosch, S.; Incel, O.D.; Scholten, H.; Havinga, P.J.M. Fusion of Smartphone Motion Sensors for Physical Activity Recognition. Sensors 2014, 14, 10146–10176. [Google Scholar] [CrossRef]
- Garcia-Ceja, E.; Osmani, V.; Mayora, O. Automatic Stress Detection in Working Environments from Smartphones’ Accelerometer Data: A First Step. IEEE J. Biomed. Health Inform. 2016, 20, 1053–1060. [Google Scholar] [CrossRef]
- Sitová, Z.; Šeděnka, J.; Yang, Q.; Peng, G.; Zhou, G.; Gasti, P.; Balagani, K.S. HMOG: New Behavioral Biometric Features for Continuous Authentication of Smartphone Users. IEEE Trans. Inf. Forensics Secur. 2016, 11, 877–892. [Google Scholar] [CrossRef]
- Carter, J.L.; Wegman, M.N. Universal Classes of Hash Functions. J. Comput. Syst. Sci. 1979, 18, 143–154. [Google Scholar] [CrossRef]
- Tan, H.; Gui, Z.; Chung, I. A Secure and Efficient Certificateless Authentication Scheme With Unsupervised Anomaly Detection in VANETs. IEEE Access 2018, 6, 74260–74276. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Brickell, E.; Pointcheval, D.; Vaudenay, S.; Yung, M. Design Validations for Discrete Logarithm Based Signature Schemes. In International Workshop on Public Key Cryptography, PKC 2000; Springer: Berlin/ Heidelberg, Germany, 2000; pp. 276–292. [Google Scholar]
- Tan, H.; Chung, I. A Secure and Efficient Group Key Management Protocol with Cooperative Sensor Association in WBANs. Sensors 2018, 18, 3930. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, L.; Ye, X.; Lin, X. Light-Weight and Robust Security-Aware D2D-Assist Data Transmission Protocol for Mobile-Health Systems. IEEE Trans. Inf. Forensics Secur. 2017, 12, 662–675. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).