Abstract
In this study, different designs of the opening pattern of computer fan grills were investigated. The objective of this study was to propose a simulation analysis and compare it to the experimental results for a set of optimized fan designs. The FLUENT computational fluid dynamics (CFD) simulation software was used to analyze the fan blade flow. The experimental results obtained by the simulation analysis of the optimized fan designs were analyzed and compared. The effect of different opening pattern designs on the resulting airflow rate was investigated. Six types of fans with different grills were analyzed. The airflow velocity distribution in the simulated flow channel indicated that the wind speed efficiency of the fan and its influence were comparable with the experimental model. The air was forced by the fan into the air duct. The flow path was separately measured by analog instruments. The three-dimensional flow field was determined by performing a wind speed comparison on nine planes containing the mainstream velocity vector. Moreover, the three-dimensional curved surface flow field at the outlet position and the highest fan rotation speed were investigated. The air velocity distribution at the inlet and the outlet of the fan indicated that among the air outlet opening designs, the honeycomb shaped air outlet displayed the optimal performance by investigating the fan characteristics and the estimated wind speed efficiency. These optimized designs were the most ideal configurations to compare these results. The air flow rate was evenly distributed at the fan inlet.
1. Introduction
The opening pattern of an axial fan grill is one of the most important factors of the resulting airflow rate. The fan grill is provided with a number of significant characteristics. From the standpoint of aerodynamic performance, the pressure rise will decrease depending on the different types of opening patterns on the axial fan grill. The increased density of the boundary layer of the fan grill opening pattern affects the exhaust flow of an axial. The resulting phenomenon is the influence of the flowing vortex when the airflow passes the fan grill. On the other hand, the style of the fan grill also affects the overall efficiency of the intake airflow when the blade design remains unchanged. A smaller aspect ratio and a higher opening ratio allow for an axial fan to generate better outflow performance. The overall airflow rate can be increased by optimizing the opening pattern of the outflow when considering the complex aerodynamic parameters [1].
The influence of different fan grill patterns on the resulting airflow velocity has been investigated. In the simulation, the airflow velocity distribution indicated the efficiency of the air velocity. The three-dimensional flow field of the experimental model was also verified from the verification of the airflow velocity. One of the most important factors that affect the resulting airflow velocity of an axial fan grill is its characteristics. Sergio Marinetti et al. 2001 carried out the investigation of the rotational speed of a fan by forcing airflow through an evaporator and two fans. The three-dimensional flow field was investigated by measuring the airflow distribution at different elevations at the evaporator inlet and outlet. The results indicated a uniform air velocity distribution at the evaporator inlet [1]. Gebrehiwot et al. 2010 applied the CFD approach to the investigation of the performance of a cross-flow fan by using three fans with similar geometry at the cross-flow opening. The fan load can be determined from the impedance curve of the perforated plates with different openings. The results of the wind tunnel testing indicated that the non-uniform airflow distribution at the air inlet along the width of a cross-flow fan was an important factor for the CFD simulation [2]. The findings from Chen’s et al. 2009 investigation indicated that the design of a distorted stator of a transonic fan presented better aerodynamic characteristics [3]. Betta et al. 2010 studied the fluid dynamic performance by comparing it to the conventional axial ventilation system and by applying the CFD analysis to the system by the k–e model [4]. Li et al. 2008 carried out the analysis and experimental investigation of the aerodynamics of forward inclined impellers and radial low pressure axial impellers. The design of the forward-inclined blades was optimized by CFD techniques and by measuring the aerodynamics and aeroacoustics of the two blades. In comparison to typical radial blades, a forward-inclined blade was proven to be able to improve the efficiency by carrying out a detailed flow rate measurement and the calculated exhaust flow field. The results indicated that a forward-inclined blade could trigger the redistribution along the radial direction and reduce the tip overload [5]. Delele et al. 2005 A CFD model was developed for the investigation of the three-dimensional airflow pattern of the ground velocity of the cross-flow air sprayer. The researchers conducted a simulation of the rotational speed of two different fans, and the results of the instant cross-sectional velocity distribution and simulation of the maximum vertical exhaust velocity and the change in directions indicated good consistency. This is due to the fact that the magnitude of the exhaust velocity of the jet flow is larger and the change in direction is greater [6]. The flow allocation and performance investigation were carried out by CFD approaches and anemometers in order to determine the effect of the balanced split vortex walls between two grid points. The results indicated that a two-dimensional CFD model could be used to predict fan performance to an acceptable level, especially at the portion between two outlets. The modification indicated a more uniform air vortex distribution at the walls and the mass flow rate between the two outlets affected the rotor exhaust air to a greater extent [7]. Li et al. 2011 carried out the comparison between two impellers with diameters 5% and 10% larger than the original impeller by both numerical analysis and experimental study. The numerical simulation of the internal characteristics indicated that the flow speed and total pressure increased, so the axial power and sound pressure also increased. When the efficiency decreased, the impeller needed to have a larger diameter for a better operating point [8]. The fan assembly could keep the average level of the components of the heat transfer coefficient. The results indicated that if a fan design could resolve the problem of cross-flow environment, the heat transfer efficiency could be improved by 30% [9]. Other studies have implemented CFD approaches in the flow field of axial fans and their performance and characteristics. The deviation of the fan performance curve obtained by experimental results reached the horizontal DFR method, and the use of static meshes and moving meshes was less than 3% and 1.5%, respectively. This presents significant improvement to the conventional approach, which has a significant deviation of 26% [10,11]. Hu et al. 2013 the calculation includes three steps: firstly, the unsteady viscous flow around the blades is calculated using the CFD method to acquire the noise source information; secondly, the radiated sound pressure is calculated using the acoustic analogy Curle equation in the frequency domain; lastly, the scattering effect of the duct wall on the propagation of the sound wave is expressed using the thin-body BEM method [12]. Owen 2013 a comparison of test data collected at an existing ACC (cooling performance of an air-cooled condenser) and numerical data generated in a CFD analysis of the flow around the same ACC shows a discrepancy in the predicted effects of wind on fan inlet temperature. Careful analysis of the test data indicates the potential involvement of atmospheric temperature distributions in fan inlet temperature deviations. A numerical case study is conducted considering four differing atmospheric temperature distributions [13]. Detailed flow measurement and computation were performed for outlet flow field for investigating the responsible flow mechanisms. Yang et al. 2008 The results show the forward-skewed blade can cause a spanwise redistribution of flow toward the blade mid-span and reduce tip loading [14]. Carolus et al. 2007 In the limits of the necessary assumptions the SEM (a simple semi-empirical noise prediction model) predicts the noise spectra and the overall sound power surprisingly well without any further tuning of parameters; the influence of the fan operating point and the nature of the inflow is obtained. Naturally, the predicted spectra appear unrealistically “smooth”, since the empirical input data are averaged and modeled in the frequency domain. By way of contrast the LES (The numerical large eddy simulation) yields the fluctuating forces on the blades in the time domain. Details of the source characteristics and their origin are obtained rather clearly. The predicted effects of the ingested turbulence on the fluctuating blade forces and the fan noise compare favorably with experiments [15].
The objective of this study is to investigate the performance of different gap designs of fan grills. The flow field of an axial fan was investigated by CFD simulation and the result was compared to experimental one. The airflow velocity of the resulting airflow was determined in the three-dimensional flow field. The maximum rotating speed at the fan outlet was also measured. The distribution of the airflow velocity at the fan inlet and outlet was analyzed in order to determine the effect of different gap designs. The objective is to generate uniform airflow velocity at the fan inlet so that an optimal configuration can be created.
2. Research Model
Configuration of Model Parameters
The dimension of the target fan model was 35 mm (L) × 95 mm (W) × 146 mm (H), as shown in Figure 1. The main components of the external structure included a casing or housing, impeller, and exhaust housing. A fan operates by creating a pressure difference by the rotating blades so that the surrounding fluid is forced to move. Therefore, its energy is transferred to the surrounding fluid in a dynamic way. The main effect is to overcome the system impedance by the air pressure that is created by the fan.

Figure 1.
New fan model.
Typically, when designing an impeller, various parameters and equations that affect the fan performance need to be considered since the geometry of the impeller deals with three-dimensional surfaces. A fan designer is required to design based on the criteria of geometrical form design and needs to carry out the design process again if a resulting impeller does not meet the performance criteria. Axial fan parameters were collected for the investigation in this study with the relevant theories and equations summarized for further review to determine the optimal impeller design and parameters such as the inner and outer diameters. With further configuration of other detailed parameters, a designer can quickly generate the required impeller without much effort in the calculation and modification. The final impeller design can be determined by the curve-fitting results and its geometric parameters, as shown in Table 1.

Table 1.
Configuration parameters of the new fan model.
One of the most important factors that affect the flow rate of a fan is the opening pattern. In order to make the overall evaluation framework more complete, the parameters and curve equations that affect the fan performance should be considered when designing the blade profile. The conditions of the geometric shapes were listed, and the simulation results of the new fan models were compared with the real test results as shown in Figure 1. Therefore, after analyzing the fans that are available on the market, a variety of new fan grill designs were created in this study. These new grill designs were screened out according to the ergonomic design principle that human fingers do not penetrate the grill gaps. Moreover, the qualified designs need to present symmetric and regular curve patterns. A total of six grill patterns were determined to be the qualified ones and were analyzed by CFD simulation in order to determine the most optimal fan grill design. The geometric parameters of the new fan blade designs are shown in Table 1. Of all the new opening pattern designs, six were selected for further simulation. The six different opening pattern designs are shown in Figure 2 as follows.

Figure 2.
The six different opening patterns.
The purpose of this study was to investigate the design of the opening patterns. A fan rotates to move air to the opening, and the domain of the upstream and downstream of the fan should be included into the numerical simulation to obtain more accurate numerical results. The symmetric air velocity measurement points on the fan model is shown in Figure 3. Along the centerline of the fan model, there were a total of nine measurement points marked as Points A to I, among which Points C to F were the points located within the fan itself. Points A and I were located at the inlet and outlet of this flow field to determine the flow pattern of the region close to the opening. The velocity component V can be determined as these points are located at the boundary of this solution domain. The velocity along the vertical axis can be obtained from the numerical analysis and can be later compared to the real measurement results. The numerical model was based on the standard k–ε model. The vertical component V indicates a larger difference than the component along the flow direction. This is the main purpose of optimizing the opening pattern design in order to obtain satisfactory results.
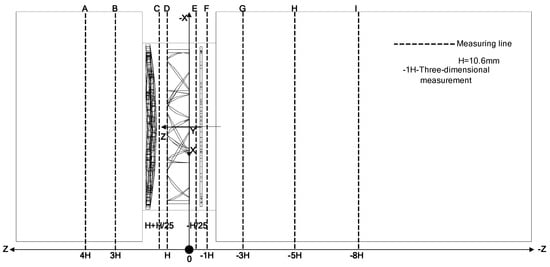
Figure 3.
Symmetric air velocity measurement points on the model.
3. Research Methodology
3.1. Numerical Analysis
When a numerical method is used for the simulation and analysis, some fundamental and reasonable assumptions need to be made in order to simplify the complexity of the numerical simulation. These assumptions are described as follows.
3.1.1. Governing Equations
In the 3D Cartesian coordinate system, the governing equations are as follows [16,17,18].
Continuity equation:
Momentum equation:
X direction:
Y direction:
Z direction:
Energy equation:
The governing equations can be represented by the general equations as follows:
is the convective term;
is the diffusive term; S is the source term; and is the unsteady term [19]. This term is not considered under the steady-state assumption. The symbol φ represents dependent variables such as u, v, w, k, ε, and T in Table 2 [20]. Γ is the corresponding diffusivity of each physical variable [12]. u, v, and w are the velocity components in the x, y, and z directions, respectively.

Table 2.
List of independent variables.
Based on the fundamentals of the finite-volume method, the computational domain must be partitioned into many small control volumes. After a volume integral, the equations of the mass, energy, and momentum of fluids can then be transformed into algebraic equations as follows:
where is the convective term; is the diffusive term; is the generation term; and is the unsteady term. This term is not considered under the steady-state assumption.
3.1.2. Theory of Turbulence Model
Since turbulence causes the exchange of momentum, energy, and concentration variations between the fluid medium, it causes quite a few fluctuations. Such fluctuations are of a small scale and with high frequency. Therefore, for real engineering calculations, a direct simulation requires very high-end computer hardware [13]. Therefore, when simulating turbulent flows, manipulations of the control equations are required to filter out turbulence components that are at an extremely high frequency or of extremely small scale. However, the modified equations may comprise variables that are unknown to us, while the turbulence model requires the use of known variables to confirm these variables [21].
3.1.3. Standard k–ε Turbulence Model
The standard k–ε is a type of semi-empirical turbulence model. It is mostly based on basic physical equations to derive the transport equations that describe the turbulent flow transmission of turbulence kinetic energy (k) and dissipation (ε) [22]. These equations are as follows [23]:
Turbulence kinetic energy equation (k):
Dissipation equation (ε):
(3) Coefficient of turbulent viscosity :
In the equation, Gk indicates the turbulence kinetic energy generated by the velocity gradient of laminar flow. Gb is the turbulence kinetic energy generated by the buoyancy. In compressible turbulent flows, YM is the fluctuation generated by the excessive diffusion. σk and σε are the turbulent Prandtl numbers of turbulence kinetic energy and turbulent dissipation; and C1ε, C2ε, and C3ε are the empirical constants. The recommended values of these coefficients are shown in Table 3 [24].

Table 3.
Coefficients of the standard k–ε turbulence model.
The k–ε model is based on the resulting equations by assuming that the flow field is completely at the turbulence state and the condition in which the molecular viscosity is negligible. Therefore, the standard k–ε model provided a better result for calculating the fully turbulent flow fields [25].
3.1.4. RNG k−ε Turbulence Model
The RNG k−ε model is derived from the mathematical method of renormalization group in combination with the transient Navier-Stokes equations (N-S equations). This model is similar to the standard model and its analytical characteristics directly evolved from the standard model. The main difference between the RNG model and the standard one is due to the consideration of the turbulent vortex by the RNG model. This consideration enhances the calculation precision on the vortex. Moreover, the turbulent Prandtl number also provides a comprehensive analytical equation. A condition is also included into the turbulent diffusion equation in order to improve the precision of the standard model. The flow field can be presented in a more precise way. The equation of the RNG model is described as follows [18].
Equation of turbulence kinetic energy (k)
Equation of diffusivity (ε)
where and are the turbulence Prandtl number of the turbulence kinetic energy and the turbulence diffusivity, is the coefficient of equivalent turbulence viscosity, is the parameter of the modified turbulence viscosity, the constants are = 1.42, = 1.68 respectively.
The main difference between the RNG model and the standard model is described as follows. The RNG model is used to build up a new equation based on the condition of low Reynolds number. The equation is as follows.
where , .
The equation depicts how the Reynolds number affects the coefficient of equivalent turbulence viscosity so that a model could perform better at a low Reynolds number. At conditions with a higher Reynolds number, the turbulence velocity equation of the standard model is still used, except that the parameter is set as 0.0845 according to the RNG theoretical calculation.
Moreover, since the turbulence in a uniform flow is also affected by the vortex, the turbulence viscosity is also modified to compensate for this influence. The equation is as follows.
Here is the quantity that is not modified from the original equation of the turbulence viscosity coefficient. Ω is a characteristic parameter that is used by the FLUENT software. is a vortex constant and its value is determined form the vortex intensity of the flow condition. For a moderate vortex flow state, is set as 0.05. For a stronger vortex flow, a larger value can be used.
For the turbulence Prandtl number, the RNG theory supplies a comprehensive analytical equation that can be used to calculate and as follows.
where = 1.0 and = 1.393 for a larger Reynolds number.
Finally, the conditional parameter of is also included into the diffusivity equation. This parameter leads to the main difference from the standard model and the equation is as follows.
where η = , , β = 0.0 = 0.012.
Since the RNG model provides a comprehensive definition and correction to several parameters, the RNG model can react to the flow field with immediate changes and curved streamlines. This is also the reason why the RNG can present better performance in this type of flow field.
3.2. Performance Testing Equipment for Fans
From the aspect of performance measurements in this experiment, the detailed configuration of the measuring equipment and apparatus and the corresponding operations were described separately as shown in Figure 4. The main device of the performance testing equipment for the fans used adopted the outlet-chamber wind tunnel according to the AMCA 210-99 standard. This type of wind tunnel is composed of a main body, flow setting means, multiple nuzzles, and a flow-rate regulating device [14]. Its major function is to simulate various types of the air-flow condition downstream of the fan and supply a good and stable flow field for measurement in order to obtain the complete performance curves [26].
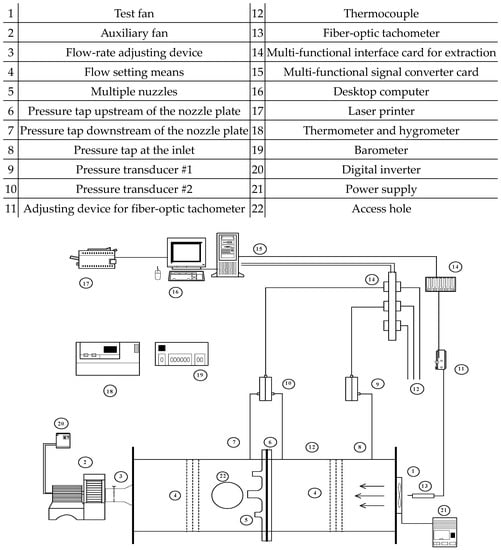
Figure 4.
Configuration of the fan performance testing system and specifications of the major instruments.
3.2.1. Calculation of Flow Rates
According to the calculation by the standard equations and flow-rate measurements by the National Laboratory, the errors can be obtained through a comparison with the measurement readings. The standard equations are as follows [27].
The pressure difference between the nozzle outlet and inlet PL5 and PL6 can be obtained. The flow rates on the cross-sections of the nozzles can be determined with varying nozzle coefficients as shown in Figure 5. If there is a need to calculate the outlet flow rate of the fan under test, then the effect of density variations must be considered, the measurement of which is as follows [28].
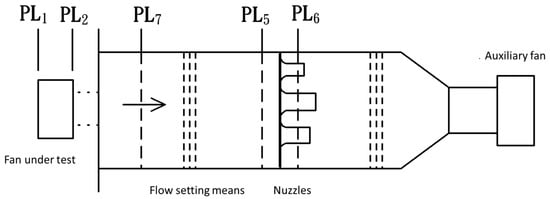
Figure 5.
Definition of various measurement planes.
The equation for the calculation of flow rates in a test chamber with multiple nuzzles is
where is the total flow rate measured by a bank of nozzles, CMM; is the pressure difference across the nozzles, mm-Aq; is the air density upstream of the nozzles, kg/m3; is the expansion factor; is the discharge coefficient of the nth nozzle; and is the cross-sectional area of the nth nozzle’s throat, m2.
3.2.2. Calculation of Air Pressures
Typical pressure readings can be directly measured by instruments, but requires understanding the definition of a fan’s static pressure (ΔPs) and total pressure (ΔPt). The static pressure, defined as the difference between the fan’s static pressure at typical pressure readings, can be directly measured by instruments, but understanding (Ps2) and the static pressure at inlet (Ps1) is required. The total pressure is the difference between the fan’s total pressure at outlet (Pt2) and the total pressure at inlet (Pt1). The equations for measurement and calculation are explained respectively as follows.
Since the outlet and inlet planes of the fan under test are PL2 and PL1, respectively, they can be defined as follows [29]:
where Ps is the static pressure of the fan under test; Pt is the total pressure of the fan under test; Pν is the dynamic pressure of the fan under test; Pt2 is the total pressure at the fan’s outlet (or plane ); and Pt1 is the total pressure at the fan’s inlet (or plane ).
Since in this experiment there was no duct at the inlet of the fan under test, therefore . On the other hand, the measured static pressure at the outlet is the same as the static pressures measured at the measuring plane PL7. Therefore, .
It can be concluded from the above equation that the static pressure of the fan under test happened to be equal to the static pressure obtained at the outlet test chamber Pt7. The Type A method (a test method with no duct at either the outlet or the inlet) that was carried out at the outlet test box is a special case of testing. When carrying out different types of tests or different equipment, the equation of the static pressure of the fan under test is thus more complicated. The calculation of dynamic pressure is as follows [30]:
where Pν2 is the outlet dynamic pressure of the fan under test, mm-Aq; V2 is the outlet air velocity of the fan under test, m/s; ρ2 is the outlet air density of the fan under test, kg/m3; and where Q2 is the outlet flow rate of the fan under test, CMM; Q is the standard flow rate of the fan under test, CMM; A2 is the outlet cross-sectional area of the fan under test, m2; ρ is the density of air at STP (1.2 kg/m3); and .
3.2.3. Fan Performance Power and Efficiency
The calculation of power can be obtained from torque and rotation speed. By measuring the torque of a fan by a torque gauge and measuring the rotation speed by a fiber-optic tachometer, the fan input power (W) can be obtained. The fan efficiency can also be obtained from the air pressure and the flow rate. It can be estimated by the equations as follows:
4. Numerical Simulation
The flow passage of the numerical model of the target axial fan is shown in Figure 6. Within the entire range of the flow rate, the model was composed of not only one flow passage. It is known that the flow field behavior follows the continuity equation and the momentum equation. The axial fan is composed of the inlet cone, impeller, and the fan housing. The resulting mesh structure contains structured meshes as the majority and unstructured meshes as the minority. After further mesh refinement and coupling, the final number of the mesh contained 750,000 cells as shown in Figure 7. The mesh structure contained a rotating mesh system between the inlet and the outlet. The outlet boundary had a uniform pressure of 1 atm. The rotation speed of the rotating mesh was 2000 RPM. The pressure and velocity coupling wind-facing difference method was selected as the simple algorithm. The maximum residual was defined as <10−3 for convergence.
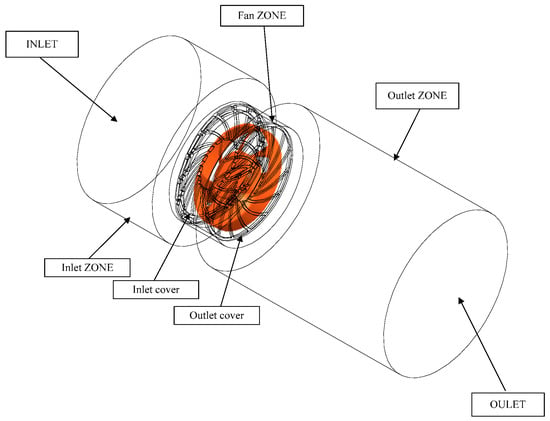
Figure 6.
Numerical model of the target axial fan.
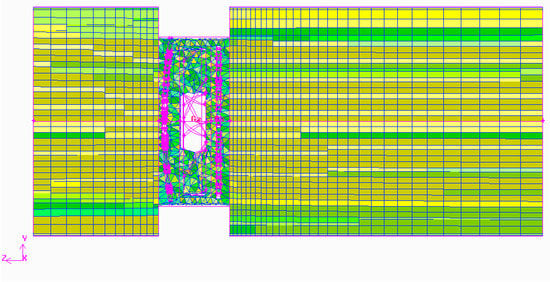
Figure 7.
Mesh structure along the cross-section of the numerical model of the axial fan.
Since this is a problem for rotating machinery, the commercial CFD software FLUENT6.3 was used for the simulation. The selected region was configured to rotate against an axis so the momentum equation could be rectified automatically. The source terms were automatically added into the relevant equations for calculation. The configuration of the boundary conditions needs to consider the operating condition of a real object, i.e., to comply with the physical phenomenon. Otherwise, the accuracy of the calculated result might be affected. The boundary conditions of this simulation include the inlet boundary condition, outlet boundary condition, and wall boundary condition. Their descriptions are listed in Table 4 as follows as shown in Figure 8 [15,28,31].

Table 4.
Boundary conditions of the fan model for simulation.
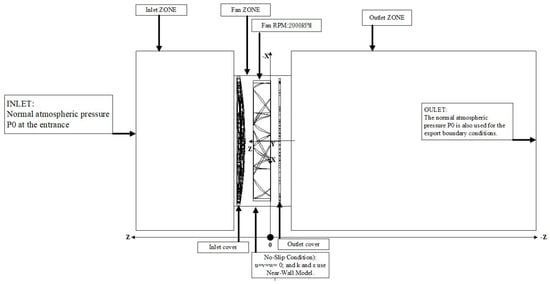
Figure 8.
Boundary conditions.
5. Verification of the Case Study and Numerical Analysis
5.1. Verification between Numerical Simulation and Experiment Testing
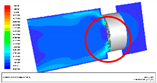
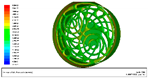
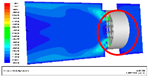
After the completion of the numerical simulation, we compared the results to the experiment in order to determine whether the trend corresponded to each other. Furthermore, the accuracy of the numerical simulation in this study was also verified as shown in Figure 9. First, to verify the accuracy of the numerical simulation, it is known from the comparison of the numerical results to the experimental ones in Table 5 that the numerical results were on average 3% smaller than the experimental ones. After exploring the reason, it was found that the deviations occurred most from the difference between the configuration of the real test environment and that of the simulated environment. This is due to the fact that when testing a real fan, the air impedance varies according to different operating points. It is also known from the experimental results that the average fan speed during the real tests was 3% larger than the design fan speed, so that it could be closer to the real test result [34].
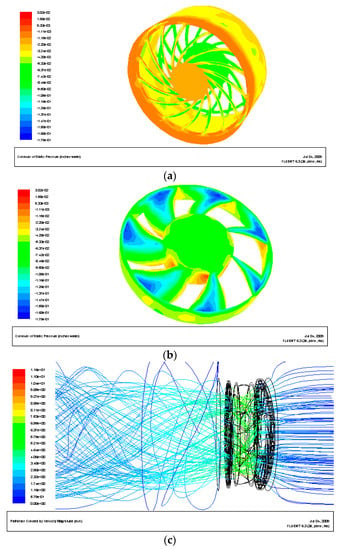
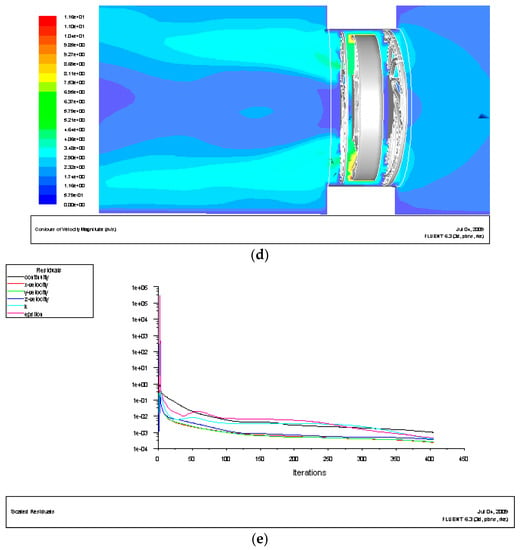
Figure 9.
Resulting plots of CFD simulation for the numerical fan model. (a) Pressure distribution on top and bottom covers; (b) pressure distribution on the fan; (c) distribution of stream lines; (d) distribution for flow field; and (e) program convergence plot.

Table 5.
Comparison of the numerical simulation result and the experimental result.
By comparing the numerical simulation results to the experimental results, the non-dimensional air velocity at the inlet, as shown in Figure 10, served as a good reference for analyzing the flow field distribution of these six opening patterns. From the average value at the inlet and the pulse velocity distribution, the correct air velocity can be determined from Figure 10. The results indicated that the deviation of the non-dimensional velocity at the inlet 4H was the same for the six opening patterns on the boundary. Therefore, the mesh structure was valid for the simulation in this study.
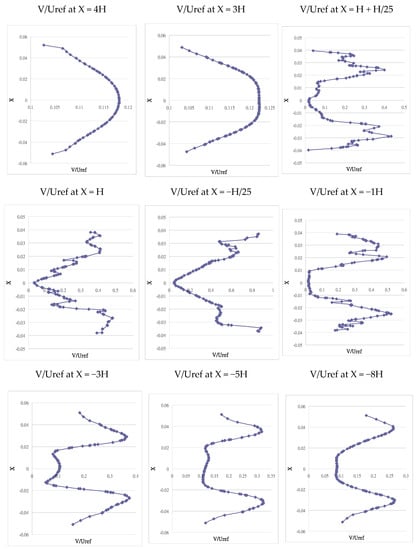
Figure 10.
Non-dimensional velocity V/Uref at nine planes along the vertical centerline of the model for the numerical simulation.
Figure 11 indicates the non-dimensional velocity V along the vertical direction from A to I. Since the air flow rate of a fan is affected by the gaps at the outlet, the relative location of the intake channel is different according to its air velocity. The velocity component of the six curves on 4H in Figure 11 was consistent with those in Figure 10. The velocity component V at 10 mm in front of the fan was almost uniform. The variation in the air velocity was due to the interference of the direction of the rear gaps. At a distance of −1H, the velocity started to vary and the change in the air velocity was in the same direction. A similar trend could be observed at the eight vertical lines at the rear end of −3H. The V component was larger at both the left and right sides and was negative at the centerline of the fan. It is known that the magnitude of the velocity component at −5H is relatively smaller than the left and right sides. The results also indicated that the velocity component of the Idea-D magnitude remained at the highest air velocity from the measurement line between E and I. Under this condition, the boundary layer effect of the velocity component could be clearly observed. The magnitude of the velocity component was gradually increased and the Idea-D can be viewed as the optimal factor of the opening pattern design.
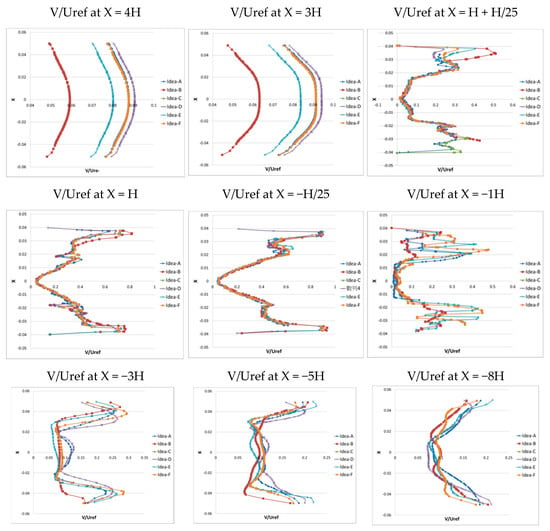
Figure 11.
Non-dimensional velocity V/Uref at nine planes along the vertical centerline of the model for the numerical simulation for these six opening patterns.
5.2. Design Cases and Comparison between Simulation Results
Figure 12 indicates the qualitative velocity distribution on the three-dimensional plane at location F of the outlet opening. The purpose of this figure is to understand the velocity pattern on these six planar regions. As the results clearly indicated a cone-shaped distribution, the velocity distribution at the outlet region was the most apparent. Moreover, Figure 12 also indicates that the out ring of the distribution of Idea-C revealed a low air velocity. In contrast, the air velocity at the peak was the highest. The Idea-D had the largest number of peaks and this indicates that this region was the region with the highest air velocity and the distribution had a more focused region in the central region. For the velocity distribution of Idea-B, E, and F, since they were affected by the non-uniform gaps, the air flow velocity was reduced. When the fan was rotating, the air layers also rotated. The air at the central region was affected by the viscosity and molecular attraction, so the rotating effect was transferred to the air on the out ring of the flow field.
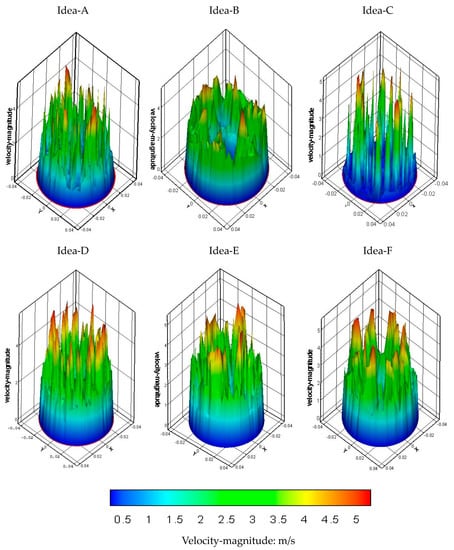
Figure 12.
Three-dimensional distribution of the air velocity at the outlet.
The results of the simulation for the six opening patterns are shown in Table 6. The effect of different opening patterns can be evaluated by a comparison of the numerical results. The variation in the flow field of six different opening patterns and the change in the performance were reviewed from the inlet and outlet of each streamline. Table 6 reveals that the high velocity regions were on the left and right sides of the flow field. This phenomenon also directly affected the outflow of the air between the blades. This is the same phenomenon that reduced the range of higher air velocity on the downstream of the fan. For Idea-A, the expansion of the opening pattern provided some improvement and became more and more apparent. The region of low air velocity extended inward so that the velocity along the inner diameter increased gradually. For Idea-B and E, the region of the highest air velocity at the outlet reduced gradually. The region of low air velocity also expanded along the downstream direction. The downstream flow field of the Idea-D honeycomb type opening still remained smooth, but not affected by the opening gap. The flow field revealed high velocity at the middle portion and downstream portion. On the overall distribution, the outlet of the impeller still remained at the high air velocity.

Table 6.
Comparison of the numerical simulation results for six different cases.
Moreover, the flow field of those six opening patterns indicated a trend of moving downstream toward the outlet. A non-ideal velocity distribution at the outlet could severely affect the total air flow rate. It is known from Table 6 that Idea-B presented a very non-uniform velocity distribution. Most of the fluid aggregated to the left and right sides of the circular region. Reverse airflow and low air velocity can be found at the central region. The total air flow rate of the fan was not greatly affected by this phenomenon, and therefore this portion could be excluded.
The comparison of the resulting flow rate of the six opening patterns is shown in Figure 13. At the outlet of Idea-D with the honeycomb shape, the flow rate obtained from the numerical simulation was 18CFM. Similarly, the resulting flow rate of Idea-A was 16CFM. Figure 13 also reveals that the air flow rate of Idea-D was 2CFM larger than Idea-A. For the static pressure, the A4 model had the highest static pressure of 1.87 mm-H2O. The result static pressure of Idea-A was 1.74 mm-H2O. From the aspect of overall air flow rate, the simulation results indicated that Idea-D had the largest air flow rate.
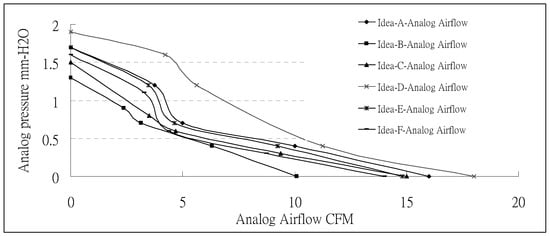
Figure 13.
Comparison of air flow rate and static pressure of new fan designs by simulation.
6. Conclusions
In this study, the aerodynamic performance of axial fans was investigated to determine the effect of different opening patterns. As the air flow rate decreases with increasing pressure, the fan’s aerodynamic performance is affected if the density of the opening pattern is increased, so the boundary layer is affected. The cross-sectional flow field of an axial fan was reviewed and investigated. The flow field could be improved by making the streamlines smoother. Some reverse flows were also observed at the outlet of the fan. Conclusions of the investigation of the flow field along the radial direction and at the outlet are as follows.
- The distribution at the inlet can be smoother.
- After passing through the inlet, the air pressure will increase at some portions about 1/2 of the impeller height.
- The maximum velocity at each cross-sectional plane occurs closer to the outlet.
- The change in the outlet location makes the air velocity increase and move toward the outlet direction.
- At the outlet plane of Idea-B, C, and E, many regions were found to have a low air velocity and recirculation. This phenomenon indicates inferior outlet conditions.
- Idea-D, with the honeycomb shape, had the most uniform air velocity among the six opening patterns. From the aspect of the leaving flow rate, it was also the most optimal opening pattern.
- If a fan is not improved by the airfoil design, the assessment can be carried out on the design factors of the outlet pattern.
There are many design parameters when desigrning the opening patterns of a fan outlet. The analysis in this study investigated six factors in order to provide future fan designs with a good reference for the optimization of the opening pattern. The results indicate that the honeycomb-shaped opening pattern can be beneficial to the performance enhancement of an axial fan. The parameters of the inlet design can also be included for further investigation on design optimization.
Author Contributions
The author contributed to the paper. H.-H.L. Collects and organizes data and acts as the corresponding author, J.-H.C. and the authors propose methods.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marinetti, S.; Cavazzini, G.; Fedele, L.; De Zan, F.; Schiesaro, P. Air velocity distribution analysis in the air duct of a display cabinet by PIV technique. Int. J. Refrig. 2012, 35, 2321–2331. [Google Scholar] [CrossRef]
- Gebrehiwot, M.G.; De Baerdemaeker, J.; Baelmans, M. Effect of a cross-flow opening on the performance of a centrifugal fan in a combine harvester: Computational and experimental study. Biosyst. Eng. 2010, 105, 247–256. [Google Scholar] [CrossRef]
- Chen, F.; Li, S.; Su, J.; Wang, Z. Experimental Study of Bowed-twisted Stators in an Axial Transonic Fan Stage. Chin. J. Aeronaut. 2009, 22, 364–370. [Google Scholar]
- Betta, V.; Cascetta, F.; Musto, M.; Rotondo, G. Fluid dynamic performances of traditional and alternative jet fans in tunnel longitudinal ventilation systems. Tunn. Undergr. Space Technol. 2010, 25, 415–422. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Ouyang, H.; Du, Z.-H. Internal flow Mechanism and Experimental Research of low Pressure Axial fan with Forward-Skewed Blades. J. Hydrodyn. 2008, 20, 299–305. [Google Scholar] [CrossRef]
- Delele, M.; De Moor, A.; Sonck, B.; Ramon, H.; Nicolaï, B.; Verboven, P. Modelling and Validation of the Air Flow generated by a Cross Flow Air Sprayer as affected by Travel Speed and Fan Speed. Biosyst. Eng. 2005, 92, 165–174. [Google Scholar] [CrossRef]
- Gebrehiwot, M.G.; De Baerdemaeker, J.; Baelmans, M. Numerical and experimental study of a cross-flow fan for combine cleaning shoes. Biosyst. Eng. 2010, 106, 448–457. [Google Scholar] [CrossRef]
- Chunxi, L.; Ling, W.S.; Yakui, J. The performance of a centrifugal fan with enlarged impeller. Energy Convers. Manag. 2011, 52, 2902–2910. [Google Scholar] [CrossRef]
- Stafford, J.; Walsh, E.; Egan, V. The effect of global cross flows on the flow field and local heat transfer performance of miniature centrifugal fans. Int. J. Heat Mass Transf. 2012, 55, 1970–1985. [Google Scholar] [CrossRef]
- Liu, S.H.; Huang, R.F.; Lin, C.A. Computational and experimental investigations of performance curve of an axial flow fan using downstream flow resistance method. Exp. Therm. Fluid Sci. 2010, 34, 827–837. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, J.; Zhang, Z. Prediction and measurement of axial flow fan aerodynamic and aeroacoustic performance in a split-type air-conditioner outdoor unit. Int. J. Refrig. 2013, 36, 1098–1108. [Google Scholar] [CrossRef]
- Hu, B.-B.; Ouyang, H.; Wu, Y.-D.; Jin, G.-Y.; Qiang, X.-Q.; Du, Z.-H. Numerical prediction of the interaction noise radiated from an axial fan. Appl. Acoust. 2013, 74, 544–552. [Google Scholar] [CrossRef]
- Owen, M.; Kröger, D.G. Contributors to increased fan inlet temperature at an air-cooled steam condenser. Appl. Ther. Eng. 2013, 50, 1149–1156. [Google Scholar] [CrossRef]
- Moonen, P.; Blocken, B.; Roels, S.; Carmeliet, J. Numerical modeling of the flow conditions in a closed-circuit low-speed wind tunnel. J. Wind Eng. Ind. Aerodyn. 2006, 94, 699–723. [Google Scholar] [CrossRef]
- Carolus, T.; Schneider, M.; Reese, H. Axial flow fan broad-band noise and prediction. J. Sound Vib. 2007, 300, 50–70. [Google Scholar] [CrossRef]
- Bredell, J.; Kröger, D.; Thiart, G. Numerical investigation of fan performance in a forced draft air-cooled steam condenser. Appl. Eng. 2006, 26, 846–852. [Google Scholar] [CrossRef]
- Hsiao, S.-W.; Lin, H.-H.; Lo, C.-H. A study of thermal comfort enhancement by the optimization of airflow induced by a ceiling fan. J. Interdiscip. Math. 2016, 19, 859–891. [Google Scholar] [CrossRef]
- Hsiao, S.W.; Lin, H.H.; Lo, C.H.; Ko, Y.C. Automobile shape formation and simulation by a computer-aided systematic method. Concurr. Eng. Res. Appl. 2016, 24, 290–301. [Google Scholar] [CrossRef]
- Lin, H.H.; Huang, Y.Y. Application of ergonomics to the design of suction fans. In Proceedings of the 1st IEEE International Conference on Knowledge Innovation and Invention, Jeju Island, South Korea, 23–27 July 2018; pp. 203–206. [Google Scholar]
- Andrea, T. On the theoretical link between design parameters and performance in cross-flow fans. A numerical and experimental study. Comput. Fluids 2005, 34, 49–66. [Google Scholar]
- Hurault, J.; Kouidri, S.; Bakir, F. Experimental investigations on the wall pressure measurement on the blade of axial flow fans. Exp. Fluid Sci. 2012, 40, 29–37. [Google Scholar] [CrossRef]
- Lin, H.H.; Hsiao, S.W. A Study of the Evaluation of Products by Industrial Design Students. Eurasia J. Math. Sci. Technol. Educ. 2018, 14, 239–254. [Google Scholar] [CrossRef]
- Shih, Y.-C.; Hou, H.-C.; Chiang, H. On similitude of the cross flow fan in a split-type air-conditioner. Appl. Eng. 2008, 28, 1853–1864. [Google Scholar] [CrossRef]
- Kim, J.-H.; Hur, N.; Kim, W. Development of algorithm based on the coupling method with CFD and motor test results to predict performance and efficiency of a fuel cell air fan. Renew. Energy 2012, 42, 157–162. [Google Scholar] [CrossRef]
- Jason, S.; Walsh, E.; Egan, V.; Grimes, R. Flat plate heat transfer with impinging axial fan flows. Int. J. Heat Mass Transfer. 2010, 53, 5629–5638. [Google Scholar]
- Greenblatt, D.; Avraham, T.; Golan, M. Computer fan performance enhancement via acoustic perturbations. Int. J. Heat Fluid Flow 2012, 34, 28–35. [Google Scholar] [CrossRef]
- Lin, H.-H. Improvement of Human Thermal Comfort by Optimizing the Airflow Induced by a Ceiling Fan. Sustainability 2019, 11, 3370. [Google Scholar] [CrossRef]
- Lin, S.-C.; Tsai, M.-L. An integrated performance analysis for a backward-inclined centrifugal fan. Comput. Fluids 2012, 56, 24–38. [Google Scholar] [CrossRef]
- Stinnes, W.H. Effect of cross-flow on the performance of air-cooled heat exchanger fans. Appl. Ther. Eng. 2002, 22, 1403–1415. [Google Scholar] [CrossRef]
- Casarsa, L.; Giannattasio, P. Experimental study of the three-dimensional flow field in cross-flow fans. Exp. Fluid Sci. 2011, 35, 948–959. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M. Development of simplified in-situ fan curve measurement method using the manufacturers fan curve. Build. Environ. 2013, 48, 77–83. [Google Scholar] [CrossRef]
- Hurault, J.; Kouidri, S.; Bakir, F.; Rey, R. Experimental and numerical study of the sweep effect on three-dimensional flow downstream of axial flow fans. Flow Meas. Instrum. 2010, 21, 155–165. [Google Scholar] [CrossRef]
- Chen, T.Y.; Shu, H.T. Flow structures and heat transfer characteristics in fan flows with and without delta-wing vortex generators. Exp. Ther. Fluid Sci. 2004, 28, 273–282. [Google Scholar] [CrossRef]
- Stafford, J.; Walsh, E.; Egan, V. Local heat transfer performance and exit flow characteristics of a miniature axial fan. Int. J. Heat Fluid Flow 2010, 31, 952–960. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).