Abstract
We introduce and discuss a dynamics of interaction of risky assets in a portfolio by resorting to methods of statistical mechanics developed to model the evolution of systems whose microscopic state may be augmented by variables which are not mechanical. Statistical methods are applied in the present paper in order to forecast the dynamics of risk/return efficient frontier for equity risk. Specifically, we adopt the methodologies of the kinetic theory for active particles (KTAP) with stochastic game-type interactions and apply the proposed model to a case study analyzing a subset of stocks traded in Milan Stock Exchange. In particular, we evaluate the efficient risk/return frontier within the mean/variance portfolio optimization theory for 13 principal components of the Milan Stock Exchange and apply the proposed kinetic model to forecast its short-term evolution (within one year). The model has the aim to pave the way to many different research perspectives and applications discussed eventually in the paper. In particular, the case of efficient frontier obtained by minimizing the Conditional Value-at-Risk (CVaR) is introduced and a preliminary result is proposed.
1. Introduction
The interest in the measurement and mathematical modelization of market risk is strongly supported by the information that it can provide to market stability and portfolio management in general. In fact, the global financial crisis of 2007–2008 raised many issues about prudential regulations and witnessed the importance of resorting to mathematical modeling to test and eventually verify regulatory rules as those of Basel Accords [1].
Financial dynamics resemble the scaling laws that characterize physical systems with large numbers of interacting units [2]. It is worth noticing that, as many complex systems, financial systems reflect the dynamic interaction of a large number of interacting agents, resulting in a systemic behaviour difficult to predict and control [3,4].
Many well established models of economic systems apply methods of statistical mechanics and many of them come from the kinetic theory of rarefied gas, thus adopting the Boltzmann Equations [5,6]. In Reference [5], for instance, power law tails of Pareto type has been retrieved for the wealth distribution obtained as quasi-stationary solution and one of the authors introduced kinetic model of welfare dynamics in Reference [7].
Methods of statistical mechanics and of the kinetic theory’s approach have been developed by Helbing, who modeled individual interactions by methods of game theory. A unified approach, suitable to link methods of the statistical mechanics, kinetic theory and game theory, is proposed in Reference [8], where master equations are derived to provide a quantitative information on the dynamics of many different social systems. Modeling the overall dynamics of modern societies, where hard sciences such as mathematics and physics can contribute to improve the quality of life is one of the main purposes of the scientific research by Helbing and coworkers [9]. A parallel approach can be found in Reference [10], which uses Boltzmann-type equations where the velocity is replaced by internal variables related to the specific social systems under consideration. Moreover, one can refer to a more specific framework of the generalized kinetic theory which is given by the Fokker-Planck approach which has been applied by various authors to modeling social sciences [11,12].
We adopt here the mathematical approach of the kinetic theory of active particles [13,14], according to which the interacting entities are called active particles, in short a-particles. In some applications, the overall system may be clustered into groups of interest called functional subsystems, while the strategy expressed by the a-particles is depicted by an internal variable at the microscopic state called activity which is heterogeneously distributed among them.
The collective state of the system is modeled by a probability distribution over the microscopic state, while the interaction dynamics is modeled by suitable developments of theoretical tools of game theory [15,16,17,18,19,20], where the main feature is that players are probability distribution and the output of interactions is delivered in probability. Moreover, applications can include space dynamics [21,22].
The development of this approach to modeling social systems, which evolved through various applications to a system approach, has been recently reviewed in References [13,14]. We recall here, as significant examples, applications to collective learning towards opinion formation, started in References [23,24,25,26,27]; support-opposition to governments [3,10,28,29,30] and competition between cells of the immune system and carriers of pathology [31,32,33,34].
We cite here Reference [4] which ends with: “The main challenge is whether and to which extent the kinetic approach is suitable for modelling and forecasting these incentives and dynamics.” In this paper we propose a basic model within the kinetic theory approach to approach the technical issue of dynamic potfolio theory, which is traditionally solved within the theory of stochastic dynamic programming, suffering, however of the “curse of dimensionality” [35].
The paper continues with four more sections and a short appendix. Section 2 introduces the basics of the Markowitz theory of portfolio management and optimization and in particular the risk/return efficient frontier whose dynamical evolution is analyzed in the paper. Section 3 describes the proposed model by introducing the mathematical structure governing the dynamics of the efficient frontier within the KTAP theory approach. The general model is then applied to a case study in which the efficient frontier is constructed by considering 13 principal components of the Milan Stock Exchange and the model is applied to forecast the time evolution of the risk distribution of 13 optimal portfolios which are derived by optimizing the return, given the risk, within the Markowitz theory approach. Section 5 discusses significant limitations of the model when applied in the context of the Markowitz portfolio theory and introduces a different possible application by considering the efficient frontier evaluated optimizing the Conditional Value-at-Risk (CVaR). A short appendix, briefly describing a fundamental property of the CVaR measure, closes the paper.
2. The Risk/Return Efficient Frontier in Portfolio Management
Market risk has been traditionally measured by the variance (or standard deviation) of portfolio returns and credit risk management adopted this point of view as well. We will discuss later in the paper different measures of risk that are now more commonly used in risk management. However, we initially set our model within the classical Markowitz portolio optimization framework [36,37], that is, using variance (or standard deviation) as a measure of risk and discuss in the paper generalizations of a coherent measure of risk [38] (see the Appendix A: CVaR as a coherent measure of risk).
We here briefly recall some basic assumptions of portfolio optimization and, at the same time, set the notation that will be used throughout the paper.
Suppose having a portfolio of n risky assets whose composition is determined by the weights , normalized such that . Markowitz portfolio theory characterizes return and risk of the portfolio through a weighted average of the first and second moment, respectively, of the time series of returns of the risky assets. Specifically, if is the i-th asset mean return and the covariance between any pair of assets i and j, the return of the portfolio of risky asset is the sum of the returns of the individual assets, scaled by the weights, that is,
and its variance is
Passing to the matrix notation, the loss is therefore
where and the superscript indicate the transpose of the vector . In our modelling setting another important quantity is the Pearson correlation coefficient, which for each pair of assets reads
with and with variance of the i-th asset in the portfolio.
Portfolio theory in the mean-variance approach is mostly based on some basic assumptions; one of them being the “compactness”of the distributions of stock returns, which can be viewed as the continuity of stock prices [39]. Of course, for instance assuming the presence of transaction costs, should mean that skewness and other higher moments shouldn’t be entirely ignored. Moreover, some dramatic events determining high percentages of loss in the stock market prices are ruled out. However, in a first approach we will consider that the conditions for mean-variance (or mean-standard deviation) apply. In the research perspectives we will discuss some details about generalizing these quite restrictive assumptions. Another point worth mentioning is that the theory assumes the normality of stock returns distributions [39]. This is not the case usually, but an argument is that even if asset returns are not exactly normal, the distribution of returns of a large portfolio should resemble a normal distribution.
Efficient Frontier
A main goal of quantitative investment managers and risk managers is to choose the proportions of various assets to be held in a portfolio by using methods of portfolio optimization, which aims to maximize a measure or proxy for a portfolio’s return contingent on a measure or proxy for a portfolio’s risk [36,37]. Basically, Markowitz theory is based on a portfolio choice problem in which one looks for the minimum risk related to a given level of return or the maximum return related to a given level of risk. Portfolios satisfying these criteria are said to be efficient and the line connecting point in the risk/return plane characterizing the risks and returns of these portfolios forms a curve called the efficient frontier. The risk/return efficient frontier characterizes the risk/return opportunities available to an investor with the minimum variance, once the return of the portfolio is fixed, or, vice versa, with the maximum return, fixed the variance, that is, the risk of the portfolio. For any portfolio below the line of the efficient frontier, there is a portfolio that has the same variance (i.e., “riskiness”) but a greater expected return, that is, it is inefficient.
3. Statement of the Problem and Derivation of the Mathematical Structure
In our model we are facing the topic regarding diversification in a portfolio, that is, the case in which investments are made in a wide variety of assets in order to limit the exposure to risk of a particular security.
Due to the fact that our focus is on diversification, we simplify our analysis to the case of idiosyncratic risk without considering systemic risk, which is non-diversifiable.
We derive a mathematical structure to model the resulting collective dynamics of n efficient portfolios of assets by adopting the KTAP approach [13,14]. The mathematical structure is the discretization of a class of integro-differential equations modelling the evolution of the probability distribution over the microscopic state of the interacting entities. By assuming the Markowitz modelling framework we characterize risk by the variance and return by the mean and, in particular, each asset represented by an a-particle possesses a microscopic characteristic representing its variance (asset volatility). The variance at the current time is evaluated from the historical time series of the market prices of the asset.
Following Reference [39], we adopt the point of view that the proper way to assess the risk of an individual asset is through its impact on the volatility of the entire portfolio.
A portfolios’ riskiness is discretized, so that it assumes n integer values , ranging from the portfolio with the lowest risk to the one with the highest risk (assuming a reasonable minimal and maximal value). As a consequence, we have chosen a discrete activity variable as a natural choice in this problem in which the activity variable is going to characterize the ‘riskiness’ of a finite and discrete number of efficient portfolios.
The overall state of the system is described, according to the KTAP approach, by the discrete probability (see Reference [7] for instance for an application in wealth distribution):
representing the (normalized) distribution of risk of a given number of efficient portfolios, say n portfolios, and satisfying the following constraint
for a fixed time interval .
From an applicative point of view, given a set of assets, we use their historical time series of market prices, and solve n optimization problems that allows one to choose n optimal portfolios among the feasible set of portfolios, each of them characterized by an increasing level of riskiness. The optimal portfolios are then the efficient ones, that is, each of them is maximizing the return given the risk (the vice versa situation of minimizing the risk, given the return follows an analogous procedure).
By balancing in the elementary volume of the space of micro-state the inlet and the outlet fluxes one gets the following system of ordinary differential equations (ODEs):
with the initial condition
An appropriate interpretation of the phenomenology is needed in order to derive the appropriate explicit expression of the following quantities:
- - the interaction rate, that is, the frequency of interactions of the test a-particle with a field a-particle;
- - the probability that the test a-particle in the h-th risk state shifts to the i-th risk state due to an encounter with a field a-particle in the k-th risk state.
Transition probabilities satisfy the following natural constraints
and the encounter rate is such that
Modelling the Dynamics of Risky Assets in a Portfolio
To derive the model for the dynamics of portfolios’ riskiness, we need to trasfer the interpretation of the phenomenology of the observed system into a heuristic specification for the transition probabilities and the interaction rates. Then, by introducing the explicit terms into the general mathematical structure (7) we get the desired model.
To set the explicit epression for the transition probabiliies, we have chosen an approach borrowing tools derived from game theory [15,16,17,18,19,20], and assuming a stochastic outcome for any binary interaction, typically related to the presence of risk, that is, to uncertainty.
The hallmarks that we use to model the transition probability density that characterizes the probability of the interacting agents to shift their riskiness status, that is, to change (by lowering or rising) their riskiness, are illustrated in the following.
When a pair of assets “interacts”, i.e., they belong to the same efficient portfolio, the output of the interaction determines a (possible) increase in riskiness if the correlation coefficient between them is positive and a (possible) decrease in the riskiness if the correlation coefficient is negative. Eventually, if the two assets are uncorrelated, there is no shift in the portfolio risk to which they belong. The frequency of interactions depends on the weights of the interacting a-particle in each portfolio. Then, we can say that each a-particle, that is, each asset in the portfolio, has binary interactions with the other a-particles, delivering a hiding-chasing stochastic game driven by the correlations between each pair of involved a-particles.
According to the above guidelines, the transition probabilities are constructed by distinguishing among three cases:
- Interactions between uncorrelated a-particles (), or of an a particle with itself ():
- Interactions between positively correlated a-particles ():
- if then
- if then
- Interactions between negatively correlated a-particles ():
- if then
- if then
It is straightforward to verify that the above introduced transition probabilities verify the properties (9,10). In proposing the basic model, binary interactions are assumed to be linear, depending on the correlation coefficient which is assumed to be the constant one measured at the current time. However, a research perspective would be that of considering that the correlation coefficient between any pair of assets updates with the time evolution of the portfolio, maybe leading to a more precise forecasting.
The encounter rate determines the frequency of interactions of pairs of a-particles, that is, of assets belonging to the same portfolio. Among different possibilities to model it, we have chosen to apply the following reasoning: the frequency of interactions roughly speaking “weights ”the effect of one asset with respect to another one in the portfolio and then, we model the encounter rate through the average of the weights of the interacting asset in the different portolios of the efficient frontier, that is,
where the vector characterizes the weights of the h-th asset, each component representing the weight in the corresponding efficient portfolio of the risk-return frontier. Then, for instance the first component of is the weight of the h-th asset in the first portfolio of the efficient frontier. It is worth noticing that by adopting this viewpoint, the frequency of interaction depends only on the test a-particle (with index h in this case).
4. A Case Study on Principal Components of Milan Stock Exchange
To derive a short-term evolution of the risk profile of n efficient portfolios we use as initial condition in the mathematical structure (7) the (normalized) frequency distribution of risk obtained by applying the Markowitz portfolio optimization, with the simplifying constraint of no short positions allowed (i.e., ), on the following randomly chosen 13 stocks traded in the Milan Stock Exchange (Table 1):

Table 1.
Stocks of the case study.
We used monthly historical time series of prices for the above listed 13 components of the FTSE.mib over a time period of 5 years, ranging from 30/06/2014 to 28/06/2019, using 61 time recording of the market prices for the above introduced 13 stocks. The histograms of distributions of logarithmic returns are summarized in Figure 1:
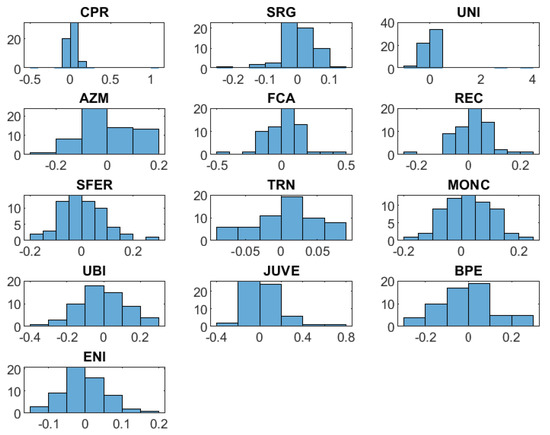
Figure 1.
Logarithmic return distributions for each stock of the panel data (logarithmic return on the abscissa and frequency on the ordinate).
where for each stock the related histogram represents the logaritmic return of the asset (i.e., with price at time t) on the market (in the abscissa) and the corresponding frequency of observation.
Among them, we derive the weights of the portfolio maximizing the Sharpe ratio , with risk-free rate of return. The risk and return of this portfolio is a point in the risk/return plane, indicated by the yellow star in Figure 2. The risk free rate has been fixed at 0.01. Although the risk proxy in mean-variance is the variance of portfolio returns, the standard deviation of portfolio returns is usually displayed, and we adopt the same notation here.

Figure 2.
Efficient frontier for the given panel of data evaluated on 13 portfolios.
5. Results and Discussion
We use the risk distribution obtained by the mean-variance optimization performed on the given panel data of stock returns as initial data in the system of Equation (7) with the proposed modellization of the probabilities of transition and encounter rate. The vector of correlation coefficients for each pair of asset has been evaluated through the covariance matrix obtained from the historical time series of the panel data for the 13 stocks of the Milan Stock Exchange given in Table 1 using a time window of 5 years. The initial condition (8) representing the risk profile for the 13 efficient portfolios obtained with the 13 stocks is graphically represented on the left of Figure 3 below. Once evaluated the matrices of transition probabilities and encounter rate, we plug them into the system of ODEs (7). A graphical representation of the solution at time (months) is showed on the right part of the figure.
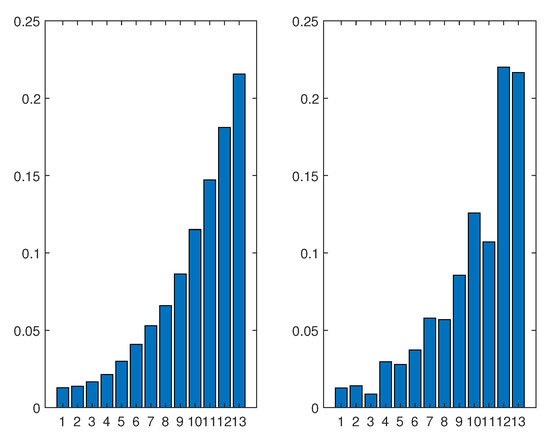
Figure 3.
Risk distribution for the 13 efficient portfolios of the risk-return frontier (on the abscissa) of the case study with the mean-variance optimization at time (left) and its evolution at the time horizon (months) (right).
Moreover, in this section we discuss future research directions within the framework of our model and propose some preliminary numerical experiments.
Basel Committee Capital Accords and the CVaR as Risk Measure
Basel Accords [1] try to define rules in order to evaluate the capital necessary to support a bank’s portfolio. Basically, regulators need to ensure clear rules to measure the minimal capital requirements. The first document has been introduced in 1988 and then revisioned in Basel II and Basel III and set the guidelines and rules for measuring, managing and reporting the banks’ risk exposures, fundamentally requiring the use of analytical approaches.
The evalution of minimal capital requirements depends on the calculation of the probability distribution of the portfolio loss. In fact, the equity capital allocated to the portfolio must be equal to the percentile of the distribution of the portfolio loss that corresponds to the desired probability (e.g., about 0.001 for the AA quality). Credit risk modelling has the goal to obtain an estimate of the risk, expressed as statistics (usually quantiles) of the potential loss distribution within a chosen time period (in the financial industry, it is usually taken as one year). At the basis of Basel Accords there is the model introduced by Vasicek [40].
There exist different measures to evaluate potential losses. Value-at-Risk (VaR), for instance, calculates the maximum potential loss at a certain confidence level (e.g., a 97.5% VaR measures a loss that is expected to be exceeded only 2.5% of the time), while Conditional Value-at-Risk (CVaR) evaluates the average loss above the same confidence level (e.g., a 97.5% CVaR measures the average of the worst 2.5% of losses). VaR calculates then the losses at a single threshold in the distribution (e.g., 97.5%), whereas CVaR averages all losses exceeding the thereshold in the distribution. For this reason, CVaR is more efficient than VaR measures to capture the tail risks. As a consequence, even if the same threshold is used, the value of CVaR is higher than the value of VaR. The importance of this point is expecially relevant in presence of fat-tailed distributions. As a consequence, in the revised risk management framework, the 97.5th percentile CVaR is roughly equivalent to the 99th percentile VaR used in Basel 2.5.
Measures of risk can be used as (extra) capital requirements to regulate the risk, however, how to measure financial risk is a long debated topic with primary focus on coherence properties [38] of the proposed quantities, in particular subaddittivity (see the Appendix B at the end of the paper).
The Basel Committee has proposed to substitute the VaR with the CVaR in the regulatory framework on market risks. Having this in mind, in the following we show the graphical representation of the efficient frontier obtained by minimizing the CVaR [41] to make the comparison with the mean/variance efficient frontier, for the proposed panel of data. To describe the probability distribution of returns we used a finite sample of return scenarios , where each is a vector that contains the returns for each of the n assets under the scenario s [41]. The efficient frontiers obtained with the mean-variance optimization (dashed-line) and with the CVaR optimization (solid line) are showed in Figure 4. Moreover, we graphically compare the weights for the 13 portfolios obtained with the two different approaches in Figure 5.

Figure 4.
Conditional Value-at-Risk (CVaR) vs mean-variance optimization for the given panel of data.
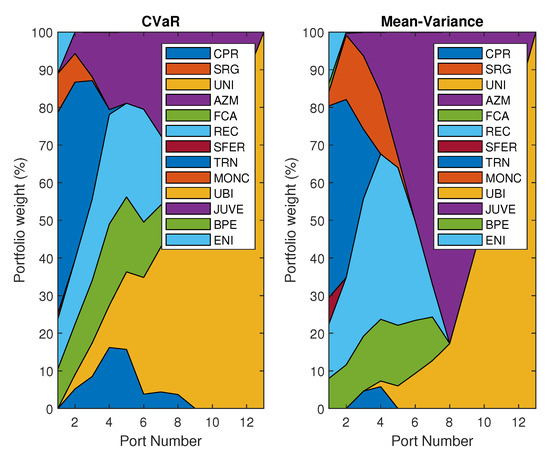
Figure 5.
Portfolio weights of CVaR VS Mean-Variance optimization for the given panel of data.
We now use the risk distribution obtained by the CVaR optimization on the same panel of stock returns as initial data in the system of Equation (7), with the proposed modellization of the transition probabilities and encounter rate and, of course, the same vector of correlation coefficients as previously. The initial condition (8) representing the risk profile for the 13 efficient portfolios obtained with the 13 stocks is graphically represented on the left of Figure 6 below. We then apply the some procedure as in the case of the mean-variance efficient frontier. A graphical representation of the solution at time (months) is showed on the right part of Figure 6.
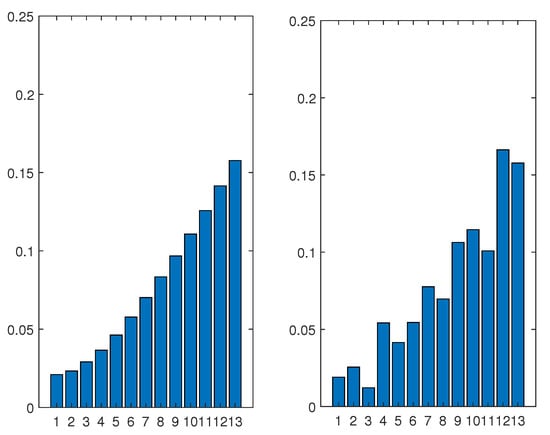
Figure 6.
Risk distribution for the 13 efficient portfolios of the risk-return frontier (on the abscissa) of the case study with the CVaR optimization at time (left) and its evolution at the time horizon (months) (right).
We have proposed the model in its simplest form, in order to express the underlying logic. It is worth noticing, however, that the KTAP approach is suitable to be applied in a more general way, allowing the better management of the heterogeneity of the different efficient portfolios. In particular, the concept of functional subsystem, applied by two of the authors of Reference [30], may be usefully applied to enhance the effect of the heterogeneity of the portfolios and of possible network interactions among them. Another research perspective might be that of introducing non linear transition probabilities by considering that the correlation coefficient between any pair of assets updates with the time evolution of the portfolio, so that it will depend of the probability distribution of the activity variable itself. This source of nonlinearity would allow the model to be more consistent with real-world features of the market. Introducing a continuous probability distribution for the activity variable representing risk would also lead to interesting research perspectives, mainly from a mathematical point of view. Finally, we just notice here that we have simply chosen randomly the basket of stocks among the 30 principal components of the Milan Stock Exchange. However, basing on the theory of portfolios’ management, we imagine that the more the distribution of returns of a stock differs from a normal distribution, the more the two methods based on VaR or CVaR differ. Of course, this simple intuition has to be supported by quantitative measurements and we plan to investigate in this direction in a next future.
Author Contributions
Conceptualization, M.D., L.L. and E.M.; Methodology, M.D.; Supervision, L.L. and E.M.; Writing—original draft, M.D., L.L. and E.M.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank the anonymous referees for their very valuable suggestions that allowed us to increase the quality of the final version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. CVaR as a Coherent Measure of Risk
Conditional Value-at-Risk, known also as Expected shortfall (ES), is a coherent measure of risk used to evaluate the credit risk of a portfolio. CVaR at the % level, is the portfolio return in the worst % of cases, that is, the focus is on the less profitable outcomes. If we consider a set V of real-valued random variables, a risk measure is a real-valued function . Sub-addittivity provides that
with the simple meaning of “a merger does not create risk” [38]. The global risk of a portfolio will always be less than the sum of its partial risks due to diversification, unless it is equal when it is triggered by concurrent events. In any case it is not “natural” the possibility that the global risk is higher than the sum of the partial risks. In Reference [42] one can find the simple example of a bank made of several branches; once the capital requirement of each branch is evaluated, the regulator has to be confident that also the overall bank capital is an adequate one, without allowing the possibility that the whole bank risk turn out to be much bigger than the sum of the branches’ risks. Moreover, a measure of risk should consider the entire shape of the tail of losses beyond the VaR [43], such as in the case of CVaR
measuring the mean of losses conditional to the exceedence of the VaR. One could also express the CVaR with the analytical formula
so that the CVaR with level of confidence is the average of all the VaR with confidence.
Appendix B. Materials and Methods
All data and computer codes associated with the publication are available to readers. Monthly historical series of prices have been downloaded from the website Yahoo Finance (https://it.finance.yahoo.com). Efficient frontiers, both using the mean-variance approach and the CVaR portfolio optimization, have been evaluated using the Financial Toolbox and the Optimization Toolbox of Matlab. The Cauchy’s problem given by the ODEs (7), with the transitions probabilities and encounter rate (12)–(17) and with the initial conditions (8) given by the risk of the efficient portfolios, has been solved using the Forward Euler method for differential equations. All graphs have been plotted using Matlab.
References
- Basel Committee on Banking Supervision 2005. International Convergence of Capital Measurement and Capital Standards, a Reviewed Framework. Available online: https://www.bis.org/publ/bcbs128.htm (accessed on 9 June 2019).
- Lux, T.; Marchesi, M. Scaling and criticality in a stochastich multi-agent model of a financial market. Nature 1999, 397, 498–500. [Google Scholar] [CrossRef]
- Dolfin, M.; Leonida, L.; Outada, N. Modeling human behavior in economics and social science. Phys. Life Rev. 2017, 22–23, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Kapetanios, G.; Muzzupappa, E. Regulatory capture and financial crisis. Phys. Life Rev. 2017, 22–23, 44. [Google Scholar] [CrossRef] [PubMed]
- Cordier, S.; Pareschi, L.; Toscani, G. On a kinetic model for a simple market economy. J. Stat. Phys. 2005, 120, 263–277. [Google Scholar] [CrossRef]
- Düring, B.; Pareschi, L.; Toscani, G. Kinetic models for optimal control of wealth inequalities. Eur. Phys. J. B 2018, 91, 265. [Google Scholar] [CrossRef]
- Dolfin, M.; Lachowicz, M. Modeling altruism and selfishness in welfare dynamics: The role of nonlinear interactions. Math. Model. Methods Appl. Sci. 2014, 24, 2361–2381. [Google Scholar] [CrossRef]
- Helbing, D. Quantitative Sociodynamics. Stochastic Methods and Models of Social Interaction Processes, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Helbing, D.; Yu, W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc. Natl. Acad. Sci. USA 2009, 106, 3680–3685. [Google Scholar] [CrossRef] [PubMed]
- Pareschi, L.; Toscani, G. Interacting Multiagent Systems: Kinetic Equations and Monte Carlo Methods; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Furioli, G.; Pulvirenti, A.; Terraneo, E.; Toscani, G. Fokker-Planck equations in the modeling of socio-economic phenomena. Math. Model. Methods Appl. Sci. 2017, 27, 115–158. [Google Scholar] [CrossRef]
- Gualandi, S.; Toscani, G. Call center service times are lognormal: A Fokker-Planck description. Math. Model. Methods Appl. Sci. 2018, 8, 1513–1527. [Google Scholar] [CrossRef]
- Ajmone Marsan, G.; Bellomo, N.; Gibelli, L. Stochastic evolutionary differential games toward a systems theory of behavioral social dynamics. Math. Model. Methods Appl. Sci. 2016, 26, 1051–1093. [Google Scholar] [CrossRef]
- Bellomo, N.; Knopoff, D.; Soler, J. On the difficult interplay between life, “complexity” and mathematicl sciences. Math. Model. Methods Appl. Sci. 2013, 23, 1861–1913. [Google Scholar] [CrossRef]
- Allen, B.; Nowak, M.A. Games on Networks. EMS Surv. Math. Sci. 2013, 1, 113–151. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Gintis, H. Game Theory Evolving, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Nash, J. Essentials of Game Theory; Elgar: Cheltenham, UK, 1996. [Google Scholar]
- Nowak, M.A. Evolutionary Dynamics. Exploring the Equations of Life; Harward University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Bellomo, N.; Bellouquid, A.; Knopoff, D. From the microscale to collective crowd dynamics. Multiscale Model. Simul. 2013, 11, 943–963. [Google Scholar] [CrossRef]
- Bellomo, N.; Ha, S.-Y. A quest toward a mathematical theory of the dynamics of swarms. Math. Model. Methods Appl. Sci. 2017, 27, 745–770. [Google Scholar] [CrossRef]
- Brugna, C.; Toscani, G. Kinetic models of opinion formation in the presence of personal conviction. Phys. Rev. E 2015, 92, 052818. [Google Scholar] [CrossRef]
- Burger, M.; Caffarelli, L.; Markowich, P. Partial differential equation models in the socio-economic sciences. Phylos. Trans. R. Soc. 2014, 372, 20130406. [Google Scholar] [CrossRef]
- Burini, D.; De Lillo, S.; Gibelli, L. Collective learning modeling based on the kinetic theory of active particles. Phys. Life Rev. 2016, 16, 123–139. [Google Scholar] [CrossRef]
- Dolfin, M.; Lachowicz, M. Modeling opinion dynamics: how the network enhances consensus. Netw. Heterogeneous Med. 2015, 10, 877–896. [Google Scholar] [CrossRef]
- Toscani, G. Kinetic models of opinion formation. Commun. Math. Sci. 2006, 4, 481–496. [Google Scholar] [CrossRef]
- Bellomo, N.; Herrero, M.; Tosin, A. On the dynamics of social conflicts: Looking for the black swan. Kinet. Relat. Models 2013, 6, 459–479. [Google Scholar]
- Bertotti, M.L.; Modanese, G. From microscopic taxation and redistribution models to macroscopic income distributions. Physica A 2011, 390, 3782–3793. [Google Scholar] [CrossRef]
- Dolfin, M.; Knopoff, D.; Leonida, L.; Maimone Ansaldo Patti, D. Escaping the trap of ‘blocking’: A kinetic model linking economic development and political competition. KInet. Rel. Mod. 2017, 10, 423–443. [Google Scholar] [CrossRef]
- Bellouquid, A.; Delitala, M. Modelling Complex Biological Sytems: A Kinetic Theory Approach, Series: Modeling and Simulation in Science, Engineering and Technology; Birkhäuser: Boston, Switzerland, 2006. [Google Scholar]
- Bellouquid, A.; De Angelis, E.; Knopoff, D. From the modeling of the immune hallmarks of cancer to a black swan in biology. Math. Model. Methods Appl. Sci. 2013, 23, 949–978. [Google Scholar] [CrossRef]
- De Angelis, E. On the mathematical theory of post-Darwinian mutations, selection and evolution. Math. Model. Methods Appl. Sci. 2014, 24, 2723–2742. [Google Scholar] [CrossRef]
- De Lillo, S.; Delitala, M.; Salvatori, M. Modelling epidemics and virus mutations by methods of the mathematical kinetic heory for active particles. Math. Model. Methods Appl. Sci. 2009, 19, 1405–1425. [Google Scholar] [CrossRef]
- Brandt, M.W. Portfolio Choice Problems. In Handbook of Financial Econometrics; Aït-Sahalia, Y., Hansen, L.P., Eds.; Elsevier: Oxford, UK, 2010; pp. 269–336. [Google Scholar]
- Markowitz, H.M. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1959. [Google Scholar]
- Artznerm, P.; Delbaen, F.; Eber, J.-M.; Heat, D. Coherent measures of risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Bodie, Z.; Kane, A.; Marcus, A.J. Investments and Portfolio Management; The Mac-Graw-Hill Europe: New York, NY, USA, 2010. [Google Scholar]
- Vasicek, O. The Distribution of Loan Portfolio Value. Risk 2002, 15, 160–172. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional Value-at-risk. J. Risk 1998, 2, 21–24. [Google Scholar] [CrossRef]
- Acerbi, C.; Scandolo, G. Liquidity risk theory and coherent measures of risk. Quant. Financ. 2008, 8, 681–692. [Google Scholar] [CrossRef]
- Christoffersen, P.F. Elements of Financial Risk Management; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).