Particle Creation and Thermal Aspects of Viscous Generalized Cosmic Chaplygin Gas
Abstract
1. Introduction
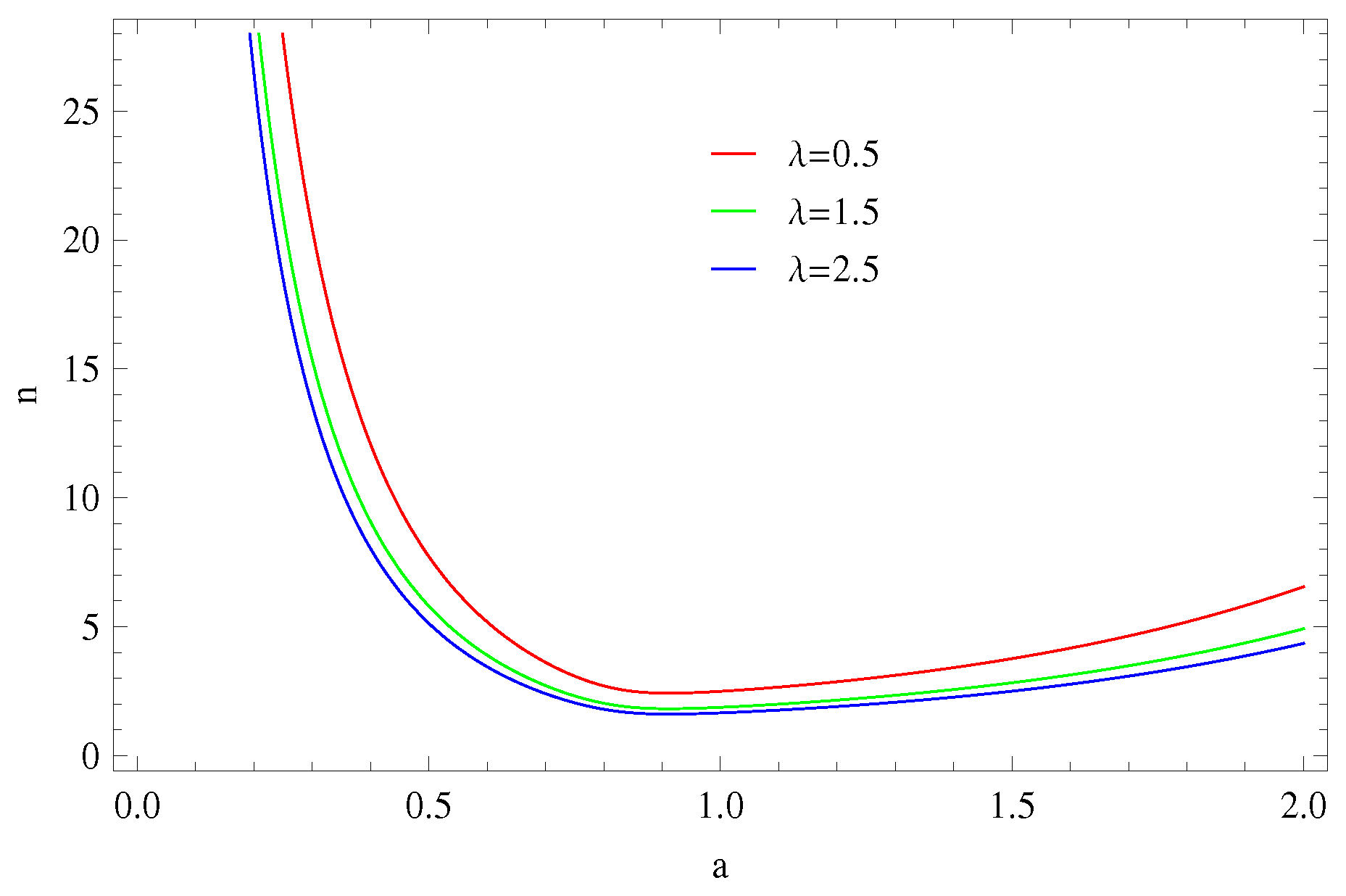
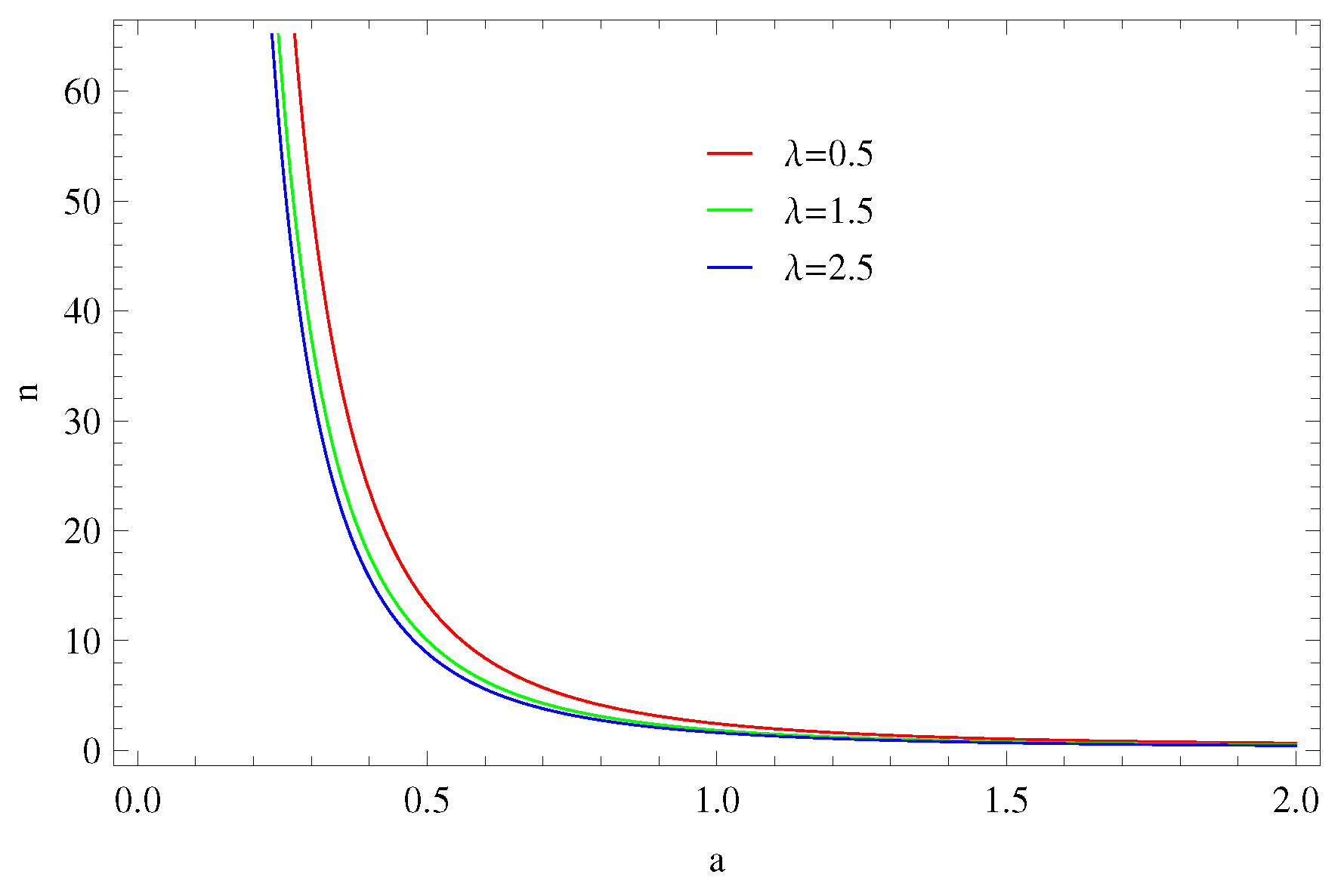
2. Particle Creation and GCCG
- Model 1:
- Model 2:
- Model 3: .
2.1. Model 1:
2.2. Model 2:
2.3. Model 3:
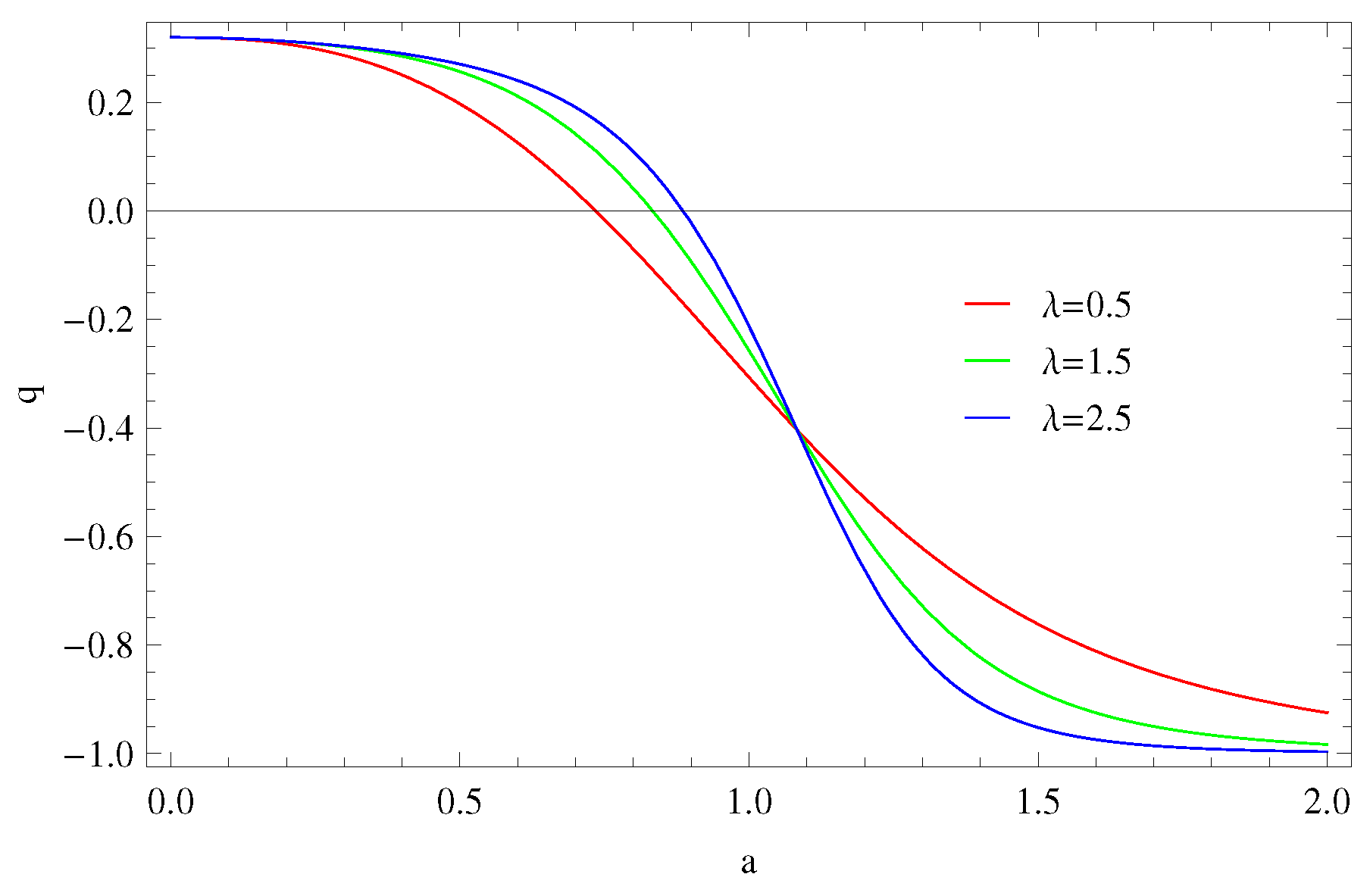
3. Entropy Production
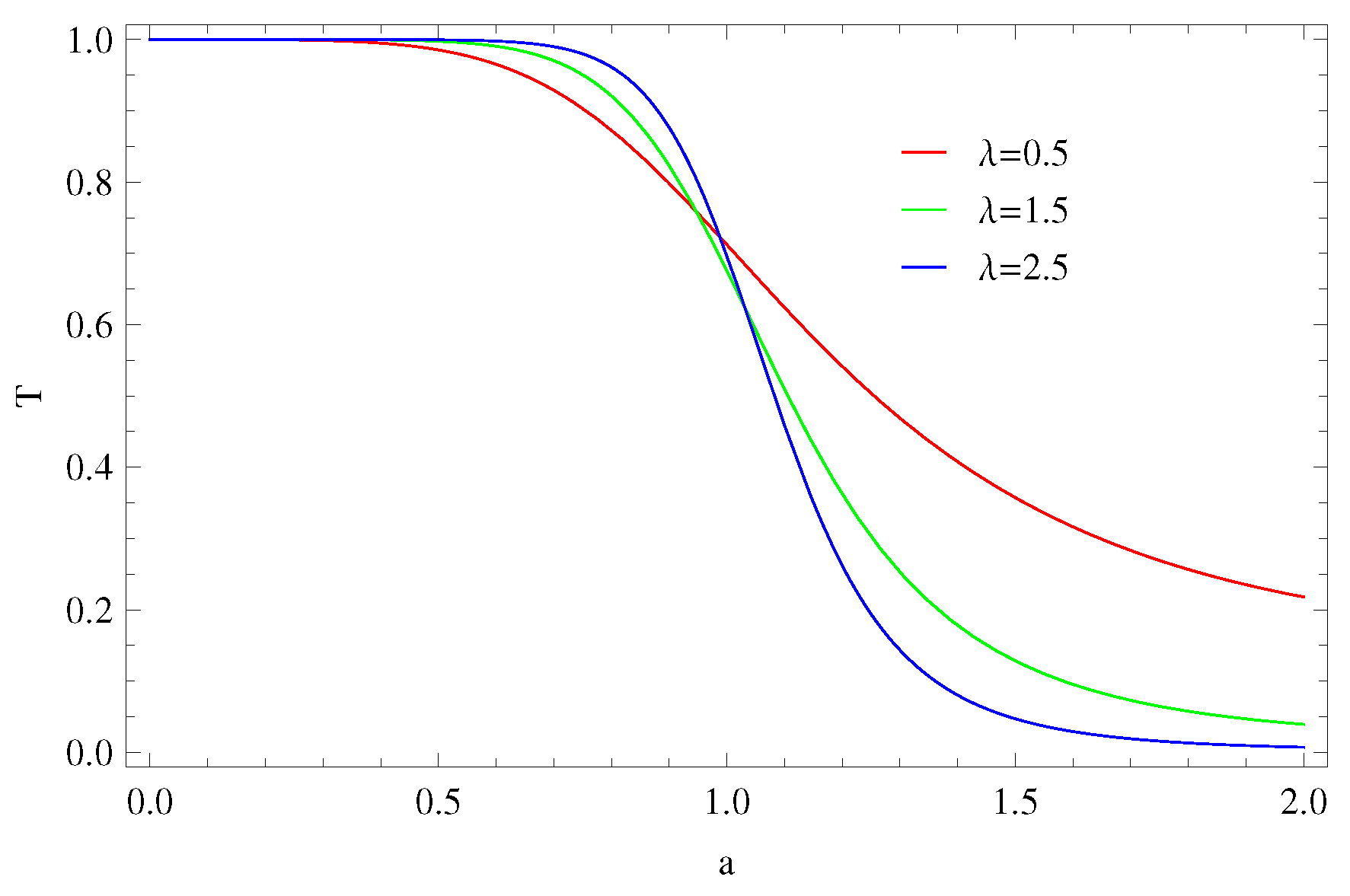
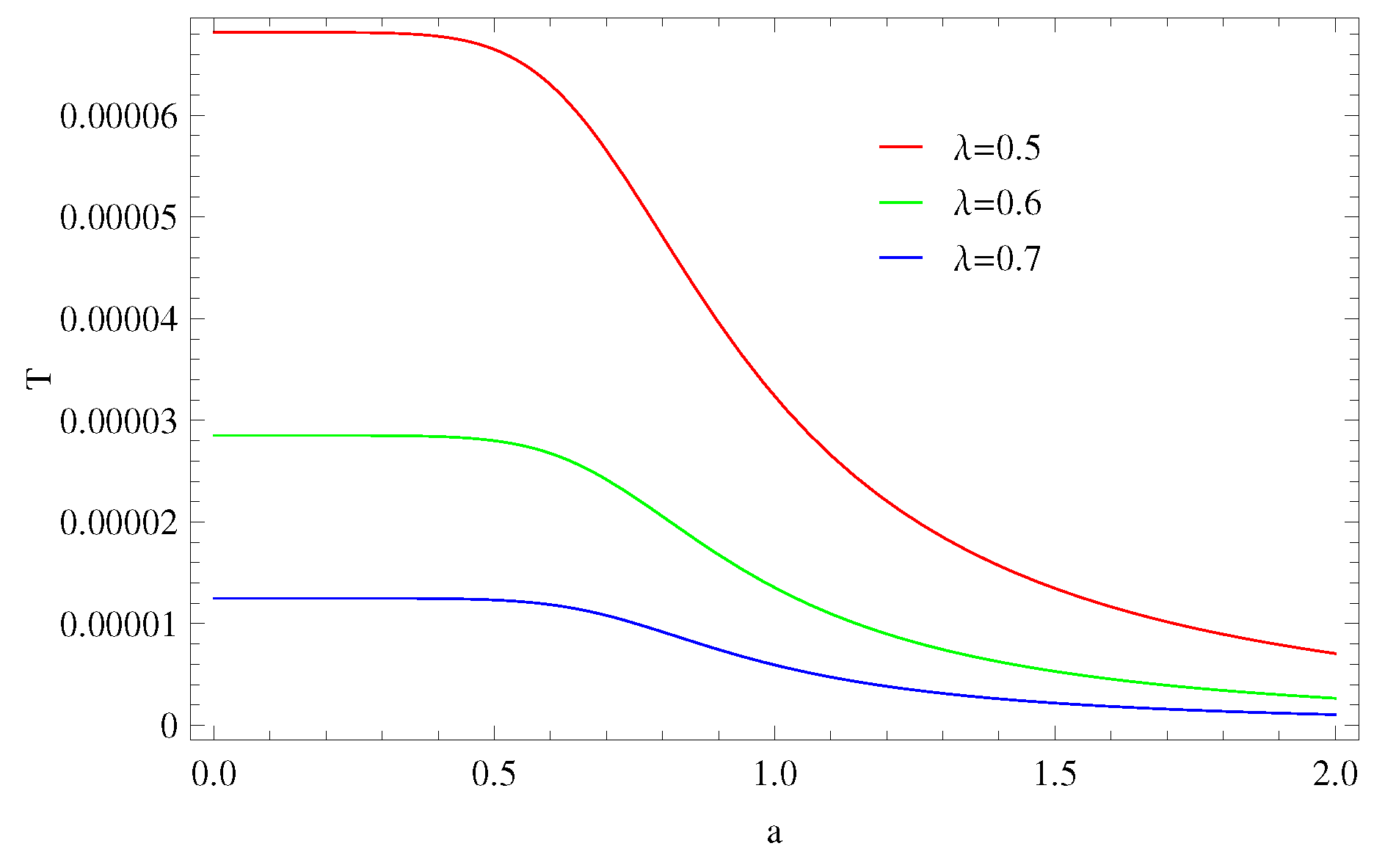
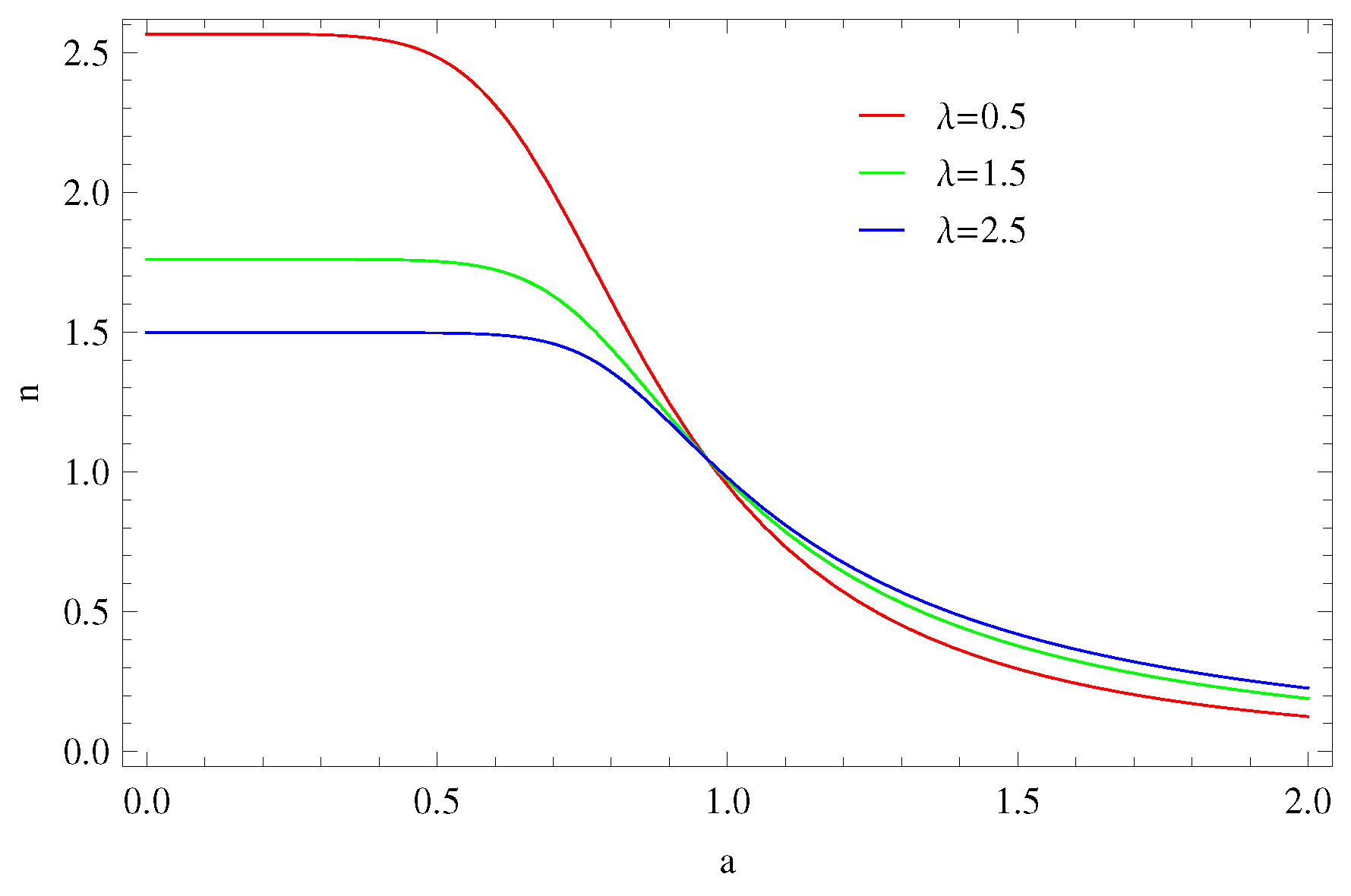
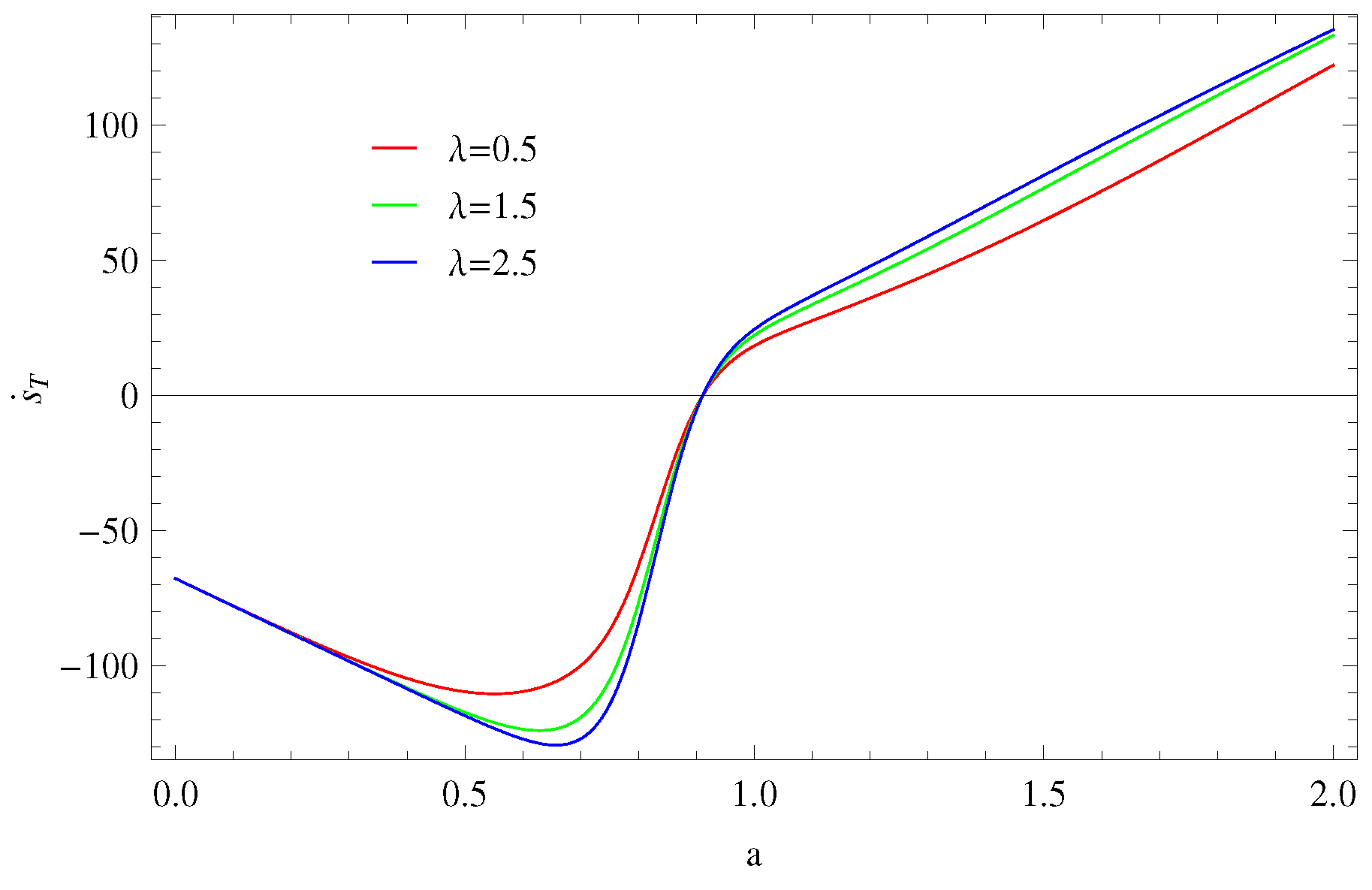
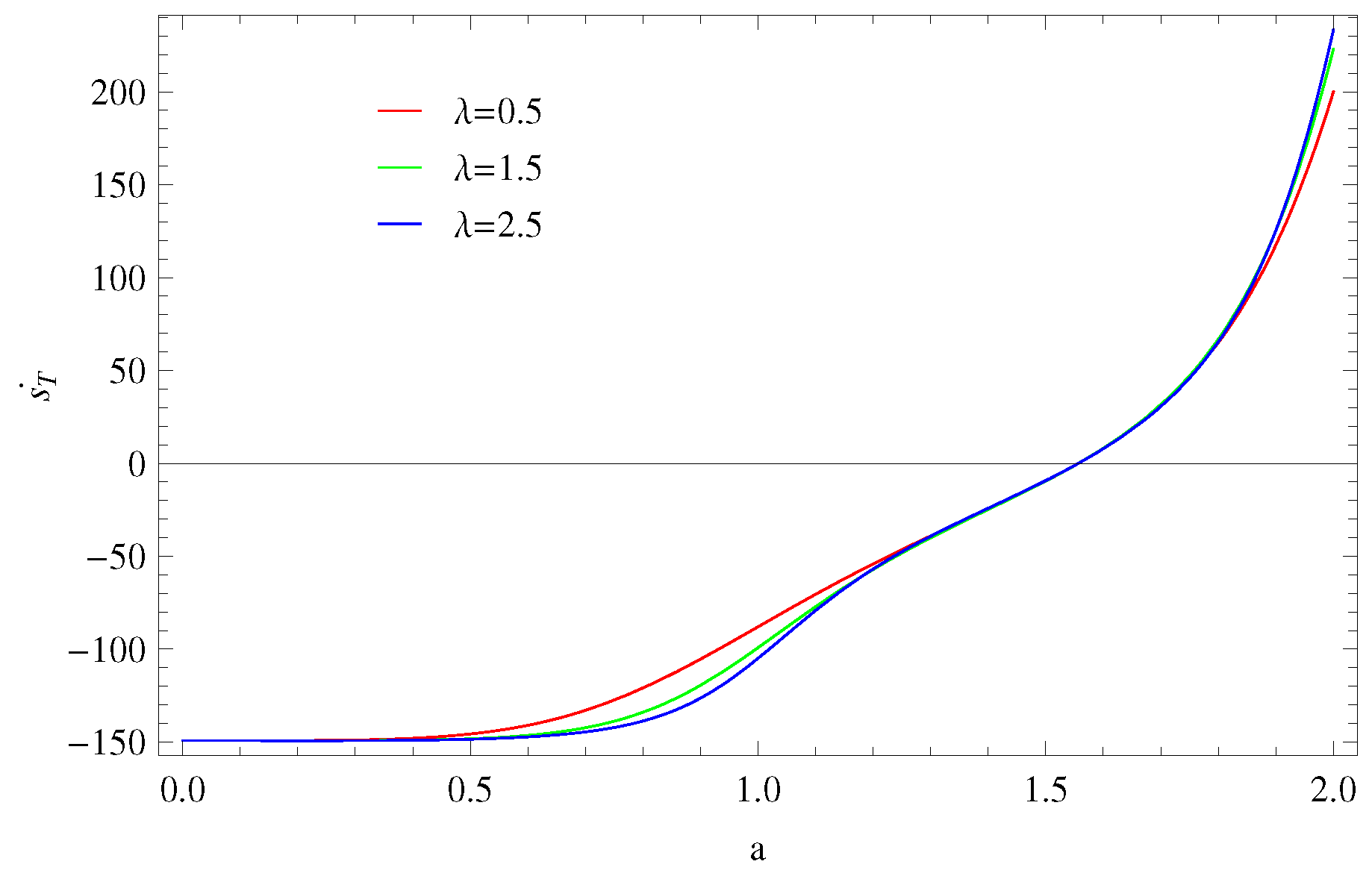
4. Thermodynamical Analysis
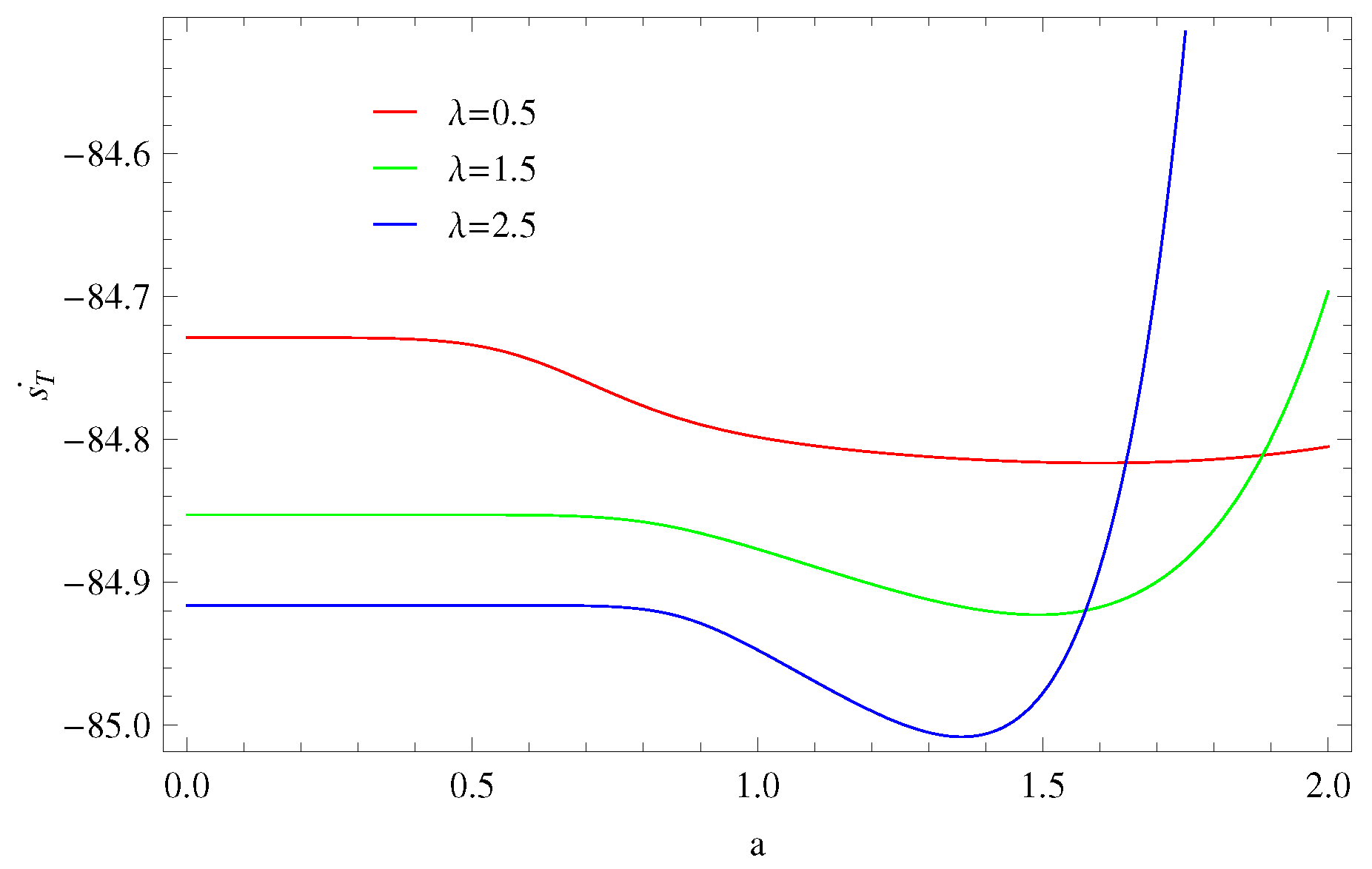
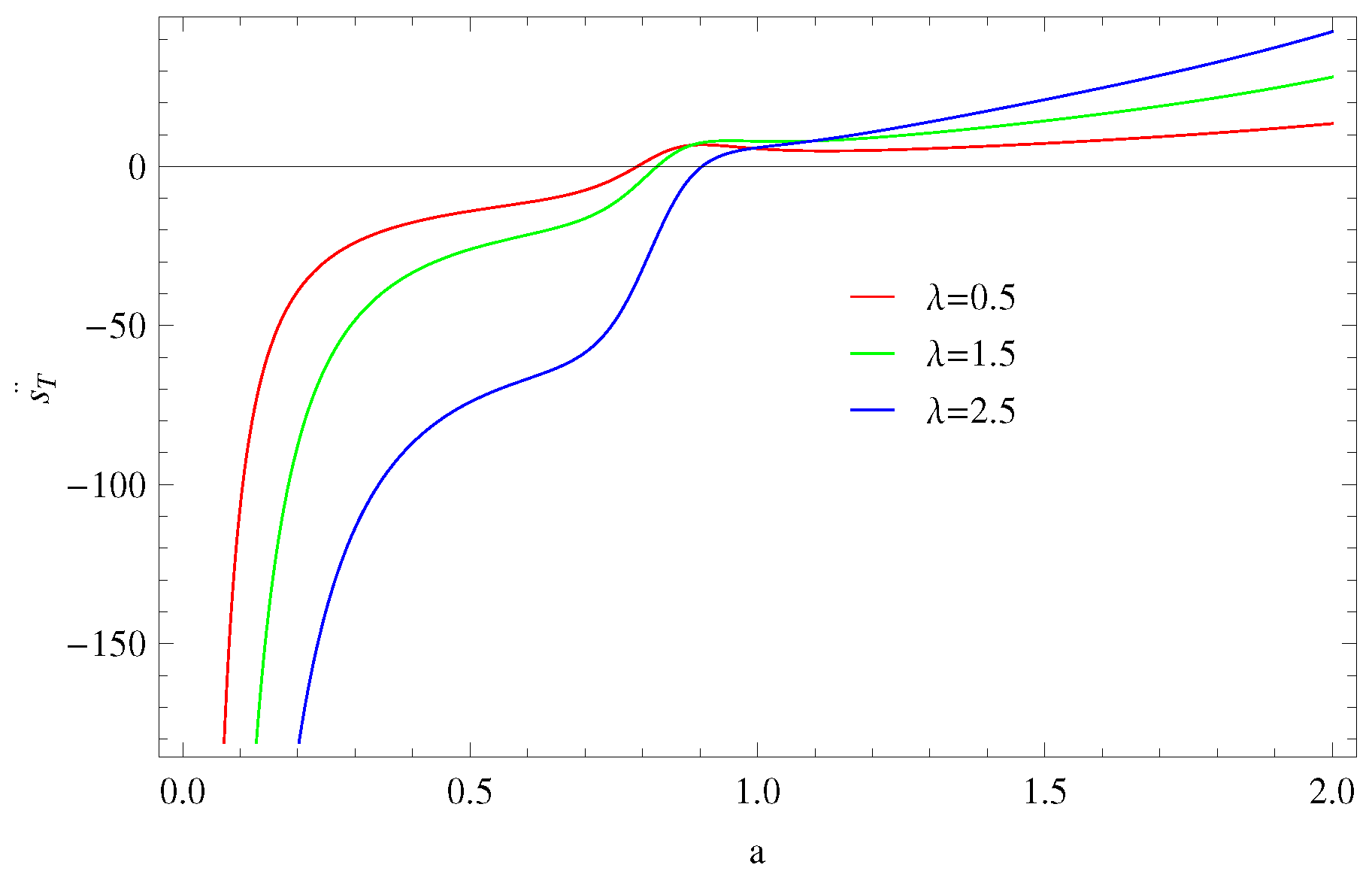
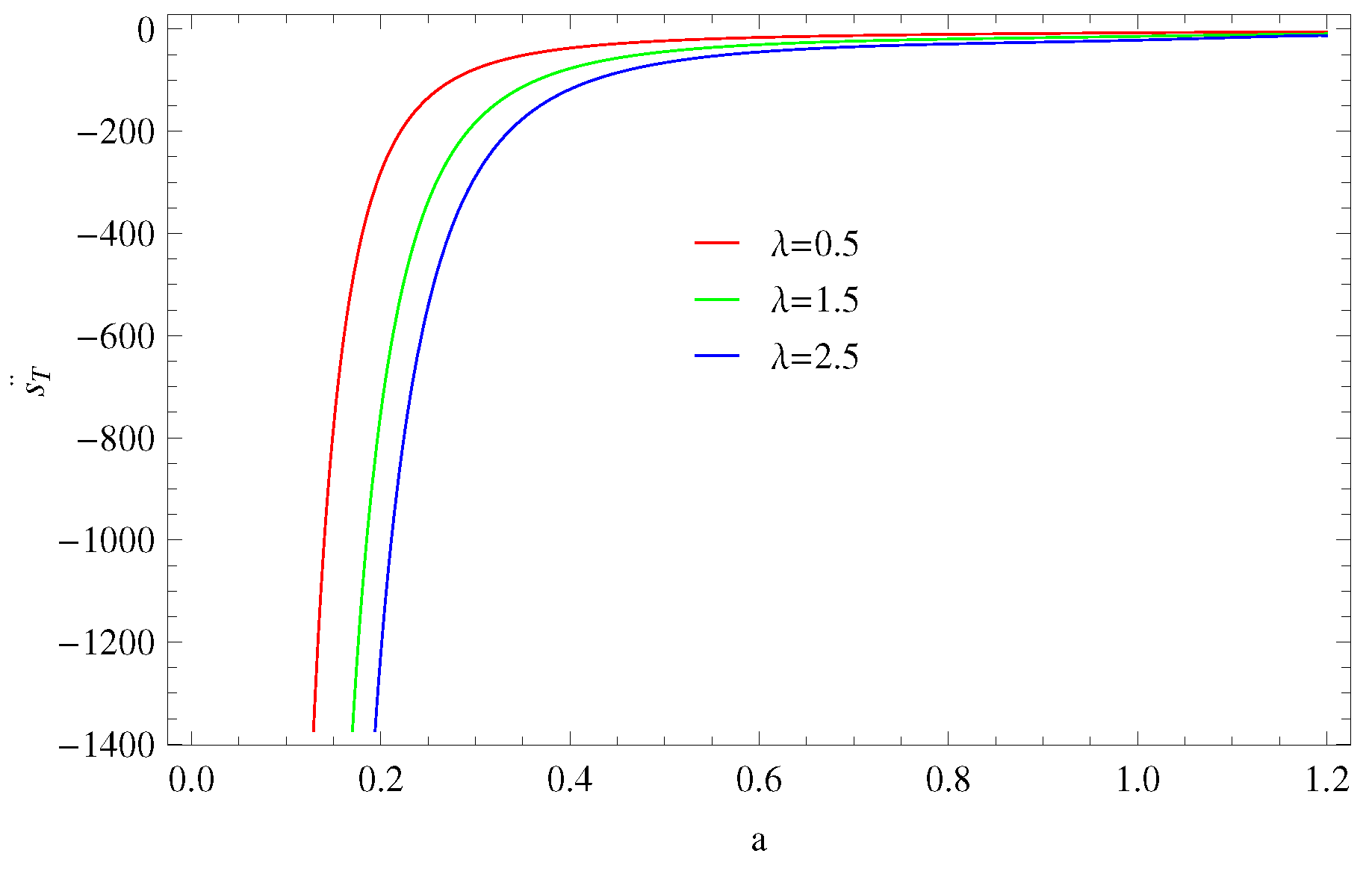
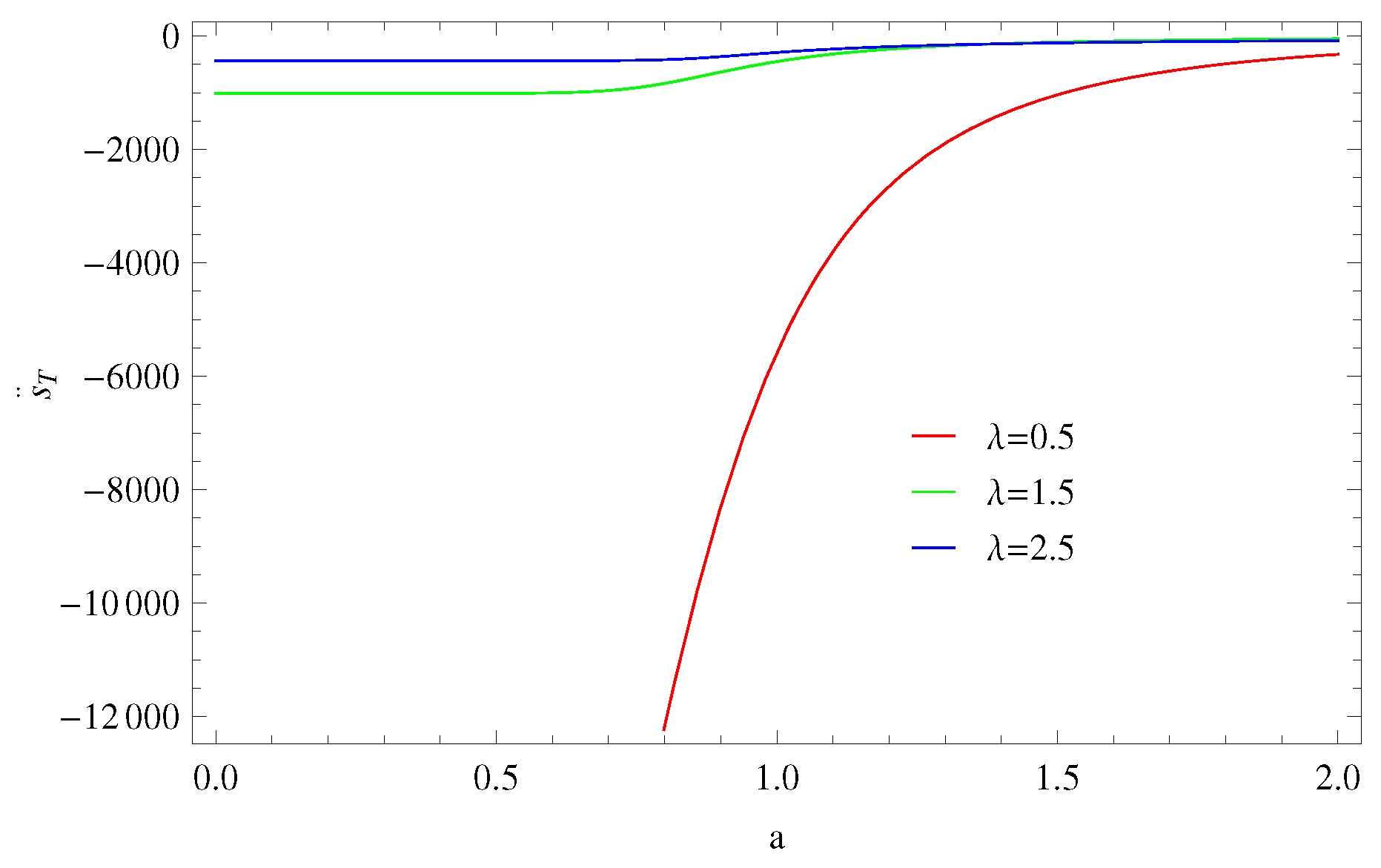
4.1. Thermal Equilibrium
4.1.1. Model 1:
4.1.2. Model 2:
4.1.3. Model 3:
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Muller, I.; Physik, Z. Zum Paradoxon der Warmeleitungstheorie. Z. Phys. 1967, 198, 329–344. [Google Scholar] [CrossRef]
- Israel, W. Nonstationary irreversible thermodynamics: A Causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J.M. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Stability and causality in dissipative relativistic fluids. Ann. Phys. 1983, 151, 446–496. [Google Scholar] [CrossRef]
- Pavon, D.; Jou, D.; Casas-Vazquesz, J. On a covariant formulation of dissipative phenomena. Ann. Inst. H Poineer Sec. A 1982, 36, 79–88. [Google Scholar]
- Pavon, D.; Bafaluy, J.; Jou, D. Causal Friedmann-Robertson-Walker cosmology. Astron. J. 1991, 8, 347. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Adelman-McCarthy, J.K.; Agüeros, M.A.; Allam, S.S.; Prieto, C.A.; Anderson, K.S.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bailer-Jones, C.A.L.; Baldry, I.K.; et al. The Sixth Data Release of the Sloan Digital Sky Survey. Astrophys. J. Suppl. 2008, 175, 297. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a Positive Cosmological Lambda-term. Int. J. Mod. Phys. A 2000, 9, 373. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. 100 years of Gravity and Accelerated Frames, The deepest insights of Einstein and Yang-Mills. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant-the weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odinstov, S.D. Late-time cosmology in a (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. D 2004, 70, 043539. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef]
- Anisimov, A.; Babichev, E.; Vikman, A. B-inflation. J. Cosmol. Astropart. Phys. 2005, 06, 006. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Turner, M.S. Making Sense of The New Cosmology. Int. J. Mod. Phys. A 2002, 17, 180–196. [Google Scholar] [CrossRef]
- Sahni, V. The Cosmological Constant Problem and Quintessence. Class. Quant. Grav. 2002, 19, 3435. [Google Scholar] [CrossRef]
- Setare, M.R. Interacting generalized Chaplygin gas model in non-flat universe. Eur. Phys. J. C 2007, 52, 689–692. [Google Scholar] [CrossRef]
- Bernardini, A.E.; Bertolami, O. Perturbative approach for mass varying neutrinos coupled to the dark sector in the generalized Chaplygin gas scenario. Phys. Rev. D 2008, 77, 083506. [Google Scholar] [CrossRef]
- Bernardini, A.E. Dynamical neutrino masses in the generalized Chaplygin gas scenario with mass varying CDM. Astropart. Phys. 2011, 34, 431–437. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Hsu, S.D.H. Entropy Bounds and Dark Energy. Phys. Lett. B 2004, 594, 13. [Google Scholar] [CrossRef]
- Li, M. A Model of Holographic Dark Energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Mimetic Gravity: A Review of Recent Developments and Applications to Cosmology and Astrophysics. Adv. High Energy Phys. 2017, 2017, 3156915. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Gauss-Bonnet dark energy. Phys. Rev. D 2005, 71, 123509. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.I.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophy. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Debnath, U.; Banerjee, A.; Chakraborty, S. Chakraborty, S. Role of Modified Chaplygin Gas in Accelerated Universe. Class. Quantum Grav. 2004, 21, 5609. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Sen, A.A.; Scherrer, R.J. Generalizing the generalized Chaplygin gas. Phys. Rev. D 2005, 72, 063511. [Google Scholar] [CrossRef]
- Benaoum, H.B. Modified Chaplygin Gas Cosmology with Bulk Viscosity. Int. J. Mod. Phys. D 2014, 23, 1450082. [Google Scholar] [CrossRef]
- Lu, J.; Xu, L.; Wu, Y.; Liu, M. Constraints on modified Chaplygin gas from recent observations and a comparison of its status with other models. Phys. Lett. B 2008, 662, 87–91. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bertolami, O.; Duvvuri, V. Chaplygin inspired Inflation. Phys. Lett. B 2006, 640, 121–125. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, P.F. You need not be afraid of phantom energy. Phys. Rev. D 2003, 68, 021303. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260. [Google Scholar] [CrossRef]
- Padmanabhan, T. Classical and Quantum Thermodynamics of horizons in spherically symmetric spacetimes. Class. Quantum Grav. 2002, 19, 5387. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Cai, R.G.; Kim, S.P. First Law of Thermodynamics and Friedmann Equations of Friedmann-Robertson-Walker Universe. JHEP 2005, 02, 050. [Google Scholar] [CrossRef]
- Banerjee, R.; Modak, S.K. Quantum Tunneling, Blackbody Spectrum and Non-Logarithmic Entropy Correction for Lovelock Black Holes. JHEP 2009, 073, 0911. [Google Scholar] [CrossRef]
- Sheykhi, A.; Jamil, M. Power-Law entropy corrected holographic dark energy model. Gen. Relativ. Gravit. 2011, 43, 2661. [Google Scholar] [CrossRef]
- Karami, K.; Ghaffari, S.; Soltanzadeh, M.M. The generalized second law of gravitational thermodynamics on the apparent and event horizons in FRW cosmology. Class. Quantum Grav. 2010, 27, 205021. [Google Scholar] [CrossRef]
- Jamil, M.; Saridakis, E.N.; Setare, M.R. Thermodynamics of dark energy interacting with dark matter and radiation. Phys. Rev. D 2010, 81, 023007. [Google Scholar] [CrossRef]
- Zeldovich, Y.A. The Neutrino Mass in Elementry particle physics and in Bing Bang Cosmology. Sov. Astron. Lett. 1981, 7, 332. [Google Scholar]
- Prigogine, I.; Geheniau, J.; Gunzig, E.; Nardone, P. Thermodynamics and cosmology. Gen. Relativ. Gravit. 1989, 21, 767. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Jesus, J.F.; Oliveira, F.A. CDM accelerating cosmology as an alternative to ΛCDM model. J. Cosmol. Astropart. Phys. 2010, 11, 027. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, S. Complete cosmic scenario from inflation to late time acceleration: Nonequilibrium thermodynamics in the context of particle creation. Phys. Rev. D 2014, 90, 123505. [Google Scholar] [CrossRef]
- Chakraborty, S. Is emergent universe a consequence of particle creation process? Phys. Lett. B 2014, 732, 81–84. [Google Scholar] [CrossRef]
- Brevik, I. Cosmology for Early- and Late-Time Universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Halder, S.; Chakraborty, S. Evolving cosmic scenario in modified Chaplygin gas with adiabatic matter creation. Ann. Phys. 2018, 388, 443–455. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S.; Rafique, S. Thermodynamics of Various Entropies in Specific Modified Gravity with Particle Creation. Eur. Phys. J. C 2018, 78, 79. [Google Scholar] [CrossRef]
- Steigman, G.; Santos, R.C.; Lima, J.A.S. An Accelerating Cosmology Without Dark Energy. J. Cosmol. Astropart. Phys. 2009, 06, 033. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Graef, L.L.; Pavon, D.; Basilakos, S. Cosmic acceleration without dark energy: Background tests and thermodynamic analysis. J. Cosmol. Astropart. Phys. 2014, 10, 042. [Google Scholar] [CrossRef]
- Chakraborty, S.; Pan, S.; Saha, S. A third alternative to explain recent observations: Future deceleration. Phys. Lett. B 2014, 738, 424–427. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pavon, D. Phantom behavior via cosmological creation of particles. Phys. Rev. D 2015, 91, 063526. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Basilakos, S. Constraints on cold dark matter accelerating cosmologies and cluster formation. Phys. Rev. D 2010, 82, 023504. [Google Scholar]
- Lima, J.A.S.; Basilakos, S.; Costa, F.E.M. New cosmic accelerating scenario without dark energy. Phys. Rev. D 2012, 86, 103534. [Google Scholar] [CrossRef]
- Jesus, J.F.; Oliveira, F.A.; Basilakos, S.; Lima, J.A.S. Newtonian perturbations on models with matter creation. Phys. Rev. D 2011, 84, 063511. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S. Cosmological consequences of an adiabatic matter creation process. Mon. Not. R. Asron. Soc. 2016, 459, 673–682. [Google Scholar] [CrossRef]
- Nunes, R.C. Connecting inflation with late cosmic acceleration by particle production. Int. J. Mod. Phys. D 2016, 25, 1650067. [Google Scholar] [CrossRef]
- Fabris, J.C.; Pacheco, J.A.F.; Piattella, O.F. Is the continuous matter creation cosmology an alternative to ΛCDM? J. Cosmol. Astropart. Phys. 2014, 06, 038. [Google Scholar] [CrossRef]
- Abramo, L.R.W.; Lima, J.A.S. Inflationary Models Driven by Adiabatic Matter Creation. Class. Quant. Grav. 1996, 13, 2953. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Pavon, D. Entropy evolution of universes with initial and final de Sitter eras. Phys. Rev. D 2013, 87, 047302. [Google Scholar] [CrossRef]
- Gunzig, E.; Maartens, R.; Nesteruk, A.V. Inflationary cosmology and thermodynamics. Class. Quant. Grav. 1998, 15, 923. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, O.; Luongo, H.Q. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Modak, S.K.; Singleton, D. Inflation with a graceful exit and entrance driven by Hawking radiation. Phys. Rev. D 2012, 86, 123515. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jawad, A.; Rani, S.; Sultan, M.A. Particle Creation and Thermal Aspects of Viscous Generalized Cosmic Chaplygin Gas. Symmetry 2019, 11, 1039. https://doi.org/10.3390/sym11081039
Jawad A, Rani S, Sultan MA. Particle Creation and Thermal Aspects of Viscous Generalized Cosmic Chaplygin Gas. Symmetry. 2019; 11(8):1039. https://doi.org/10.3390/sym11081039
Chicago/Turabian StyleJawad, Abdul, Shamaila Rani, and M. Adeel Sultan. 2019. "Particle Creation and Thermal Aspects of Viscous Generalized Cosmic Chaplygin Gas" Symmetry 11, no. 8: 1039. https://doi.org/10.3390/sym11081039
APA StyleJawad, A., Rani, S., & Sultan, M. A. (2019). Particle Creation and Thermal Aspects of Viscous Generalized Cosmic Chaplygin Gas. Symmetry, 11(8), 1039. https://doi.org/10.3390/sym11081039




