Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code
Abstract
:1. Introduction
2. Numerical Model of Combined Coal-Rock by Particle Flow Code
2.1. Particle Flow Code (PFC)
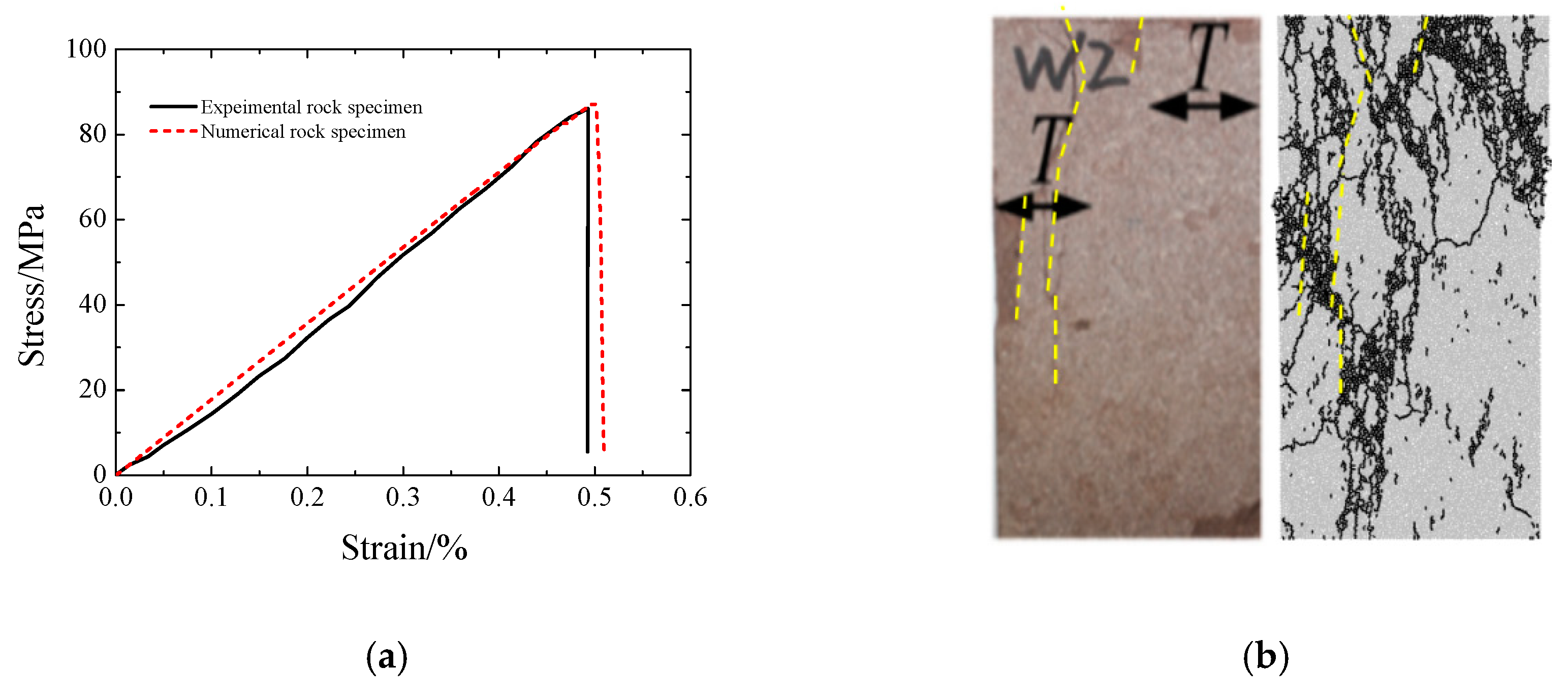
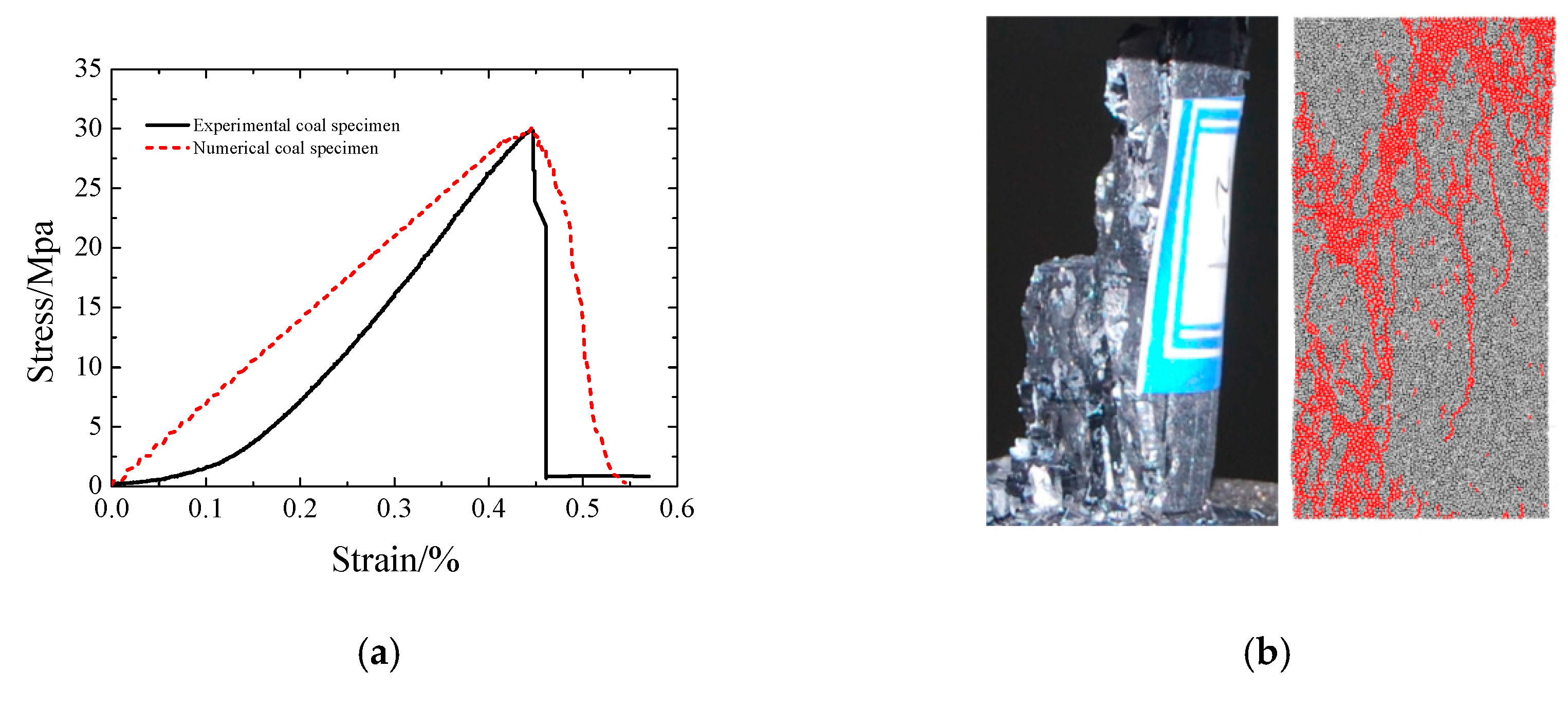
2.2. Meso-Mechanical Parameters of Combined Coal-Rock Model
2.3. Numerical Acoustic Emission (AE) Based on Bonds Breakages
2.4. Numerical Combined Coal-Rock Model
3. Result Analysis
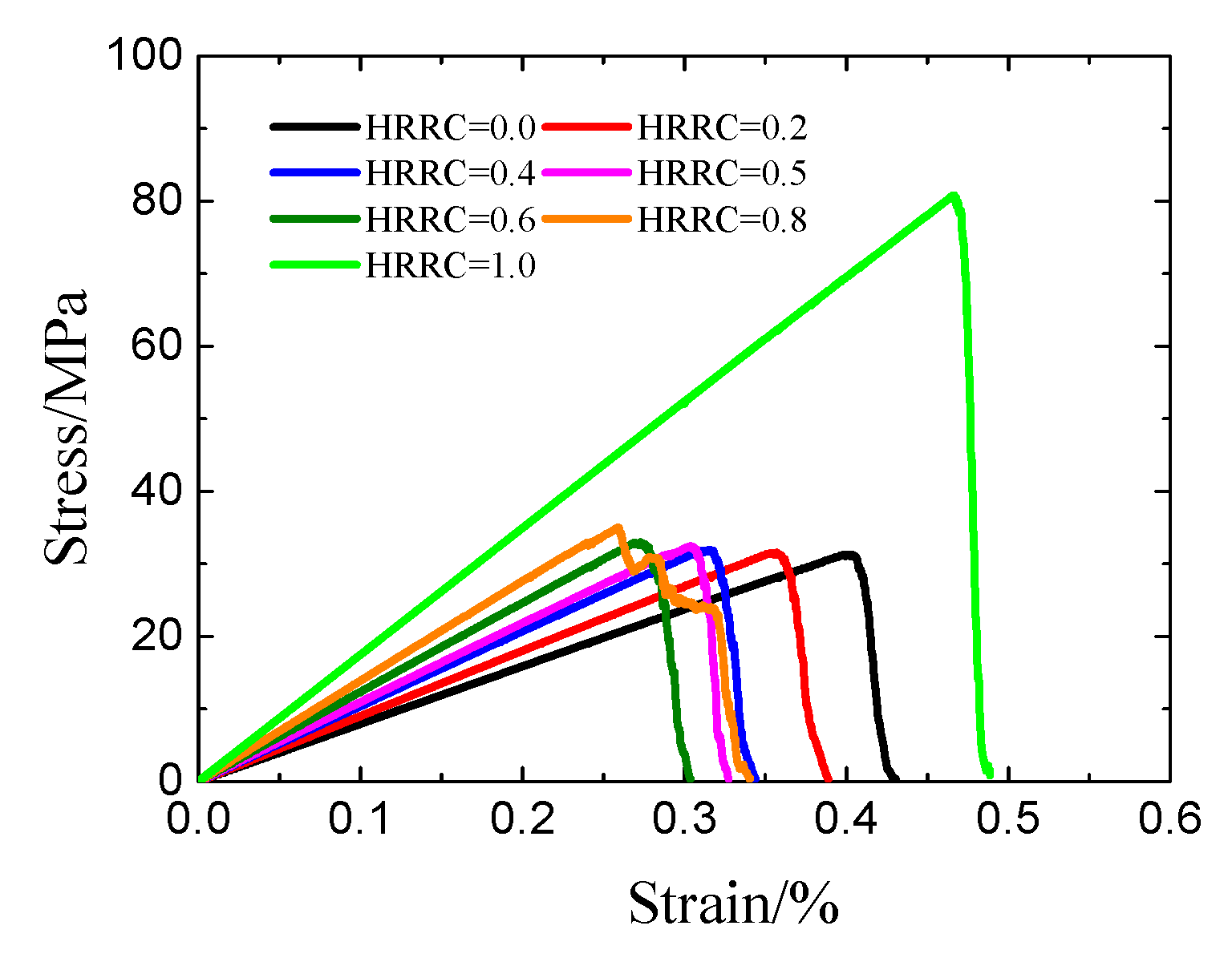
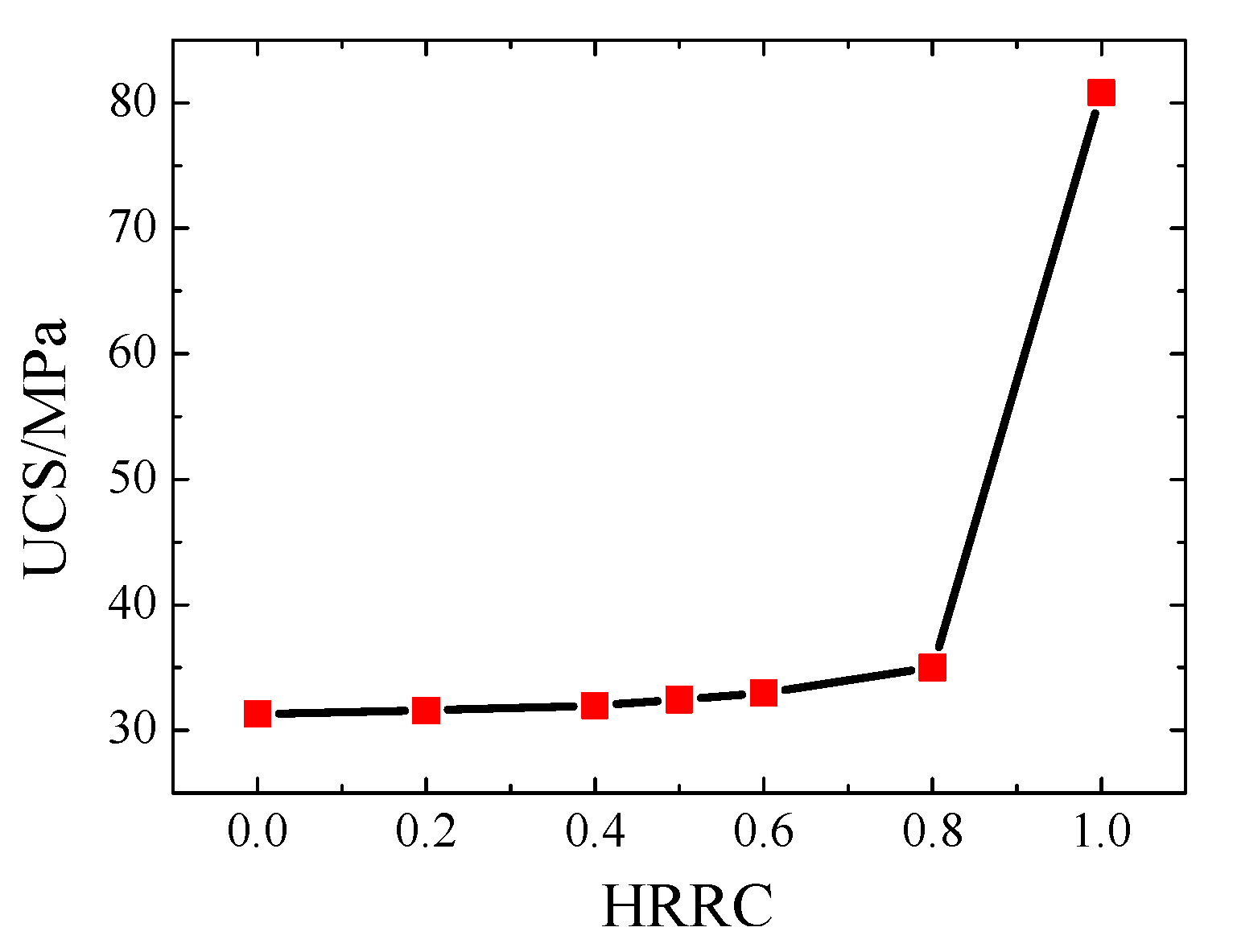
3.1. Mechanical Behavior of Coal-Rock Combined Bodies
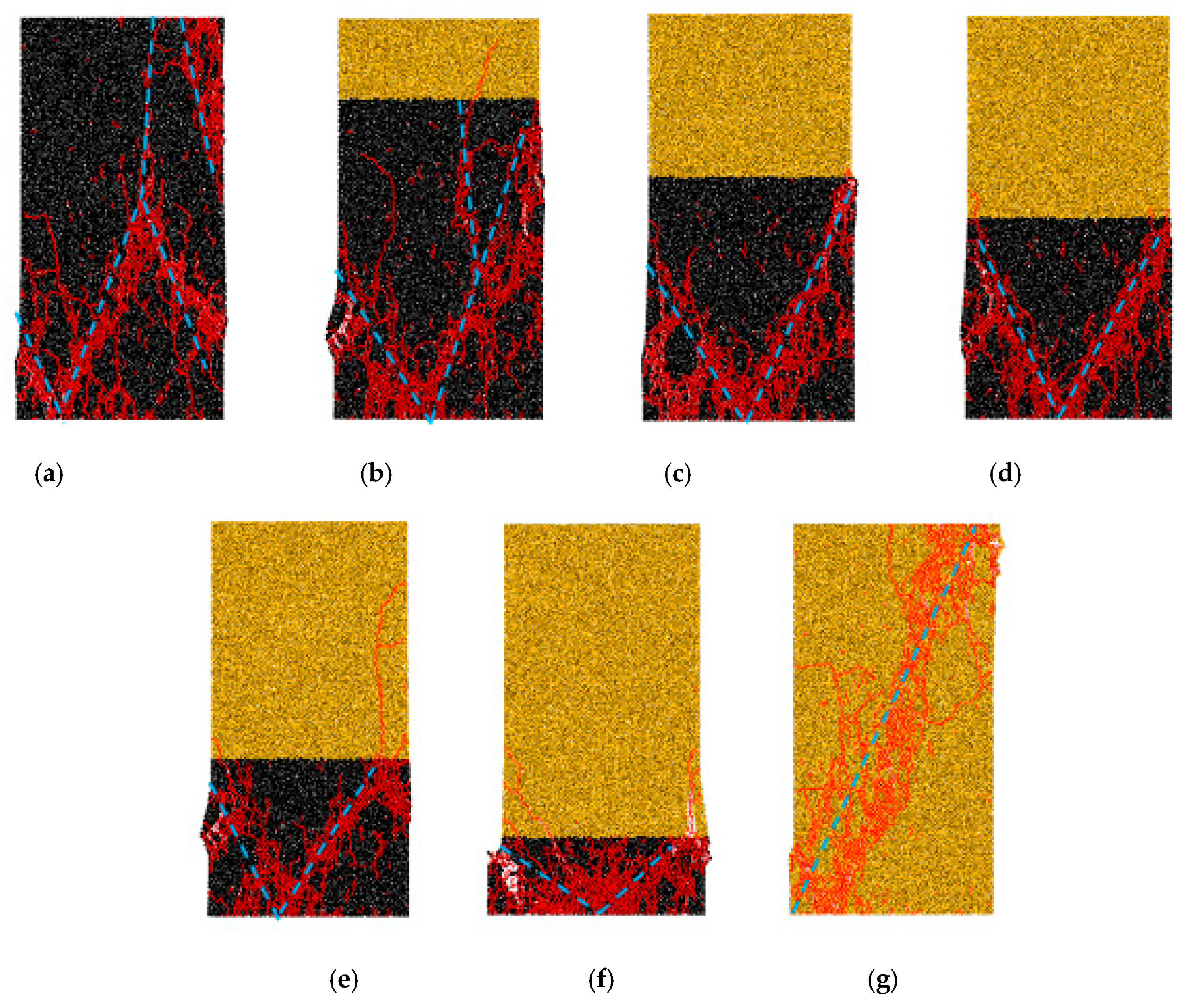
3.2. Failure Mode of Coal-Rock Combined Bodies
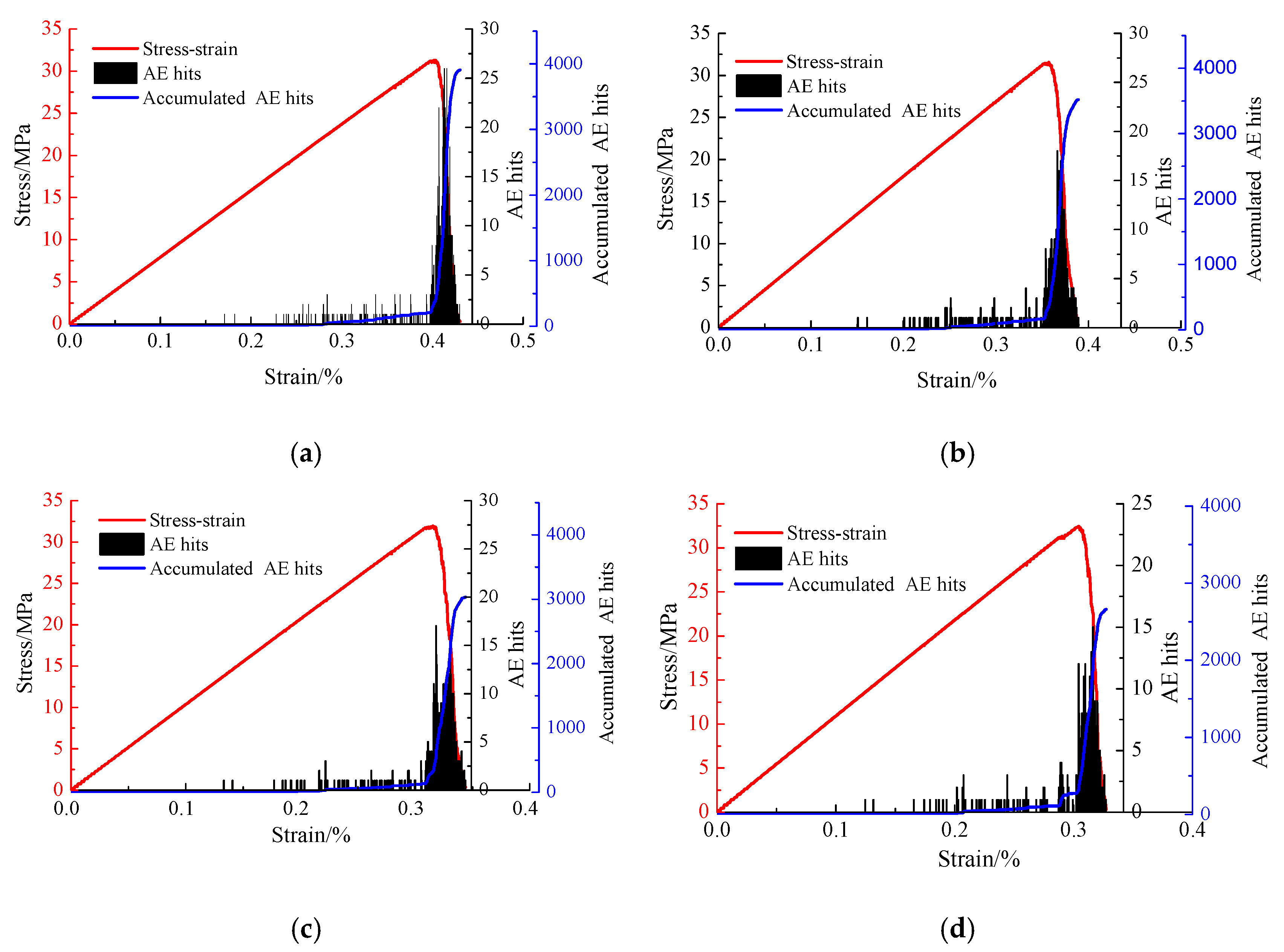
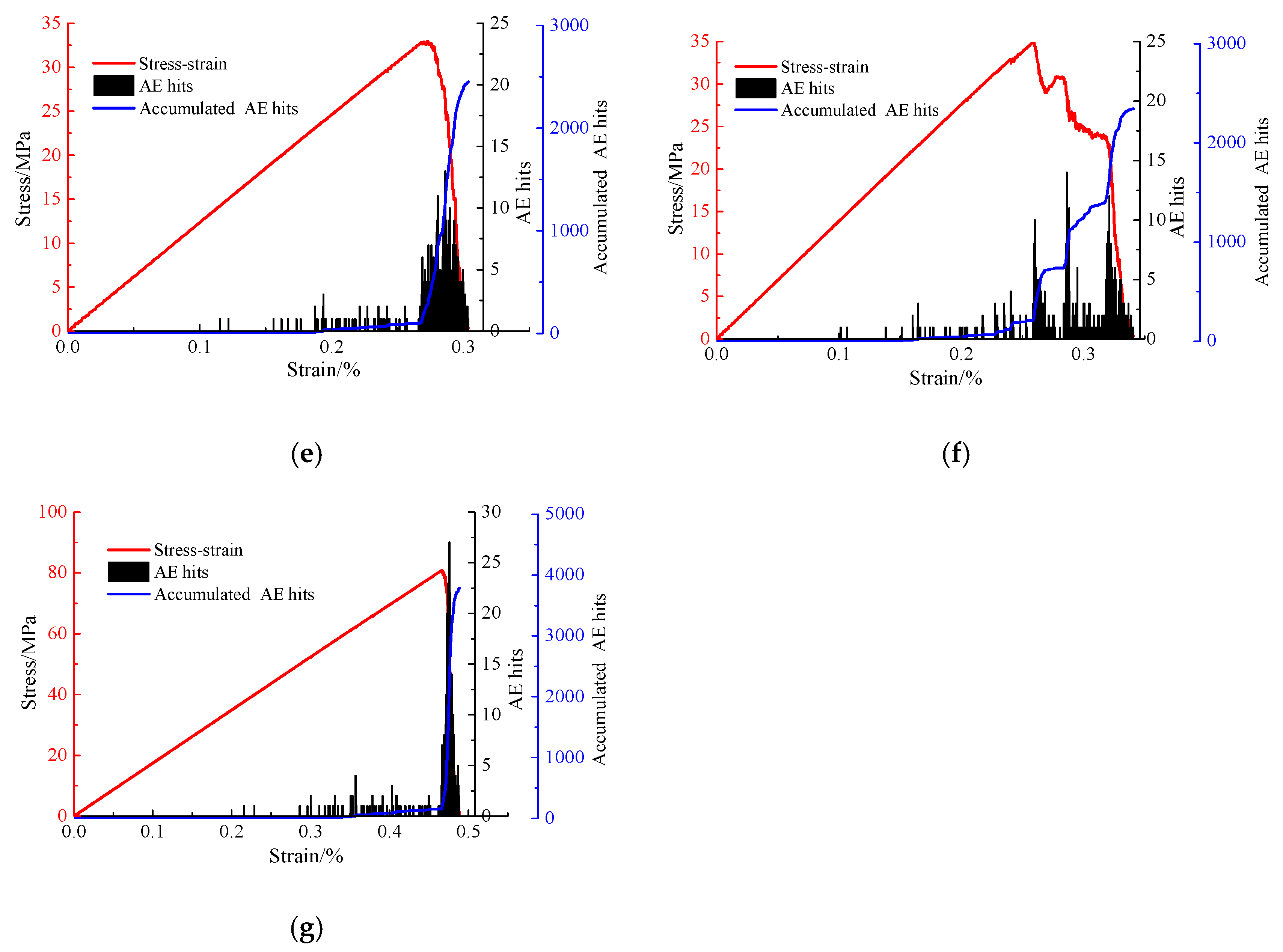
3.3. AE Characteristics of Coal-Rock Combined Bodies
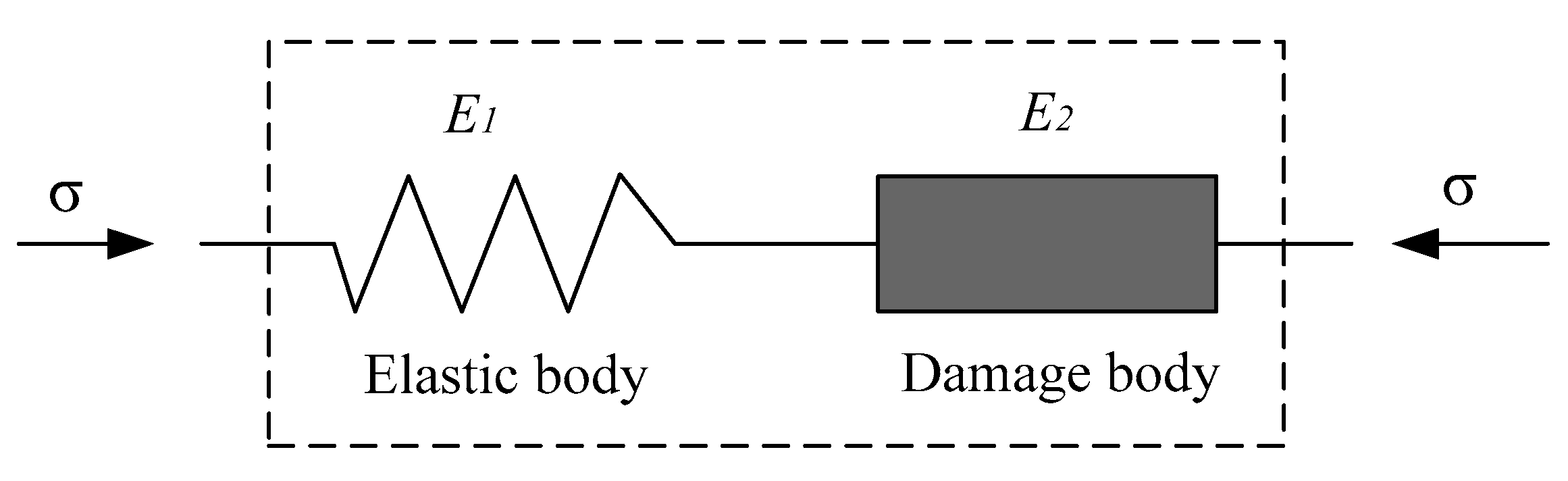
4. Damage Constitutive Model of Coal-Rock Combined Bodies
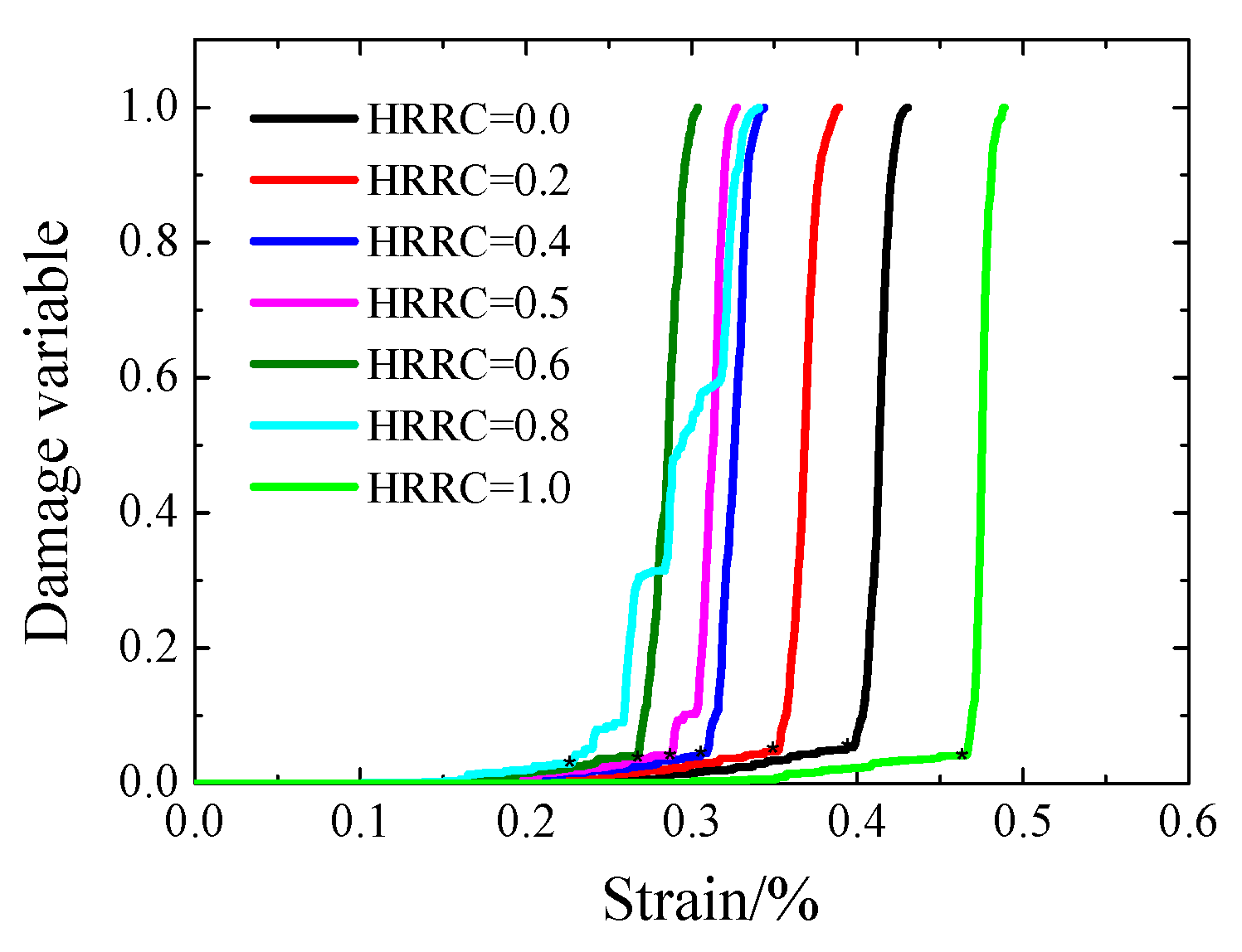
4.1. Damage Variable Based on AE Hits
4.2. Damage Constitutive Model of Coal-Rock Combined Bodies Based on AE Hits
5. Conclusions
- (1)
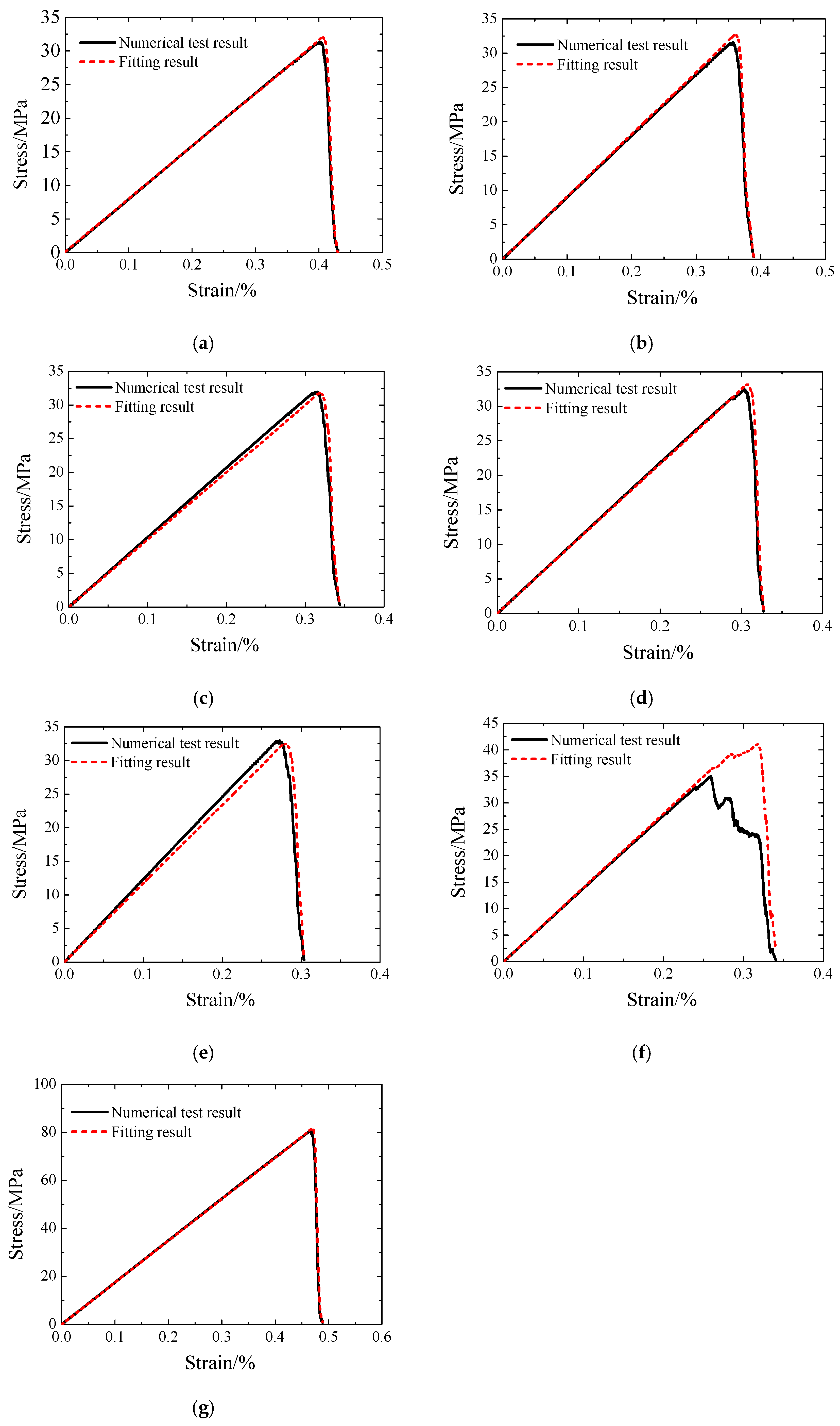
- With the increase of the HRRC, the UCS and the E of the combined coal-rock bodies increase. The difference of UCS between coal-rock combined bodies (HRRC = 0.2, 0.4, 0.5, 0.6, 0.8) and coal specimen is very small, less than 4 MPa, and this shows that the strength of the coal-rock combined bodies is mainly determined by the strength of the coal body. As for E, the increase is gradual with the increase of HRRC, and this illustrates that the influence of HRRC of coal-rock combined bodies on the E is higher than on UCS.
- (2)
- The failure of coal-rock combined bodies mainly focuses on the coal body, and this shows that the failure modes of coal-rock combined bodies are mainly controlled by the coal body. Besides HRRC = 0.0 and 1.0, the failure modes of coal-rock combined bodies are similar and have a “V” shape, and the opening of “V” become lager with the increase of the HRRC. When HRRC = 0.8, the failure parts of rock mass and coal mass expand outward, which may be the reason for the peak fluctuation of the stress-strain curve when HRRC = 0.8. When HRRC is equal to 0.0, the failure modes have an inverted “V” or inverted “Y” shape. When HRRC is equal to 1.0, the rock mass is inclined to splitting failure.
- (3)
- Apart from HRRC = 0.8, the evolution law of AE hits of coal-rock combined bodies are similar. The evolution law of AE hits of coal-rock combined bodies have three stages, named the stable stage, rapid ascending stage, and rapid descending stage. The maximum AE hits number of the stress-strain-AE hits curves and the total accumulated AE hits number decrease with the increase of HRRC (except HRRC = 1.0). As for HRRC = 0.8, the evolution law of the AE hits curve and accumulated AE hits curve is different from the others, and they fluctuate with the fluctuating of the stress-strain curve. The reason also comes from the failure modes of this coal-rock combined body.
- (4)
- The damage variable curves of coal-rock combined body have two stages, named slowly damage stage and sharply damage stage. In the slowly damage stage, with the increase of HRRC (expert HRRC = 1.0), the damage variable of the combined coal-rock bodies becomes shorter. As for the sharply damage stage, with the increase of HRRC (expert HRRC = 0.8), the damage variables of the combined coal-rock bodies are similar. The damage variable curve fluctuates in the sharply damage stage of HRRC and is equal to 0.8, and the reason for this is also related to the failure of the rock part in the coal-rock combined body.
- (5)
- The damage constitutive relation based on Equation (9) can well reflect the stress-strain relationships with a lower HRRC. However, for a higher HRRC (such as 0.8 or larger than 0.8), the damage constitutive equation is not accurately and the damage of the rock part in the coal-rock-combined body should be considered.
Author Contributions
Funding
Conflicts of Interest
References
- Skoczylas, N.; Wierzbicki, M. Evaluation and management of the gas and rock outburst hazard in the light of international legal regulations. Arch. Min. Sci. 2014, 59, 1119–1129. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Shen, B.; Sun, X.; Gao, L. Effective evaluation of pressure relief drilling for reducing rock bursts and its application in underground coal mines. Int. J. Rock Mech. Min. Sci. 2019, 114, 7–16. [Google Scholar] [CrossRef]
- Ren, F.; Zhu, C.; He, M. Moment Tensor Analysis of Acoustic Emissions for Cracking Mechanisms During Schist Strain Burst. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Guo, W.; Gu, Q.; Tan, Y.; Hu, S. Case studies of rock bursts in tectonic areas with facies change. Energies 2019, 12, 1330. [Google Scholar]
- Wang, X.; Meng, F. Statistical analysis of large accidents in China’s coal mines in 2016. Nat. Hazards 2018, 92, 311–325. [Google Scholar] [CrossRef]
- Chen, S.; Guo, W.; Zhou, H.; Shen, B.; Liu, J. Field investigation of long-term bearing capacity of strip coal pillars. Int. J. Rock Mech. Min. Sci. 2014, 70, 109–114. [Google Scholar] [CrossRef]
- Newman, D. A case history investigation of two coal bumps in the southern appalachian coalfield [C]. In Proceedings of the 21st International Conference on Ground Control in Mining, West Virginia University, Morgantown, WV, USA, 6–8 August 2002; pp. 90–97. [Google Scholar]
- Liu, J.; Tang, C.; Zhu, W.; Yang, T. Rock-coal model for studying the rockburst. Chin. J. Geotech. Eng. 2004, 26, 276–280. [Google Scholar]
- Li, J.; Qi, Q.; Mao, D.; Wang, Y. Discussion on evaluation method of bursting liability with composite model of coal and rock. Chin. J. Rock Mech. Eng. 2005, 24, 4805–4810. [Google Scholar]
- Zuo, J.; Wang, Z.; Zhou, H.; Pei, J.; Liu, J. Failure behavior of a rock-coal-rock combined body with a weak coal interlayer. Int. J. Min. Sci. Technol. 2013, 23, 907–912. [Google Scholar] [CrossRef]
- Guo, W.; Tan, Y.; Yu, F.; Zhao, T.; Hu, S.; Huang, D.; Qin, Z. Mechanical behavior of rock-coal-rock specimens with different coal thicknesses. Geomech. Eng. 2018, 15, 1017–1027. [Google Scholar]
- Agioutantis, Z.; Kaklis, K.; Mavrigiannakis, S.; Verigakis, M.; Vallianatos, F.; Saltas, V. Potential of acoustic emissions from three point bending tests as rock failure precursors. Int. J. Min. Sci. Technol. 2016, 26, 155–160. [Google Scholar]
- Shkuratnik, V.L.; Filimonov, Y.L.; Kuchurin, S.V. Experimental investigations into acoustic emission in coal samples under uniaxial loading. J. Min. Sci. 2004, 40, 458–464. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, W.; Gu, Q.; Zhao, T.; Yu, F.; Hu, S.; Yin, Y. Research on the rockburst tendency and AE characteristics of inhomogeneous coal-rock combination bodies. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Yin, D.; Chen, S.; Liu, X.; Ma, H. Effect of joint angle in coal on failure mechanical behaviour of roof rock–coal combined body. Q. J. Eng. Geol. Hydrogeol. 2018, 51, 202–209. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Procházka, P.P. Application of discrete element methods to fracture mechanics of rock bursts. Eng. Fract. Mech. 2004, 71, 601–618. [Google Scholar]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2015, 18, 1–28. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Wang, X.; Tian, L. Mechanical and crack evolution characteristics of coal-rock under different fracture-hole conditions: A numerical study based on particle flow code. Environ. Earth Sci. 2018, 77, 297. [Google Scholar]
- Liu, W. Experimental and Numerical Study of Rock Stratum Movement Characteristics in Longwall Mining. Shock Vib. 2019. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.; Tian, L.G.; Huang, D.M. Analysis of Mechanical and AE Characteristics of Rock Materials with Double-hole Defects Based on Particle Flow Code. Shock Vib. 2018. [Google Scholar] [CrossRef]
- Wang, X.; Wen, Z.; Jiang, Y. Time—Space effect of stress field and damage evolution law of compressed coal-rock. Geotech. Geol. Eng. 2016, 34, 1933–1940. [Google Scholar] [CrossRef]
- Khazaei, C.; Hazzard, J.; Chalaturnyk, R. Damage quantification of intact rocks using acoustic emission energies recorded during uniaxial compression test and discrete element modeling. Comput. Geotech. 2015, 67, 94–102. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Q.; Wu, S. Acoustic emission characteristics of the rock-like material containing a single flaw under different compressive loading rates. Comput. Geotech. 2017, 83, 83–97. [Google Scholar] [CrossRef]
- Huang, D.; Chang, X.; Tan, Y.; Zhou, J.; Yin, Y. Numerical Study of the Mechanical and Acoustic Emissions Characteristics of Red Sandstone under Different Double Fracture Conditions. Symmetry 2019, 11, 772. [Google Scholar] [CrossRef]
- Zuo, J.; Xie, H.; Wu, A.; Liu, J. Investigation on failure mechanisms and mechanical behaviors of deep coal-rock single body and combined body. Chin. J. Rock Mech. Eng. 2011, 30, 84–92. [Google Scholar]
- Murti, V.; Zhang, W.; Valliappan, S. Stress invariants in an orthotropic damage space. Eng. Fract. Mech. 1991, 40, 985–990. [Google Scholar] [CrossRef]
- Kim, J.; Yi, J.; Kim, J.; Zi, G.; Kong, J.S. Fatigue life prediction methodology using entropy index of stress interaction and crack severity index of effective stress. Int. J. Damage Mech. 2013, 22, 375–392. [Google Scholar]
- Kupchella, R.; Stowe, D.; Xiao, X.; Algoso, A.; Cogar, J. Incorporation of material variability in the Johnson Cook model. Procedia Eng. 2015, 103, 318–325. [Google Scholar] [CrossRef]
- Mizuno, M.; Okayasu, M.; Odagiri, N. Damage evaluation of piezoelectric ceramics from the variation of the elastic coefficient under static compressive stress. Int. J. Damage Mech. 2010, 19, 375–390. [Google Scholar] [CrossRef]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mech. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Wang, X.; Wen, Z.; Jiang, Y.; Huang, H. Experimental study on mechanical and acoustic emission characteristics of rock-like material under non-uniformly distributed loads. Rock Mech. Rock Eng. 2018, 51, 729–745. [Google Scholar] [CrossRef]
- Zong, Y.; Han, L.; Wei, J.; Wen, S. Mechanical and damage evolution properties of sandstone under triaxial compression. Int. J. Min. Sci. Technol. 2016, 26, 601–607. [Google Scholar]
- Liu, X.; Tan, Y.; Ning, J.; Lu, Y.; Gu, Q. Mechanical properties and damage constitutive model of coal in coal-rock combined body. Int. J. Rock Mech. Min. Sci. 2018, 110, 140–150. [Google Scholar] [CrossRef]
- Lemaitre, J.; Sermage, J.P.; Desmorat, R. A two scale damage concept applied to fatigue. Int. J. Fract. 1999, 97, 67–81. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Minimum particle diameter (mm) | 0.4 | Porosity | 0.1 |
| Particle diameter ratio | 1.5 | Parallel bond friction angle (°) | 38 |
| Density (kg/m3) | 2440 | Parallel bond tensile strength (MPa) | 27.8 |
| Contact modulus of the particle (GPa) | 4.0 | Normal critical damping ratio | 0.5 |
| Parallel bond Deformation modulus (GPa) | 27 | Parallel bond Cohesive force (MPa) | 39 |
| Contact bond gap (mm) | 0.05 | Stiffness ratio | 1.0 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Minimum particle diameter/mm | 0.3 | Porosity | 0.1 |
| Particle diameter ratio | 1.66 | Coefficient of friction | 0.46 |
| Density/(kg/m3) | 1800 | Parallel bond Compressive strength/MPa | 10 |
| Contact modulus of the particle/GPa | 1.0 | Parallel bond friction angle/degree | 25 |
| Parallel bond Deformation modulus/GPa | 12 | Parallel bond Cohesive force/MPa | 16 |
| Contact bond gap/mm | 0.05 | Stiffness ratio | 1.0 |
| Normal critical damping ratio | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Yuan, W.; Yan, Y.; Wang, X. Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code. Symmetry 2019, 11, 1040. https://doi.org/10.3390/sym11081040
Liu W, Yuan W, Yan Y, Wang X. Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code. Symmetry. 2019; 11(8):1040. https://doi.org/10.3390/sym11081040
Chicago/Turabian StyleLiu, Wanrong, Wei Yuan, Yatao Yan, and Xiao Wang. 2019. "Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code" Symmetry 11, no. 8: 1040. https://doi.org/10.3390/sym11081040
APA StyleLiu, W., Yuan, W., Yan, Y., & Wang, X. (2019). Analysis of Acoustic Emission Characteristics and Damage Constitutive Model of Coal-Rock Combined Body Based on Particle Flow Code. Symmetry, 11(8), 1040. https://doi.org/10.3390/sym11081040






