Abstract
Molecular conformation as a subproblem of the geometrical shaping of the molecules is essential for the expression of biological activity. It is well known that from the series of all possible sugars, those that are most naturally occurring and usable by living organisms as a source of energy—because they can be phosphorylated by hexokinase, the first enzyme in the glycolysis pathway—are D-sugars (from the Latin dextro). Furthermore, the most naturally occurring amino acids in living cells are L-sugars (from the Latin laevo). However, a problem arises in dealing with the comparison of their conformers. One alternative way to compare sugars is via their molecular alignment. Here, a solution to the eigenproblem of molecular alignment is communicated. The Cartesian system is rotated, and eventually translated and reflected until the molecule arrives in a position characterized by the highest absolute values of the eigenvalues observed on the Cartesian coordinates. The rotation alone can provide eight alternate positions relative to the reflexes of each coordinate.
1. Introduction
The topological description of a molecule requires knowledge of the adjacencies (the bonds) between the atoms as well as their identities (the atoms). If this problem is simplified to the extreme, by disregarding the bond types and atom identities, then the adjacencies are simply expressed as 0 or 1 in the vertex adjacency matrix ([Ad]) and the identities are expressed as 0 or 1 in the identity matrix ([Id]). The characteristic polynomial (ChP) is the natural construction of a polynomial in which the eigenvalues of the [Ad] are the roots of the ChP, as follows:
λ is an eigenvalue of [Ad] ↔ it follows that [v] ≠ 0 eigenvector such that λ·[v] = [Ad]·[v]
(λ·[Id] − [Ad])·[v] = 0); since v ≠ 0 → [λ·Id − Ad] is singular → det([λ·Id − Ad]) = 0.
Therefore, the characteristic polynomial is defined by:
The characteristic polynomial is a polynomial in λ of the degree of the number of atoms. The eigenproblem (the determination of eigenvalues and eigenvectors) is applicable to any Hessian [1] matrix [A] ([Ad] → [A]). The mixed derivatives of a scalar-valued function f are the entries off the main diagonal in the Hessian. Assuming that the derivatives are continuous, the order of differentiation does not matter (a result known as Schwarz’s, Clairaut’s, or Young’s theorem), and then the Hessian of f is a symmetric matrix.
Indeed, this is the case (a symmetric matrix) for the (vertex) adjacency matrix, and for the distance matrix—both topological (by bonds) and geometrical (by the atom coordinates).
Related to this problem is the issue of determining the best rotation to relate two sets of vectors. To this issue, a solution was proposed by calculating a symmetric matrix of Lagrange multipliers which is used to minimize the residuals of the linear association between the vectors [2]. Later, different approaches were proposed, such as geometric hashing [3], clique detection [4], the embedding problem [5], Gaussian molecular representation, Gaussian overlap optimization [6], and others covered in [7]. Some of the proposed solutions go a different way, involving physical means forcing the alignment [8,9], while the formulation of similarity metrics was one of the most recently proposed computational alternatives [10]. The alignment serves as a tool for other studies, including similarity analysis [11], docking [12], and structure–activity relationships [13].
The eigenproblem in relation to geometrical alignment was stated before in the context of surface analysis and control [14], and also can go another direction into the context of the molecule. In this context, the molecule is seen as more than a simple unweighted undirected molecular graph with undistinguishable atoms [15].
The eigenproblem of molecular alignment is analyzed in this paper.
2. Materials and Methods
The alignment of molecules can be stated in many ways, as listed in the introduction. For instance, one approach is to search for topological alignment, and another is to search for geometrical alignment. To anticipate the type of molecular alignment, it is necessary to employ the latter method—to search for geometrical alignment.
A molecule is taken here as an example from PubChem CID 444173 ((2R,3S,4R,5R)-oxane-2,3,4,5-tetrol), as shown in Figure 1.
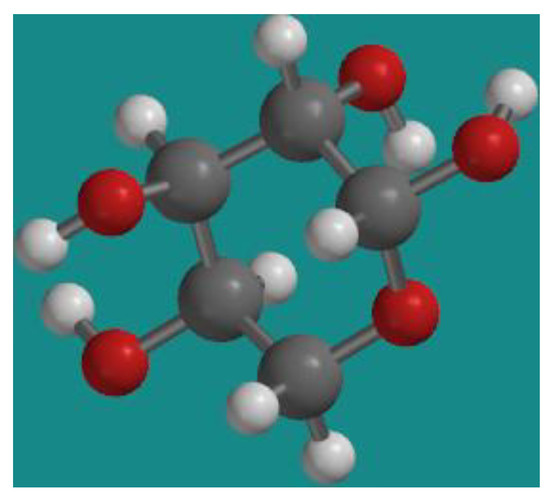
Figure 1.
3D representation of the model of PubChem CID 444173.
For convenience, hydrogen atoms are excluded from the data and the analysis. The next table (Table 1) contains the relevant information for the heavy atoms in the reference molecule.

Table 1.
3D structural data for CID 444173 (heavy atoms, geometric coordinates, and atom symbols).
The general way of constructing a characteristic polynomial is to provide an identity matrix [Id] and a Hessian matrix (herein labeled as [A]). If considering the topology of the molecule, then it is necessary to have the information regarding the connections between the atoms (e.g., bonds). Since all bonds are single bonds for the selected molecule, listing the atoms pairs of the bonds is enough (Table 2).

Table 2.
Topology data for CID 444173 (list of bonds between heavy atoms).
A deeper look into the eigenproblem (|λ∙I − A| = 0) is performed in the next section, with a specific focus on changing of the mathematical properties of the eigenproblem when the adjacencies in [A] change from symmetric to anti-symmetric.
3. Results and Discussion
From Table 2, the adjacency matrix [Ad] is immediate—zeros represent the entries without a bond between the labeled atoms, while ones appear otherwise. The adjacency matrix is Hessian. For convenience, its characteristic polynomial is:
ChP(λ; CID444173, “[Ad]”) = 1∙λ10 − 10∙λ8 + 31∙λ6 − 35∙λ4 + 11∙λ2 − 1∙λ0.
As can be seen, the degree of the polynomial is 10, which is equal to the number of the (connected) atoms in the molecule. The general rule is that a characteristic polynomial is always of a degree equal to the size of the square matrices [I] and [A] (see the before given equation), from which it was derived.
The same strategy can be applied if the adjacency matrix [Ad] is replaced by the distance matrix [Di]. For convenience, Table 3 lists these two matrices.

Table 3.
Adjacency and distance matrices for CID 444173 (heavy atoms).
It can be checked (but is also true for the general case) that the distance matrix is Hessian, and therefore a characteristic polynomial can be computed for it as well. The next equation lists the ChP computed for the distance matrix [Di]:
ChP(λ; CID444173, ”[Di]”) = 1∙λ10 − 313∙λ8 + 3488∙λ7 − 15456∙λ6 − 34720∙λ5 − 40832∙λ4 − 23808∙λ3 − 5376∙λ2
The natural extension of this matrix is to employ 3D distances instead of topological distances. Of course, one consequence of this is that the characteristic polynomial would no longer have integer coefficients.
The next table lists the 3D distance matrix (distances were cut to four significant digits) and the roots of the associated characteristic polynomial.
One interesting remark to the data listed in Table 4 is that all roots are real (this is the general behavior for the roots of a characteristic polynomial).

Table 4.
3D distance matrix and its eigenvalues for CID 444173 (heavy atoms).
Up until this point, the ideas presented in this paper have been reported before. Herein follows the extension to the extant knowledge. What if the same formula is applied to define the ChP for Cartesian coordinate distance matrices instead of for the Euclidian distance matrix?
Next three tables (Table 5, Table 6 and Table 7) list those results (the number of digits is displayed according to the input data—see Table 1).

Table 5.
First Cartesian coordinate (“x”) distances matrix for CID 444173 (heavy atoms).

Table 6.
Second Cartesian coordinate (“y”) distances matrix for CID 444173 (heavy atoms).

Table 7.
Third Cartesian coordinate (“z”) distances matrix for CID 444173 (heavy atoms).
It can be observed that the Cartesian coordinates distance matrices are no longer symmetric matrices, but are in fact anti-symmetric, meaning that Mi,j = −Mj,i.
The beauty of the result shown by taking a look at the eigenvalues. The next table (Table 8) lists the eigenvalues for all matrices.

Table 8.
Eigenvalues for CID 444173 (heavy atoms).
It should be noted that the values listed in Table 7 reveal some computational errors. It is obvious (and it is so) that 3.6 × 10−15 is actually a “0” and it is necessary to be aware of this type of error coming from “machine epsilon” [16] which is about 10−7 for “single” precision, 10−16 for “double” precision, and about 10−19 for “extended” precision. Most floating-point implementations use “double” precision and thus the listed value (3 × 10−15) “fits in range”.
More important, as can be observed (see Table 7), the eigenvalues of [Dx], [Dy], [Dz] are all 0 excepting (always) two—which are (always) paired and (always) imaginary (i = √−1, see Table 8). This is the opposite of the traditional case of symmetric matrices, when the values are (always) real. This is the beauty of the result.
Moreover, it should be noted that the polynomial can be expressed with real-value coefficients as a product of a polynomial of degree 2 and a monomial of degree (n − 2), as listed in Table 9.

Table 9.
The polynomials of [Dx], [Dy], and [Dz] for CID 444173 (heavy atoms).
A consequence is hidden behind this result—to obtain those two coefficients (which are actually the first and third coefficients, independent of how many atoms are in the molecule) it is necessary to obtain their roots. Therefore, it is not necessary to run an “eigenvalues” routine to obtain them; it is enough to run only two steps of a coefficient determination program (such as that described in [17]), which will produce a result much more quickly.
So, what if we conduct a rotation of the molecule?
For example, by rotating the molecule by 15° (15/180 radians; coordinates are given in Table 1), the values for the polynomials are changed—see Table 10. First it should be pointed out that the polynomial is no longer invariant due to the choice of the system of coordinates. If invariants are sought, this is not a good situation—but for the purpose of addressing the alignment problem, this setup is very useable.

Table 10.
The polynomials of [Dx], [Dy], and [Dz] rotated (15°, 15°, 15°) for CID 444173 (heavy atoms).
In the general case, with a1, a2, and a3 as rotation angles defining the rotation matrices (given below), it is necessary to maximize the variance along the axes of coordinates.
This results a two-step algorithm, described below:
- Since rotation by a0 leaves untouched the “z” coordinate, the first problem is to find a value of a0 such that the squared sum of the eigenvalue(s) for the [Dx] matrix is minimized (or its coefficient from Table 9, which is x1·x2 = x1· = −x12 = −x22, is maximized);
- Next, we need to leave untouched the “x” coordinate—which was already fitted in the first step. For this, we may want to employ rotation by a2, such that the squared sum of the eigenvalue(s) for the [Dy] matrix is minimized (or its coefficient from Table 9 is maximized);
- There is no third step involving the third rotation matrix, because by maximizing (or minimizing) the first two coordinates, we have already employed all coordinates (x and y in the first step; y and z in the second).
Therefore, at this point we have the alignment of the molecule.
The problem of molecular 3D alignment involving the modified characteristic polynomial (eigenproblem) becomes a combinatorial problem since, after eigenvector minimization by each (two out of three) Cartesian coordinate, we obtain the molecules in their proper alignment or in the mirror of the proper alignment, when “xi ← −xi” and/or “yi ← −yi” and/or “zi ← −zi” transformation will align it.
Of course, a question may arise: what is the meaning of such alignment? This research is ongoing, but so far it has been found that this alignment corresponds to the minimization of the rotation inertia of the coordinates. In other words, the thinnest part of the molecule aligns with one coordinate, and then the thinnest part of what remains (so the molecule can be rotated around that axis) aligns with the second coordinate.
Revising the results communicated here, it should be noted that the classical eigenproblem is addressed to symmetric matrices—such as are the topological adjacency and topological distance matrices (shown in Table 3) and the geometrical distance matrix (Table 4). The peculiarity of the Cartesian distance matrices (shown in Table 5, Table 6 and Table 7) is the fact that they are anti-symmetric, sometimes called skew-symmetric matrices. This is, in mathematical terms, a strong property—as strong as the property of symmetry (please note that here the symmetry describes the matrices—namely, matrix A is symmetric if A = AT and it is anti-symmetric if A = −AT). On the other hand, the elements of the Cartesian coordinate matrices are mirrored relative to the main diagonal—this property is called reflection symmetry, line symmetry, or mirror symmetry—which makes these matrices very suitable for the same set of operations that are typically employed for symmetric matrices. Further, among the known properties of skew-symmetric matrices is the fact illustrated in Table 8—If A is a real skew-symmetric matrix and λ is a real eigenvalue, then λ = 0, i.e., the nonzero eigenvalues of a skew-symmetric matrix are purely imaginary”. Since a skew-symmetric matrix is similar to its own transposition, they must have the same eigenvalues. It follows that the eigenvalues (λ) of a skew-symmetric matrix always come in pairs (±λ), a property which is also illustrated in Table 8.
It should be noted that the generation of Cartesian coordinates from the diagonalization of adjacency or distance-related matrices is quite standard in mathematical chemistry. For instance, the methods to generate fullerene cages from Schlegel diagrams are normally embedded in fullerene sw packages (see for example [18]). Thus, the results communicated here may have useful applications in this regard.
4. Conclusions
The change from symmetry to anti-symmetry in the adjacency matrix of the eigenproblem moves the eigenvalues from real space into imaginary space. When the eigenequation is applied to the Cartesian space of the molecule instead of the topological or Euclidean spaces, the resultant roots (corresponding to the eigenvalues) are all 0 (multiple roots) excepting two, which are always imaginary (and complementary). The rotation of a molecule induces into the Cartesian space a way of aligning the molecule by maximizing the magnitude of the roots in a preselected order of the Cartesian axes. This property can be further exploited for the alignment of multiple molecules, when for highly symmetric molecules the alignment problem is turned into the (S2)3 conformational problem.
Though the programs provided in the Supplementary Materials can be used to align any molecule, they are not communicated as a novel tool. Aligning a molecule by its Cartesian coordinates via the simultaneous alignment of many molecules—such as for molecular docking purposes—will require further study.
Supplementary Materials
The datafile for CID 444173 and the MATLAB program implementing the Cartesian alignment of a molecule are available online at https://www.mdpi.com/2073-8994/11/8/1027/s1.
Author Contributions
The author designed and made the study and also wrote the paper.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Sylvester, J.J. On the theorem connected with Newton’s rule for the discovery of imaginary roots of equations. Messenger Math. 1880, 9, 71–84. [Google Scholar]
- Kabsch, W. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. 1976, A32, 922–923. [Google Scholar] [CrossRef]
- Lamdan, Y.; Wolfson, H.J. Geometric Hashing: A General and Efficient Model-based Recognition Scheme. In Proceedings of the Second International Conference on Computer Vision Proceedings, Tampa, FL, USA, 5–8 December 1988; pp. 238–249. [Google Scholar]
- Martin, Y.C.; Bures, M.G.; Danaher, E.A.; DeLazzer, J.; Lico, I.; Pavlik, P.A. A fast new approach to pharmacophore mapping and its application to dopaminergic and benzodiazepine agonists. J. Comput. Aided Mol. Des. 1992, 7, 83–102. [Google Scholar] [CrossRef]
- Mrippen, G.M.; Havel, T.F. Distance Geometry and Molecular Conformation; Research Studies Press: Taunton, UK; Wiley: New York, NY, USA, 1988; pp. 1–541. [Google Scholar]
- Kearsley, S.K.; Smith, G.M. An alternative method for the alignment of molecular structures: Maximizing electrostatic and steric overlap. Tetrahedron Comput. Methodol. 1990, 3, 615–633. [Google Scholar] [CrossRef]
- Lemmen, C.; Lengauer, T. Computational methods for the structural alignment of molecules. J. Comput. Aided Mol. Des. 2000, 14, 215–232. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, B.; Herschbach, D. Alignment and trapping of molecules in intense laser fields. Phys. Rev. Lett. 1995, 74, 4623–4626. [Google Scholar] [CrossRef] [PubMed]
- Larsen, J.J.; Hald, K.; Bjerre, N.; Stapelfeldt, H.; Seideman, T. Three dimensional alignment of molecules using elliptically polarized laser fields. Phys. Rev. Lett. 2000, 85, 2470–2473. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Gong, J.; Liu, X.; Gao, D.; Li, H. SimG: An alignment based method for evaluating the similarity of small molecules and binding sites. J. Chem. Inf. Model. 2013, 53, 2103–2115. [Google Scholar] [CrossRef]
- Wang, N.; DeLisle, R.K.; Diller, D.J. Fast small molecule similarity searching with multiple alignment profiles of molecules represented in one-dimension. J. Med. Chem. 2005, 48, 6980–6990. [Google Scholar] [CrossRef][Green Version]
- Benyamini, H.; Shulman-Peleg, A.; Wolfson, H.J.; Belgorodsky, B.; Fadeev, L.; Gozin, M. Interaction of C60-fullerene and carboxyfullerene with proteins: Docking and binding site alignment. Bioconj. Chem. 2006, 17, 378–386. [Google Scholar] [CrossRef]
- Cramer, R.D., III; Patterson, D.E.; Bunce, J.D. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J. Am. Chem. Soc. 1988, 110, 5959–5967. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Ma, J.; Liu, X.; Kobbelt, L.; Bao, H. Spectral Quadrangulation with Orientation and Alignment Control. In Proceedings of the ACM SIGGRAPH Asia 2008 Papers, Singapore, 10–13 December 2008. [Google Scholar]
- Joiţa, D.M.; Jäntschi, L. Extending the Characteristic Polynomial for Characterization of C20 Fullerene Congeners. Mathematics 2017, 5, 84. [Google Scholar] [CrossRef]
- Goldberg, D. What every computer scientist should know about floating-point arithmetic. ACM Comput. Surv. 1991, 23, 5–48. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.D. 7. Characteristic Polynomial (CHARACT-POLY). In New Frontiers in Nanochemistry: Concepts, Theories, and Trends, 3-Volume Set: Volume 2: Topological Nanochemistry; Putz, M.V., Ed.; Apple Academic Press: Waretown, NJ, USA, 2019; pp. 95–117. [Google Scholar]
- Schwerdtfeger, P.; Wirz, L.; Avery, J. Fullerene—A software package for constructing and analyzing structures of regular fullerenes. J. Comput. Chem. 2013, 34, 1508–1526. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).