1. Introduction
In Ref. [
1] a general model of swarming behavior of an individual population was proposed and studied. The main aim in that paper was to study the macroscopic (so-called “
hydrodynamic”) limit. The mathematical structure proposed therein seems very rich and interesting from the mathematical point of view—see the analysis of its simplification in Refs. [
2,
3,
4].
In the present paper, we study the time evolution of the probability density
f. The function
is the distribution of an internal, microscopic state
at time
of a (statistical or test) agent. Such a description has then a
mesoscopic nature. An arbitrary vector
can be related to a biological state, activity, opinion (e.g., political opinion), a social state of a test agent, etc.—cf. [
1,
5,
6,
7] and references therein,
. The model has therefore a wide range of possible applications in various applied sciences, such as biology, medicine, social or political sciences.
Because some results of the present paper may have a particular importance in the description in social sciences, we will refer the parameter u to as the opinion of (test) agent.
The time evolution is defined by the general nonlinear integro-differential Boltzmann-like equation, see Ref. [
1] and references therein,
where
The nonlinear operator
Q describes interactions between agents causing a change of opinion. The turning rate
measures the rate for an agent with opinion
u to change it into
v. A simpler equation, with two possible states only, was studied in Ref. [
8]—see also Ref. [
6]. It is a typical kinetic (microscopic or more precisely, mesoscopic) way of describing large (social) populations. Instead of dealing with the states of all separated agents involved in the population evolution, we deal with the statistical state of one (
test) agent. This state is described by the probability density
f that is a solution of Equation (
1). The main aim is to describe general dispersion–concentration phenomena resulting from individual opinions of agents. The dispersion results in the presence of various opinions in a society, whereas the concentration represents a kind of uniformity of opinions. The main advantage of the class of models given by Equation (
1) is that it can capture many scenarios that are known in social sciences.
There is an increasing interest in a kinetic approach in a similar context. Ref. [
9] is dedicated to the modeling and simulation of swarms, where interactions at the microscopic scale are modeled by stochastic games. Ref. [
10] describes the state of the art of swarming at the individual–based level and the macroscopic level. Ref. [
5] models ensembles of social agents as behavioral, evolutionary, complex systems referring to the complexity features of living systems. Individual–based approaches based on stochastic processes are proposed in Refs. [
7,
11,
12]. Ref. [
13] studies the local stability of Dirac masses for a kinetic model of alignment. See also references therein.
The modeling process leads to a proper choice of the turning rate. In the present paper, we are going to study two different and somehow opposite choices.
Case 1. (A conformist society). Letwhere is a given number. Throughout the paper we assume that
is a symmetric function of its arguments, i.e.,
This assumption, which may be related to a symmetric nature of interactions between agents, is essential for the mathematical theory presented here. In fact relaxing of the assumption leads to a completely different behavior and different macroscopic limits. In such a case one may expect first order terms that dominate in the macroscopic picture causing a drift towards some states.
The rate of transition from opinion
u to opinion
v is proportional to
-power of the actual probability of having opinion
v. The higher the probability, the larger the chance of a change. Therefore it is natural to refer to such a society as a
conformist society (or a
collectivistic society). The interaction kernel
corresponds to the tendency of agents to change opinion. In particular, it may restrict the interactions to close opinions only—see Ref. [
4]. The (sensitivity) parameter
describes the level of sensitivity of interactions. The greater
, the more sensitive interactions.
The models defined by Case 1 was proposed in Ref. [
1], and then studied in various directions in Refs. [
2,
3,
4]. Ref. [
1] proposed results of global existence in the space homogeneous case for
, whereas
was considered in Ref. [
2,
3,
4]. Assuming that
yields a trivial model, thus it is excluded. Alternatively, we may propose:
Case 2. (A moderately anti-conformist society). Letwhere is a given number. The rate of transition from opinion u to opinion v is proportional to the product of -power of the actual probability of having opinion u and the actual probability of having opinion v. The higher the product, the larger the chance of a change. Therefore, we may refer to such a society as a moderately anti-conformist society (or a individualistic society). As before, the interaction kernel corresponds to the tendency of agents to change opinion.
One may note that the following choice of leads to the same kinetic equation, again justifying its name (the moderately anti-conformist society) (or individualistic society).
Case 3. Letwhere is a given number and . Both Cases 1 and 2 (or 3) can be put together as the following equation
where
. Condition
corresponds to Case 1, whereas
to Case 2 (or Case 3).
The main Equation (
3) reads
,
, whereby
we denote the convolution-like product, i.e.,
The
-norm is denoted by
. We may state the following existence–uniqueness result for solutions to Equation (
4).
Proposition 1. Let . If is a probability density such that , then there exists such that the solution to (4) exists and is unique in on the interval . The solution preserves the positivity and -norm (i.e., it is a probability density) on . Moreover, - 1.
If the solution is global and possesses all finite -norms, , and the functions are decreasing;
- 2.
If the solution, depending on initial data, is either global () or local (), it possesses all finite -norms on , , and the functions are increasing for .
Proof. The proof follows from Ref. [
1]. First we observe that the operator on the right-hand side of Equation (
4) is locally Lipschitz-continuous in the
-setting. Therefore, the existence in this setting on some interval
follows. It is easy to see that the solution
preserves positivity and
-norm of the initial datum,
.
Let
,
. Then the solution
a priori satisfies
Therefore, the conclusion follows. □
Moreover, we need the smoothness of the solutions. Let and be the Banach spaces—the classical Sobolev space (a subspace of ) and the space of m-differentiable functions, respectively, with the usual norms denoted by and , respectively.
Let
,
, and
be defined
In particular, for , we write and .
Proposition 2. Let the assumption of Proposition 1 be satisfied and additionally andfor some . Then the solution (given by Proposition 1) satisfies for all . Proof. The proof follows again by the standard application of Lipschitz-continuity in . □
2. Formal Diffusive and Anti-Diffusive Limits
In the present section we study (only in a formal way) the macroscopic limits of Equation (
4) with both
and
. As we will see, the case
corresponds to the diffusive macroscopic behavior, whereas
—to the anti-diffusive behavior.
Suppose that the support of
is concentrated close to the diagonal
, i.e.,
where
is the normalizing coefficient, i.e.,
d-dimensional volume of the unit ball (centered at 0).
We are going to consider
, because we are interested in the limit as the “
support tends to the diagonal” and the non-zero values of
tend to infinity. We may note that
defined in Equation (
6) satisfies Equations (
5). The essential role here is again played by the symmetric nature of interactions. Without this nature, the limit could be completely different.
Let the solution of Equation (
4), for fixed
, be denoted by
and be in
. If
tends to
f in
, then
f is a solution to the following partial differential equation
with the positive constant
where
is the unit ball. Taking
as well as
, Equation (
7) is the classical porous medium equation—see Refs. [
14,
15,
16] and references therein. On the other hand, taking
and
we obtain a nonlinear anti-diffusion equation. A linear anti-diffusion equation was also formally obtained as in a hydrodynamic limit in Ref. [
8]—see (4.19) and (4.20) therein. Considering regular solutions (i.e.,
with respect to
u), Equation (
7) is equivalent to
where
is the Laplace operator. We generalize the above argument to Equation (
4) with
given by
We do not assume that is a probability density but we refer to the notion of generalized moments as well as the generalized covariance matrix in a standard way.
Assumption 1. We assume
- 1.
The function is bounded, non-negative and symmetric, i.e., ;
- 2.
The first, second, third, and fourth generalized moments are bounded, i.e., - 3.
The matrixthe generalized covariance matrix of , is positive definite.
If
is a probability density, then the generalized moments and the generalized covariance of
become just moments and covariance of
. Assumption 1 is satisfied for
in Equation (
6) if
is given by
With this
we put
and easily obtain Equation (
7), which is formally equivalent to Equation (
9). We intend to obtain the following generalization of Equation (
9)
The symbol “·” stands for the inner scalar product of two
-matrices and
is the Hessian matrix (it consists of second order derivatives in
). To obtain Equation (
11) we use the Taylor expansions
Substituting these expressions to the right-hand side of Equation (
4) and taking into account Equation (
10) we obtain
From the symmetry of
, the first order terms with respect to
vanish. The second order terms yield
In the limit
we formally obtain the diffusion or anti-diffusion equation Equation (
11).
In the particular case of Equation (
6), all mixed (generalized) second moments of
are equal to zero. In that case the pure second (generalized) moments, using Equation (
8), are as follows
In this case, in the limit
, Equation (
4) formally results in the diffusion/anti-diffusion equation Equation (
9). Also, formally, Equation (
9) turns to be a porous-media equation when
. The existence, uniqueness and regularity criteria are formulated in [
15]. There is no such result for anti-diffusion equations, in particular for Equation (
9) with
.
3. Convergence Result
In this section, we are going to prove the rigorous convergence result— a diffusive limit for
. It is somehow in the spirit of the diffusive limit for a class of bilinear equations studied in Ref. [
17]. We assume stronger regularity of the initial datum
and obtain the convergence of order
. Due to the symmetry of
one can enhance the convergence rate from
to
.
Concerning Equation (
4) with
the global existence and uniqueness follows from Proposition 1, for its diffusive limit (
7)—from [
15] (by the porous-media theory), whereas the case
is almost completely unknown.
We transform Equation (
11) to a porous-media equation, for which one can state an existence result in the diffusive case
. Since the matrix
is symmetric and positive–definite, there is a
-matrix
B such that
. We can now define a new function
and establish the relations between the derivatives
Herewith Equation (
11) transforms to
The initial condition is given by
. It follows
In this way we arrive at an equation which is formally equivalent to Equation (
11) and reduces to a porous-media equation
The respective function
satisfies the porous-media equation
We are ready to formulate an existence result.
Proposition 3. Let , and be a probability density on such that . Let moreover satisfy Assumption 1. Then Equation (17) with the initial condition has a unique solution in , on some interval . Proof. By the substitution
Equations (
17) reduces to (
18), in other words
with the initial condition
. The assertion follows from the porous-media existence theory. □
Theorem 1. Let , as well as be a probability density on such that . Let moreover be a non-negative function satisfying Assumption 1 and let defined on be a solution of Equation (4) with the initial datum and with If in X is a solution to Equation (17) with the same initial datum , thenwith some constant . Proof. Let
be the solution to Equation (
4) with
defined by (
10). The idea of the proof is as follows:
the kinetic equation is transformed into an equation formally equivalent to a porous-media equation with a small perturbation;
the perturbed porous-media equation is reduced to its standard form by the change of variables ;
the comparison principle for porous-media equations is applied.
We fix
. Using the Taylor expansions to Equation (
4) as in
Section 2, we obtain the right-hand side given by Equation (
12). From the symmetry of
, the first and third order terms with respect to
vanish. The second order terms yield
Hence Equation (
12) reads
where
where
consists of all fourth-order partial derivatives
and
is the 4-linear form
acting on four copies of the vector
. The remainder
can be estimated by
and the
X-norm can be estimated by
where
C is a constant depending on the fourth moments of
and the
-norm of
.
Finally, we attempt to a comparison of
with
f. The above consideration leads to a perturbed porous-media equation for
Alike the transformation
, one can define
, which satisfies
with the initial condition
. Since
F satisfies the porous-media Equation (
18) with the same initial datum, one can apply classical comparison theorems for porous media, see [
18,
19]. This leads to the estimate
Since the matrix B is non-singular, we obtain a similar estimate for . This completes the proof. □
If mixed moments (or mixed generalized moments) of
vanish, the covariance matrix
is a diagonal matrix. Therefore, the diffusive/anti-diffusive limit equation, i.e., Equation (
9), is a particular case of Equation (
11). This fact in the case
we state in the following:
Corollary 1. Let , as well as be a probability density on such that . Let defined on be solutions of Equation (4) with the initial datum and with β given by (6). If in X, , is a solution to Equation (7) with the same initial datum, on , thenwith some constant . Proof. It is sufficient to put
. This is a probability density. Then the covariance matrix
is proportional to the identity matrix
I and the matrix operation
provides
. It is seen that Equation (
7) is a particular case of Equation (
17). □
4. Numerical Examples
The properties of the solutions to the considered equations can be illustrated by some numerical examples. Take
,
and
. Since Equation (
7) is a limit equation for Equation (
4), one can apply some numerical methods such as the finite differences or the method of lines
with
. As a matter of fact, this is a continuous version of the method of lines. For
this is an approximation of a porous-media PDE, which is a parabolic equation. One can investigate the convergence.
If we rearrange Equation (
19), it turns out that it coincides with an agent-based model corresponding to kinetic equations
One can see that the solutions to (
20) preserve non-negativity of the initial datum as well as
-norm. In both cases
and
one can pass to the limit with
. Its derivation resembles the diffusive limit for (
4).
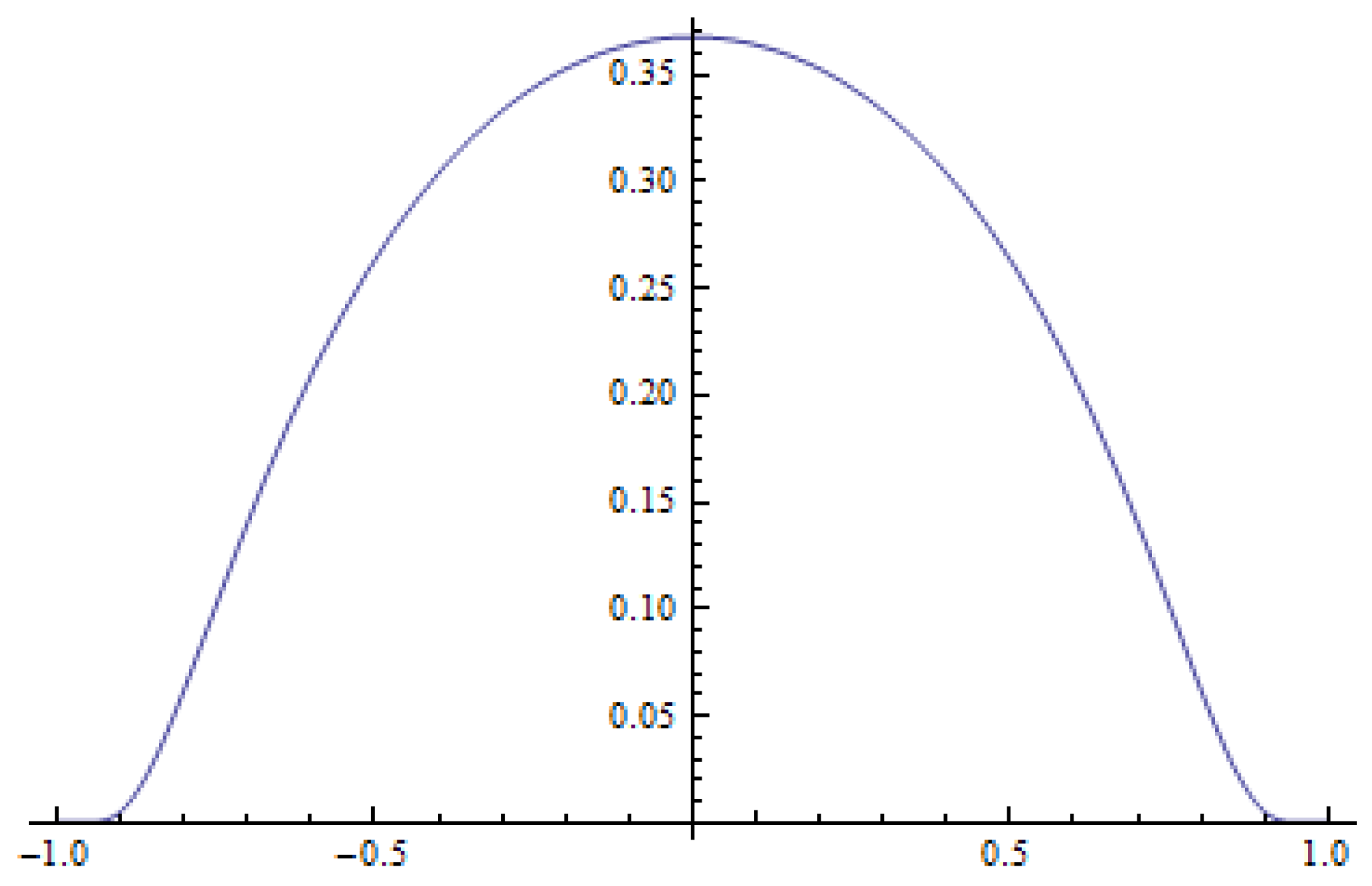
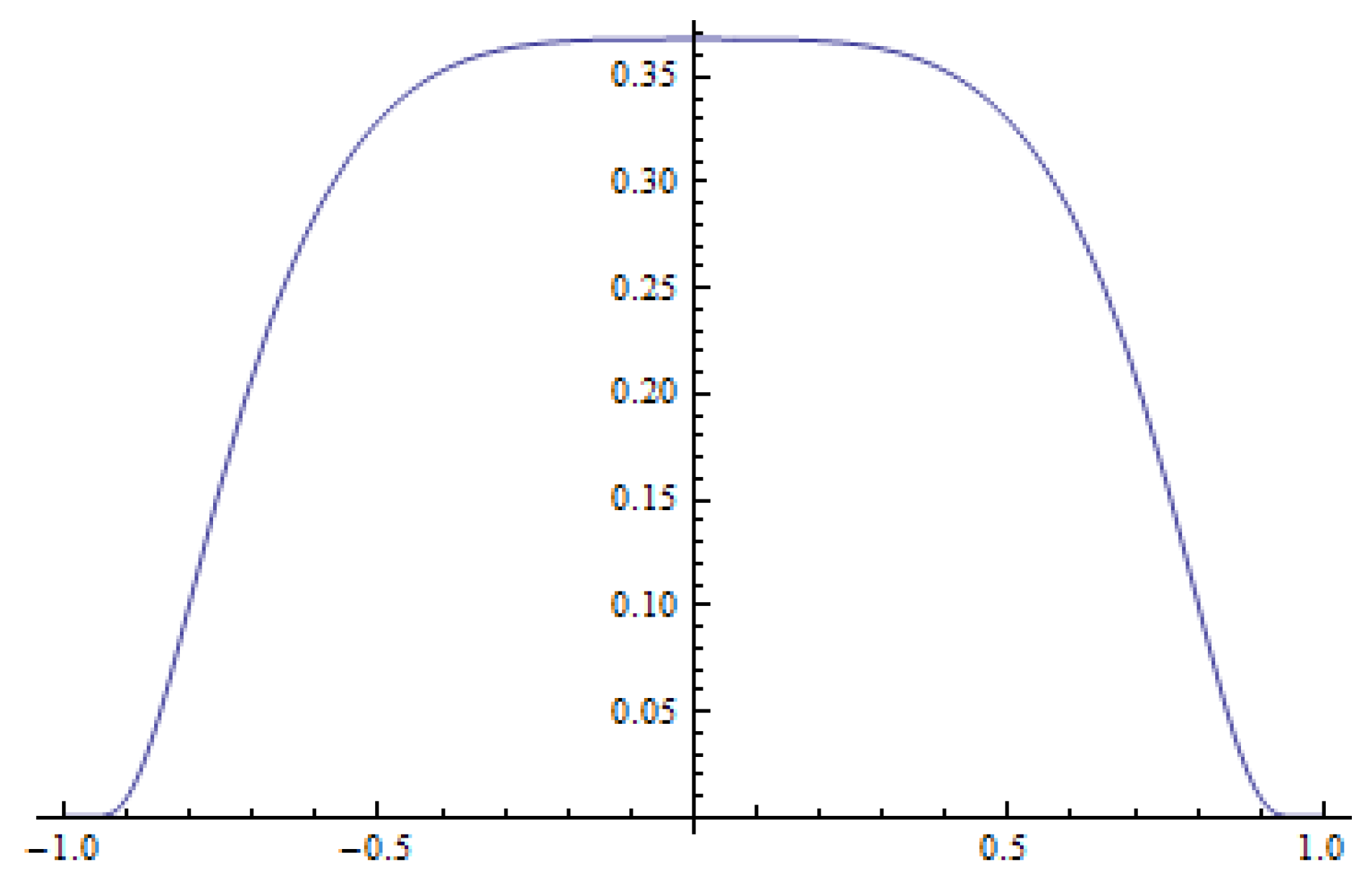
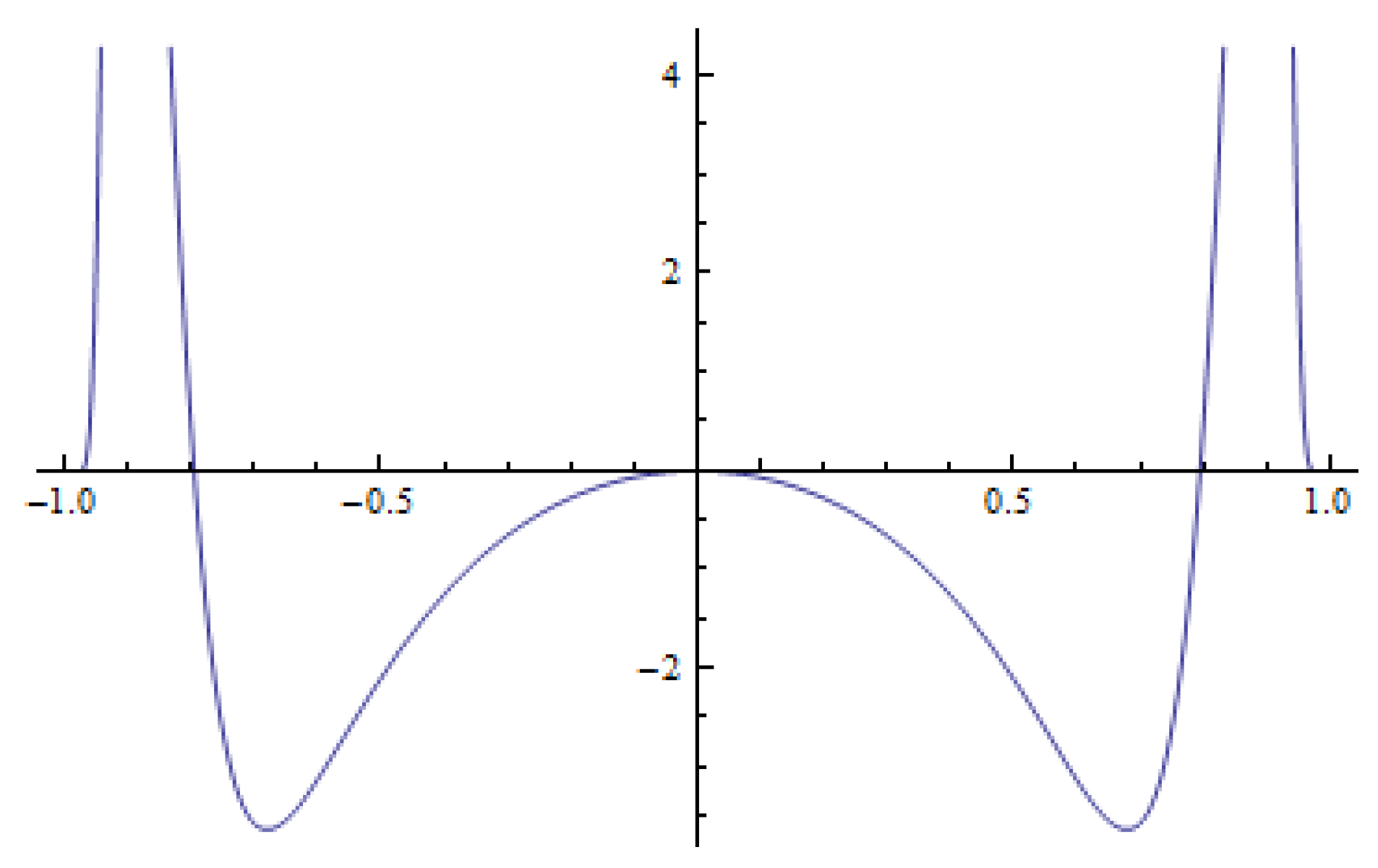
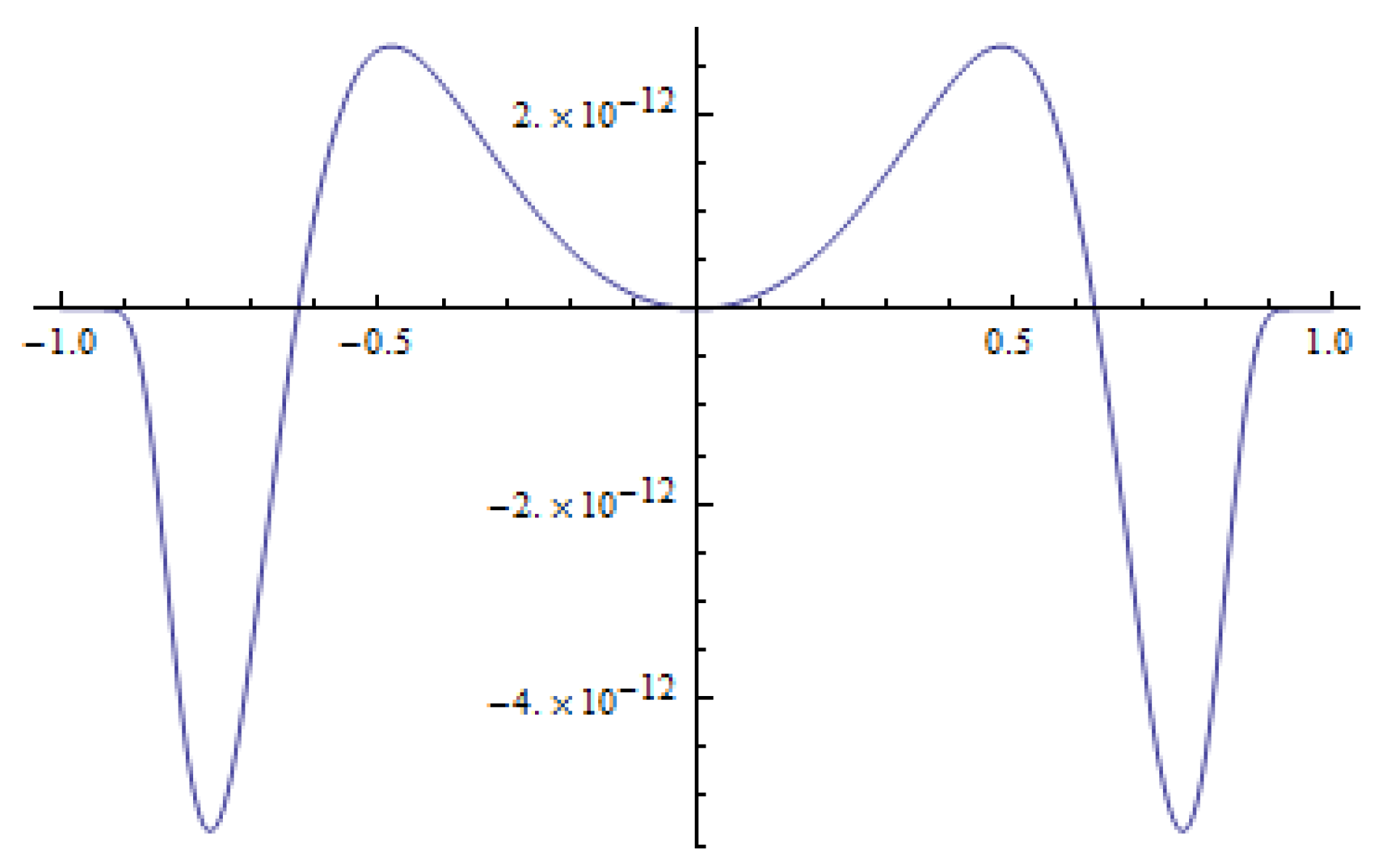
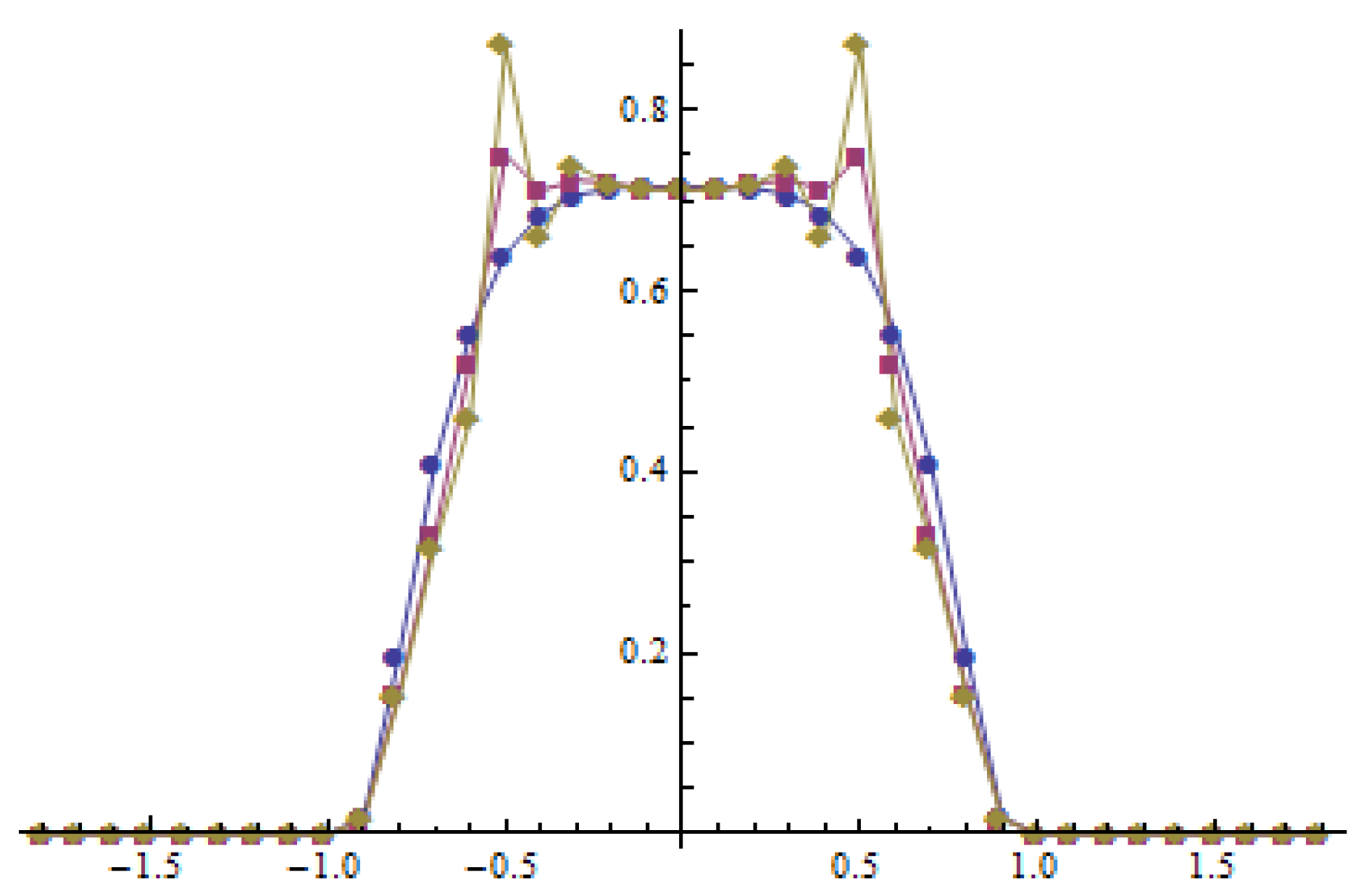
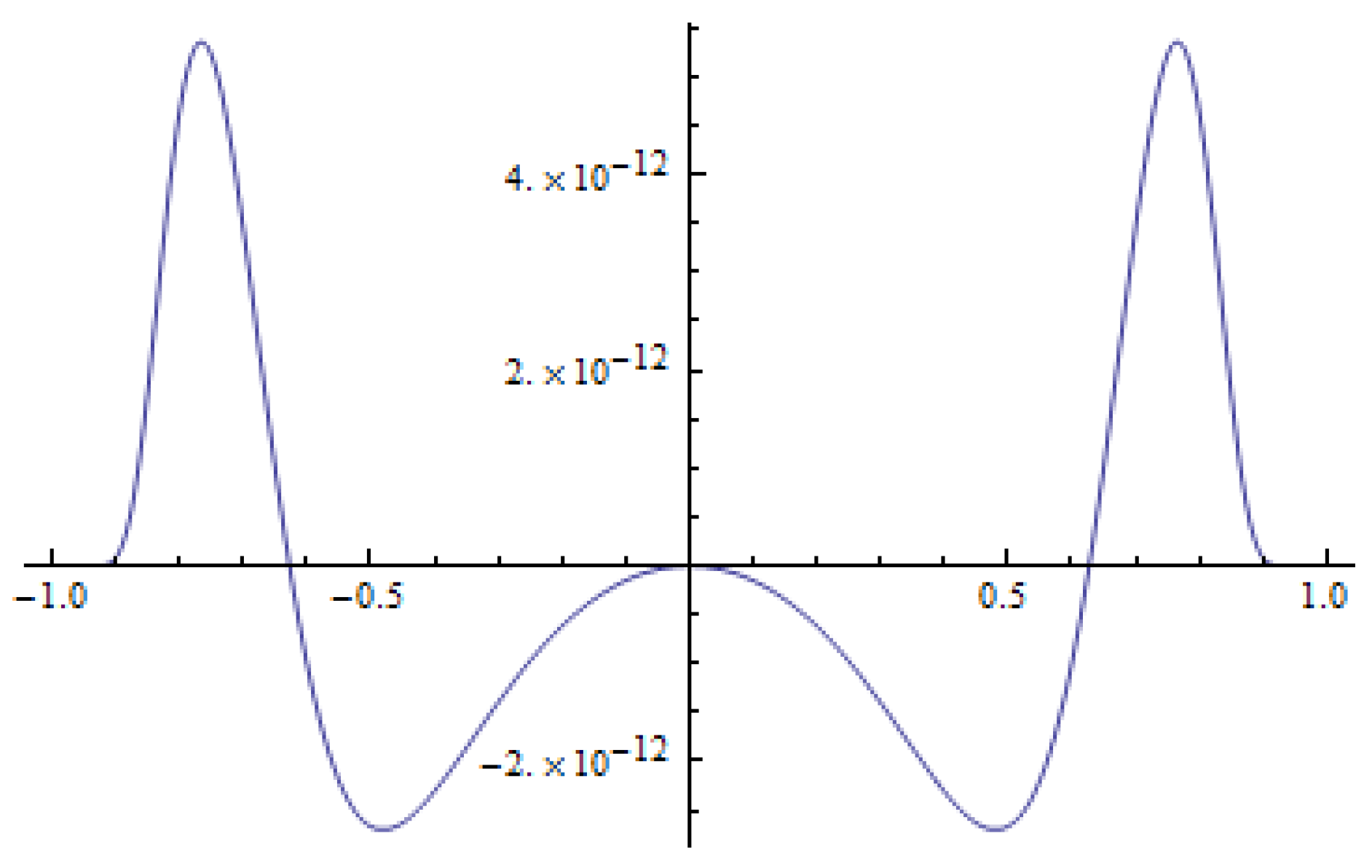
Example 1. We consider the initial datum in the formwhere is a normalizing coefficient. The initial datum is an even function and has a single global maximum at (see Figure 1). Then the solution to the method of lines (19) has unique global maximum at zero. Please note that
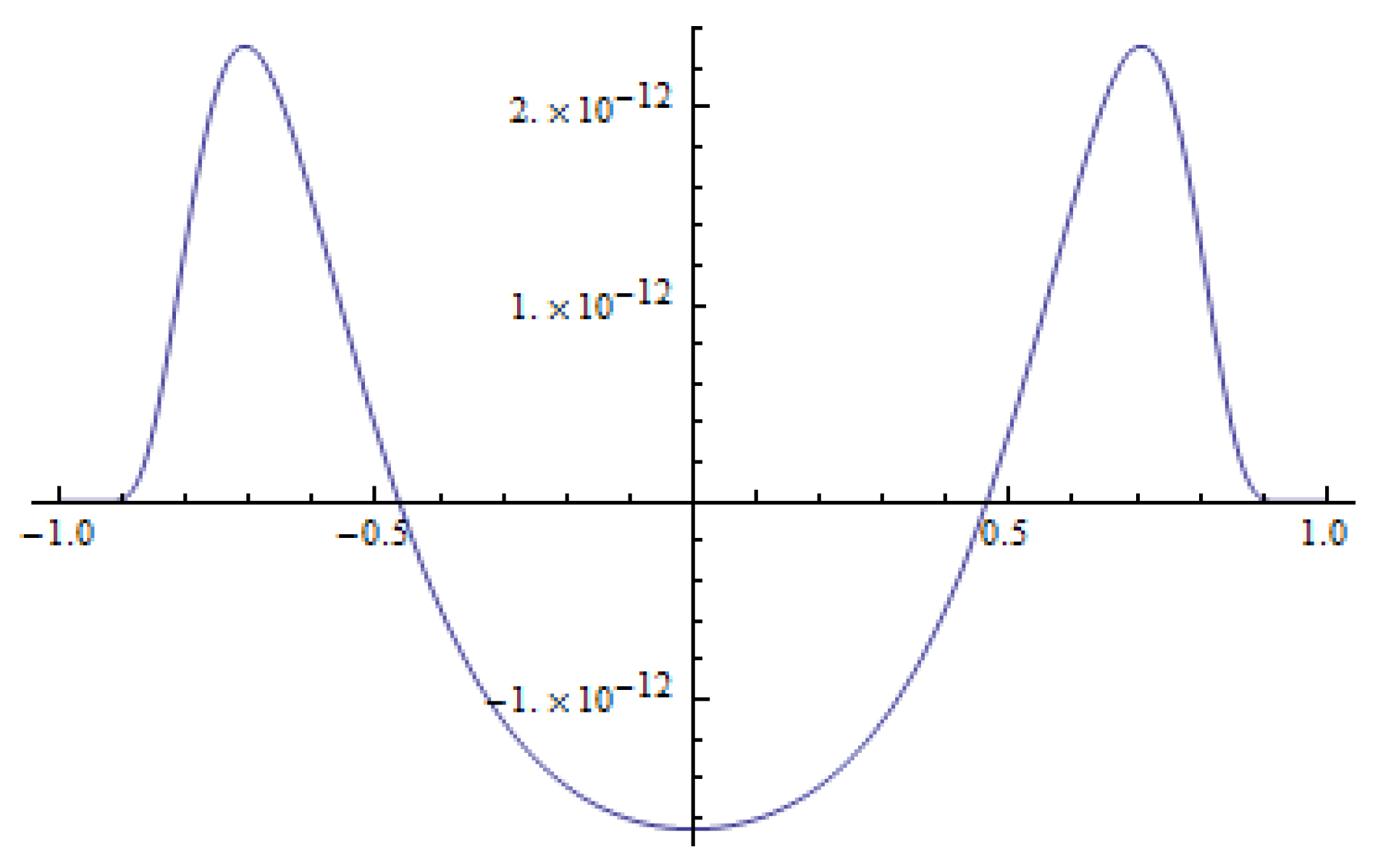
If the time derivative is negative in a neighborhood of zero and
(see
Figure 2), then the maximum of the initial function is transformed into a smaller value (see
Figure 3). Therefore, the solution to (
19) with
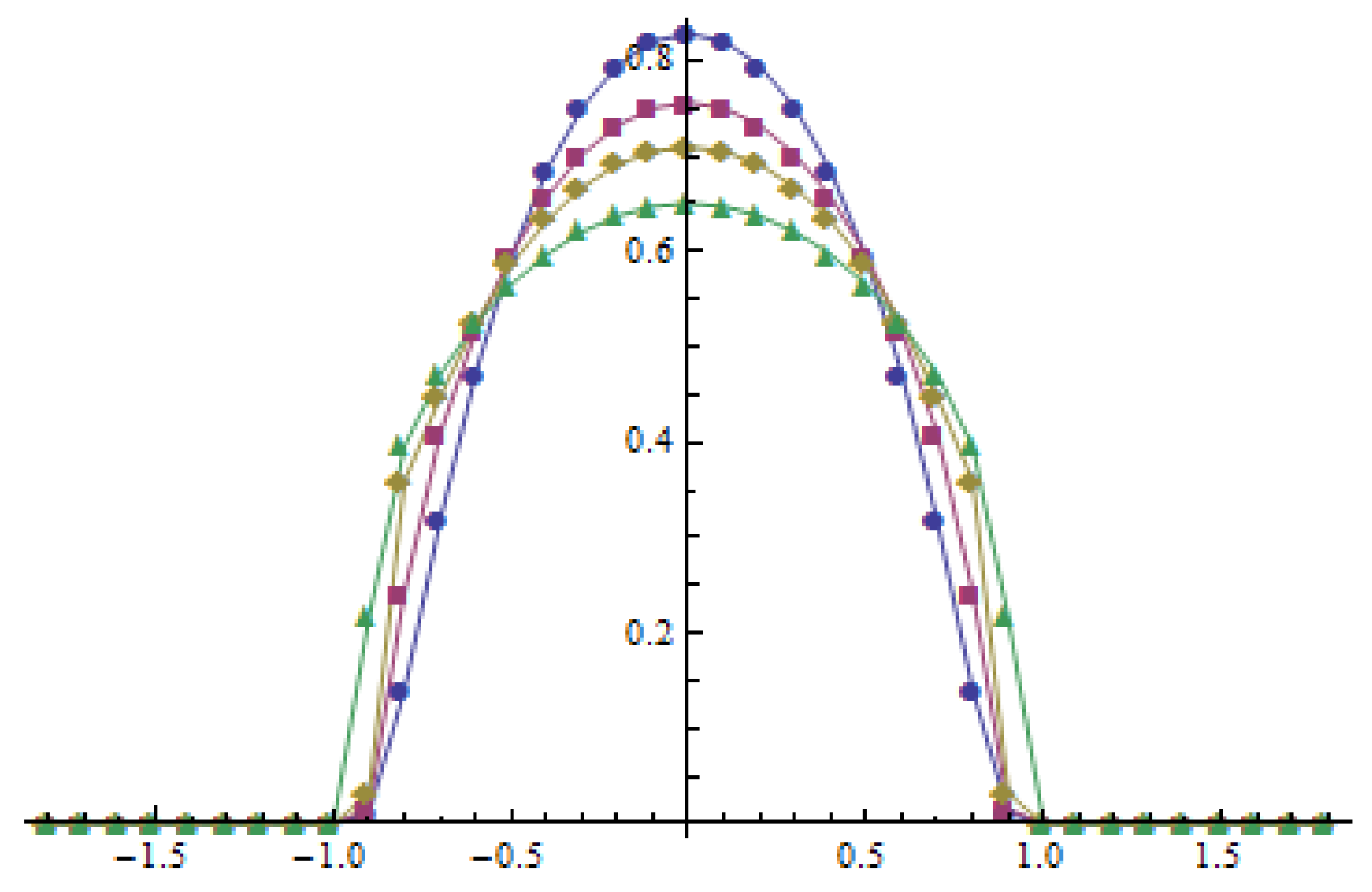
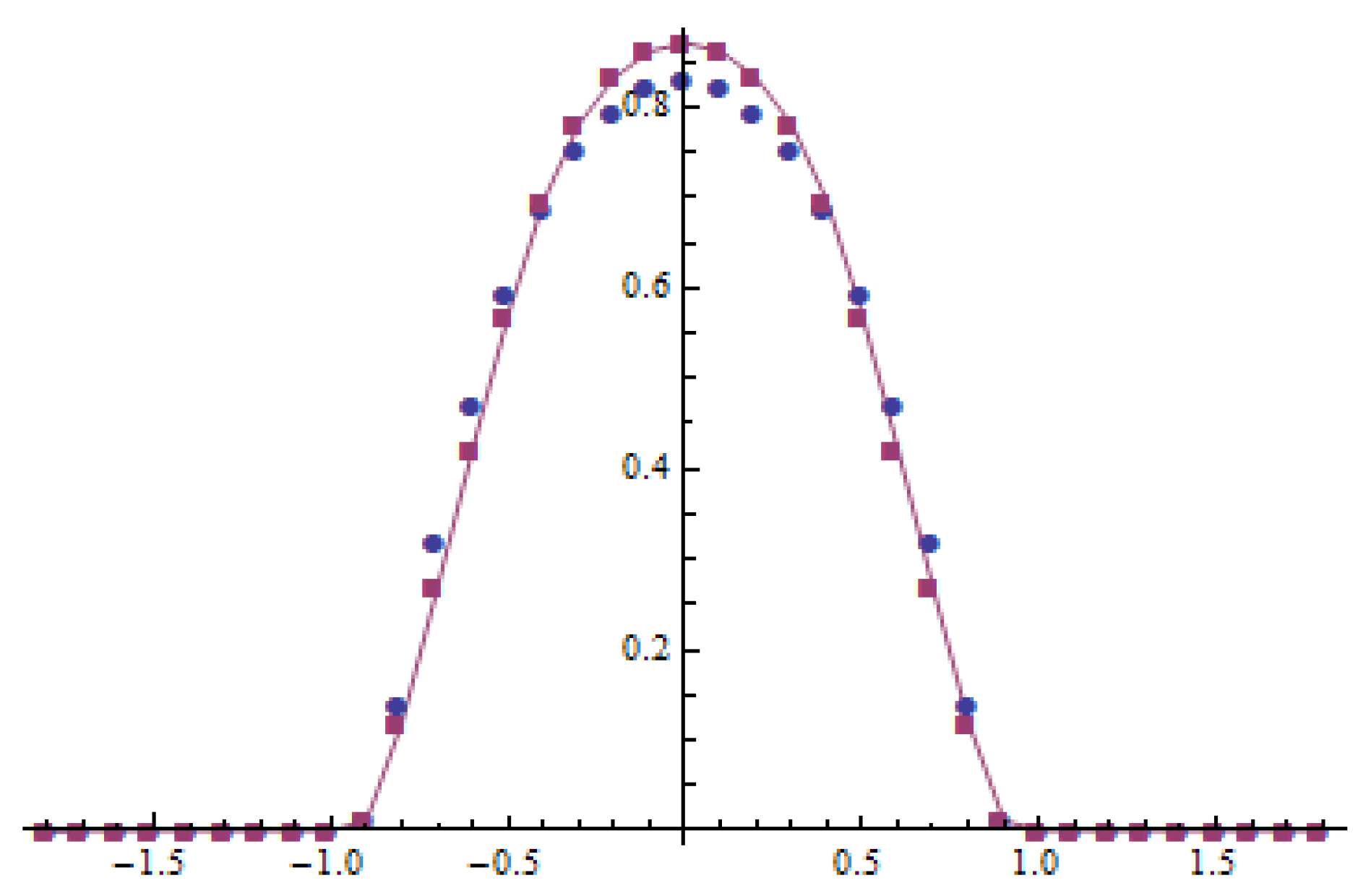
is dispersive. Otherwise, the maximum of the solution to (
19) is increasing (
, see
Figure 4 and
Figure 5), and the solutions are not dispersive. The time derivative of the solution for
does not have any positive twin peaks in the neighborhood of
(see
Figure 4), which indicates that the solution for anti-diffusion is unipolar. This follows from the fact that the initial datum and its derivatives satisfy the conditions given in [
4] (cf. Theorem 3.1).
Consider
. It follows from Proposition 1 that for
the
-norm and non-negativity of the solution are preserved. The same properties remain for
. The method of lines for
is stable, unlike for
. The evolution of the solution is presented at
Figure 3 and
Figure 5.
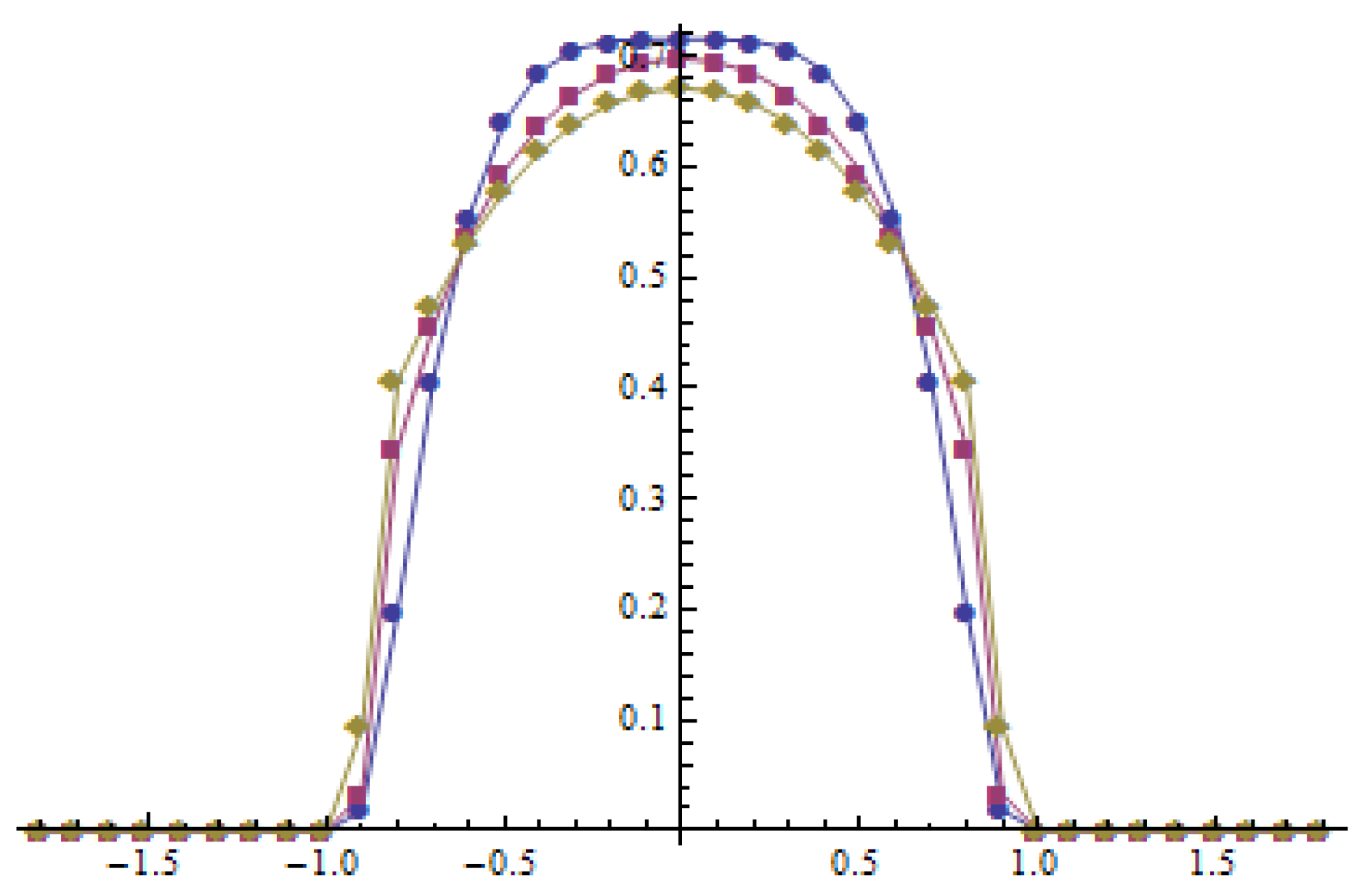
Example 2. We consider the following initial datumwhere is the normalizing coefficient. The initial datum has a single peak in the middle of the interval (see Figure 6), moreover, which has the second order derivative that is equal to zero in (see Figure 7). Therefore, the initial datum is “weakly” concave. The behavior of and its second order derivative is presented in Figure 6 and Figure 7. One can see that the initial datum satisfies conditions given in [4] (see Theorem 3.1). Therefore, the method of lines for anti-diffusion transforms the unipolar initial function into the bipolar solution with twin peaks which move away from zero. The bipolarity can also be observed in the context of the time derivative for the initial function. The initial function in “
weakly” concave in
. The time derivative for
and
has symmetric positive twin peaks (see
Figure 8). Using the formula (
21) one can observe that the values of the time derivative given in the twin peaks added to the values of the initial function in the same points are significantly increasing the value of the initial function. Therefore, the bipolar behavior is observed (see
Figure 9).
Considering
, the time derivative is presented in
Figure 10, and the dispersive evolution is shown in
Figure 11.
As before, for
, the
-norm and non-negativity of the solution are preserved. The same properties remain for
. The method of lines for
is stable, unlike for
. The evolution of the solution to the method of lines for
is presented in
Figure 9 and
Figure 11.
Our numerical experiments with the method of lines applied to kinetic models in social sciences indicate the possibility of a reliable approximation of short-range interaction opinions in the case of non-conformist societies (). It has a natural interpretation that the model with short interactions is replaced by a discrete model with discrete opinions influencing neighboring opinions. This replacement is constrained by appropriate scaling according to diffusive limits. Concerning the conformist society case (), our numerical simulations show numerical instability. However, we observed the unipolar and bipolar phenomenon on a very small time interval.
5. Conclusions
In the paper we studied a class of nonlinear integro-differential kinetic equations that can describe the opinion dynamics for two types of societies— the conformist and anti-conformist . An anti-diffusive (concentration) and a diffusive (dispersive) macroscopic pictures were observed, respectively.
The solutions to the kinetic Equation (
4) are a priori positive and preserve
-norm in both considered cases. For
the existence result is global, whereas for
it is only local (see Proposition 1), which can be related to a strong concentration (self-organization) in the latter case.
Assuming that
(given by (
6)) belongs to
,
,
, we conclude that the solutions to the kinetic equation are convergent in
X to the solution of a diffusion or (formally) anti-diffusion equations.
In Ref. [
4] some bipolar phenomena are described for the kinetic Equation (
4). It is a very well-known phenomenon in political sciences (see [
4] and references therein).
The present paper opens new interesting problems related to the description of concentration-dispersive phenomena on the mesoscopic scale that may be related to various processes observed in life and social sciences.