Abstract
We study the problem of the influence of one-sided different noisy channels to the quantum correlations decay in a symmetric bosonic system. We concentrate on one type of these correlations—the entanglement. The system under consideration is composed of two nonlinear oscillators coupled by two-boson interactions and externally driven by a continuous coherent field. Our low-dimensional system can be treated as 2-qutrit one. Two different noisy channels (the amplitude and the phase-damping reservoirs) are applied to both of the system’s modes. We show that there is a noticeable difference in the quantum entanglement in 2-qubit subspaces of the whole system decrease after swapping the reservoirs between the modes of the considered symmetric system. It appears also that the degree of obtained entanglement depends crucially on the position of the appropriate type of reservoir. The origin of the observed asymmetry is also explained.
1. Introduction
Obtaining low-dimensional optical systems is still one of the challenges in contemporary quantum optics. Systems evolving among a strictly limited number of quantum states play an important role, e.g., in quantum cryptography [1,2], state teleportation [3,4], and quantum information processing [5].
The methods leading to the state truncation rely mainly on the applications of nonlinear media of various types. In the literature we may find both theoretical and experimental examples of low-dimensional bosonic systems obtained with the help of effective nonlinearities of various orders and strengths [6,7,8,9]. One of such methods makes use of quantum effects leading to the phenomena known as photon blockade (or more generally, boson blockade). This is the phenomenon in which the Hilbert space of the considered system is significantly truncated in such a way that only a very limited number of bosonic states is available for the whole system. Such a truncation can be obtained in two different ways, and two different physical mechanisms lead to photon blockades.
In the first mechanism, which is known as conventional photon blockade, the origin of truncation lies in obtaining an effective nonlinearity in the Hamiltonian describing the system [10,11,12,13]. This nonlinearity is responsible for the non-equidistant eigenstates spectrum of the system. An external driving resonant with one transition is not resonant with others, and thus, the number of allowed states is limited (truncated). For example, the effective nonlinearity of a cavity field–atom interaction leads to the anharmonicity of the Jaynes–Cummings ladder of eigenstates. The presence of single photon in this optical cavity suppresses the appearance of the second one in the system, because a second photon at the same frequency is not resonant with the next transitions in the ladder [10]. This mechanism works properly only if the second photon is detuned from each of those next transitions by amounts that are much larger than the respective linewidths. Therefore, strong nonlinearities, and thus strong light–matter regimes, are necessary in this first mechanism. Large nonlinearities may be problematic from an experimental point of view, but many examples have already been presented in which strong effective nonlinearities are generated, e.g., due to: cavity field–atom interactions in the dispersive limit [10], optomechanical interactions [14], interactions between the atoms in optical lattices [15], nanoresonators [16], and interactions in superconducting circuit-QED systems [17,18].
In the weak light–matter regime, where the effective nonlinearity is weak, the second mechanism (known as unconventional photon blockade) is necessary [19,20,21]. It is a strongly resonant effect and requires a minimum input intensity to operate [22]. The physical origin of this blockade effect is the result of multipath destructive interference, which is responsible for uncoupling of some of the states.
In the considerations presented in this paper, we apply the systems characterized by strong nonlinearities to make use of the physical mechanism leading to the conventional photon blockade. Such systems are also known in the literature as nonlinear quantum scissors, due to their properties resulting in truncation of the Hilbert space [23,24,25]. Due to the presence of strong nonlinearity, which changes the energy spectrum of the considered system, there is only a limited number of resonant states, and finally the effective state truncation is possible.
In many papers the limited number of two-mode states is the starting point of the discussion of entanglement formation. Such possibility was reported for example in papers dealing with nonlinear quantum scissors, which exploited strongly nonlinear media (with much larger than other parameters describing the interactions) to obtain 2-qubit, qutrit-qubit or 2-qutrit systems [26,27,28]. Various external driving mechanisms were also analyzed: continuous excitation, performed by a laser field [24,26]; intense optical field generating two modes by parametric down-conversion process [27]. Pulsed laser driving with constant or different pulse widths was also analyzed [29]. In all these cases, generation of maximally or almost maximally entangled states were reported. It was also shown that changes in the duration of laser pulse or even random perturbations in pulse duration can improve the ability of the nonlinear system to produce entangled states [29]. It may be of special worth especially for real experimental situations when some perturbations in maintaining the precise and stable timing of pulse laser sources can occur.
In the present paper, a coupled oscillatory system evolving among limited number of quantum states externally driven in both modes by a coherent field is presented. We concentrate on an open system evolution of coupled nonlinear media and apply different (amplitude and phase) noisy channels to both modes of the considered system. We show that we may influence the rate of disentanglement and the values of entanglement created in the qubit subspaces of the whole system by swapping the noisy channels between the modes. Such changes in the environment type, which influence the entangled qubits, may occur when both parts of the entangled pair are sent through different paths and therefore may encounter various local disturbances. The observed asymmetry in the response of the analyzed 2-mode system may give some information on which type of environment the system’s parts were exposed to and which of the qubits was affected by a specific type of noise. The influence of the reservoir and the reservoir combinations on the symmetry of quantum correlation were analyzed for example in [30] for some mixed states under the influence of depolarizing channel. For the specified X state, the problem of symmetry in correlations decay was reported for example in [31].
2. The Model
The systems we are dealing with consist of coupled quantum nonlinear media with external excitations, which in general can be of various types. Such systems are well known as the potential sources of maximally or almost maximally entangled states. Various types of coupling and external driving have already been discussed [26,27,28,32]. In all of those cases it appeared that it was possible to restrict the evolution of the whole coupled system to several bosonic states only—therefore, under the assumptions of weak interactions (as compare with the nonlinearity), truncation of the appropriate wave function was possible. In consequence it has also been shown that such nonlinear systems can be treated as pairs of qubits, or qutrits or qutrit-qubit pairs. It has also been shown that under some assumptions, creation of for example Bell-type [24,26] or W-states [32] was possible.
Such models can be realized either in the quantum optical domain with media characterized by ultra-strong Kerr nonlinearities, or more often in the systems described by effective Hamiltonians including nonlinearities of the Kerr type.
Each of the parts forming the coupled system is characterized by the following nonlinear Hamiltonian in the interaction picture:
where a and b label two modes of the system, and are the photon number operators in those modes. In general, both parts can have different nonlinear properties: .
In our considerations of the decay asymmetry we will concentrate on the nonlinear exchange between the bosonic modes. In the optical counterparts of such a system that type of interaction is realized by two-photon processes:
where describes the strength of the mutual interaction. Apart from the interactions between nonlinear parts, we assume that the system is driven by coherent laser fields with intensities and . Therefore, the appropriate Hamiltonian has the following form:
Under assumptions of weak internal and external interactions (if compared to Kerr-type nonlinearity), the evolution of the discussed system is closed within a few two-mode states only, despite the continuous excitations. To make use of the nonlinear bosonic exchange between the modes of a coupled oscillatory system we prepare it in the initial excited state , and when symmetrically exciting both modes the adequate wave function takes the following form:
and forms a 2-qutrit system, as in both modes only states , and are populated. The appropriate fidelity for obtaining the wave function (4) is plotted in Figure 1. We calculate fidelities between the two wave functions of the system: the truncated wave function for the specified subspace and the whole numerically obtained wave function in an extended basis. We can easily see that our nonlinear coupled system evolves only between the states belonging to two subspaces: (solid line) and (dashed line). Therefore, the influence of the states other than (4) is negligible and we can treat the state truncation as fully justified.
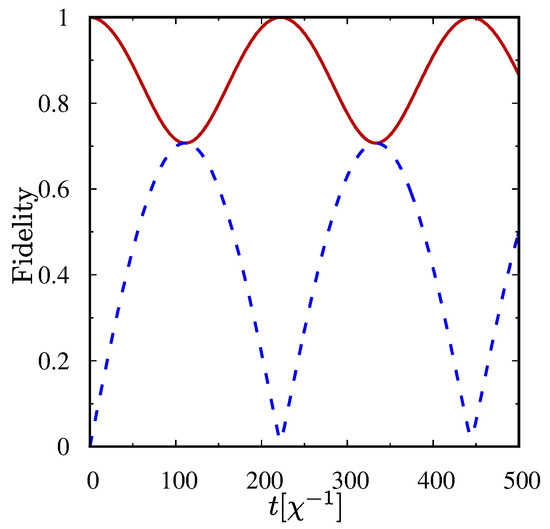
Figure 1.
Fidelity between the numerically obtained wave function describing the whole two-mode system in an extended basis and the truncated wave function for the subspace — solid line, and for the subspace — dashed line. The initial state of the system is a two-photon state , ; .
The analysis of formation of maximally entangled states within the system, given in [25,26], enables us to claim that the coupled oscillators form the following entangled states with probabilities equal to unity () or slightly less than unity ( for which fidelity ). As also the mode b is externally driven by a coherent field, additionally the state is included in the evolution. Consequently, also states can be obtained, but with lower probabilities. These maximally entangled states are defined by:
3. Entanglement Decay under Dissipation Channel Combinations
The analysis of the influence of various dissipation channels on the system’s dynamics can be described by standard techniques when considering master equation for the density matrix of the system. For our purpose we will assume two-sided different noisy channels. We will focus on the amplitude and phase channels applied to both of the system’s modes. In particular, we will concentrate on the problem of the decay of the created entangled states for the symmetrically driven system. The amplitude damping in Born and Markov approximations for a specified mode can be obtained by adding an appropriate Liouvillian to the master equation:
For the phase-damping channel, the adequate master equation has the following form:
where denotes the specified mode of the system, and we additionally assume zero temperature reservoirs. The Hamiltonian consists of the nonlinear part (1), the Hamiltonian (2) describing the interactions within the oscillatory system, and the Hamiltonian (3) with excitations performed in both modes. The whole coupled system is fully symmetric, as depicted in Figure 2, and for our analysis we will assume switching the location of the reservoir with specified type of noise between the qubits which we can create the entangled states and look for the symmetry in the quantum correlations dynamics.
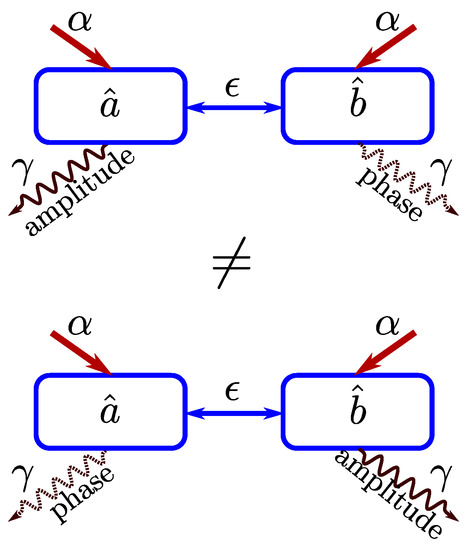
Figure 2.
Visualization of different location of noise in the model of the symmetric coupled oscillatory system.
We will focus on one type of quantum correlations, namely the entanglement. For the analysis of entanglement, we can apply negativity [33,34], which is a measure of entanglement degree in 2-qubit and qubit-qutrit systems
where is the i-th eigenvalue of a matrix . This matrix is obtained by performing partial transpose of the matrix of the whole quantum system with respect to one of the subsystems, a or b. Using that measure we can identify the maximally entangled states (in the systems of 2 qubits and qubit-qutrit) as those for which the negativity equal to unity is obtained. holds for separable states. In further considerations we will analyze the process of entanglement creation within the 2-qubit subsystem of the whole system. Therefore we restrict ourselves to the subspace spanned by the following two-mode states: ; is the abbreviation for the negativity defined according to (9), with the matrix describing this 2-qubit subsystem. The second 2-qubit subsystem is related to the states: and the appropriate negativity .
It is well known that the amplitude reservoir describes the process of energy dissipation induced by the environment. Therefore, the decrease in the states’ populations leads consequently to the decay of quantum correlations such as for example quantum entanglement. Phase-damping reservoir, on the other hand, describes the process of a random change in time of relative phases of the superposed states. In that process the number of photons remains unchanged and the energy is preserved. Nevertheless, the dephasing process is also responsible for quantum correlations destruction, but without changes of the total energy of the system. When looking at the density matrix—the phase-damping channel affects the off-diagonal elements only, while the amplitude damping channel influences the diagonal as well as the off-diagonal elements.
In [35] the influence of symmetrically applied amplitude and phase-damping channels was analyzed and it was shown that the dephasing channel, although it leads to the decrease of entanglement (measured by the negativity) but the rate of such a process is much slower than for the system exposed to the amplitude damping environment. Also, the entanglement sudden death, observed when energy dissipation is allowed, was not possible due to the dephasing process only. Another interesting feature of the analyzed qutrit-qubit system was also noticed. Specifically, the state appeared to be helpful in restoring the degree of entanglement when the system is exposed to the amplitude damping process. It is possible because of constant external driving and formation of the entangled state , which involves . Therefore, the negativity can be periodically increased due to the presence of correlations, which depend on the external coherent field of the amplitude . Correlations can therefore flow out of the considered 2-qubit subspace and return, due to the interactions with the additional two-mode state. Actually, our coupled nonlinear system is a higher-dimensional one. When only unitary evolution is assumed, the wave function can be expressed by (4), therefore we must consider 2-qutrits instead of just a qutrit-qubit system. Apart from the state there is also nonzero probability of obtaining the state , and other entangled states are also possible to obtain.
The state is a common state for both of the 2-qubit subspaces, therefore it is evident that they are not independent and correlations obtained in one of them may influence the correlations observed in the other one.
We assume that the whole system is fully symmetrical — nonlinear media are of the same type, , they are symmetrically driven with the same strengths (see Figure 2). We apply different damping channels to both modes a and b and look for any differences under swapping the channels, which affect both parts of the whole considered system.
Still we concentrate mainly on the entanglement created only between the states () and between the states (). We are going to ask ourselves the question, whether it is possible in a real physical system composed of these states to see any asymmetrical behavior of negativity decay by switching the damping channels between the modes a and b. The appropriate figures (Figure 3) presenting the time dependence of negativities calculated for 2-qubit subspace for various relations between the mutual () and the external () interactions, are presented. First of all, it can be easily seen that there is an evident difference between the values of negativities obtained and the rate of decay under the symmetric channel swapping. Therefore, a fully symmetrical quantum system can exhibit a clear asymmetry in evolution of quantum correlations when applying and swapping different types of reservoirs.
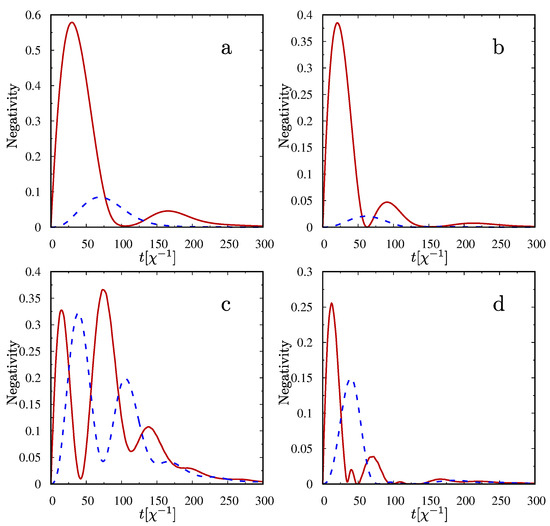
Figure 3.
Negativities for 2-qubit subspaces— (solid line) and (dashed line) versus time scaled in units for combinations of damping channels. In (a) and (c) the mode a is exposed to the amplitude damping channel and mode b into the phase-damping channel. In (b) and (d) the channels are swapped. The initial state of the system is a two-photon one , for (a) and (b); and for (c) and (d).
As seen in Figure 3, for all the considered cases larger values of entanglement characterized by and , are possible, when the mode a is exposed to the amplitude damping channel and the mode b decays to the phase reservoir (Figure 3a,c), than when the reservoirs are swapped between the modes (Figure 3b,d). There is also a noticeable difference in the time span for which the system can be considered to be an entangled one. Again, longer times for disentangling of the qubits are necessary if the mode a decays to the reservoir with amplitude damping and the mode b to the phase than for the case with the mode a decaying to the dephasing channel and the mode b to the amplitude channel. Therefore, there is a certain asymmetry in the response of the coupled system to the exchange of the damping channels between the parts of the whole system. We can also see that the presence of correlations is connected mainly with the subspace . In all the considered cases (in various damping channels configurations) the values of negativities are noticeably higher than appropriate negativities for the second considered subspace. Additionally, the decrease in the value of is obviously connected with the increase of . Thus, there is some kind of flow of entanglement between the considered subspaces of the whole system.
Next we will address the problem of the specific entangled states (5)–(6) formation to decide, which of them are responsible for nonzero negativities and which influence the observed asymmetry in and dependencies after exchanging the reservoirs between the modes a and b.
It is evident that all the states (5)–(6) should be possible to observe during the time evolution of the system. States are created due to the 2-photon interactions, states are obtained as a consequence of additional external excitation, which is responsible for populating the states and .
In Figure 4 the evolutions of appropriate entangled states are plotted. When the mode a is decaying into the amplitude damping channel, the states oscillate with almost the same frequencies, simultaneously obtaining maxima and minima. When the mode a is exposed to the dephasing process, the evolution of state is slightly perturbed by another frequency. From the behavior of entangled states presented, it comes out that a complete decay of negativity is related to the higher probability of obtaining the states —in such a case the correlations initially created in the subspace are transferred out of the considered subspace. Due to the presence of one common state belonging to both subspaces of the whole system, correlations can be significantly transferred to the subspace . It happens in shorter time for the situation when the mode a is exposed to the dephasing process, as it is easier to populate the state by an external field, while the mode a does not lose its population. The presence of the state is therefore crucial in obtaining the asymmetry in correlations, measured by the negativity decay introduced by swapping the reservoirs between the qubits forming the entangled states. As seen from Figure 4, the evolution of the created entangled states strongly depends on the type of reservoir applied to each of the modes. Such a difference is obviously seen in the values of negativities for the qubit subspaces and results in the asymmetry in correlations decay.
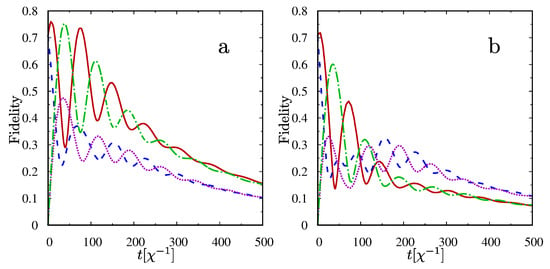
Figure 4.
Fidelities for obtaining the entangled states for , and the initial state . In (a) the mode a is exposed to the amplitude damping channel and the mode b to the phase-damping channel. In (b) the channels are swapped. —solid line; —dashed line; —dashed-dotted line and —dotted line.
It appears that the state plays a crucial role in formation and behavior of the entanglement in the coupled system. Its presence influences significantly the time of disentanglement and indirectly the values of — higher probabilities of decrease the probabilities of . When the mode a of the state decays by the amplitude channel to the state , it increases the probability of generating the states and results in higher values of . On the other hand, the mode a is externally pumped by the linear interaction and again the state can be formed.
4. Conclusions
We discussed a coupled nonlinear system whose parts are driven by coherent laser fields. We additionally assumed that interactions between the nonlinear media are performed via two-boson exchange. Such systems, when appropriate conditions describing relations between the strengths of the interactions and the nonlinearity are fulfilled, evolve only between a limited number of states despite the constant energy supply. We have shown that the model we are dealing with can be treated as a 2-qutrit system and the unitary evolution can be described by a truncated wave function. As the nonlinearity describing the interacting media must be large (as compared to other interactions), in that sense the possibility of the Hilbert space truncation may be regarded as the conventional photon blockade. We have discussed the problem of the entanglement decay under the influence of different noisy channels. Both parts of the considered coupler (the mode a and the mode b) were exposed to the local amplitude or phase-damping environments. Our goal was to show that despite the symmetry of our system, it is possible to differentiate the decay rates and the values of the entanglement obtained within 2-qubits subspaces by appropriately choosing the type of system-environment interactions. For that purpose, we have analyzed the time evolution of negativities after first applying and then swapping different noisy channels to the modes a and b. We have identified the asymmetry in the response of the system to the interactions with the reservoirs. There is a noticeable difference in the rate at which entanglement decreases, due to the location of the noise between the qubits.
Author Contributions
Conceptualization and Formal analysis, A.K.-K.; Software, Validation and Investigation, A.K.-K. and G.C.; Visualization, G.C.; Writing—original draft, A.K.-K.; Writing—review & editing, G.C.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Bartkiewicz, K.; Černoch, A.; Chimczak, G.; Lemr, K.; Miranowicz, A.; Nori, F. Experimental quantum forgery of quantum optical money. npj Quantum Inf. 2017, 3, 7. [Google Scholar] [CrossRef]
- Özdemir, Ş.K.; Bartkiewicz, K.; Liu, Y.X.; Miranowicz, A. Teleportation of qubit states through dissipative channels: Conditions for surpassing the no-cloning limit. Phys. Rev. A 2007, 76, 042325. [Google Scholar] [CrossRef]
- Chimczak, G.; Tanaś, R. High-fidelity atomic-state teleportation protocol with non-maximally-entangled states. Phys. Rev. A 2009, 79, 042311. [Google Scholar] [CrossRef]
- Chimczak, G. Efficient generation of distant atom entanglement via cavity decay. Phys. Rev. A 2005, 71, 052305. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Maccone, L.; Paris, M.; Sacchi, M. Optical Fock-state synthesizer. Phys. Rev. A 2000, 61, 053817. [Google Scholar] [CrossRef]
- Didier, N.; Pugnetti, S.; Blanter, Y.M.; Fazio, R. Detecting phonon blockade with photons. Phys. Rev. B 2011, 84, 054503. [Google Scholar] [CrossRef]
- Wang, H.; Gu, X.; Liu, Y.X.; Miranowicz, A.; Nori, F. Tunable photon blockade in a hybrid system consisting of an optomechanical device coupled to a two-level system. Phys. Rev. A 2015, 92, 033806. [Google Scholar] [CrossRef]
- Peřinová, V.; Lukš, A.; Křapelka, J. Dynamics of nonclassical properties of two- and four-mode Bose-Einstein condensates. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 195301. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon blockade in an optical cavity with one trapped atom. Nature 2005, 436, 87–90. [Google Scholar] [CrossRef]
- Faraon, A.; Fushman, I.; Englund, D.; Stoltz, N.; Petroff, P.; Vučković, J. Coherent generation of non-classical light on a chip via photon-induced tunnelling and blockade. Nat. Phys. 2008, 4, 859–863. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.X.; Zagoskin, A.M.; Nori, F. State-dependent photon blockade via quantum-reservoir engineering. Phys. Rev. A 2014, 90, 033831. [Google Scholar] [CrossRef]
- Zhu, C.J.; Yang, Y.P.; Agarwal, G.S. Collective multiphoton blockade in cavity quantum electrodynamics. Phys. Rev. A 2017, 95, 063842. [Google Scholar] [CrossRef]
- Bose, S.; Jacobs, K.; Knight, P.L. Preparation of nonclassical states in cavities with a moving mirror. Phys. Rev. A 1997, 56, 4175–4186. [Google Scholar] [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Tai, M.E.; Lukin, A.; Rispoli, M.; Greiner, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Miranowicz, A.; Gao, Y.B.; Bajer, J.; Sun, C.P.; Nori, F. Qubit-induced phonon blockade as a signature of quantum behavior in nanomechanical resonators. Phys. Rev. A 2010, 82, 032101. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Srinivasan, S.J.; Schmidt, S.; Spietz, L.; Aumentado, J.; Türeci, H.E.; Houck, A.A. Dispersive Photon Blockade in a Superconducting Circuit. Phys. Rev. Lett. 2011, 107, 053602. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.; Miranowicz, A.; Nori, F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Liew, T.C.H.; Savona, V. Single Photons from Coupled Quantum Modes. Phys. Rev. Lett. 2010, 104, 183601. [Google Scholar] [CrossRef]
- Bamba, M.; Imamoğlu, A.; Carusotto, I.; Ciuti, C. Origin of strong photon antibunching in weakly nonlinear photonic molecules. Phys. Rev. A 2011, 83, 021802. [Google Scholar] [CrossRef]
- Hamsen, C.; Tolazzi, K.N.; Wilk, T.; Rempe, G. Two-Photon Blockade in an Atom-Driven Cavity QED System. Phys. Rev. Lett. 2017, 118, 133604. [Google Scholar] [CrossRef] [PubMed]
- Flayac, H.; Gerace, D.; Savona, V. An all-silicon single-photon source by unconventional photon blockade. Sci. Rep. 2015, 5, 11223. [Google Scholar] [CrossRef] [PubMed]
- Leoński, W.; Tanaś, R. Possibility of producing the one-photon state in a kicked cavity with a nonlinear Kerr medium. Phys. Rev. A 1994, 49, R20–R23. [Google Scholar] [CrossRef] [PubMed]
- Leoński, W.; Miranowicz, A. Kerr nonlinear coupler and entanglement. J. Opt. B 2004, 6, S37–S42. [Google Scholar] [CrossRef]
- Leoński, W.; Kowalewska-Kudłaszyk, A. Quantum Scissors–Finite-Dimensional States Engineering. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 56, pp. 131–185. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Leoński, W. Finite-dimensional states and entanglement generation for a nonlinear coupler. Phys. Rev. A 2006, 73, 042318. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Leoński, W.; Peřina, J., Jr. Photon-number entangled states generated in Kerr media with optical parametric pumping. Phys. Rev. A 2011, 83, 052326. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Leoński, W. Nonlinear coupler operating on Werner-like states; entanglement creation, its enhancement, and preservation. J. Opt. Soc. Am. B 2014, 31, 1290–1297. [Google Scholar] [CrossRef]
- Kalaga, J.; Kowalewska-Kudłaszyk, A.; Jarosik, M.; Szczȩśniak, R.; Leoński, W. Enhancement of the entanglement generation via randomly perturbed series of external pulses in a nonlinear Bose–Hubbard dimer. Nonlinear Dyn. 2019, 1–15. [Google Scholar] [CrossRef]
- Życzkowski, K.; Horodecki, P.; Horodecki, M.; Horodecki, R. Dynamics of quantum entanglement. Phys. Rev. A 2001, 65, 012101. [Google Scholar] [CrossRef]
- Lyyra, H.; Karpat, G.; Li, C.; Guo, G.; Piilo, J.; Maniscalco, S. Symmetry in the open-system dynamics of quantum correlations. Sci. Rep. 2017, 7, 8367. [Google Scholar] [CrossRef]
- Said, R.S.; Wahiddin, M.R.B.; Umarov, B.A. Generation of three-qubit entangled W state by nonlinear optical state truncation. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 1269–1274. [Google Scholar] [CrossRef]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413–1415. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A. Dephasing in nonlinear quantum scissors systems. Opt. Commun. 2012, 285, 5543–5548. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).