A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives
Abstract
1. Introduction
2. Proposed Methods and Their Convergence Analysis
3. Numerical Performance of Proposed Schemes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mathai, A.M.; Haubold, H.J. Fractional and Multivariable Calculus. In Model Building and Optimization Problems; Springer Optimization and Its Applications 122; Springer: Berlin, Germany, 2017. [Google Scholar]
- Ross, B. A brief history and exposition of the fundamental theory of fractional calculus. In Fractional Calculus and Its Applications; Ross, B., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1975; Volume 457, pp. 1–36. [Google Scholar]
- Atanackovic, T.M.; Pilipovic, S.; Stankovic, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles; Wiley: London, UK, 2014. [Google Scholar]
- Khan, M.A.; Ullah, S.; Farhan, M. The dynamics of Zika virus with Caputo fractional derivative. AIMS Math. 2019, 4, 134–146. [Google Scholar] [CrossRef]
- Brambila, F.; Torres, A. Fractional Newton-Raphson Method. arXiv 2017, arXiv:1710.07634v3. [Google Scholar]
- Akgül, A.; Cordero, A.; Torregrosa, J.R. A fractional Newton method with 2th-order of convergence and its stability. Appl. Math. Lett. 2019, 98, 344–351. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Lombardero, A. Cálculo Fraccionario y dinámica newtoniana. Pensam. Mat. 2014, IV, 77–106. [Google Scholar]
- Caputo, M.C.; Torres, D.F.M. Duality for the left and right fractional derivatives. Signal Process 2015, 107, 265–271. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations and Systems of Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Magreñan, A.Á. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]
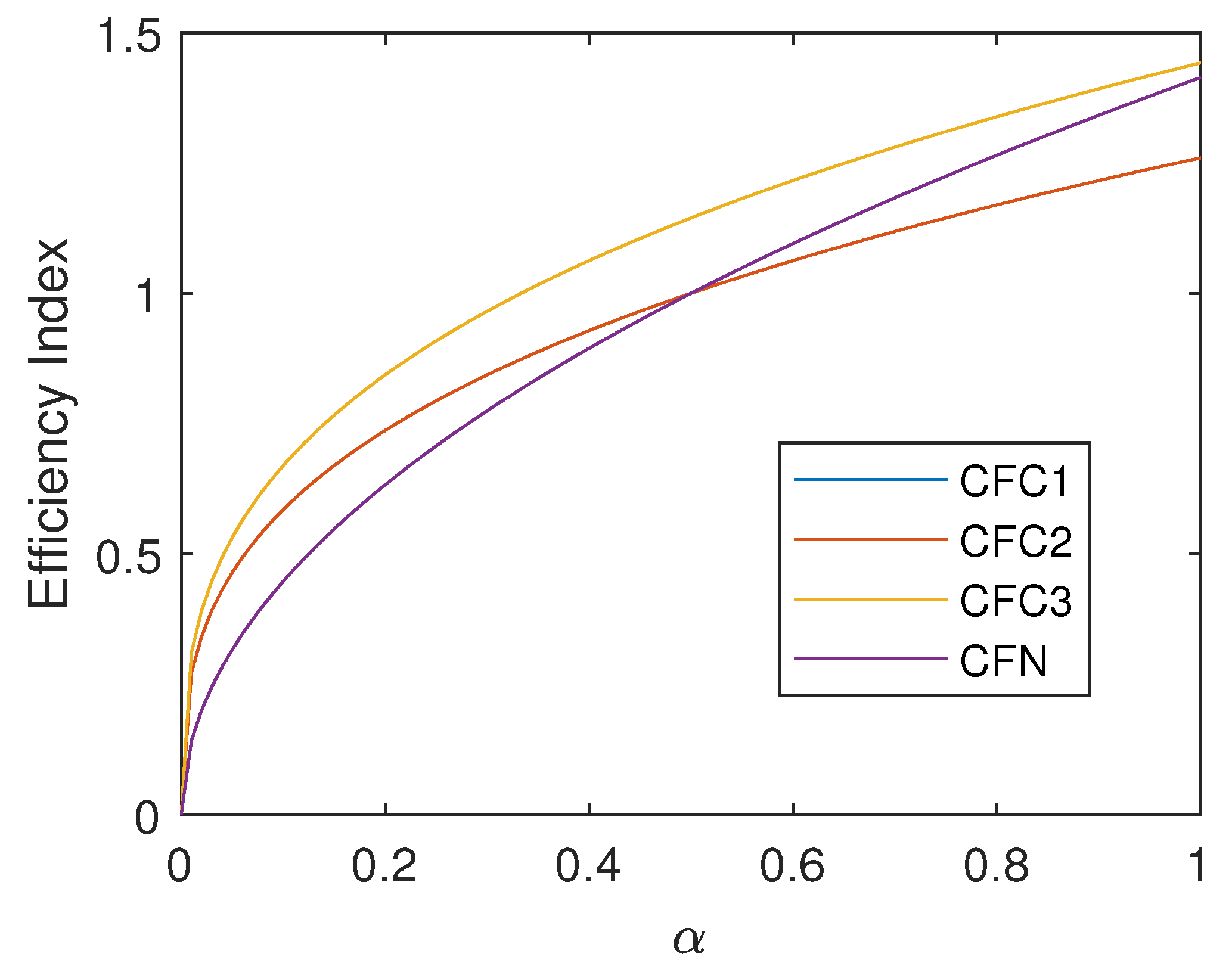
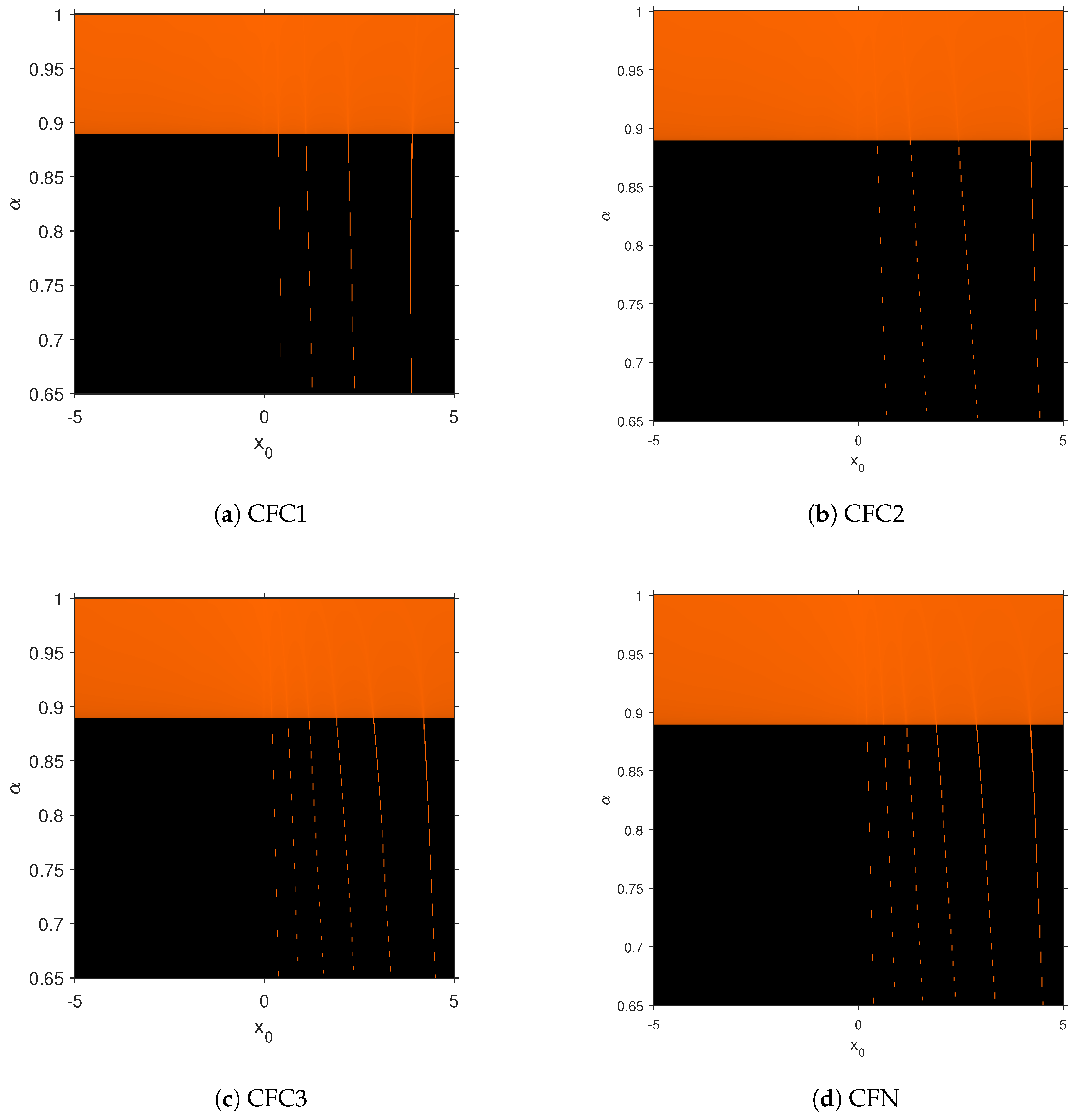

| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1274e-05+i4.6093e-04 | 9.2186e-04 | 4.6804e-04 | 250 |
| 0.91 | −3.2556e-05+i2.0787e-04 | 4.1575e-04 | 2.1041e-04 | 250 |
| 0.92 | −1.0632e-05+i7.7354e-05 | 1.5471e-04 | 7.8081e-05 | 250 |
| 0.93 | −2.5978e-06+i2.1869e-05 | 4.3739e-05 | 2.2023e-05 | 250 |
| 0.94 | −4.1185e-07+i4.0939e-06 | 8.1878e-06 | 4.1145e-06 | 250 |
| 0.95 | −1.6155e-08-i9.1923e-07 | 1.9214e-06 | 9.1937e-07 | 23 |
| 0.96 | 1.4985e-07-i7.7007e-07 | 1.9468e-06 | 7.8451e-07 | 13 |
| 0.97 | 3.4521e-07-i7.6249e-07 | 2.6824e-06 | 8.3699e-07 | 9 |
| 0.98 | 2.7084e-07-i3.4599e-07 | 1.9608e-06 | 4.3939e-07 | 7 |
| 0.99 | −6.3910e-07+i2.1637e-07 | 6.4318e-06 | 6.7474e-07 | 5 |
| 1.00 | −2.9769e-08+i0.0000e+00 | 3.0994e-03 | 2.9769e-08 | 3 |
| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1270e-05+i4.6090e-04 | 9.2190e-04 | 4.6800e-04 | 250 |
| 0.91 | −3.2560e-05+i2.0790e-04 | 4.1570e-04 | 2.1040e-04 | 250 |
| 0.92 | −1.0630e-05+i7.7350e-05 | 1.5470e-04 | 7.8080e-05 | 250 |
| 0.93 | −2.5980e-06+i2.1870e-05 | 4.3740e-05 | 2.2020e-05 | 250 |
| 0.94 | −4.1180e-07+i4.0940e-06 | 8.1880e-06 | 4.1150e-06 | 250 |
| 0.95 | −1.6680e-07+i9.2200e-07 | 1.9640e-06 | 9.3690e-07 | 22 |
| 0.96 | −3.4850e-07+i7.2840e-07 | 2.0220e-06 | 8.0750e-07 | 12 |
| 0.97 | 5.5470e-07-i6.3310e-07 | 2.6850e-06 | 8.4180e-07 | 7 |
| 0.98 | −3.1400e-07+i2.0370e-07 | 1.6820e-06 | 3.7430e-07 | 7 |
| 0.99 | 1.2990e-07-i8.4600e-08 | 1.2680e-06 | 1.5500e-07 | 6 |
| 1.00 | −2.9770e-08+i0.0000e+00 | 3.0990e-03 | 2.9770e-08 | 3 |
| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1275e-05-i4.6093e-04 | 9.2187e-04 | 4.6804e-04 | 250 |
| 0.91 | −3.2556e-05-i2.0787e-04 | 4.1575e-04 | 2.1041e-04 | 250 |
| 0.92 | −1.0632e-05-i7.7354e-05 | 1.5471e-04 | 7.8081e-05 | 250 |
| 0.93 | −2.5978e-06-i2.1869e-05 | 4.3739e-05 | 2.2023e-05 | 250 |
| 0.94 | −4.1185e-07+i4.0939e-06 | 8.1878e-06 | 4.1145e-06 | 250 |
| 0.95 | 2.8656e-08-i9.4754e-07 | 1.9837e-06 | 9.4797e-07 | 23 |
| 0.96 | −3.2851e-07+i6.6774e-07 | 1.8538e-06 | 7.4418e-07 | 14 |
| 0.97 | 2.3413e-07-i4.2738e-07 | 1.5022e-06 | 4.8731e-07 | 11 |
| 0.98 | 2.0677e-07-i2.4623e-07 | 1.4017e-06 | 3.2154e-07 | 9 |
| 0.99 | 3.0668e-07-i2.2801e-07 | 3.3615e-06 | 3.8216e-07 | 7 |
| 1.00 | 1.2192e-16+i0.0000e+00 | 3.9356e-06 | 1.2192e-16 | 5 |
| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1274e-05-i4.6093e-04 | 9.2186e-04 | 4.6804e-04 | 250 |
| 0.91 | −3.2556e-05-i2.0787e-04 | 4.1575e-04 | 2.1041e-04 | 250 |
| 0.92 | −1.0632e-05-i7.7354e-05 | 1.5471e-04 | 7.8081e-05 | 250 |
| 0.93 | −2.5978e-06-i2.1869e-05 | 4.3739e-05 | 2.2023e-05 | 250 |
| 0.94 | −4.1185e-07+i4.0939e-06 | 8.1878e-06 | 4.1145e-06 | 250 |
| 0.95 | −1.1203e-07+i9.8331e-07 | 2.0799e-06 | 9.8967e-07 | 26 |
| 0.96 | −3.2473e-09-i7.0333e-07 | 1.7375e-06 | 7.0333e-07 | 19 |
| 0.97 | 5.9619e-08-i7.4110e-07 | 2.3750e-06 | 7.4349e-07 | 18 |
| 0.98 | 4.7121e-07+i7.4115e-07 | 4.1416e-06 | 8.7826e-07 | 19 |
| 0.99 | 3.9274e-08-i3.9674e-07 | 3.5758e-06 | 3.9868e-07 | 14 |
| 1.00 | 3.9559e-08+i4.8445e-07 | 7.8597e-03 | 4.8606e-07 | 8 |
| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1308e-05-i4.6100e-04 | 9.2200e-04 | 4.6811e-04 | 250 |
| 0.91 | −3.2562e-05-i2.0789e-04 | 4.1577e-04 | 2.1042e-04 | 250 |
| 0.92 | −1.0633e-05-i7.7355e-05 | 1.5471e-04 | 7.8082e-05 | 250 |
| 0.93 | −2.5978e-06-i2.1870e-05 | 4.3739e-05 | 2.2023e-05 | 250 |
| 0.94 | −4.1185e-07+i4.0939e-06 | 8.1878e-06 | 4.1145e-06 | 250 |
| 0.95 | −9.6563e-08+i9.3217e-07 | 1.9628e-06 | 9.3716e-07 | 28 |
| 0.96 | 1.3446e-08-i7.0728e-07 | 1.7477e-06 | 7.0741e-07 | 22 |
| 0.97 | −9.7497e-08+i1.0000e+00 | 1.7666e-06 | 2.1081e-07 | 15 |
| 0.98 | −1.8598e-07-i1.0000e+00 | 5.5924e-06 | 4.4631e-07 | 15 |
| 0.99 | −1.5051e-07+i5.1262e-07 | 4.9442e-06 | 5.3426e-07 | 13 |
| 1.00 | 3.9559e-08+i4.8445e-07 | 7.8597e-03 | 4.8606e-07 | 8 |
| Iterations | ||||
|---|---|---|---|---|
| 0.90 | −8.1275e-05+i4.6093e-04 | 9.2187e-04 | 4.6804e-04 | 250 |
| 0.91 | −3.2556e-05+i2.0787e-04 | 4.1575e-04 | 2.1041e-04 | 250 |
| 0.92 | −1.0632e-05+i7.7354e-05 | 1.5471e-04 | 7.8081e-05 | 250 |
| 0.93 | −2.5978e-06+i2.1869e-05 | 4.3739e-05 | 2.2023e-05 | 250 |
| 0.94 | −4.1185e-07+i4.0939e-06 | 8.1878e-06 | 4.1145e-06 | 250 |
| 0.95 | −9.1749e-08-i9.2392e-07 | 1.9434e-06 | 9.2846e-07 | 28 |
| 0.96 | 1.5946e-08+i1.0000e+00 | 6.4777e-07 | 1.0272e-07 | 12 |
| 0.97 | 1.2679e-07+i1.0000e+00 | 4.3336e-06 | 5.1715e-07 | 16 |
| 0.98 | −5.1142e-07+i7.8442e-07 | 4.5155e-06 | 9.3641e-07 | 16 |
| 0.99 | 9.3887e-08-i1.0000e+00 | 4.7305e-06 | 1.8942e-07 | 11 |
| 1.00 | −2.9297e-10-i1.0000e+00 | 1.4107e-05 | 5.9703e-10 | 9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordero, A.; Girona, I.; Torregrosa, J.R. A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives. Symmetry 2019, 11, 1017. https://doi.org/10.3390/sym11081017
Cordero A, Girona I, Torregrosa JR. A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives. Symmetry. 2019; 11(8):1017. https://doi.org/10.3390/sym11081017
Chicago/Turabian StyleCordero, Alicia, Ivan Girona, and Juan R. Torregrosa. 2019. "A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives" Symmetry 11, no. 8: 1017. https://doi.org/10.3390/sym11081017
APA StyleCordero, A., Girona, I., & Torregrosa, J. R. (2019). A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives. Symmetry, 11(8), 1017. https://doi.org/10.3390/sym11081017







