A Variant of Chebyshev’s Method with 3αth-Order of Convergence by Using Fractional Derivatives

Abstract

In this manuscript, we propose several iterative methods for solving nonlinear equations whose common origin is the classical Chebyshev’s method, using fractional derivatives in their iterative expressions. Due to the symmetric duality of left and right derivatives, we work with right-hand side Caputo and Riemann–Liouville fractional derivatives. To increase as much as possible the order of convergence of the iterative scheme, some improvements are made, resulting in one of them being of $3\alpha$-th order. Some numerical examples are provided, along with an study of the dependence on initial estimations on several test problems. This results in a robust performance for values of $\alpha$ close to one and almost any initial estimation.

1. Introduction

The concept of fractional calculus was introduced simultaneously with the development of classical one. The first references date back to 1695, the year in which Leibniz and L’Hospital came up with the concept of semi-derivative. Other researchers of the time were also interested in this idea, such as Riemann, Liouville, or Euler.

Since their early development in the XIX-th century until nowadays, fractional calculus has evolved from theoretical aspects to the appearance in many real world applications: mechanical engineering, medicine, economy, and others. They are frequently modeled by differential equations with derivatives of fractional order (see, for example [1,2,3,4] and the references therein).

Nowadays, fractional calculus has numerous applications in science and engineering. The fundamental reason for this is the greater degree of freedom of fractional calculation tools compared to classical calculation ones. This makes it the most suitable procedure for modeling problems whose hereditary properties must be preserved. In this sense, one of the most significant tools of fractional calculation is the fractional (integral) derivative.

Many times, these kinds of problems are related with systems of equations, that can be nonlinear if it is the differential equation. So, it is not strange to adapt iterative techniques for solving nonlinear equations by means of fractional derivatives of different orders, and see which is the resulting effect on the convergence. This has been studied in some previous works by Brambila et al. [5] holding the original expression of Newton’s iterative method and without proving the order of convergence. In [6], a fractional Newton’s method was deduced to achieve $2\alpha$-th order of convergence and showing good numerical properties. However, it is known (see for example the text of Traub [7]) that in point-to-point methods to increase the order of the iterative methods implies to add functional evaluations of higher-order derivatives of the nonlinear function. Our starting question is: how affects this higher-order derivative when it is replaced by a fractional one to the global order of convergence of the iterative method?

The aim of this work is to use the Chebyshev’s method with fractional derivative to solve $f\left(x\right)=0$, $f:D\subseteq \mathbb{R}\to \mathbb{R}$. Let us consider $\overline{x}\in \mathbb{R}$ as the solution of the equation $f\left(x\right)=0$, such that $f^{\prime }\left(\overline{x}\right)\ne 0$. First of all, we remind the standard Chebyshev’s method:

$$x_{k+1}=x_k-\left(1+{\displaystyle \frac{1}{2}}{L}_f\left(x_k\right)\right){\displaystyle \frac{f\left(x_k\right)}{f^{\prime }\left(x_k\right)}},k=0,1,\dots$$

(1)

being $L_f\left(x_k\right)={\displaystyle \frac{f\left(x_k\right)f^{\prime \prime }\left(x_k\right)}{f^{\prime }{\left(x_k\right)}^2}}$, known as logarithmic convexity degree. Then, we will change the first and second order integer derivatives by the notion of fractional derivative and see if is the order of convergence of the original method is held.

Now, we set up some definitions, properties and results that will be helpful in this work (for more information, see [8] and the references therein).

Definition 1.

The gamma function is defined as

$$\mathsf{\Gamma }\left(x\right)={\int }_0^{+\infty }{u}^{x-1}{e}^{-u}du,$$

whenever $x>0$.

The gamma function is known as a generalization of the factorial function, due to $\mathsf{\Gamma }\left(1\right)=1$ and $\mathsf{\Gamma }(n+1)=n!,$ when $n\in \mathbb{N}$. Let us now see the notion of fractional Riemann-Liouville and Caputo derivatives.

Definition 2.

Let $f:\mathbb{R}\to \mathbb{R}$ be an element of $L^1\left([a,x]\right)$ ($-\infty <a<x<+\infty$), with $\alpha \ge 0$ and $n=\left[\alpha \right]+1$, being $\left[\alpha \right]$ the integer part of α. Then, the Riemann–Liouville fractional derivative of order α of $f\left(x\right)$ is defined as follows:

$$\left(D_{a^{+}}^{\alpha }\right)f\left(x\right)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }(n-\alpha )}}{\displaystyle \frac{d^n}{d{x}^n}}{\int }_a^x{\displaystyle \frac{f\left(t\right)}{{(x-t)}^{\alpha -n+1}}}dt,}\hfill & \alpha \notin \mathbb{N},\hfill \\ {\displaystyle \frac{d^{n-1}f\left(x\right)}{d{x}^{n-1}}},\hfill & \alpha =n-1\in \mathbb{N}\cup \left\{0\right\}.\hfill \end{array}\right.$$

(2)

Let us remark that definition (2) is consistent if the integral of the first identity in (2) is n-times derivable or, in another case, f is $(n-1)$-times derivable.

Definition 3.

Let $f:\mathbb{R}⟶\mathbb{R}$ be an element of $C^{+\infty }\left([a,x]\right)$ ($-\infty <a<x<+\infty$), $\alpha \ge 0$ and $n=\left[\alpha \right]+1$. Thus, the Caputo fractional derivative of order α of $f\left(x\right)$ is defined as follows:

$$\left({}^C{D}_a^{\alpha }\right)f\left(x\right)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }(n-\alpha )}}{\int }_a^x{\displaystyle \frac{d^{n}f\left(t\right)}{d{t}^n}}{\displaystyle \frac{dt}{{(x-t)}^{\alpha -n+1}}},}\hfill & \alpha \notin \mathbb{N},\hfill \\ {\displaystyle \frac{d^{n-1}f\left(x\right)}{d{x}^{n-1}}},\hfill & \alpha =n-1\in \mathbb{N}\cup \left\{0\right\}.\hfill \end{array}\right.$$

(3)

In [9], Caputo and Torres generated a duality theory for left and right fractional derivatives, called symmetric duality, using it to relate left and right fractional integrals and left and right fractional Riemann–Liouville and Caputo derivatives.

The following result will be useful to prove Theorem 4.

Theorem 1.

([8], Proposition 26).Let $\alpha \ge 0$, $n=\left[\alpha \right]+1$, and $\beta \in \mathbb{R}$. Thus, the following identity holds:

$$D_{a^{+}}^{\alpha }{(x-a)}^{\beta }={\displaystyle \frac{\mathsf{\Gamma }(\beta +1)}{\mathsf{\Gamma }(\beta +1-\alpha )}}{(x-a)}^{\beta -\alpha }.$$

(4)

The following result shows a relationship between Caputo and Riemann–Liouville fractional derivatives.

Theorem 2.

([8], Proposition 31).Let $\alpha \notin \mathbb{N}$ such that $\alpha \ge 0$, $n=\left[\alpha \right]+1$ and $f\in L^1\left([a,b]\right)$ a function whose Caputo and Riemann-Liouville fractional derivatives exist. Thus, the following identity holds:

$${}^C{D}_a^{\alpha }f\left(x\right)=D_{a^{+}}^{\alpha }f\left(x\right)-\sum _{k=0}^{n-1}{\displaystyle \frac{f^{\left(k\right)}\left(a\right)}{\mathsf{\Gamma }(k+1-\alpha )}}{(x-a)}^{k-\alpha },x>a.$$

(5)

As a consequence of the two previous results, we obtain that

$${}^C{D}_{x_0}^{\alpha }{(x-x_0)}^k=D_{x_0}^{\alpha }{(x-x_0)}^k,k=1,2,\cdots$$

Remark 1.

In what follows, due to previous results and consequences, we work with Caputo fractional derivative, since all our conclusions are also valid for Riemann–Liouville fractional derivative at the same extent.

The next result shows a generalization of the classical Taylor’s theorem by using derivatives of fractional order.

Theorem 3.

([10], Theorem 3).Let us assume that ${}^C{D}_a^{j\alpha }g\left(x\right)\in \mathcal{C}\left([a,b]\right),$ for $j=1,2,\cdots ,n+1$, where $0<\alpha \le 1$. Then, we have

$$g\left(x\right)=\sum _{i=0}^n{}^C{D}_a^{i\alpha }g\left(a\right){\displaystyle \frac{{(x-a)}^{i\alpha }}{\mathsf{\Gamma }(i\alpha +1)}}+{}^C{D}^{(n+1)\alpha }g\left(\xi \right){\displaystyle \frac{{(x-a)}^{(n+1)\alpha }}{\mathsf{\Gamma }\left(\right(n+1)\alpha +1)}}$$

(6)

being $a\le \xi \le x,$ for all $x\in (a,b]$, where ${}^C{D}_a^{n\alpha }{=}^C{D}_a^{\alpha }·\cdots {·}^C{D}_a^{\alpha }$ (n-times).

When the assumptions of Theorem 3 are satisfied, the Taylor development of $f\left(x\right)$ around $\overline{x}$, by using Caputo-fractional derivatives, is

$$f\left(x\right)={\displaystyle \frac{{}^C{D}_{\overline{x}}^{\alpha }f\left(\overline{x}\right)}{\mathsf{\Gamma }(\alpha +1)}}\left[{(x-\overline{x})}^{\alpha }+C_2{(x-\overline{x})}^{2\alpha }+C_3{(x-\overline{x})}^{3\alpha }\right]+\mathcal{O}\left({(x-\overline{x})}^{4\alpha }\right),$$

(7)

being $C_j={\displaystyle \frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(j\alpha +1)}}{\displaystyle \frac{{}^C{D}_{\overline{x}}^{j\alpha }f\left(\overline{x}\right)}{{}^C{D}_{\overline{x}}^{\alpha }f\left(\overline{x}\right)}}$, for $j\ge 2$.

The rest of the manuscript is organized as follows: Section 2 deals with the design of high-order one-point fractional iterative methods and their analysis of convergence. In Section 3, some numerical tests are made in order to check the theoretical results and we show the corresponding convergence planes in order to study the dependence on the initial estimations of the proposed schemes. Finally, some conclusions are stated.

2. Proposed Methods and Their Convergence Analysis

In order to extend Chebyshev’s iterative method to fractional calculus, let us define

$${}^C{L}_f^{\alpha }\left(x\right)=\frac{f{\left(x\right)}^C{D}_a^{2\alpha }f\left(x\right)}{{\left(D_a^{\alpha }f\left(x\right)\right)}^2},$$

that we call fractional logarithmic convexity degree of Caputo-type.

Then, an iterative Chebyshev-type method using Caputo derivatives can be constructed. The following result show the convergence conditions of this new method.derivative with $2\alpha$.

Theorem 4.

Let $f:D\subset \mathbb{R}⟶\mathbb{R}$ be a continuous function with k-order fractional derivatives, $k\in \mathbb{N}$ and any α, $0<\alpha \le 1$, in the interval D. If $x_0$ is close enough to the zero $\overline{x}$ of $f\left(x\right)$ and ${}^C{D}_{\overline{x}}^{\alpha }f\left(x\right)$ is continuous and non zero in $\overline{x}$, then the local order of convergence of the Chebyshev’s fractional method using Caputo-type derivatives

$$x_{k+1}=x_k-\mathsf{\Gamma }(\alpha +1)\left(1+{\displaystyle \frac{1}{2}}{}^C{L}_f^{\alpha }\left(x_k\right)\right){\displaystyle \frac{f\left(x_k\right)}{{}^C{D}_a^{\alpha }f\left(x_k\right)}},$$

(8)

that we denote by CFC1, is at least $2\alpha$ and the error equation is

$$e_{k+1}^{\alpha }=C_2\left({\displaystyle \frac{2{\mathsf{\Gamma }}^2(\alpha +1)-\mathsf{\Gamma }(2\alpha +1)}{2{\mathsf{\Gamma }}^2(\alpha +1)}}\right)e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right),$$

(9)

being $e_k=x_k-\overline{x}$.

Proof. 

According to Theorems 1 and 3, we get that the Taylor expansion in fractional derivatives of ${}^C{D}^{\alpha }f\left(x_k\right)$ around $\overline{x}$ is

$${}^C{D}^{\alpha }f\left(x_k\right)={\displaystyle \frac{{}^C{D}_{\overline{x}}^{\alpha }f\left(x_0\right)}{\mathsf{\Gamma }(\alpha +1)}}\left[\mathsf{\Gamma }(\alpha +1)+{\displaystyle \frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(\alpha +1)}}{C}_2{e}_k^{\alpha }+{\displaystyle \frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}}{C}_3{e}_k^{2\alpha }\right]+\mathcal{O}\left(e_k^{3\alpha }\right),$$

(10)

where $C_j={\displaystyle \frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha j+1)}}{\displaystyle \frac{{}^C{D}_{\overline{x}}^{j\alpha }f\left(\overline{x}\right)}{{}^C{D}_{\overline{x}}^{\alpha }f\left(\overline{x}\right)}}$, for $j\ge 2$.

Then,

$${\displaystyle \frac{f\left(x_k\right)}{{}^C{D}_a^{\alpha }f\left(x_k\right)}}={\displaystyle \frac{1}{\mathsf{\Gamma }(\alpha +1)}}{e}_k^{\alpha }+{\displaystyle \frac{\left({\mathsf{\Gamma }}^2(\alpha +1)\right)-\mathsf{\Gamma }(2\alpha +1)}{\left({\mathsf{\Gamma }}^3(\alpha +1)\right)}}{C}_2{e}_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right).$$

(11)

On the other hand, it is clear, by identity (10), that

$${}^C{D}_{\overline{x}}^{2\alpha }f\left(x_k\right)=\frac{{}^C{D}_{\overline{x}}^{\alpha }f\left(\overline{x}\right)}{\mathsf{\Gamma }(\alpha +1)}\left[\mathsf{\Gamma }(2\alpha +1)C_2+\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(\alpha +1)}{C}_3{e}_k^{\alpha }\right]+O\left(e_k^{2\alpha }\right).$$

(12)

Therefore,

$$\begin{array}{cc}\hfill f{\left(x_k\right)}^C{D}_{\overline{x}}^{2\alpha }f\left(x_k\right)=& {\left(\frac{{}^C{D}_{\overline{x}}^{\alpha }f\left(\overline{x}\right)}{\mathsf{\Gamma }(\alpha +1)}\right)}^2\left[\mathsf{\Gamma }(2\alpha +1)C_2{e}_k^{\alpha }+\left(C_2^2\mathsf{\Gamma }(2\alpha +1)+{\displaystyle \frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(\alpha +1)}}{C}_3\right)e_k^{2\alpha }\right]+\mathcal{O}\left(e_k^{3\alpha }\right)\end{array}$$

and

$$\begin{array}{ccc}\hfill {\left({}^C{D}_a^{\alpha }f\left(x_k\right)\right)}^2& =& {\left({\displaystyle \frac{{(}^C{D}_{\overline{x}}^{\alpha }f)\left(\overline{x}\right)}{\mathsf{\Gamma }(\alpha +1)}}\right)}^2\left[{\left(\mathsf{\Gamma }(\alpha +1)\right)}^2+2\mathsf{\Gamma }(2\alpha +1)C_2{e}_k^{\alpha }\right.\hfill \\ & & +\left({\displaystyle \frac{{\left(\mathsf{\Gamma }(2\alpha +1)\right)}^2}{{\left(\mathsf{\Gamma }(\alpha +1)\right)}^2}}{C}_2^2+2{\displaystyle \frac{\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}}{C}_3\right)e_k^{2\alpha }\hfill \\ & & \left.+2{\displaystyle \frac{\mathsf{\Gamma }(2\alpha +1)\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(\alpha +1)\mathsf{\Gamma }(2\alpha +1)}}{C}_2{C}_3{e}_k^{3\alpha }\right]+\mathcal{O}\left(e_k^{4\alpha }\right).\hfill \end{array}$$

Let us now calculate the Taylor expansion of ${}^C{L}_f^{\alpha }\left(x_k\right)$ around $\overline{x}$,

$$\begin{array}{ccc}\hfill {}^C{L}_f^{\alpha }\left(x_k\right)& =& {\displaystyle \frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^2}}{C}_2{e}_k^{\alpha }\hfill \\ & & +{\displaystyle \frac{1}{\mathsf{\Gamma }{(\alpha +1)}^2}}\left[C_2^2\mathsf{\Gamma }(2\alpha +1)+{\displaystyle \frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(\alpha +1)}}{C}_3-2{\displaystyle \frac{1}{\mathsf{\Gamma }{(\alpha +1)}^2}}\mathsf{\Gamma }{(2\alpha +1)}^2{C}_2^2\right]e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right).\hfill \end{array}$$

As a consequence, we obtain that )

$$\begin{array}{ccc}\hfill 1+{\displaystyle \frac{1}{2}}{}^C{L}_f^{\alpha }\left(x_k\right)& =& 1+{\displaystyle \frac{\mathsf{\Gamma }(2\alpha +1)}{2\mathsf{\Gamma }{(\alpha +1)}^2}}{C}_2{e}_k^{\alpha }\hfill \\ & & +{\displaystyle \frac{1}{2\mathsf{\Gamma }{(\alpha +1)}^2}}\left[C_2^2\mathsf{\Gamma }(2\alpha +1)+{\displaystyle \frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(\alpha +1)}}{C}_3-2{\displaystyle \frac{1}{\mathsf{\Gamma }{(\alpha +1)}^2}}\mathsf{\Gamma }{(2\alpha +1)}^2{C}_2^2\right]e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right).\hfill \end{array}$$

Accordingly, a Chebyshev-like quotient can be obtained, and written in terms of the error at the k-th iterate $e_k=x_k-\overline{x}$.

$${\displaystyle \frac{f\left(x_k\right)}{{(}^C{D}_a^{\alpha }f)\left(x_k\right)}}\left(1+{\displaystyle \frac{1}{2}}{}^C{L}_f^{\alpha }\left(x_k\right)\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(\alpha +1)}}{e}_k^{\alpha }+C_2\left({\displaystyle \frac{2\mathsf{\Gamma }{(\alpha +1)}^2-\mathsf{\Gamma }(2\alpha +1)}{2\mathsf{\Gamma }{(\alpha +1)}^3}}\right)e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right).$$

(13)

Then, it is clear that, to make null the term of $e_k^{\alpha }$, a Caputo-fractional Chebyshev’s method should include as a factor $\mathsf{\Gamma }(\alpha +1)$ to conclude that the error expression is (9). □

Let us remark that, when $\alpha =1$, we get the classical Chebyshev method, whose order is 3. However, the iterative expression defined in (8) does not achieve the required maximum order of convergence $3\alpha$. The following theorem presents another Caputo-fractional variant of Chebyshev’s method, defined by replacing the second order derivative with a fractional one, with order $\alpha +1$, $0<\alpha \le 1$. Its proof is omitted, as it is similar to that of Theorem 4. We denote this Caputo-fractional Chebyshev variant by CFC2.

Theorem 5.

Let $f:D\subset \mathbb{R}⟶\mathbb{R}$ be a continuous function with k-order fractional derivatives, $k\in \mathbb{N}$ and any α, $0<\alpha \le 1$, in the interval D. If $x_0$ is close enough to the zero $\overline{x}$ of $f\left(x\right)$ and ${}^C{D}_{\overline{x}}^{\alpha }f\left(x\right)$ is continuous and non zero in $\overline{x}$, then the local order of convergence of the Chebyshev’s fractional method using Caputo-type derivatives (CFC2)

$$x_{k+1}=x_k-\mathsf{\Gamma }(\alpha +1){\displaystyle \frac{f\left(x_k\right)}{{}^C{D}_a^{\alpha }f\left(x_k\right)}}\left(1+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{}^C{D}_a^{\alpha +1}f\left(x_k\right)f\left(x_k\right)}{{}^C{D}_a^{\alpha }f{\left(x_k\right)}^C{D}_a^{\alpha }f\left(x_k\right)}}\right),$$

is at least $2\alpha$, being $0<\alpha <1$. On the one hand, if $0<\alpha \le \frac{2}{3}$, the error equation is

$$e_{k+1}^{\alpha }=\left({\displaystyle \frac{\mathsf{\Gamma }{(\alpha +1)}^2-\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^3}}{C}_2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{\mathsf{\Gamma }{(\alpha +1)}^2}}{\displaystyle \frac{{}^C{D}_{\overline{x}}^{\alpha +1}f\left(\overline{x}\right)}{{}^C{D}^{\alpha }f\left(\overline{x}\right)}}\right)e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha +1}\right).$$

On the other hand, if $\frac{2}{3}\le \alpha <1$, then

$$e_{k+1}^{\alpha }=\left({\displaystyle \frac{\mathsf{\Gamma }{(\alpha +1)}^2-\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }{(\alpha +1)}^3}}{C}_2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{\mathsf{\Gamma }{(\alpha +1)}^2}}{\displaystyle \frac{{}^C{D}_{\overline{x}}^{\alpha +1}f\left(\overline{x}\right)}{{}^C{D}^{\alpha }f\left(\overline{x}\right)}}\right)e_k^{2\alpha }+\mathcal{O}\left(e_k^{3\alpha }\right).$$

Can the order of fractional Chebyshev’s method be higher than $2\alpha$? In the following result it is shown that it is possible if the coefficients in the iterative expression are changed. The resulting fractional iterative scheme is denoted by CFC3. Again, the proof of the following result is omitted as it is similar to that of Theorem 4.

Theorem 6.

Let $f:D\subset \mathbb{R}⟶\mathbb{R}$ be a continuous function with k-order fractional derivatives, $k\in \mathbb{N}$ and any α, $0<\alpha \le 1$, in the interval D. If $x_0$ is close enough to the zero $\overline{x}$ of $f\left(x\right)$ and ${}^C{D}_{\overline{x}}^{\alpha }f\left(x\right)$ is continuous and non zero in $\overline{x}$, then the local order of convergence of the Chebyshev’s fractional method using Caputo-type derivatives (CFC3)

$$x_{k+1}=x_k-\mathsf{\Gamma }(\alpha +1){\displaystyle \frac{f\left(x_k\right)}{{}^C{D}_a^{\alpha }f\left(x_k\right)}}\left(A+B^C{L}_f^{\alpha }\left(x_k\right)\right),$$

(14)

is at least $3\alpha$ only if $A=1$ and $B={\displaystyle \frac{\mathsf{\Gamma }(2\alpha +1)-\mathsf{\Gamma }{(\alpha +1)}^2}{\mathsf{\Gamma }(2\alpha +1)}}$, being $0<\alpha <1$, and the error equation

$$\begin{array}{ccc}\hfill e_{k+1}^{\alpha }& =& \left[-\mathsf{\Gamma }(2\alpha +1)\left(1-\frac{\mathsf{\Gamma }(2\alpha +1)}{{\mathsf{\Gamma }}^4(\alpha +1)}\right)C_2+\frac{B\mathsf{\Gamma }(2\alpha +1)}{{\mathsf{\Gamma }}^3(\alpha +1)}\left(2-3\frac{\mathsf{\Gamma }(2\alpha +1)}{{\mathsf{\Gamma }}^2(\alpha +1)}\right)C_2^2\right.\hfill \\ & & \left.+\frac{1}{\mathsf{\Gamma }(\alpha +1)}\left(\frac{B\mathsf{\Gamma }(3\alpha +1)}{{\mathsf{\Gamma }}^3(\alpha +1)}-\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)\mathsf{\Gamma }(\alpha +1)}+1\right)C_3\right]e_k^{3\alpha }+\mathcal{O}\left(e_k^{4\alpha }\right),\hfill \end{array}$$

(15)

being $e_k=x_k-\overline{x}$.

According to the efficiency index defined by Ostrowski in [11], in Figure 1 we show that, with the same number of functional evaluations per iteration than CFC2 and CFC1 but with higher order of convergence, CFC3 has the best efficiency index, even compared with the fractional Newton’s method CFN defined in [6]. In it, let us remark that incides of CFC1 and CFC2 coincide, as they have the same order of convergence and number of functional evaluations iteration.

In the following section, we analyze the dependence on the initial guess of the different Chebyshev-type fractional methods.

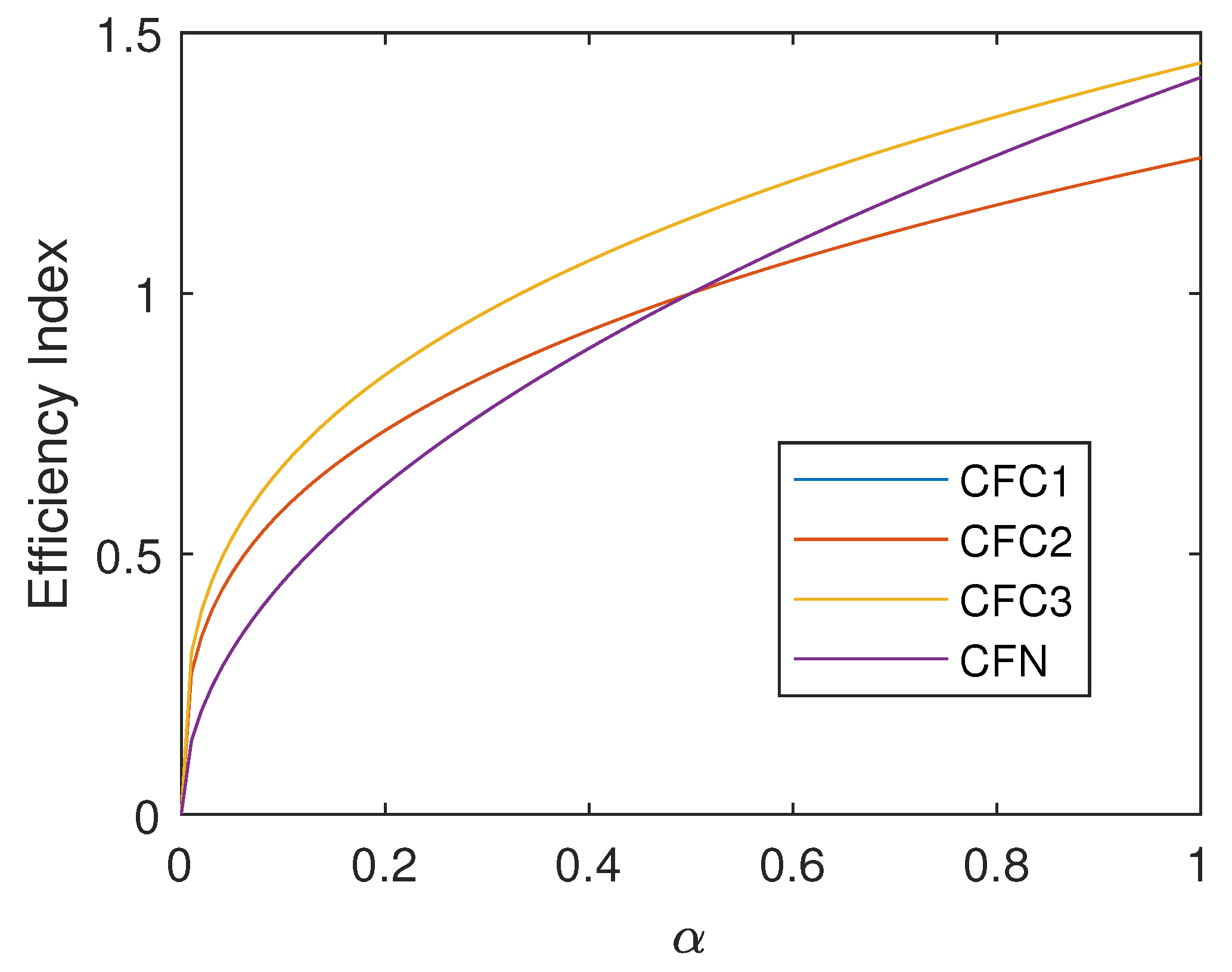
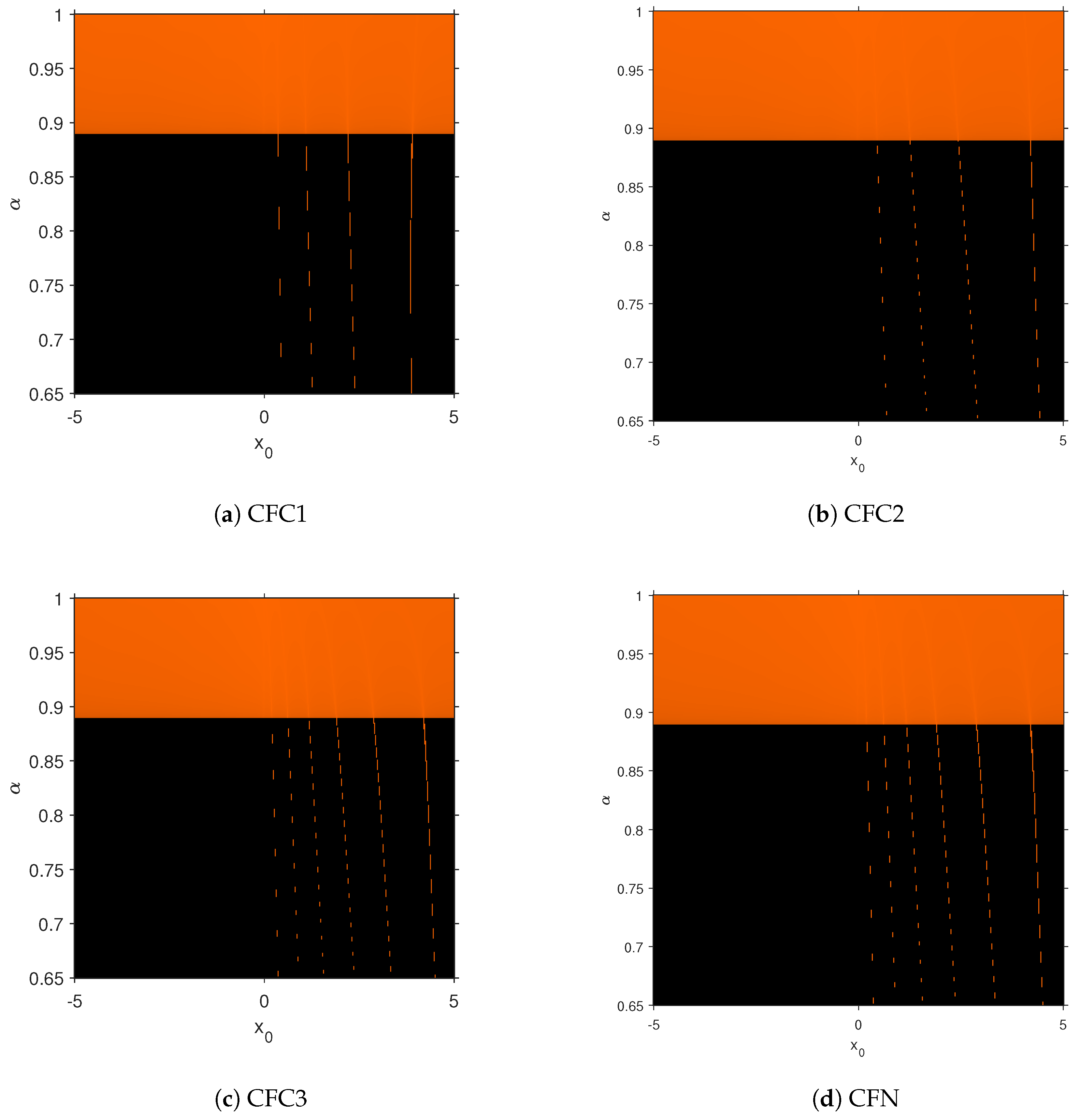
3. Numerical Performance of Proposed Schemes

In this section, we use $Matlab$ R2018b with double precision for solving different kind of nonlinear equations. The stopping criterium used is $|x_{k+1}-x_k|<{10}^{-6}$ with at most 250 iterations. The Gamma function is calculated by means of the routine made by Paul Godfrey (15 digits of accuracy along real axis and 13 elsewhere in $\mathbb{C}$. On the other hand, we use the program $mlf$ of Mathworks for computing Mittag-Lefler function that has a precission of 9 significant digits.

The first test function is $f\left(x\right)=x^3+x$, whose roots are ${\overline{x}}_1=0$, ${\overline{x}}_2=i$ and ${\overline{x}}_3=-i$. In

Table 1. CFC2 results for $f\left(x\right)=x^3+x$ with $x_0=1.1$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1274e-05+i4.6093e-04	9.2186e-04	4.6804e-04	250
0.91	−3.2556e-05+i2.0787e-04	4.1575e-04	2.1041e-04	250
0.92	−1.0632e-05+i7.7354e-05	1.5471e-04	7.8081e-05	250
0.93	−2.5978e-06+i2.1869e-05	4.3739e-05	2.2023e-05	250
0.94	−4.1185e-07+i4.0939e-06	8.1878e-06	4.1145e-06	250
0.95	−1.6155e-08-i9.1923e-07	1.9214e-06	9.1937e-07	23
0.96	1.4985e-07-i7.7007e-07	1.9468e-06	7.8451e-07	13
0.97	3.4521e-07-i7.6249e-07	2.6824e-06	8.3699e-07	9
0.98	2.7084e-07-i3.4599e-07	1.9608e-06	4.3939e-07	7
0.99	−6.3910e-07+i2.1637e-07	6.4318e-06	6.7474e-07	5
1.00	−2.9769e-08+i0.0000e+00	3.0994e-03	2.9769e-08	3

,

Table 2. CFC3 results for $f\left(x\right)=x^3+x$ with $x_0=1.1$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1270e-05+i4.6090e-04	9.2190e-04	4.6800e-04	250
0.91	−3.2560e-05+i2.0790e-04	4.1570e-04	2.1040e-04	250
0.92	−1.0630e-05+i7.7350e-05	1.5470e-04	7.8080e-05	250
0.93	−2.5980e-06+i2.1870e-05	4.3740e-05	2.2020e-05	250
0.94	−4.1180e-07+i4.0940e-06	8.1880e-06	4.1150e-06	250
0.95	−1.6680e-07+i9.2200e-07	1.9640e-06	9.3690e-07	22
0.96	−3.4850e-07+i7.2840e-07	2.0220e-06	8.0750e-07	12
0.97	5.5470e-07-i6.3310e-07	2.6850e-06	8.4180e-07	7
0.98	−3.1400e-07+i2.0370e-07	1.6820e-06	3.7430e-07	7
0.99	1.2990e-07-i8.4600e-08	1.2680e-06	1.5500e-07	6
1.00	−2.9770e-08+i0.0000e+00	3.0990e-03	2.9770e-08	3

,

Table 3. CFN results for $f\left(x\right)$ with $x_0=1.1$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1275e-05-i4.6093e-04	9.2187e-04	4.6804e-04	250
0.91	−3.2556e-05-i2.0787e-04	4.1575e-04	2.1041e-04	250
0.92	−1.0632e-05-i7.7354e-05	1.5471e-04	7.8081e-05	250
0.93	−2.5978e-06-i2.1869e-05	4.3739e-05	2.2023e-05	250
0.94	−4.1185e-07+i4.0939e-06	8.1878e-06	4.1145e-06	250
0.95	2.8656e-08-i9.4754e-07	1.9837e-06	9.4797e-07	23
0.96	−3.2851e-07+i6.6774e-07	1.8538e-06	7.4418e-07	14
0.97	2.3413e-07-i4.2738e-07	1.5022e-06	4.8731e-07	11
0.98	2.0677e-07-i2.4623e-07	1.4017e-06	3.2154e-07	9
0.99	3.0668e-07-i2.2801e-07	3.3615e-06	3.8216e-07	7
1.00	1.2192e-16+i0.0000e+00	3.9356e-06	1.2192e-16	5

,

Table 4. CFC2 results for $f\left(x\right)$ with $x_0=-1.3-i1.3$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1274e-05-i4.6093e-04	9.2186e-04	4.6804e-04	250
0.91	−3.2556e-05-i2.0787e-04	4.1575e-04	2.1041e-04	250
0.92	−1.0632e-05-i7.7354e-05	1.5471e-04	7.8081e-05	250
0.93	−2.5978e-06-i2.1869e-05	4.3739e-05	2.2023e-05	250
0.94	−4.1185e-07+i4.0939e-06	8.1878e-06	4.1145e-06	250
0.95	−1.1203e-07+i9.8331e-07	2.0799e-06	9.8967e-07	26
0.96	−3.2473e-09-i7.0333e-07	1.7375e-06	7.0333e-07	19
0.97	5.9619e-08-i7.4110e-07	2.3750e-06	7.4349e-07	18
0.98	4.7121e-07+i7.4115e-07	4.1416e-06	8.7826e-07	19
0.99	3.9274e-08-i3.9674e-07	3.5758e-06	3.9868e-07	14
1.00	3.9559e-08+i4.8445e-07	7.8597e-03	4.8606e-07	8

,

Table 5. CFC3 results for $f\left(x\right)$ with $x_0=-1.3-i1.3$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1308e-05-i4.6100e-04	9.2200e-04	4.6811e-04	250
0.91	−3.2562e-05-i2.0789e-04	4.1577e-04	2.1042e-04	250
0.92	−1.0633e-05-i7.7355e-05	1.5471e-04	7.8082e-05	250
0.93	−2.5978e-06-i2.1870e-05	4.3739e-05	2.2023e-05	250
0.94	−4.1185e-07+i4.0939e-06	8.1878e-06	4.1145e-06	250
0.95	−9.6563e-08+i9.3217e-07	1.9628e-06	9.3716e-07	28
0.96	1.3446e-08-i7.0728e-07	1.7477e-06	7.0741e-07	22
0.97	−9.7497e-08+i1.0000e+00	1.7666e-06	2.1081e-07	15
0.98	−1.8598e-07-i1.0000e+00	5.5924e-06	4.4631e-07	15
0.99	−1.5051e-07+i5.1262e-07	4.9442e-06	5.3426e-07	13
1.00	3.9559e-08+i4.8445e-07	7.8597e-03	4.8606e-07	8

and

Table 6. Fractional Newton results for $f\left(x\right)$ with $x_0=-1.3-i1.3$.

$\mathit{\alpha }$	$\overline{\mathit{x}}$	$|{\mathit{x}}_{\mathit{k}+1}-{\mathit{x}}_{\mathit{k}}|$	$\left|\mathit{f}\right({\mathit{x}}_{\mathit{k}+1}\left)\right|$	Iterations
0.90	−8.1275e-05+i4.6093e-04	9.2187e-04	4.6804e-04	250
0.91	−3.2556e-05+i2.0787e-04	4.1575e-04	2.1041e-04	250
0.92	−1.0632e-05+i7.7354e-05	1.5471e-04	7.8081e-05	250
0.93	−2.5978e-06+i2.1869e-05	4.3739e-05	2.2023e-05	250
0.94	−4.1185e-07+i4.0939e-06	8.1878e-06	4.1145e-06	250
0.95	−9.1749e-08-i9.2392e-07	1.9434e-06	9.2846e-07	28
0.96	1.5946e-08+i1.0000e+00	6.4777e-07	1.0272e-07	12
0.97	1.2679e-07+i1.0000e+00	4.3336e-06	5.1715e-07	16
0.98	−5.1142e-07+i7.8442e-07	4.5155e-06	9.3641e-07	16
0.99	9.3887e-08-i1.0000e+00	4.7305e-06	1.8942e-07	11
1.00	−2.9297e-10-i1.0000e+00	1.4107e-05	5.9703e-10	9

, we show the different solutions, the number of iterations, and the residual errors of the difference between the two last iterations and the value of function f at the last iteration. In Table 1 and Table 2 we observe the performance of Caputo-fractional Chebyshev’s method CFC2 and CFC3 estimating different roots with the initial guess $x_0=1.1$.

As we know, when $\alpha$ is near to 1 the method needs less iterations and the evaluating of the last iteration is smaller than in first values of the parameter $\alpha$. Let us now compare our proposed schemes with fractional Newton’s method designed in [6] (see Table 3).

As we can see in Table 1, Table 2 and Table 3, there are no big differences in terms of convergence to the real root but in the case of Caputo-fractional Newton’s method CFN, the number of iterations needed to converge is higher than for CFC2 and CFC3.

To end, we show the convergence plane (see [12]) in Figure 2 and Figure 3 where the abscissa axis corresponds to the initial approximations and $\alpha$ appears in the ordinate axis. We use a mesh of $400\times 400$ points. Points painted in orange correspond to initial estimations that converge to ${\overline{x}}_1$ with a tolerance of ${10}^{-3}$, a point is painted in blue if it converges to ${\overline{x}}_2$ and in green if it converges to ${\overline{x}}_3$. In any other case, points are painted in black, showing that no root is found in a maximum of 250 iterations. The estimations point are located in $[-5,5]$, although convergence to the real root is found in $[-50,50]$ paragraph has been moved, so that it can been seen before the Figure 2 shows. please check and confirm.

We show the convergence plane of Chebyshev’ and Newton’s fractional methods. In Figure 2, it can be observed that for any real initial estimation in the interval used, if $\alpha \ge 0.89$, both methods converge to one of the zeros of $f\left(x\right)$ and if $\alpha <0.89$, Newton’s and Chebyshev’s fractional methods do not converge to any solution. However, the higher order of convergence of Chebyshev’s scheme can make the difference.

However, we have got only convergence to the real root, by using real initial guesses. In what follows, we use complex initial estimations, of equal real and imaginary parts, $x_0=\lambda +i\lambda$$\lambda \in \mathbb{R}$, in order to calculate the corresponding convergence plane.

In Figure 3, we can observe that starting with complex initial values is more efficient to find all the roots of the nonlinear equation. In it, orange color means convergence to the real root ${\overline{x}}_1$, blue color is convergence to ${\overline{x}}_2$ and $(x_0,\alpha )$ in green color converge to ${\overline{x}}_3$. It is observed that it is possible to converge to ${\overline{x}}_3$ with lower values of $\alpha$ with CFC3 than using CFC1 or CFC2. Moreover, the methods converge mostly to ${\overline{x}}_3$ when the real and complex part of the initial estimation is positive, meanwhile it is possible to converge to any of the roots when the real and complex part of $x_0$ is negative.

Iterations

Also in Table 4, Table 5 and Table 6 we see that, with the same initial estimation, it is possible to approximate all the roots of the function by changing the value of $\alpha$.

4. Conclusions

In this manuscript, we have designed several Chebyshev-type fractional iterative methods, by using Caputo’s fractional derivative. We have shown that the order of convergence can reach $3\alpha$, $0<\alpha \le 1$, by means of an appropriate design in the iterative expression, including a Gamma function as a dumping parameter, but also an specific treatment of the high-order derivative derivative. It has been proven that the replacement of high-order integer derivatives by fractional ones must be carefully done, as it is not obvious that the order of convergence will be preserved. The theoretical results have been checked in the numerical section, with special emphasis on the dependence on the initial guess (that is shown in the convergence planes), comparing Newton’ and Chebyshev’s fractional methods performances. CFC3 method is not only the most efficient scheme (see Figure 1), but also converges to any of the searched roots for values of $\alpha$ lower than those needed by CFC1 and CFC2.