Abstract
A reversible cyclic process is analyzed in which the center of mass of an ideal gas is raised in a gravitational field during both an expansion phase and a subsequent contraction phase, with the gas returning to its initial height in a final step. When the properties of the gas are taken as uniform, the thermodynamic efficiency of this cycle is able to exceed that of a corresponding Carnot cycle, which is a violation of the second law of thermodynamics. The source of this discrepancy was previously claimed, when analyzing a similar heating and cooling of a sphere, to be the assumed independence of the internal energy on the gravitational field. However, this violation is only apparent since all of the effects of the gravitational field were not incorporated fully into the thermodynamic analysis of the cycle. When all the influences of the gravitational field are considered, no possible violation of the second law can occur. The evaluation of the entropy changes of the gas throughout the cycle also highlights other key inconsistencies that arise when the full effects of the gravitational field are neglected. As the analysis of the cycle provided here shows, the assumption of the independence of the internal energy, as well as other thermodynamic properties, on the gravitational field strength can still be invoked.
1. Introduction
1.1. Problem Statement: The Heating of Two Spheres in a Gravitational Field
In Reference [1], the thermodynamic analysis of the heating of two identical homogeneous spheres, labeled A and B, in a constant gravitational field was reconsidered (in the non-relativistic limit only). In the standard problem statements describing this process, although both spheres begin with the same radius and absolute temperature , the heating nonetheless occurs with sphere A always resting on a horizontal platform, while sphere B is always suspended from a thread attached to a higher horizontal platform (see Figure 1). Consequently, as the temperature of sphere A increases, its center of mass will rise in the gravitational field due to the thermal expansion of the sphere. With the thermal expansion coefficient defined as (where is the molar volume and is the pressure), the radius of sphere A will increase by the differential amount for the differential temperature increase . Assuming the horizontal platform is non-deformable, the center of mass of sphere A is therefore also raised by .
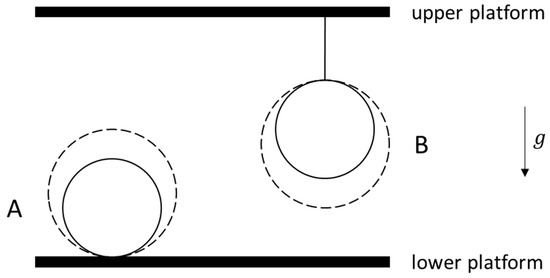
Figure 1.
Sphere A rests on a horizontal platform, while sphere B is suspended from a thread that is attached to another horizontal platform that is at a higher height in the gravitational field with strength (and pointing in the downward direction). Both spheres expand upon an increase in their temperatures, such that the center of mass of sphere A is raised, while that of B is lowered in the gravitational field.
Now, the appropriate form of the first law of thermodynamics for sphere A, which is a closed system, is:
in which is the change in the potential energy of the sphere, is the change in the sphere’s internal energy, is the differential amount of “heat added to/removed from” the sphere, and is the differential change in the volume of the sphere. While not explicitly stated, one can argue that the analysis in Reference [1] implicitly assumed the surroundings to be a constant pressure environment, so Equation (1) can be rearranged to yield:
where is the differential change in the enthalpy of the sphere for a constant pressure process. Since the mass of the sphere is unchanged, , where is the specific isobaric heat capacity [2]. Therefore:
in which is the gravitational field strength. (Despite the appearance of the factor of three and the use of a specific heat capacity, Equation (3) is essentially identical to the corresponding result appearing in Reference [1]).
In contrast, the same temperature increase of sphere B, accompanied by the same thermal expansion as sphere A, leads instead to a lowering of its center of mass by . Consequently, for sphere B:
In other words, for the same , the final temperature of sphere A will be less than the final temperature of sphere B. (As a side note, since and should have the same signs, the quantity in parentheses in Equation (4) should be positive, requiring that . For example, if the sphere is comprised of pure copper, then J/kg-K and K−1 [3,4]. For normal gravity, then m. So as long as the copper sphere is smaller than the Earth, this condition will be satisfied!).
1.2. Cyclic Process Based on the Heating of a Sphere in a Gravitational Field
Since the center of mass of sphere A rises while that of sphere B is lowered, the predicted difference in the final temperatures of the two spheres, as follows from the given first law analysis, may be an expected result. However, as argued in Reference [1], such a conclusion is problematic. The resulting temperature difference apparently implies that a cyclic process could be generated that violates the second law of thermodynamics.
To see how, start with one of the spheres at an initial radius and temperature resting on a horizontal platform. Let also be a constant, so that can be integrated to yield . Next, bring the sphere into thermal contact with a thermal reservoir at . Upon increasing the temperature of the sphere from to , the center of mass of the sphere rises a distance of , while according to Equation (3), the sphere “absorbs an amount of heat” equal to:
in which is also taken to be constant. Now, attach the sphere by a thread to another platform placed above it, and remove the bottom platform. Then, bring the sphere into thermal contact with a thermal reservoir at , reducing its temperature from back to . In this case, the center of mass of the sphere again rises a distance of , while the sphere “releases an amount of heat” equal to:
Note for this analysis that .
Nevertheless, the sphere, although returned to its initial temperature, has been raised a total distance of in the gravitational field. Therefore, an additional step is required to return the sphere to its initial height (i.e., to rest again on the first bottom platform). As the sphere falls back down, the corresponding decrease in the sphere’s potential energy allows for the generation of additional work in the amount of . The net heat and work for the entire cyclic process are and , respectively. (Since the sphere returns to its initial volume, and the surroundings are assumed to be at a constant pressure, the work done by the sphere during the initial expansion step is equal and opposite to the work done by the sphere during the subsequent compression step. Thus, the net work done around the cycle is just equal to the work produced as the sphere returns to its initial height). Therefore, we have generated a heat engine, or a cyclic process, undergoing interactions with the thermal reservoirs at and with a thermodynamic efficiency of:
As , , which is a limiting value that is independent of the temperature difference.
However, any heat engine or cyclic process operating just between two different thermal reservoirs cannot have an efficiency that exceeds that of a Carnot engine or cycle operating between the same two reservoirs. In other words, Equation (7) cannot exceed a value of . However, as , Equation (7) approaches a non-zero limiting value, while . Hence, the efficiency of the cyclic process generated with the sphere can be made to exceed that of the corresponding Carnot cycle, thereby violating the second law of thermodynamics [1].
Since such a violation cannot occur, Reference [1] then identifies the apparent source of this inconsistency: the internal energy of the sphere was assumed, as is normally done [5,6,7,8,9], to be independent of . According to Reference [1], by only letting depend upon both and can the cycle be correctly analyzed, and the violation of the second law be eliminated.
2. Thermodynamically Consistent Analysis
The analysis leading to Equation (7) is relatively straightforward, and so the temperature-independent limiting value of for this cycle does indeed appear to be a troubling result. Yet, the conclusion reached in Reference [1] must be considered tentative. Various facets of the process, and their possible impact on the actual operation of the cycle, have not been fully accounted for in the thermodynamic analysis. In particular, and an example of one feature of the cycle that may have been neglected, is the potential role of the surroundings. Consequently, the works performed during the expansion and contraction of the sphere may not have been properly determined in the analysis.
2.1. What If the Sphere Is Surrounded by the Atmosphere?
In the problem statement of the heating of the two identical spheres in a gravitational field that is provided in Reference [1], there is no specific mention of what surrounds the spheres. Likewise, in their analysis of the cyclic process with the single sphere, there is no explicit reference to what comprises the region external to the sphere and between the two platforms. As the initial problem of the heating of the two spheres discussed in Reference [1] is from the 1967 International Physics Olympiad competition, these missing details are understandable. A straightforward statement of the process, without seemingly unwarranted complexities, was presumably needed. In addition, when considering the cycle based on the heating/cooling of the single sphere, there appears to be no a priori restrictions on the surroundings in order for the cyclic process to occur.
As noted before, the surroundings in Reference [1] were implicitly assumed to be a constant pressure environment. In their analysis, only the “heat capacity” of the sphere is invoked. Since the volume of the sphere varies, this “heat capacity” cannot refer to the constant volume heat capacity. The other heat capacity of relevance in thermodynamics is the constant pressure heat capacity, which is typically employed when the volume of the system changes. Hence, one can argue that Reference [1], whether intentionally or not, assumed that the sphere was exposed to an atmosphere of fixed pressure. (Again, we note that Equation (3), which was derived after an explicit reference to a constant pressure environment, is essentially identical to the corresponding result obtained in Reference [1]).
However, now that the presence of the surrounding atmosphere is explicitly acknowledged, we must also consider that the atmosphere will be subject to the same gravitational field as the sphere, i.e., the pressure of the surroundings will vary with height. In the analysis of the cycle presented so far, with the constant pressure environment, the works of expansion and contraction of the sphere are simply equal to and , respectively (where is the magnitude of the volume change). Yet, in the presence of the gravitational field, the atmosphere no longer imposes a constant pressure. Since the local pressure exerted on the sphere varies with height, and the specific value of a given local pressure depends upon the location of the center of mass of the sphere within the gravitational field, the two works of expansion and contraction may not necessarily cancel each other out. During the contraction phase, the center of mass of the sphere is never located at a height below that of the expansion phase. In addition, because of the presence of the lower platform during the expansion, most of the volume increase occurs around the top of the sphere, where the local pressure is lower than what it is at the platform. Due to the thread during the contraction, most of the volume decrease occurs around the bottom of the sphere, where the pressure is higher. Hence, the net work around the cycle, as well as , may be different from what appears in Equation (7). Consequently, the thermodynamic efficiency of the cycle may not in fact exceed that of the corresponding Carnot cycle.
Accounting properly for the pressure variations in the surroundings may also resolve another curious aspect of the cyclic process (which may provide an explanation as to why the current analysis of the cycle appears to lead to a violation of the second law). The raising of the center of mass of the sphere occurs in two steps, both of which are thermally driven processes, i.e., the sphere’s upward movement is instigated by the heating/cooling and subsequent thermal expansion/contraction of the sphere. Yet, the heating/cooling should ultimately give rise to certain effects that induce a net mechanical action on the sphere. However the process is carried out, the upward movement of the sphere that occurs against the downward pull of gravity must be due to the forces (besides gravity)—and their corresponding displacements—that are exerted on the sphere. As these forces are responsible for the lifting of the sphere, their effect on the sphere should not vanish, and this effect should remain in the thermodynamic analysis. The resulting increase in the potential of the energy of the sphere should presumably always occur in combination with the performance of work on the sphere.
For this process, only the surrounding atmosphere exerts the relevant forces on the sphere that are needed to increase its height. (The platform and the thread also exert forces on the sphere. However, the points of contact between them and the sphere are not displaced, and so they do no work on the sphere). At the same time, the pressure of the atmosphere is assumed to be the same everywhere and constant. Hence, the atmosphere exerts the same forces on the sphere during both the expansion and contraction phases of the process. Consequently, the net work done by the atmosphere on the sphere is zero over these two steps, even though the sphere has been raised in the gravitational field. However, by considering the variation of the pressure with height, as noted before, the atmosphere may be exerting larger forces along the bottom of the sphere during the contraction phase compared to the smaller forces exerted along the top of the sphere during the expansion phase. Thus, the atmosphere may still be applying an effective upward force to displace the sphere, i.e., the net work done by the atmosphere over these two steps may not necessarily vanish.
2.2. What If There Is No Atmosphere Surrounding the Sphere?
Although the assumption that the sphere is exposed to the atmosphere is reasonable, it nonetheless adds an additional layer of complexity to the analysis of the cycle. Furthermore, its appearance in the analysis draws attention away from the impact that gravity may have on just the sphere and how those effects are not necessarily being handled properly in the standard thermodynamic description of the cycle. Perhaps then, the sphere was supposed to be placed in a vacuum, with any effects of the environment, by construction, being irrelevant. While the introduction of a vacuum potentially simplifies the analysis, it is nonetheless a rather specific restriction on the process. There is again no obvious reason why the cycle must only occur within a vacuum, with the corresponding violation arising, for some reason, only when there is no surrounding atmosphere. Nevertheless, this limiting situation does serve to highlight additional aspects of the problem that have yet to be considered, which if properly accounted for may also not result in the cycle violating the second law.
As a reminder, the radius of the sphere was taken to change by the differential amount for the differential temperature change , with the location of the center of mass of the sphere also changing by the same amount of . (In Reference [1], the differential change in the radius is determined by , with denoting the “thermal expansion coefficient”. The missing “3” suggests this is a linear, or radial, thermal expansion coefficient, as opposed to the volume-based parameter used here). However, the use of (either version of) this relation assumes that the material being heated or cooled always maintains the same shape, i.e., the system of interest is always spherical. Thus, by construction, the center of mass of the system always resides at the center of the sphere (hence its concomitant raising and lowering by ). In other words, gravity has no effect on the shape of the system. However, if the solid remains spherical, even in the presence of a gravitational field, then one is implicitly assuming that the sphere is comprised of an incompressible substance. Yet, for the problem of interest, the use of an incompressible substance gives rise to two additional thermodynamic inconsistencies.
First, incompressibility is an idealization, providing a convenient model for the solution of various problems. Yet, only certain aspects of this model are typically invoked. The full—and thermodynamically consistent—behavior of such a substance is usually not considered. For example—at least for a fluid—incompressibility implies by definition that the isothermal compressibility, , is equal to zero (i.e., there is no change in density regardless of the pressure change). Now, via the cyclic rule, we have that , which is finite for real fluids. Thus, for this model fluid, must also be taken equal to zero [10], i.e., there is only one allowed molar volume or density, independent of and , for an incompressible fluid. In other words, for an incompressible fluid, the volume of the system (of fixed mass) cannot change upon heating or cooling! (As an aside, an incompressible fluid must also have identical values of its isochoric and isobaric heat capacities [10]. As noted before, Reference [1] did not specify which type of heat capacity was invoked in the analysis, which is perhaps another indication that the sphere was implicitly assumed to be incompressible.) Similar arguments should apply for an incompressible solid. Hence, for a sphere that is presumed to be incompressible, the location of its center of mass will not vary at all during the heat and cooling stages. In this case, the resulting (and now uninteresting) cycle will certainly not violate the second law.
As the thermal expansion of the solid is of course a crucial aspect of the cycle, the substance comprising it cannot then be incompressible. However, then, the second possible inconsistency arises. With the solid now being compressible, its shape will no longer be that of a perfect sphere because of gravitational effects. Moreover, the solid’s shape will depend upon whether it is resting on the platform, or whether it is being suspended from the thread. When the solid rests on the platform, the bottom portion of the solid will have to support the weight of all the remaining higher portions of the solid. Hence, these lower layers will be compressed more than the upper layers. The solid will be squashed to some extent, resembling, although not exactly, an oblate spheroid. On the other hand, when suspended from the thread, the solid will now be under tension. In this case, the upper layers will have to support (under tension) all the remaining lower portions of the solid. Hence, the upper layers will be stretched more than the lower layers. The sphere, in this arrangement, will be more like, though again not exactly, a prolate spheroid (at least in those upper layers). Whatever its precise shape, the gravitational field will give rise to density variations within the solid, the nature of which will be different when the solid rests on the platform or when suspended by thread. These density variations must be properly accounted for when determining the change in the center of mass of the solid, or the change in the potential energy of the solid. Consequently, when the solid is heated or cooled, is no longer a relevant description of both the volume increase/decrease and the change in height of the center of mass of the solid.
There are even other aspects of the cyclic process that should be considered in more detail. For example, the lower platform and thread were assumed to be non-deformable, but consistency now requires that compressibility effects be accounted for in these systems. In addition, the shape of the solid will change in between the end of the heating stage and prior to the start of the cooling stage, simply when the thread is attached to the top of the solid and the lower platform, on which the solid had been resting, is removed. Presumably, the location of the center of mass will not remain fixed during this shape change, and the corresponding difference in the potential energy for this previously ignored step should also be included in the analysis. Finally, how the compressive and tensile forces within the sphere vary throughout this thermally-driven process is an interesting problem. These internal forces, which will vary along with the changes in the internal density profile, will give rise to internal works (which themselves are manifested as changes in the internal energy of the solid) that alter the shape of the solid and ultimately serve to raise or lower the center of mass (which here in a vacuum occurs without the aid of an external force agent, such as the atmosphere). Overall, a fully consistent analysis of this seemingly simple problem of the heating and cooling of a sphere is quite complicated. Thus, the previous conclusion that this cyclic process yields a violation of the second law, when the internal energy is assumed to be independent of the field strength, must be considered as tentative.
3. Equivalent Cyclic Process for an Ideal Gas in a Container in a Gravitational Field
Although the works of expansion/contraction of the sphere when it is surrounded by the atmosphere could be determined when the pressure of the surroundings varies with height, or the varying shape of the solid could, in principle, be determined, another analogous reversible cyclic process is instead considered in this paper. This process conveniently sidesteps various complications that arise for the solid and simplifies greatly the analysis of the various steps of the cycle. In particular, an ideal gas is chosen to replace the solid as the “working substance”, which then follows a suitably designed cyclic process. Although not identical to the process for the sphere, the net effect of this cycle for the ideal gas is the same as that for the sphere, i.e., the center of mass of the gas is raised both during an expansion phase and a subsequent contraction phase, with the gas dropping down to its initial height in a final step.
Once this new cycle is properly analyzed, in which the pressure variations with height of the ideal gas are explicitly considered (i.e., the compressibility of the gas is directly accounted for), the net work performed on the gas as its center of mass is raised in the gravitational field no longer vanishes, and is equal to the increase in the potential energy of the gas. Consequently, the net work performed around the cycle is identically equal to zero, even though the internal energy is still assumed to be independent of . Hence, no possible violation of the second law is found to occur for this process. At least for this and similar cycles, the assumption of the independence of the internal energy on does not, as of yet, give rise to an inconsistency with the laws of thermodynamics. Finally, the use of the ideal gas allows for other important thermodynamic properties to be straightforwardly determined. The determination of the entropy of the gas, for example, at various points throughout the cycle further highlights other key inconsistencies that arise when the full effects of the gravitational field are neglected.
The system and reversible cycle of interest, which is analogous to the cyclic process generated with the sphere, is presented in Figure 2. Initially, a pure component ideal gas at a uniform temperature is contained within a cylinder of constant cross-sectional area in which there is a movable piston (of negligible mass) located at a height relative to the bottom of the cylinder. A vacuum surrounds the container, while an external agent imposes a force such that the pressure on the top of the piston is equal to . (Since the gas is at equilibrium, and the piston is movable, the pressure the gas exerts on the bottom side of the piston is therefore also equal to ). The cylinder initially rests on a platform. In step 1, while the bottom of the cylinder remains on the platform, and with the pressure on the piston being kept fixed at , the temperature of the gas is increased from to . The volume of the gas increases as well, with the height of the piston increasing to . Due to the volume increase, the center of mass of the gas has also been raised in the gravitational field. (This step is similar to the expansion phase of the sphere, where its volume and the height of its center of mass are likewise increased). Next, in step 2, the piston is now held in place, being attached to a higher platform via a rigid connecting rod. Keeping the pressure of the gas on the bottom of the piston always equal to , the cylinder is now raised, decreasing the distance between the piston and the bottom of the cylinder from to while decreasing the temperature of the gas from back to . Although the gas has been restored to its initial state (i.e., initial temperature and volume), its center of mass has been, however, raised a distance of relative to its location at the beginning of step 1. (This step is similar to the contraction phase of the sphere, where its volume decreases while the height of its center of mass is still increased). Finally, in step 3, the cylinder, similar to the sphere, is returned to the lower platform, keeping the piston at its fixed height relative to the bottom of the cylinder (i.e., there is no change in the temperature and volume of the gas during this last step). All three steps together comprise a cyclic process, the net effect of which is similar to the process generated with the sphere. (Note that a vacuum outside of the container is not strictly required for the analysis. If the cylinder were exposed to the atmosphere, which would be subject to the same gravitational field, the external agent in steps 1 and 3 would therefore be required to vary its imposed external force such that the net force exerted on the top of the piston were always equal to ).
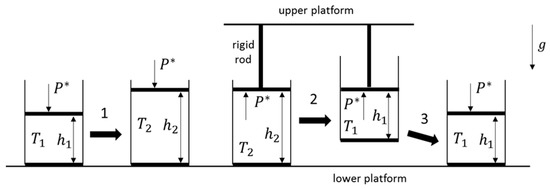
Figure 2.
An ideal gas is contained within a cylinder of a constant cross-sectional area with a movable piston of negligible mass. In the first step 1 of this reversible cyclic process, and while the cylinder remains on the lower platform, the temperature of the ideal gas is increased from to . The pressure on the piston remains at while the height of the piston also increases from to . In the second step 2, the piston is held in placed by a rigid connecting rod attached to the upper platform. While keeping the pressure on the piston again at , the temperature of the gas is decreased from to , while the relative height of the piston from the bottom of the cylinder is decreased from to . Consequently, the center of mass of the gas has been raised in the gravitational field. In the final step 3, the cylinder is returned to the lower platform without changing the temperature and volume of the gas. Hence, the center of mass of the gas has been returned to its initial height, as it was at the beginning of the cycle and prior to the start of step 1.
3.1. Ignoring the Effects of Gravity on the Properties of the Ideal Gas
To begin, let’s neglect the effects of gravity on the internal properties of the gas, i.e., the local properties of the gas are taken to be independent of their position in the gravitational field. In other words, the temperature, pressure, and density of the gas (as well as all other intensive properties) are always assumed to be uniform throughout the container. Hence, the center of mass of the gas always resides at the center of the cylinder. In this case, the thermodynamic analysis of this cycle will be quite similar to the previous analysis of the cyclic process with the sphere.
In step 1, while remaining on the platform, and with the pressure on the piston being kept fixed at , the temperature of the gas is increased from to . (With assumed uniform properties, the pressure of the gas is also equal to everywhere). The height of the piston increases to , while the center of mass of the gas is raised from to . The work done by the gas along this constant pressure expansion is simply . (In thermodynamics, work is calculated from the forces at the boundary of the system and their corresponding displacements. The only boundary of the gas that is displaced in this step is that residing just below the piston, which moves a distance , with the gas exerting a constant force at that boundary). The change in the potential energy of the gas is , where is the number of moles of the gas and is its molecular weight. For an ideal gas, and for fixed , the differential change in the internal energy of the gas is given by , regardless of the pathway taken, where is the specific isochoric heat capacity of the ideal gas [9]. Assuming that is a constant, the change in internal energy of the gas for this step is therefore . Hence, and again noting that , the “heat absorbed” by the gas in this step is:
Since the properties of the ideal gas are uniform, the pressure, temperature, and the height of the piston are related through the ideal gas equation of state, , where is the ideal gas constant. Thus, Equation (8) can be rewritten as:
where and for an ideal gas. Note the similarity between Equation (9) and Equation (3), in which is the total mass of the gas.
In step 2, while the piston is held in place, and with the pressure exerted on the bottom of the piston always equaling , the cylinder is raised. The distance between the piston and the bottom of the cylinder is decreased from to while the temperature of the gas is decreased from back to . For this step, the center of mass of the gas, relative to its location at the start of step 1, has been raised a distance of in the gravitational field. In addition, since the piston is held fixed, the gas does no work on this boundary. Rather, as the bottom of the cylinder is moved upwards, work is done on the gas at this lower boundary. At this lower boundary, the pressure of the gas is also equal to , as the intensive properties of the gas are taken as uniform, and is a constant by design. Therefore, as the volume of the gas is decreased, the work done on the gas during this step is . At the beginning of step 2, the center of mass of the gas is located at a height of with respect to the bottom platform. At the end of step 2, the center of mass is therefore at . Thus, the change in the potential energy of the gas for step 2 is . With , we have that:
Similar to what was found for the sphere, we note that .
Finally, allow the cylinder to return to the lower platform, keeping the piston at its fixed height relative to the bottom of the cylinder. From this step, the additional work is recovered. Hence, for the entire cyclic process, and . (Just like for the sphere, , even though the gas has been raised in the gravitational field over these two steps.) Therefore, a cyclic process has been generated with a thermodynamic efficiency of:
The efficiency in Equation (11), unlike what appears in Equation (7), is not a function of either or . However, similar to what was found for the sphere, Equation (11) implies that the efficiency of the cyclic process will exceed that of the corresponding Carnot cycle for appropriate values of and . Again, an apparent violation of the second law of thermodynamics is found.
As noted earlier, the above conclusion may not be valid, since the variations in the intensive properties of the gas due to gravity have not been accounted for in the analysis. At equilibrium, the pressure and other intensive properties of the gas are not necessarily uniform in a gravitational field [8], and these local variations with height must be explicitly considered when analyzing the different steps of the reversible cycle. In the next subsection, the various work, heat, and energy terms around the cycle are again determined, but now the effects of gravity on the properties of the gas are included in the analysis.
Before doing so, it is noted that neglecting the influence of gravity may seem to be a reasonable assumption when analyzing the properties of the ideal gas. As will be seen in the next section, is a characteristic length scale over which the properties of the ideal gas will observably vary in a gravitational field. Hence, for a gas within a container of height , the properties of the gas will be nearly uniform when . For nitrogen, as an example, within a container of height and a temperature of , (for ). Thus, nitrogen will appear to be, at least to the precision of what is typically observed experimentally, “uniformly” distributed throughout the container. However, such an apparent uniformity is not pertinent to a rigorous thermodynamic analysis of a given reversible process. When considering whether a particular process may or may not violate a law of thermodynamics, a distinction has to be made at the start of the analysis between “what appears to be uniform” and “what is strictly uniform”. To definitively determine if the process in question satisfies the second law, the corresponding heat, work, and energy terms must be rigorously determined, not just approximately so. The properties of the gas at equilibrium in a gravitational field must be strictly accounted for when it undergoes the reversible cycle (which, by definition, traverses a succession of equilibrium states). Only after the corresponding work, heat, and energy terms have been consistently and rigorously determined (as the possible delicate balance between these terms may not be satisfied if the system is assumed at the outset to be “essentially uniform”) can a conclusion be confidently drawn about a possible violation of the second law.
3.2. Including the Effects of Gravity on the Properties of the Ideal Gas
In a gravitational field, the variation with height of both the pressure and molar density of an ideal gas with a uniform temperature is proportional to [8], where points in the upward direction, while the gravitational force points in the (downward) direction (with located at the bottom platform). Since the container is closed, the integration of the molar density as a function of from the bottom to the top of the container must be related to , which is the total number of moles of gas in the container. Consequently, in its initial state, with a temperature and the piston at height above the bottom platform, the molar density and pressure of the ideal gas vary with height according to:
in which is still satisfied at each . Since the piston is also initially at rest, we find from Equation (13) that the pressure of the gas exerted on the bottom of the piston is related to the initial height of the piston as follows:
For given values of , , and (as well as and ), there is a unique value of .
The pressure of the gas at the bottom of the container, , is obtained by setting in Equation (13). Upon doing so, one finds that , which is just the total weight of the gas. In addition, because the density of the gas is not uniform, the center of mass of the gas is not necessarily located at the center of the container. The height of the center of mass, , can be determined using Equation (12), and is given by:
In general, only for does . However, as the same system is being compared under two different conditions (i.e., , , and are identical both with and without the effects of gravity), effectively only for just is the center of mass located at the center of the container. Again, for given values of , , and (as well as and ), there is a unique value of .
Now, during step 1, the temperature of the gas increases from to , while the height of the piston increases from to . Since the pressure on the piston is kept fixed at , the work done by the gas along this expansion is again equal to . However, while the piston height increases from to , the center of mass of the gas increases from to . Hence, the change in the potential energy of the gas is , which in general is not equal to . For an ideal gas, in the absence of a gravitational field, the molar internal energy, , is only a function of [9]. Even in the presence of the field, is likewise taken to be only a function of (and not also on ). Since is uniform, is also uniform or independent of . Thus, again assuming is a constant, for this step. Therefore, the “heat absorbed” by the gas is:
Next, for step 2, as the piston is held fixed, and the pressure of the gas at the top of the cylinder is also held fixed at , the bottom of the cylinder is moved upwards. At this lower boundary, the pressure of the gas, , is also a constant, since (for a container with a constant cross-sectional area, the pressure at the bottom must always balance both the pressure at the top of the gas, , which is constant, and the fixed weight of the gas). As the volume of the gas is decreased, and the bottom of the cylinder is displaced a distance of , the work done on the gas is . At the beginning of this step, the center of mass of the gas is located at , with respect to the bottom platform. At the end of step 2, the center of mass is at (where was determined when the cylinder was in contact with the bottom platform with a piston height of ). Thus, the change in the potential energy for step 2 is . With , we have that:
Unlike what was found for the sphere or the case of uniform gas properties, and .
The balancing of these two “heat flows”, along with a non-zero net work interaction at this stage of the process, is a physically appealing result. At the completion of step 2, the gas has been fully returned to its initial internal state, and has simply been raised in the gravitational field. Even though the overall process is thermally driven, the raising of an object in a gravitational field, without changing any other of its properties, should presumably occur without a net “heat flow” into the system. Since only the height of the gas has been increased, the expected net effect of completing both steps 1 and 2 should only be a non-zero work interaction (whether or not these two steps are initiated by a heating of the gas). Moreover, this non-vanishing work interaction should be consistent with the change in potential energy of the gas. In fact, for the current analysis, , with the latter being identical to the potential energy change of the gas after the completion of steps 1 and 2.
Finally, for step 3, we allow the cylinder to return to the lower platform, keeping the piston at its fixed height relative to the bottom of the cylinder. From this step, one recovers the additional work, . For the entire cyclic process, and , and there is no net work produced for this cyclic process.
Hence, there is no possibility for this cyclic process to violate the second law, since its thermodynamic efficiency is always equal to zero. This conclusion is reached when the effects of the gravitational field are consistently incorporated into the thermodynamic analysis, i.e., the various work and potential energy terms are determined using the equilibrium properties of an ideal gas under gravity. Moreover, the internal energy is still assumed to be independent of .
4. Evaluation of the Entropy Changes of the Ideal Gas Around the Cycle
Taking into account all the gravitational effects in the analysis of the cycle eliminates another thermodynamic inconsistency that appears when the properties of the gas are taken to be uniform. When the intensive properties of the gas are assumed to be uniform, a discrepancy appears between two necessarily equivalent ways of determining the entropy change of the gas for the various steps of the cycle. This discrepancy does not arise because of the assumed independence of the entropy on , and is eliminated simply by considering the full effects of the gravitational field. Finally, this inconsistency may also explain why the net heat around the cycle, and by extension the net work, is not zero for the case of uniform gas properties.
To begin, consider the case of non-uniform gas properties, in which all the gravitational effects are determined. Identical to the internal energy, the entropy of the gas is taken to be independent of . Since the molar density of the gas varies with height, the molar entropy, , of the gas also varies with height. Thus, start with the following form of the differential change in the molar entropy of an ideal gas (which for a pure component ideal gas will only be a function of the changes in two other intensive variables, which are chosen here to be changes in and ) [8]:
Selecting the molar entropy at a temperature and molar density to be an arbitrary reference state, and again letting be a constant, then:
Since the above molar entropy is a function of height , the total (extensive) entropy of the ideal gas, , at a particular temperature and total height of the container (or location of the piston relative to the bottom of the container) is given by [8]:
Substituting Equation (12) into Equation (19), and then into Equation (20), yields upon evaluation:
Now, using Equation (21), the entropy change of the gas for step 1 of the cycle is given by (in which and ):
The reference state does not appear in Equation (22), as expected, but the above expression appears to directly contradict the assumed independence of the entropy on . However, equation (14) indicates that since is constant for step 1, will also be constant as the gas expands. Furthermore, since is constant, Equation (15) likewise requires that be constant for this step. Therefore, each of the last two terms on the right hand side of Equation (22) is equal to zero, and the entropy change reduces to:
Even though the pressure of the gas varies with height, the gas always exerts a fixed local pressure on the piston (equal to ). Interestingly, the entropy change (with non-uniform properties) becomes identical to what is expected for an ideal gas with uniform properties undergoing a constant pressure process [2]. However, note that the isochoric and isobaric heat capacities of an ideal gas are, in general, only functions of temperature. In the current analysis, they are both taken to be constant. Hence, the pressure of the ideal gas (even if it varies) is irrelevant for the chosen value of . Thus, Equation (23) is perhaps an expected result.
Now, the entropy change of the gas can also be obtained directly from the definition of the differential change in the entropy [9]:
which is to be evaluated along a reversible pathway. (Since is uniform during the process, the above makes use of the “heat added to/removed from” the entire system, which is the same term that appears in the earlier first law analysis of the cycle.) Returning to Equation (16), one finds for step 1 that:
and so:
The above differential expression initially appears to be difficult to integrate directly, as the explicit dependence of and on must be known, while Equations (14) and (15) provide only the corresponding implicit dependence. However, remembering that both and are constants for this step, then and for step 1. Hence, Equation (26) can be rewritten as:
The above can now be directly integrated, although an additional simplification of Equation (27) can first be performed. With equations (14) and (15), one finds that:
Thus, Equation (27) reduces to:
An integration of Equation (29) for step 1 yields a result that matches Equation (23), as it must.
Equation (29), or its integrated form in Equation (23), is also applicable to step 2 of the process (as the pressure on the bottom of the piston is again constant and equal to ). At the end of step 2, the gas has been returned to the same internal state that it had at the very start of the cycle, i.e., the net effect of steps 1 and 2 is simply the raising of the gas without any other changes in its properties. With this internal state again described by the same temperature and initial volume, based again on the height of the piston relative to the bottom of the container, the gas should also have the same value of the entropy, regardless of it having been raised in a gravitational field. As follows from Equation (23) or Equation (29), the entropy change of the gas for step 1 is equal and opposite to the entropy change of the gas for step 2. Hence, the entropy change across both steps is zero, which is a result that is consistent with (along with the same temperature change of to in step 1 and to in step 2). Finally, since the gas simply falls back down to the bottom platform for step 3, there is no additional entropy change of the gas during this step. Thus, as expected, there is no change in the entropy of the gas as it undergoes the complete cyclic process.
Moreover, there are changes in the entropy of the two thermal reservoirs as the cycle is completed. Since the “heat added” to the gas during step 1 is “taken from” the thermal reservoir at , the entropy change of this thermal reservoir is equal to for this step. Likewise, the entropy change of the thermal reservoir at is equal to for step 2. Consequently, the entropy change of the universe for the cyclic process is equal to:
where again, , and and . As required by the second law, the entropy of the universe never decreases for this process (with the positive change occurring because of the irreversible heat transfer between the gas and the reservoirs, i.e., the heat transfer occurs directly between two bodies whose temperatures differ by finite amounts). Again, these thermodynamically consistent conclusions are found even upon invoking the assumption that the thermodynamic properties of the ideal gas are independent of .
Finally, let’s analyze the cycle for the case in which the properties of the gas are always taken to be uniform. Returning to Equations (18) to (20), but now letting the molar density be independent of location within the cylinder, Equation (23) is again obtained, as expected for a constant pressure process for a uniform ideal gas. However, for this case, as follows from Equation (8):
where, again for the assumption of uniform properties, . Now, a division of Equation (31) by to obtain does not yield, upon integration, Equation (23), or for the chosen reversible path. This result, which may be the reason why for this case, again highlights the thermodynamically inconsistent analysis of the cycle when the properties of the gas are taken to be uniform. The role of gravity is invoked when determining the change in the potential energy of the gas, but its effects on the intensive properties of the gas are ignored. Since the entropy changes and various “heat flows” are not consistently calculated, the resulting violation of the second law is only apparent, and is not an actual consequence of the process.
5. Conclusions
A cycle utilizing an ideal gas, similar to the process presented in Reference [1], was proposed and consistently analyzed. When the effects of gravity are properly accounted for during each step of this cycle, while still assuming that the internal energy of the system is independent of , no violation of the second law is found to occur. As of yet, there is no need to invoke a different assumption, whereby the internal energy and entropy, for example, are taken to be explicit functions of the gravitational field.
While the cycle discussed in Reference [1] was not directly analyzed here, the conclusions drawn for the cycle using the ideal gas also suggest that no violation will arise for the process with the sphere when all the effects of gravity are properly included. However, a thermodynamically consistent analysis of the cycle in Reference [1] should be done to confirm this conclusion, and would make for an interesting and worthwhile—albeit complicated—exercise.
The fundamental principles of thermodynamics indicate that the energy of a system is a state function, and therefore will be a function of other relevant properties or variables of the system. For many systems of interest, this energy function can be expressed as a sum of other functions, each of which depends only on a distinct subset of relevant properties. While not required, this splitting of the energy into separate terms is nevertheless done for convenience, and each of these separate functions are then labeled as different “existence forms” of energy [11], such as kinetic, potential, and “internal”. Within macroscopic thermodynamics, which makes no explicit reference to the underlying constituents of a material system, the implied meaning of “internal energy” has been those contributions to the total energy of the system that are related to some essential aspects or intrinsic characteristics of the system itself. Moreover, these “internal” properties of the system are presumably not influenced by any bulk motion of the system nor dependent upon a specific location in an “external” field [9]. For the gravitational field generated by the Earth, the amount of matter normally considered in a system of interest is so small by comparison that the gravitational field, or the gravitational potential at each location, is not altered by the presence of the system. In other words, the gravitational field, being considered as arising from something “external” to and fully distinct from the system, is regarded as completely independent of the “internal” thermodynamic state of the system [5]. Conversely, the thermodynamic state of the system, and hence the internal energy, is considered to be independent of the external field. Consequently, the internal energy is represented by a function only of other intrinsic system properties, such as the temperature, pressure, density, composition, etc. It is typically not considered to be explicitly dependent on the system’s velocity and specific position in a field or on the field strength.
However, this assumed independence of the internal energy (and other thermodynamic properties) on the gravitational field does seem to contradict one of the key aspects of the heating/cooling of the sphere, which was the original problem of interest. As discussed before, when placed on the lower platform, gravity will serve to compress the solid, with the lower layers being compressed more than the upper layers. Therefore, the material in these lower layers will have a different (local) value of its internal energy compared to the material in the upper layers. Thus, is the internal energy of the solid not a function of the gravitational field? Although gravity is indeed compressing the solid, one may argue that the internal energy is an implicit—rather than a strictly explicit—function of the field. The (local) internal energy does not depend upon by the field per se, but rather is an immediate function of the local density variation that arises in the solid as a consequence of the gravitational field. If there were no field present, but some external agent or some restrictive boundary were instead compressing the solid to the same shape that it would have in the presence of the field, the resulting density variations within the solid would be identical to those that develop with gravity. Hence, the internal energy of the solid would be the same (at least for this non-relativistic analysis). The local density variations are intrinsic characteristics of the system. Therefore, the local internal energy, which as noted before is considered to be representative of the internal state of the system, is taken to be a function of just the local density, with the effects of gravity on the solid being instead accounted for through its influence on the local density. This is similar to how the pressure variations and entropy were determined in the analysis of the ideal gas, having been obtained directly from just the local density variation. This definition of the internal energy, when consistently applied, does not lead to any loss of information about the “internal” thermodynamic state of the system. Of course, due to this implicit influence, the internal energy could be redefined to directly include these gravitational effects (as was done in Reference [1]). However, this redefinition is, as of yet, not strictly required and, arguably for the sake of simplicity, it is not necessary.
Admittedly, the chosen independence of the internal energy, and other related thermodynamic properties, on the gravitational, or other external, field is ultimately an assumption, the justification of which follows from the correspondence between the thermodynamic predictions that are obtained from it and empirical results [8]. Many thermodynamic analyses have invoked this selected form of a field-free internal energy [12,13,14], the results of which do not appear to contradict our experience. Even so, the chosen definition of the internal energy does not follow from any thermodynamic reasoning. Hence, as noted above, nothing strictly precludes the extension of this definition to include variables related to a given external field, as was done in Reference [1].
Of course, nowadays, we are cognizant of the molecular constituents of the system, and so tend to associate “internal energy” with those contributions to the total energy arising from the molecular properties of the system. Therefore, the dependent variables of the internal energy function are selected to be those macroscopic properties (e.g., temperature) that somehow modify these molecular properties [9]. However, a simple connection between these macroscopic and molecular properties may not arise in certain cases, such as what occurs for an ideal gas within a gravitational field in which the number of particles comprising the gas is small and the total energy of the gas is fixed. For this system, the location and velocity of a given particle are not statistically independent variables [15]. However, in the thermodynamic limit, the height and velocity of a particle become uncorrelated, and so the molecular-based analysis of an ideal gas in a gravitational field matches the results obtained from standard (macroscopic) thermodynamic analyses [15].
From a molecular perspective, there are arguably only two “existence forms” of energy in most cases: kinetic and potential. When a molecular-based analysis of the first law of thermodynamics is performed [16], only these two forms appear, in which the energy of the system can be separated into terms related to the gravitational potential energy of the particles, the kinetic energy due to the motion of the center of mass of the system, the kinetic energy due to the motion of the particles relative to the motion of the center of mass, and the potential energy arising from the interaction forces between the particles (and we are neglecting the contributions due to the internal degrees of freedom of the molecules themselves, such as rotational and vibrational). The latter two energies, being invariant to changes in the bulk velocity or location in a gravitational field, are combined together and relabeled as the “internal energy”; these are the contributions arising from the internal characteristics of the system itself (i.e., the molecules comprising the system), rather than from some other external body (as is the case for the gravitational field and the gravitational potential energy term) [17]. Hence, the standard choice that is made in nearly all thermodynamic analysis in which the “internal energy” is assumed not to be a function of the field strength. Again, this is an assumption based on the apparent non-influence of the field on the internal state of the system (at least for non-relativistic systems). Furthermore, this assumption has not as of yet been shown to lead to an inconsistency with the laws of thermodynamics.
Funding
This research received no external funding.
Acknowledgments
I would like to thank Mark Uline for interesting and helpful discussions on an earlier and partial version of this manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- De Palma, G.; Sormani, M.C. Counterintuitive effect of gravity on the heat capacity of a solid sphere: Re-examination of a well-known problem. Am. J. Phys. 2015, 83, 723–729. [Google Scholar] [CrossRef][Green Version]
- Koretsky, M.D. Engineering and Chemical Thermodynamics, 2nd ed.; John Wiley& Sons, Inc.: New York, NY, USA, 2013; pp. 70, 152. [Google Scholar]
- Specific Heat Capacity Table. Available online: http://www2.ucdsb.on.ca/tiss/stretton/database/specific_heat_capacity_table.html (accessed on 23 June 2018).
- Thermal Expansion Coefficients at 20 °C. Available online: http://hyperphysics.phyastr.gsu.edu/hbase/Tables/thexp.html (accessed on 23 June 2018).
- Guggenheim, E.A. Modern Thermodynamics by the Methods of Willard Gibbs; Methuen & Co. LTD.: London, UK, 1933; pp. 153–159. [Google Scholar]
- Koenig, F.O. Note on thermodynamic equilibrium in the gravitational field. J. Phys. Chem. 1936, 40, 373–378. [Google Scholar] [CrossRef]
- Hatsopoulos, G.N.; Keenan, J.H. Principles of General Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1965; pp. 509–517. [Google Scholar]
- Reiss, H. Methods of Thermodynamics; Dover Publications, Inc.: Mineola, NY, USA, 1996; pp. 89, 180, 183, 184. [Google Scholar]
- Tester, J.W.; Modell, M. Thermodynamics and Its Applications, 3rd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997; pp. 38, 41, 81, 876–877. [Google Scholar]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 6th ed.; McGraw Hill: New York, NY, USA, 2001; pp. 203–204. [Google Scholar]
- Falk, G.; Herrmann, F.; Bruno Schmid, G. Energy forms or energy carriers? Am. J. Phys. 1983, 51, 1074–1077. [Google Scholar] [CrossRef]
- Andrews, F.C. Gravitational effects on concentrations and partial pressures in solutions: A thermodynamic analysis. Science 1972, 178, 1199–1201. [Google Scholar] [CrossRef] [PubMed]
- Debenedetti, P.G. Thermodynamic stability of single-phase fluids and fluid mixtures under the influence of gravity. J. Chem. Phys. 1988, 89, 6881–6888. [Google Scholar] [CrossRef]
- Berberan-Santos, M.N.; Bodunov, E.N.; Pogliani, L. Liquid-vapor equilibrium in a gravitational field. Am. J. Phys. 2002, 70, 438–443. [Google Scholar] [CrossRef]
- Román, F.L.; White, J.A.; Velasco, S. Microcanonical single-particle distributions for an ideal gas in a gravitational field. Eur. J. Phys. 1995, 16, 83–90. [Google Scholar] [CrossRef]
- DeVoe, H. Particle model for work, heat, and the energy of a thermodynamic system. J. Chem. Educ. 2007, 84, 504–512. [Google Scholar] [CrossRef]
- Alonso, M.; Finn, E.J. On the notion of internal energy. Phys. Educ. 1997, 32, 256–264. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).