1. Introduction
Client credit assessment is an important reference for developing bank financial services and loan approval procedures. Its main purpose is to determine the probability of default and to help banks reduce risk. The earliest client credit assessment method was empirical discriminant provided by credit analysts. This qualitative analysis method relies too much on the professional quality and experience of the evaluators and lacks objectivity.
With the digital technology applications available in banking, a large amount of client data and their credit information are collected. Many studies using machine learning algorithms have been conducted [
1], such as linear discriminant analysis (LDA) [
2], logistic regression (LR) [
3], decision trees (DTs) [
4], naive Bayes (NB) [
5], artificial neural networks (ANNs) [
6,
7], support vector machines (SVMs) [
8], and ensemble approaches [
4,
9], to achieve automatic credit assessment. The essence of the client credit assessment is a classification problem. According to the default risk, clients are divided into two categories: “good” and “risk” [
10].
In actual situations, client data are collected in chronological order as the bank transaction proceeds. The relationship between client characteristics and credit assessment results is not static. With the developing market environment and economic cycles, the relationship between client characteristics and credit assessment results may vary [
11]. Traditional machine learning algorithms create a learning model based on historical client data and then use the model to predict new client data. In addition, the actual applications also require the evaluation speed of the credit assessment model. Traditional machine learning algorithms cannot update the model in real-time as new client data arrives. Therefore, the learning model learns only the old relationships. A learning model established by traditional machine learning methods will have a good credit assessment ability for new clients if there is no change in the relationship between client characteristics and credit assessment results. Once the relationship has changed, the traditional machine learning models are likely to make incorrect assessments, which could create risks and cause economic losses. To ensure that the learning model can be updated with the latest client data and make an accurate assessment, this paper proposes applying online learning methods in the field of client credit assessment. In contrast to traditional machine learning methods, online learning methods process the training instance once “on arrival” without storing and make predictions using the current model at each time step [
12]. Therefore, online learning algorithms can immediately capture potential changes in the relationship between client characteristics and credit assessment. Additionally, online learning has been proven to achieve good performance in practical applications [
13,
14].
Online learning is often challenged by the joint issue of concept drift and class imbalance in the field of client credit assessment. In contrast to traditional machine learning algorithms that are trained on static datasets, online learning algorithms address the arriving training instances from the data stream one by one. Suppose the data stream has an underlying probability distribution
Pt(
x,
yi) [
15], and the instances in the data stream are generated by it. Once the distribution
Pt(
x,
yi) varies, the characteristic of the instances will change and concept drift will occur. In general, concept drift can be classified into sudden drift and gradual drift according to the changing concept speed [
16].
As noted, in the field of credit assessment, the relationship between the client characteristics and the credit assessment results is not static. Many client characteristics, such as income, expenditure, asset value, capital gain, and expected income, are susceptible to macroeconomic and market conditions. The income and asset value of a client with good credit in an economic expansion cycle will be significantly difference to that of the same client in an economic contraction. This phenomenon constitutes concept drift in the client credit assessment data stream. Although existing research [
11] has recognized potential concept drift in client credit assessment, it has used only a simple integrated approach to improve the overall accuracy.
Another important challenge is the imbalanced class distribution in the client credit assessment data [
17,
18]. In an actual credit business, many possible default clients are directly rejected in the initial screening, leading to a different number of “good” clients and “risk” clients in the data collection period. The number of good clients is larger than the number of risk clients leading to a problem of asymmetry. Moreover, the cost of misclassifying risk clients as good clients, and misclassifying good clients as risk clients is different. Misclassification of risk clients is more expensive and should be avoided as much as possible. Therefore, the learning model must focus on the minority class (risk clients). To address the class imbalance in the field of client credit assessment, many algorithms apply sampling techniques to balance the training dataset. Brown and Mues [
2] applied simple random undersampling and oversampling methods to deal with the class imbalance. Zieba et al. [
19] used the synthetic minority oversampling technique (SMOTE) to generate risk clients and achieved better performance than the random sampling methods. However, introducing too much synthetic client data will create more subjective factors. In addition, these sampling methods based on static datasets cannot be used in online learning conditions. In summary, the main challenges of credit assessment are the evaluation speed, the concept drift problem and the class imbalance problem.
Many online learning algorithms have been proposed to address concept drift and class imbalance in data streams. Online learning algorithms for concept drift are commonly categorized into active approaches and passive approaches [
20]. Active approaches [
21] apply a drift detection mechanism to identify the occurrence of concept drift and then take action to address it, which can handle sudden concept drift better. However, passive approaches [
22,
23] evolve the classifier continuously without detecting concept drift and are good at overcoming gradual drift. In an actual client credit assessment data stream, the type of concept drift is unknown, which requires the learning model to be capable of handling different types of concept drift. To handle the class imbalance in online learning conditions, Wang et al. [
24] proposed a time-decayed indicator to evaluate the real-time class imbalance degree of the data stream. Then the indicator was used to change the sampling times of the ensemble learning algorithm online bagging (OB) [
25] to propose oversampling online bagging (OOB) and undersampling online bagging (UOB).
In this paper, a novel sample-based online learning ensemble for client credit assessment is proposed to solve the deficiencies of traditional machine learning methods and handle concept drift and class imbalance in the credit assessment data stream. First, a novel multiple time scale ensemble classifier is proposed that contains a stable classifier and dynamic classifiers. To address gradual concept drift, the stable classifier learns the whole data streams from the moment the learning procedure begins. To handle sudden drift, the dynamic classifier exists for only a period and learns a partial concept. Second, to overcome the class imbalance, a novel sample-based online class imbalance learning procedure is proposed, which combines both oversampling for the minority instances and undersampling for the majority instances. Two bank client credit assessment cases, Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD) and Gateway Mobile Switching Centre (GMSC), are analyzed. The proposed sample-based online learning ensemble (SOLE) is compared with other state-of-the-art online learning methods by multiple metrics, such as accuracy, recall, F-score, G-mean and prequential area under the curve (PAUC). Two base classifiers, the Hoeffding tree and the naive Bayes, are used to test the preference of the online learning algorithms for the base classifier. The time and memory consumption of the algorithms are also reported. In general, the proposed SOLE achieves better performance using fewer computing resources and shows high adaptability for different base classifiers. In addition, to verify the feasibility of SOLE in practical applications, the credit scoring model and Kolmogorov–Smirnov (KS) test are applied. The results show that SOLE is suitable for practical application and can help services that need fast credit assessments, such as the E-commerce, online loan approval and financial security testing.
The rest of this paper is organized as follows.
Section 2 proposes the multiple time scale ensemble classifier. SOLE is proposed in
Section 3. Then, the experimental results and analysis reports are presented in
Section 4.
Section 5 provides the conclusion.
2. Multiple Time Scale Ensemble Classifier
Online learning algorithms should have the ability to handle potential concept drift in the client credit assessment data stream. In this section, a novel multiple time scale ensemble classifier is proposed to solve this issue. The main contribution of the ensemble method is that it is capable of different types of concept drift. As the sudden concept drift varies immediately, a learning algorithm that only learns the latest instances can adapt to the new concept rapidly, while a classifier that learns more instances can help handle gradual concept drift [
26]. In addition, if the old concept reappears, the learning model that is trained over a long time and has learned the old concept will perform better. Therefore, the proposed ensemble classifier has base classifiers of different time scales to address different potential concept drifts.
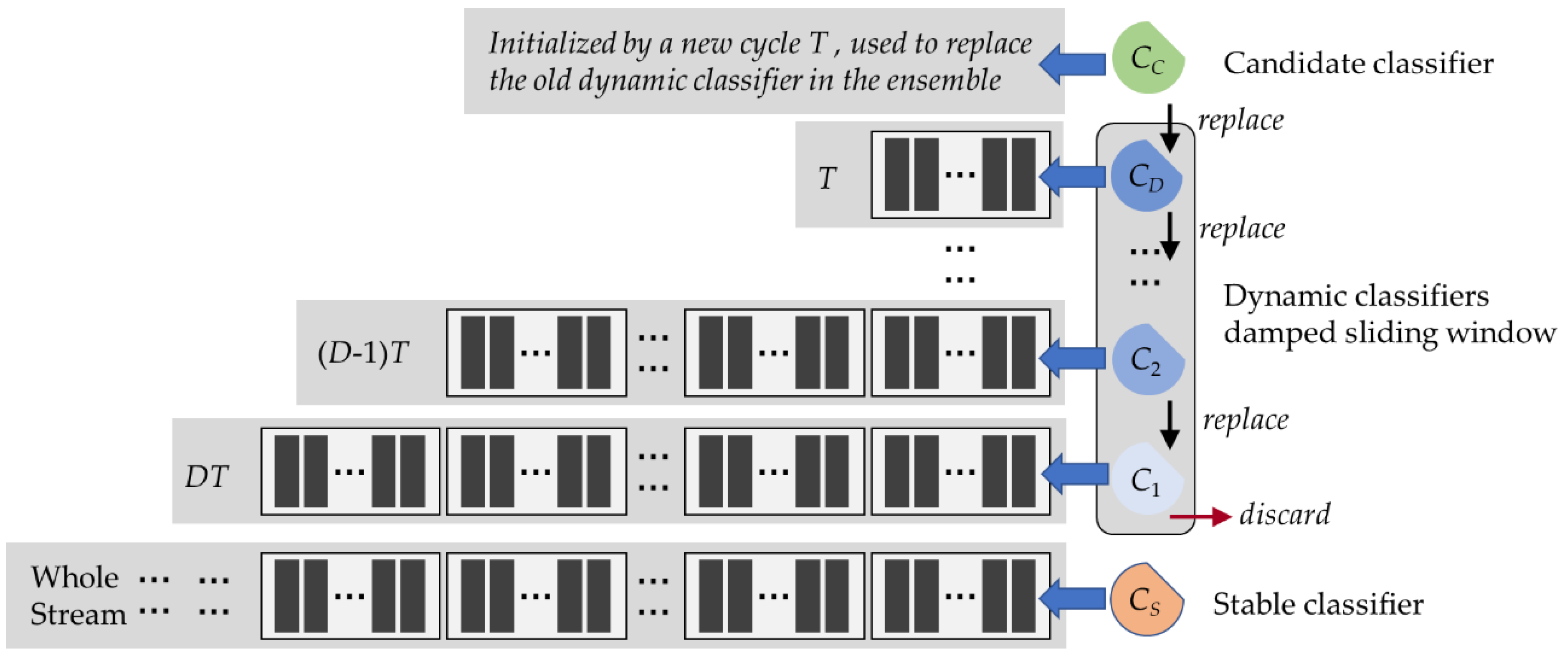
Figure 1 shows the structure of the multiple time scale ensemble classifier.
From
Figure 1, the multiple time scale ensemble classifier has a long-term stable classifier
Cs, and a dynamic classifier damped sliding window
Cd (
d = 1, 2, …,
D). Suppose
S is an unlimited data stream …,
xi,
xi+1,
xi+2, …. The real label of the instances
xt, which arrives at time
t, is
yt. To capture the concept of the data stream at different times, each
I instance of the data stream is seen as a time cycle
T. Therefore, as instances continuously come from the data stream, the data stream can be regarded as consequent time cycles
T1,
T2, …
Tn,
Tn+1 ….
Base classifiers in the multiple time scale ensemble classifier learn different time scale instances. The stable classifier
Cs learns all the instances since the learning procedure handles the gradual and cyclic concept drift of the data stream. The dynamic classifier
Cd learns only instances in the limited time cycle, which is defined as:
where the current time cycle is
Tn. The stable classifier and dynamic classifiers learn instances of different time scales: those learned by the stable classifier are given by
Ss and those by the dynamic classifier are given by
Sd. The dynamic classifier
Cd learns only instances of the most recent
D-d+1 time cycle. Each classifier in the ensemble classifier has its predictive weight, and the actual prediction result is the weighted combination of all classifiers:
where
is the ensemble prediction that the instance
x belongs to class
l,
ws is the weight of the stable classifier and
wd (
d = 1, 2, …,
D) are the weights of the dynamic classifiers. The weight of the stable classifier
ws is a constant, but the weight of dynamic classifiers
wd decreases over time. The initial weight of the newly created dynamic classifier is 1/
D, and the weight of the old dynamic classifiers decreases repeatedly according to the creation time, which is shown in Equation (3).
Therefore, old dynamic classifiers have less predictive weight than the new dynamic classifier, which helps the ensemble classifier to focus more on the latest instances of the data stream. Additionally, the stable classifier and dynamic classifiers both have a half predictive weight when the ensemble classifier makes predictions. The SOLE learning procedure is shown in Algorithm 1.
| Algorithm 1. Learning Procedure |
Inputs:
1. S: data stream
2. I: number of instances in a time cycle
3. D: number of the dynamic classifiers
4. α: sampling parameter
Output: Ensemble classifier E
Initiation:
1. p = 0: the indicator of processed instances
2. k = 0: the indicator of dynamic classifier
3. The stable classifier Cs
4. The candidate classifier Cc
Process: |
1. while (S. hasNext()) do
2. xnew = S. getnextInstance()
3. TrainOnInstance(xnew,α,DCRI[l])
4. p = p + 1
5. if (p%I == 0) then // reach a new time cycle
6. K = k + 1
7. if (k > D) then //number of dynamic classifiers beyond D
8. Cd ← Cd+1 (d = 1, …, D-1)
9. CD ← Cc
10. else
11. Ck ← Cc //copy Cc as the new dynamic classifier
12. end if
13. Cc. resetlearning() //reset the candidate classifier
14. end if
15. Calculate weight of classifiers according to equation (3)
16. Compute the damped class imbalance ratio by (4)
17. end if
18. end while |
At the early stages of the learning procedure, a stable classifier Cs and a candidate classifier Cc are created. The stable classifier exists during the whole learning procedure. The candidate classifier learns only instances of a time cycle. Whenever a new time cycle occurs (line 5), the candidate classifier trained by the last time cycle is copied as a new dynamic classifier and included in the dynamic classifier damped sliding window. Then, the candidate classifier is reset. If the number of dynamic classifiers is greater than D (lines 7–9), the subsequent classifier replaces the former classifiers one by one, Cd ← Cd+1 (d = 1, …, D−1), to keep the number of dynamic classifiers at D. The candidate classifier is used as the new dynamic classifier CD. Then, the algorithm updates the weight of the classifiers according to Equation (3) and calculates the damped class imbalance ratio using Equation (4). In the dynamic classifier damped sliding window, older dynamic classifiers are trained by more former arriving instances and have less predictive weight, which helps the ensemble classifier always attach importance to the latest data stream concept. The stable classifier exists for the whole learning process and can address gradual concept drift and cyclic concept drift better.
3. Sample-Based Online Class Imbalance Learning Procedure
If a data stream is class imbalanced, the model will lack minority class training instances. The sampling technique is a commonly used method to address class imbalance learning. However, traditional sampling techniques, such as random sampling or smart sampling [
2,
19], are not applicable to online learning conditions because that online learning requires the learning model to address one instance for each time step. For the online learning condition, sampling methods can be realized by changing the instance training times. OB [
25] is an online ensemble learning algorithm that modifies offline bagging, which contains multiple base classifiers. For each instance, the base classifier is updated
K times, following the
Poisson(
λ = 1) distribution. For the class imbalance learning condition, the categories are divided into a majority (negative) and a minority (positive) according to their amounts. To balance the class imbalance ratio, the proposed sample-based online class imbalance learning procedure oversamples the positive instances and undersamples the negative instances according to the real-time class imbalance ratio of the data stream. Therefore, the classifier can be trained by a nearly equal number of instances of different classes.
To determine the training times of an instance, the damped class imbalance ratio (
DCIR) which calculates the class imbalance ratio in real time, is proposed. The candidate classifier is copied as the dynamic classifier to the ensemble classifier. As the candidate classifier is trained by instances of a time cycle, each dynamic classifier
Cd has its part of initialization instances
Rd. The class distribution
Hd(
l) of
Rd is also calculated. Therefore, the
DCIR is calculated as:
where
wd is the weight of the dynamic classifier
Cd. First, the number of the instances of each class (0: negative, 1: positive) in the initialization dataset
Rd is summed, and
DCIR(
l) is the weighted summation of class
l divided by the weighted summation of total classes. According to Equation (3), the weight of dynamic classifier
wd is time-decayed and the earlier generated dynamic classifier has a lower weight. Therefore, the
DCIR is mainly determined by the latest class imbalance ratio of the data stream. The sample-based online class imbalance learning procedure is shown in Algorithm 2.
| Algorithm 2. TrainOnInstance(x,α,DCRI[l]) |
Input:
1. x: instance to be processed
2. α: sampling parameter
3. DCIR[l]: damped class imbalance ratio (l = negative, positive)
Output: The classifier Cnew
Process: |
1. y = getreallabel(x)
2. if (y →negative) then
3. sampleweight = DCIR[positive]/DCIR[negative]
4. else
5. sampleweight = DCIR[negative]/DCIR[positive]
6. end if
7. For each classifier in the ensemble, set K ~ Poisson(sampleweight*α). Then, update the classifier with x for K times
|
For a new instance x from the data stream, the algorithm obtains the real label y of the instance x. Then, the algorithm determines whether instance x belongs to the minority class. If x belongs to the majority class (i.e., x is negative) (line 2), the algorithm applies undersampling to learn instance x. The sample weight is set to DCIR [positive] divided by DCIR [negative] (line 3). Otherwise, the algorithm applies the oversampling method to instance x (line 5). The sampleweight influences the λ of the Poisson distribution. Finally, the stable classifier, candidate classifier and all the dynamic classifiers train on the instance x K times by the Poisson distribution (sampleweight*α). In general, the classifiers train more times on the positive instance and train fewer times on the minority class, which can balance the training set in the online learning condition. Particularly, this sampling method is based on only the latest instances without using historical information, which can avoid using the instances of an old concept.
4. Experiments
In this section, a systematic experiment comparison of online learning algorithms for credit assessment is presented. The proposed SOLE is compared with other state-of-the-art online learning algorithms on two real-world client credit assessment cases by multiple evaluation metrics.
Section 4.1 introduces the client credit assessment cases and experimental materials.
Section 4.2 presents the evaluation metrics. The comparative algorithms and the contrast base classifier are shown in
Section 4.3. The experimental results of SOLE compared with other online learning algorithms are presented in
Section 4.4.
Section 4.5 applies the credit scoring model and KS test to verify the practicality of SOLE in actual client credit assessment applications. Finally,
Section 4.6 presents the resource consumption.
4.1. Research Cases and Materials
Two bank credit assessment cases, PAKDD [
11] and GMSC [
22], are used in the experimental comparison. GMSC is a classic credit assessment case that comes from the Kaggle competition. GMSC contains the data of bank clients, such as age, monthly income, number of credit cards, and dependents, which are used to determine whether a loan should be granted. GMSC contains 150,000 instances, 10 explanatory attributes and 1 predictive attribute. PAKDD is another commonly used benchmark data stream in online learning. It comes from the PAKDD 2009 competition and mainly tests the impact of market changes in several business years on the performance of the classifier. The class distribution of PAKDD is also imbalanced. PAKDD contains 50,000 instances, 28 explanatory attributes and 1 predictive attribute.
Table 1 shows the main characteristics of the two experimental credit assessment cases.
Traditional machine learning evaluation methods divide a dataset into a training set and testing set. The model is trained on the static training set and then used to predict the testing set. Online learning methods obtain instances one by one, and the learning models can only learn one instance at each time step, which is a more challenging learning condition. In the comparative experiments, prequential evaluation is used: when a new instance arrives, first test it and then train on it. All the experiments are carried out on the Massive Online Analysis (MOA) [
27], which is designed for online learning conditions. The experimental machine has an eight-core CPU (Intel i7-6700) and 32 GB RAM.
4.2. Evaluation Metrics
Traditional overall accuracy and error rate are commonly used indicators to evaluate classification performance. However, when the learning datasets are class imbalanced, they can only reflect the overall performance. Therefore, other metrics have been adopted in the binary class imbalance learning condition [
28]. Generally, the minority class is treated as the positive class, and the majority class is usually treated as negative.
Table 2 shows the confusion matrix of the binary classification problem, which generates four numbers on the testing data.
Then, the recall is defined as:
Recall is the ratio of the True Positive rate with the positive instance percentage. Precision is the proportion of the True Positive rate with respect to the sum of the True Positive rate and the False Positive rate. The best situation of online class imbalance learning is improving recall without decreasing precision. However, it is conflicting to improve recall and precision together. Thus, the F-score is used to show the trade-off between them:
where
β is the relative importance factor of recall and precision, and which is usually set to 1. G-mean is also an indicator to replace overall accuracy:
The area under the curve (AUC) computes the area under the receiver operating characteristic (ROC) curve, which is also a good measurement for class imbalance learning condition. However, AUC is only suitable for the offline learning situation. To improve the traditional AUC for online learning conditions, Brzezinski et al. [
29] modified the AUC and proposed the prequential area under the curve (PAUC). The value of the indicator is continually updated in the online learning situation. Whenever an instance is processed, the indicator changes. Overall, the experiments in this paper compare the performance of the proposed SOLE with online learning algorithms on traditional accuracy, recall, F-score, G-mean and PAUC.
4.3. Comparative Methods
In this section, the comparative methods in the experiments are introduced. The selected comparative methods are all state-of-the-art online learning methods for concept drift and class imbalance. As the ensemble method tends to be more accurate than the base classifier, all the applied algorithms are ensemble online learning methods. Overall, Leveraging Bagging (LB) [
23], learn
++NIE [
26], OOB, UOB [
24], Online Accuracy Update Ensemble (OAUE) [
30] and Adaptive Random Forest (ARF) [
22] are compared. To control the performance of the base classifier for all algorithms, all the comparative algorithms use the same base classifiers except ARF. The Hoeffding tree and the naive Bayes are used as the base classifier for comparison. The default parameter settings of the base classifier are shown in
Table 3.
The Hoeffding tree is an incremental, anytime DT induction algorithm, it is very efficient and suitable for the classification of large amounts of data. The naive Bayes classifier is a relatively simple probability classifier based on Bayes’ theorem and has a low computational resource cost. Both the Hoeffding tree and the naive Bayes are widely used as the base classifiers in studies of the online learning situation. In particular, ARF uses the ARFHoeffding tree, which specifically modifies the traditional Hoeffding tree as the base classifier. OAUE can only apply the Hoeffding tree as a base classifier.
4.4. Experimental Results
4.4.1. Comparison of Online Learning Algorithms
In this section, the experimental results of all the comparison methods are presented using different metrics. All the comparative experiments are carried out 10 times and the average is taken as the result. All the ensemble methods use 10 base classifiers. The default parameters of SOLE are
D = 10,
T = 500, and ε = 1.
D is the number of dynamic classifiers.
T is the size of the time cycle, and
α is the sampling parameter.
Table 4 shows the results using the Hoeffding tree and the ARFHoeffding tree as the base classifiers, including SOLE, LB, learn
++NIE, OOB, UOB, OAUE and ARF. And the bold number is the optimal results.
For the GMSC (imbalance ratio: 1/14), LB and ARF achieve the same best accuracy, which is 0.2% higher than the learn++NIE accuracy. However, accuracy reflects only the overall classification performance. For the recall, three sample-based methods, SOLE, OOB and UOB, perform better than other online learning methods, which proves the effectiveness of the sampling technique in dealing with class imbalance. SOLE obtains the highest recall, which is 7.9% higher than UOB. Compared with the accuracy and recall, it can be concluded that while the overall classification performance is good, the actual classification performance on the minority class may be poor. In addition, SOLE achieves first place in all three metrics, F-score, G-mean, and PAUC. SOLE, OOB and UOB perform better than the other methods for these three metrics. Furthermore, learn++NIE and OAUE achieve recall values of only 2.2% and 0.0%, which shows that the algorithm predicts nearly all instances as the majority class. Thus, learn++NIE and OAUE lose their judgment capacity and cannot be used in practical applications.
As for the PAKDD (imbalance ratio: 1/4), learn++NIE and OAUE achieve first place in accuracy, which is 0.1% higher than the LB accuracy. The accuracy of SOLE is lower than that of LB, learn++NIE, OAUE and ARF, but higher than that of the other sampling methods, OOB and UOB. For the recall metric, LB, learn++NIE, OAUE and ARF obtain very low values, meaning that these algorithms regard almost all the instances as the majority. UOB has the best recall value, of 68.1%, which is 12.4% higher than SOLE. However, the overall accuracy of UOB is only 53.5, which means that UOB misclassifies almost half of the instances. Therefore, it can be concluded that UOB obtains a better classification performance for the minority class (i.e., recall value) at the expense of misclassifying many majority class instances. In practical client credit assessment applications, treating too many good clients as risk clients will cause adverse effects on the business. For the F-score, G-mean, and PAUC metrics, SOLE achieves first place and is better than the other algorithms.
For the experiments using the naive Bayes as the base classifier, only SOLE, LB, learn
++NIE, OOB, and UOB are included in the comparison.
Table 5 shows the average results using the naive Bayes as the base classifier. For the GMSC (imbalance ratio: 1/14), LB achieves the best classification accuracy, which is 0.2% higher than OOB and UOB. SOLE obtains the highest value on the recall metric, which is 0.4% higher than learn
++NIE. LB, OOB and UOB achieve only low recall values, which means they perform poorly for the minority class. In addition, SOLE performs best on the F-score, G-mean, and PAUC metrics and is better than the other algorithms. For the PAKDD (imbalance ratio: 1/4), LB also achieves the best performance for the accuracy metrics but obtains the lowest recall value. OOB achieves the best recall value of 79.7%, and UOB achieves the second place of 79.4%. However, their classification accuracy is lower than 50%, reflecting the fact that they acquire a better performance for the minority class at the expense of poor performance for the majority class. Moreover, SOLE achieves first place for three metrics: F-score, G-mean, and PAUC. SOLE performs better because it proposed a multi-time scale ensemble classifier and a sample-based learning method to address the joint problem of concept drift and class imbalance, while other state-of-the-art methods only focus on solving one problem.
4.4.2. Base Classifier Preference
Compared with the performances of the algorithms using different base classifiers, it can be concluded that the algorithms have preferences for the base classifier. The base class is also biased against the dataset.
Table 6 shows the bias of the base classifier by using different colors. The values in the table are the results using the Hoeffding tree as the base classifier minus the results using the naive Bayes as the base classifier. A positive value means that an algorithm performs better using the Hoeffding tree as the base classifier. A negative value means that an algorithm performs better using the naive Bayes as the base classifier. Orange cells indicate that the Hoeffding tree performs better, and green cells indicate that the naive Bayes performs better. The depth of the color has three levels according to the size of the value (0–10%, 10–20%, >20%).
First, the performance for different credit assessment cases is compared. It can be concluded that the number of green cells for PAKDD is larger than that for GMSC. This phenomenon may be related to the class imbalance ratio or the characteristics of the dataset. Second, the preferences of different algorithms are compared. Learn++NIE performs better using the naive Bayes as the base classifier. The performance gap between using the two base classifiers is apparent. LB performs better using the Hoeffding tree for GMSC, while it achieves a better performance using the naive Bayes for PAKDD. SOLE, OOB and UOB achieve better results using the Hoeffding tree. In general, SOLE has the best adaptability, as the performance gaps of SOLE between different base classifiers are minimal.
4.4.3. PAUC–Time Curves
In this section, to intuitively show the classification performance of different algorithms, the PAUC–time curves are plotted.
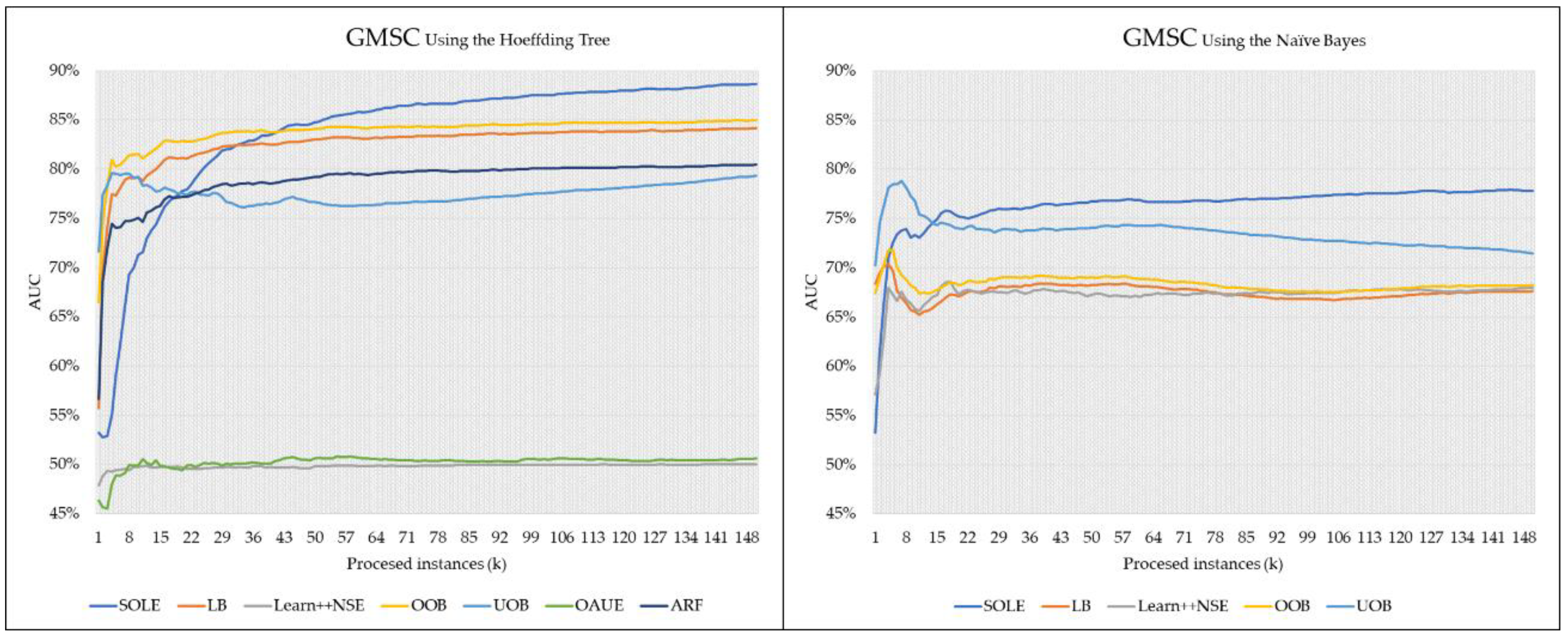
Figure 2 shows the PAUC–time curves for GMSC using different base classifiers. SOLE achieves the highest PAUC using both the Hoeffding tree and the naive Bayes as the base classifier. For the PAUC–time curves using the Hoeffding tree as the base classifier, SOLE achieves a low value at the beginning of the learning process. The PAUC value of SOLE continues growing and obtains first place at the end of the process. For the PAUC–time curves using the naive Bayes as the base classifier, the UOB achieves first place at the beginning. However, the PAUC of UOB continues to decrease, and the PAUC of SOLE continues to increase. Thus, SOLE performs better than UOB after approximately the 15 k time step.
Figure 3 shows the PAUC–time curves for PAKDD using different base classifiers. SOLE achieves the highest PAUC for both using the Hoeffding tree and the naive Bayes as the base classifier. For the PAUC–time curves using the Hoeffding tree as the base classifier, SOLE achieves fourth place at the beginning. Additionally, the SOLE PAUC value continues to increase, but the PAUC of the other algorithms is stable. Therefore, SOLE achieves the highest PAUC at the end. Then, for the PAUC–time curves using the naive Bayes as the base classifier, SOLE is better than the other algorithms throughout the whole learning procedure.
4.4.4. Parameter Sensitivity of SOLE
To explore the impact of parameter settings on the classification performance of SOLE, in this section, the parametric comparison experiment is carried out. Experiments compare the main parameters, number of dynamic classifiers
D, time cycle
T, and the sampling parameter
α whose default settings are
D = 10,
T = 500, and ε = 1. As for each group of parameter settings, the comparative experiments are carried out in parallel 10 times on both the cases and the averages are calculated.
Table 7 shows the average results with different parameter settings by using the Hoeffding tree as the base classifier. Only the Hoeffding tree as the base classifier is presented because of the same phenomena as using the naive Bayes as the base classifier.
From
Table 7, all the parameters have an impact on the classification performance of SOLE. First, increasing the number of dynamic classifiers can help improve the performance to some extent. Within the results of all the parameters,
D = 15 is the best setting for GMSC, and
D = 20 is the best setting for PAKDD. Second, SOLE performs better at time cycles of 500 and 750 for PAKDD, but the time cycle shows no apparent influence on GMSC. It shows that the best value of the time cycle is influenced by the features of the data streams. Finally, the classification accuracy improves when the algorithm uses a larger sampling parameter. However, the classification recall shows the opposite situation. Intuitively, the larger sampling parameter will increase the classification performance for the majority class but decrease the classification performance for the minority class.
4.5. Feasibility Analysis in Practical Application
4.5.1. Credit Scoring Model
The traditional credit assessment models provide only the classification probability that a client is a good clients or a risk clients. However, they are not easy to understand and use in practical applications. To present the credit condition of each client, the credit score is calculated based on the predicted probability provided by the proposed SOLE. The credit score is calculated as [
31]:
where
P is the probability that a client is a good clients, 1−
P is the probability that a client is a risk clients,
factor is the linear transform coefficient, which is usually a logarithmic value, and
offset is the adjustment constant that keeps the credit score in the target interval.
4.5.2. Bad Debts and the KS Test
To verify the feasibility of SOLE in practical applications, the credit scores of the clients for GMSC are calculated. The learning model is SOLE using the naive Bayes as the base classifier.
factor is set to
ln60, and
offset is set to 600. The credit score results are sorted from high to low and then divided into ten intervals. Each score interval has 15 k clients.
Table 8 shows the distribution of credit scores.
As shown in
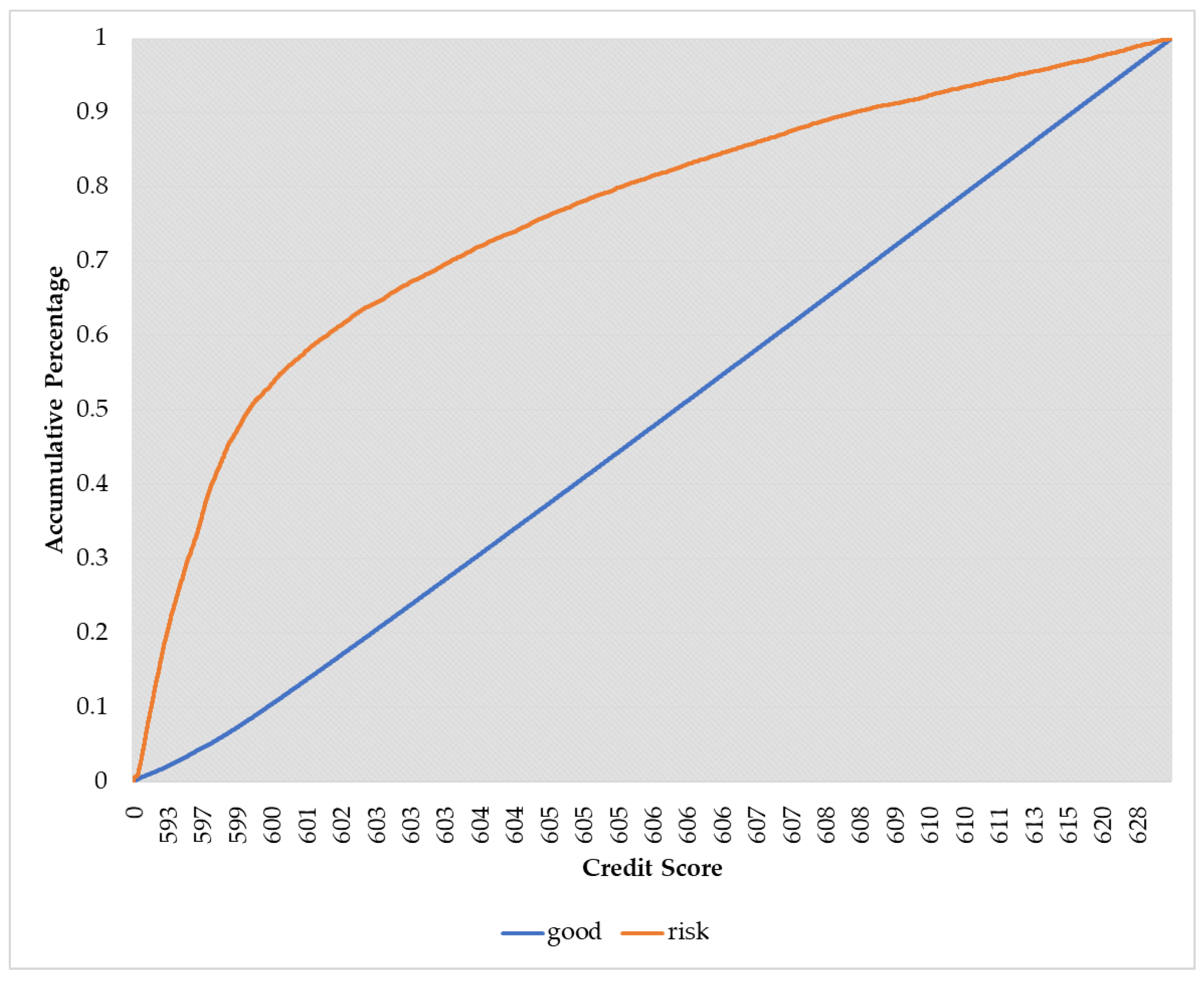
Table 8, risk clients are mainly distributed in the score intervals under the credit score of 604.6. As the credit score increases, the bad debt ratio decreases rapidly. Therefore, SOLE effectively reflects the real credit condition of the clients. The credit score can be used as the basis to assess the credit condition of the clients. In the actual financial risk control business, the KS test is usually used to evaluate the performance of a model. The KS test uses the difference between the accumulative percentage of good clients and the accumulative percentage of risk clients to show the distinguishing ability of a model. The larger the value of the KS test, the better the distinguishing ability.
Table 9 shows the relationship between the KS test and distinguishing ability [
31].
Figure 4 shows the KS curves for the GMSC of SOLE using the naive Bayes as the base classifier. The KS value is 0.47, which represents a high distinguishing ability. Thus, it proves that SOLE can be used in practical credit assessment.
4.6. Resources Consumption
For online learning models, resource consumption is an important feature for verifying whether the algorithms are capable of real-world applications.
Table 10 shows the resource consumption of the algorithms for the two cases. In general, SOLE consumes the least time and memory for both GMSC and PAKDD using the naive Bayes as the base classifier. It also consumes the least time and memory for GMSC using the Hoeffding tree as the base classifier. For the experiments on PAKDD using the Hoeffding tree as the base classifier, learn
++NIE costs the least time, OAUE costs the least memory, and SOLE also has a good performance on the resource consumption.
First, the resource consumption results by using the Hoeffding tree as the base classifier are compared. LB and ARF consume significantly more resources than other methods, meaning that LB and ARF will have more delays in real-time practical applications. OOB costs more time and memory than UOB because of the different sampling strategy. As the class imbalance ratio increases, OOB will require more resources for minority class instances, but UOB will cost less resources by undersampling the majority class instances. Therefore, the resource consumption of OOB for GMSC is higher than that for PAKDD.
Second, the experimental results are compared by using the naive Bayes as the base classifier. Learn++NIE costs significantly more time and memory. As the naive Bayes is a simpler base classifier than the Hoeffding tree, all the comparative methods except learn++NIE consume fewer resources using the naive Bayes as the base classifier. Therefore, it can be concluded that the learn++NIE has its preference by using the naive Bayes as the base classifier. By using the naive Bayes as the base classifier, learn++NIE will consume more resources and achieve better performance. In summary, the datasets, algorithm characteristics and the base classifiers all affect the source consumption.