1. Introduction
In recent times, many novel cryptosystems based on Group Theory have been proposed. Even when the ideas behind these group-based cryptosystems are interesting in their own right, these cryptosystems cannot yet compete with more standardized schemes such as Diffie-Hellman or RSA.
The word problem and the conjugacy problem are two of the fundamental decision problems in group theory proposed by Max Dehn in 1911 [
1]. The study and understanding of these problems in particular groups have played an important role on group-based cryptosystems.
Braid groups (see Reference [
2]), for example, are the mathematical structures behind many cryptographic schemes proposed in the last thirty years. One of the main reasons why these groups are suitable to be used in cryptography is the existence of
normal forms that facilitates an efficient solution of the word problem [
3].
The conjugacy search problem (i.e., given two elements
x and
y of a group
G that are conjugated, find the element
such that
) is the ground from which it is possible to build an scheme similar to ElGalmal in braid groups ([
4]).
Solving the conjugacy problem in braid groups is the most direct way to attack this scheme. Garside ([
5]) proposed the first algorithm in 1969 to solve this problem in a braid group. However, Garside’s proposal is not efficient and a polynomial time algorithm has not been found yet. Heuristics algorithms (as proposed by Hofheinz and Steinwandt in Reference [
6]) have achieved a large quota of success though.
Another example of key agreement protocol where the conjugacy search problem plays an important role was proposed by Anshel et al. [
7] in 1999. Broadly speaking, in this protocol the two parties agree on a common key by computing a commutator. It was first proposed for braid groups for two reasons: the existence of normal forms and the fact that the conjugacy search problem is considered difficult in these groups.
Cryptography based on group theory has brought about new and interesting pure mathematical questions. The word problem and the conjugacy problem play an important role in some cryptographic schemes based in group theory. Therefore, its study in particular groups seems unavoidable.
Let us consider now an arbitrary group
G and a word in the free group of rank
r,
, with
r a natural number. We can define the map
where each tuple
is mapped to
.
We denote the image of the map by . The verbal subgroup of G related to is defined as the subgroup generated by .
The surjectivity of the map , the cardinality of the set , if the verbal subgroup or if it is possible to find a constant k for which are essential questions to answer.
In 1951, O. Ore proved ([
8]) that every element in an alternating group
, with
, can be written as a commutator in
.
In other words, Ore’s result states that if we consider the word in the free group of rank 2, , then , for every .
In the same work, he proposed a conjecture: “Every element in a finite simple group G is a commutator in G”. This is known as the Abstract Ore’s Conjecture and was an open question until 2010.
One initial progress on this conjecture was done in 1994 by Wilson [
9]. He proved that for any finite simple group, there exists a constant
k such that,
.
In this line of work, some new results were obtained considering the word
, with
n a natural number. In 1996, Martínez and Zelmanov [
10] and in 1997, Saxl and Wilson [
11] proved, independently, that for every finite simple group big enough, there exists a constant
k such that
.
In 2010, M. W. Liebeck, E. A. O’Brien, A. Shalev and P. H. Tiep [
12] published the proof of the Ore Conjecture. They proved that for every finite simple group
G,
, where
denotes the commutator. The proof of this result is highly non trivial and makes use of Character Theory and computation where algebraic computer programs were specially designed.
Once this conjecture was proved, it seems natural to consider Engel words of arbitrary length instead of the commutator . That is considering the word . Ore’s Conjecture can be easily extended to Engel words, is it still true that for every finite simple group G and any natural number m?
In Reference [
13], a first approach was given for alternating simple groups. The author proved that every element in
, with
, can be written as a product of at most two Engel words of arbitrary length, that is
for any natural numbers
and
. However, the general case for alternating groups (if
for any natural numbers
and
) remains unknown.
In
Section 2 and
Section 3 two new approaches to this problem are presented. First, in
Section 2, we study special sequences of Engel words, getting interesting properties about their length. In
Section 3 we define a graph, depending on an alternating group and a fixed permutation and study the relation between this graph and the fact of an element
being an Engel word of arbitrary length.
In
Section 4, we work with an alternating group
,
and a fixed permutation
y in
. We build a graph related to them in order to empirically study the Engel words
in
.
2. Engel Chains
In this section, we define a particular type of sequence of Engel words and study some of their properties. We also analyze computationally the maximal length of these sequences for small alternating groups.
Let
y be a fixed element in the alternating group
,
. For each element
we can consider the following sequence of Engel words
There always exist two integers
such that
in
. Let us consider the first occurrence of
and
and the set
Definition 1. Let x and y be two fixed elements in . The set is called the y-Engel Chain associated to the element x and is called y-Engel Loop associated to the element x.
The length of the Chain is and the length of the loop is .
Lemma 1. Given we have that for every Proof. Given
, for every
we have that
That is, the product of two consecutive Engel words in the Chain is an Engel word of the Chain .
Definition 2. Given two elements , with , the Engel loop is stable by y-conjugation if .
We give now a characterization of an y-Engel loop stable by y-conjugation.
Lemma 2. Given , with , the loop is stable by y-conjugation if an only if for every we have that Proof. It is enough to see that
and that
.
Applying Lemma 1 we get the result. □
Let G be a group and let us consider an element . From now on, denotes the order of the element g and denotes the centralizer of g of the group G.
Lemma 3. Let y be a cycle with maximal length in and a loop stable by y-conjugation. Let us take , we have that
- 1.
For every we have that .
- 2.
For every we have that .
Proof. is evident. To prove
, as
we have that
and therefore, it is also true for every power of
y. □
Using Lemma 3, we know that if we consider an element in a loop stable by y-conjugation, every element in the set produces the same element when it is commuted by y. Note that is the only element in the set which belongs to .
Furthermore, every element in the set
belongs to the loop
when it is commuted by
y and since
y is a cycle with maximal length in
, we have that
Therefore condition in Lemma 3 is necessary and sufficient to guarantee that the loop is stable by y-conjugation.
Let us study the amount of conjugated loops in an alternating group , with p prime.
Lemma 4. Let p be a prime number and a p-cycle. If the loop is not stable by y-conjugation, it has exactly p conjugated loops in the set .
Proof. Let us consider the following action
We have that is exactly .
Then if is not stable by y-conjugation, we have that and then . □
Fix an element
y in an alternating group
,
and consider the loop
associated to the element
x in
, we have that
where
.
Let us fix
z an element in the loop
, since
for some element
, we have that
for every
. Therefore, the set of elements that, when commuted by
y, produces
z as a result is
Since z and are elements in , we have that there is only one element in A which also belongs to : .
Then, for every element in the loop , we have that there is only one element in such that, when commuted by y, the result is and there are elements outside of the loop such that commuted by y gives as a result .
Definition 3. Given an element y in an alternating group , , we define the annihilator of y as the set of elements x in such that there exists with . We denote this set by .
The annihilator of
y is the set of elements in
whose chain ’finishes’ in the identity element. If
defines the set of elements in
whose chain goes to a loop different from the identity element, we have that
We also know that
, where
is the set of non-identity elements that belong to the loop
,
is the set of elements in
which do not belong to
but its commutator with
y belongs to
and, inductively,
Note that there exists an index such that .
We performed a brute-force search (using GAP) to study the length of the y-Engel chains that finishes in the identity element for small alternating groups , .
The results we obtained were that the maximal length of these chains were 2 or 3 for the considered alternating groups. We summarize all the information in
Table 1.
This output is quite interesting as it seems to indicate that the y-Engel Chains that finish in the identity element are usually short.
In the following lines, we prove that under certain conditions, the maximal length of an Engel Chain that end in the identity element is 2. Note that denotes the normalizer of in .
Lemma 5. Let us consider the group , odd and take , a cycle with maximal length in . We have that and that is either or , where φ is the Euler’s totient function.
Proof. The number of conjugated elements of an
n-cycle in
is
. Then,
. We have that
Since
, we have that
. In the group
, there exist exactly
elements with the same decomposition as a product of disjoint cycles as
y, so we have that
.
By definition,
. If for every
i with
we have that the elements
y and
are conjugated in
, the number of groups in
conjugated to the group
would be half of the number of groups in
conjugated to
. So
and then
If half of the powers of
y are conjugated to
y in
, we have that there exists
such that
Then,
□
Lemma 6. Let p be a prime number greater than 3. Let us consider y, a cycle of maximal length in . The annihilator of y, , in is the group .
Proof. Consider
and
. We define
and inductively
Note that if and only if , that is, . Then, is an element of and therefore ; is an element of , that is, .
We have proved that if an only if . We will prove by induction that if an only if .
if and only if that is (by induction), and therefore, .
Then , that is, and by definition we have that .
We have two chains:
Since p is a prime number we have that and, since is selfnormalizer, we have that .
If we take x an element in , we have that and . Then we have that and therefore . So, .
Since
, we have that
□
Lemma 7. Let n be a positive integer such that and let y be a n-cycle in . The annihilator of y, , in is the group .
Proof. Let be a prime divisor of n. Given , we have that and since we have that is the only subgroup of with order n.
Using the arguments from Lemma 5, we have that . □
Corollary 1. Let n be a positive integer such that and y be a cycle of maximal length in . Then the maximal length of an Engel Chain which ends in the identity element is 2.
Proof. If we have that . Also we have that .
Thanks to Lemma 7, we have that is self-normalizing. Then the maximal length of the chain is . □
3. Engel Graphs
Let
y be a fixed element in an alternating group
, with
and a
, let us consider the following set of Engel words of length
m:
Since for every we have that , is a descending chain of subsets in .
Let us fix
and consider the set
as
, where
. Then, if
we have that
Let us consider the set
. We can define the following map
It is easy to see that for every and every element , , the map is well defined and bijective.
Then, we can study the sets by working with the set of all right cosets of in .
Note that as is a descending chain of sets and is a finite group, there exists such that .
We are going to define a directed graph which will allow us the study of Engel words in . Let us consider the set of nodes and let us define the set of arrows by the following relation:
Given , there exists an arrow from to if an only if .
Definition 4. Let y be an element in an alternating group , the graph is called Engel graph associated to the element y and the group .
It is possible to use this graph in the study of Engel words in an alternating group as:
If we consider a path of length k in the graph, starting in the node and finishing in the node , we have that . Once the graph is built, it is possible to easily compute Engel words of high lengths.
Reciprocally, if we want to compute
, it is enough to consider a path of length
k starting in the node
and commute by
y any element of the coset associated to the last node of the path
. We have that
We can study the ’dynamic’ of the set by studying the ’dynamic’ of the graph .
Once the graph is constructed, we want to use it to know whether or not an element in the alternating group , , can be written as an Engel word of type for . The following lemma shows the relation between the graph and the fact of an element in the alternating group being an Engel word of arbitrary length.
Lemma 8. Let be the map defined in (1) with . If is a directed cycle of , every element in the set can be written as an Engel word of arbitrary length. Proof. Consider , a directed cycle in the Engel graph .
Fixing an arbitrary element
in
W, we have that
As W is a directed cycle, there exists such that .
Take an arbitrary and a permutation in . We have that for and there exists such that , with .
It is enough to take to get that for some . □
Lemma 8 implies that given an alternating group , and y an element in , if we compute of the directed cycles in the Engel graph we get a subset of in which every element can be written as an Engel word of arbitrary length.
Corollary 2. If is a directed cycle of and the map defined in (1) with , every element can be written as an Engel word of arbitrary length in . Proof. This result can be directly deduced from Reference [
13] and Lemma 8. □
The following results shows some of the properties that Engel Graphs have.
Lemma 9. If and is the natural embedding, the image by ϕ of a directed cycle in an Engel graph , is a directed cycle in the Engel graph .
Proof. Fix and let be a directed cycle of the Engel graph . Given a node of , we can consider the directed cycle of that contains the node .
If there exists an arrow between two nodes
x,
z of
, we have that
Then for every . Then there is an arrow between the nodes and in . As is a directed cycle, we have that is also a directed cycle of the same length that . □
Corollary 3. Every element in that can be written as an Engel word of arbitrary length in , is also an Engel word of arbitrary length in , for every .
A sufficient condition for two Engel graphs to be isomorphic is presented in the following result.
Lemma 10. If we have that the Engel graphs and are isomorphic.
Proof. Denote
for some
. We define the next map
If
, we have that
. Then
so
and then
is injective.
Surjectivity is obvious, so is a bijection.
Consider two nodes and in , such that there is an arrow from to , that is .
If there is an arrow between two nodes in , there is also an arrow between the image of these nodes by in . Then is a isomorphism of graphs. □
4. Engel Graphs for Small Alternating Groups
In this section, we use an Engel graph to prove that for every and every . We show here the explicit method performed for the alternating group . For , the procedure is analogous and we show the computational results at the end of this section.
Some results from Reference [
13] are necessary to prove Theorem 2. We summarize those results in the following lemma.
Lemma 11. Let , , be a permutation of one of the following types: a product of two transpositions, a 3-cycle or a product of two 3-cycle. Then σ is an Engel word of arbitrary length in .
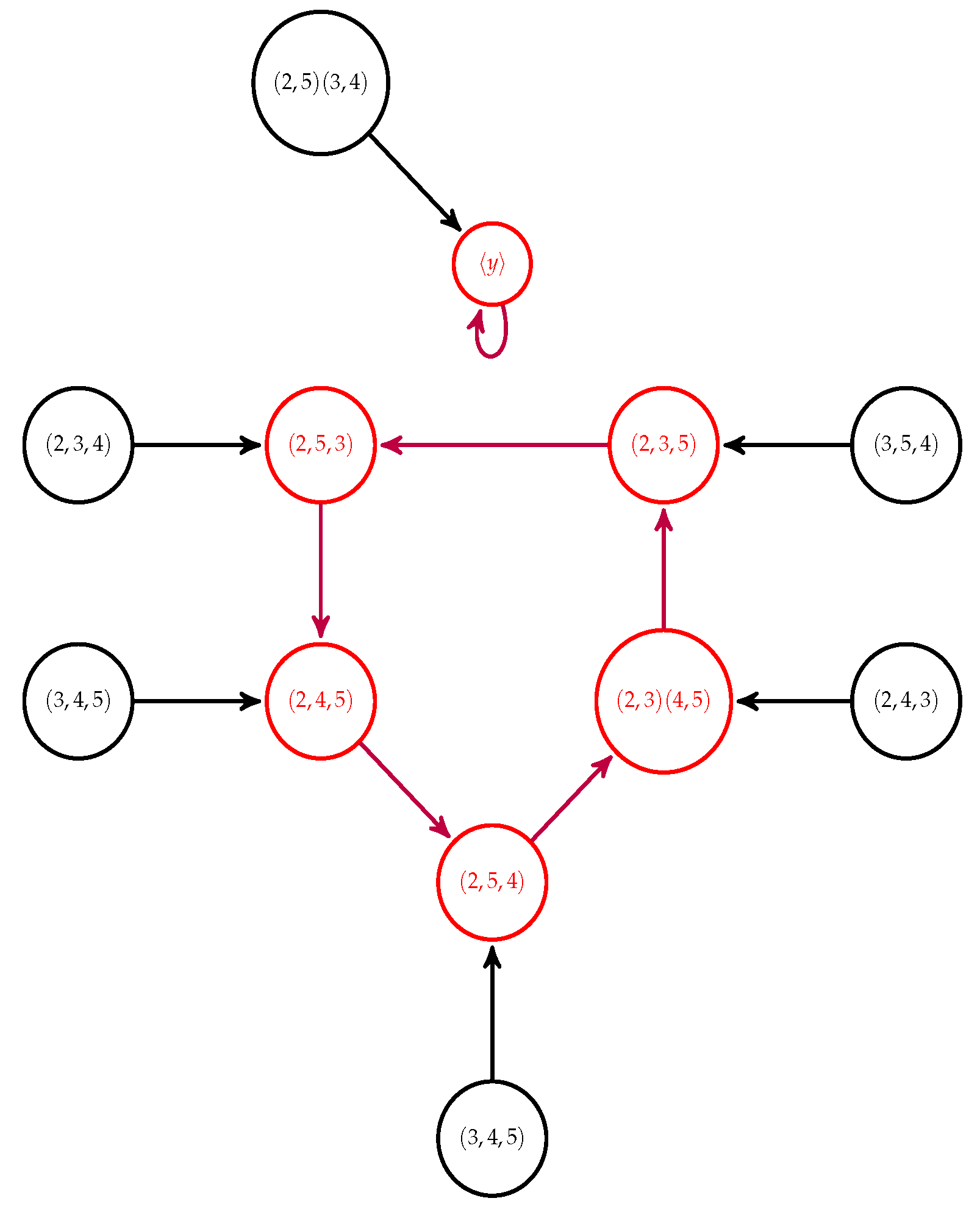
Consider a 5-cycle in . We have that , the cyclic group of order 5, so is a set of order .
Let us build the Engel graph
in
Figure 1. As we know, each node is associated to a coset module
. We denote each node
by a permutation of the set
.
The graph has two directed cycles. The first one, , is a cycle with five elements and the other one, , is only the identity node, .
By using Lemma 8, we just need to compute the sets
and
to get another set of elements in
which can be written as an Engel word of arbitrary length in
. We have that:
Thanks to Corollary 2 we have that every 5-cycle in can be written as an Engel word of arbitrary length in .
This result together with Lemma 11 allows us to prove the following theorem:
Theorem 1. Every element in can be written as an Engel word of arbitrary length. That is, for every we have that .
It is also possible to use the adjacency matrix of the Engel graph to study which nodes belong to a directed cycle. If we consider the adjacency matrix of the Engel graph , it is known that the element of the matrix gives us the number of directed paths of length k from the node i to the node j in the graph.
Computing the powers of the adjacency matrix and looking for the elements in the diagonal of that are different to 0, we can compute which elements of the graph belong to a cycle.
Let us consider the graph
, with
. Its associated adjacency matrix
is:
If we compute
, the result is:
It is possible to see that there are 6 nodes in the Engel graph that belong to a directed cycle. However, as the size of the matrix corresponds to the number of nodes in the Engel graph, working with these kinds of matrices becomes impractical when we consider alternating groups of higher order. As an example, for in the set has elements. For and y a 7-cycle, we get 360.
To study bigger alternating groups, we used GAP to compute the directed cycles of the Engel graph associated to the group and the element .
Later, we computed the set for each directed cycle in the graph . Then, we find out which types of permutations belongs to . To finish, we list every type of permutations in that does not belong to .
This final list contains every type of permutation that cannot be written as an Engel word of arbitrary length of type .
Let us fix a cycle y of maximal length in , . We use the previous algorithm to search the directed cycles of the Engel graph in order to see if Theorem 1 is also true for bigger alternating groups.
We will compute the set , where is the set of directed cycles in the Engel graph and we will see what types of permutations do not appear in .
Using the algorithm described above in GAP for
and
, we get that the types of permutations in
which do not appear in
are
Applying Lemma 11, we can get Theorem 1 for the group .
If we take , with and we repeat the same process for , if n is odd but if n is even, there is only one type of permutation that does not appear in the set : .
And again, we can easily get the Theorem 1 for the groups , with .
We summarise all the results we have got computationally in
Table 2.
Theorem 2. Every element in an alternating group , , can be written as an Engel word of arbitrary length in . That is,for every . In this work, we have provided two new approaches that can be used in the study of Engel words in alternating groups: Engel chains and Engel graphs. Using them (and GAP), we have also proved that every element in an alternating group , , can be written as an Engel word of arbitrary length.
It is still unknown whether Theorem 2 holds for . However, computational results seems to indicate some consistency in the “behaviour” of the Engel words in an alternating group and it is possible that a similar theorem holds for any alternating group , . The techniques proposed in this paper might be helpful in the further study of the general problem.