Segmentation of Laterally Symmetric Overlapping Objects: Application to Images of Collective Animal Behavior
Abstract
1. Introduction
2. Binary Image Data Acquisition
2.1. Design of Experiments on Fish
2.2. Acquisition of Binary Masks of Fish in Overlap
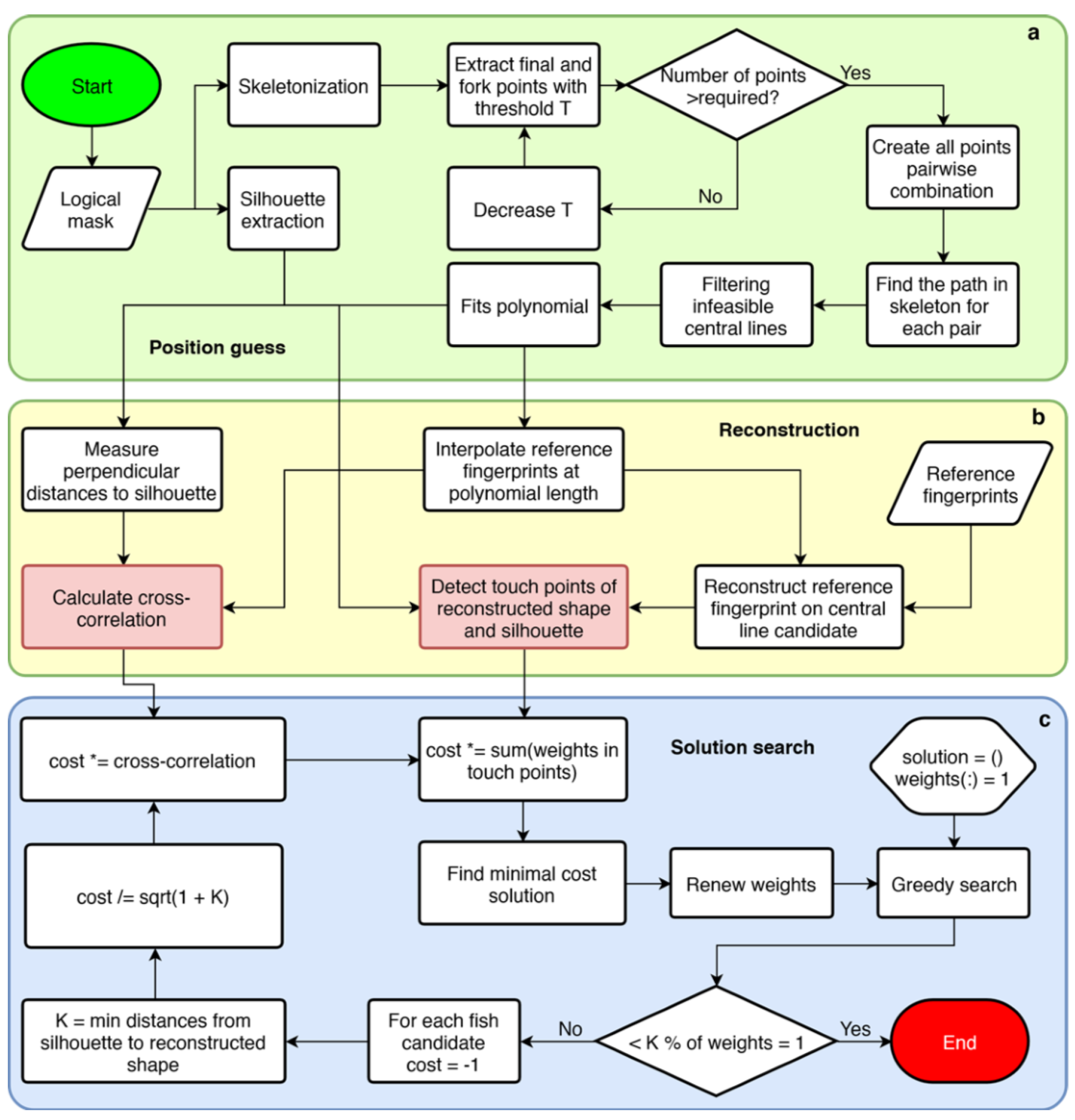
3. Segmentation of Binary Images of Symmetric Objects in Overlap
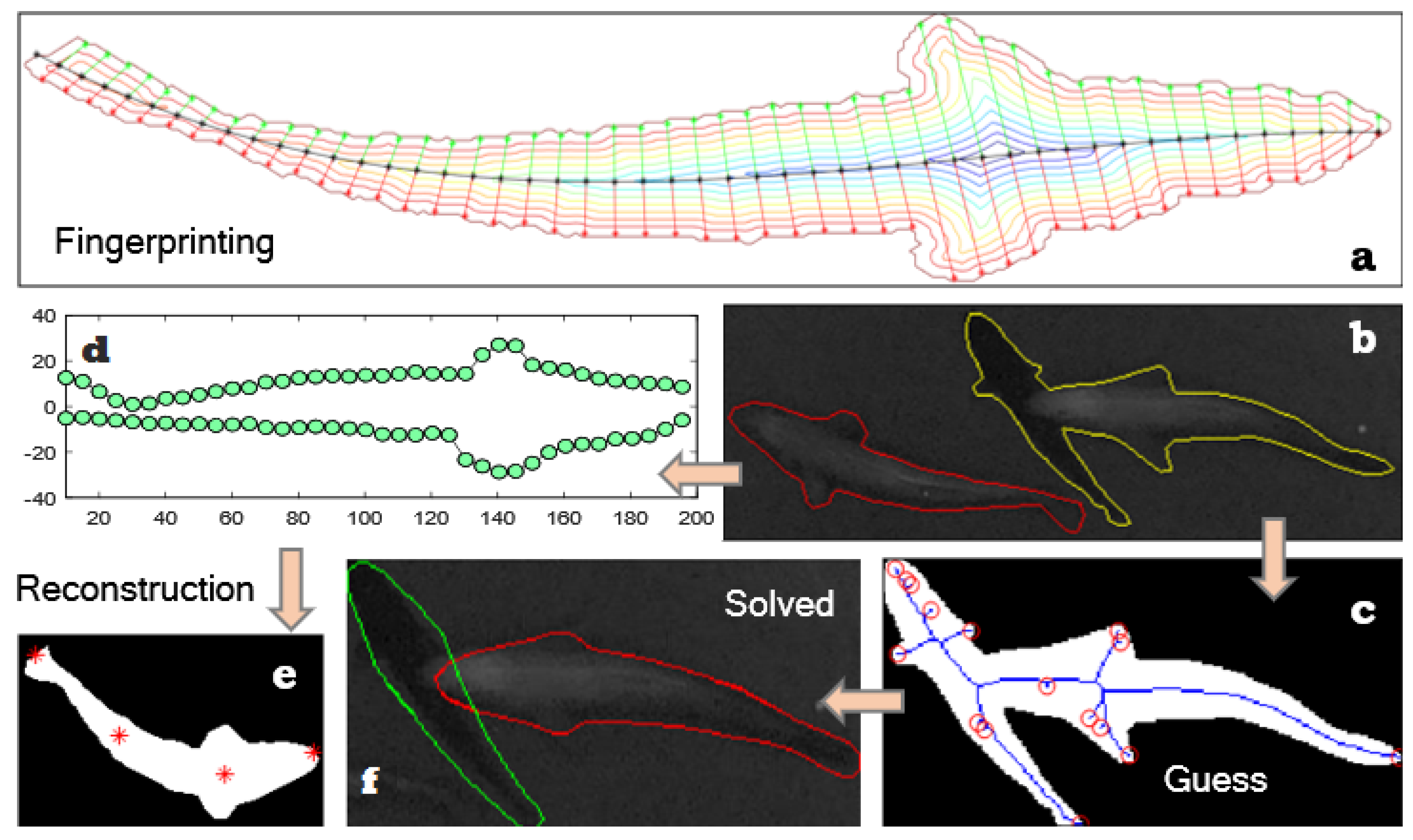
3.1. Morphological Fingerprinting
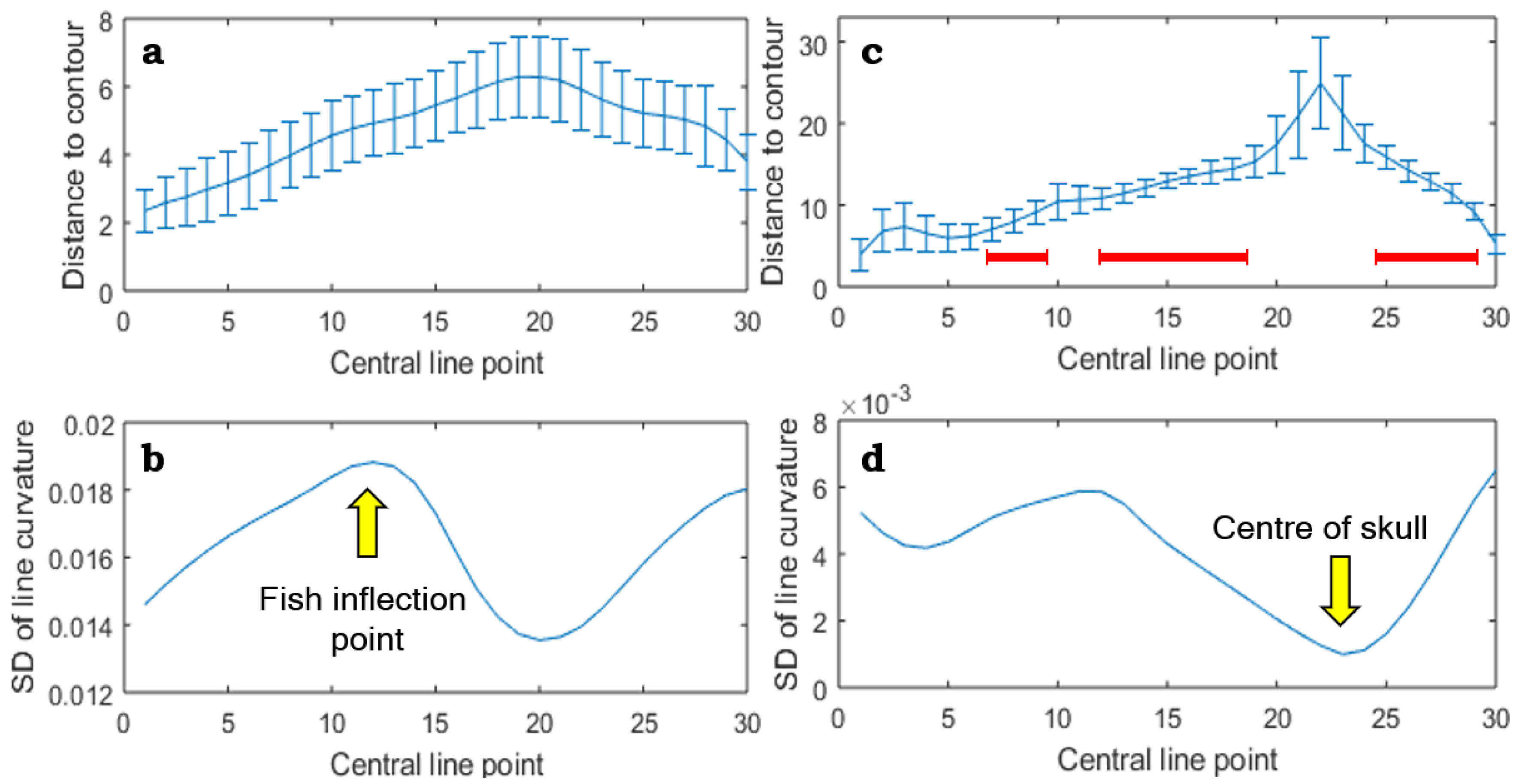
3.2. Dynamic Pattern Extraction
3.3. Position Guess
3.4. Solution Search
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| index of the value in computation of the degree of uniqueness | |
| A | area of binary mask |
| area of all detected binary masks, including fish overlaps | |
| total cost, i.e., total accuracy of the reconstruction method | |
| distance from the central line to the n-th point of the overlapping contour | |
| d | diameter of the fish circular tank |
| set of distances from the central line to the reconstructed object contour | |
| distance from the central line to the m-th point of the reconstructed object contour | |
| expected value | |
| discrepancy between the solution and the contour | |
| F | number of relevant lengths of the fingerprint central line |
| global cost, i.e., median of distances between intact points of in an overlapping contour and the reconstructed fingerprint contour | |
| image height | |
| stop criterion in calculation of the unknown number of objects in the solution search | |
| K | minimum from the set of distances from the central line to the reconstructed object contour |
| range of acceptable lengths of the central lines in the training set | |
| set of lengths of the central lines in the training set | |
| local cost, i.e., comparison of the perpendicular distances with the overlapping contour with the reference length | |
| m | order of the doubled equidistant points |
| M | doubled (below and above) number of equidistant points on the fingerprint central line |
| n | order of the pixel in the contour |
| N | count of pixels in an overlapping contour |
| number of equidistant points on the polynomial representation of the central line | |
| P | count of the points per fingerprint central line in dynamic pattern extraction |
| reference distance in calculation of the local cost | |
| reference distance of the s-th, forward or backward, orientation | |
| robustness of the solution search method | |
| s | orientation, forward or backward, of the reference distance |
| T | optimal count of skeleton points, i.e., the level of detail (LoD) |
| degree of solution uniqueness of the reconstruction method | |
| U | dispersion of fish sizes in the experiment |
| image width | |
| weight of the n-th pixel in the contour |
References
- Dennis, R.L.; Newberry, R.C.; Cheng, H.W.; Estevez, I. Appearance matters: Artificial marking alters aggression and stress. Poultry Sci. 2008, 87, 1939–1946. [Google Scholar] [CrossRef] [PubMed]
- Delcourt, J.; Denoel, M.; Ylieff, M.; Poncin, P. Video multitracking of fish behaviour: A synthesis and future perspectives. Fish. Fish. 2012, 14, 186–204. [Google Scholar] [CrossRef]
- Li, T.; Chang, H.; Wang, M.; Ni, B.; Hong, R.; Yan, S. Crowded scene analysis: A survey. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 367–386. [Google Scholar] [CrossRef]
- Kok, V.J.; Lim, M.K.; Chan, C.S. Crowd behavior analysis: A review where physics meets biology. Neurocomputing 2016, 177, 342–362. [Google Scholar] [CrossRef]
- Jolles, J.W.; Boogert, N.J.; Sridhar, V.H.; Couzin, I.D.; Manica, A. Consistent individual differences drive collective behavior and group functioning of schooling fish. Curr. Biol. 2017, 27, 2862–2868. [Google Scholar] [CrossRef] [PubMed]
- Delcourt, J.; Becco, C.; Vandewalle, N.; Poncin, P. A video multitracking system for quantification of individual behavior in a large fish shoal: Advantages and limits. Beh. Res. Methods 2009, 41, 228–235. [Google Scholar] [CrossRef] [PubMed]
- Morais, E.; Campos, M.; Padua, F.; Carceroni, R. Particle filter-based predictive tracking for robust fish counting. In Proceedings of the IEEE XVIII Brazilian Symposium on Computer Graphics and Image Processing, Natal, Brazil, 9–12 October 2005. [Google Scholar] [CrossRef]
- Raj, A.; Sivaraman, A.; Bhowmick, C.; Verma, N.K. Object tracking with movement prediction algorithms. In Proceedings of the 2016 IEEE 11th International Conference on Industrial and Information Systems (ICIIS), Roorkee, India, 3–4 December 2016. [Google Scholar] [CrossRef]
- Tang, W.Q.; Jiang, Y.L. Target tracking of the robot fish based on adaptive fading Kalman filtering. In Proceedings of the 2013 IEEE International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20–22 December 2013. [Google Scholar] [CrossRef]
- Perez-Escudero, A.; Vicente-Page, J.; Hinz, R.C.; Arganda, S.; de Polavieja, G.G. idTracker: Tracking individuals in a group by automatic identification of unmarked animals. Nat. Methods 2014, 11, 743–748. [Google Scholar] [CrossRef] [PubMed]
- Terayama, K.; Habe, H.; aki Sakagami, M. Multiple fish tracking with an NACA airfoil model for collective behavior analysis. IPSJ Trans. Comp. Vis. Appl. 2016, 8. [Google Scholar] [CrossRef]
- Butail, S.; Paley, D.A. Three-dimensional reconstruction of the fast-start swimming kinematics of densely schooling fish. J. R. Soc. Interface 2011, 9, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Saverino, C.; Gerlai, R. The social zebrafish: Behavioral responses to conspecific, heterospecific, and computer animated fish. Behav. Brain Res. 2008, 191, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Calfee, R.D.; Puglis, H.J.; Little, E.E.; Brumbaugh, W.G.; Mebane, C.A. Quantifying fish swimming behavior in response to acute exposure of aqueous copper using computer assisted video and digital image analysis. J. Vis. Exp. 2016, 53477. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, C.; Grimson, W. Adaptive background mixture models for real-time tracking. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), Fort Collins, CO, USA, 23–25 June 1999. [Google Scholar] [CrossRef]
- KaewTraKulPong, P.; Bowden, R. An improved adaptive background mixture model for real-time tracking with shadow detection. In Video-Based Surveillance Systems; Springer: New York, NY, USA, 2002; pp. 135–144. [Google Scholar] [CrossRef]
- van den Boomgaard, R.; van Balen, R. Methods for fast morphological image transforms using bitmapped binary images. CVGIP Graph. Models Image Process. 1992, 54, 252–258. [Google Scholar] [CrossRef]
- Holló, G. A new paradigm for animal symmetry. Interface Focus 2015, 5, 20150032. [Google Scholar] [CrossRef] [PubMed]
- Maurer, C.; Qi, R.; Raghavan, V. A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 265–270. [Google Scholar] [CrossRef]
- Mojekwu, T.O.; Anumudu, C.I. Advanced techniques for morphometric analysis in fish. J. Aquac. Res. Dev. 2015, 06, 354. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- van Eede, M.; Macrini, D.; Telea, A.; Sminchisescu, C.; Dickinson, S. Canonical skeletons for shape matching. In Proceedings of the 18th IEEE International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Csurka, G.; Larlus, D.; Perronnin, F. What is a good evaluation measure for semantic segmentation? In Proceedings of the British Machine Vision Conference, Bristol, UK, 9–13 September 2013; BMVA Press: Durham, UK, 2013; pp. 32.1–32.11. [Google Scholar] [CrossRef]
- Lonhus, K.; Štys, D.; Saberioon, M.; Rychtáriková, R. Segmentation of laterally symmetric overlapping objects: Application to images of collective animal behavior. arXiv 2018, arXiv:1811.01373. [Google Scholar]

| Series | Imgs. | Mean BF | JAC | Dice | Count [%] | Centroid e. [%] | Orient. [] |
|---|---|---|---|---|---|---|---|
| T. barb | 187 | 89.30 | |||||
| E. bass | 147 | 84.35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lonhus, K.; Štys, D.; Saberioon, M.; Rychtáriková, R. Segmentation of Laterally Symmetric Overlapping Objects: Application to Images of Collective Animal Behavior. Symmetry 2019, 11, 866. https://doi.org/10.3390/sym11070866
Lonhus K, Štys D, Saberioon M, Rychtáriková R. Segmentation of Laterally Symmetric Overlapping Objects: Application to Images of Collective Animal Behavior. Symmetry. 2019; 11(7):866. https://doi.org/10.3390/sym11070866
Chicago/Turabian StyleLonhus, Kirill, Dalibor Štys, Mohammadmehdi Saberioon, and Renata Rychtáriková. 2019. "Segmentation of Laterally Symmetric Overlapping Objects: Application to Images of Collective Animal Behavior" Symmetry 11, no. 7: 866. https://doi.org/10.3390/sym11070866
APA StyleLonhus, K., Štys, D., Saberioon, M., & Rychtáriková, R. (2019). Segmentation of Laterally Symmetric Overlapping Objects: Application to Images of Collective Animal Behavior. Symmetry, 11(7), 866. https://doi.org/10.3390/sym11070866






