A New Lightweight Stream Cipher Based on Chaos

Abstract

A chaotic system and two Nonlinear Feadback Shift Registers (NFSRs) are used to generate a new stream cipher in this paper. This design can be used for efficient encryption in resource-constrained devices or environments. The chaotic system is quantified and integrated with two NFSRs based on the technology of Field Programmable Gate Array (FPGA). Many analyses are made from the angle of entropy in order to verify the cryptographic characteristics of the stream cipher, and National Institute of Standards and Technology (NIST) statistical test is completed to analyze the cipher. The test results show that the stream cipher here has good cryptographic characteristics.

1. Introduction

In recent years, many resource-constrained equipment has been widely used. A device with limited computing power, storage space, and energy sources is called a resource-constrained device, such as smart cards Radio Frequency Identification (RFID) tag, wireless sensor, and personal digital power terminal. How to use secure and effective ciphers on these devices is a challenging problem. Many traditional ciphers are difficult to implement in this resource-constrained environment because of their own characteristics. Therefore, lightweight ciphers have attracted increasing attention. In 2013, National Institute of Standards and Technology (NIST) launched the lightweight stream ciphers project to study the performance of existing lightweight ciphers and to establish standards. In March 2017, NIST released the Lightweight Cryptography Report, which introduced the implementation of the project and the related achievements, and planned to develop the corresponding standards for lightweight cryptographic algorithms. As early as November 2004, the European Network of Excellent for Cryptology (ECRYPT) initiated the research project of eSTREAM [1], and convened the implementation of stream cipher algorithms for both hardware and software. Finally, four hardware-oriented winners were identified in 2008. Sprout [2], Fruit [3], LIZARD [4], Plantlet [5], Trivium [6], MICKEY [7], and Grain series ciphers [8,9,10] are some lightweight stream ciphers. However, as time goes on, a lot of progresses have been made in decoding areas, and some of the lightweight stream ciphers have been proved to be unsafe [11,12,13,14,15,16,17]. As a new cryptographic theory, chaotic cryptography has been paid more and more attention by many cryptographers. Chaotic cryptography is widely used in image encryption [18,19,20,21,22], secure communication [23,24,25,26,27], neural network, and economics. However, a few scholars have tried to introduce chaotic systems into the field of lightweight encryption [28,29], and no one has tried to apply chaotic systems to lightweight stream ciphers.

This paper combines chaotic system with Nonlinear Feadback Shift Register (NFSR) for the first time on the basis of studying a large number of lightweight stream ciphers, and produces a new lightweight stream cipher system that is based on chaos. The methods of entropy analyses [30,31,32,33] and NIST statistical tests are used to verify the performance of the lightweight stream cipher in order to verify the characteristics of the cipher. The results show that the lightweight cipher here is of better performance.

The structure is arranged, as follows: Section 2 describes the digitization process of Logistic chaotic sequence; Section 3 puts forward a lightweight stream cipher based on Logistic chaotic sequence; Section 4 elaborates the design principle of the lightweight stream cipher Logic; Section 5 carries out the entropy analyses of the system; Section 6 carries out the NIST statistical tests of the system; and Section 7 analyzes the hardware resources of the lightweight stream cipher. Section 8 analyzes the security of Logic system and Section 9 summarizes the whole paper.

2. Chaotic Sequence and Quantization

Chaos theory in non-linear science has been widely studied and applied in cryptography. Chaotic systems have a series of good cryptography properties, such as extreme sensitivity to initial conditions, pseudo-random behavior, and long-period instability, which are similar to the principles of diffusion and confusion in modern cryptography. A method of chaotic digitization is introduced in order to overcome the effect of finite precision. The expression of Logistic chaotic map is shown as:

$$x(n+1)=\mu x(n)[1-x(n)]\mu \in [0,4],x(n)\in (0,1].$$

(1)

It can be expressed by a floating point and integer. Single precision floating point cannot meet the requirements of chaos. Double precision floating point occupies too much resources. Here, the integer expression is used, and decimal $x(n)$ is written into binary expression.

$$x={\displaystyle \sum _{i=0}^{\infty }{a}_i{2}^{-(i+1)}}=(a_1{a}_2\cdot \cdot \cdot \cdot \cdot \cdot ).$$

(2)

The top $L$ positions are taken because of the accuracy requirement, then

$$x={\displaystyle \sum _{i=0}^{\infty }{a}_i{2}^{-(i+1)}}\approx (a_1{a}_2\cdot \cdot \cdot \cdot \cdot \cdot a_{L-1})=2^{-L}{\displaystyle \sum _{i=0}^{L-1}{a}_i{2}^{L-i-1}}=2^{-L}X.$$

(3)

Here

$$X={\displaystyle \sum _{i=0}^{L-1}{a}_i{2}^{L-i-1}}.$$

(4)

Each of $x(n)$ corresponds to a $L$-bit of binary $X$. In fact, $X$ is the decimal representation of $x(n)$, which takes $L$-bit and shifts to the right, so the Logistic chaotic map sequence can be expressed as:

$$X_{n+1}=4X_n(2^L-X_n)/2^L.$$

(5)

Here $L=32$, $\mu =4$, which can satisfy the requirements of chaos and map to the whole interval $(0,1]$.

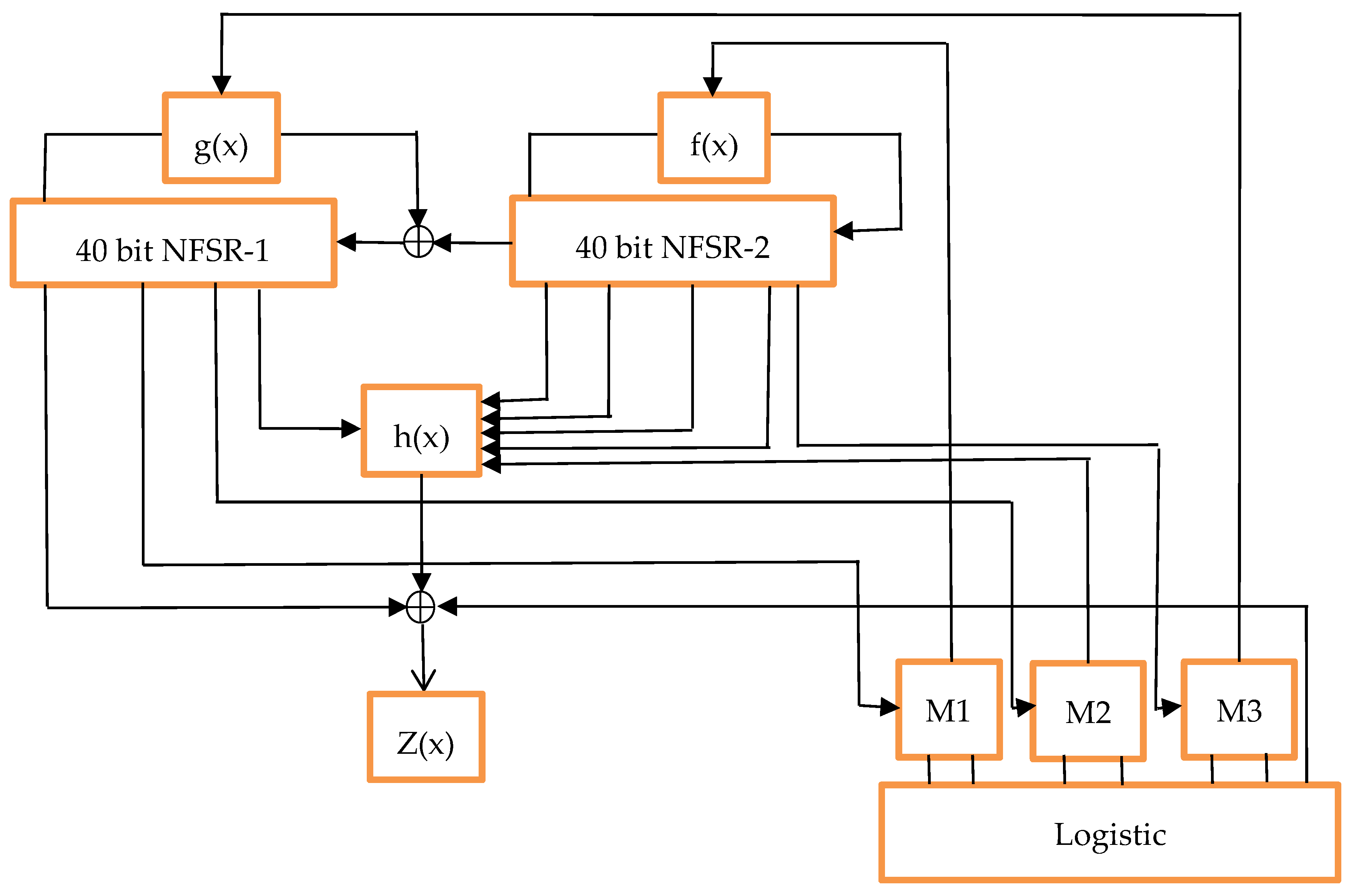
3. Logic Lightweight Stream Cipher

This paper presents a lightweight stream cipher, named Logic based on chaotic system and NFSR. Here, the algorithm is a hardware-oriented lightweight stream cipher algorithm, which can be applied in situations where hardware resources (gate number, energy consumption, and storage) are very limited. The algorithm uses 80-bit secret key. The main part of the algorithm is composed of Logistic chaotic system, two 40-level NFSRs, and three multiplexers. The structure diagram of Logic is shown in Figure 1.

As you can see from Figure 1, this is an efficient fusion of classical Grain series ciphers [4,8,9,10] with Logistic chaotic ciphers. Different from Grain lightweight ciphers, the Logic cipher here adopts two NFSRs and extract Logistic chaotic ciphers effectively to affect the following three functions: the feedback polynomial $g(x)$ of NFSR-1, the feedback polynomial $f(x)$ of NFSR-2, and the filtering function $h(x)$, so as to disturb the whole NFSRs system.

The states of NFSR-1 and NFSR-2 at time $i$ are $(b_i,b_{i+1},\cdot \cdot \cdot ,b_{i+39})$ and $(s_i,s_{i+1},\cdot \cdot \cdot ,s_{i+39})$.

The feedback polynomial $g(x)$ of NFSR-1 is defined as:

$$\begin{array}{ll}g(x)=& 1\oplus x^{15}\oplus x^{19}\oplus x^{23}\oplus x^{28}\oplus x^{34}\oplus x^{11}{x}^{24}\oplus x^{20}{x}^{29}\oplus x^{31}{x}^{37}\oplus x^{13}{x}^{18}{x}^{26}\\ & \oplus x^{22}{x}^{28}{x}^{35}\oplus x^{14}{x}^{24}{x}^{30}{x}^{37}\oplus x^{18}{x}^{27}{x}^{31}{x}^{36}.\end{array}$$

(6)

The feedback polynomial $f(x)$ of NFSR-2 is defined as:

$$\begin{array}{ll}f(x)=& 1\oplus x^{16}\oplus x^{18}\oplus x^{21}\oplus x^{35}\oplus x^{12}{x}^{19}\oplus x^{15}{x}^{23}\oplus x^{21}{x}^{37}\oplus x^{11}{x}^{23}{x}^{35}\oplus x^{19}{x}^{26}{x}^{33}\\ & \oplus x^{12}{x}^{23}{x}^{32}{x}^{37}\oplus x^{15}{x}^{26}{x}^{29}{x}^{35}.\end{array}$$

(7)

The filtering function $h(x)$ of Logic system is a balanced boolean function with five variables and four orders, and its nonlinearity reaches a maximum of 12. It is defined as:

$$\begin{array}{ll}h(x)=& x_1\oplus x_3\oplus x_1{x}_4\oplus x_1{x}_5\oplus x_2{x}_3\oplus x_2{x}_5\oplus x_3{x}_4\oplus x_1{x}_2{x}_3\oplus x_1{x}_2{x}_3{x}_4\oplus x_1{x}_2{x}_3{x}_5\\ & \oplus x_1{x}_2{x}_4{x}_5\oplus x_1{x}_3{x}_4{x}_5\oplus x_2{x}_3{x}_4{x}_5.\end{array}$$

(8)

The variables $x_0$, $x_1$, $x_2$, $x_3$ and $x_4$ correspond to the state bits $s_{i+2}$, $s_{i+17}$, $s_{i+29}$, $c_{i+2}$ and $b_{i+32}$, respectively.

The output function is defined as:

$$z_i={\displaystyle \sum _{k\in A}{b}_{i+k}}\oplus h(s_{i+2}\oplus s_{i+17}\oplus s_{i+29}\oplus c_{i+2}\oplus b_{i+32})\oplus c_{i+4}.$$

(9)

where $A=\left\{3,7,4,15,23,28,34,37\right\}$.

Before it outputs, Logic initializes the key stream. Let the secret key bits be $k_i$ and $0\le i\le 79$. The initial loading of registers is shown as

$$\begin{array}{c}(b_0,b_1,\cdot \cdot \cdot ,b_{39})\leftarrow (k_0,k_1,\cdot \cdot \cdot ,k_{39}),\\ (s_0,s_1,\cdot \cdot \cdot ,s_{39})\leftarrow (k_{40},k_{41},\cdot \cdot \cdot ,k_{79}).\end{array}$$

(10)

In the initialization phase, Logic feeds back the output to both NFSR-1 and NFSR-2 for updating, and it starts to output the key stream after 80 runs.

4. Design Principles

The Logic stream cipher consists of four components: two NFSR combinations, a chaotic module, a filter function, and three multiplexers.

4.1. Two NFSRs

There are two NFSRs in this part, in which NFSR-2 feeds back data to the LSB of NFSR-1. Both of the NFSRs are initialized with the same clock. The initial secret key is generated by the chaotic sequence. The initial value of chaotic sequence is set in order to avoid zero state. After initialization, NFSR-1 and NFSR-2 update and flip state driven by the clock.

4.2. Digital Chaotic Module

The Logistic chaotic sequence is relatively simple and it consumes less hardware resources. Therefore, the chaotic sequence is chosen as the disturbance and obfuscation module of the whole system in the Logic stream cipher. The system is decomposed into a 32-bit digital chaotic system after initialization and digitization, then the bits $l_{i+4}$, $l_{i+8}$, $l_{i+10}$, $l_{i+16}$, $l_{i+20}$, $l_{i+24}$, and $l_{i+28}$ are separately extracted for the multiplexer unit to select and extract. Subsequently, the data of NFSR-1, NFSR-2, filter function, and output function are disturbed and confused.

4.3. Filter Function

The five bits, $b_{i+32}$ of NFSR-1, $s_{i+2}$, $s_{i+17}$, and $s_{i+29}$ of NFSR-2, $c_{i+2}$ of Logistic digital chaotic module are used to construct the filter function module. The filter function with five variables and algebraic degree 4 is a balanced Boolean function, which is of a maximum non-linearity of 12.

4.4. Multiplexer Unit

The multiplexer unit is composed of three multiplexers, namely C1 (MUX2-1), C2 (MUX2-1), and C3 (MUX2-1). The selection bits of C1 are from $s_{i+19}$ of NFSR-1, the input bits are from $l_{i+4}$, and $l_{i+8}$ of Logistic digital chaotic module. The selection bits of C2 are from $s_{i+27}$ of NFSR-1, the input bits are from $l_{i+10}$ and $l_{i+16}$ of Logistic digital chaotic module. The selection bit of C3 are from $b_{i+11}$ of NFSR-2, and the input bits are from $l_{i+20}$ and $l_{i+24}$ of the Logistic digital chaotic module. $\mathrm{MUX}2-1(l_1{l}_2,s)$ is defined as a two-choice multiplexer with input signal $l_1$ and $l_2$ and $s$ represents the selection signal.

$$\begin{array}{c}\mathrm{C}1=\mathrm{MUX}2-1(l_{i+4}{l}_{i+8},s_{i+19}),\\ \mathrm{C}2=\mathrm{MUX}2-1(l_{i+10}{l}_{i+16},s_{i+27}),\\ \mathrm{C}3=\mathrm{MUX}2-1(l_{i+20}{l}_{i+24},b_{i+11}).\end{array}$$

(11)

5. Entropy Analyses

In this part, entropy analyses are completed by comparing the lightweight cipher based on the chaotic Logistic function with our own Logic cipher system.

5.1. Permutation Entropy

Permutation entropy [34] is used to measure the complexity of the time series. It introduces the idea of permutation when calculating the complexity of reconstructed sub sequence.

• There is a discrete time series $x(1)$, $x(2)$, …, $x(N)$ with length N, then an embedding dimension $m$ and a time delay τ are specified.
• By reconstructing the original sequence, each sub-sequence is represented as $X(i)$, and $X(i)=x(i)$, $x(i+\tau )$, …, $x(i+(m-1)\tau )$.
• Subsequently, incremental sorting is performed on each interior $X(i)$, i.e., $x(i+(j_1-1)\tau )\le x(i+(j_2-1)\tau )\le \dots \le x(i+(j_m-1)\tau )$, if the two values are equal, the order is based on the subscripts $n$ in $j_n$. In this way, $X(i)$ is mapped to (j₁, j₂, …, j_m), which is just one of $m!$ permutations. In other words, each subsequence $X(i)$ of dimension $m$ is mapped to one of $m!$ permutations.
• Through the above steps, the continuous $m$ dimensional subspace is represented by a sequence of such symbols, in which the number of these symbols is $m!$. The probabilities of all symbols are expressed by $p_1$, $p_2$, …, $p_k$, where $k\le m!$.
• The permutation entropy of the time series $x(1)$, $x(2)$, …, $x(N)$ is:

  $$H(m)=-{\displaystyle \sum _{j=1}^k{p}_j\ln }{p}_j.$$

  (12)

When $p_k=1/m!$, each symbol has the same probability, and the complexity of time series is the highest, so the permutation entropy is the highest. In addition, for the convenience of presentation, $H(m)$ is usually normalized by dividing by $\ln (m!)$. The analysis results are shown in

Table 1. Permutation entropy value.

Time Series	$\mathit{m}$	$\mathit{\tau }$	PE
Logistic	3	1	0.3854
Logic	3	1	0.5982

.

$$0\le \frac{H(m)}{\ln (m!)}\le 1.$$

(13)

5.2. Approximate Entropy

Approximate Entropy (ApEn) [35] is a non-linear dynamic parameter that is used to quantify the regularity and unpredictability of time series fluctuations. It uses a non-negative number to represent the complexity of a time series and it reflects the possibility of new information occurring in the time series. The more complex the time series is, the greater the approximate entropy becomes. The algorithm is described, as follows:

• Let $U(1)$, $U(2)$, …, $U(N)$ be a time series of dimension $N$, which is obtained by sampling at equal intervals.
• The relevant parameters $m$ and $r$ of the algorithm are defined, in which $m$ is an integer that represents the length of comparison vectors and $r$ is a real number using the measure of similarity.
• Here, the $m$ dimension vectors are reconstructed as $Y(1)$, $Y(2)$, …, $Y(N-m+1)$, where $Y(i)=[U(i),U(i+1),\dots ,U(i+m-1)]$.
• For $1\le i\le N-m+1$, the number of vectors satisfying the following conditions is counted.

  $$C_i^m(r)=\frac{1}{N-m+1}SUM[d(i,j)\le r].$$

  (14)

Here, $d(i,j)=\underset{a}{\max }\left|U(a)-U^{*}(a)\right|$, $\left|U(a)\right|$ is the element of a vector, which represents the distance between the vectors $Y(i)$ and $Y(j)$, which is determined by the maximum difference between the corresponding elements, and the range of $j$ is $\left[1,N-m+1\right]$, where $j$ and $i$ can be equal.

5.

Let us define

$${\mathsf{\Phi }}^m(r)=\frac{1}{N-m+1}{\displaystyle {\sum }_{i=1}^{N-m+1}\log }(C_i^m(r)).$$

(15)

6.

The approximate entropy (ApEn) is defined as

$$ApEn={\mathsf{\Phi }}^m(r)-{\mathsf{\Phi }}^{m+1}(r).$$

(16)

In the aspect of parameter selection, the parameter $m$ is defined as $m=2$, and the selection of $r$ depends on the practical application scenarios, usually $r=0.2*std$, in which $std$ represents the standard deviation of the original time series. According to the relevant literatures [31,32], it can be selected in practical application that $d(i,j)\le r$. If a time series is of significant regularity, its ApEn is relatively small. Correspondingly, a more complex time series corresponds to a larger entropy value. The analysis results are shown in

Table 2. Approximate entropy test.

Time Series	$\mathit{m}$	$\mathit{r}=0.2\mathit{s}\mathit{t}\mathit{d}$	$\mathit{N}$	ApEn
Logistic	2	0.1013	2048	0.6655
Logic	2	0.1015	2048	0.9442

.

5.3. Information Entropy

Information Entropy [36] is used to measure the uncertainty of random variables, which is directly related to the changing characteristics of the research. $\log (1/p)$ can be used to measure uncertainty. Here, $p$ is the probability of something happening. The greater the probability is, the smaller the uncertainty becomes. The formula of information entropy, in fact, is the expectation of $\log (1/p)$, namely, the expectation of uncertainty. It represents the uncertainty of a system. The random variables under distribution $X$ are independent of each other. The default base of $\log$ is 2, which is because the stream cipher system is binary. The expected coding length for coding samples according to the true distribution is illustrated as [33]

$$H={\displaystyle \sum _{i=1}^{n}p(i)\ast \log \frac{1}{p(i)}}.n=2,$$

(17)

as there are only two values for binary stream ciphers. The information entropy should be non-negative and have the maximum entropy value of 1. The analysis results are shown in

Table 3. Information entropy value.

Time Series	InEn
Logistic	0.5951
Logic	0.9238

.

From the above entropy analyses, it can be concluded that the entropy of the cryptographic system in this paper is significantly better than that of the lightweight stream cipher that is based on the chaotic Logistic function alone, which also proves that the combination of NFSR and chaotic cryptography can improve the entropy characteristics of the overall cryptography.

6. Statistical Tests

The NIST SP 800-22 test package provided by the National Institute of Standards and Technology of the United States is used in this paper in order to verify the statistical performance of the Logic stream cipher. The test program is a statistical package, which includes 16 testing methods. These methods can be used to test the randomness of binary sequences of arbitrary length that are generated by software and hardware of secret random or pseudo random number generator. These testing methods are mainly devoted to determine the various non-randomness that may exist in the cipher. Some of these tests can be decomposed into multiple sub-tests. The randomness test belongs to the black-box test. Here, the test is regarded as a black-box. The randomness test does not go deep into the inside of the algorithm, nor does it care about the structure of the algorithm itself. It only determines the output characteristics of the algorithm by observing the external behavior. All of the test results are determined by the $P-value$. If the results are calculated as $P<0.01$, the stream cipher is regarded to be non-random. If $P\ge 0.01$, the stream cipher is regarded as random. It is proven that the stream cipher that is generated by the system can be used in encryption applications. The test results are shown in

Table 4. National Institute of Standards and Technology (NIST) Statistical Tests.

Test	$\mathit{P}-\mathit{v}\mathit{a}\mathit{l}\mathit{u}\mathit{e}$	Test
Frequency Test	0.400908	Success
Frequency Test within a Block	0.861626	Success
Runs Test	0.475849	Success
Test for the Longest Run of Ones in a Block	0.199175	Success
Binary Matrix Rank Test	0.949536	Success
Discrete Fourier Transform Test	0.232884	Success
Non-Overlapping Template Matching Test	0.815009	Success
Overlapping Template Matching Test	0.751585	Success
Maurer’s “Universal Statistical” Test	0.139146	Success
Linear Complexity Test	0.359316	Success
Serial Test	0.067079	Success
Approximation Entropy Test	0.011645	Success
Cumulative Sums Test	0.557894	Success
Random Excursions Test	0.459642	Success
Random Excursions Variant Test	0.254816	Success

.

7. Hardware Implementation Analysis

7.1. Comparison of Implementation Results

Lightweight cryptography is a cryptosystem with strict requirements regarding cost, energy consumption, and storage. It can be used in smart cards, radio frequency identification tags, wireless sensors, and personal digital assistant terminals. Therefore, how to use hardware and software to achieve system performance is the primary consideration in order to meet the above security requirements. Lightweight cryptography includes hardware-oriented design, software-oriented design, and hardware-software platform design. In this paper, we use hardware-oriented design to implement the Logic lightweight stream cipher. There are many metrics for hardware implementation, such as area, energy consumption, throughput, longest path, clock cycle, and so on.

Table 5. Comparison with other lightweight ciphers.

Cipher	Key Size (bits)	Area Size (GEs)	Throughput (Kb/s)	Platform
Trivium [6]	80	2580	100	0.13μmCMOS
DES [37]	56	2309	100	0.18μmCMOS
Grain-v1 [8]	80	1294	100	0.13μmCMOS
Lizard [4]	120	1161	100	0.18μmCMOS
HIGHT [37]	128	3048	100	0.25μmCMOS
Mickey 2.0 [7]	80	3188	100	0.13μmCMOS
Logic (Our work)	80	2258	100	0.13μmCMOS

shows the performance comparison of the Logic stream cipher and several other lightweight stream ciphers.

7.2. Throughtput Analysis

Logic stream cipher uses two NFSRs and a chaotic sequence. After initialization, all of the components work under the drive of the same clock. After compiling, the throughput of the system can reach 78.98 Kbps at 100 kHz.

8. Security Evaluation

8.1. Algebraic Attack

A deterministic cipher cryptanalysis method was proposed at the EUROCRYPT2003 conference [38], which is called algebraic attack. The main idea of this method is to define the security of a cryptographic algorithm as solving a set of overdetermined multivariable nonlinear equations. The complexity of algebraic attack is mainly determined by the complexity of establishing large-scale multivariable nonlinear equations and solving the equations. The problem of solving large-scale multivariable nonlinear equations is an important problem in computational algebra. A new cryptographic criterion of boolean function, namely algebraic immunity, is proposed, with the development of algebraic attack. See [39,40] for research progress on algebraic immunity. The system can continuously improve the nonlinear degree of cryptography algorithm through self-feedback iterative update since the cipher here uses two NFSR in this paper, which greatly increases the difficulty for attackers to establish and solve nonlinear equations, which makes it difficult for algebraic attacks to obtain better analysis results for this system.

8.2. TMDTO Attack

In 2000, Biryukov, Shamir and Wagner [41] proposed a new time/memory/data trade-off (TMDTO) attack against cipher cryptography. TMDTO has become an important method in restoring the internal state of cipher cryptography. Set as the mapping of the bit internal state to the output continuous bit key stream, the problem of restoring the internal state can be transformed into the problem of inverting a one-way function using the TMDTO method. The internal state restoration attack is a cipher text only attack method. The target of the attack is to restore the the internal state of the sequence cipher at a certain moment in the key flow generation stage. The internal state at subsequent moments can be calculated by the state update function according to the internal state at this moment, thus predicting the key flow. If the state update function is reversible, the internal state of the previous moment can be obtained, or even the key can be restored. In fact, Grain v1 [42] and MICKEY 1.0 [43] all suffered from internal state restoration attacks that were based on TMDTO. Among them, the analysis results of MICKEY 1.0 directly led to the design to improve the algorithm to get MICKEY 2.0. The secret key space of each NFSR is $2^{40}$ since the system is composed of two independent NFSRs, so the secret key space of the whole system is $2^{80}$. Assuming that each key generates a $2^{16}$ key stream, in the first step of the attack, if an attacker can obtain a $2^{15}$ key stream, then the attacker will look for conflicts in the table. Here is the probability that the attacker cannot find the conflict. The calculation process is as follows.

$${\left(1-\frac{2^{15}}{2^{80}}\right)}^{2^{15}}.$$

(18)

The attacker can repeat the first two steps to obtain a different key, then he can find the probability of the conflict calculation process, as follows.

$$1-{\left({\left(1-\frac{2^{15}}{2^{80}}\right)}^{2^{15}}\right)}^{2^{50}}\approx 0.63.$$

(19)

The amount of data of this attack is $2^{16}\times 2^{50}\times 80=2^{72.3}$, and the computational complexity is $2^{16}\times 2^{50}=2^{66}$. If the cryptographic system can generate a stream of $2^{16}$ key stream under each secret key, it can resist certain TMDTO attacks.

8.3. Fault Attack

Fault attack refers to the introduction of fault in cryptography algorithm in cryptography chip device, which results in wrong results of the cryptography device, and the analysis of the wrong results to obtain the key. It is known that such attacks have been successfully applied to Grain ciphers [44]. It requires that the attacker insert a single bit error in the NFSR during the initialization phase, so that the attacker can reset the password and obtain the correct key flow. This kind of error attack can be prevented if mirror image or mask is used in the hardware, since the two-stage NFSR is adopted in the hardware design of this system [45].

8.4. Linear Approximation Attack

As mentioned in reference [46], the Grain cipher cryptography will resist the linear approximation attack if the NFSR used and the output function of the cryptography system have high nonlinearity and good elasticity. The NFSRs and system output function that were selected in this paper have high nonlinearity and good elasticity. Therefore, the system can resist certain linear approximation attacks.

8.5. Correlation Attack

Complexity theory can be used to analyze the computational complexity of cryptography and algorithms. The linear complexity of a periodic random time series is similar to its periodic length. Logic stream ciphers use two NFSRs, a chaotic system, and three multiplexers. According to empirical tests, the approximate period length should be above $O(2^{80})$. Therefore, it can be estimated that its linear complexity is also above $O(2^{80})$, and it can be considered as a lifetime secret key. In terms of related attacks, since NFSR-2 performs XOR calculations with NFSR-1 through feedback function $g(x)$, it is inferred that all the bits in NFSR-1 are balanced, and it can be assumed that NFSR-2 is independent of each bit that is generated in NFSR-1. In the aspect of algebraic attack, the filter function $h(x)$ here is a five-variable four-order balanced boolean function. Due to the use of two sets of NFSRs, and the input of the filter being exclusive or obtained from NFSR-1, NFSR-2, and chaotic sequence, the system is greatly improved and the system can resist correlation attack.

9. Conclusions

In this paper, the chaotic system is added to the lightweight stream cipher cryptosystem for the first time. Digitizing the Logistic chaotic sequence and combining it with NFSRs and multiplexers generate a new lightweight stream cipher cryptosystem. The tests of permutation entropy, approximate entropy, and information entropy of the cipher show that the system has good complexity. The NIST statistical test shows that the stream cipher that is generated by the system has good statistical characteristics. The analysis of hardware resource and throughput proves that the design can be effectively applied in resource-constrained devices or environments for encryption.