Fixed Coeficient A(α) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations
Abstract
1. Introduction
2. Derivation of the Method
2.1. Order of the Method
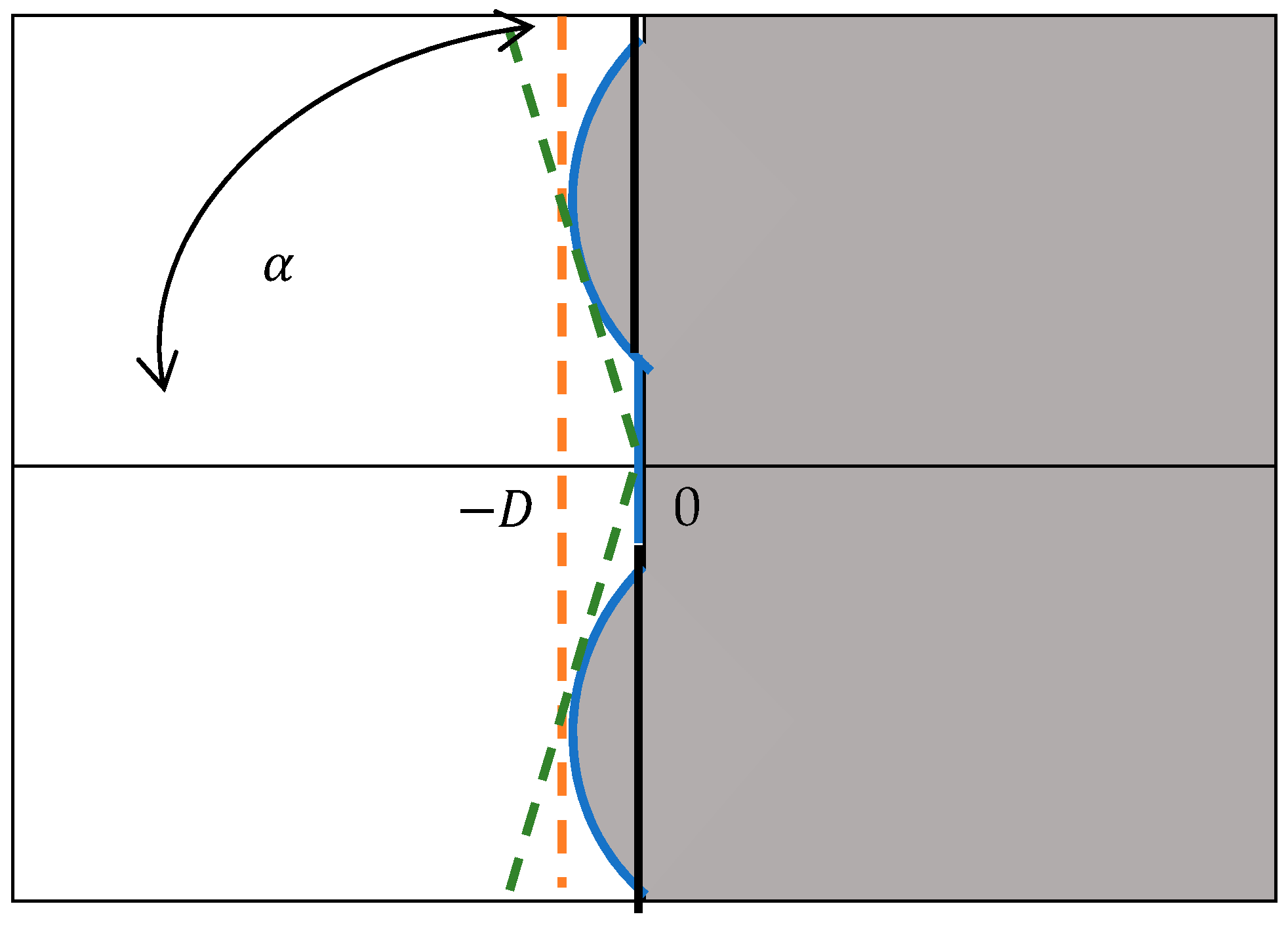
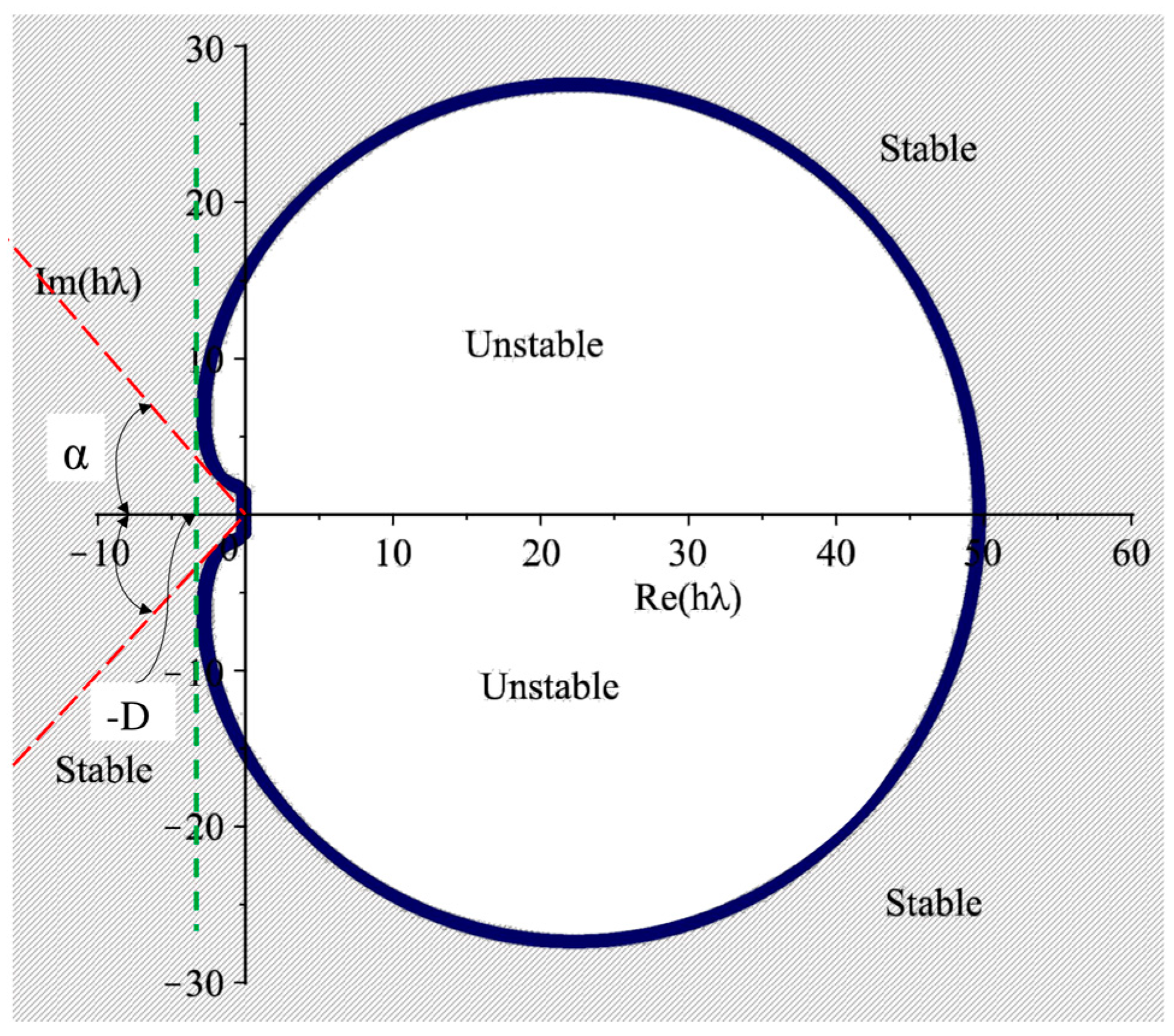
3. Stability Analysis
3.1. Zero Stability
3.2. Stability Region
3.3. Convergence of the Method
4. Implementation
- Step 1.
- Predict: are developed explicitly.
- Step 2.
- Evaluate:
- Step 3.
- Correct: by
- Step 4.
- Evaluate:
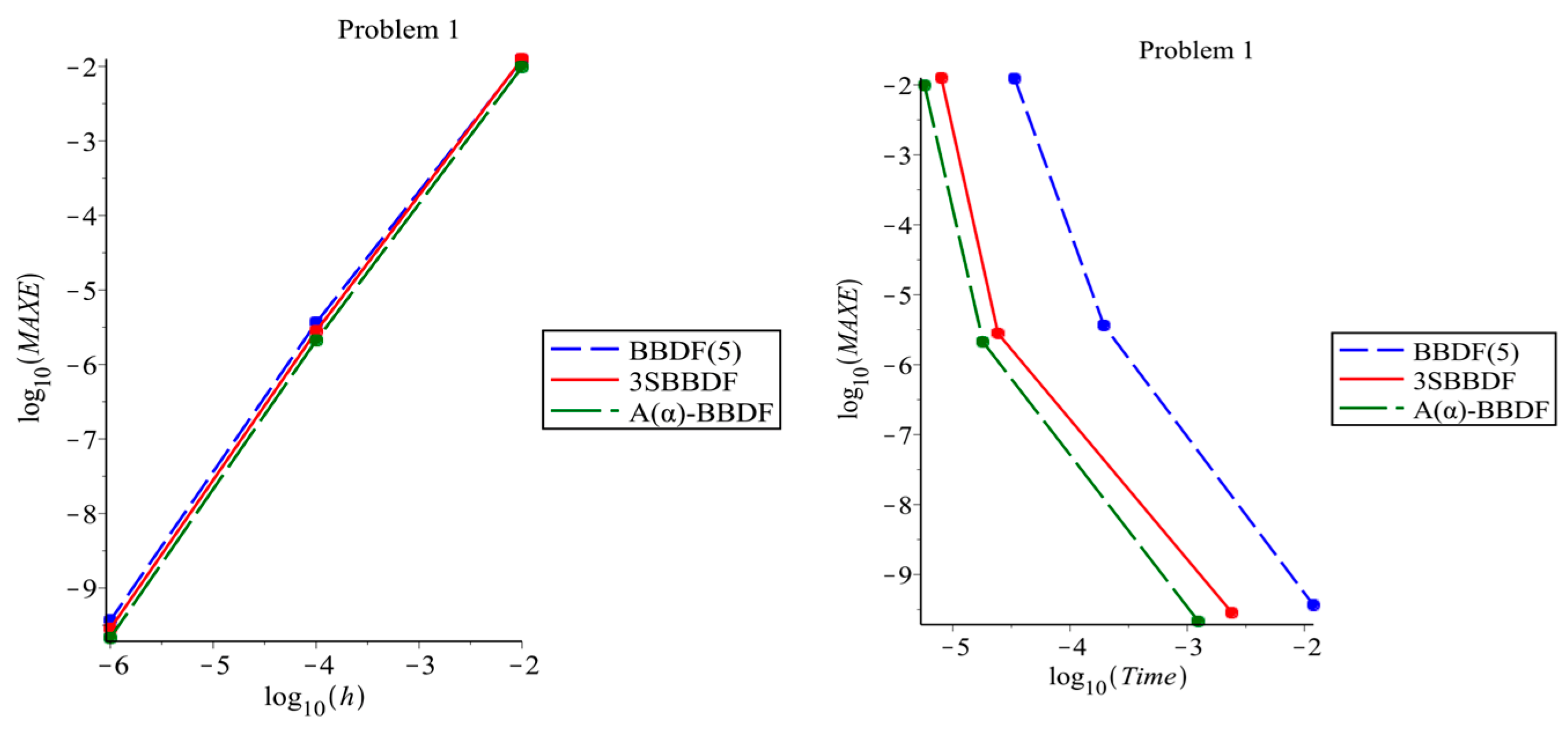
5. Numerical Results
| BBDF(5) | : | Fifth order Block Backward Differentiation Formula in [12] |
| 3SBBDF | : | 3-point Superclass of Block Backward Differentiation Formula in [14] |
| -BBDF | : | New 3-point BBDF |
| NS | : | Number of steps |
| : | Step size | |
| T | : | Computing time in seconds |
| MAXE | : | Maximum error |
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bui, T.D. Solving stiff differential equations in the simulation of physical systems. Simulation 1981, 37, 37–46. [Google Scholar] [CrossRef]
- Aiken, J.C. Stiff Review. In Proceedings of the International Conference on Stiff Computation, Park City, UT, USA, 12–14 April 1982. [Google Scholar]
- Chu, M.T.; Hamilton, H. Parallel solution of ODE’s by multi-block methods. SIAM J. Sci. Stat. Comput. 1987, 8, 342–353. [Google Scholar] [CrossRef]
- Aceto, L.; Trigiante, D. On the A-stable methods in the GBDF class. Nonlinear Anal. Real World Appl. 2002, 3, 9–23. [Google Scholar] [CrossRef]
- Dahlquist, G. A Special Stability Problem for Linear Multistep Methods. BIT 1963, 3, 27–43. [Google Scholar] [CrossRef]
- Majid, Z.A.; Suleiman, M.B.; Ismail, F.; Othman, M. 2-Point Implicit Block One-Step Method Half Gauss-Seidel For Solving First Order Ordinary Differential Equations. Matematika 2003, 19, 91–100. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. Implicit r-point block backward differentiation formula for solving first-order stiff ODEs. Appl. Math. Comput. 2007, 186, 558–565. [Google Scholar] [CrossRef]
- Majid, Z.A.; Suleiman, M.; Omar, Z. 3-Point Implicit Block Method for solving ordinary differential equations. Bull. Malays. Math. Sci. Soc. Second Ser. 2006, 29, 29–31. [Google Scholar]
- Ismail, F.; Ken, Y.L.; Othman, M. Explicit and implicit 3-point block methods for solving special second order ordinary differential equations directly. Int. J. Math. Anal. 2009, 3, 239–254. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. 2-point block predictor-corrector of backward differentiation formulas for solving second order ordinary differential equations directly. Chiang Mai J. Sci. 2012, 39, 502–510. [Google Scholar]
- Ibrahim, Z.B.; Othman, K.I.; Suleiman, M. Derivation of diagonally implicit block backward differentiation formulas for solving stiff initial value problems. Math. Probl. Eng. 2015, 2015, 179231. [Google Scholar] [CrossRef]
- Shampine, L.F.; Watts, H.A. Block implicit one-step methods. Math. Comp. 1969, 23, 731–740. [Google Scholar] [CrossRef]
- Nasir, N.A.A.; Ibrahim, Z.B.; Othman, K.I.; Suleiman, M.B. Numerical Solution of First Order Ordinary Differential Equations Using Fifth Order Block Backward Differentiation Formulas. Sains Malays. 2012, 41, 489–492. [Google Scholar]
- Asnor, A.I.; Yatim, S.A.M.; Ibrahim, Z.B. Formulation of Modified Variable Step Block Backward Differentiation Formulae for Solving Stiff Ordinary Differential Equations. Indian J. Sci. Technol. 2017, 10, 1–7. [Google Scholar] [CrossRef][Green Version]
- Iskandar Shah, M.Z.; Ibrahim, Z.B. Convergence Properties of pth Order Diagonally Implicit Block Backward Differentiation Formulas. Chiang Mai J. Sci. 2018, 45, 601–606. [Google Scholar]
- Musa, H.; Suleiman, M.B.; Senu, N. Fully Implicit 3-point Block Extended Backward Differentiation Formulas for Stiff Initial value Problems. Appl. Math. Sci. 2012, 6, 4211–4228. [Google Scholar]
- Babaginda, B.; Musa, H.; Ibrahim, L.K. A New Numerical Method For Solving Stiff Initial Value Problems. Fluid Mech. Open Access 2016, 3, 1–5. [Google Scholar]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1973; pp. 154–196. [Google Scholar]
- Fatunla, S.O. Block methods for second order ODEs. Int. J. Comput. Math. 1991, 41, 55–63. [Google Scholar] [CrossRef]
- Butcher, J.C. Forty-Five Years of A-stability. J. Numer. Anal. Ind. Appl. Math. 2009, 4, 1–9. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 7th ed.; Brooks/Cole: Belmont, CA, USA, 2001. [Google Scholar]
- Alvarez, J.; Rojo, J. An improved class of generalized Runge- Kutta methods for stiff problems. I. The scalar case. Appl. Math. Comput. 2002, 130, 537–560. [Google Scholar] [CrossRef]
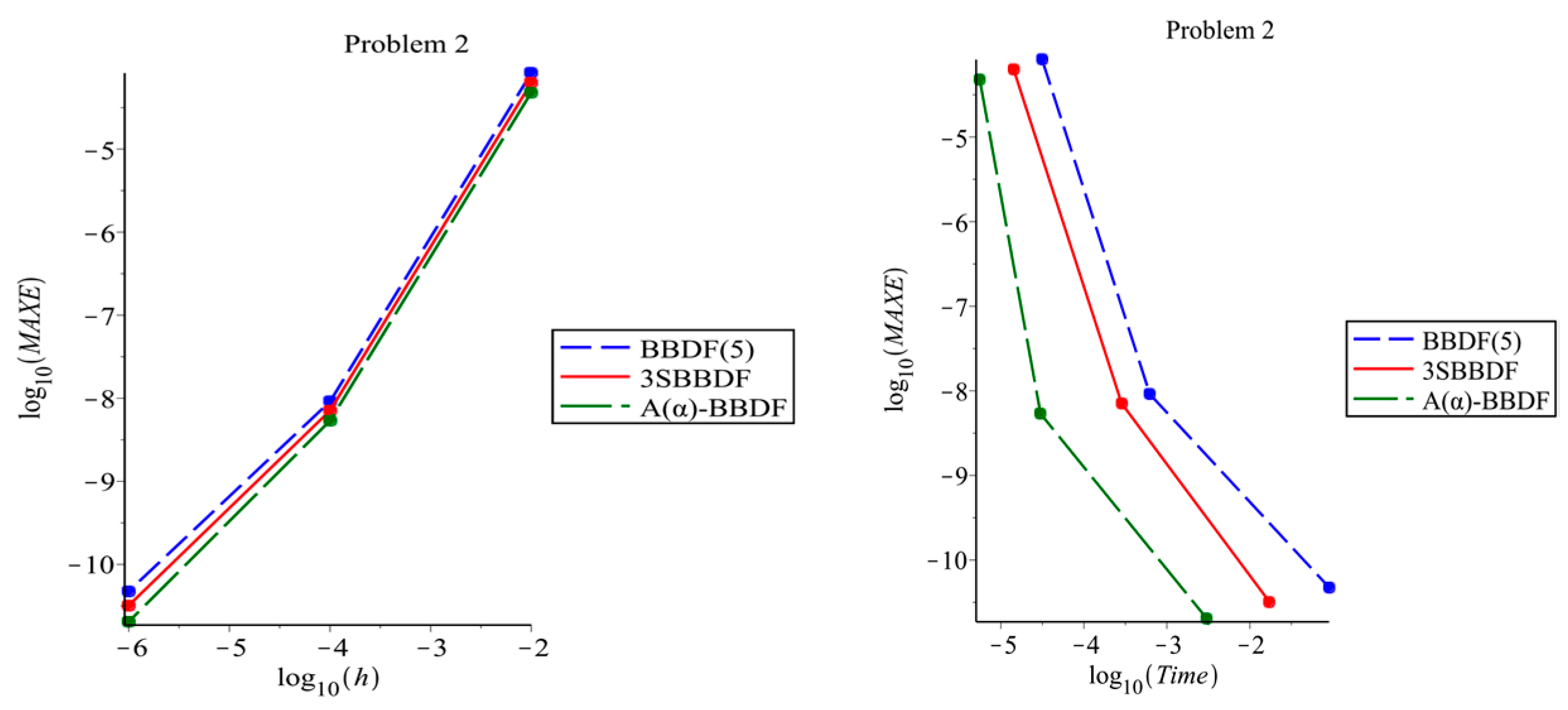
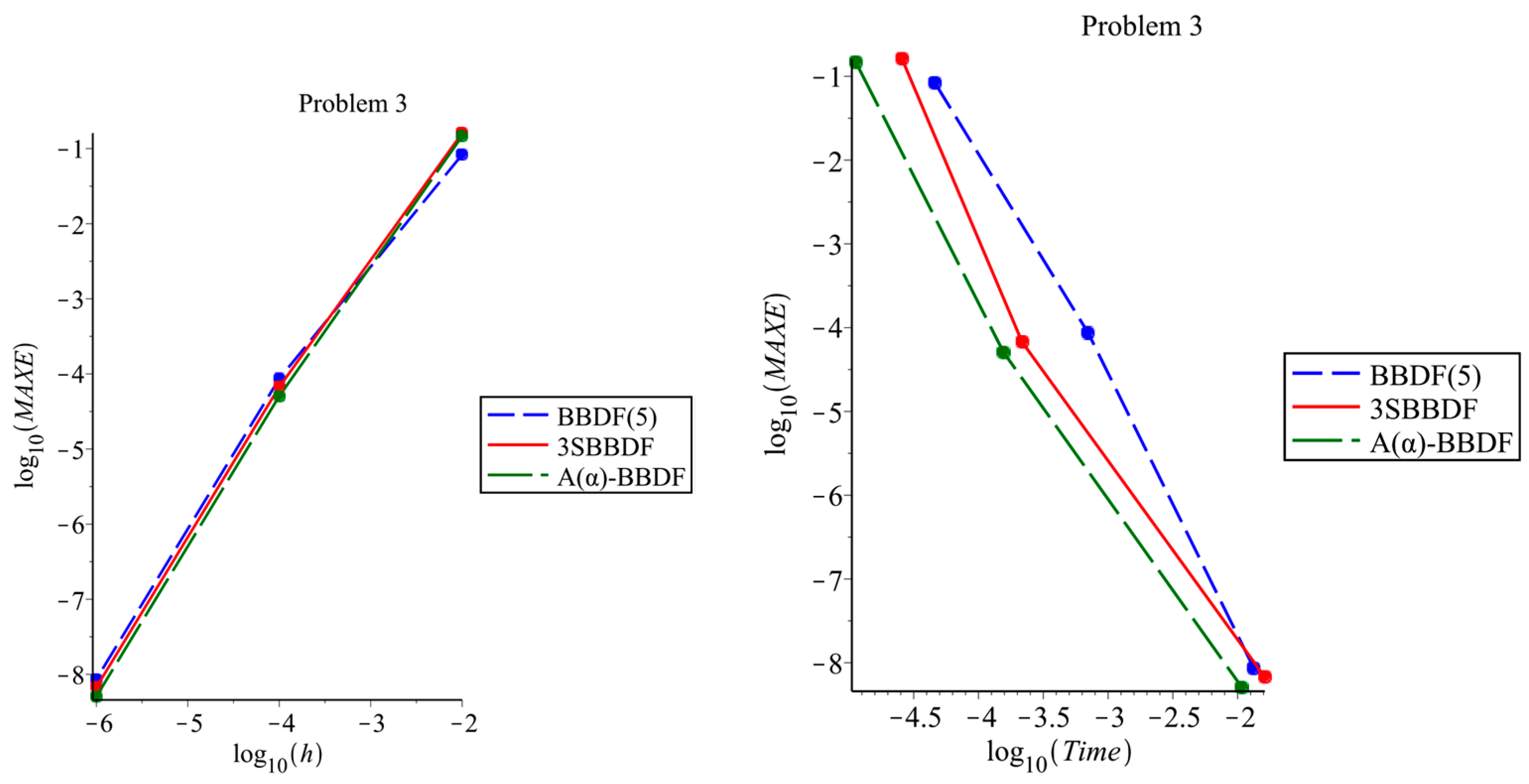
| 1 | ||||||||
| 1 | ||||||||
| 1 |
| Method | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 50 | 1.22077 (02) | 3.38123 × 10−5 | |
| 3SBBDF | 34 | 1.25970 (02) | 7.97504 × 10−6 | |
| -BBDF | 34 | 9.80872 (03) | 5.74054 × 10−6 | |
| BBDF(5) | 5,000 | 3.61596 (06) | 1.95107 × 10−4 | |
| 3SBBDF | 3334 | 2.78963 (06) | 2.43208 × 10−5 | |
| -BBDF | 3334 | 2.10240 (06) | 1.81288 × 10−5 | |
| BBDF(5) | 500,000 | 3.65378 (10) | 1.19412 × 10−2 | |
| 3SBBDF | 333,334 | 2.84503 (10) | 2.40965 × 10−3 | |
| -BBDF | 333,334 | 2.15115 (10) | 1.24343 × 10−3 |
| Methods | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 250 | 8.22989 (05) | 3.13736 × 10−5 | |
| 3SBBDF | 167 | 6.27205 (05) | 1.42650 × 10−5 | |
| -BBDF | 167 | 4.80218 (05) | 5.55058 × 10−6 | |
| BBDF(5) | 25,000 | 9.13120 (09) | 6.23244 × 10−4 | |
| 3SBBDF | 16,667 | 7.10257 (09) | 2.84914 × 10−4 | |
| -BBDF | 16,667 | 5.36673 (09) | 3.00451 × 10−5 | |
| BBDF(5) | 2,500,000 | 4.75320 (11) | 8.99541 × 10−2 | |
| 3SBBDF | 1,666,667 | 3.20597 (11) | 1.71905 × 10−2 | |
| -BBDF | 1,666,667 | 2.04591 (11) | 3.01268 × 10−3 |
| Methods | NS | MAXE | TIME | |
|---|---|---|---|---|
| BBDF(5) | 50 | 8.31685 (02) | 4.61774 × 10−5 | |
| 3SBBDF | 34 | 1.60854 (01) | 2.57089 × 10−5 | |
| -BBDF | 34 | 1.46790 (01) | 1.13065 × 10−5 | |
| BBDF(5) | 5000 | 8.63685 (05) | 7.02594 × 10−4 | |
| 3SBBDF | 3334 | 6.71328 (05) | 2.17249 × 10−4 | |
| -BBDF | 3334 | 5.06905 (05) | 1.56282 × 10−4 | |
| BBDF(5) | 500,000 | 8.64038 (09) | 1.33371 × 10−2 | |
| 3SBBDF | 333,334 | 6.72941 (09) | 1.62222 × 10−2 | |
| -BBDF | 333,334 | 5.08898 (09) | 1.07846 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, Z.B.; Mohd Noor, N.; Othman, K.I. Fixed Coeficient A(α) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry 2019, 11, 846. https://doi.org/10.3390/sym11070846
Ibrahim ZB, Mohd Noor N, Othman KI. Fixed Coeficient A(α) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry. 2019; 11(7):846. https://doi.org/10.3390/sym11070846
Chicago/Turabian StyleIbrahim, Zarina Bibi, Nursyazwani Mohd Noor, and Khairil Iskandar Othman. 2019. "Fixed Coeficient A(α) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations" Symmetry 11, no. 7: 846. https://doi.org/10.3390/sym11070846
APA StyleIbrahim, Z. B., Mohd Noor, N., & Othman, K. I. (2019). Fixed Coeficient A(α) Stable Block Backward Differentiation Formulas for Stiff Ordinary Differential Equations. Symmetry, 11(7), 846. https://doi.org/10.3390/sym11070846





