A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested
Abstract
1. Introduction
2. Materials and Methods
3. Proposed Outlier Detection Statistic
4. Simulation Study
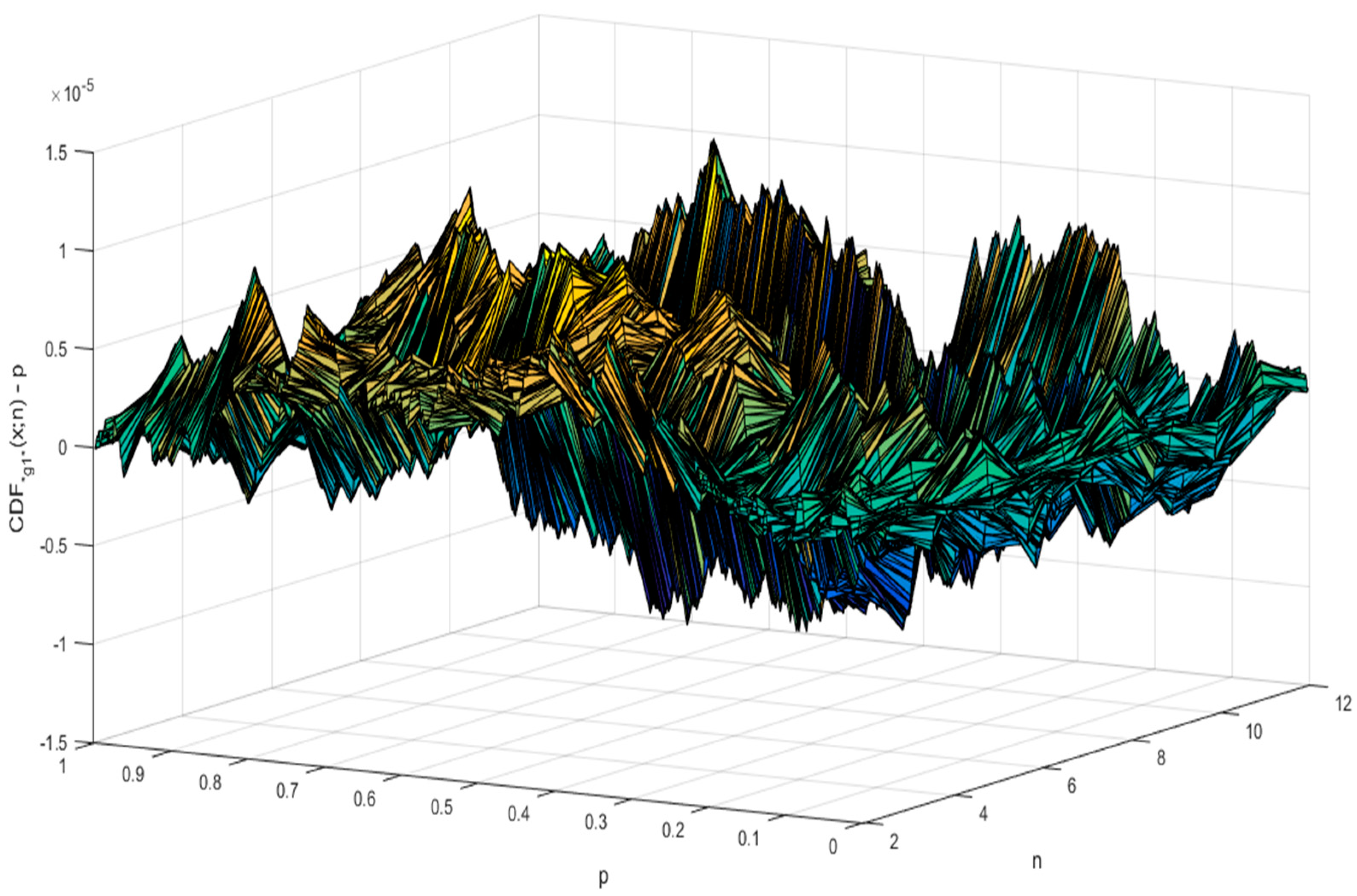
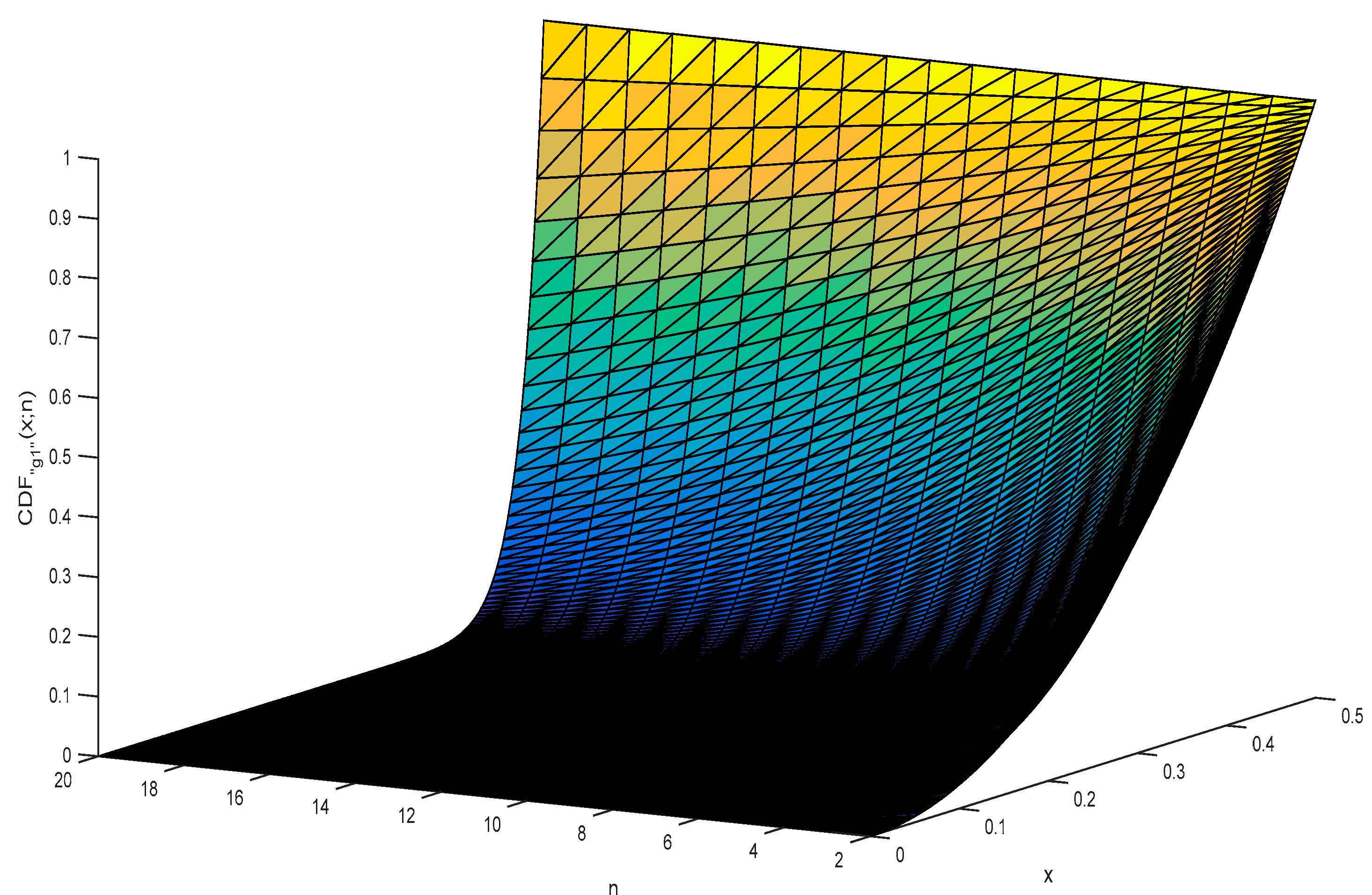
5. The Analytical Formula of CDF for g1
6. Simulation Results for the Distribution of the “g1” Statistic
7. from “g1” Statistic to “g1” Confidence Intervals for the Extreme Values
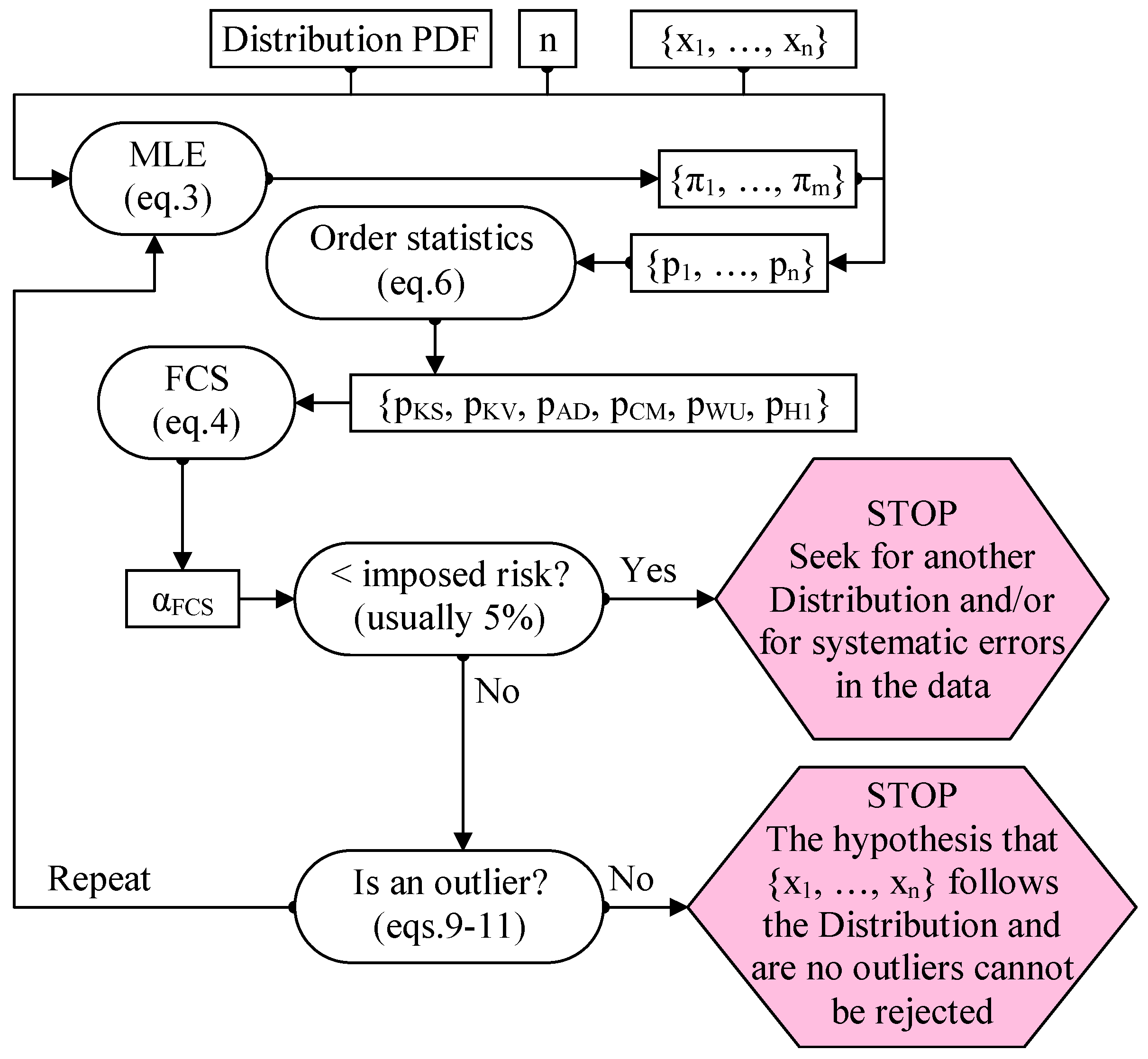
8. Proposed Procedure for Detecting the Outliers
9. Second Simulation Assessing “Grubbs” and “g1” Outlier Detection Alternatives
10. Going Further with the Outlier Analysis
11. Further Discussion
12. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Gauss, C.F. Theoria Motus Corporum Coelestium; (Translated in 1857 as “Theory of Motion of the Heavenly Bodies Moving about the Sun in Conic Sections” by C. H. Davis. Little, Brown: Boston. Reprinted in 1963 by Dover: New York); Perthes et Besser: Hamburg, Germany, 1809; pp. 249–259. [Google Scholar]
- Tippett, L.H.C. The extreme individuals and the range of samples taken from a normal population. Biometrika 1925, 17, 151–164. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest and smallest member of a sample. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Thompson, W.R. On a criterion for the rejection of observations and the distribution of the ratio of the deviation to the sample standard deviation. Ann. Math. Stat. 1935, 6, 214–219. [Google Scholar] [CrossRef]
- Pearson, E.; Sekar, C.C. The efficiency of the statistical tools and a criterion for the rejection of outlying observations. Biometrika 1936, 28, 308–320. [Google Scholar] [CrossRef]
- Grubbs, F.E. Sample criteria for testing outlying observations. Ann. Math. Stat. 1950, 21, 27–58. [Google Scholar] [CrossRef]
- Grubbs, F.E. Procedures for detecting outlying observations in samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Nooghabi, M.; Nooghabi, H.; Nasiri, P. Detecting outliers in gamma distribution. Commun. Stat. Theory Methods 2010, 39, 698–706. [Google Scholar] [CrossRef]
- Kumar, N.; Lalitha, S. Testing for upper outliers in gamma sample. Commun. Stat. Theory Methods 2012, 41, 820–828. [Google Scholar] [CrossRef]
- Lucini, M.; Frery, A. Comments on “Detecting Outliers in Gamma Distribution” by M. Jabbari Nooghabi et al. (2010). Commun. Stat. Theory Methods 2017, 46, 5223–5227. [Google Scholar] [CrossRef]
- Hartley, H. The range in random samples. Biometrika 1942, 32, 334–348. [Google Scholar] [CrossRef]
- Bardet, J.-M.; Dimby, S.-F. A new non-parametric detector of univariate outliers for distributions with unbounded support. Extremes 2017, 20, 751–775. [Google Scholar] [CrossRef]
- Gosset, W. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar]
- Jäntschi, L.; Bolboacă, S.-D. Computation of probability associated with Anderson-Darling statistic. Mathematics 2018, 6, 88. [Google Scholar] [CrossRef]
- Fisher, R. On an Absolute Criterion for Fitting Frequency Curves. Messenger Math. 1912, 41, 155–160. [Google Scholar]
- Fisher, R. Questions and answers #14. Am. Stat. 1948, 2, 30–31. [Google Scholar]
- Bolboacă, S.D.; Jäntschi, L.; Sestraș, A.F.; Sestraș, R.E.; Pamfil, D.C. Supplementary material of ’Pearson-Fisher chi-square statistic revisited’. Information 2011, 2, 528–545. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.D. Performances of Shannon’s Entropy Statistic in Assessment of Distribution of Data. Ovidius Univ. Ann. Chem. 2017, 28, 30–42. [Google Scholar] [CrossRef]
- Davis, P.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA, 1975; pp. 51–198. [Google Scholar]
- Pearson, K. Note on Francis Gallon’s problem. Biometrika 1902, 1, 390–399. [Google Scholar]
- Cramér, H. On the composition of elementary errors. Scand. Actuar. J. 1928, 1, 13–74. [Google Scholar] [CrossRef]
- Von Mises, R.E. Wahrscheinlichkeit, Statistik und Wahrheit; Julius Springer: Berlin, Germany, 1928; pp. 100–138. [Google Scholar]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. Giornale dell’Istituto Italiano degli Attuari 1933, 4, 83–91. [Google Scholar]
- Kolmogorov, A. Confidence Limits for an Unknown Distribution Function. Ann. Math. Stat. 1941, 12, 461–463. [Google Scholar] [CrossRef]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A Test of Goodness-of-Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Kuiper, N.H. Tests concerning random points on a circle. Proc. Koninklijke Nederlandse Akademie van Wetenschappen Series A 1960, 63, 38–47. [Google Scholar] [CrossRef]
- Watson, G.S. Goodness-Of-Fit Tests on a Circle. Biometrika 1961, 48, 109–114. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. A 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Jäntschi, L. Distribution fitting 1. Parameters estimation under assumption of agreement between observation and model. Bull. UASVM Hortic. 2009, 66, 684–690. [Google Scholar]
- Jäntschi, L.; Bolboacă, S.D. Distribution fitting 2. Pearson-Fisher, Kolmogorov-Smirnov, Anderson-Darling, Wilks-Shapiro, Kramer-von-Misses and Jarque-Bera statistics. Bull. UASVM Hortic. 2009, 66, 691–697. [Google Scholar]
- Bolboacă, S.D.; Jäntschi, L. Distribution fitting 3. Analysis under normality assumption. Bull. UASVM Hortic. 2009, 66, 698–705. [Google Scholar]
- Liu, K.; Chen, Y.Q.; Domański, P.D.; Zhang, X. A novel method for control performance assessment with fractional order signal processing and its application to semiconductor manufacturing. Algorithms 2018, 11, 90. [Google Scholar] [CrossRef]
- Paiva, J.S.; Ribeiro, R.S.R.; Cunha, J.P.S.; Rosa, C.C.; Jorge, P.A.S. Single particle differentiation through 2D optical fiber trapping and back-scattered signal statistical analysis: An exploratory approach. Sensors 2018, 18, 710. [Google Scholar] [CrossRef] [PubMed]
- Teunissen, P.J.G.; Imparato, D.; Tiberius, C.C.J.M. Does RAIM with correct exclusion produce unbiased positions? Sensors 2017, 17, 1508. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Liu, L.; Qiu, X.; Lei, B. Fast vessel detection in Gaofen-3 SAR images with ultrafine strip-map mode. Sensors 2017, 17, 1578. [Google Scholar] [CrossRef] [PubMed]
- Vergura, S.; Carpentieri, M. Statistics to detect low-intensity anomalies in PV systems. Energies 2018, 11, 30. [Google Scholar] [CrossRef]
- Chen, L.; He, J.; Sazzed, S.; Walker, R. An investigation of atomic structures derived from X-ray crystallography and cryo-electron microscopy using distal blocks of side-chains. Molecules 2018, 23, 610. [Google Scholar] [CrossRef] [PubMed]
- Bolboacă, S.D.; Jäntschi, L. The effect of leverage and influential on structure-activity relationships. Comb. Chem. High Throughput Screen. 2013, 16, 288–297. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Porta, A.; Nollo, G.; Javorka, M. Information decomposition in multivariate systems: Definitions, implementation and application to cardiovascular networks. Entropy 2017, 19, 5. [Google Scholar] [CrossRef]
- Li, G.; Wang, J.; Liang, J.; Yue, C. Application of sliding nest window control chart in data stream anomaly detection. Symmetry 2018, 10, 113. [Google Scholar] [CrossRef]
- Paolella, M.S. Stable-GARCH models for financial returns: Fast estimation and tests for stability. Econometrics 2016, 4, 25. [Google Scholar] [CrossRef]
| Sample statistic (G) | Associated probability (pG = 1-αG) | Equation |
|---|---|---|
| (1) | ||
| (2) |
| Parameter | Meaning | Setting |
|---|---|---|
| n | sample size of the observed | from 2 to 12 |
| m | sample size of the MC simulation | 108 |
| p | control points for the probability | 999 |
| resa | internal resamples (repetitions) | 10 |
| repe | external repetitions | 7 |
| n | SE | ||||
|---|---|---|---|---|---|
| 2 | 2.9 × 10−6 | −7.9 × 10−6 | at p = 0.694 | 5.7 × 10−6 | at p = 0.427 |
| 3 | 5.6 × 10−6 | −1.2 × 10−5 | at p = 0.787 | 1.6 × 10−6 | at p = 0.118 |
| 4 | 2.2 × 10−6 | −5.6 × 10−6 | at p = 0.234 | 3.7 × 10−6 | at p = 0.613 |
| 5 | 6.0 × 10−6 | −1.2 × 10−5 | at p = 0.546 | 2.3 × 10−6 | at p = 0.080 |
| 6 | 3.5 × 10−6 | −5.8 × 10−6 | at p = 0.797 | 9.2 × 10−6 | at p = 0.196 |
| 7 | 5.0 × 10−6 | −9.6 × 10−6 | at p = 0.777 | 3.8 × 10−6 | at p = 0.035 |
| 8 | 4.2 × 10−6 | −8.4 × 10−6 | at p = 0.675 | 3.9 × 10−6 | at p = 0.948 |
| 9 | 3.3 × 10−6 | −9.1 × 10−6 | at p = 0.269 | 7.9 × 10−6 | at p = 0.689 |
| 10 | 2.8 × 10−6 | −6.4 × 10−6 | at p = 0.443 | 6.6 × 10−6 | at p = 0.652 |
| Step | Results |
|---|---|
| Dataset (given for convenience) | 4.151; 4.401; 4.421; 4.601; 4.941; 5.021; 5.023; 5.150; 5.180; 5.295; 5.301; 5.311; 5.311; 5.335; 5.343; 5.404; 5.421; 5.447; 5.452; 5.452; 5.481; 5.504; 5.517; 5.537; 5.537; 5.551; 5.561; 5.572; 5.577; 5.577; 5.627; 5.637; 5.637; 5.667; 5.667; 5.671; 5.677; 5.677; 5.691; 5.717; 5.743; 5.751; 5.757; 5.761; 5.767; 5.767; 5.787; 5.811; 5.817; 5.827; 5.867; 5.897; 5.897; 5.904; 5.943; 5.957; 5.957; 5.987; 6.041; 6.047; 6.047; 6.047; 6.057; 6.077; 6.091; 6.111; 6.117; 6.117; 6.137; 6.137; 6.137; 6.137; 6.137; 6.142; 6.167; 6.177; 6.177; 6.177; 6.204; 6.207; 6.221; 6.227; 6.227; 6.231; 6.237; 6.257; 6.267; 6.267; 6.267; 6.291; 6.304; 6.327; 6.357; 6.357; 6.367; 6.367; 6.371; 6.427; 6.457; 6.467; 6.487; 6.497; 6.511; 6.517; 6.517; 6.523; 6.532; 6.547; 6.583; 6.587; 6.587; 6.587; 6.607; 6.611; 6.647; 6.647; 6.647; 6.647; 6.647; 6.657; 6.657; 6.671; 6.671; 6.677; 6.677; 6.677; 6.697; 6.704; 6.717; 6.717; 6.737; 6.737; 6.737; 6.747; 6.767; 6.767; 6.767; 6.797; 6.827; 6.857; 6.867; 6.897; 6.897; 6.937; 6.937; 6.957; 6.961; 6.997; 7.027; 7.027; 7.027; 7.057; 7.071; 7.087; 7.087; 7.117; 7.117; 7.117; 7.121; 7.123; 7.147; 7.151; 7.177; 7.177; 7.187; 7.187; 7.207; 7.207; 7.207; 7.211; 7.247; 7.247; 7.277; 7.277; 7.277; 7.281; 7.304; 7.307; 7.307; 7.321; 7.337; 7.367; 7.391; 7.427; 7.441; 7.467; 7.516; 7.527; 7.527; 7.557; 7.567; 7.592; 7.627; 7.627; 7.657; 7.657; 7.717; 7.747; 7.751; 7.933; 8.007; 8.164; 8.423; 8.683; 9.143; 9.603 |
| For n = 206 calculate the probability that the extreme values contain an outlier by using Equation (13) | At α = 5% risk being in error InvCDF“g1”(1-0.05; 206) = 0.498755 |
| Calculate the critical probabilities for the extreme values by using Equations (9) and (10) | g1 = 0.498755 → |0.5 - pmin/max| = 0.498755 → 1 - 2pmin/max = ± 0.99751 → pmin = 0.0001245; pmax = 0.9998755 |
| Estimate the parameters of the distribution fitting the dataset (distribution: Gauss-Laplace; μ - location parameter; σ - scale parameter; k - shape parameter) | Initial estimates (from a hybrid CM & MLE method): μ = 6.4806; σ = 0.83076; k = 1.4645; MLE estimates (by applying eq.3): μ = 6.47938; σ = 0.82828; k = 1.79106; |
| Calculate the lower and the upper bound for the extreme values by using InvCDF of the distribution fitting the data (Equation (15)) | InvCDF“GL”(0.0001245; μ = 6.47938, σ = 0.82828, k = 1.79106) = 3.2409 InvCDF“GL”(0.9998755; μ = 6.47938, σ = 0.82828, k = 1.79106) = 9.7178 |
| Make the conclusion regarding the outliers | Since the smallest value in the dataset is 4.151 (> 3.24) and the largest value is 9.603 (< 9.71), at 5% risk being in error there are no outliers in the dataset on the assumption that data follows the Gauss-Laplace distribution |
| Step | Action (step 0 is setting the dataset; α ← 0.05) |
|---|---|
| 1 | Estimate (with MLE, Equation (3)) parameters (μ, σ) of the Normal distribution; calculate the associated CDFs (Equation (18)) |
| 2 | Calculate the order statistics, their associated risks being in error, FCS and pFCS (Equations (6) and (4)) |
| 3 | For n and α calculate the confidence intervals for the extreme values by using (a) Equation (6) and (17) and (b) Equation (19) |
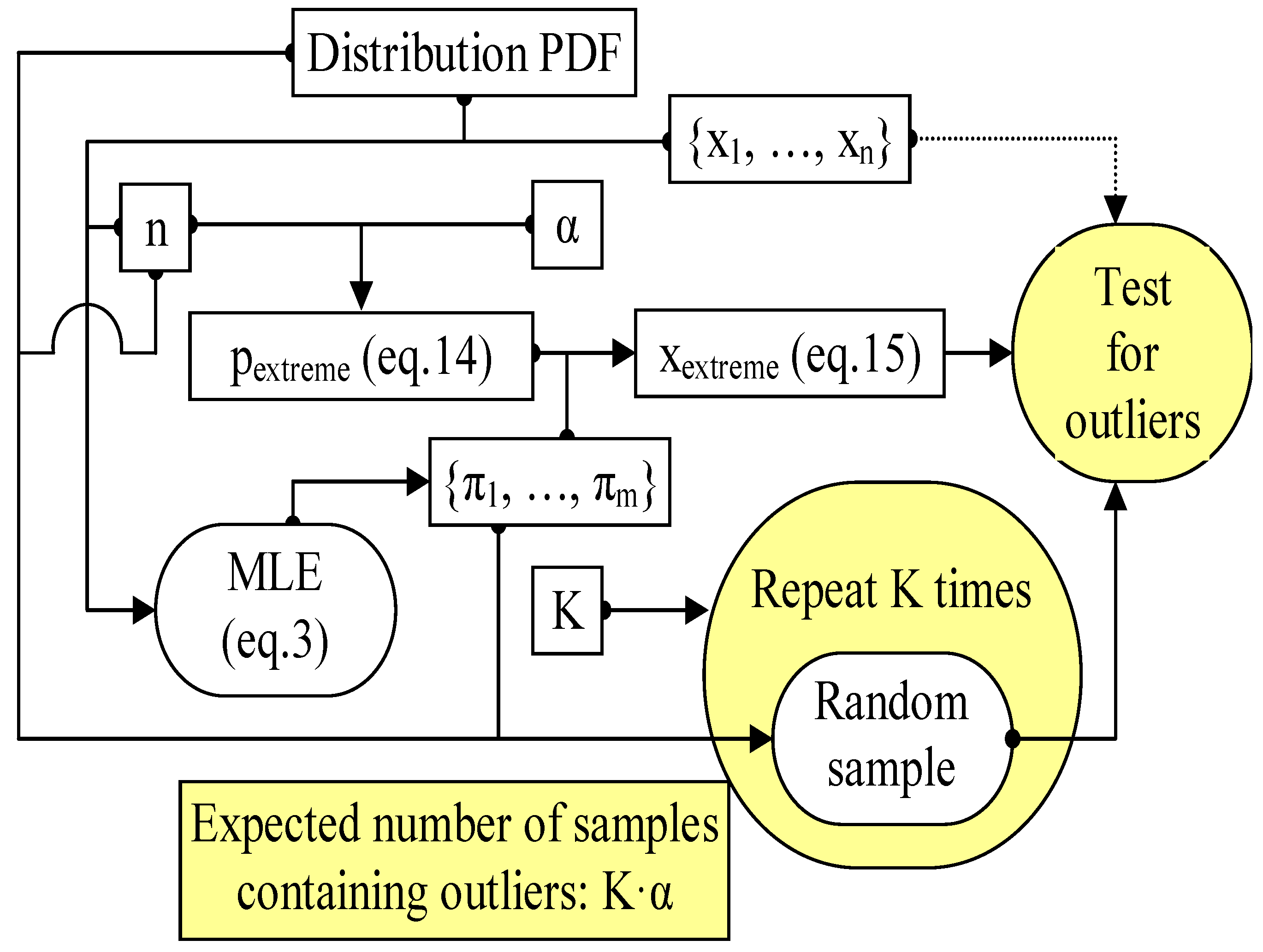
| 4 | Run the MC experiment (Figure 4) for K = 10000 (and then the expected number of outliers is 500) samples and count the samples containing outliers for the existing method (Grubbs, Equation (19); with μ and σ from CM method) and for the proposed method (g1, Equations (13)–(15) and (17); with μ and σ from the MLE method) |
| Step | Results (for α = 5%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | μ = 575.2; σ = 8.256 (MLE) → CPs = {0.1916, 0.2644, 0.2644, 0.2644, 0.3492, 0.3492, 0.3492, 0.6328, 0.8568, 0.9941} | |||||||||
| 2 | Statistic | AD | KS | CM | KV | WU | H1 | FCS | ||
| Value | 1.137 | 1.110 | 0.206 | 1.715 | 0.182 | 5.266 | 12.293 | |||
| αStatistic | 0.288 | 0.132 | 0.259 | 0.028 | 0.049 | 0.343 | 0.056 | |||
| 3 | xcrit(5%) = 575.2 ± 2.29·8.7025; pextreme(5%) = 0.5 ± InvCDF“g1”(1-0.05; 10); xextreme(5%) = {552.086, 598.314} | |||||||||
| 4 | Number of samples containing outliers | Existing method (Grubbs) | Proposed method (g1) | |||||||
| First run | 1977 (19.77%) | 510 (5.1%) | ||||||||
| Second run | 2009 (20.09%) | 526 (5.26%) | ||||||||
| Step | Results (for α = 5%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | μ = 572.889; σ = 4.725 (MLE) → CPs = {0.1504, 0.2705, 0.2705, 0.2705, 0.4254, 0.4254, 0.4254, 0.8603, 0.9907} | |||||||||
| 2 | Statistic | AD | KS | CM | KV | WU | H1 | FCS | ||
| Value | 0.935 | 1.057 | 0.174 | 1.535 | 0.155 | 4.678 | 9.715 | |||
| αStatistic | 0.389 | 0.167 | 0.327 | 0.082 | 0.088 | 0.394 | 0.137 | |||
| 3 | xcrit(5%) = 572.89 ± 2.215·5.011; pextreme(5%) = 0.5 ± InvCDF“g1”(1-0.05; 9); xextreme(5%) = {559.822, 585.956} | |||||||||
| 4 | Number of samples containing outliers | Existing method (Grubbs) | Proposed method (g1) | |||||||
| First run | 2341 (23.41%) | 563 (5.63%) | ||||||||
| Second run | 2333 (23.33%) | 543 (5.43%) | ||||||||
| Sample | {568, 570, 570, 570, 572, 572, 572, 578, 584, 596} | {568, 570, 570, 570, 572, 572, 572, 578, 584} |
|---|---|---|
| At 5% risk being in error can the hypothesis that the sample was drawn from a normal distribution be rejected? | No (αFCS = 7%) | No (αFCS = 15.8%) |
| Grubbs confidence interval for ‘no outliers’ at 5% risk being in error | (555.27, 595.13) 596 is detected as being outlier | (561.79, 583.99) 584 is detected as being outlier |
| g1 confidence interval for ‘no outliers’ at 5% risk being in error | (552.08, 598.32) no outliers | (559.82, 585.96) no outliers |
| Step | Results (for α = 5%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | From the CM method: μ = 575.7; σ = 10.067; from MLE method: μ = 575.7; σ = 9.550 | |||||||||
| 2 | Statistic | AD | KS | CM | KV | WU | H1 | FCS | ||
| Value | 1.267 | 1.109 | 0.225 | 1.774 | 0.198 | 5.411 | 13.652 | |||
| αStatistic | 0.241 | 0.132 | 0.226 | 0.018 | 0.035 | 0.254 | 0.034 | |||
| 3 | Grubbs confidence interval for ’no outliers’ at 5% risk being in error: (552.647,598.753); 601 is an outlier g1 confidence interval for ’no outliers’ at 5% risk being in error: (548.963, 602.437); no outliers | |||||||||
| Step | Results (for α = 5%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | From the CM method: μ = 576.0; σ = 10.914; from MLE method: μ = 576.0; σ = 10.354 | |||||||||
| 2 | Statistic | AD | KS | CM | KV | WU | H1 | FCS | ||
| Value | 1.348 | 1.108 | 0.238 | 1.803 | 0.209 | 5.481 | 14.468 | |||
| αStatistic | 0.216 | 0.133 | 0.206 | 0.015 | 0.028 | 0.215 | 0.025 | |||
| 3 | Grubbs confidence interval for ’no outliers’ at 5% risk being in error: (551.00, 601.00); 604 is an outlier g1 confidence interval for ’no outliers’ at 5% risk being in error: (547.01, 604.99); no outliers | |||||||||
| Step | Results (for α = 5%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Table 5 Dataset; Normal distribution → CM: μ = 6.481; σ = 0.831; MLE: μ = 6.481; σ = 0.829 | |||||||||
| 2 | Statistic | AD | KS | CM | KV | WU | H1 | FCS | ||
| Value | 0.439 | 0.484 | 0.049 | 0.952 | 0.047 | 104.2 | 1.276 | |||
| αStatistic | 0.812 | 0.965 | 0.886 | 0.852 | 0.743 | 0.641 | 0.973 | |||
| 3 | Grubbs confidence interval for ’no outliers’ at 5% risk being in error: (3.492, 9.470); 9.603 is an outlier g1 confidence interval for ’no outliers’ at 5% risk being in error: (3.444, 9.517); 9.603 is an outlier | |||||||||
| 4 | Number of samples containing outliers | Existing method (Grubbs) | Proposed method (g1) | |||||||
| First run | 637 (6.37%) | 511 (5.11%) | ||||||||
| Second run | 630 (6.3%) | 481 (4.81%) | ||||||||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jäntschi, L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry 2019, 11, 835. https://doi.org/10.3390/sym11060835
Jäntschi L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry. 2019; 11(6):835. https://doi.org/10.3390/sym11060835
Chicago/Turabian StyleJäntschi, Lorentz. 2019. "A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested" Symmetry 11, no. 6: 835. https://doi.org/10.3390/sym11060835
APA StyleJäntschi, L. (2019). A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry, 11(6), 835. https://doi.org/10.3390/sym11060835





