Time-Fractional Heat Conduction in Two Joint Half-Planes
Abstract
1. Introduction
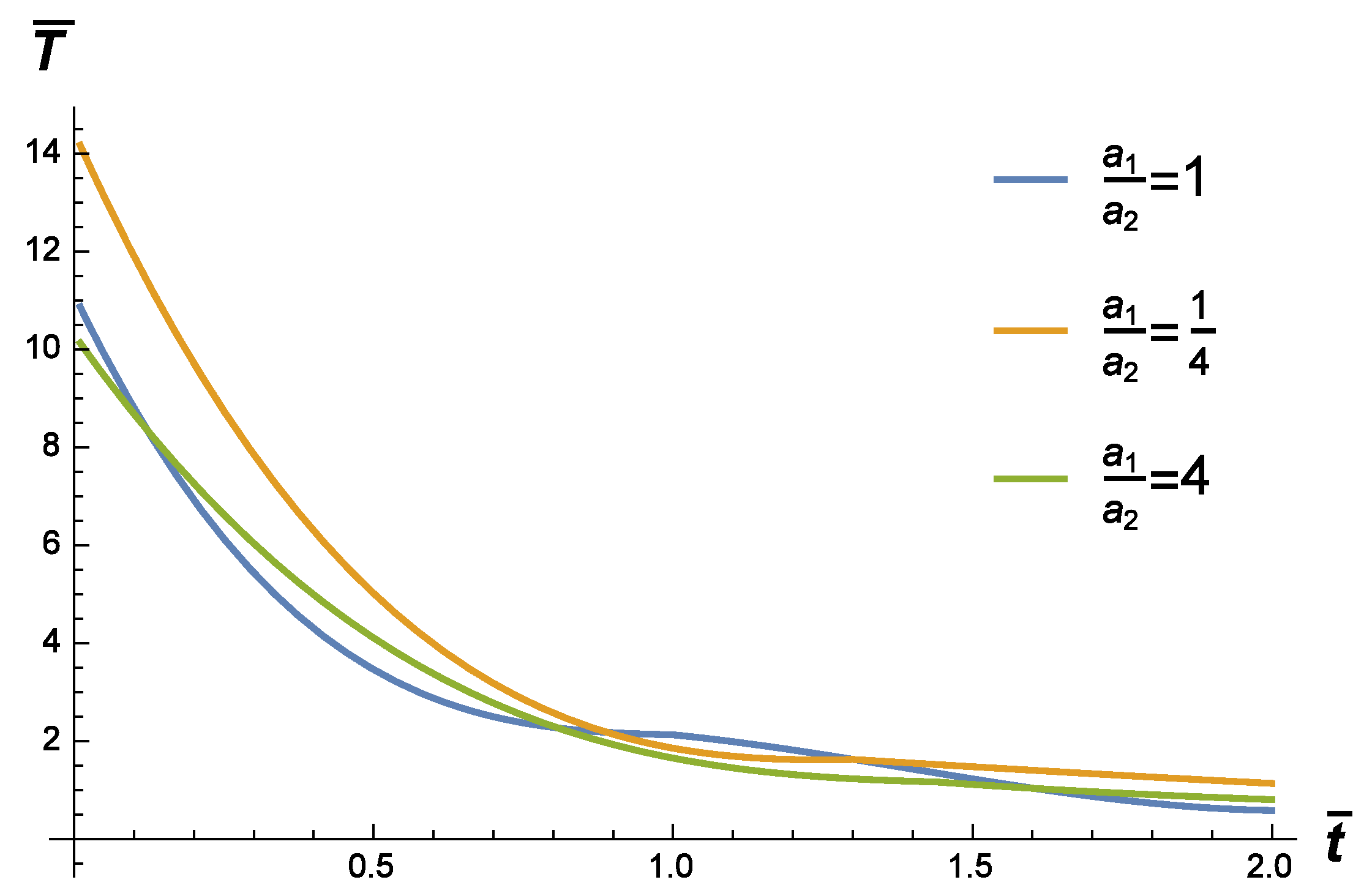
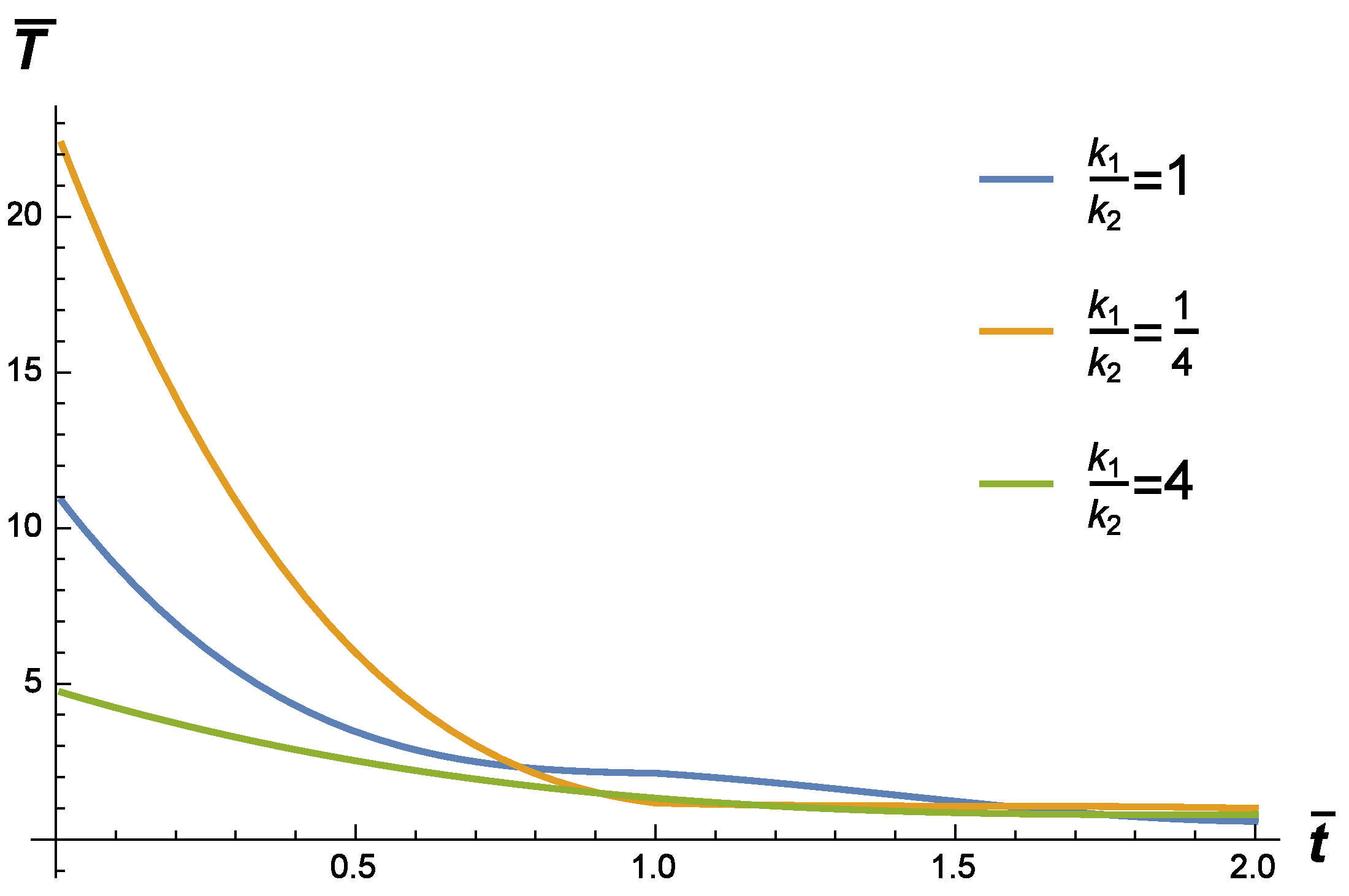
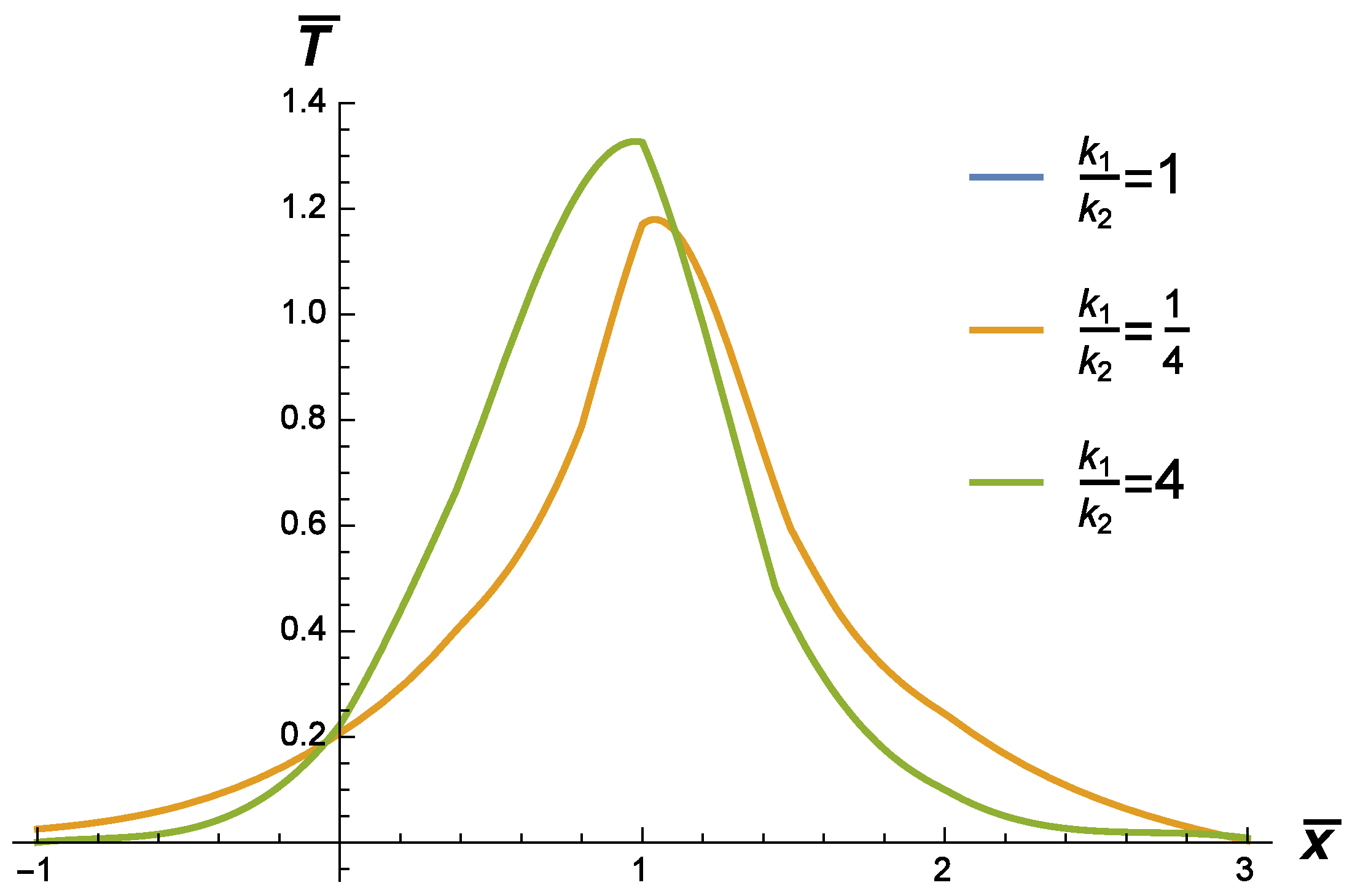
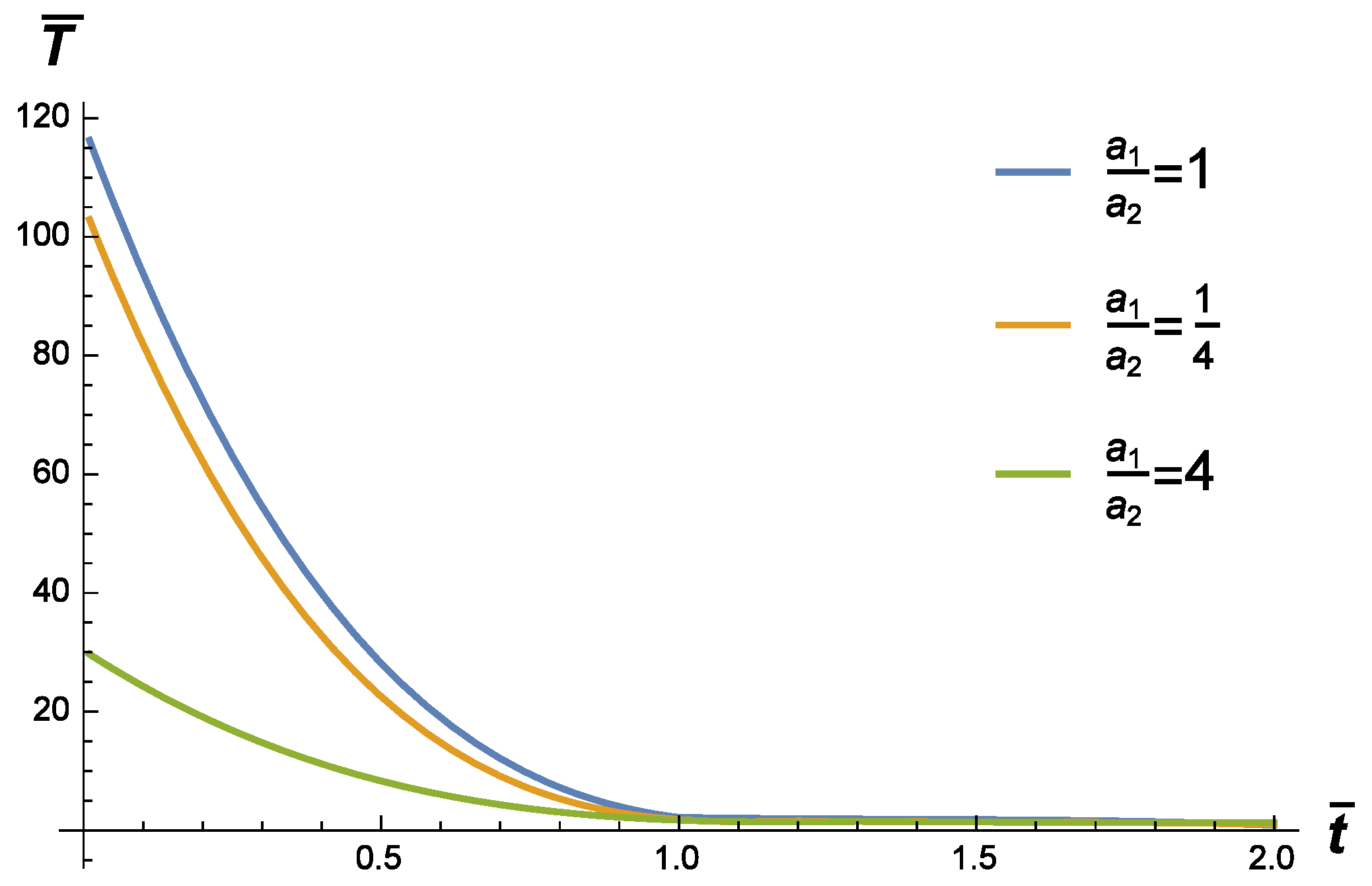
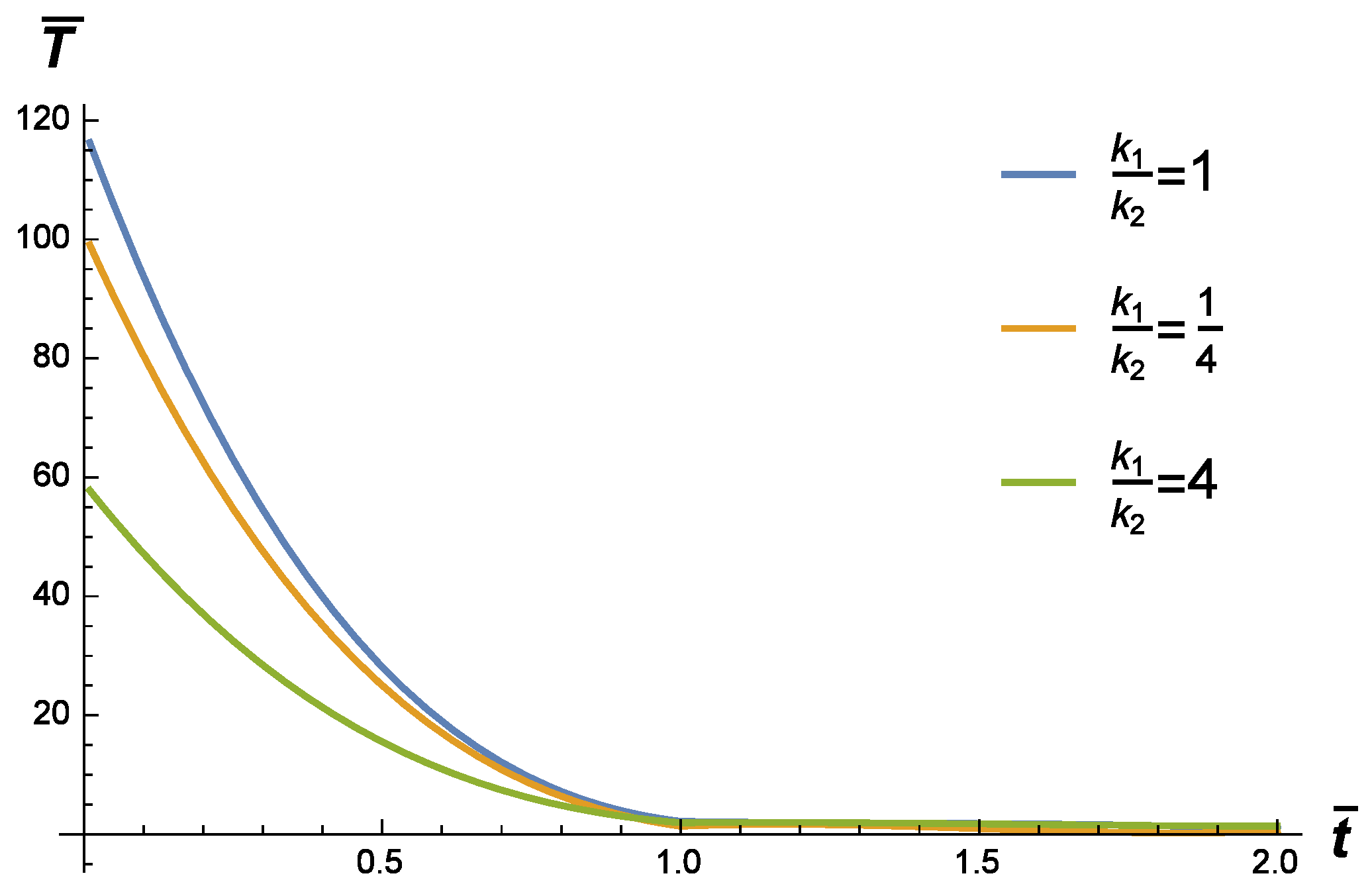
2. The Fundamental Solution to the Cauchy Problem
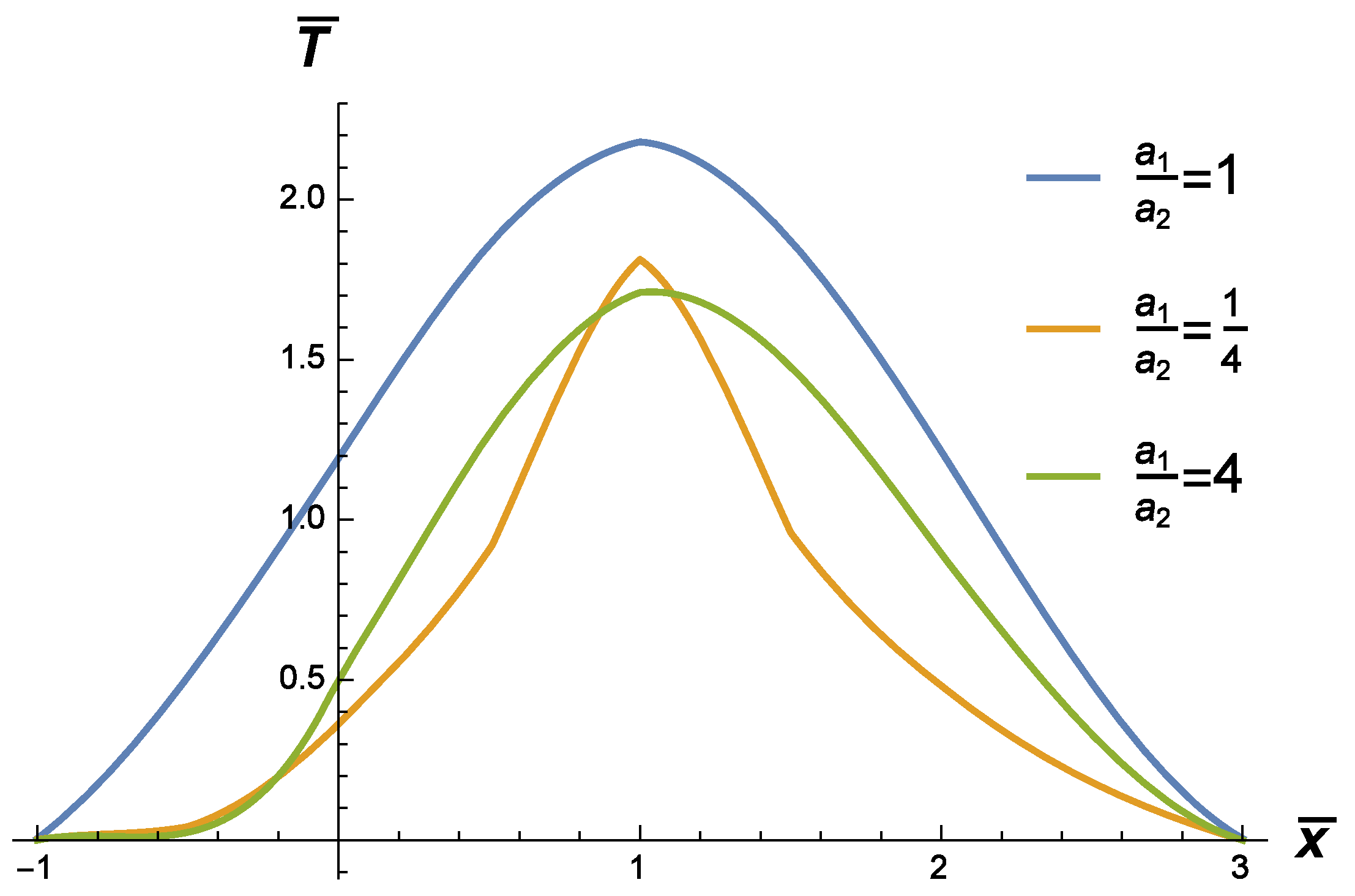
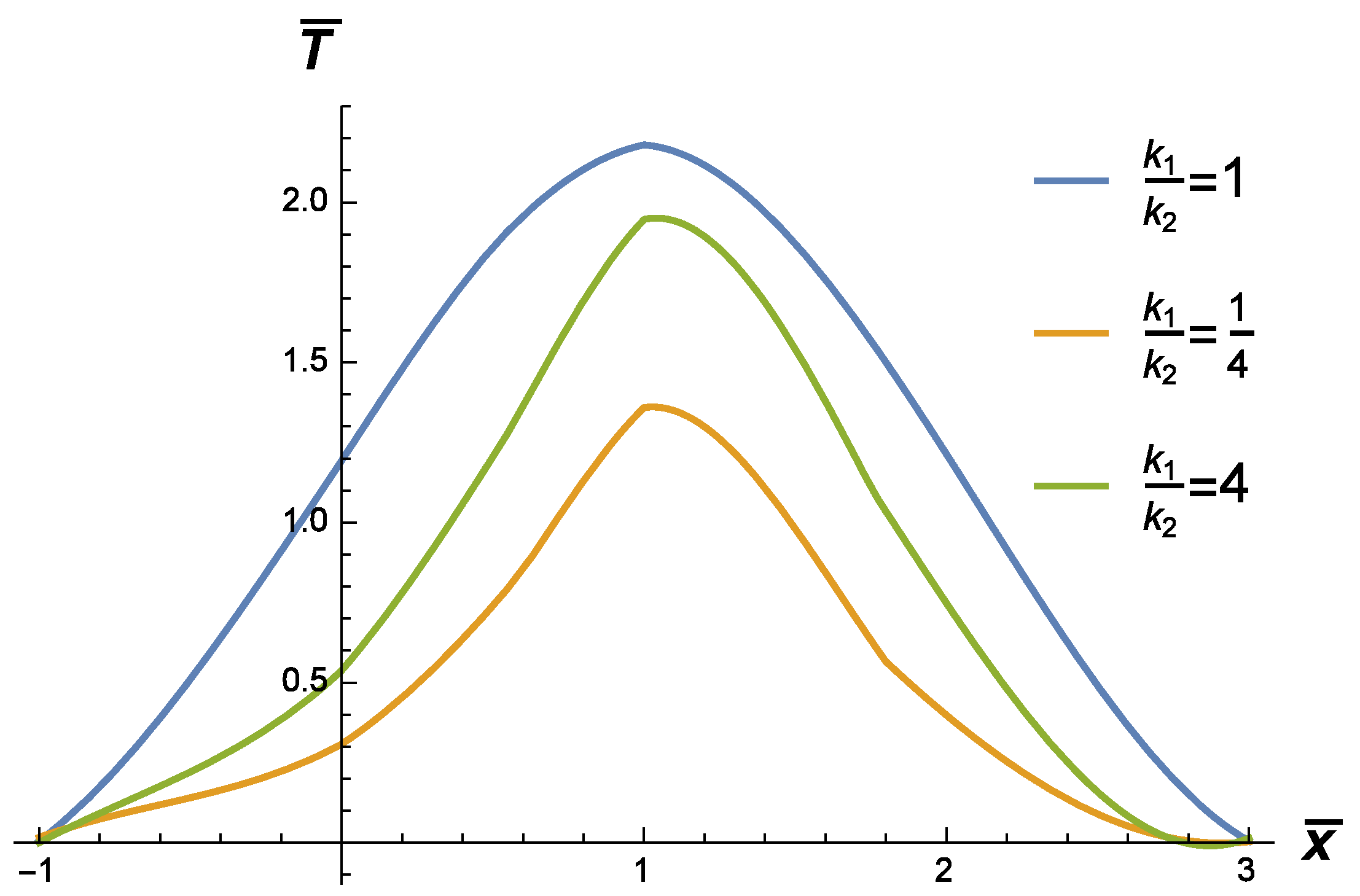
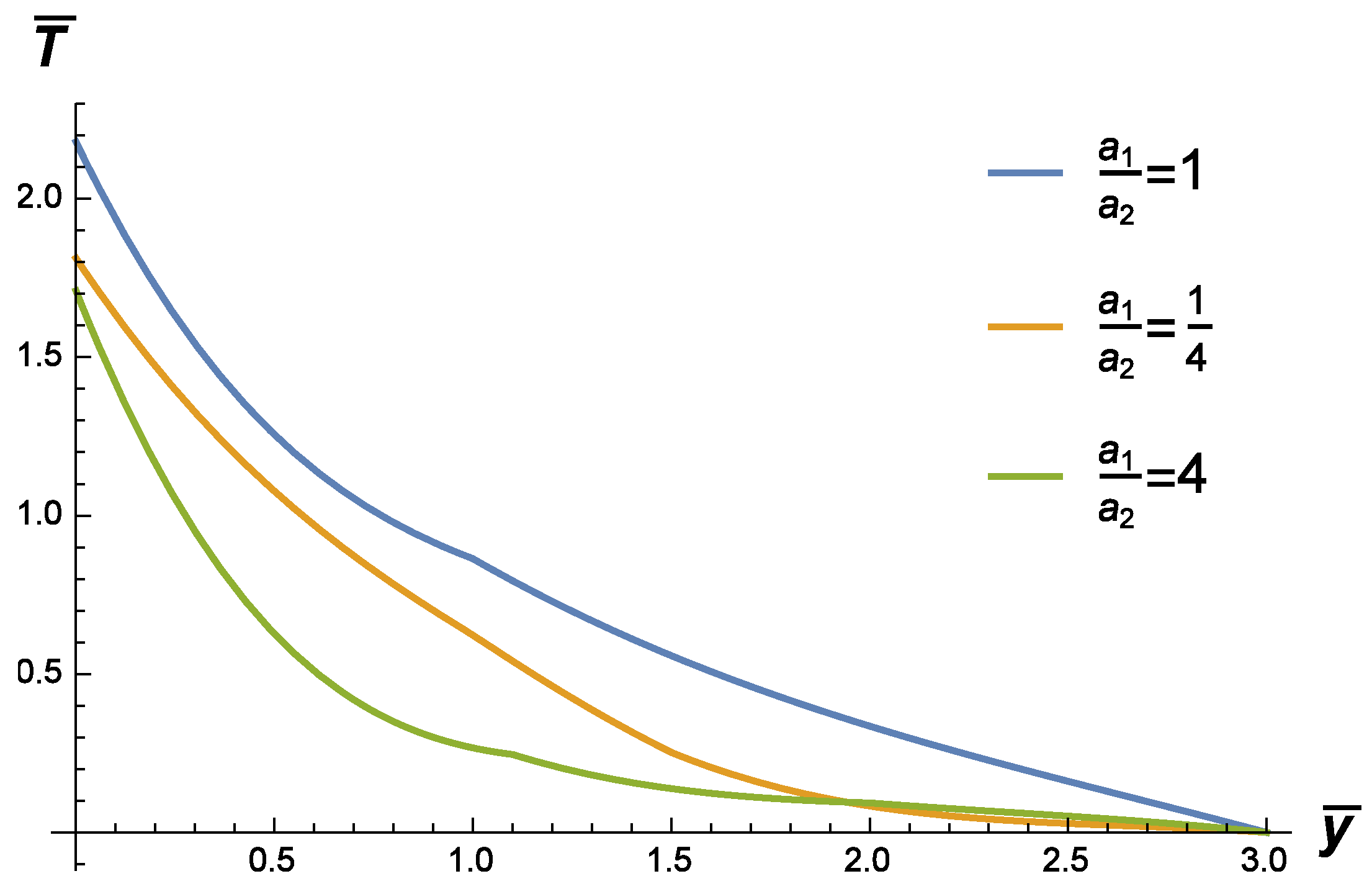
3. The Fundamental Solution to the Source Problem
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gurtin, M.E.; Pipkin, A.C. A general theory of heat conduction with finite wave speeds. Arch. Ration. Mech. Anal. 1968, 31, 113–126. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. To the theoretical explanation of the “universal response”. Phys. Stat. Sol. 1984, 123, 739–745. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. On the theory of relaxation for systems with “remnant” memory. Phys. Stat. Sol. 1984, 124, 389–393. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional heat conduction equation and associated thermal stresses. J. Therm. Stress. 2005, 28, 83–102. [Google Scholar] [CrossRef]
- Povstenko, Y. Thermoelasticity which uses fractional heat conduction equation. J. Math. Sci. 2009, 162, 296–305. [Google Scholar] [CrossRef]
- Povstenko, Y. Theory of thermoelasticity based on the space-time fractional heat conduction equation. Phys. Scr. 2009, 136, 014017. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional Cattaneo-type equations and generalized thermoelasticity. J. Therm. Stress. 2011, 34, 97–114. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional thermoelasticity. In Encyclopedia of Thermal Stresses; Hetnarski, R.B., Ed.; Springer: New York, NY, USA, 2014; Volume 4, pp. 1778–1787. [Google Scholar]
- Rukolaine, S.A. Unphysical effects of the dual-phase-lag model of heat conduction. Int. J. Heat Mass Transf. 2014, 78, 58–63. [Google Scholar] [CrossRef]
- Kovács, R.; Ván, P. Thermodynamical consistency of the dual-phase-lag heat conduction equation. Contin. Mech. Thermodyn. 2018, 30, 1223–1230. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers, Inc.: Redding, CA, USA, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Tenreiro Machado, J.A. (Eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Baleanu, D.; Güvenç, Z.B.; Tenreiro Machado, J.A. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Datsko, B.; Luchko, Y.; Gafiychuk, V. Pattern formation in fractional reaction-diffusion systems with multiple homogeneous states. Int. J. Bifurcat. Chaos 2012, 22, 1250087. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Datsko, B.; Gafiychuk, V.; Podlubny, I. Solitary travelling auto-waves in fractional reaction–diffusion systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 378–387. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Povstenko, Y. Neumann boundary-value problems for a time-fractional diffusion-wave equation in a half-plane. Comput. Math. Appl. 2012, 64, 3183–3192. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional heat conduction in infinite one-dimensional composite medium. J. Therm. Stress. 2013, 36, 351–363. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional heat conduction in an infinite medium with a spherical inclusion. Entropy 2013, 15, 4122–4133. [Google Scholar] [CrossRef]
- Povstenko, Y. Fundamental solutions to time-fractional heat conduction equations in two joint half-lines. Cent. Eur. J. Phys. 2013, 11, 1284–1294. [Google Scholar] [CrossRef]
- Gaver, D.P. Observing stochastic processes, and approximate transform inversion. Oper. Res. 1966, 14, 444–459. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368 Numerical inversion of Laplace transform. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Stehfest, H. Remark on algorithm 368 Numerical inversion of Laplace transform. Commun. ACM 1970, 13, 624. [Google Scholar] [CrossRef]
- Kuznetsov, A. On the convergence of Gaver–Stehfest algorithm. SIAM J. Numer. Anal. 2013, 51, 2984–2998. [Google Scholar] [CrossRef]
- Rani, D.; Mishra, V.; Cattani, C. Numerical inverse Laplace transform for solving a class of fractional differential equations. Symmetry 2019, 11, 530. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Bryčkov, Y.A.; Maričev, O.I. Integrals and Series, Vol 1: Elementary Functions; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1986. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Povstenko, Y.; Klekot, J. Time-Fractional Heat Conduction in Two Joint Half-Planes. Symmetry 2019, 11, 800. https://doi.org/10.3390/sym11060800
Povstenko Y, Klekot J. Time-Fractional Heat Conduction in Two Joint Half-Planes. Symmetry. 2019; 11(6):800. https://doi.org/10.3390/sym11060800
Chicago/Turabian StylePovstenko, Yuriy, and Joanna Klekot. 2019. "Time-Fractional Heat Conduction in Two Joint Half-Planes" Symmetry 11, no. 6: 800. https://doi.org/10.3390/sym11060800
APA StylePovstenko, Y., & Klekot, J. (2019). Time-Fractional Heat Conduction in Two Joint Half-Planes. Symmetry, 11(6), 800. https://doi.org/10.3390/sym11060800