Symmetric Networks with Geometric Constraints as Models of Visual Illusions
Abstract
1. Introduction
1.1. Neuroscientific and Image-Recognition Context
1.2. Overview of the Paper
2. Wilson Networks
2.1. Geometric Consistency
3. Rate Equations for the Dynamics
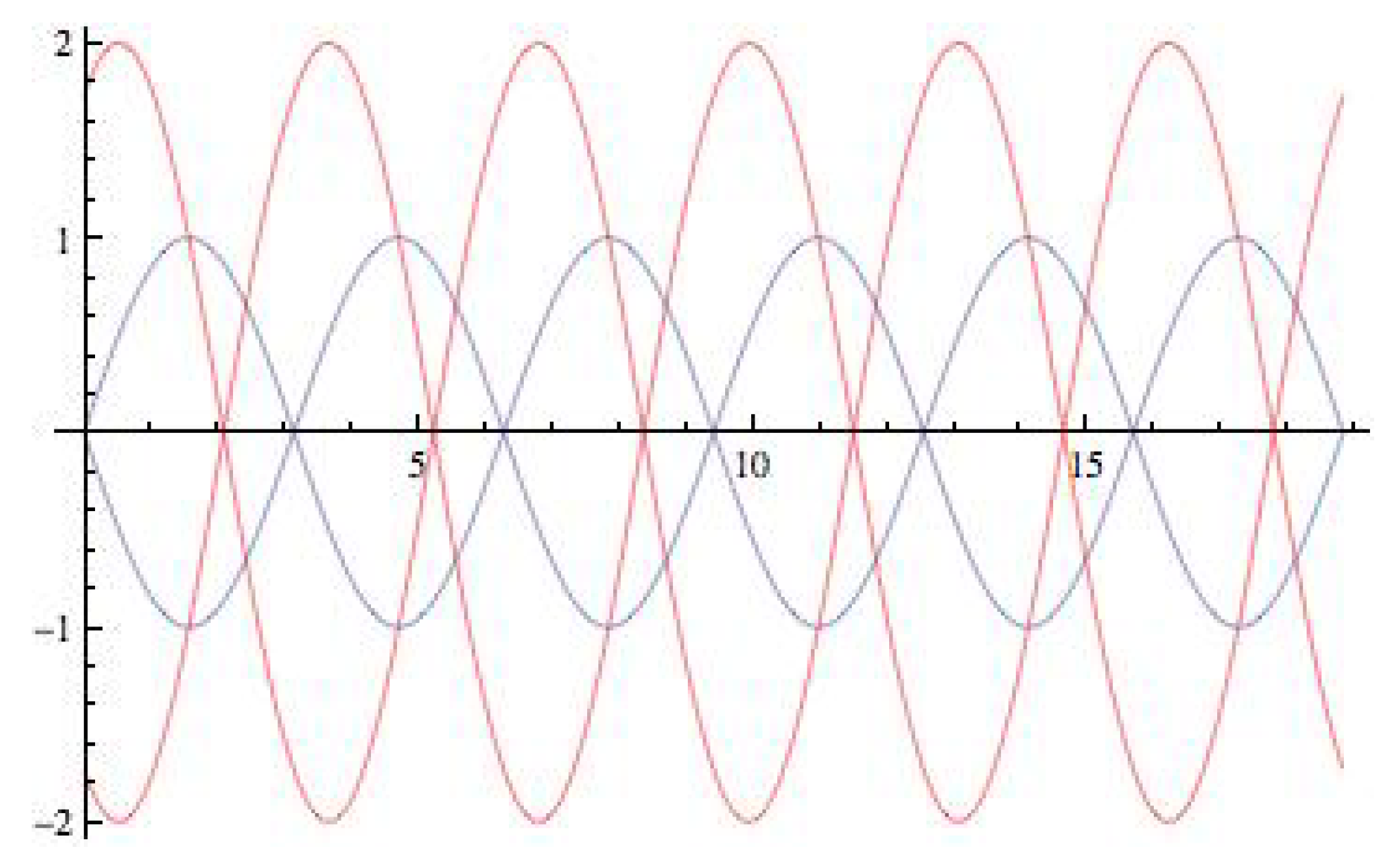
3.1. Symmetry-Breaking Hopf Bifurcation
- (1)
- where V is absolutely irreducible.
- (2)
- W is irreducible of type or .
4. Examples of Illusions
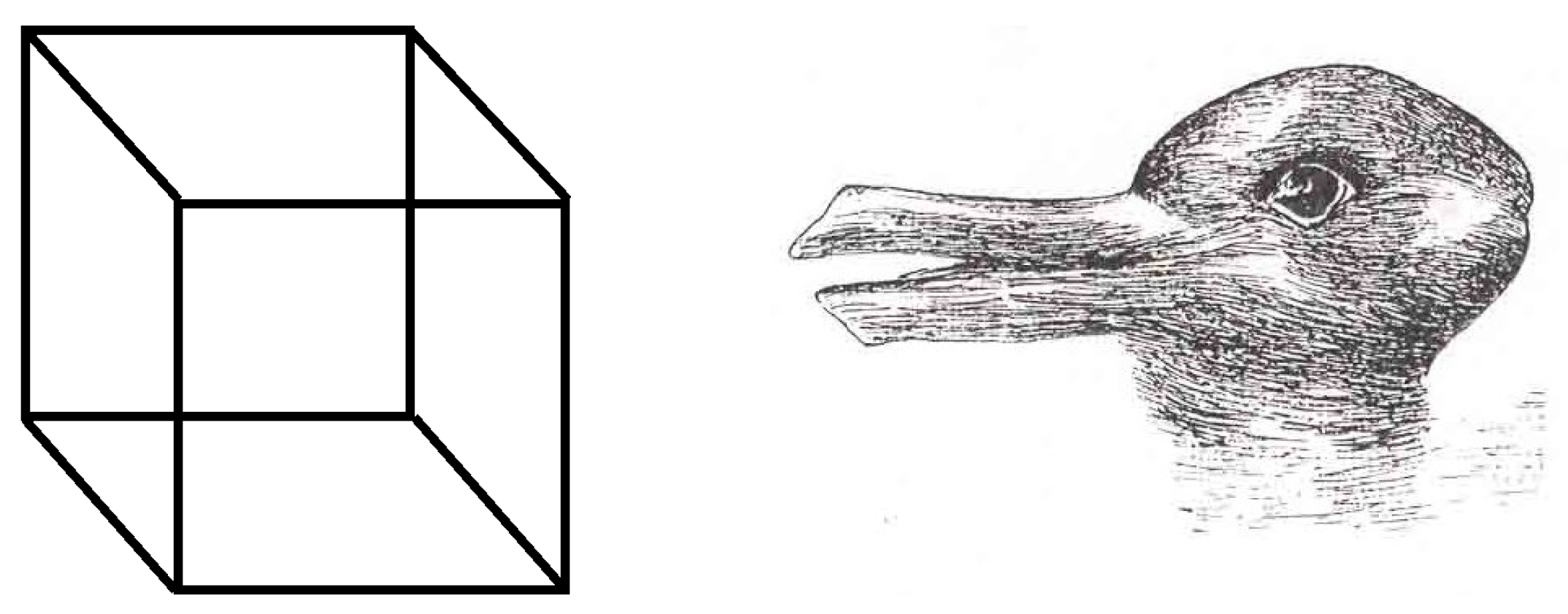
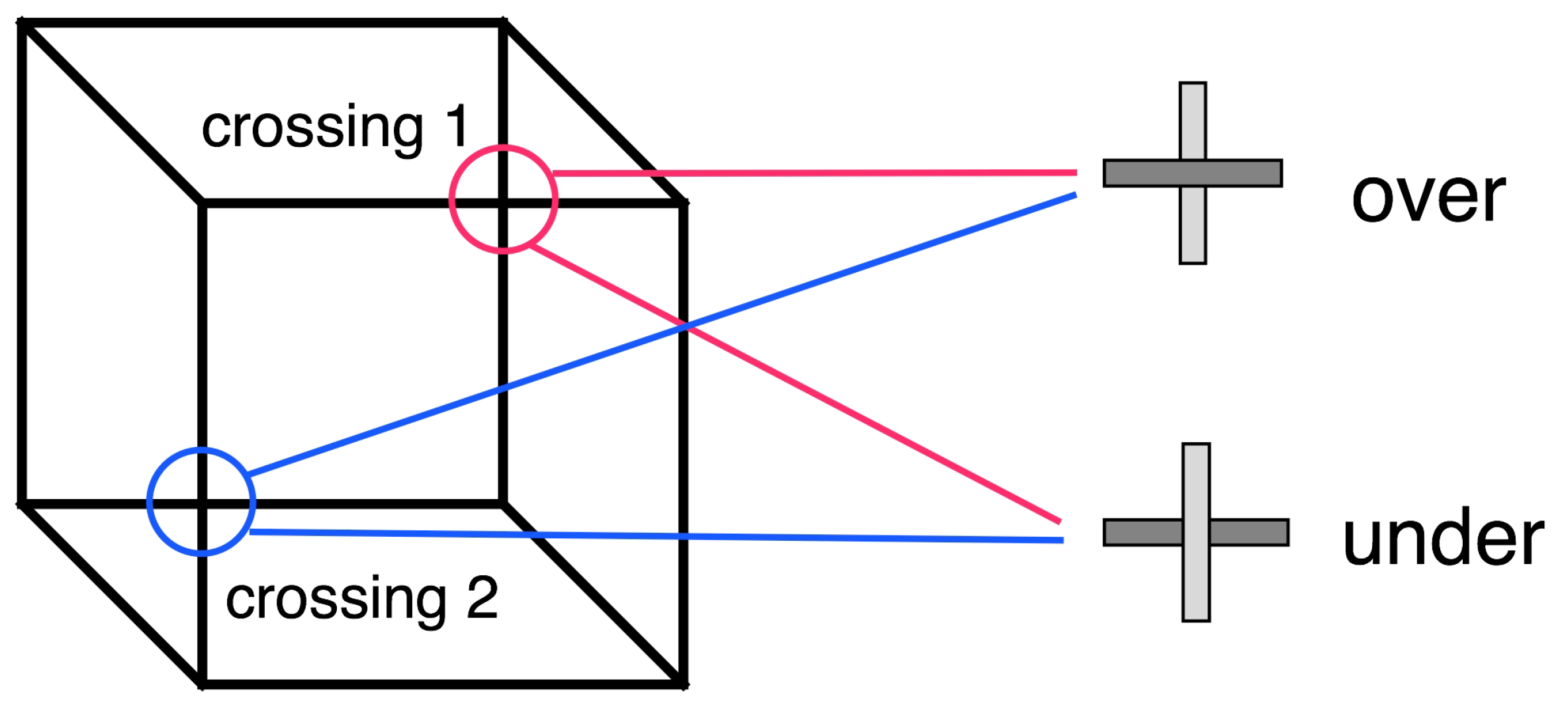
4.1. Necker Cube
4.2. Rabbit/Duck
4.3. Model-Independent Analysis
- ears + head facing right = rabbit
- beak + head facing right = transitional percept
- beak + head facing left = duck
- ears + head facing left = transitional percept
- ears + head facing right = rabbit
- ears + head facing left = transitional percept
- beak + head facing left = duck
- beak + head facing right = transitional percept
4.4. Model-Dependent Analysis
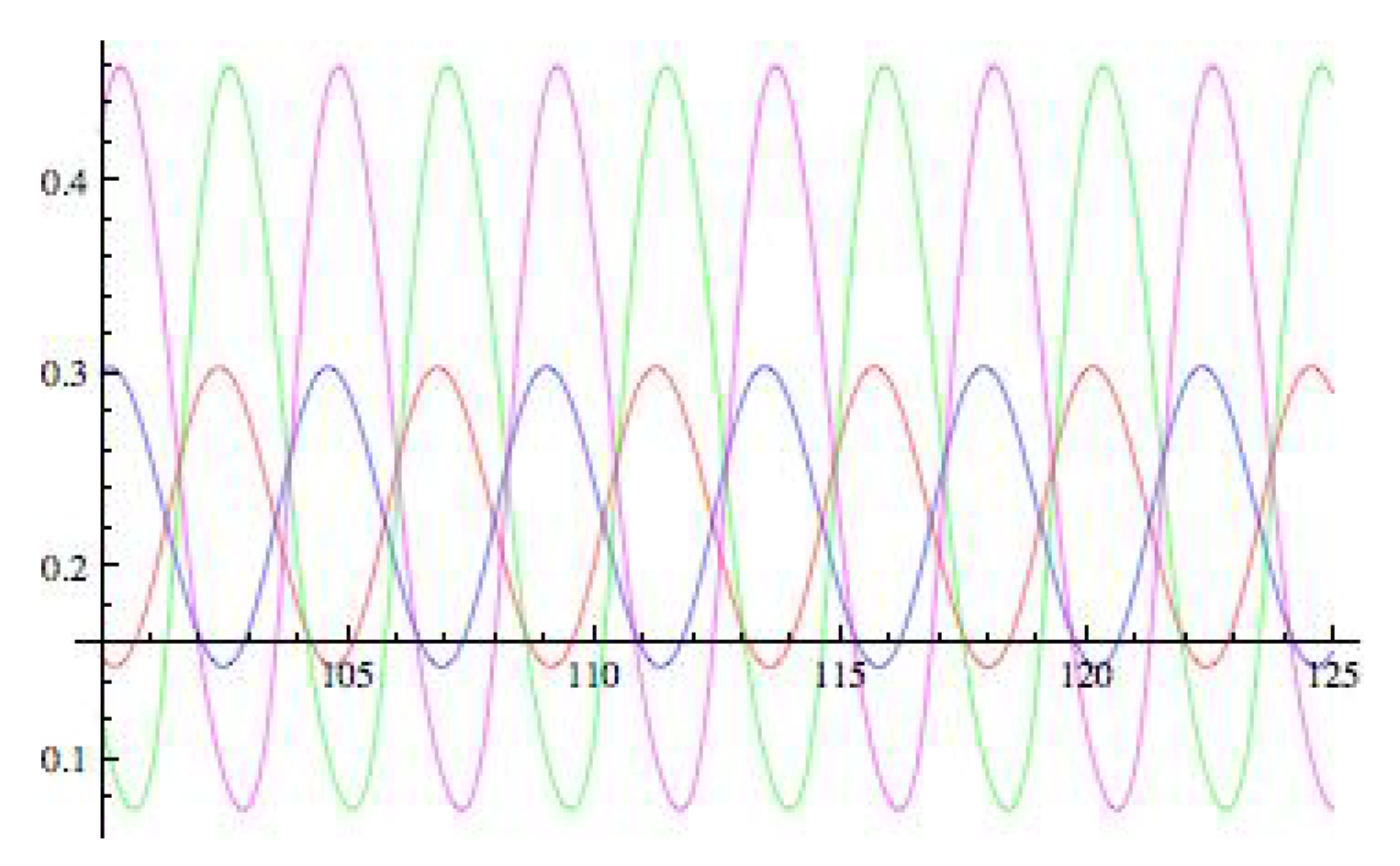
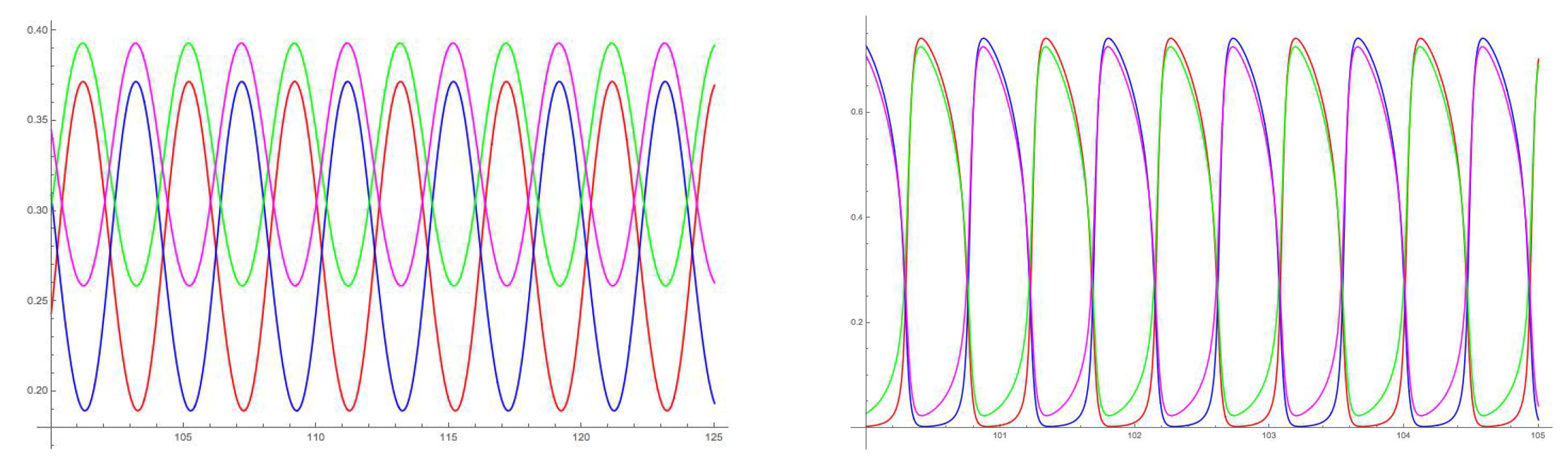
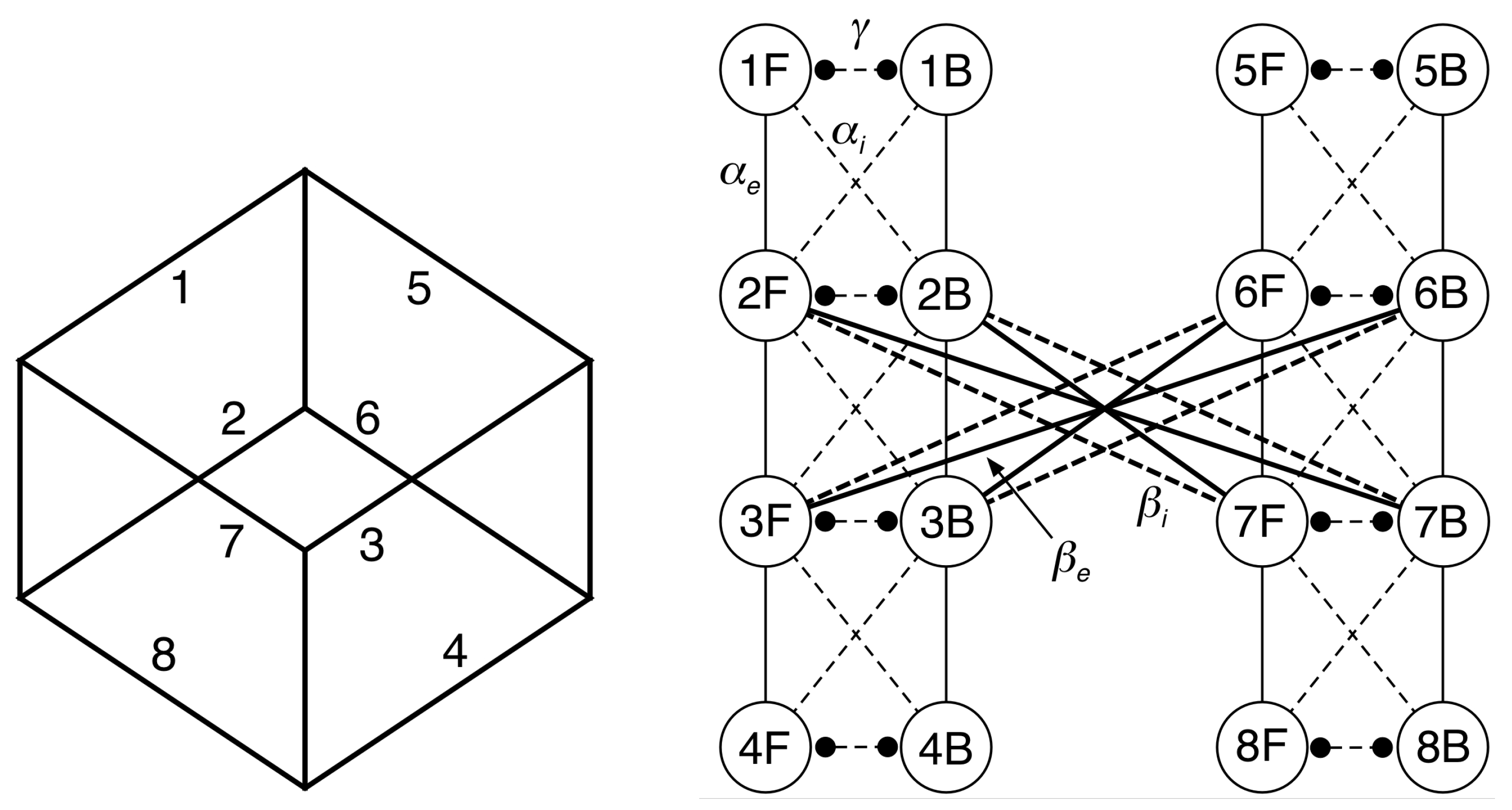
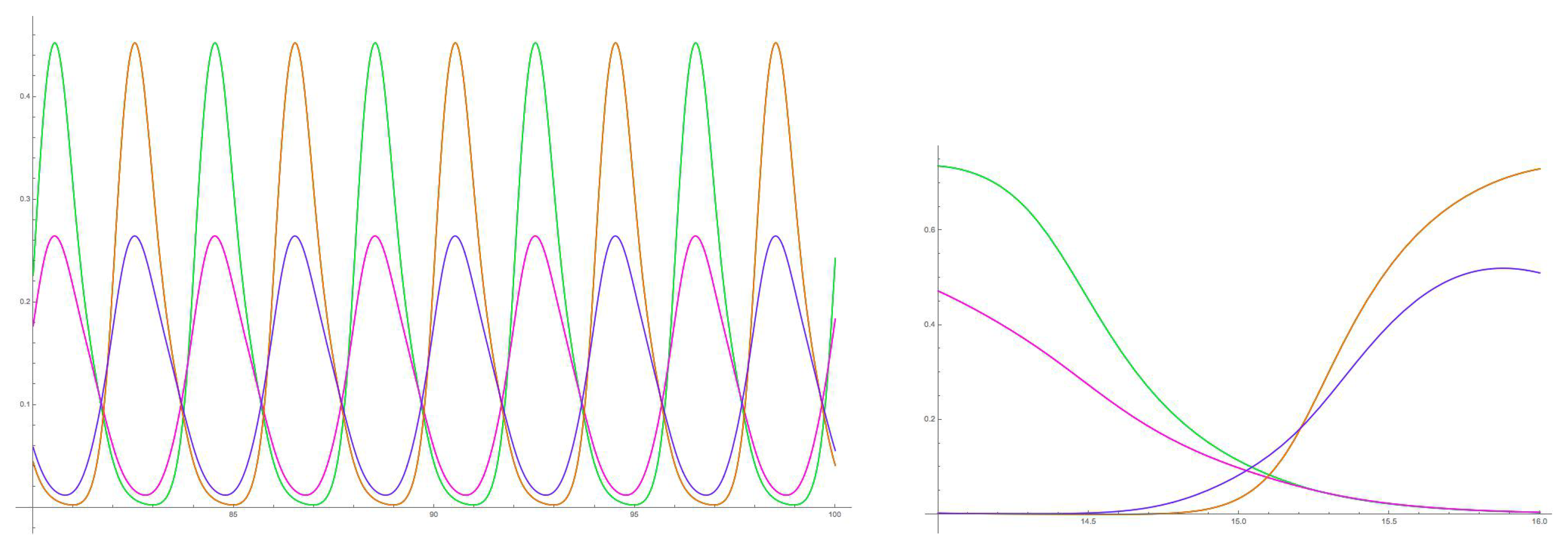
5. 16-Node Necker Cube Network
- (1)
- Lines that are (near) vertical in the image are (near) vertical in the 3-dimensional object detected as the percept. There is much evidence that the vertical direction is special in vision; see for example Quinn [83].
- (2)
- Lines that are (near) parallel in the image are (near) parallel in the 3-dimensional object detected as the percept.
- (3)
- Lines that are not (near) parallel in the image are not (near) parallel in the 3-dimensional object detected as the percept.
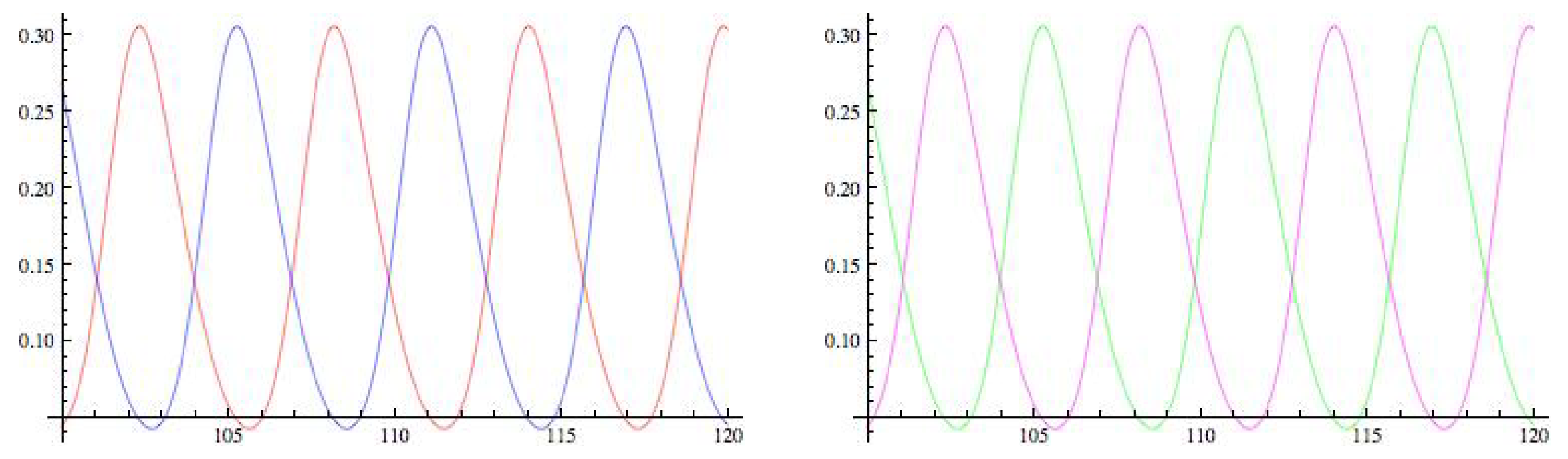
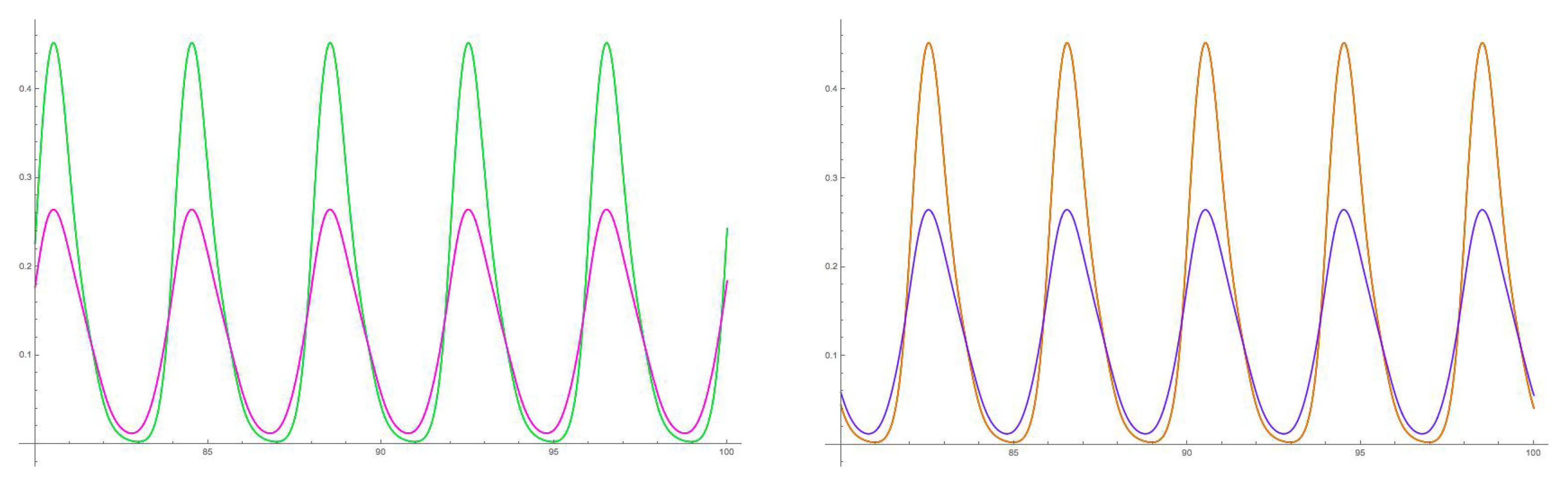
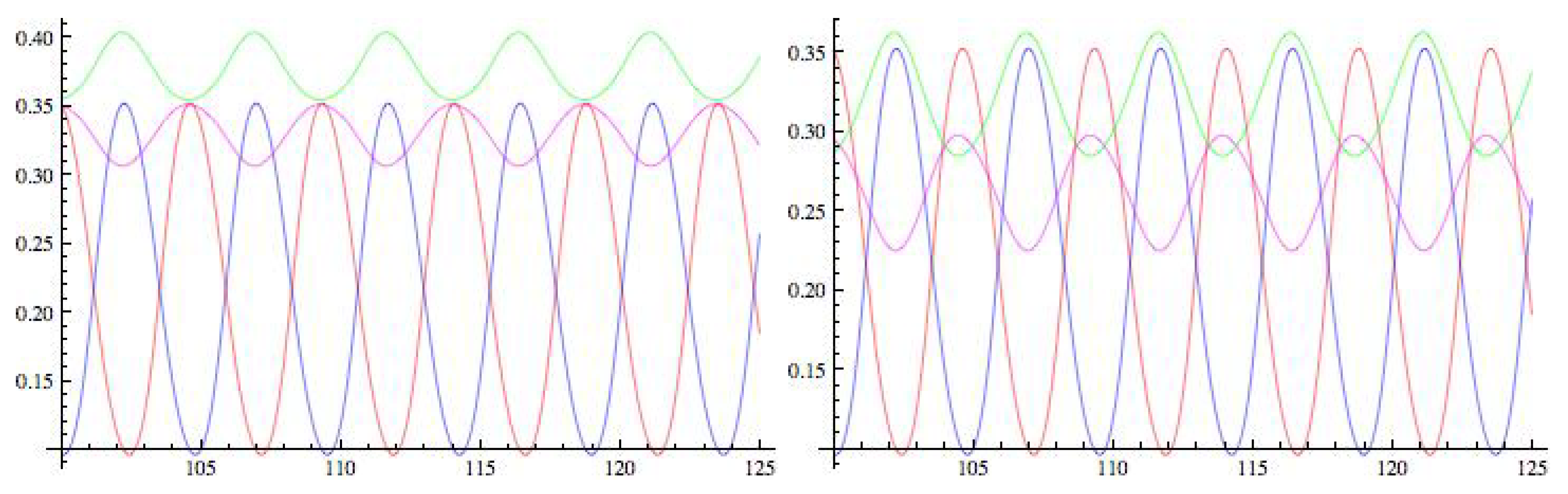
5.1. Symmetry-Breaking Hopf Bifurcation
6. Analysis of the Rate Model
6.1. Eigenstructure of the Adjacency Matrix
6.2. Spatiotemporal Symmetries of Critical Eigenspaces
- Reflects the diagram left-right.
- Reflects the diagram top-bottom.
- interchanges F and B in each pair of nodes with the same number.
6.3. Special Model
7. Analysis of the Special Model
Conditions for First Bifurcation
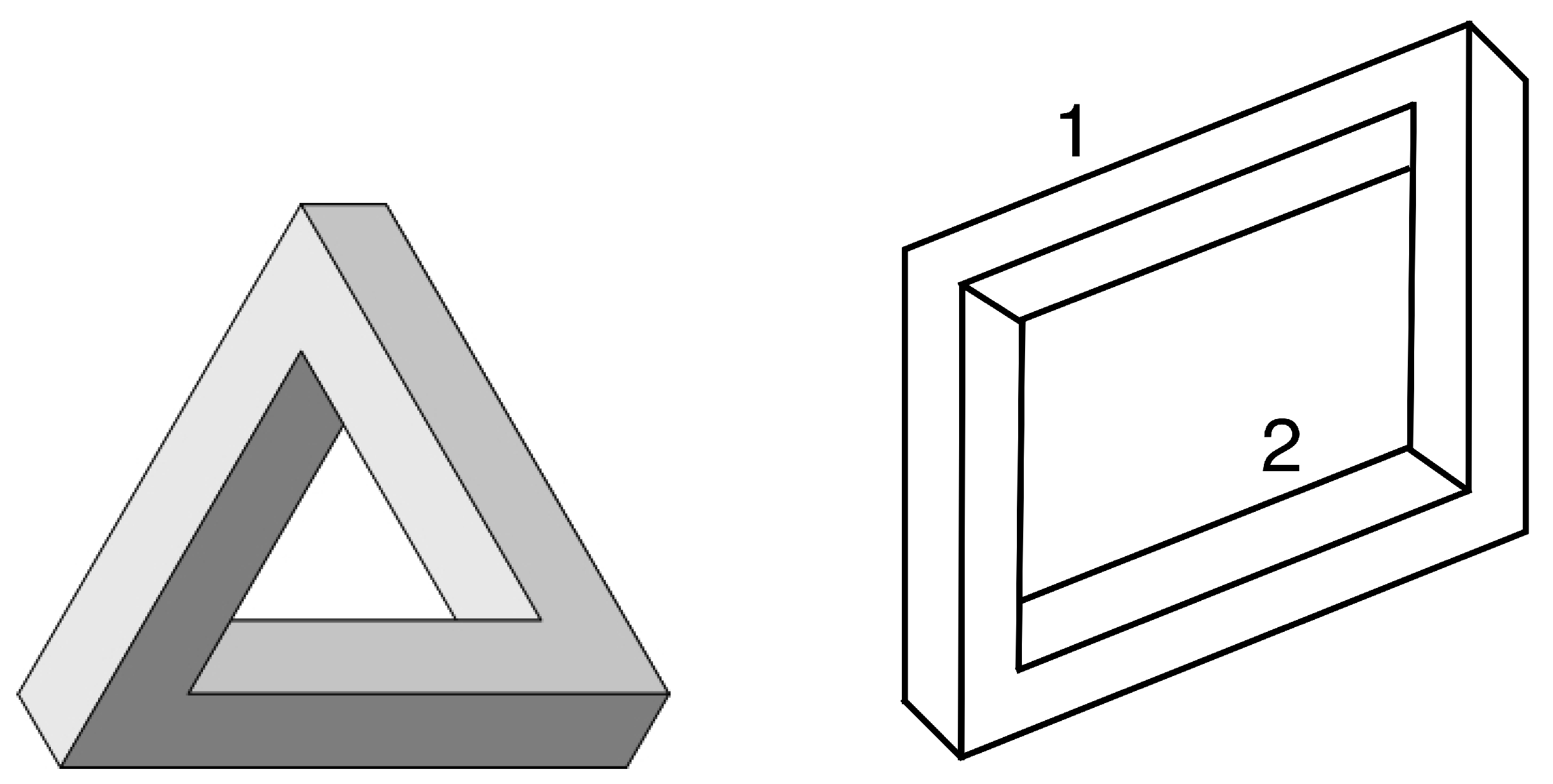
8. Transitional States Are Impossible Figures
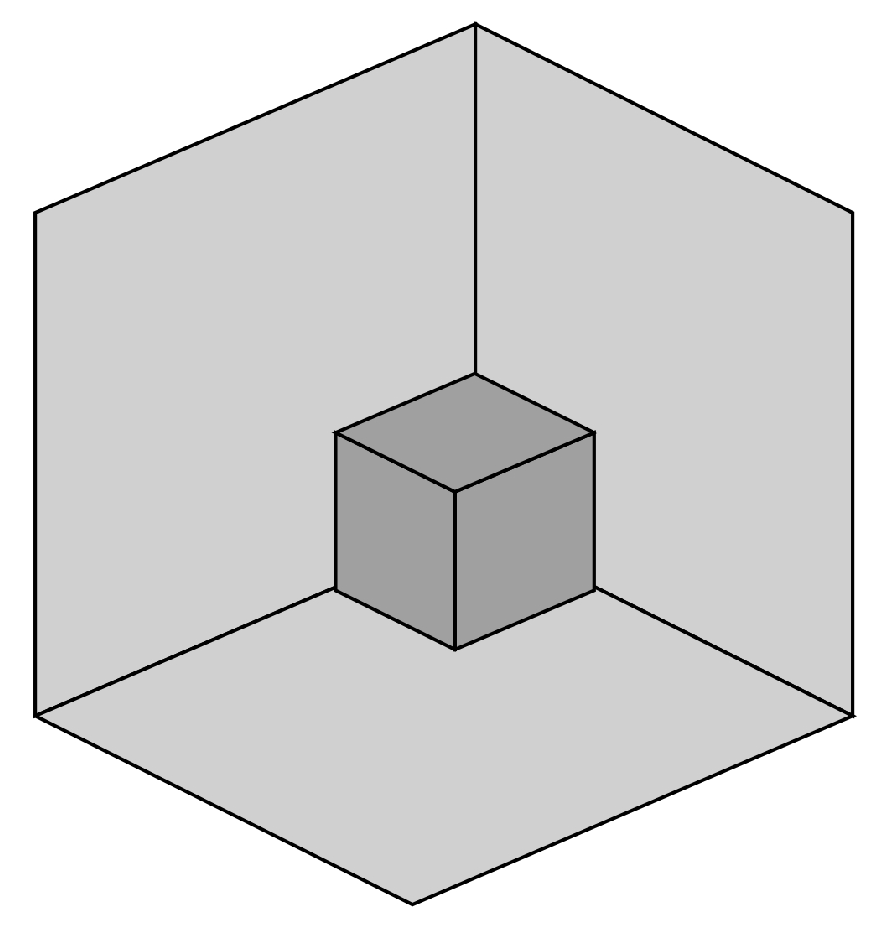
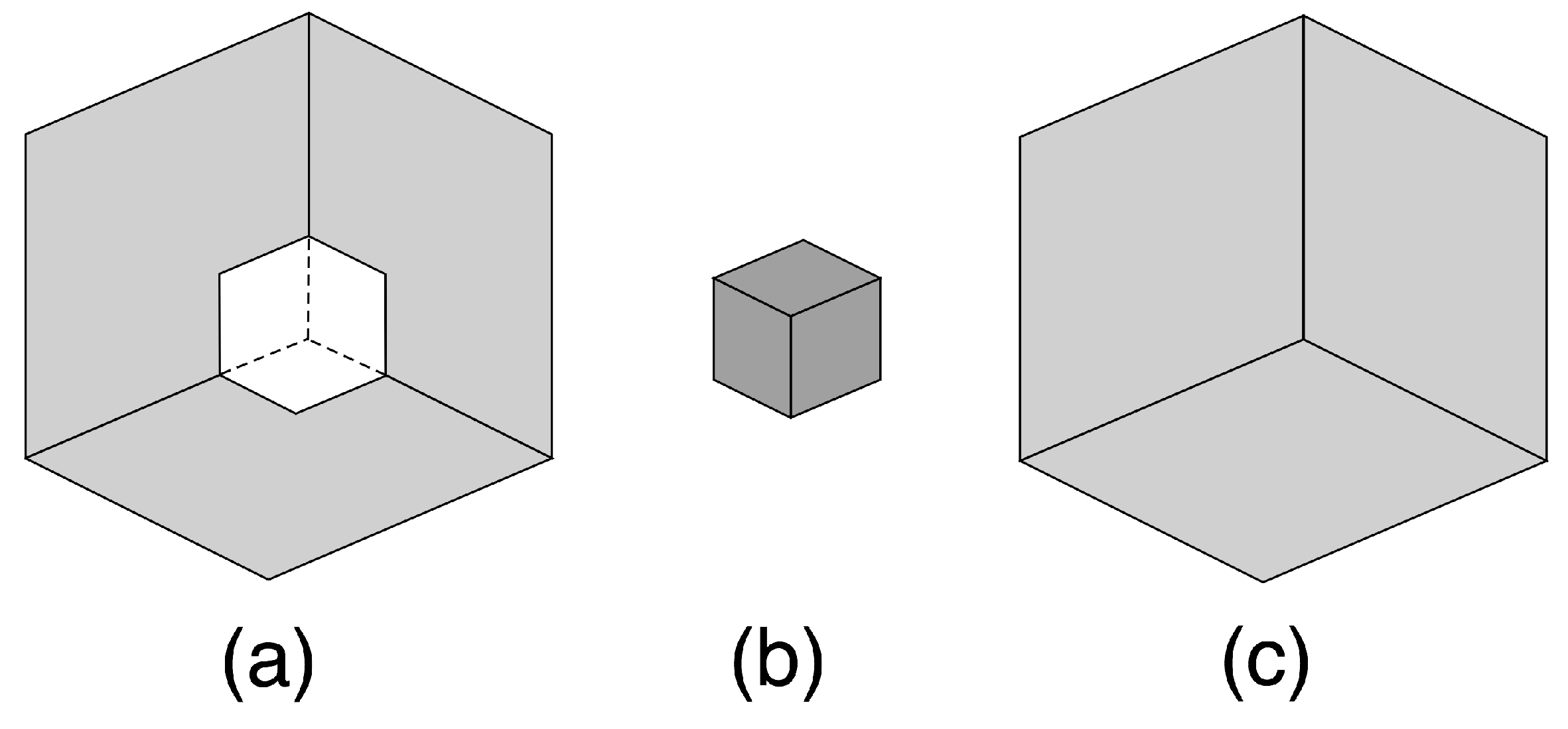
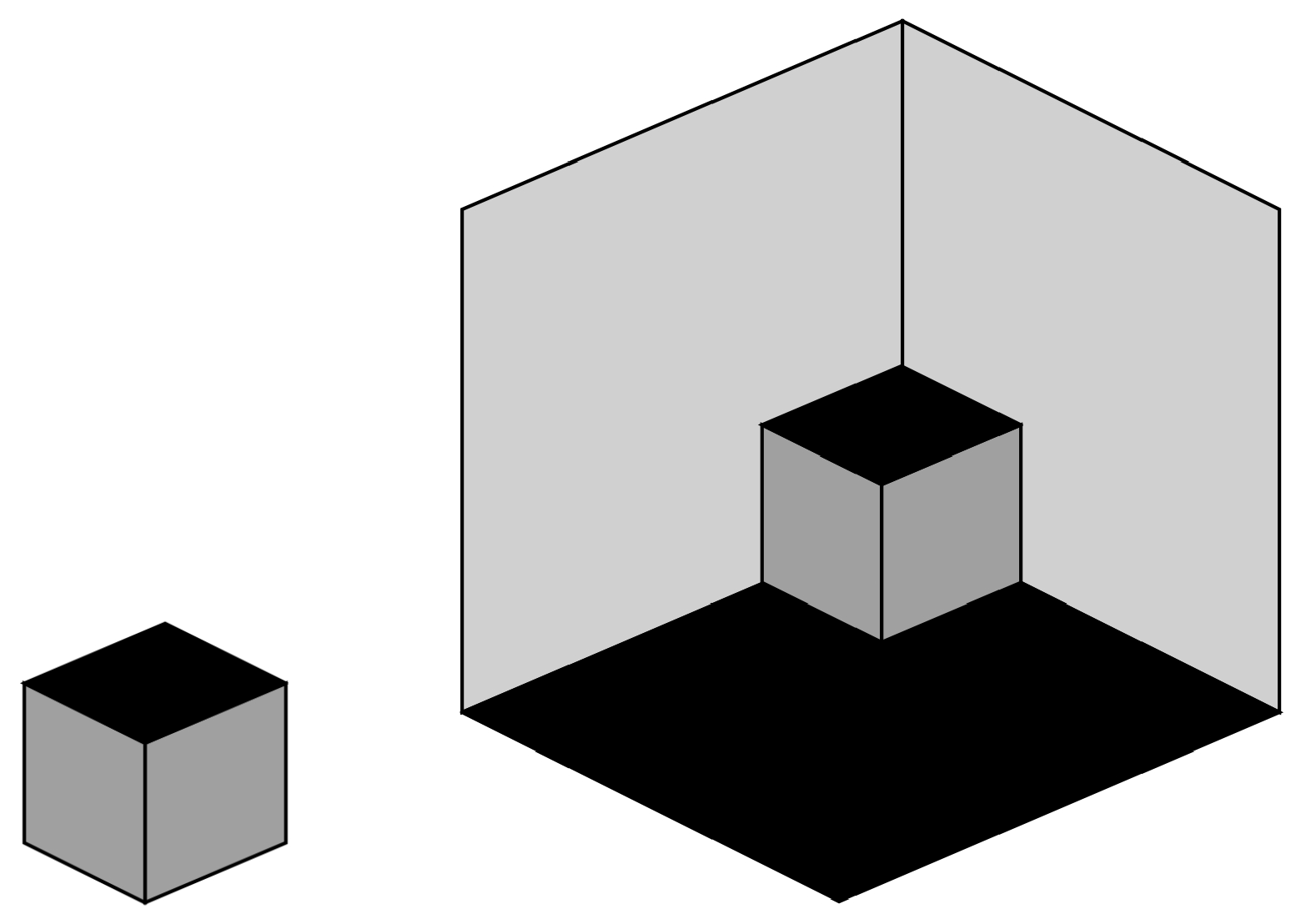
9. Tristable Necker-Like Figure
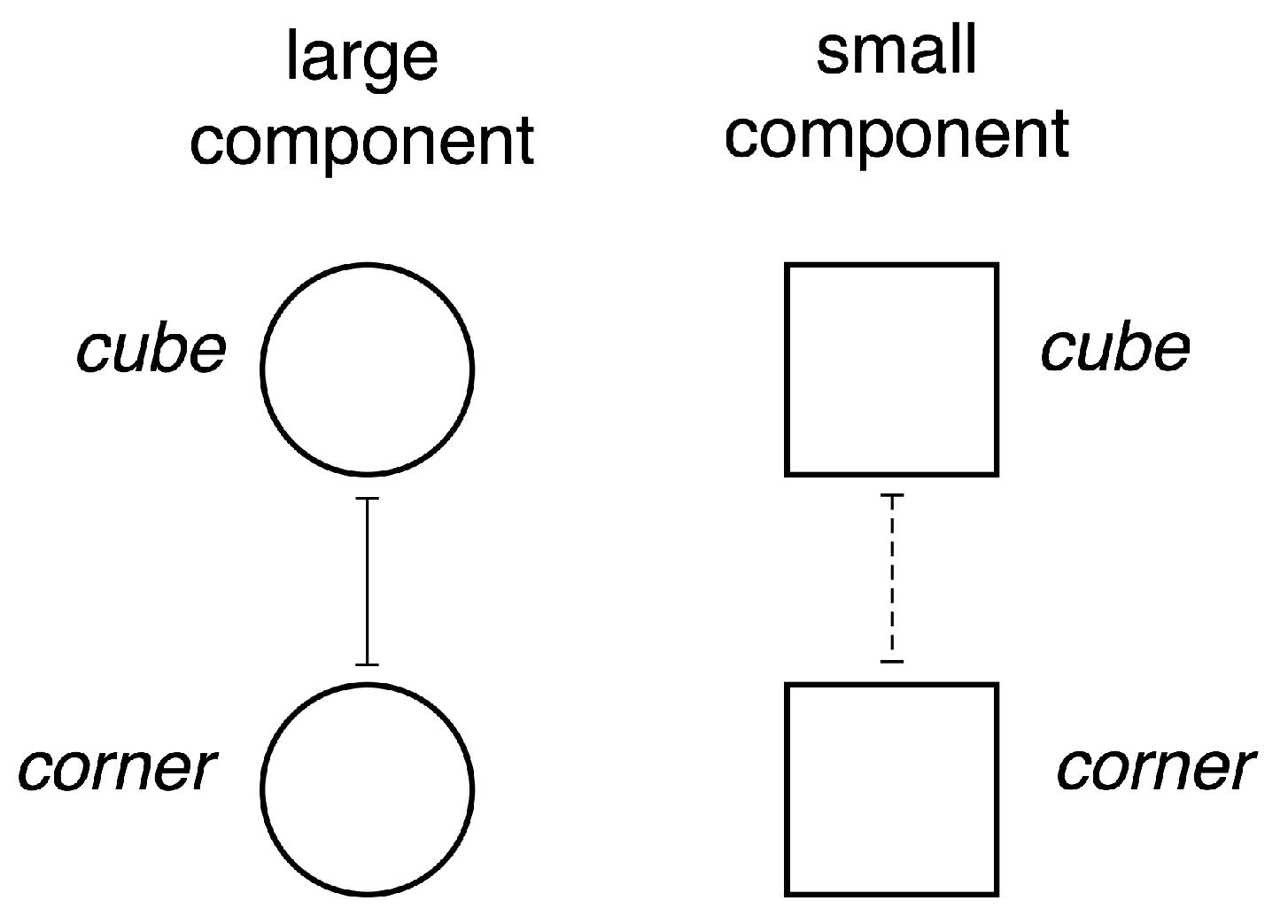
- A small cube (dark grey) in a ‘room’—a corner where three rectangles meet (light grey).
- A small cubical hole (dark grey) removed from a cube (light grey).
- A small cube (dark grey) in front of a large cube (light grey).
9.1. Why Is No Fourth Percept Observed?
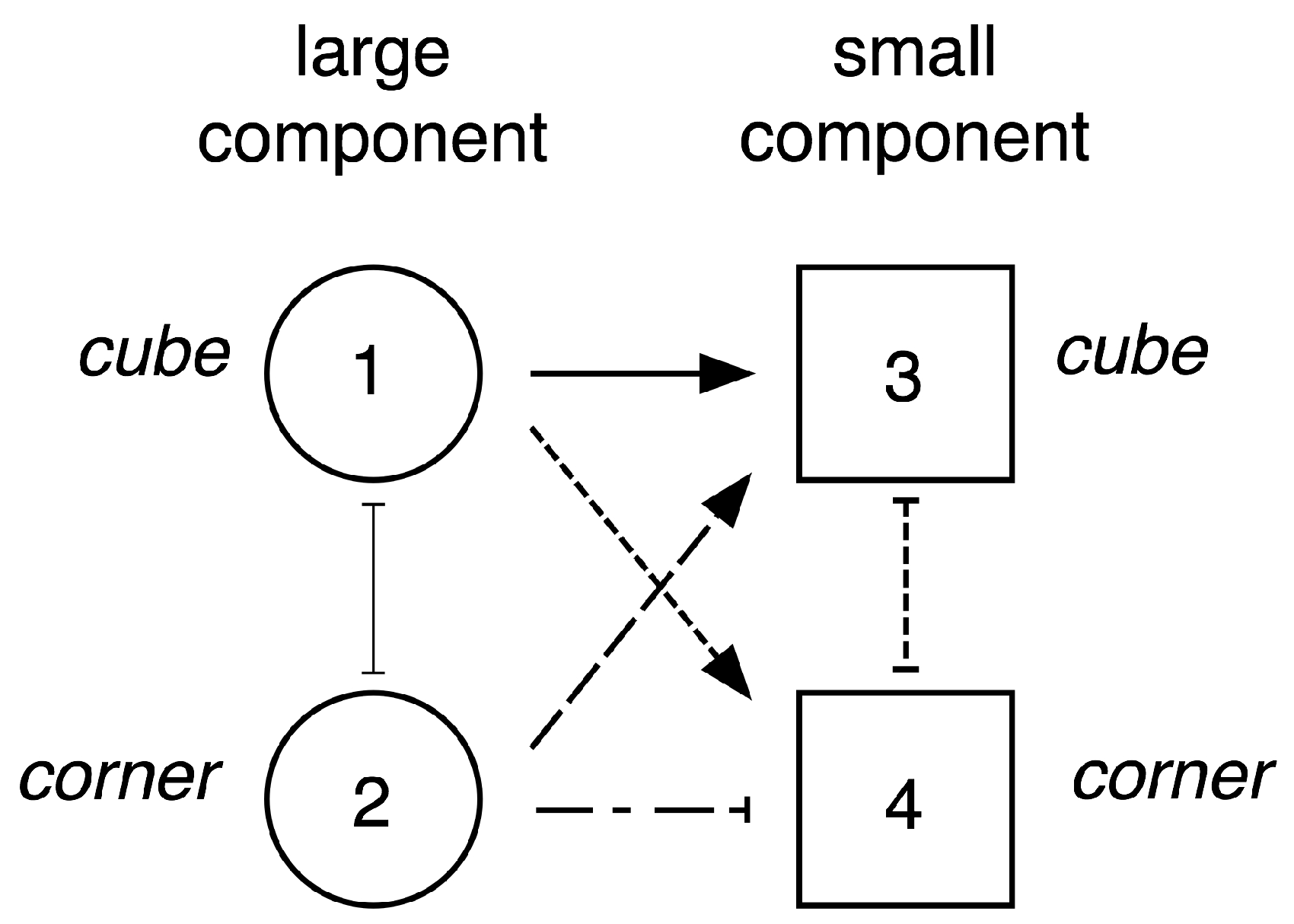
9.2. Completing the Network
- If the large component is at level cube then the small component can reasonably occur at either level cube or corner, so we insert excitatory connections from node 1 to nodes 3 and 4.
- If the large component is at level corner then by the above discussion the small component can occur in a structurally stable manner only at level cube, so we insert an excitatory connection from node 2 to node 3 and an inhibitory connection from node 2 to node 4.
10. Further Remarks and Summary
11. Conclusions
- Wilson networks with natural geometric consistency conditions are capable of modelling the perception of multistable illusions.
- A relatively small number of local geometric consistency conditions can generate the observed global form of the percepts.
- A potentially important type of geometric consistency is a form of structural stability: the percept should not depend on features of the image that can be destroyed by small perturbations.
- Important features of rate models, such as the first Hopf bifurcation from a fully synchronous equilibrium, can be understood analytically, even for quite complicated networks, provided connection strengths are gain-homogeneous and the network has sufficient symmetry.
- In particular, the first bifurcation from a fusion state in the 16-node Necker cube model selects a unique spatiotemporal pattern that matches observations.
- However, in some cases (including the 16-node model) transitional states occur that do not satisfy the geometric consistency conditions used to construct the model. These percepts correspond to impossible figures, but probably occur so briefly that they would be difficult to observe.
Author Contributions
Funding
Conflicts of Interest
References
- Blake, R.; Logothetis, N.K. Visual competition. Nat. Rev. Neurosci. 2002, 3, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Breese, B.B. Binocular rivalry. Psychol. Rev. 1909, 16, 410–415. [Google Scholar] [CrossRef]
- Wilson, H. Computational evidence for a rivalry hierarchy in vision. Proc. Nat. Acad. Sci. USA 2003, 100, 14499–14503. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H. Minimal physiological conditions for binocular rivalry and rivalry memory. Vis. Res. 2007, 47, 2741–2750. [Google Scholar] [CrossRef] [PubMed]
- Eagleman, D.M. Visual illusions and neurobiology. Nat. Rev. Neurosci. 2001, 2, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Leopold, D.A.; Logothetis, N.K. Multistable phenomena: changing views in perception. Trends Cog. Sci. 1999, 3, 254–264. [Google Scholar] [CrossRef]
- Penrose, L.S.; Penrose, R. Impossible objects: A special type of optical illusion. Brit. J. Psych. 1958, 49, 31–33. [Google Scholar] [CrossRef]
- Wikipedia. Penrose triangle. Available online: https://en.wikipedia.org/wiki/Penrose̲triangle (accessed on 1 June 2019).
- Sherman, D.A. Optical illusions. Cornell U. 2015. Available online: http://people.cornellcollege.edu/dsherman/illusions/ (accessed on 1 June 2019).
- Wilson, H.R. Requirements for conscious visual processing. In Cortical mechanisms of vision; Jenkin, M., Harris, L., Eds.; Cambridge University Press: Cambridge, UK, 2009; pp. 399–417. [Google Scholar]
- Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef]
- Yoon, M.J.; Shen, J.J. First-order modeling and stability analysis of illusory contours. Visual Comm. Image Representation 2008, 19, 42–55. [Google Scholar]
- Naber, M.; Gruenhage, G.; Einhäuser, W. Tri-stable stimuli reveal interactions among subsequent percepts: rivalry is biased by perceptual history. Vision Res. 2010, 50, 818–828. [Google Scholar] [CrossRef]
- Poston, P.; Stewart, I. Nonlinear modelling of multistable perception. Behavioral Science 1978, 23, 318–334. [Google Scholar] [CrossRef] [PubMed]
- Wallis, G.; Ringelhan, S. The dynamics of perceptual rivalry in bistable and tristable perception. Journal of Vision 2013, 24, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Necker, L.A. Observations on some remarkable optical phænomena seen in Switzerland; and on an optical phænomenon which occurs on viewing a figure of a crystal or geometrical solid. London and Edinburgh Philosophical Magazine and Journal of Science 1832, 1, 329–337. [Google Scholar] [CrossRef]
- Jastrow, J. The mind’s eye. Popular Science Monthly 1889, 54, 299–312. [Google Scholar]
- Ermentrout, G.B.; Terman, D.H. Mathematical Foundations of Neuroscience; Springer: New York, NY, USA, 2010. [Google Scholar]
- Diekman, C.; Golubitsky, M. Network symmetry and binocular rivalry experiments. J. Math. Neuro. 2014, 4. [Google Scholar] [CrossRef]
- Diekman, C.; Golubitsky, M.; McMillen, T.; Wang, Y. Reduction and dynamics of a generalized rivalry network with two learned patterns. SIAM J. Appl. Dynam. Sys. 2012, 11, 1270–1309. [Google Scholar] [CrossRef]
- Diekman, C.; Golubitsky, M.; Wang, Y. Derived patterns in binocular rivalry networks. J. Math. Neuro. 2013, 3. [Google Scholar] [CrossRef]
- Gregory, R.L. Putting illusions in their place. Perception 1991, 20, 1–4. [Google Scholar] [CrossRef]
- Gregory, R.L. Visual illusions classified. Trends in Cognitive Sciences 1997, 1, 190–194. [Google Scholar] [CrossRef]
- Changizi, M.A.; Hsieh, A.; Nijhawan, R.; Kanai, R.; Shinsuke, S. Perceiving the present and a systematization of illusions. Cognitive Science 2008, 32, 459–503. [Google Scholar] [CrossRef]
- Bach, M.; Poloschek, C.M. Optical Illusions. Adv. Clin. Neurosci. Rehabil. 2006, 6, 20–21. [Google Scholar]
- Zöllner, F. Ueber eine neue Art von Pseudoskopie und ihre Beziehungen zu den von Plateau und Oppel beschrieben Bewegungsphaenomenen. Annalen der Physik 1860, 186, 500–525. [Google Scholar] [CrossRef]
- Wikipedia. Zöllner illusion. Available online: https://en.wikipedia.org/wiki/Zöllner̲illusion (accessed on 1 June 2019).
- Fraser, J. A new visual illusion of direction. British J. Psych. 1908, 2, 307–320. [Google Scholar] [CrossRef]
- Wikipedia. Fraser spiral illusion. Available online: https://en.wikipedia.org/wiki/Fraser_spiral_illusion (accessed on 1 June 2019).
- Wikipedia. Poggendorff illusion. Available online: https://en.wikipedia.org/wiki/Poggendorff̲illusion (accessed on 1 June 2019).
- Maffei, L.; Fiorentini, A. The unresponsive regions of visual cortical receptive fields. Vis. Res. 1976, 16, 1131–1139. [Google Scholar] [CrossRef]
- Allman, J.; Miezin, F.; McGuinness, E. Stimulus specific responses from beyond the classical receptive field: neurophysiological mechanisms for local-global comparisons in visual neurons. Annu. Rev. Neurosci. 1985, 8, 407–430. [Google Scholar] [CrossRef]
- Howe, C.Q.; Yang, Z.; Purves, D. The Poggendorff illusion explained by natural scene geometry. Proc. Nat. Acad. Sci. USA 2005, 102, 7707–7712. [Google Scholar] [CrossRef] [PubMed]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Wikipedia. Spinning Dancer. Available online: https://en.wikipedia.org/wiki/Spinning̲Dancer (accessed on 1 June 2019).
- Bernal, B.; Guillen, M.; Marquez, J. The spinning dancer illusion and spontaneous brain fluctuations: An fMRI study. Neurocase 2014, 20, 627–639. [Google Scholar] [CrossRef]
- Troje, N.F.; McAdam, M. The viewing-from-above bias and the silhouette illusion. i-Perception 2010, 1, 143–148. [Google Scholar] [CrossRef]
- Grossberg, S.; Pinna, B. Neural dynamics of gestalt principles of perceptual organization: from grouping to shape and meaning. Gestalt Theory 2012, 34, 399–482. [Google Scholar]
- Pinna, B.; Gregory, R.L. Shifts of edges and deformations of patterns. Perception 2002, 31, 1503–1508. [Google Scholar] [PubMed]
- Logothetis, N.K.; Schall, J.D. Neuronal correlates of subjective visual perception. Science 1989, 245, 761–763. [Google Scholar] [CrossRef]
- Leopold, D.A.; Logothetis, N.K. Activity changes in early visual cortex reflect monkeys? percepts during binocular rivalry. Nature 1996, 379, 549–553. [Google Scholar] [CrossRef]
- Sheinberg, D.L.; Logothetis, N.K. The role of temporal cortical areas in perceptual organization. Proc. Nat. Acad. Sci. USA 1997, 94, 3408–3413. [Google Scholar] [CrossRef] [PubMed]
- Laing, C.R.; Frewen, T.; Kevrekidis, I.G. Reduced models for binocular rivalry. J. Comput. Neurosci. 2010, 28, 459–476. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Bote, R.; Rinzel, J.; Rubin, N. Noise-induced alternations in an attractor network model of perceptual bistability. J. Neurophysiology 2007, 98, 1125–1139. [Google Scholar] [CrossRef] [PubMed]
- Logothetis, N.K.; Leopold, D.A.; Sheinberg, D.L. What is rivalling during binocular rivalry? Nature 1996, 380, 621–624. [Google Scholar] [CrossRef]
- Dayan, P. A hierarchical model of binocular rivalry. Neural Comput. 1998, 10, 1119–1135. [Google Scholar] [CrossRef]
- Tong, F.; Engel, S.A. Interocular rivalry revealed in the human cortical blind-spot representation. Nature 2001, 411, 195–199. [Google Scholar] [CrossRef]
- Lumer, E.D.; Friston, K.J.; Rees, G. Neural correlates of perceptual rivalry in the human brain. Science 1998, 280, 1930–1934. [Google Scholar] [CrossRef]
- Tong, F.; Nakayama, K.; Vaughan, J.T.; Kanwisher, N. Binocular rivalry and visual awareness in human extrastriate cortex. Neuron 1998, 21, 753–759. [Google Scholar] [CrossRef]
- Stewart, I. Symmetry-breaking in a rate model for a biped locomotion central pattern generator. Symmetry 2014, 6, 23–66. [Google Scholar] [CrossRef]
- Stewart, I. Spontaneous symmetry-breaking in a network model for quadruped locomotion. Internat. J. Bif. Chaos 2017, 27, 1730049. [Google Scholar] [CrossRef]
- Hong, S.W.; Shevell, S.K. Resolution of binocular rivalry: perceptual misbinding of color. Vis. Neurosci. 2006, 23, 561–566. [Google Scholar] [CrossRef] [PubMed]
- Kovács, I.; Papathomas, T.V.; Yang, M.; Fehér, A. When the brain changes its mind: interocular grouping during binocular rivalry. Proc. Natl. Acad. Sci. USA 1996, 93, 15508–15511. [Google Scholar] [CrossRef] [PubMed]
- Shevell, S.K.; St Clair, R.; Hong, S.W. Misbinding of color to form in afterimages. Vis. Neurosci. 2008, 25, 355–360. [Google Scholar] [CrossRef]
- Wiesel, T.N.; Hubel, D.H. Single-cell responses in striate cortex of kittens deprived of vision in one eye. J. Neurophysiol. 1963, 26, 1003–1017. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, H.V.B.; Spinelli, D.N. Visual experience modifies distribution of horizontally and vertically oriented receptive fields in cats. Science 1970, 168, 869–871. [Google Scholar] [CrossRef]
- Iacaruso, M.F.; Gasler, I.T.; Hofer, S.B. Synaptic organisation of visual space in primary visual cortex. Nature 2017, 547, 449–452. [Google Scholar] [CrossRef]
- Bressloff, P.C.; Cowan, J.D.; Golubitsky, M.; Thomas, P.J.; Wiener, M.C. Geometric visual hallucinations, Euclidean symmetry, and the functional architecture of striate cortex. Phil. Trans. R. Soc. London B 2001, 356, 299–330. [Google Scholar] [CrossRef]
- Golubitsky, M.; Shiau, L.-J.; Török, A. Bifurcation on the visual cortex with weakly anisotropic lateral coupling. SIAM J. Appl. Dyn. Syst. 2003, 2, 97–143. [Google Scholar] [CrossRef]
- Blasdel, G.G. Orientation selectivity, preference, and continuity in monkey striate cortex. J. Neurosci. 1992, 12, 3139–3161. [Google Scholar] [CrossRef] [PubMed]
- Golubitsky, M.; Stewart, I. Nonlinear dynamics of networks: the groupoid formalism. Bull. Amer. Math. Soc. 2006, 43, 305–364. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.; Török, A. Patterns of synchrony in coupled cell networks with multiple arrows. SIAM J. Appl. Dynam. Sys. 2005, 4, 78–100. [Google Scholar] [CrossRef]
- Stewart, I.; Golubitsky, M.; Pivato, M. Symmetry groupoids and patterns of synchrony in coupled cell networks. SIAM J. Appl. Dynam. Sys. 2003, 2, 609–646. [Google Scholar] [CrossRef]
- Ta’eed, L.K.; Ta’eed, O.; Wright, J.E. Determinants involved in the perception of the Necker cube: An application of catastrophe theory. Behavioral Sci. 1998, 33, 97–115. [Google Scholar]
- Peregoy, P.; Stewart, I. Catastrophe theory modelling in psychology. Psych. Bull. 1983, 94, 336–362. [Google Scholar]
- Seely, J.; Chow, C.C. The role of mutual inhibition in binocular rivalry. J. Neurophysiol. 2011, 106, 2136–2150. [Google Scholar] [CrossRef]
- Liu, L.; Tyler, C.W.; Schor, C.M. Failure of rivalry at low contrast: evidence of a suprathreshold binocular summation process. Vis. Res. 1992, 32, 1471–1479. [Google Scholar] [CrossRef]
- Shpiro, A.; Curtu, R.; Rinzel, J.; Rubin, N. Dynamical characteristics common to neuronal competition models. J. Neurophysiol. 2007, 97, 462–473. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Hassard, B.D.; Kazarinoff, N.D.; Wan, Y.-H. Theory and Applications of Hopf Bifurcation; London Mathematical Society Lecture Note series; Cambridge University Press: Cambridge, UK, 1981; Volume 41. [Google Scholar]
- Golubitsky., M.; Stewart, I. The Symmetry Perspective; Progress in Mathematics; Birkhäuser: Basel, Switzerland, 2002; Volume 200. [Google Scholar]
- Golubitsky., M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory II; Applied Mathematics Series; Springer: New York, NY, USA, 1988; p. 69. [Google Scholar]
- Curtu, R. Singular Hopf bifurcations and mixed-mode oscillations in a two-cell inhibitory neural network. Phys. D 2010, 239, 504–514. [Google Scholar] [CrossRef]
- Curtu, R.; Shpiro, A.; Rubin, N.; Rinzel, J. Mechanisms for frequency control in neuronal competition models. SIAM J. Appl. Dyn. Syst. 2008, 7, 609–649. [Google Scholar] [CrossRef]
- Kalarickal, G.J.; Marshall, J.A. Neural model of temporal and stochastic properties of binocular rivalry. Neurocomputing 2000, 32, 843–853. [Google Scholar] [CrossRef]
- Laing, C.; Chow, C. A spiking neuron model for binocular rivalry. J. Comput. Neurosci. 2002, 12, 39–53. [Google Scholar] [CrossRef]
- Lehky., S.R. An astable multivibrator model of binocular rivalry. Perception 1988, 17, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, K. The dynamic model of binocular rivalry. Biol. Cybern. 1984, 49, 201–208. [Google Scholar] [CrossRef]
- Mueller, T.J. A physiological model of binocular rivalry. Vis. Neurosci. 1990, 4, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Noest, A.J.; van Ee, R.; Nijs, M.M.; van Wezel, R.J.A. Percept-choice sequences driven by interrupted ambiguous stimuli: a low-level neural model. J. Vis. 2007, 7(8), 10. [Google Scholar] [CrossRef]
- Shpiro, A.; Moreno-Bote, R.; Rubin, N.; Rinzel, J. Balance between noise and adaptation in competition models of perceptual bistability. J. Comput. Neurosci. 2009, 27, 37–54. [Google Scholar] [CrossRef]
- Lappin, J.S.; Craft, W.D. Foundations of spatial vision: from retinal images to perceived shapes. Psychol. Rev. 2000, 107, 6–38. [Google Scholar] [CrossRef]
- Quinn, P.C. Visual perception of orientation is categorical near vertical and continuous near horizontal. Perception 2004, 33, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Adams, D. The Hitch Hiker’s Guide to the Galaxy; Pan: London, UK, 1979. [Google Scholar]
- Khoh, C.W.; Kovesi, P. Animating impossible objects. Computer Science & Software Engineering, U of Western Australia 1999. Available online: http://www.csse.uwa.edu.au/~pk/Impossible/impossible.html (accessed on 1 June 2019).
- Smale, S. Differentiable dynamical systems. Bull. Amer. Math. Soc. 1967, 73, 747–817. [Google Scholar] [CrossRef]
- Thom, R. Structural Stability and Morphogenesis; Benjamin: Reading MA, USA, 1975. [Google Scholar]
- Blake, R.; Yu, K.; Lokey, M.; Norman, H. What is suppressed during binocular rivalry? Perception 1980, 9, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Blake, R. A fresh look at interocular grouping during binocular rivalry. Vis. Res. 2004, 44, 983–991. [Google Scholar] [CrossRef]
- Papathomas, T.V.; Kovács, I.; Conway, T. Interocular grouping in binocular rivalry: Basic attributes and combinations. In Binocular Rivalry; Alais, D., Blake, R., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 155–168. [Google Scholar]





| Pattern | Eigenvalue |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
| No. | Spatial K | Eigenvector Structure (Activity Variable Only) | |||
|---|---|---|---|---|---|
| 1 | + | + | + | ||
| 2 | − | + | + | ||
| 3 | + | − | + | ||
| 4 | − | − | + | ||
| 5 | − | + | − | ||
| 6 | + | + | − | ||
| 7 | − | − | − | ||
| 8 | + | − | − |
| Pattern | Eigenvalue | Symbol |
|---|---|---|
| 1 | [multiplicity 2] | |
| 2 | [multiplicity 2] | |
| 3 | [multiplicity 2] | |
| 4 | [multiplicity 2] | |
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stewart, I.; Golubitsky, M. Symmetric Networks with Geometric Constraints as Models of Visual Illusions. Symmetry 2019, 11, 799. https://doi.org/10.3390/sym11060799
Stewart I, Golubitsky M. Symmetric Networks with Geometric Constraints as Models of Visual Illusions. Symmetry. 2019; 11(6):799. https://doi.org/10.3390/sym11060799
Chicago/Turabian StyleStewart, Ian, and Martin Golubitsky. 2019. "Symmetric Networks with Geometric Constraints as Models of Visual Illusions" Symmetry 11, no. 6: 799. https://doi.org/10.3390/sym11060799
APA StyleStewart, I., & Golubitsky, M. (2019). Symmetric Networks with Geometric Constraints as Models of Visual Illusions. Symmetry, 11(6), 799. https://doi.org/10.3390/sym11060799




