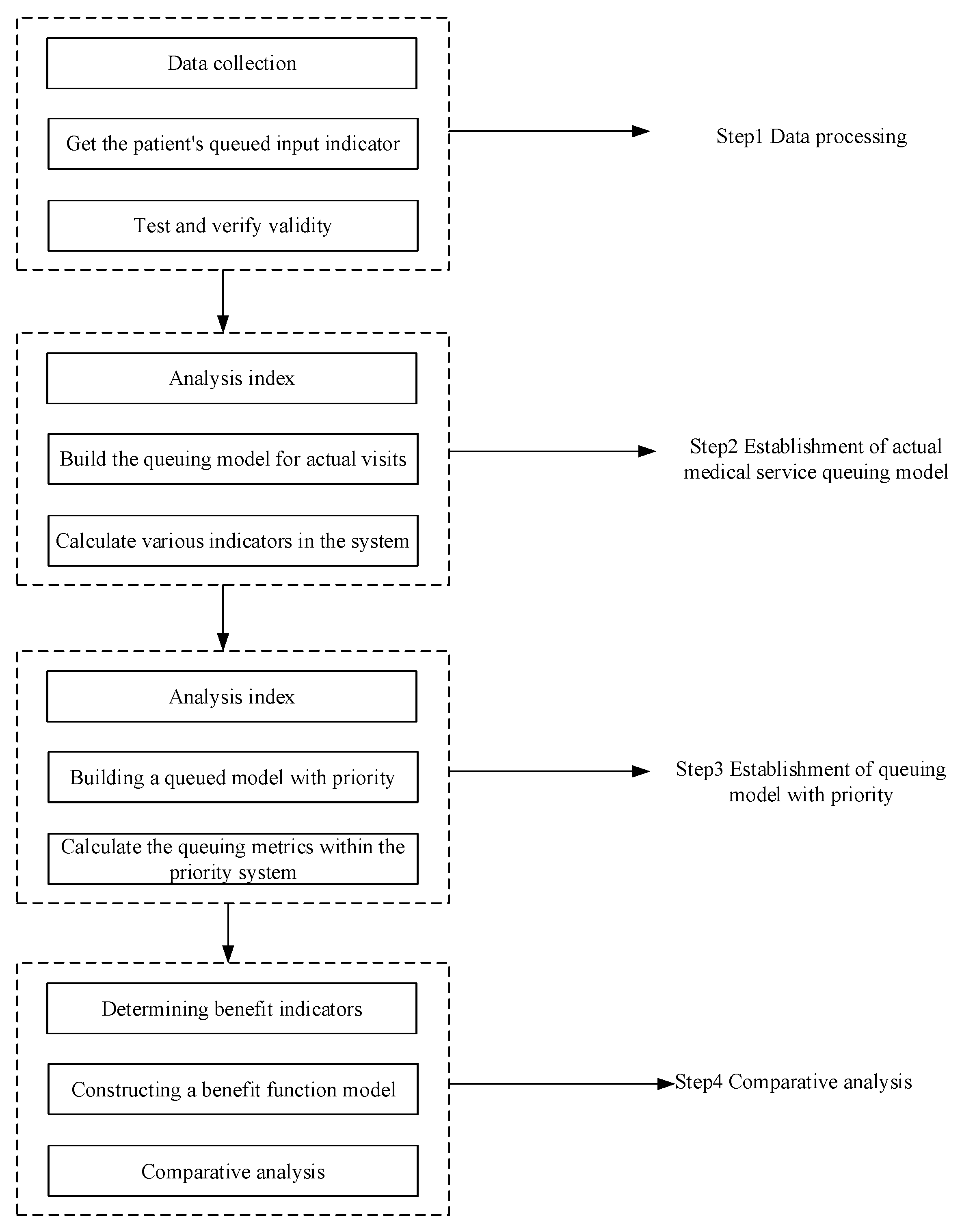
4.2.1. Calculation of Queued Indicators
According to the collated data, this paper obtains the relevant queuing indicators because an infinitely long queue is generated when the service strength in the system is greater than 1. We calculated the service intensity and found the number of beds c to be 3.6. In order to obtain more sample data for normalization, we use the number of beds as the variable to obtain multiple sets of the selected indicators. The number of services selected in this paper is 5, 7, 9, 11, and 14.
According to the queuing model formula obtained in the fourth section, we use MATLAB to solve all the queuing indicators under the first-come-first-served system, the relevant queuing indicators of the emergency patient with the priority system, and the non-emergency patient. The relevant queuing indicators and the total queuing indicators under the priority system are individually represented in
Table 7,
Table 8,
Table 9 and
Table 10.
4.2.2. Comparison of Queuing Systems
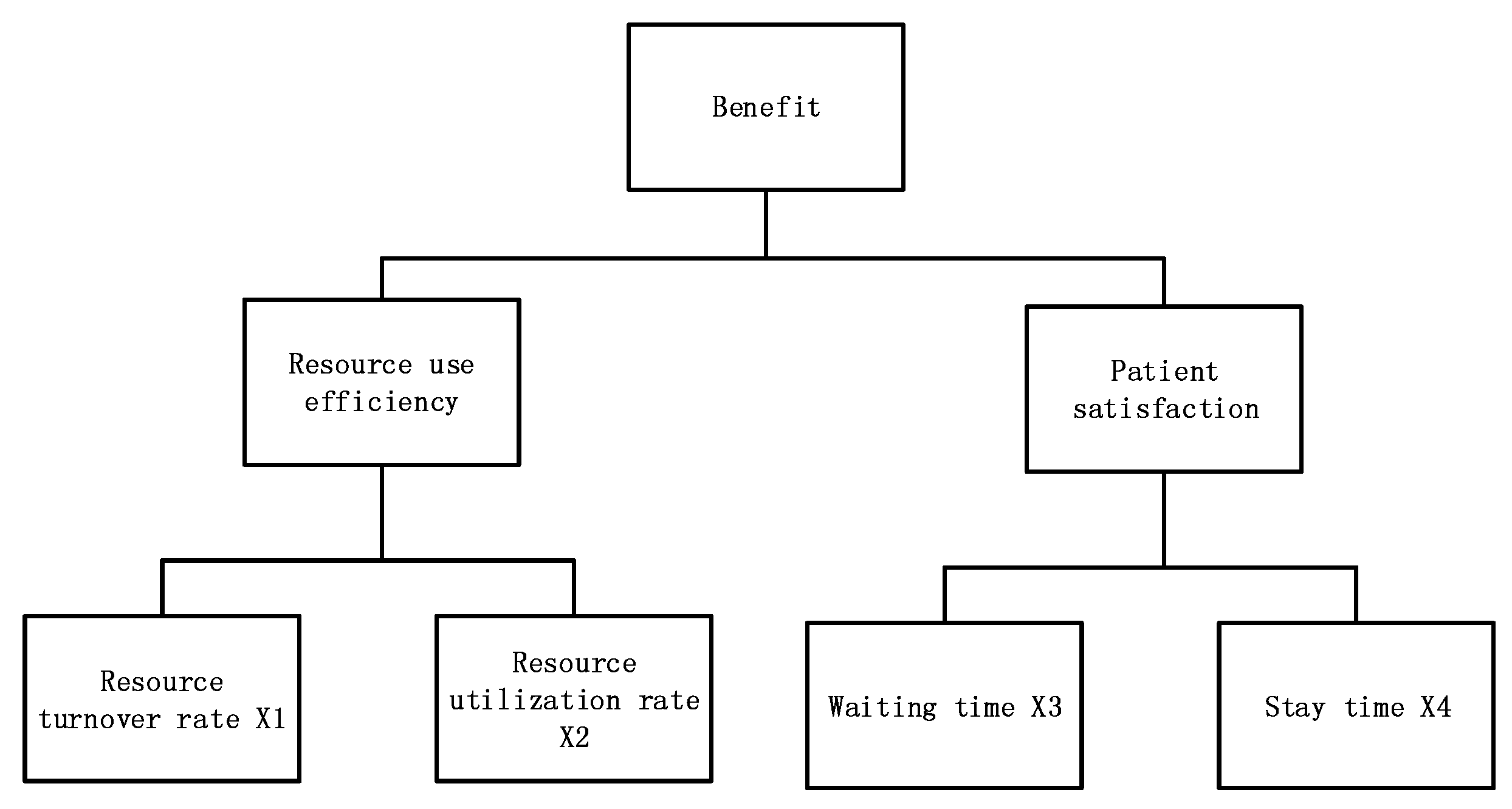
First, after normalizing the queuing theory in 4.2.1, it is brought into the benefit function formula 13 to obtain the benefit function
under the first-come-first-served and the benefit function
under the priority system.
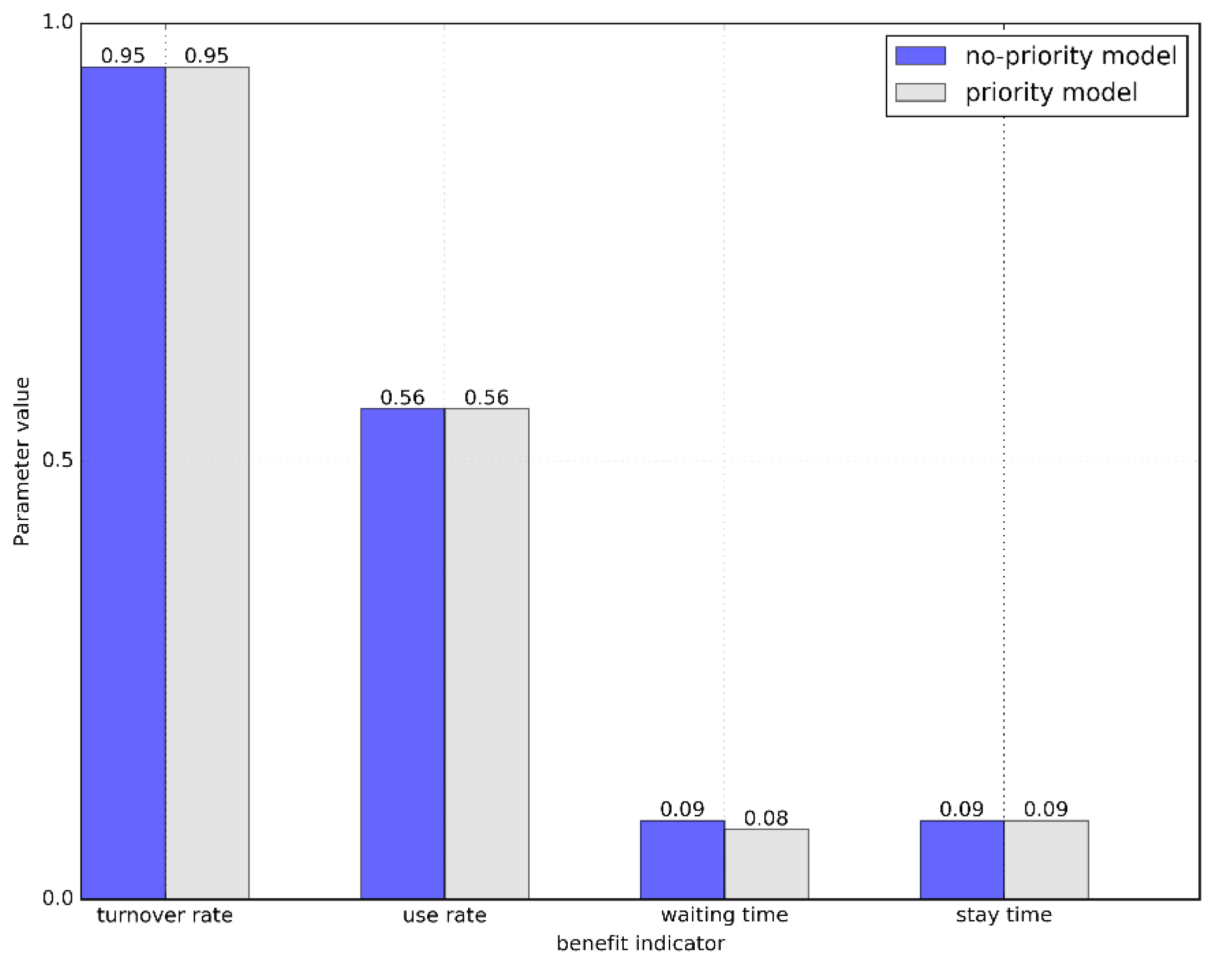
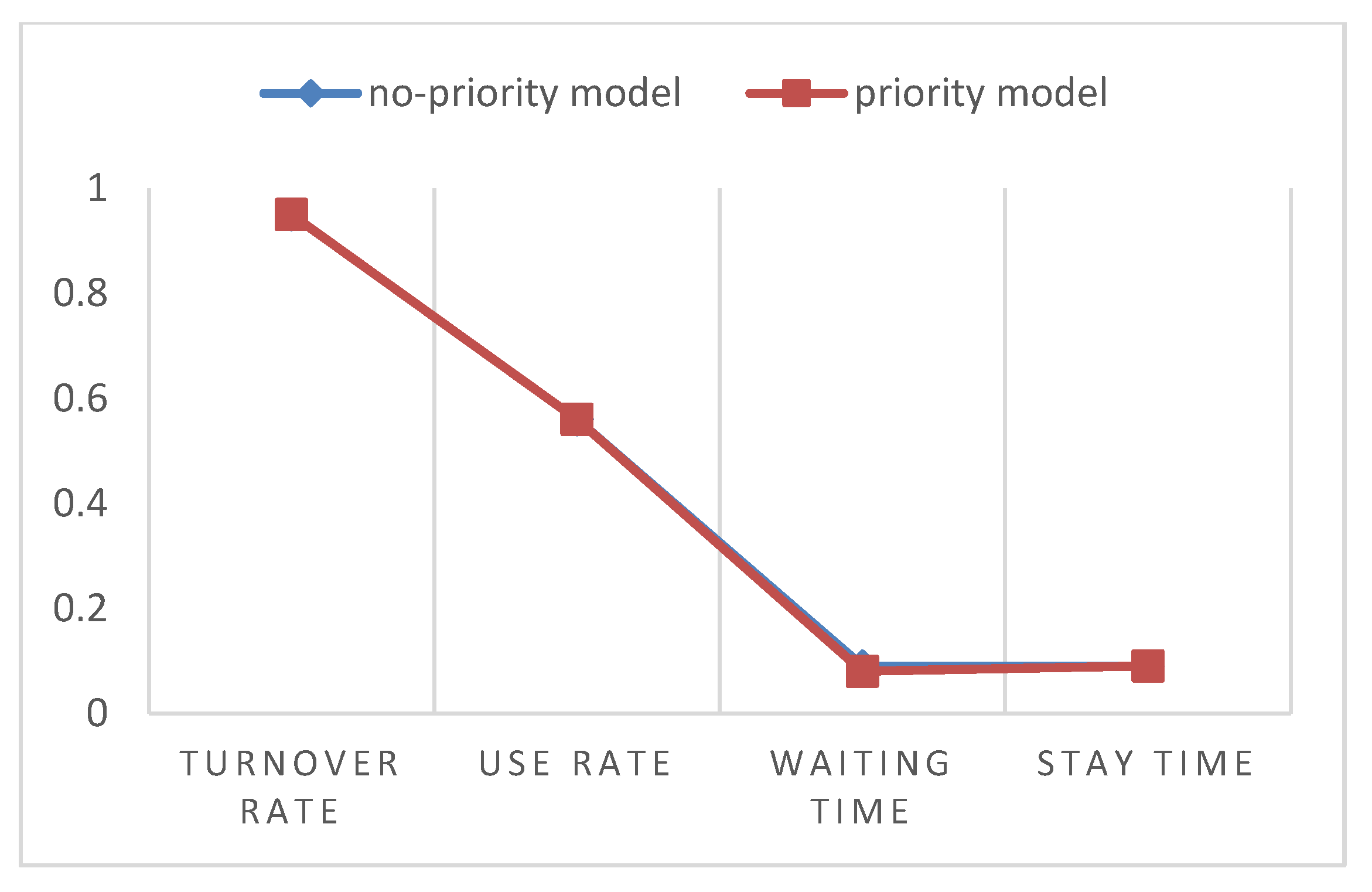
Based on the above results, it is found that the benefit value of the bed has not changed correspondingly to the bed lining system under the existing first-come-first-served rules after giving the emergency patient non-preemptive priority. Since there is basically no difference in the benefit value, we need to compare the various queuing factors that determine the benefit value. Since the index values have been normalized, we use the form of the chart here to make a more intuitive comparison in
Figure 3 and
Figure 4.
According to the above comparison results, it can be found that when the first-come-first-served and the prioritized queuing system are balanced, not only are the overall benefits not significantly changed, but the relevant indicators in the system are also basically the same. Then it can be shown that priority does not change the integrity and balance of the system.
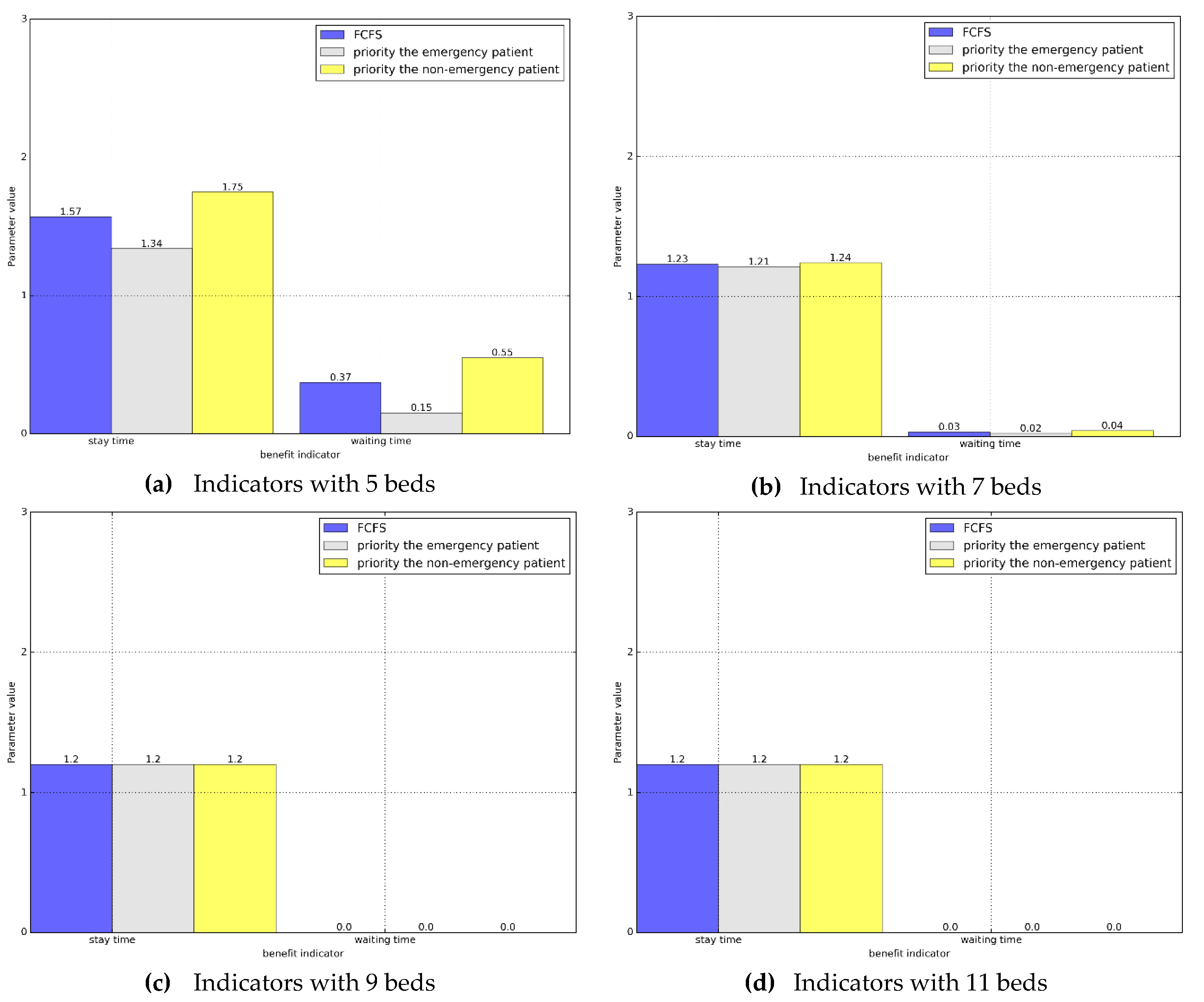
Since there is no difference in the overall indicators, we will discuss then the indicators of the two queuing systems for the emergency patient and non-emergency patient. Based on the relevant data obtained in
Section 4.2.1, we first compare the wait time with the stay time, and we present the data as a histogram in
Figure 5.
According to the histogram, we can clearly see that compared with the current queuing method, after waiting for the priority of the emergency department, the waiting time and stay time are significantly reduced. At the same time, for non-emergency patients, although the relevant indicators have increased, though not obviously, and when the number of resources reaches a certain number, there is no difference between emergency patients and non-emergency patients in the priority system.
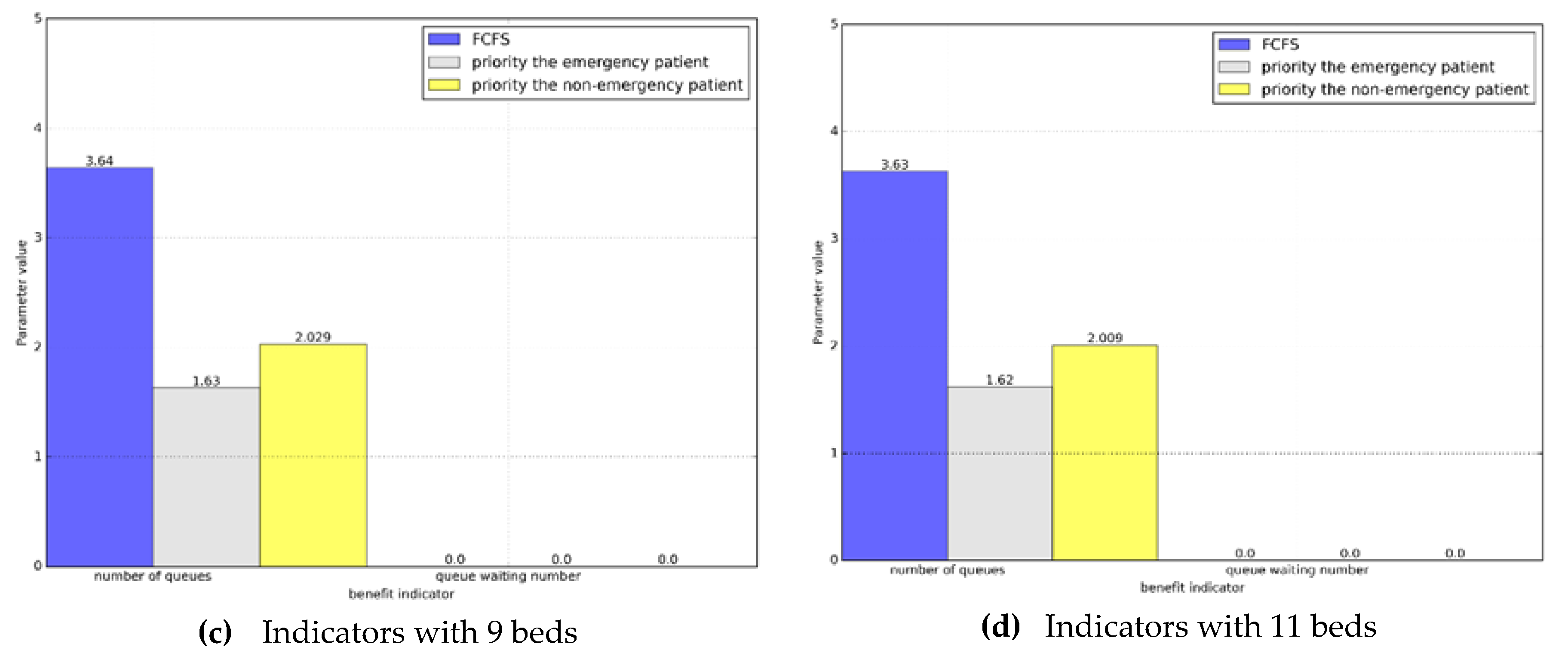
Next, we will compare the queue length and the waiting numbers. Similarly, we will display it in the form of a histogram in
Figure 6.
Based on the comparison, we can see that in the priority system the average number of waiting patients and the average number of queues in the emergency department are less than those in the non-emergency patients. At the same time, we find that when the system reaches a steady state, in the priority system, the total number of emergency and non-emergency patients is the same as the number of patients in the actual situation.
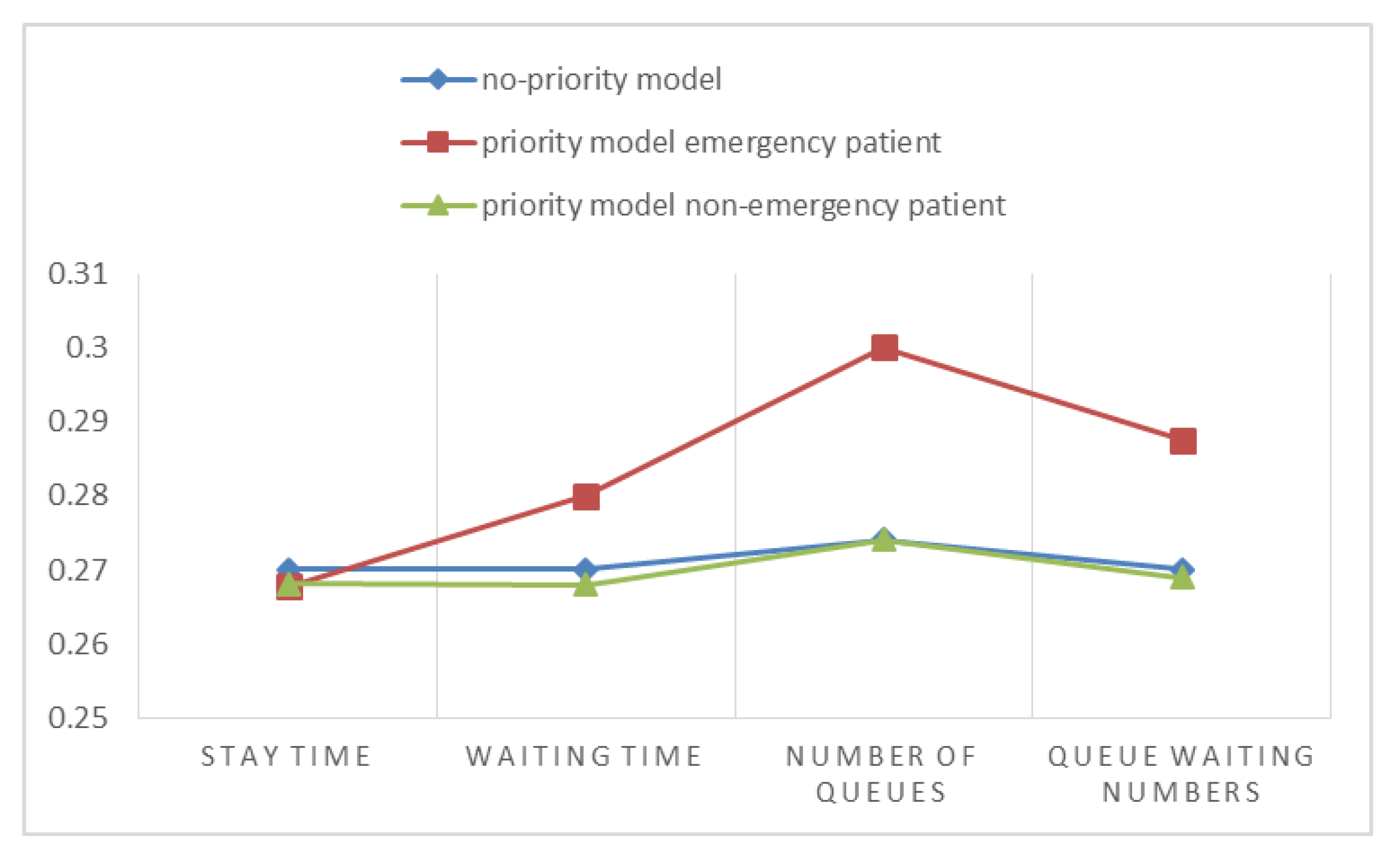
Comparing these two sets of indicators, it can be found that in the priority system, the emergency service patient’s service index is indeed optimized, but it does not reflect the specific changes of the emergency service indicators of non-emergency patients. Hence, we compare them next by normalizing the data in
Figure 7.
After normalization, we find that when priority is given to the emergency patients, the trend is very obvious compared with the actual situation which is the same as the above conclusion. More importantly, non-emergency patients did not change their relative indicators after the two systems reached a steady state, indicating that giving priority to emergency patients did not have a significant impact on non-emergency patients.
We now summarize the comparative analysis. After giving emergency patients a certain priority, their queuing indicators are optimized, such as the average waiting time and the length of stay in the emergency department, so that the emergency patient’s condition will not be delayed and they can get treatment earlier. At the same time, there has not been a significant change in the indicators of visits to non-emergency patients. Therefore, it can be concluded that the queuing system with priority has a certain improvement effect on the medical service of the emergency department.