Theoretical Model of the Axial Residual Velocity of PELE Projectiles Penetrating Thin Metal Targets

Abstract

With the increase of battlefield target diversity and protection mobility, the disadvantages of traditional armor piercing warheads have gradually become prominent. The conception of the PELE (penetration with enhanced lateral efficiency) projectile was thus proposed. The axial residual velocity of the projectile is a very important indicator of a PELE projectile, which mainly reflects the penetration ability of the PELE projectile. The PELE projectile is a symmetrical structure, so the collision problem can be simplified to plane collision. Furthermore, the two-dimensional plane is axisymmetric, and so it can be further simplified to one-dimensional collision. Based on simplification and assumptions, the mechanism of a PELE projectile penetrating a thin metal target plate was studied using the shock wave theory, and a theoretical model of axial residual velocity has been established in this article. The energy loss during the penetration process was divided into the following parts: the kinetic energy increment of the target plug in the impact region, the internal energy increment of the outer casing and inner core, and the shear energy dissipation of the projectile against the target plate. In addition, the specific methods of determining the energy loss of each part are given in detail. According to the conservation of energy, the approximate calculation formulae of the axial residual velocity of a PELE projectile have been deduced. Finally, the theoretical results were compared with the experimental results under different working conditions, and the results were in good agreement. Therefore, the theoretical model has application value and guiding significance in the field of engineering.

1. Introduction

The PELE (penetration with enhanced lateral efficiency) projectile is a new type of penetrating body proposed in recent years. This new type of ammunition is the result of a cooperation between the French-German Research Institute Saint Louis, the GEKE Technology in Freiburg, and the Diehl Munitionssysteme. PELE projectiles have the advantage of being able to convert axial velocity into radial velocity without any pyrotechnical agents. They are mainly composed of a high density outer casing and a low density inner core; a simplified schematic diagram is shown in Figure 1. The outer casing is usually made of heavy metals such as steel or tungsten, which can achieve good penetration performance when impacting the metal target plate. The inner core is made of inert materials such as plastic or aluminum, which are relatively weak in penetration. When the PELE projectile impacts the metal target plate, the inner core moves slowly forward and is squeezed between the crater and outer casing. The rising pressure in the inner core causes the surrounding casing to expand and produce a radial force on the casing, as shown in Figure 2a. As the projectile perforates the target plate, the radial force of the inner core is released, and the outer casing is broken down into large numbers of fragments radially, as shown in Figure 2b. Therefore, the PELE projectile not only has stronger penetration ability, but also has stronger lateral damage performance [1,2].

The axial residual velocity of the projectile, the radial scattering velocity, and the spatial distribution of fragments are important indicators used to measure damage efficiency. Many experts and scholars [3,4,5,6,7,8] have studied the factors that affect the lateral effect of PELE projectiles, such as the impact velocity, the intersection posture between the projectile and target plate, the material of the inner core, and so on. However, experiments only reflect changes in state, which cannot give the specific changes in the process. In order to reach a clearer and more intuitive understanding of the penetration process of the PELE projectile and its mechanism of action, Paulus [3], Verreault [9], and other scholars [10,11,12] carried out a lot of numerical simulations of the penetration process of PELE projectiles using the finite element simulation software Autodyn (Century Dynamics, FortWorth, TX, USA) and LS-DYNA (Livermore Software Technology Corporation, Livermore, CA, USA), and obtained the key factors that affect the damage power of PELE projectiles. Neither experiments nor simulations can describe the penetration process of PELE projectiles theoretically. By using elastic wave theory and energy conservation, Paulus [3] established the calculation model of the axial residual velocity and the radial scattering velocity after PELE projectile penetrating of a target plate. Zhu [13] and Du [14] analyzed from experimental and theoretical perspectives the fragmentation effect of PELE after penetrating a metal target plate. However, the theoretical analysis models they built adopted the acoustic approximation, ignoring the multiple wave interactions at the inner core/target interface. According to shock wave theory and Motto fragment distribution theory [15,16], Verreault [9,17,18] established the theoretical model of the radial scattering velocity after PELE projectile penetrating of a target plate. Fan [19] developed a two-stage to estimate the radial velocity of PELE projectiles after perforating the target plate by using the shock wave theory.

Based on the above literature investigation, it can be found that most of the previous works on the penetration process of PELE projectiles have focused on experiments and numerical simulations. Moreover, there are some limitations in the theoretical analysis when using one-dimensional linear elastic wave theory to analyze the penetration process of PELE projectiles. The residual velocity of the projectile, the radial scattering velocity, and the spatial distribution of fragments are three important aspects of PELE projectiles. The residual velocity of the projectile mainly reflects the penetration ability of the PELE projectile. Although PELE projectiles are usually aimed at thinner targets, they are often used as a penetrating body to penetrate thicker targets or even multi-layer targets, whereupon the projectile velocity will also be greatly attenuated. Therefore, it is necessary to establish a theoretical model of the residual velocity of a projectile with a wider range of speeds. In view of this, the main research work of this paper was based on shock wave theory and energy conversion; the energy dissipation during the penetration process were analyzed in detail. On this basis, the theoretical model of axial residual velocity of a PELE projectile penetrating a metal thin target plate was established, and the theoretical model was validated by experiments.

2. Establishment of the Theoretical Model of Axial Residual Velocity

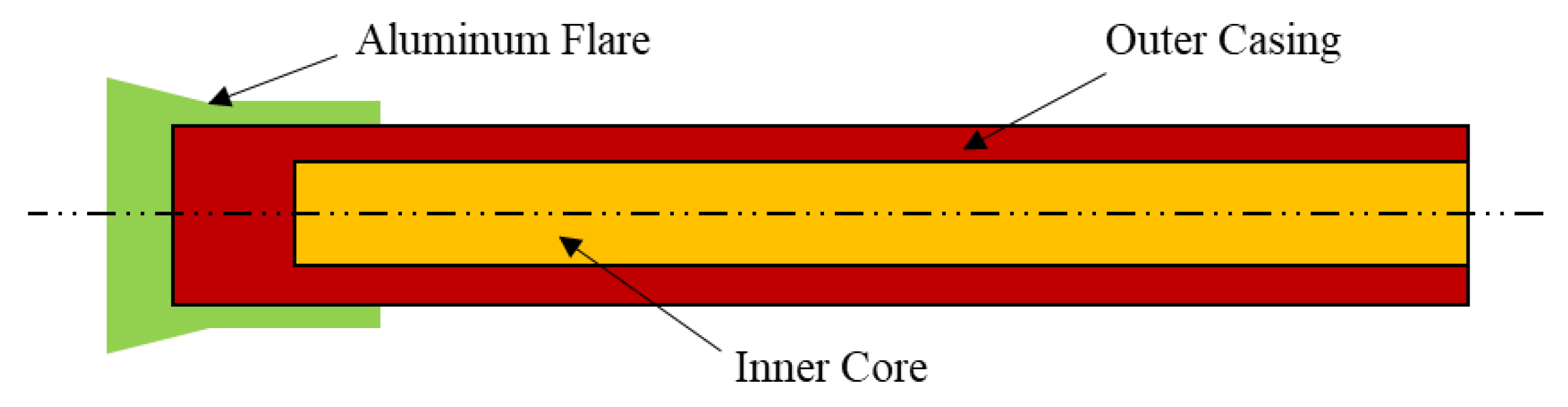
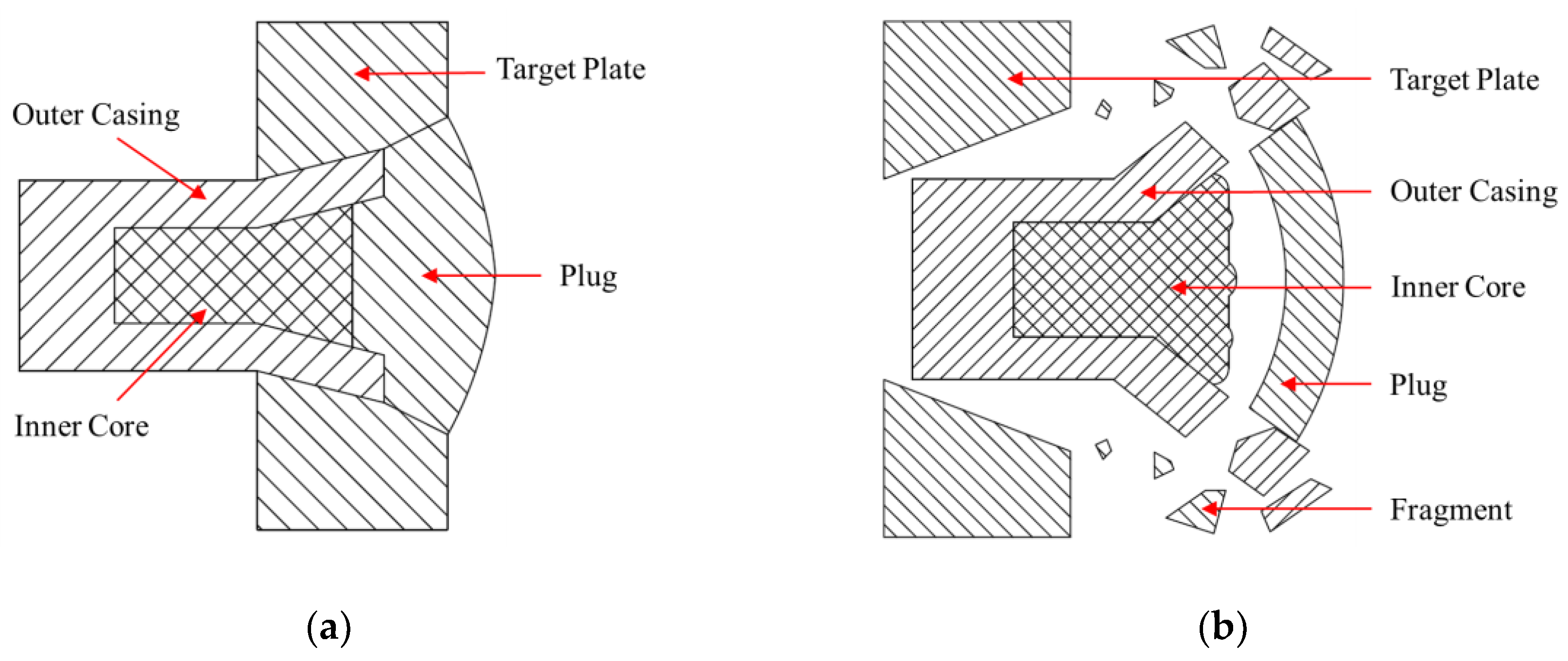
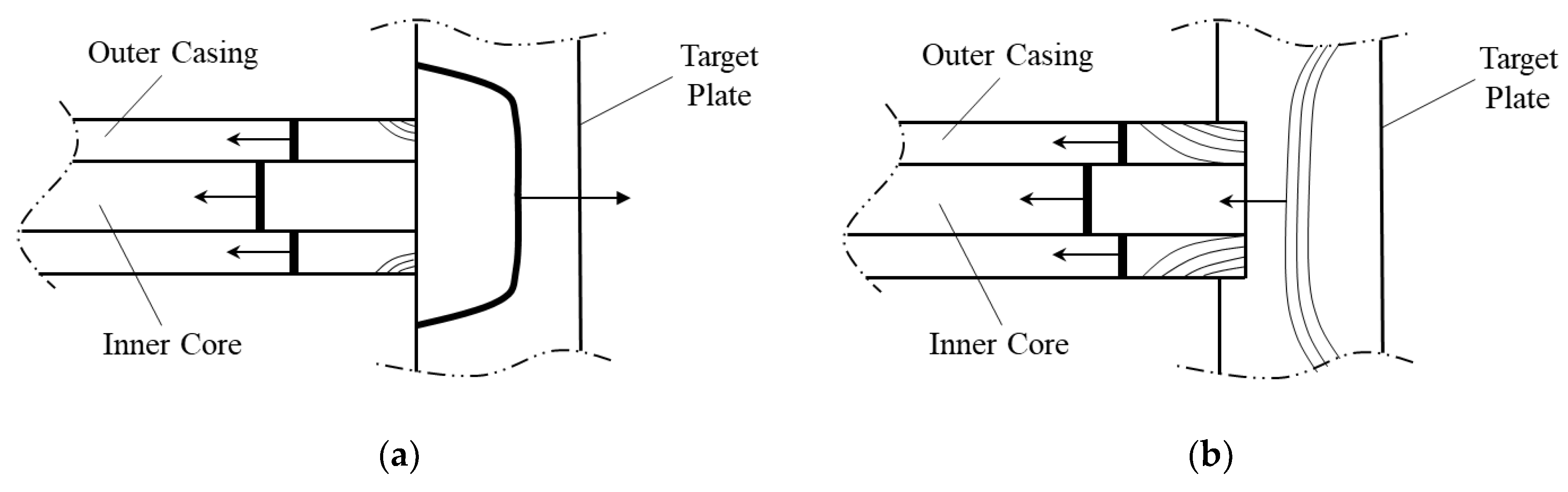
2.1. Plane Shock Wave Assumption of PELE Projectile Penetrating Against Target Plate

Since the PELE projectile has a symmetrical structure, the collision between the projectile and the target plate can be simplified to a plane collision problem. When the PELE projectile impacts the target plate, two shock waves are generated at the contact interface between the projectile and target plate. The shock waves propagate to the rear of the projectile and the target plate respectively, as shown in Figure 3a. Since the target thickness is much smaller than the projectile length, the shock waves in the target plate first reach the free interface of the target plate and reflect rarefaction waves to the contact interface, as shown in Figure 3b. In order to facilitate the division of the penetration process, the following definitions are made: t₀ represents the moment when the projectile has just touched the target plate; t₁ represents the moment when the rarefaction waves from the back side of the target plate reach the contact interface; t₂ represents the moment when the PELE projectile just perforates the target plate. The time range t₀–t₁ is defined as the impact stage, and the time range t₁–t₂ is defined as the plug shear stage. Thus, the process of the PELE projectile penetrating the target plate can be divided into two stages: projectile impact stage and plug shear stage.

On the moment of impact between the PELE projectile and target plate, one shock wave is produced in the target plate and propagates to the back of the target plate, and another shock wave, opposite to the projectile’s flight direction, is generated in the projectile. Due to the inner core material being different from the outer casing, the intensity and shock wave velocity of the inner core and outer casing are different. After the plane shock wave, the rarefaction wave propagates radially from the interface to the projectile interior, which causes the projectile to expand radially. The plane shock wave relationship is obtained under the one-dimensional stress condition. To analyze the process of a PELE penetrating a target plate using the plane shock wave theory, the following assumptions are required:

(1) Neglecting the influence of shearing force on the impact wave intensity. The shearing force is caused by the difference of particle velocity between the projectile and target plate, which makes the impact velocity decrease and the impact pressure increase. For a thin target plate, the shearing force is smaller than the impact pressure, so it can be neglected.

(2) The radial expansion of projectile is neglected before the projectile perforates the target plate. After the shock wave, the projectile casing will expand radially under the action of the rarefaction wave. However, within the time range of investigation, the radial expansion value of the projectile is limited, and it is considered that the radial deformation of the outer casing is limited by the target plate. Therefore, the radial expansion of the projectile is neglected in the perforation process.

Since both the PELE projectile and the target plate have symmetrical structures, when analyzing the stress state of the projectile and the target plate, it can be simplified into a 2D (two-dimensional) plane problem and the 2D plane is axisymmetric. In this paper, the axial residual velocity of the projectile is mainly studied, not the radial dispersion of fragments after the projectile perforates the target plate. Therefore, combined with the above two basic assumptions, the study of the axial residual velocity of projectile can be further simplified to a 1D (one-dimensional) collision problem. The penetration process of the PELE projectile against a thin metal target plate is similar to that of the flat head projectile, and the penetration process can be analyzed using the shear resistance model of the flat head projectile. The shear resistance model divides the energy loss during the penetration process into two parts: the impact energy dissipation between the projectile and the target plate, and the shear energy dissipation of the plug in the perforation process.

According to shock wave theory, the impact energy dissipation can be divided into the following parts: impact compression potential energy of the plug, the kinetic energy of particles after the shock wave, and the impact compression potential energy of the outer casing and inner core etc. Based on the characteristics of the PELE projectile, the shear energy dissipation of the plug is divided separately into the inner edge and outer edge of projectile casing shear of the target plate.

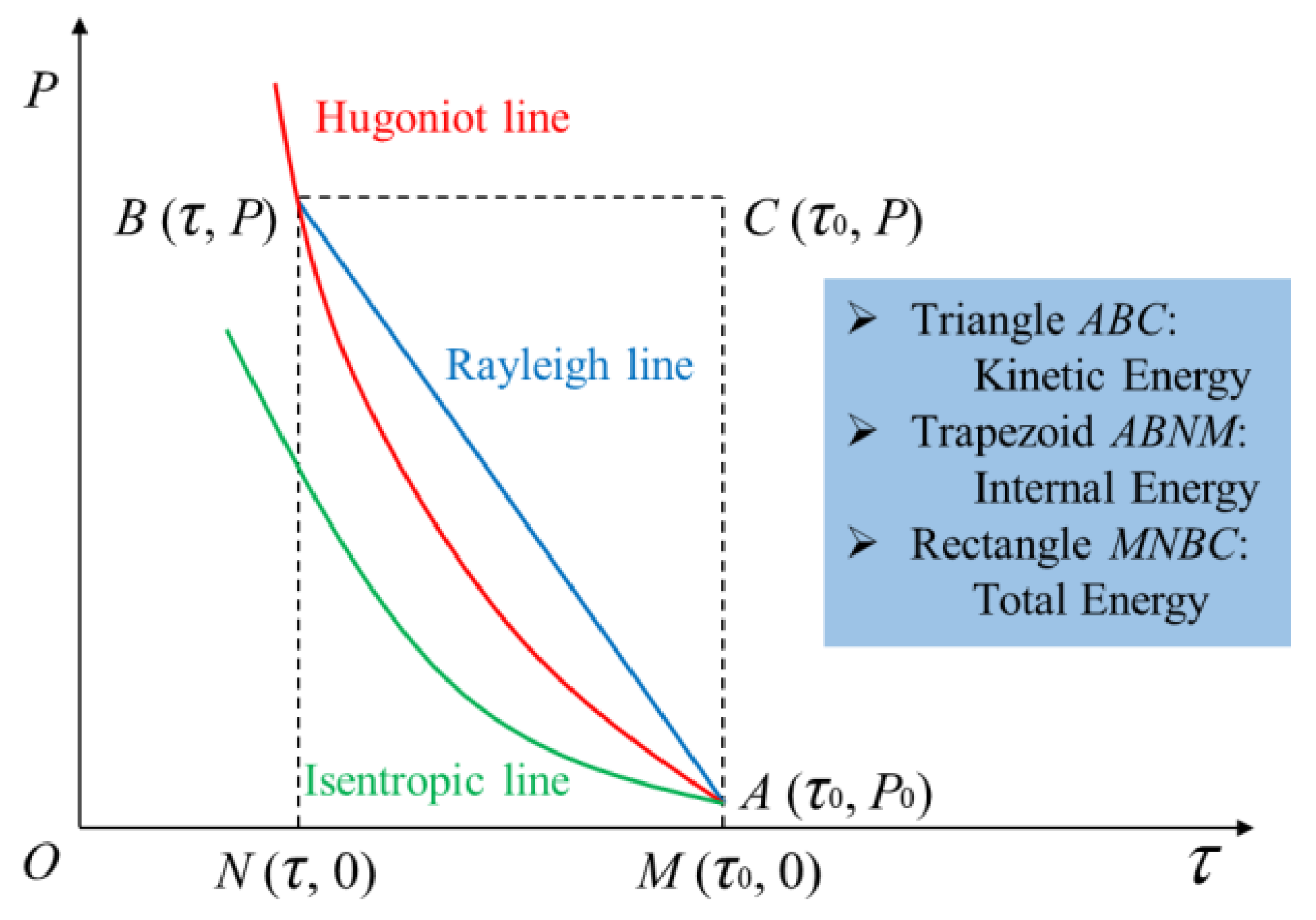
2.2. Internal Energy and Kinetic Energy Increment of the Target Plate Plug after Shock Waves

Before the rarefaction wave reflects from the back side of the target plate, the impact between the projectile and the target plate can be approximately considered a coaxial impact problem, as shown in Figure 4. The projectile comprises two parts, outer casing and inner core, and their internal shock wave intensities are different because the materials are different. Correspondingly, the shock wave intensities in different impact regions of the target plate are different.

It is assumed that then the projectile impacts the target plate with the mass m and velocity u₀, the initial velocity and pressure of the target plate and the initial pressure of the projectile are both zero. Here, the following definitions are made. P stands for the pressure per unit area, ρ is the material density, D represents the shock wave velocity, u is the particle velocity, E means the energy, c, and λ represents the Hugoniot constant of the material. In addition, the subscript j is an abbreviation for “jacket,” and it is used to denote the parameters of the projectile outer casing material; the subscript f is an abbreviation for “filling,” and it is used to denote the parameters of the inner core material; the subscript t represents the parameters of the target plate, and it is an abbreviation for “target.” The subscript tj represents the post-wave state of target plate after the collision between the outer casing and target plate, and the subscript tf represents the post-wave state of the target plate after the collision between the inner core and target plate. The subscript 0 indicates the wave-front state of the material, and the subscript 1 indicates the post-wave state of the material. According to the interaction of the shock wave, the following relationships can be obtained.

(1) Take the projectile outer casing as the main body of research. The initial state of the outer casing is P_0j, ρ_0j, u_0j, c_0j, and a left shock wave is generated in the outer casing after the impact, and the post-wave state is P_1j, ρ_1j, u_1j, c_1j. Thus, the following relationships can be obtained through the shock wave discontinuous equation and the linear shock equation.

$$P_{1j}={\rho }_{0j}\left(D_j-u_0\right)\left(u_{1j}-u_0\right)$$

(1)

$$D_j-u_0=-c_{0j}+{\lambda }_j\left(u_{1j}-u_0\right)$$

(2)

(2) Take the projectile inner core as the main body of research. The initial state of the inner core is P_0f, ρ_0f, u_0f, c_0f, and a left shock wave is generated in the inner core after the impact, and the post-wave state is P_1f, ρ_1f, u_1f, c_1f. Similarly, the following relationships can be obtained by the shock wave discontinuous equation and the linear shock equation.

$$P_{1f}={\rho }_{0f}\left(D_f-u_0\right)\left(u_{1f}-u_0\right)$$

(3)

$$D_f-u_0=-c_{0f}+{\lambda }_f\left(u_{1f}-u_0\right)$$

(4)

(3) Take the target plate as the main body of research. The initial state of the target plate is P_0t, ρ_0t, u_0t, c_0t, and a right shock wave is generated in the target plate after the impact. The post-wave state is divided into two regions, as follows.

(a) The interaction region between the outer casing and the target plate. In this case, the corresponding post-wave state is P_tj, ρ_tj, u_tj, c_tj. Similarly, the following relationships can be obtained through the shock wave discontinuous equation and the linear shock equation.

$$P_{tj}={\rho }_{0t}{D}_{tj}{u}_{tj}$$

(5)

$$D_{tj}=c_{0t}+{\lambda }_t{u}_{tj}$$

(6)

(b) The interaction region between the inner core and the target plate. In this case, the corresponding post-wave state is P_tf, ρ_tf, u_tf, c_tf. Similarly, the following relationships can be obtained through the shock wave discontinuous equation and the linear shock equation.

$$P_{tf}={\rho }_{0t}{D}_{tf}{u}_{tf}$$

(7)

$$D_{tf}=c_{0t}+{\lambda }_t{u}_{tf}$$

(8)

According to the mechanical equilibrium conditions of the interaction region, the velocity and pressure on both sides of the discontinuity are equal. Hence, the following relationships can be obtained.

(a) The balance condition between the outer casing and the target plate, P_tj = P_1j, u_tj = u_1j. When Equations (1), (2), (5), and (6) are combined together, the expression of the particle velocity of the target plate after the shock wave is as follows.

$$\left({\rho }_{0j}{\lambda }_j-{\rho }_{0t}{\lambda }_t\right)u_{tj}^2-\left(2{\rho }_{0j}{\lambda }_j{u}_0+{\rho }_{0j}{c}_{0j}+{\rho }_{0t}{c}_{0t}\right)u_{tj}+{\rho }_{0j}{\lambda }_j{u}_0^2+{\rho }_{0j}{c}_{0j}{u}_0=0$$

(9)

By solving Equation (9), the particle velocity after the impact between the outer casing and the target plate can be obtained.

$$u_{tj}=\frac{\left(2{\rho }_{0j}{\lambda }_j{u}_0+{\rho }_{0j}{c}_{0j}+{\rho }_{0t}{c}_{0t}\right)-\sqrt{{\left(2{\rho }_{0j}{\lambda }_j{u}_0+{\rho }_{0j}{c}_{0j}+{\rho }_{0t}{c}_{0t}\right)}^2-4\left({\rho }_{0j}{\lambda }_j-{\rho }_{0t}{\lambda }_t\right)\left({\rho }_{0j}{\lambda }_j{u}_0^2+{\rho }_{0j}{c}_{0j}{u}_0\right)}}{2\left({\rho }_{0j}{\lambda }_j-{\rho }_{0t}{\lambda }_t\right)}$$

(10)

(b) The balance condition between the inner core and the target plate, P_tf = P_1f, u_tf = u_1f. When Equations (3), (4), (7), and (8) are combined together, the particle velocity after the impact between the inner core and the target plate can be obtained as follows.

$$u_{tf}=\frac{\left(2{\rho }_{0f}{\lambda }_f{u}_0+{\rho }_{0f}{c}_{0f}+{\rho }_{0t}{c}_{0t}\right)-\sqrt{{\left(2{\rho }_{0f}{\lambda }_f{u}_0+{\rho }_{0f}{c}_{0f}+{\rho }_{0t}{c}_{0t}\right)}^2-4\left({\rho }_{0f}{\lambda }_f-{\rho }_{0t}{\lambda }_t\right)\left({\rho }_{0f}{\lambda }_f{u}_0^2+{\rho }_{0f}{c}_{0f}{u}_0\right)}}{2\left({\rho }_{0f}{\lambda }_f-{\rho }_{0t}{\lambda }_t\right)}$$

(11)

Thus, the kinetic energy increase of the target plate in the impact region of the projectile and the target plate can be obtained after the shock wave.

$$E_{tj}=\frac{1}{2}\pi \left(R^2-r^2\right)h{\rho }_{0t}{u}_{tj}^2$$

(12)

$$E_{tf}=\frac{1}{2}\pi r^{2}h{\rho }_{0t}{u}_{tf}^2$$

(13)

where R is the projectile outer casing radius, r is the inner core radius, and h is the target plate thickness.

Under the experimental conditions, the projectile and the target plate system are at normal pressure and normal temperature, and the shock wave pressure formed by the impact process is relatively high, P >> P₀. The relation between the material pressure and the specific volume under the impact adiabatic condition is shown in Figure 5. The relationship P >> P₀ is reflected in Figure 5 where point A is very close to point M, which means that the AB line can be considered to be the diagonal of the rectangular MNBC. Under this state, the influence of the initial pressure can be neglected, and it can be assumed that the total work of the shock compression is evenly distributed between the internal energy and kinetic energy.

2.3. Internal Energy Increment of Projectile after Shock Waves

Combined with the shock wave relationship, the shock wave velocity D_tj, D_tf, D_j, and D_f can be obtained. Where D_tj represents the shock wave velocity of target plate under the impact between outer casing and target plate, D_tf represents the impact wave velocity of target plate under the impact between inner core and target plate, and D_j and D_f represent the shock wave velocity of outer casing and inner core, respectively. The duration of the shock wave between the projectile and target plate is determined by the time from the projectile impacting the target plate to the rarefaction wave reaching the impact interface. It is assumed that the shock wave intensity unloading of the impact interface is completed once, and then the shock wave pressure duration t_j and t_f of the outer casing and the inner core can be expressed as follows.

$$t_j=\frac{h}{D_{tj}}+\frac{\left(h-u_{tj}{t}_j\right)}{c_{0t}-u_{tj}}$$

(14)

$$t_f=\frac{h}{D_{tf}}+\frac{\left(h-u_{tf}{t}_f\right)}{c_{0t}-u_{tf}}$$

(15)

According to the Hugoniot relations, combined with the particle velocity of target plate after the shock wave, the internal energy change of the outer casing and the inner core during t_j and t_f can be expressed by the kinetic energy change.

$$E_{1j}=\frac{1}{2}{u}_{1j}^2\pi \left(R^2-r^2\right)D_j{t}_j{\rho }_{0j}$$

(16)

$$E_{1f}=\frac{1}{2}{u}_{1f}^2\pi r^2{D}_f{t}_f{\rho }_{0f}$$

(17)

2.4. Shear Energy Dissipation of the Target Plate Plug

Since the shock wave impedance of the outer casing is higher than that of the inner core, the velocity of the annular contact interface between the outer casing and target plate is faster than that of the contact interface between the inner core and target plate during the penetration process. The working distance of the shear force is determined by the velocity difference and the movement time of the two contact interfaces.

It is assumed that the velocities of all the particles on the impact interface are always the same before the rarefaction wave propagates to the impact contact interface, and so the distance difference Δh between the two interfaces during this period can be expressed as follows.

$$∆h=\left(u_{tj}-u_{tf}\right)t_f$$

(18)

According to the calculation theory of a flat head projectile penetrating a target plate [20], the shear energy dissipation of the outer edge of outer casing on the target plate E_τj and that of the inner edge of outer casing on the target plate E_τf can be expressed as follows.

$$E_{\tau j}=\frac{1}{\sqrt{3}}\pi R{\sigma }_Y^D{h}^2$$

(19)

$$E_{\tau f}=\frac{1}{\sqrt{3}}\pi r{\sigma }_Y^D∆h^2$$

(20)

2.5. Axial Residual Velocity of PELE Projectile after Perforating Against the Target Plate

It is assumed that the internal energy increment of projectile by the shock wave is completely dissipated in the process of plastic deformation and rupture of the casing material and the kinetic energy of fragments, and cannot be converted into the kinetic energy of projectile again. In addition, the energy increment of the target plate plug under the action of the shock wave and the shear energy dissipation of the projectile on the target plate are both the loss of the kinetic energy of projectile. Since the target metal thickness is very thin, the mass loss of the PELE projectile can be neglected during the penetration process, and the mass of the residual projectile is approximately the same as the initial projectile mass, namely $m_0=m_{\mathrm{res}}$. Therefore, the axial residual velocity of projectile after perforating against the target plate can be determined by the principle of energy conservation.

$$E_0=E_{res}+E_{tj}+E_{tf}+E_{1j}+E_{1t}+E_{\tau j}+E_{tf}$$

(21)

$$u_{res}=\sqrt{u_0^2-\frac{2}{m_0}\left(E_{tj}+E_{tf}+E_{1j}+E_{1t}+E_{\tau j}+E_{tf}\right)}$$

(22)

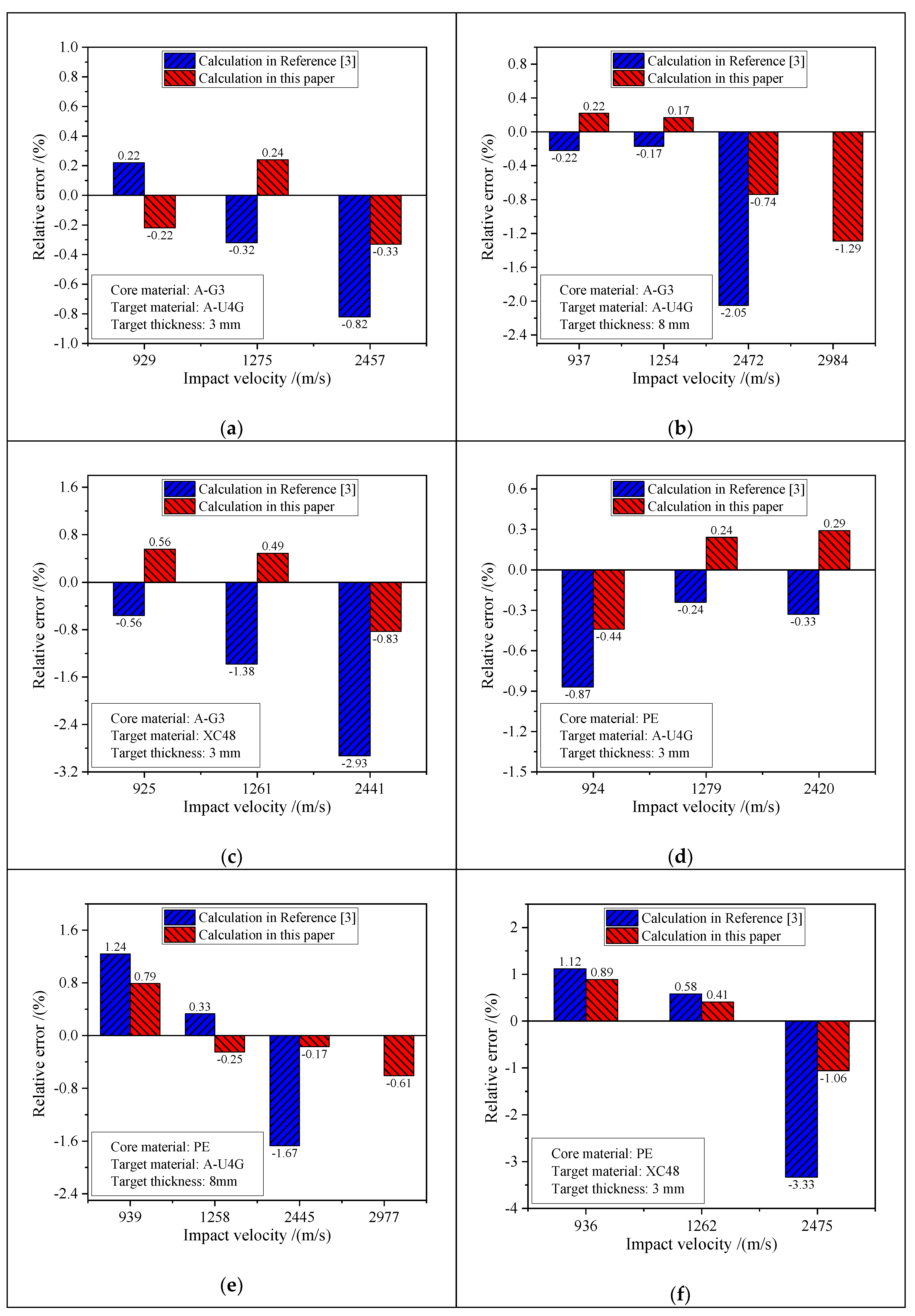
3. Verification and Analysis of the Theoretical Model

3.1. Literature Verification and Analysis of the Theoretical Model

In Reference [3], the residual velocity of PELE projectiles with different inner cores penetrating metal thin target plates was measured. In the reference, the PELE projectiles were divided into two groups. The first group had an impact velocity less than 2500 m/s, total length of projectile of 50 mm, projectile diameter of 10 mm, and inner core diameter of 6 mm. The second group had an impact velocity higher than 2500 m/s, total length of projectile of 40 mm, projectile diameter of 8 mm, and inner core diameter of 4 mm. The outer casing materials in the two groups were tungsten alloy (D180K), and the inner core materials used were aluminum (A-G3) and polyethylene (PE) material. The target plates were made of aluminum (A-U4G) with 3 mm and 8 mm thickness, and steel target (XC48) with 3 mm thickness. The performance parameters of the projectiles and target plates are shown in

Table 1. Material properties of project and target plate [3,21].

Material Properties	Outer Casing Material	Inner Core Material		Target Plate Material
	D180K	A-G3	PE	A-U4G	XC48
Density ρ0 (g/cm3)	18.0	2.65	0.92	2.8	7.82
Sound velocity c0 (m/s)	4029	5176	2187	5106	4797
Hugoniot constant λ	1.24	1.35	1.48	1.35	1.49
Dynamic yield stress σyD (Gpa)	--	--	--	1.16	2.16

.

Based on the above established theoretical model of axial residual velocity and the material parameters, the residual velocity of the PELE projectile under different conditions can be obtained. The comparison between the calculated results and the experimental results are shown in

Table 2. Residual velocity of experiment and calculation for A-G3 core material.

Target Plate		Experimental Initial Velocity (m/s)	Experimental Residual Velocity (m/s)	Calculated Residual Velocity in Reference [3] (m/s)	Calculated Residual Velocity in this Paper (m/s)
Material	Thickness (mm)
A-U4G	3	929	914	916	912
		1275	1261	1257	1264
		2457	2444	2424	2436
	8	937	900	898	902
		1254	1208	1206	1210
		2472	2434	2384	2416
		2984	2945	--	2907
XC48	3	925	895	890	900
		1261	1231	1214	1237
		2441	2423	2352	2403

and

Table 3. Residual velocity of experiment and calculation for PE core material.

Target Plate		Experimental Initial Velocity (m/s)	Experimental Residual Velocity (m/s)	Calculated Residual Velocity in Reference [3] (m/s)	Calculated Residual Velocity in this Paper (m/s)
Material	Thickness (mm)
A-U4G	3	924	918	910	914
		1279	1263	1260	1266
		2420	2394	2386	2401
	8	939	887	898	894
		1258	1203	1207	1200
		2445	2393	2353	2389
		2977	2952	--	2934
XC48	3	936	889	899	897
		1262	1206	1213	1211
		2475	2462	2380	2436

, respectively. In the comparison verification, all the parameters of the model established in this paper are derived from Reference [3], not from self-measurement. The measurements in Reference [3] do not give the uncertainty. Paulus’s calculation results [3] also do not take into account the uncertainty, directly substituting. In order to maintain the same significant digits as Paulus’s calculation results, the calculation results of this paper also follow the idea of directly substituting all the parameters into the solution, and then rounding off and retaining the significant digits to units. It is worth noting that this article follows the principle of significant figure retention in the intermediate calculation process.

Paulus [3] assumed that weak shock waves will be generated in the PELE projectile when it impacts the target plate. Combined with the Recht-Ipson model and the Mott model, the residual velocity of projectile, the radial scattering velocity and the spatial distribution of fragments were then obtained. To make a more intuitive comparative analysis, the results calculated by the theoretical model in this paper are compared with those calculated by the theoretical model in Reference [3], taking the experimental results in Reference [3] as reference data. In order to characterize the degree of difference between the calculated results and the experimental results, we need to analyze the relative error, and the relative error α is defined as follow.

$$\alpha =\frac{\left(u_{ref}-u_{exp}\right) or \left(u_{cal}-u_{exp}\right)}{u_{exp}}\times 100\%$$

(23)

where u_ref represents the calculation result corresponding to the model established in Reference [3], u_cal represents the calculation result corresponding to the model established in this paper, and u_exp represents the experimental result in Reference [3].

When using the relative error to compare the model established in this paper with that in Reference [3], they must be under the same initial conditions. Based on the relative error, the relationship between the residual velocity and the impact velocity of a projectile penetrating a target plate under different working conditions can be obtained intuitively, as shown in Figure 6. From the comparison of the experimental results in Reference [3] and the calculated results in Table 2, Table 3, and Figure 6, the calculated results obtained by the theoretical model of axial residual velocity in this paper are in good agreement with the measured experimental results in Reference [3].

In addition, it was found that the calculated results based on the elastic wave theory used in Reference [3] are close to the experimental results at lower velocity. When the impact velocity is higher than 2500 m/s, elastic wave theory is not suitable for penetration calculation of PELE projectiles, and so the calculation results were not given in Reference [3]. However, the theoretical model established in this paper can be well matched for both lower and higher velocities. Since the theoretical model established in Reference [3] is based on elastic wave theory, the premise is that the deformation of the projectile and target should be subject to Hooke’s law, which determines that the model is more suitable for the low-speed collision. When the impact velocity is high, the dynamic pressure generated by the projectile during the penetration process is very high, and the projectile and the target plate will undergo large deformation. At this point, the elastic moduli of the projectile and target material will no longer be constant, but will become a function of stress or strain. Therefore, there are limitations in using elastic wave theory to analyze the penetration process of projectile and target. This paper uses one-dimensional shock wave theory to analyze the penetration process of projectile and target, which can solve this problem well. Obviously, the calculated results based on shock wave theory in this paper are better than that based on the elastic wave theory in Reference [3], especially in high velocity conditions. The above comparative analysis can further confirm the rationality of the theoretical model established in this paper.

3.2. Experiment Verification and Analysis of the Theoretical Model

To further verify the rationality of the theoretical model established in this paper, two groups of experiments were designed and the axial residual velocities of projectiles were measured experimentally. In the experiments, the material of outer casing was tungsten alloy, and the length of projectile was 40 mm, the inner radius was 3 mm, the outer radius was 5 mm, and the depth of inner hole was 37 mm. The materials of the inner core were Al (6061Al) and PTFE, with a radius of 3 mm and a height of 37 mm. The material of target plate was Al (2024Al), with a thickness of 3 mm. The material parameters of projectile and target plate are shown in

Table 4. Material properties of project and target plate [3,22].

Material Properties	Outer Casing Material	Inner Core Material		Target Plate Material
	Tungsten	6061Al	PTFE	2024Al
Density ρ0 (g/cm3)	18.0	2.7	2.15	2.8
Sound velocity c0 (m/s)	4029	5350	1682	5370
Hugoniot constant λ	1.24	1.34	1.82	1.3
Dynamic yield stress σyD (Gpa)	--	--	--	1.2

.

The projectile was wrapped with a layer of 1.5 mm thick copper, to ensure close integration between the experimental projectiles and launch gun rifles. The overall projectile is shown in Figure 7a, and the experimental launch gun is shown in Figure 7b. To measure the impact velocity of projectile, a light curtain was placed between the target plate and the launch gun, as shown in Figure 7c. The 3 mm Al (2024Al) target plate was placed behind the light curtain target, and was in the field of view of the high-speed photography. In addition, two copper foil targets were placed behind the target plate to test the residual axial velocity of the projectile, as shown in Figure 7d. In order to ensure the accuracy of the experimental data, the experiment was conducted twice in each condition, and four groups of tests were conducted. At the end of the entire experimental setup, a water tank was placed to recover the fragments and residual projectile. The overall arrangement of the experimental equipment is shown in Figure 8.

In order to more visually display the fragmentation effect of the PELE projectile after perforating the thin metal target plate, the fragments of the PELE projectile outer casing were collected from the water tank, as shown in Figure 9. Moreover, the quantity and total mass of recycled fragments were counted, as shown in

Table 5. Quantity and total mass of recycled fragments.

Inner Core Material	Test Number	Quantity of Recycled Fragments	Total Mass of Recycled Fragments	Percentage of Recovery Mass of Outer Casing (%)
Al	1#	45	34.0	90.2
	2#	42	34.4	91.2
PTFE	1#	34	31.7	84.1
	2#	29	31.8	84.4

.

From Figure 9, it can be seen that the PELE projectile was broken into a lot of fragments after perforating the target, the structure of the Al inner core was relatively complete, and plastic deformation occurred only in the head; the PTFE inner core was completely broken and the corresponding debris was not recovered in the water tank. Moreover, from the shape of fragments in Figure 9, the rupture of the projectile outer casing did not occur in the direction of thickness; only circumferential and axial rupture occurred. The above phenomena can well explain the difference between PELE projectiles and traditional armor piercing projectiles, that is, they possess a certain penetration ability and also have a certain lateral fragmentation effect.

Assuming that the time taken for the PELE projectile to pass through the two copper foil targets is t, and the distance between the two copper foil targets is L₀, the axial residual velocity of the projectile can be expressed as follows.

$$u_{res}=\frac{L_0}{t}$$

(24)

The theoretical and experimental results of the residual velocity of PELE projectiles are shown in

Table 6. Residual velocity of experiment and calculation for PTFE and Al core material.

Inner Core Material	Test Number	Experimental Initial Velocity (m/s)	Experimental Residual Velocity (m/s)	Calculated Residual Velocity (m/s)
Al	1#	806	788	779
	2#	798	780	772
PTFE	1#	809	790	784
	2#	802	787	776

and Figure 10a. According to the relative error formula defined above, the relative error between the experiment results and the calculation results of the different inner cores is shown in Figure 10b. It can be obviously seen that the calculation results and the experimental results coincide well for the two kinds of PELE projectiles with different inner cores, which also illustrates the rationality of the theoretical model established in this paper.

4. Conclusions

Since the PELE projectile is a symmetrical structure, the collision between the projectile and the target plate can be simplified to a plane collision problem. Moreover, because the two-dimensional plane is axisymmetric, it can be further simplified to one-dimensional collision. Based on shock wave theory, the shock wave discontinuous equation, and the linear shock equation, the theoretical model of the axial residual velocity of a PELE projectile penetrating thin metal targets was established. In order to verify the rationality of the theoretical model, we compared the calculation results obtained by the theoretical model with the experimental results in Reference [3] and the self-designed experimental results. The comparison results show that they are in good agreement, and we can also draw the following conclusions:

(1) Based on the experimental results in Reference [3], the theoretical model established in this paper can be well matched for both lower and higher velocities, but the calculated results based on the elastic wave theory used in Reference [3] were close to the experimental results at lower velocity. Therefore, the calculated results based on shock wave theory in this paper are better than those based on elastic wave theory in Reference [3], especially in high velocity conditions. Through comparative analysis, we confirmed the rationality of the theoretical model established in this paper.

(2) Four groups of tests were self-designed to further verify the theoretical model, and the impact velocity of the PELE projectile was about 800 m/s. The results show that the experimental results were in good agreement with the calculated results, and the error between them was within 1.5%.

The above two verification methods all illustrate that the theoretical model established in this paper is scientific and reasonable. In addition, by comparing the theoretical results and experimental data in Reference [3], it was also found that when the projectile impact velocity is below 3000 m/s, the theoretical model established in this paper can be applied very well.