Framework for Onboard Bus Comfort Level Predictions Using the Markov Chain Concept
Abstract
1. Introduction
2. Literature Review
2.1. Predictive Framework for ATIS Subsystem
2.2. Prediction Methods in Public Transportation
3. Onboard Bus Comfort Level and Markov Chain Concept
3.1. Bus Comfort Level
- Comfort level A (corresponding to a factor of discomfort )—means that: approximately 10–70% of the vehicle seats are occupied; each passenger has a guaranteed seating position without being forced to travel in the immediate vicinity of another passenger; passengers travel without difficulty in carrying luggage, trolleys, bicycles, etc.
- Comfort level B (corresponding to a factor of discomfort ) means that: all or almost all seating positions are occupied (70–100%); possibility to easily carry a baggage, trolleys, bicycles, etc.
- Comfort level C (corresponding to a factor of discomfort ) means that: the small number of standing places is occupied, but it is possible to have free movement within the vehicle: easy access to the punch (up to 2 persons/m2).
- Comfort level D (corresponding to a factor of discomfort ) indicates that the onboard occupancy level results in a difficulty of free movement in the vehicle and in access problems to the punch (up to 4 persons/m2).
- Comfort level E (corresponding to the discomfort factor ) indicates an already high onboard congestion causing very difficult access to the punch (up to 6–7 persons/m2).
- Comfort level F (corresponding to a factor of discomfort is characterised by: very high in-vehicle congestion, during which it is not possible to cancel the ticket; the ride involves a large physical effort, with standing passengers pressing into the seating area; there are large difficulties in closing the door and incidental damages to the closing device; it is necessary to give way to passengers getting off their seats (over 7 persons/m2).
3.2. Short-Term In-Vehicle Occupation Predictions Based on Markov Chains Model
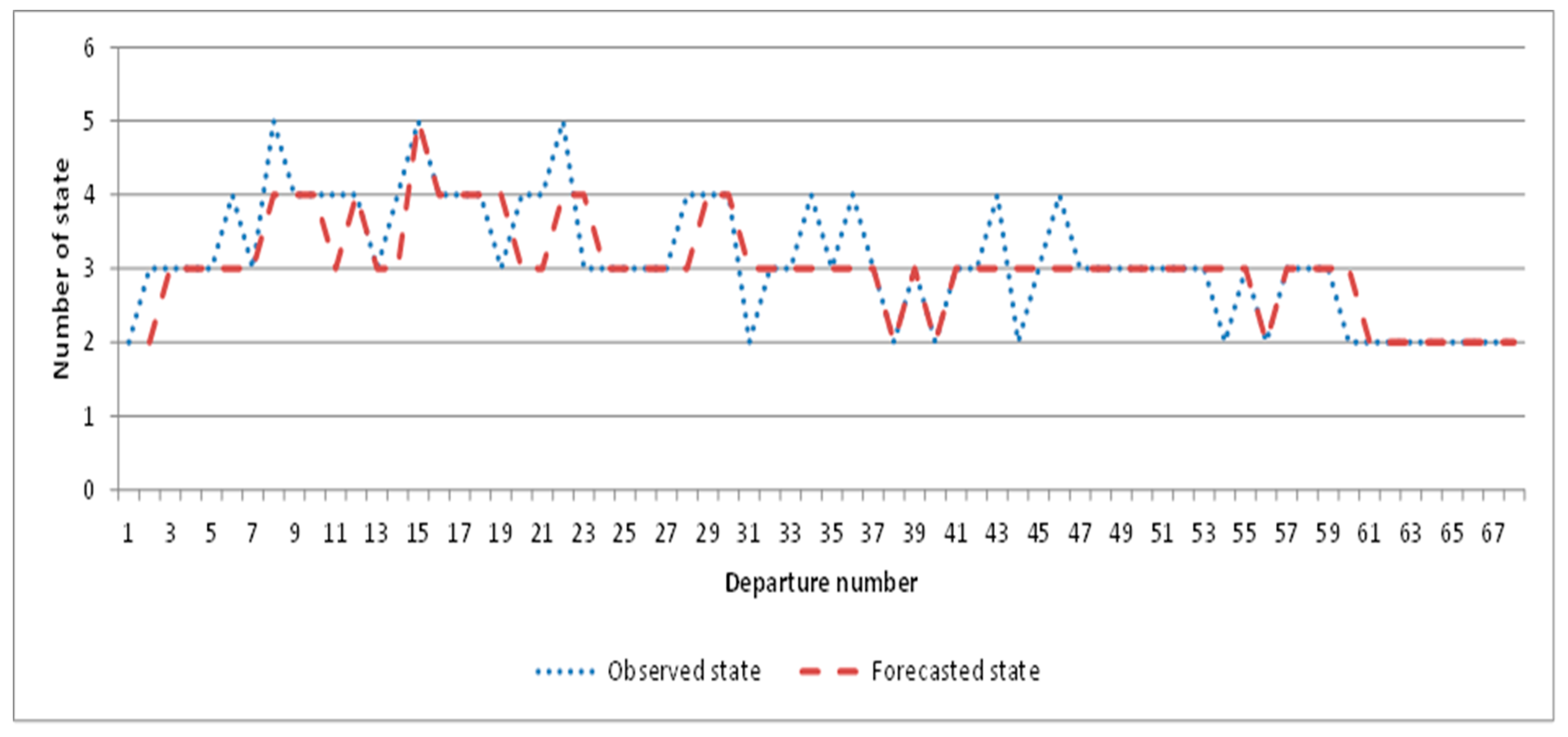
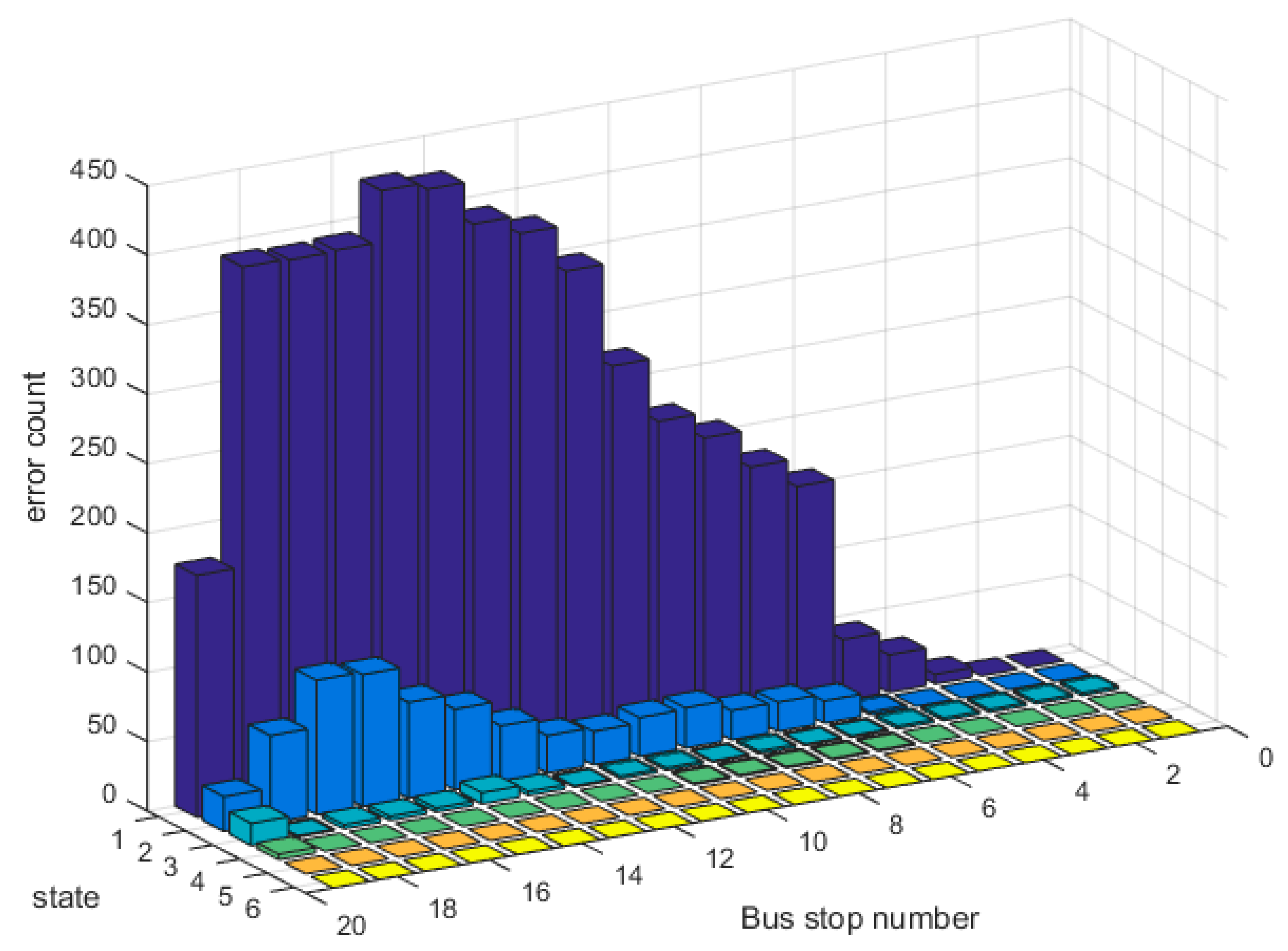
4. Case Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adamski, A. Inteligentne Systemy Transportowe: Sterowanie, Nadzór i Zarządzanie; Uczelniane Wydaw. Nauk.-Dydakt. AGH im. S. Staszica: Kraków, Poland, 2003. [Google Scholar]
- Bifulco, G.N.; Di Pace, R.; Viti, F. Evaluating the effects of information reliability on travellers’ route choice. Eur. Transp. Res. Rev. 2013, 6, 61–70. [Google Scholar] [CrossRef]
- Zito, P.; Amato, G.; Amoroso, S.; Berrittella, M. The effect of Advanced Traveller Information Systems on public transport demand and its uncertainty. Transportmetrica 2011, 7, 31–43. [Google Scholar] [CrossRef]
- Balakrishna, R.; Ben-Akiva, M.; Bottom, J.; Gao, S. Information Impacts on Traveler Behavior and Network Performance: State of Knowledge and Future Directions. In Advances in Dynamic Network Modeling in Complex Transportation Systems; Springer: New York, NY, USA, 2013; Volume 2, pp. 193–224. [Google Scholar]
- Polydoropoulou, A.; Gopinath, D.A.; Ben-Akiva, M. Willingness to Pay for Advanced Traveler Information Systems SmarTraveler Case Study. Transp. Res. Rec. J. Transp. Res. Board 1997, 1588, 1–9. [Google Scholar] [CrossRef]
- Chorus, C.G.; Molin, E.J.E.; Van Wee, B. Use and Effects of Advanced Traveller Information Services (ATIS): A Review of the Literature. Transp. Rev. 2006, 26, 127–149. [Google Scholar] [CrossRef]
- Blasum, U.; Bussieck, M.R.; Hochstattler, W.; Moll, C.H.; Scheel, H.; Winter, T. Scheduling trams in the morning. Math. Methods Oper. Res. 1999, 49, 137–148. [Google Scholar]
- Haase, K.; Deaulniers, G.; Desrosiers, J. Simultanous vehicle and crew scheduling in urban mass transit systems. Transp. Sci. 2001, 35, 215–343. [Google Scholar] [CrossRef]
- Kidwai, F.A.; Marwah, B.R.; Deb, K.; Karim, M.R. A genetic algorithm based bus scheduling model for Transit network. Proc. East. Asia Soc. Transp. Stud. 2005, 5, 477–489. [Google Scholar]
- Jimenez, F.; Roman, A. Urban bus fleet-to-route assignment for pollutant emissions minimization. Transp. Res. Part E 2016, 85, 120–131. [Google Scholar] [CrossRef]
- Li, L.; Lo, H.K.; Cen, X. Optimal bus fleet management strategy for emissions reduction. Transp. Res. Part D 2015, 41, 330–347. [Google Scholar] [CrossRef]
- Beltran, B.; Carrese, S.; Cipriani, E.; Petrelli, M. Transit network design with allocation of green vehicles: A genetic algorithm approach. Transp. Res. Part C 2009, 17, 475–483. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Bull, S. A Survey on Robustness in Railway Planning. Eur. J. Oper. Res. 2017, 266, 1–15. [Google Scholar] [CrossRef]
- Gancarz, T. Intelligent transport systems. Res. Tech. Pap. Pol. Assoc. Transp. Eng. Crac. 1998, 27, 75. [Google Scholar]
- Cejrowski, M.; Krych, A.; Pawłowski, M. Support for transport management using BIMBA-BIT and VISUM-PT procedures. Res. Tech. Pap. Pol. Assoc. Transp. Eng. Crac. 1998, 27, 59–68. [Google Scholar]
- Moreira, J.M.; De Sousa, J.F. Planning and control indicators for mass transit companies. Model. Manag. Transp. 1999, 2, 177. [Google Scholar]
- Oziomek, J.; Rogowski, A. The optimal allocation of the buses to the suburban lines in Ostrowiec Świętokrzyski. Autobusy Tech. Eksploat. Syst. Transp. 2016, 4, 14–19. [Google Scholar]
- Oziomek, J.; Rogowski, A. Planning the allocation of the buses to the lines in terms of minimizing fuel consumption based on the example of MPK Ostrowiec Świętokrzyski. TTS Tech. Transp. Szyn. 2015, 12, 1175–1179. [Google Scholar]
- Papierkowski, K. Traffic control in public transport in Scandinavia based on the example of the KON-FRAM system. Res. Tech. Pap. Pol. Assoc. Transp. Eng. Crac. 1998, 27, 203. [Google Scholar]
- Li, J.Q.; Head, K.L. Sustainability provisions in the bus-scheduling problem. Transp. Res. Part D Transp. Environ. 2009, 14, 50–60. [Google Scholar] [CrossRef]
- Mo, Y.; Su, Y. Neural networks based on real-time transit passenger volume prediction. In Proceedings of the 2009 2nd Conference on Power Electronics and Intelligent Transportation System(PEITS), Shenzhen, China, 19–20 December 2009; pp. 303–306. [Google Scholar]
- Li, Y. Predict the Volume of Passenger Transport of Railway Based on Grey Markov Chain Model. Adv. Mater. Res. 2014, 1030–1032, 2069–2072. [Google Scholar] [CrossRef]
- Zhao, S.Z.; Ni, T.H.; Wang, Y.; Gao, X.T. A new approach to the prediction of passenger flow in a transit system. Comput. Math. Appl. 2011, 61, 1968–1974. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R.C. A novel passenger flow prediction model using deep learning methods. Transp. Res. Part C Emerg. Technol. 2017, 84, 74–91. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Sun, S.; Ma, X.; Lu, G. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks. Transp. Res. Part C Emerg. Technol. 2017, 77, 306–328. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, D.; Tu, L.; Zhang, F.; Xu, C.; Wang, Y.; Tian, C.; Li, X.; Huang, B.; Li, Z. A real-time passenger flow estimation and prediction method for urban bus transit systems. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3168–3178. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Zhao, J. The use of LS-SVM for short-term passenger flow prediction. Transport 2011, 26, 5–10. [Google Scholar] [CrossRef]
- Xue, R.; Sun, D.J.; Chen, S. Short-term bus passenger demand prediction based on time series model and interactive multiple model approach. Discret. Dyn. Nat. Soc. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Zhou, C.; Dai, P.; Li, R. The passenger demand prediction model on bus networks. In Proceedings of the IEEE 13th International Conference on Data Mining Workshops, Dallas, TX, USA, 7–10 December 2013; pp. 1069–1076. [Google Scholar]
- Ma, Z.; Xing, J.; Mesbah, M.; Ferreira, L. Predicting short-term bus passenger demand using a pattern hybrid approach. Transp. Res. Part C 2014, 39, 148–163. [Google Scholar] [CrossRef]
- Tsai, T.H.; Lee, C.K.; Wei, C.H. Neural network based temporal feature models for short-term railway passenger demand forecasting. Expert Syst. Appl. 2009, 36, 3728–3736. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, C.; Zang, C. Short-term passenger flow prediction on bus stop based on the hybrid model. Adv. Eng. Res. 2017, 140, 343–347. [Google Scholar]
- Roos, J.; Bonnevay, S.; Gavin, G. Short-term urban rail passenger flow forecasting: A dynamic bayesian network approach. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 1034–1039. [Google Scholar]
- Zhang, W.; Zhu, J. Passenger traffic forecast based on the Grey-Markov method. In Proceedings of the 2009 IEEE International Conference on Grey Systems and Intelligent Services (GSIS 2009), Nanjing, China, 10–12 November 2009; pp. 630–633. [Google Scholar]
- Xiao, Z.S.; Mao, B.H.; Zhang, T. Integrated predicting model for daily passenger volume of rail transit station based on neural network and Markov chain. In Proceedings of the 2018 3rd IEEE International Conference on Cloud Computing and Big Data Analysis (ICCCBDA), Chengdu, China, 20–22 April 2018; pp. 578–583. [Google Scholar]
- Altinkaya, M.; Zontul, M. Urban bus arrival time prediction: A review of computational models. Int. J. Recent Technol. Eng. (IJRTE) 2013, 2, 164–169. [Google Scholar]
- Wang, D.; Sun, X.; Li, Y. Using Markov process for passenger structure prediction within comprehensive transportation channel. J. Comput. 2013, 8, 1072–1077. [Google Scholar] [CrossRef]
- Celikoglu, H.B.; Cigizoglu, H.K. Public transportation trip flow modeling with generalized regression neural networks. Adv. Eng. Softw. 2007, 38, 71–79. [Google Scholar] [CrossRef]
- Rudnicki, A. Jakość Komunikacji Miejskiej; Zeszyty Naukowo-Techniczne Oddziału SITK w Krakowie: Seria, Brunei, 1999; p. 71. [Google Scholar]


| Issues Raised in the Papers | Articles |
|---|---|
| Optimal queuing of rolling stock at depots for line departure | Blasum M. Bussieck M.R., Hochstattler W., Moll C.H., Scheel H., Winter T. [7] |
| Optimising the number of vehicles serving the urban public transport system | Haase K., Deaulniers G., Denosiers J. [8] Kidwai F.A., Marwah B.R., Deb K., Karim M.R. [9] |
| Optimisation of the allocation of rolling stock to lines - environmental criteria | Jimenez F., Roman A., (2016), Li J.Q., Head K.L. [10] Li L., Lo H.K., Cen X. [11] Beltran B., Carrese S., Cipriani E., Petrelli M. [12] |
| Allocation of rolling stock to lines, as part of public transport planning, day by day planning | Lusby R.M., Larsen J., Bull S. [13] |
| Characteristics of management systems for the allocation of rolling stock to lines | Gancarz T. (1998), Papierkowski K. [14] Cejrowski M., Krych A., Pawłowski M. [15] Moreira J.M., de Sousa J.F. [16] |
| Optimisation of the allocation of rolling stock to lines to minimise fuel consumption | Oziomek J., Rogowski A. [17,18] |
| Author(s) | Methodology | Type | Modes |
|---|---|---|---|
| Y. Mo, Y. Su [21] | Neural networks | Transit passenger Flow | Bus |
| Y. Li [22] | Grey Markov Chain model | Flow | Railway |
| S. Z. Zhao, T. H. Ni, Y. Wang, X. T. Gao [23] | Wavelet analysis, Neural networks | Flow | Transit system |
| L. Liu, R. C. Chen [24] | Deep learning method | Flow | Bus rapid transit |
| Y. Li, X. Wang, S. Sun, X. Ma, G. Lu [25] | Multiscale radial basis function networks | Flow | Subway |
| J. Zhang, D. Shen, L. Tu, F. Zhang, C. Xu, Y. Wang, C. Tian, X. Li, B. Huang, Z. Li [26] | Extended Kalman filter model | Flow | Bus transit system |
| Q. Chen, W. Li, J. Zhao [27] | Least Squares Support Vector Machine | Flow | Bus |
| R. Xue, D. J. Sun, S. Chen [28] | Time series and interactive multiple model (IMM) | Demand | Bus |
| C. Zhou, P. Dai, R. Li [29] | Time-varying Poisson model, Weighted time-varying Poisson model, ARIMA | Demand | Bus |
| Z. Ma, J. Xing, M. Mesbah, L. Ferreira [30] | Interactive Multiple, Model-based Pattern Hybrid (IMMPH) | Demand | Bus |
| T. H. Tsai, C. K. Lee, C. H. Wei [31] | Neural network | Demand | Railway |
| Z. Wang, C. Yang, C. Zang [32] | Hybrid model (BP neural network & time series model) | Flow prediction | Bus stop |
| J. Roos, S. Bonnevay, G. Gavin [33] | Dynamic Bayesian network | Flow forecasting | Metro |
| Z. Wei, Z. Jinfu [34] | Grey-Markov Method | Passenger traffic | Passenger turnover |
| Z. S. Xiao, B. H. Mao, T. Zhang [35] | Hybrid model—BP neural network and Markov Chain | Daily passenger volume | Rail transit station |
| MEAN ABSOLUTE PERCENTAGE ERRORS [%] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANALYZED TIME HORIZON [days] | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| Number of bus stop | 1 | 0,0 | 0,0 | 0,0 | 1,8 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 2 | 0,0 | 0,0 | 0,0 | 1,8 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| 3 | 0,0 | 0,5 | 0,5 | 2,3 | 1,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,5 | 0,5 | 0,0 | 0,0 | |
| 4 | 0,5 | 2,5 | 0,5 | 3,3 | 0,5 | 1,4 | 0,0 | 0,5 | 1,5 | 1,5 | 3,5 | 0,0 | 0,0 | |
| 5 | 2,0 | 2,2 | 1,0 | 3,8 | 1,0 | 4,2 | 2,1 | 2,5 | 2,5 | 3,0 | 2,2 | 0,5 | 0,7 | |
| 6 | 6,5 | 9,5 | 3,5 | 11,3 | 7,2 | 9,4 | 2,1 | 8,2 | 10,4 | 9,5 | 12,4 | 5,5 | 2,4 | |
| 7 | 8,5 | 11,7 | 4,7 | 12,3 | 8,2 | 5,2 | 20,8 | 7,5 | 10,0 | 9,5 | 12,3 | 7,7 | 5,2 | |
| 8 | 9,2 | 10,9 | 5,5 | 14,0 | 11,2 | 5,9 | 6,3 | 9,5 | 16,3 | 14,5 | 15,7 | 8,5 | 7,3 | |
| 9 | 10,2 | 11,4 | 7,2 | 12,2 | 12,4 | 9,7 | 7,6 | 11,2 | 19,5 | 18,2 | 15,8 | 10,7 | 7,3 | |
| 10 | 11,7 | 12,2 | 8,0 | 17,3 | 13,2 | 20,0 | 6,3 | 15,0 | 23,8 | 25,2 | 18,7 | 9,7 | 9,7 | |
| 11 | 19,0 | 21,6 | 12,2 | 23,7 | 24,9 | 23,1 | 14,2 | 21,7 | 24,2 | 21,7 | 23,3 | 12,9 | 8,0 | |
| 12 | 22,5 | 24,4 | 20,4 | 15,6 | 20,6 | 18,5 | 21,0 | 19,5 | 24,3 | 19,0 | 22,6 | 20,8 | 13,9 | |
| 13 | 22,8 | 23,3 | 25,4 | 20,6 | 17,8 | 13,3 | 22,4 | 19,9 | 23,3 | 20,9 | 20,1 | 20,1 | 24,5 | |
| 14 | 23,0 | 24,7 | 36,8 | 19,5 | 21,1 | 17,5 | 25,5 | 18,7 | 21,4 | 27,2 | 18,6 | 18,7 | 25,8 | |
| 15 | 24,5 | 24,0 | 32,0 | 21,0 | 22,9 | 17,3 | 19,4 | 16,6 | 21,1 | 25,1 | 22,4 | 20,2 | 26,3 | |
| 16 | 25,8 | 23,0 | 27,1 | 19,3 | 18,0 | 19,3 | 17,8 | 19,3 | 22,5 | 30,1 | 21,6 | 18,7 | 26,9 | |
| 17 | 24,4 | 23,3 | 26,8 | 20,1 | 19,4 | 17,9 | 18,1 | 18,0 | 22,2 | 28,9 | 19,1 | 19,0 | 26,9 | |
| 18 | 19,4 | 18,7 | 24,5 | 19,7 | 20,9 | 15,3 | 14,4 | 18,1 | 17,5 | 30,5 | 21,1 | 20,7 | 17,8 | |
| 19 | 7,5 | 10,1 | 10,2 | 8,1 | 8,8 | 12,7 | 4,5 | 6,5 | 11,7 | 27,3 | 10,3 | 10,4 | 12,2 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Więcek, P.; Kubek, D.; Aleksandrowicz, J.H.; Stróżek, A. Framework for Onboard Bus Comfort Level Predictions Using the Markov Chain Concept. Symmetry 2019, 11, 755. https://doi.org/10.3390/sym11060755
Więcek P, Kubek D, Aleksandrowicz JH, Stróżek A. Framework for Onboard Bus Comfort Level Predictions Using the Markov Chain Concept. Symmetry. 2019; 11(6):755. https://doi.org/10.3390/sym11060755
Chicago/Turabian StyleWięcek, Paweł, Daniel Kubek, Jan Hipolit Aleksandrowicz, and Aleksandra Stróżek. 2019. "Framework for Onboard Bus Comfort Level Predictions Using the Markov Chain Concept" Symmetry 11, no. 6: 755. https://doi.org/10.3390/sym11060755
APA StyleWięcek, P., Kubek, D., Aleksandrowicz, J. H., & Stróżek, A. (2019). Framework for Onboard Bus Comfort Level Predictions Using the Markov Chain Concept. Symmetry, 11(6), 755. https://doi.org/10.3390/sym11060755





