Study on a Novel Fault Diagnosis Method Based on VMD and BLM
Abstract
1. Introduction
2. Basic Method
2.1. VMD
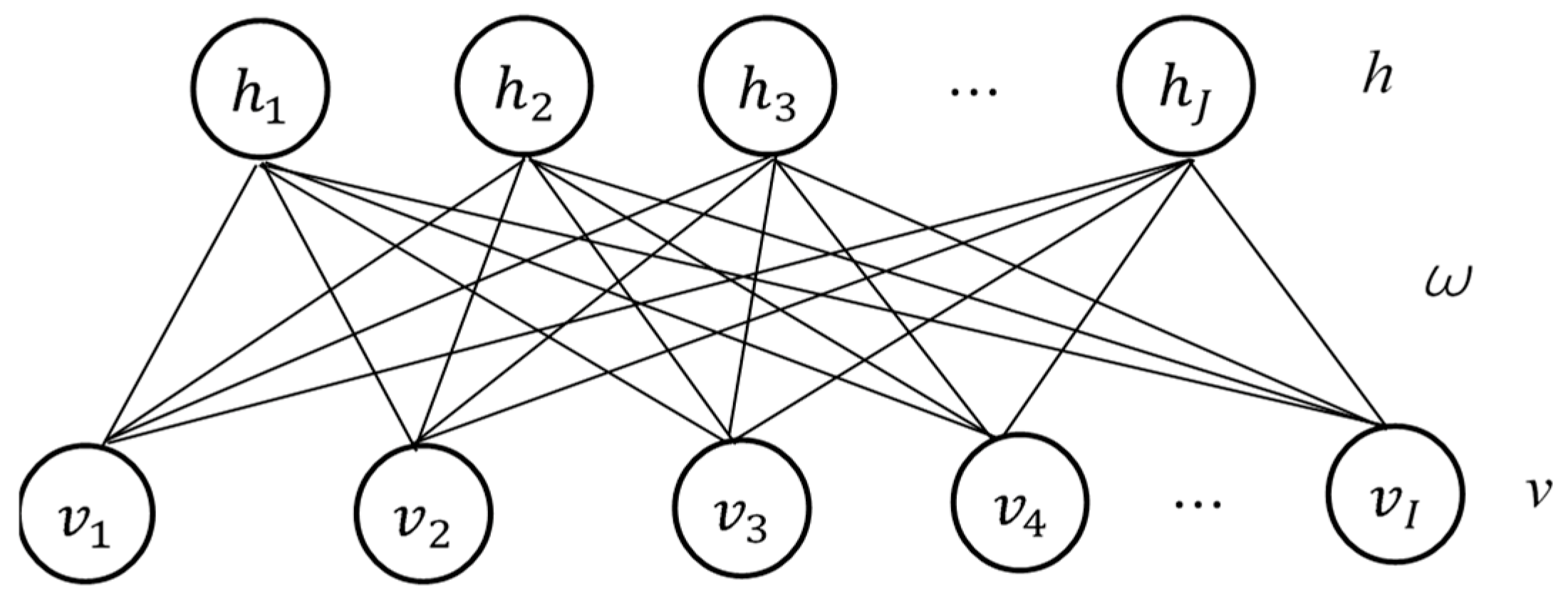
2.2. Deep Belief Network
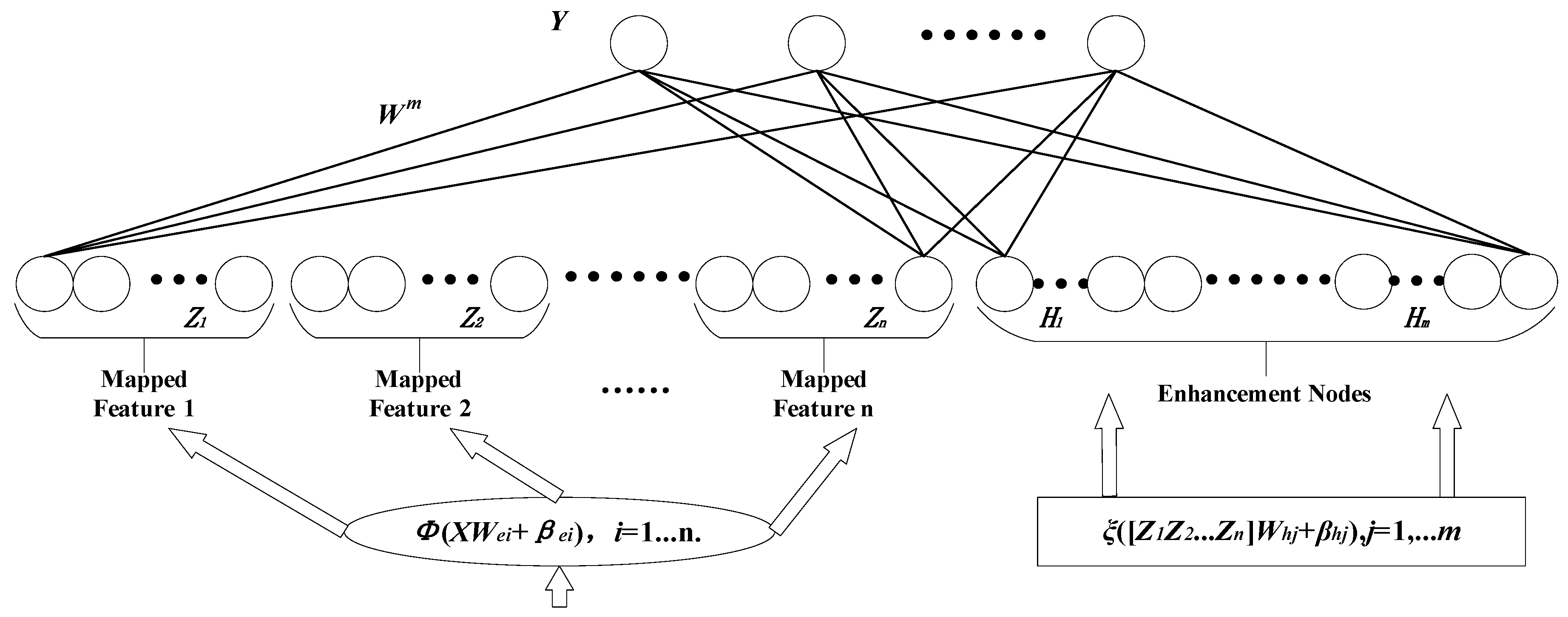
2.3. Broad Learning Model
3. A New Fault Diagnosis Method Based on VMD, HT and BLM
3.1. The Idea of the VHBLFD Method
3.2. The Fault Diagnosis Model and Steps
3.3. The Steps of the Fault Diagnosis Method
4. Validation and Analysis of the VHBLFD Method
4.1. Experiment Data and Environment
4.2. Feature Extraction
4.3. Fault Diagnosis Results
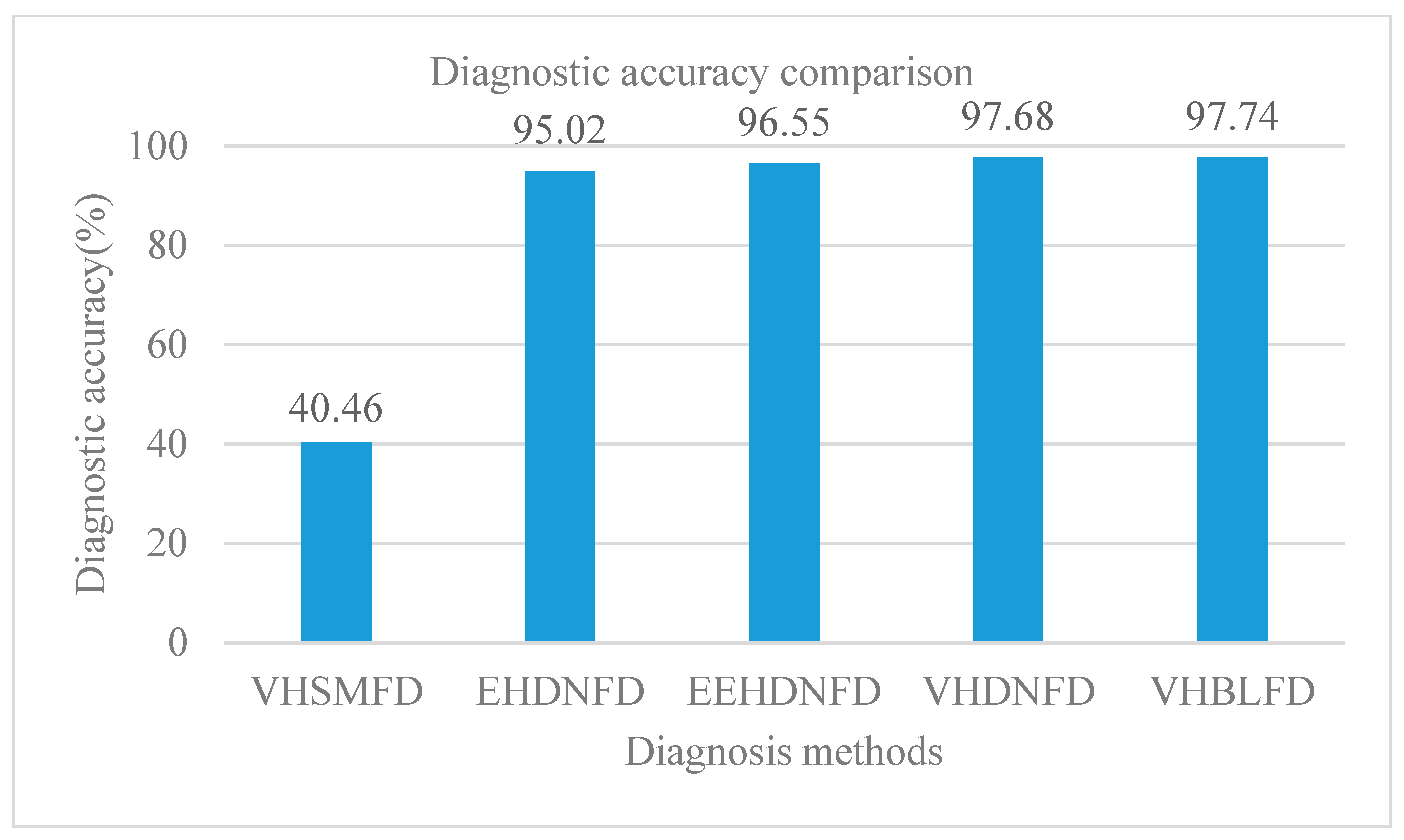
4.4. Comparision and Analysis for Diagnosis Results
4.5. The Influences of Parameters in BLM for Diagnosis Accuracy
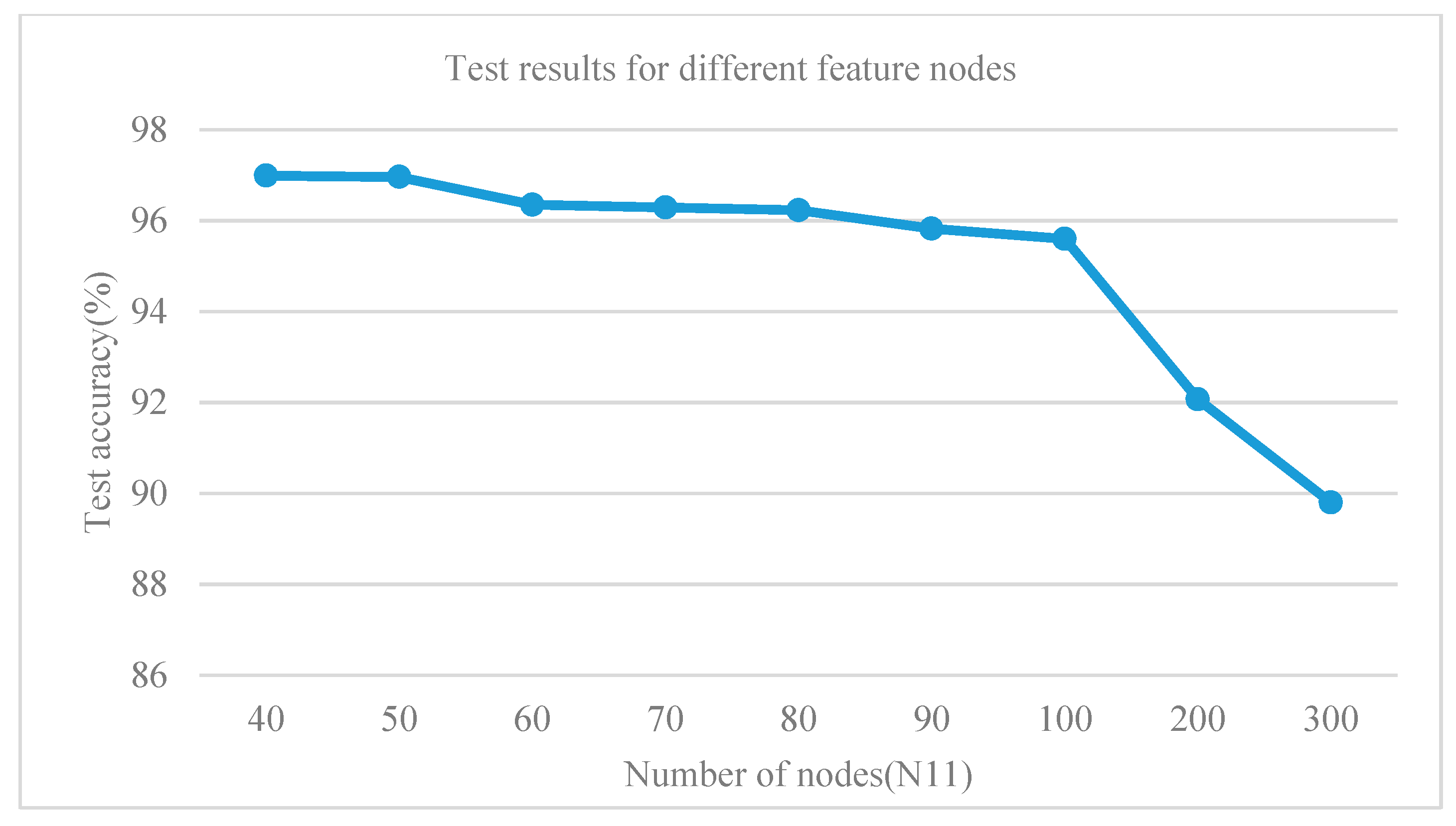
4.5.1. The Influences of the Number of Feature Nodes for Diagnosis Accuracy
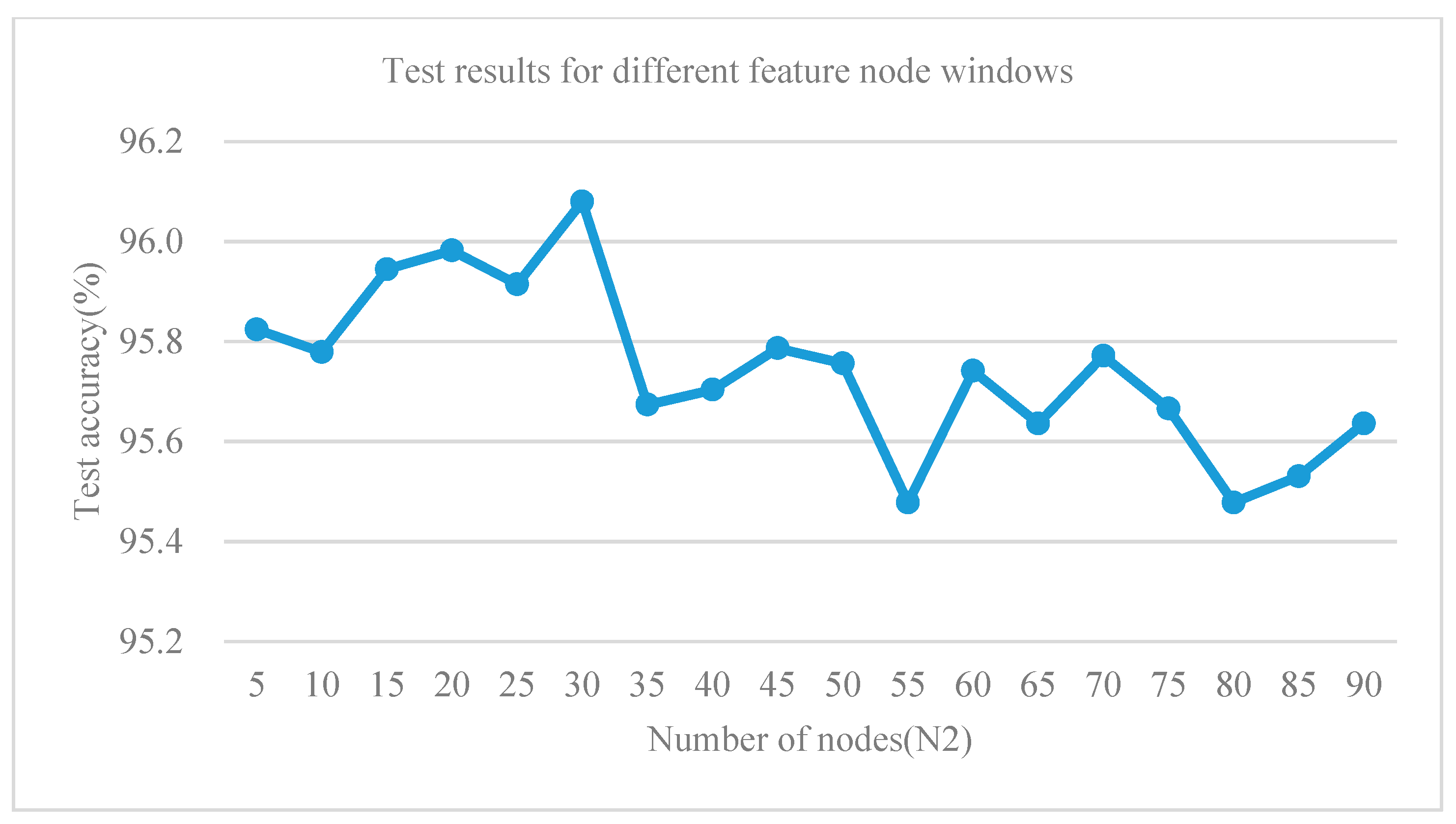
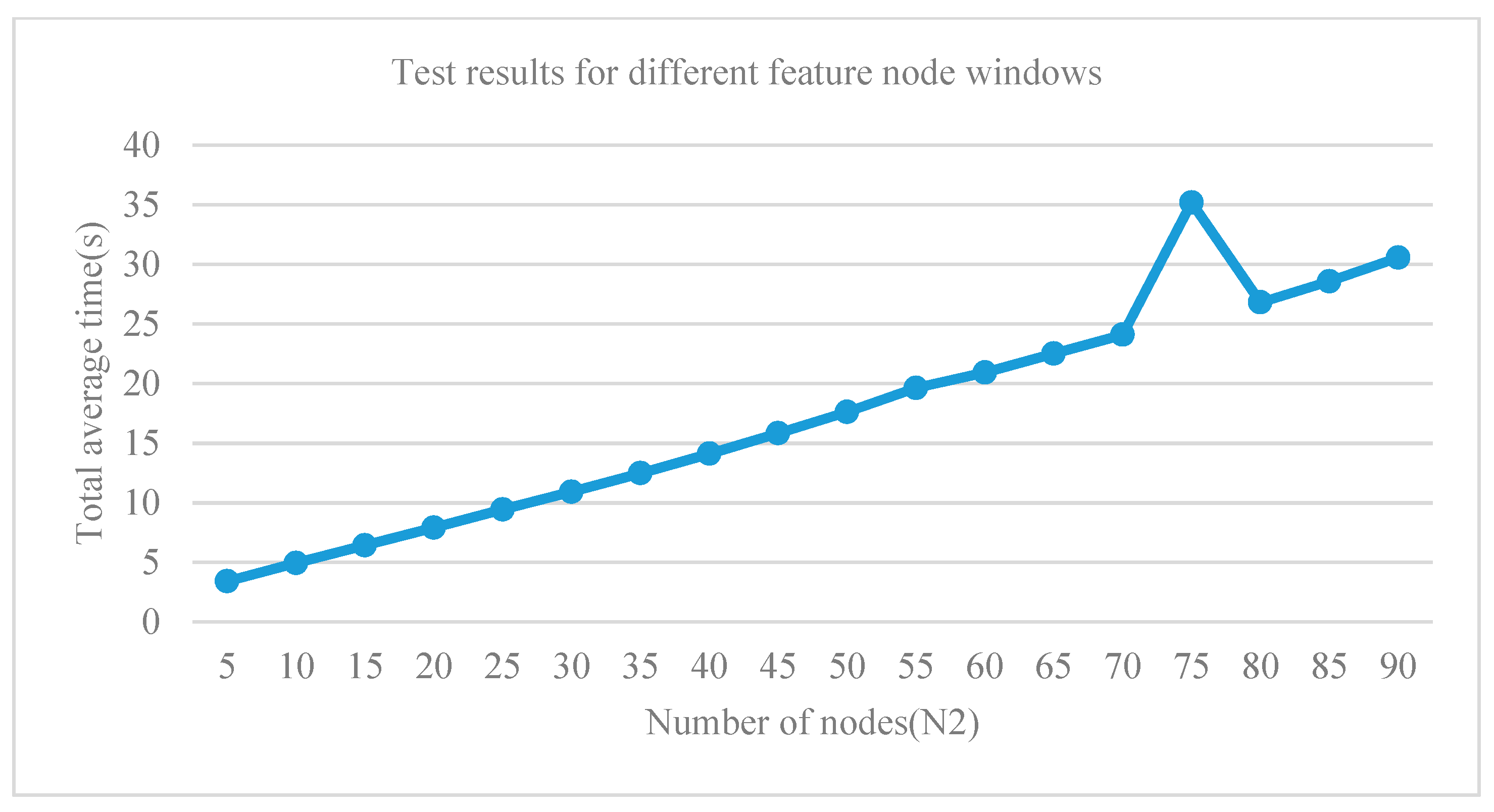
4.5.2. The Influences of the Number of Feature Node Windows for Diagnosis Accuracy
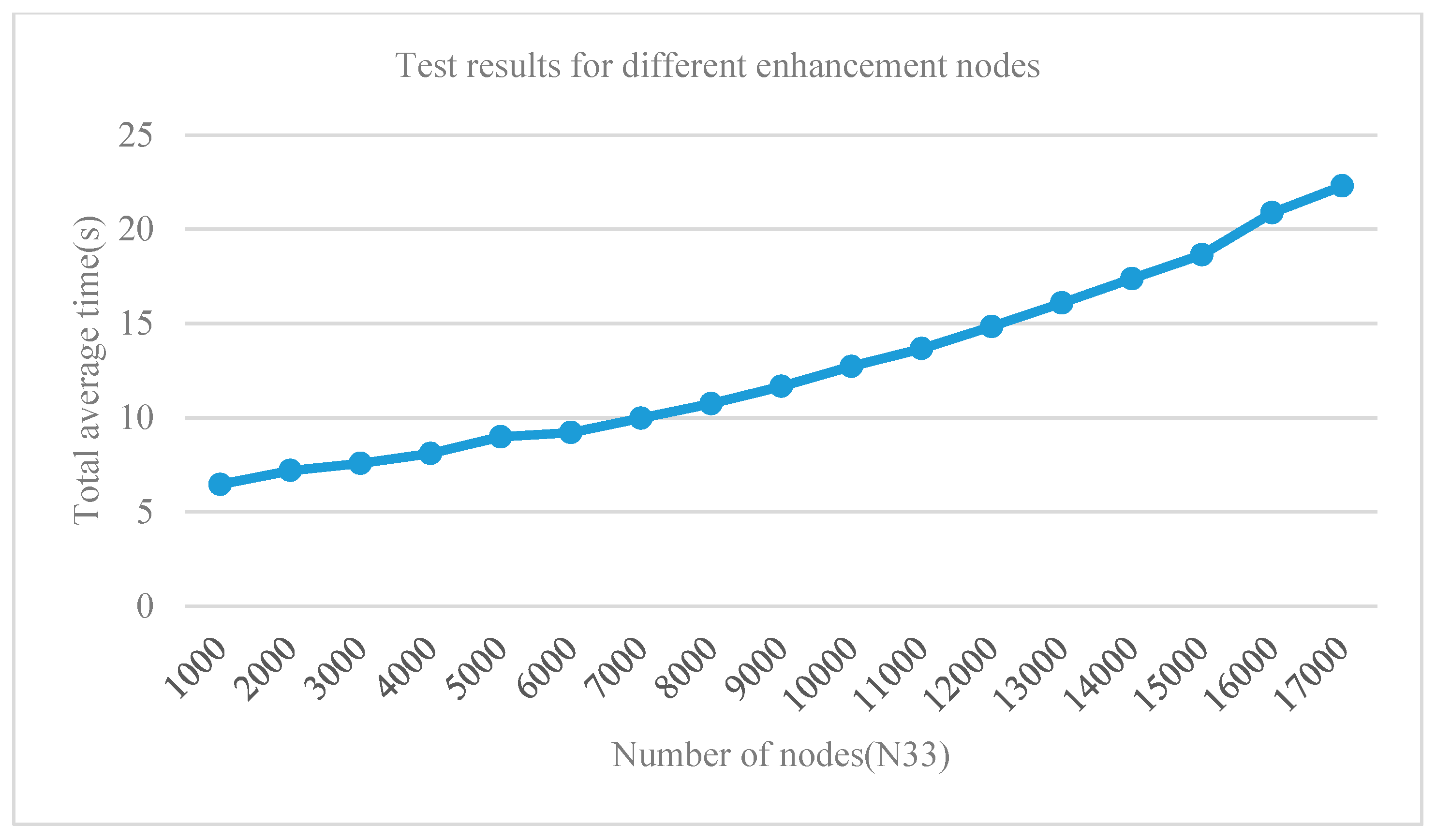
4.5.3. The Influences of the Number of Enhancement Nodes for Diagnosis Accuracy
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, S.L.; He, Q.B.; Zhang, H.B.; Kong, F.R. Rotating machine fault diagnosis through enhancement stochastic resonance by full-wave signal construction. Mech. Syst. Signal Process. 2017, 85, 82–97. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.J.; Zhao, H.M.; Yang, X.H. A novel fault diagnosis method based on integrating empirical wavelet transform and fuzzy entropy for motor bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Guo, S.K.; Chen, R.; Wei, M.M.; Li, H.; Liu, Y.Q. Ensemble data reduction techniques and Multi-RSMOTE via fuzzy integral for bug report classification. IEEE Access 2018, 6, 45934–45950. [Google Scholar] [CrossRef]
- Yu, J.; Ding, B.; He, Y.J. Rolling bearing fault diagnosis based on mean multigranulation decision-theoretic rough set and non-naive Bayesian classifier. J. Mech. Sci. Technol. 2018, 32, 5201–5211. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Yi, X.K.; Chen, R.; Zhai, Z.G.; Gu, J.X. Feature extraction based on information gain and sequential pattern for English question classification. IET Softw. 2018, 12, 520–526. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.M.; Yang, X.H.; Li, G.Y. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]
- Ren, Z.R.; Skjetne, R.; Jiang, Z.Y.; Gao, Z.; Verma, A.S. Integrated GNSS/IMU hub motion estimator for offshore wind turbine blade installation. Mech. Syst. Signal Process. 2019, 123, 222–243. [Google Scholar] [CrossRef]
- Chen, H.L.; Xu, Y.T.; Wang, M.J.; Zhao, X.H. Chaos-induced and Mutation-driven algorithm for constrained engineering design problems. Appl. Math. Model. 2019, 71, 45–59. [Google Scholar] [CrossRef]
- Lu, S.L.; Zhou, P.; Wang, X.X.; Liu, B.Y.; Liu, F.; Zhao, J.W. Condition monitoring and fault diagnosis of motor bearings using undersampled vibration signals from a wireless sensor network. J. Sound Vib. 2018, 414, 81–96. [Google Scholar] [CrossRef]
- Xie, H.M.; Yang, K.; Li, S.W.; Yin, S.; Peng, J.; Zhu, F.; Li, H.; Zhang, L. Microwave heating-assisted pyrolysis of mercury from sludge. Mater. Res. Express 2019, 6, 015507. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.J.; Zhao, H.M. An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem. IEEE Access 2019, 7, 20281–20292. [Google Scholar] [CrossRef]
- Yu, J.; He, Y.J. Planetary gearbox fault diagnosis based on data-driven valued characteristic multigranulation model with incomplete diagnostic information. J. Sound Vib. 2018, 429, 63–77. [Google Scholar] [CrossRef]
- Osman, S.; Wang, W. A normalized Hilbert-Huang transform technique for bearing fault detection. J. Vib. Control 2014, 22, 2771–2787. [Google Scholar] [CrossRef]
- Wang, L.H.; Zhao, X.P.; Wu, J.X.; Xie, Y.Y.; Zhang, Y.H. Motor fault diagnosis based on short-time Fourier transform and convolutional neural network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Pan, Y.N.; Chen, J. The changes of complexity in the performance degradation process of rolling element bearing. J. Vib. Control 2016, 22, 344–357. [Google Scholar] [CrossRef]
- Li, T.; Hu, Z.; Jia, Y.; Wu, J.; Zhou, Y. Forecasting crude oil prices using ensemble empirical mode decomposition and sparse Bayesian learning. Energies 2018, 11, 1882. [Google Scholar] [CrossRef]
- Ren, Z.; Skjetne, R.; Gao, Z. A crane overload protection controller for blade lifting operation based on model predictive control. Energies 2019, 12, 50. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Jiang, S.; Fu, H.; Wang, L.; Jiang, W. Double entropy joint distribution function and its application in calculation of design wave height. Entropy 2019, 21, 64. [Google Scholar] [CrossRef]
- Zhao, H.M.; Sun, M.; Deng, W.; Yang, X.H. A new feature extraction method based on EEMD and multi-scale fuzzy entropy for motor bearing. Entropy 2017, 19, 14. [Google Scholar] [CrossRef]
- Chen, R.; Guo, S.K.; Wang, X.Z.; Zhang, T.L. Fusion of multi-RSMOTE with fuzzy integral to classify bug reports with an imbalanced distribution. IEEE Trans. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Zhao, H.M.; Yao, R.; Xu, L.; Yuan, Y.; Li, G.Y.; Deng, W. Study on a novel fault damage degree identification method using high-order differential mathematical morphology gradient spectrum entropy. Entropy 2018, 20, 682. [Google Scholar] [CrossRef]
- Sun, F.R.; Yao, Y.D.; Li, X.F. The heat and mass transfer characteristics of superheated steam coupled with non-condensing gases in horizontal wells with multi-point injection technique. Energy 2018, 143, 995–1005. [Google Scholar] [CrossRef]
- Guo, S.K.; Chen, R.; Li, H.; Zhang, T.L.; Liu, Y.Q. Identify severity bug report with distribution imbalance by CR-SMOTE and ELM. Int. J. Softw. Eng. Knowl. Eng. 2019, 29, 139–175. [Google Scholar] [CrossRef]
- Zhou, Y.R.; Li, T.Y.; Shi, J.Y.; Qian, Z.J. A CEEMDAN and XGBOOST–based approach to forecast crude oil prices. Complexity 2019. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.M.; Yang, X.H.; Xiong, J.X.; Sun, M.; Li, B. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl. Soft Comput. 2017, 59, 288–302. [Google Scholar] [CrossRef]
- Guo, J.H.; Mu, Y.; Xiong, M.D.; Liu, Y.Q.; Gu, J.X. Activity feature solving based on TF-IDF for activity recognition in smart homes. Complexity 2019. [Google Scholar] [CrossRef]
- Fu, H.; Li, Z.; Liu, Z.; Wang, Z. Research on big data digging of hot topics about recycled water use on micro-blog based on particle swarm optimization. Sustainability 2018, 10, 2488. [Google Scholar] [CrossRef]
- Tang, G.; Zhang, Y.; Wang, H.Q. Multivariable LS-SVM with moving window over time slices for the prediction of bearing performance degradation. J. Intell. Fuzzy Syst. 2018, 34, 3747–3757. [Google Scholar] [CrossRef]
- Kim, K.J.; Cho, S.B. Ensemble Bayesian networks evolved with speciation for high-performance prediction in data mining. Soft Comput. 2017, 21, 1065–1080. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.M.; Zou, L.; Li, G.Y.; Yang, X.H.; Wu, D.Q. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2017, 21, 4387–4398. [Google Scholar] [CrossRef]
- Wang, H.C.; Chen, J. Performance degradation assessment of rolling bearing based on bispectrum and support vector data description. J. Vib. Control 2014, 20, 2032–2041. [Google Scholar] [CrossRef]
- Yu, J.; Bai, M.Y.; Wang, G.N.; Shi, X.J. Fault diagnosis of planetary gearbox with incomplete information using assignment reduction and flexible naive Bayesian classifier. J. Mech. Sci. Technol. 2018, 32, 37–47. [Google Scholar] [CrossRef]
- Gao, H.Z.; Liang, L.; Chen, X.G.; Xu, G.H. Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization. Chin. J. Mech. Eng. 2015, 28, 96–105. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, B.; Chen, B.Q.; Cao, H.; Zi, Y.; He, Z. Weak fault signature extraction of rotating machinery using flexible analytic wavelet transform. Mech. Syst. Signal. Process. 2015, 64, 162–187. [Google Scholar] [CrossRef]
- Kabla, A.; Mokrani, K. Bearing fault diagnosis using Hilbert-Huang transform (HHT) and support vector machine (SVM). Mech. Ind. 2016, 17, 308. [Google Scholar] [CrossRef]
- Yuan, J.; Ji, F.; Gao, Y.; Zhu, J.; Wei, C.; Zhou, Y. Integrated ensemble noise-reconstructed empirical mode decomposition for mechanical fault detection. Mech. Syst. Signal Process. 2018, 104, 323–346. [Google Scholar] [CrossRef]
- Du, Y.C.; Du, D.P. Fault detection and diagnosis using empirical mode decomposition based principal component analysis. Comput. Chem. Eng. 2018, 115, 1–21. [Google Scholar] [CrossRef]
- Fei, S.W.; He, Y. A multi-layer KMC-RS-SVM classifier and DGA for fault diagnosis of power transformer. Recent Pat. Comput. Sci. 2012, 5, 238–243. [Google Scholar] [CrossRef]
- Kang, L.; Zhao, L.; Yao, S.; Duan, C.X. A new architecture of super-hydrophilic β-SiAlON/graphene oxide ceramic membrane for enhanced anti-fouling and separation of water/oil emulsion. Ceram. Int. 2019. [Google Scholar] [CrossRef]
- Cheng, J.S.; Peng, Y.F.; Yang, Y.; Wu, Z. Adaptive sparsest narrow-band decomposition method and its applications to rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2017, 85, 947–962. [Google Scholar] [CrossRef]
- Huang, W.Y.; Cheng, J.S.; Yang, Y. Rolling bearing performance degradation assessment based on convolutional sparse combination learning. IEEE Access 2019, 7, 17834–17846. [Google Scholar] [CrossRef]
- Huang, W.Y.; Cheng, J.S.; Yang, Y. Rolling bearing fault diagnosis and performance degradation assessment under variable operation conditions based on nuisance attribute projection. Mech. Syst. Signal Process. 2019, 114, 165–188. [Google Scholar] [CrossRef]
- Van Tung, T.; AlThobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar]
- Guo, X.J.; Chen, L.; Shen, C.Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Qi, Y.M.; Shen, C.Q.; Wang, D.; Shi, J.; Jiang, X.; Zhu, Z. Stacked sparse autoencoder-based deep network for fault diagnosis of rotating machinery. IEEE Access 2017, 5, 15066–15079. [Google Scholar] [CrossRef]
- Shao, H.D.; Jiang, H.K.; Wang, F.A.; Wang, Y. Rolling bearing fault diagnosis using adaptive deep belief network with dual-tree complex wavelet packet. ISA Trans. 2017, 69, 187–201. [Google Scholar] [CrossRef]
- Li, S.B.; Liu, G.K.; Tang, X.H.; Lu, J.; Hu, J. An ensemble deep convolutional neural network model with improved d-s evidence fusion for bearing fault diagnosis. Sensors 2017, 17, 1729. [Google Scholar] [CrossRef]
- Shao, H.D.; Jiang, H.K.; Zhang, H.Z.; Duan, W.; Liang, T.; Wu, S. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing. Mech. Syst. Signal Process. 2018, 100, 743–765. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.B.; Chen, X.F. Sparse deep stacking network for fault diagnosis of motor. IEEE Trans. Ind. Inform. 2018, 14, 3261–3270. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.H.; Peng, G.L.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Shao, H.D.; Jiang, H.K.; Zhang, H.Z.; Liang, T. Electric locomotive bearing fault diagnosis using a novel convolutional deep belief network. IEEE Trans. Ind. Electron. 2018, 65, 2727–2736. [Google Scholar] [CrossRef]
- Wang, Z.R.; Wang, J.; Wang, Y.R. An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition. Neurocomputing 2018, 310, 213–222. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W.; Zhong, Y.T.; Tang, H. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Process. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.Z.; Xu, Y.H.; Zheng, Y.; Peng, X.; Jiang, W. Unsupervised fault diagnosis of rolling bearings using a deep neural network based on generative adversarial networks. Neurocomputing 2018, 315, 412–424. [Google Scholar] [CrossRef]
- Zhao, X.L.; Jia, M.P. A novel deep fuzzy clustering neural network model and its application in rolling bearing fault recognition. Meas. Sci. Technol. 2018, 29, 125005. [Google Scholar] [CrossRef]
- Hu, Z.X.; Jiang, P. An imbalance modified deep neural network with dynamical incremental learning for chemical fault diagnosis. IEEE Trans. Ind. Electron. 2019, 66, 540–550. [Google Scholar] [CrossRef]
- Li, Z.P.; Chen, J.L.; Zi, Y.Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Jiang, X.X.; Shen, C.Q.; Shi, J.J.; Zhu, Z. Initial center frequency-guided VMD for fault diagnosis of rotating machines. J. Sound Vib. 2018, 435, 36–55. [Google Scholar] [CrossRef]
- Li, J.M.; Yao, X.F.; Wang, H.; Zhang, J. Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Wang, C.G.; Li, H.K.; Huan, G.J.; Ou, J. Early fault diagnosis for planetary gearbox based on adaptive parameter optimized VMD and singular kurtosis difference spectrum. IEEE Access 2019, 7, 31501–31516. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Lei, T.S.; Li, J.H.; Cai, X.; Shao, X.; Chang, J.; Tian, F. Real-time calibration and registration method for indoor scene with joint depth and color camera. J. Pattern Recognit. Artif. Intell. 2018, 32, 1854021. [Google Scholar] [CrossRef]
- Guo, S.K.; Liu, Y.Q.; Chen, R.; Sun, X.; Wang, X.X. Using an improved SMOTE algorithm to deal imbalanced activity classes in smart home. Neural Process. Lett. 2018. [Google Scholar] [CrossRef]
- Wen, J.; Zhong, Z.F.; Zhang, Z.; Fei, L.K.; Lai, Z.H.; Chen, R.Z. Adaptive locality preserving regression. IEEE Trsns. Circ. Syst. Vid. 2018. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Wang, X.X.; Zhai, Z.G.; Chen, R.; Zhang, B.; Jiang, Y. Timely daily activity recognition from headmost sensor events. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.Q.; Wang, Z.W.; Chang, J.; Zhang, J.; Tian, F. A fast framework construction and visualization method for particle-based fluid. EUPASIP J. Image Video Process. 2017, 2017, 79. [Google Scholar] [CrossRef]
- Huang, F.; Yao, C.; Liu, W.; Li, Y.; Liu, X. Landslide susceptibility assessment in the nantian area of china: A comparison of frequency ratio model and support vector machine. Geomat. Nat. Haz. Risk 2018, 9, 919–938. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, Y. Temperature dependent photoluminescence of surfactant assisted electrochemically synthesized ZnSe nanostructures. J. Alloy Compd. 2019, 781, 201–208. [Google Scholar] [CrossRef]
- Liu, G.; Chen, B.; Gao, Z.; Fu, H.; Jiang, S.; Wang, L.; Yi, K. Calculation of joint return period for connected edge data. Water 2019, 11, 300. [Google Scholar] [CrossRef]
- Zhou, J.; Du, Z.; Yang, Z.; Xu, Z. Dynamic parameters optimization of straddle-type monorail vehicles based multiobjective collaborative optimization algorithm. Vehicle Syst. Dyn. 2019. [Google Scholar] [CrossRef]
- Lin, J.; Yuan, J.S. Analysis and simulation of capacitor-less ReRAM-based stochastic neurons for the in-memory spiking neural network. IEEE Trans. Biomed Circ. Syst. 2018, 12, 1004–1017. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Fang, X.Z.; Cui, J.R.; Fei, L.K.; Yan, K.; Chen, Y.; Xu, Y. Robust sparse linear discriminant analysis. IEEE Trans. Circ. Syst. Vid. 2019, 29, 390–403. [Google Scholar] [CrossRef]
- Chen, H.L.; Jiao, S.; Heidarib, A.A.; Wang, M.J.; Chen, X.; Zhao, X.H. An opposition-based sine cosine approach with local search for parameter estimation of photovoltaic models. Energ. Convers. Manage. 2019, 195, 927–942. [Google Scholar] [CrossRef]
- Yu, W.J.; Zeng, Z.; Peng, B.; Yan, S.; Huang, Y.H.; Jiang, H.; Li, X.B.; Fan, T. Multi-objective optimum design of high-speed backplane connector using particle swarm optimization. IEEE Access 2018, 6, 35182–35193. [Google Scholar] [CrossRef]
- Luo, J.; Chen, H.L.; Zhang, Q.; Xu, Y.T.; Huang, H.; Zhao, X.H. An improved grasshopper optimization algorithm with application to financial stress prediction. Appl. Math. Model. 2018, 64, 654–668. [Google Scholar] [CrossRef]
- Liu, G.; Gao, Z.; Chen, B.; Fu, H.; Jiang, S.; Wang, L.; Koi, Y. Study on Threshold selection methods in calculation of ocean environmental design parameters. IEEE ACCESS 2019, 7, 39515–39527. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.P.; Liu, Z.L. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef]
- Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 13 July 2017).







| No. | Inner Race | Outer Race | Rolling Element |
|---|---|---|---|
| 1 | −0.0830 | 0.0085 | −0.0028 |
| 2 | −0.1957 | 0.4235 | −0.0963 |
| 3 | 0.2334 | 0.0130 | 0.1137 |
| 4 | 0.1040 | −0.2652 | 0.2573 |
| 5 | −0.1811 | 0.2372 | −0.0583 |
| 6 | 0.0556 | 0.5909 | −0.1260 |
| 7 | 0.1738 | −0.0930 | 0.2074 |
| 8 | −0.0469 | −0.4069 | 0.1727 |
| 9 | −0.1119 | 0.2794 | −0.2199 |
| 10 | 0.0596 | 0.4370 | −0.1561 |
| 11 | 0 | −0.3529 | 0.2240 |
| … | … | … | … |
| 2041 | 0.2305 | 0.0309 | 0.2375 |
| 2042 | 0.0461 | 0.1186 | −0.0271 |
| 2043 | −0.5122 | −0.0061 | −0.1327 |
| 2044 | 0.1481 | −0.0979 | 0.0929 |
| 2045 | 0.6280 | 0.0914 | 0.1106 |
| 2046 | −0.2043 | 0.1494 | −0.1499 |
| 2047 | −0.2640 | −0.2355 | −0.1108 |
| 2048 | 0.4662 | −0.3224 | 0.1467 |
| Fault Diagnosis Method | Diagnostic Accuracy (%) | Test Time (s) |
|---|---|---|
| VHBLFD1 (100,5,1000) | 95.99 | 6.45 |
| VHBLFD2 (100,15,17000) | 97.74 | 22.29 |
| Diagnosis Methods | Diagnostic Accuracy (%) | Test Time (s) |
|---|---|---|
| VHSMFD | 40.46 | 274.71 |
| EHDNFD | 95.02 | 664.57 |
| EEHDNFD | 96.55 | 630.37 |
| VHDNFD | 97.68 | 459.21 |
| VHBLFD | 97.74 | 22.29 |
| (N11, N2, N33) | Test Accuracy (%) | Total Average Time (s) |
|---|---|---|
| 40, 15, 3000 | 96.9902 | 4.8618 |
| 50, 15, 3000 | 96.9601 | 5.2248 |
| 60, 15, 3000 | 96.3506 | 5.6163 |
| 70, 15, 3000 | 96.2904 | 6.0630 |
| 80, 15, 3000 | 96.2302 | 6.5115 |
| 90, 15, 3000 | 95.8239 | 7.0634 |
| 100, 15, 3000 | 95.5982 | 7.5683 |
| 200, 15, 3000 | 92.0692 | 15.0772 |
| 300, 15, 3000 | 89.7968 | 21.7082 |
| Number of Nodes (N11, N2, N33) | Test Accuracy (%) | Total Average Time (s) |
|---|---|---|
| 100, 5, 1000 | 95.8239 | 3.4090 |
| 100, 10, 1000 | 95.7787 | 4.9404 |
| 100, 15, 1000 | 95.9443 | 6.4226 |
| 100, 20, 1000 | 95.9819 | 7.9057 |
| 100, 25, 1000 | 95.9142 | 9.4303 |
| 100, 30, 1000 | 96.0797 | 10.9200 |
| 100, 35, 1000 | 95.6734 | 12.4819 |
| 100, 40, 1000 | 95.7035 | 14.1060 |
| 100, 45, 1000 | 95.7863 | 15.8277 |
| 100, 50, 1000 | 95.7562 | 17.6226 |
| 100, 55, 1000 | 95.4778 | 19.6315 |
| 100, 60, 1000 | 95.7411 | 20.9249 |
| 100, 65, 1000 | 95.6358 | 22.5161 |
| 100, 70, 1000 | 95.7712 | 24.0979 |
| 100, 75, 1000 | 95.6659 | 35.2004 |
| 100, 80, 1000 | 95.4778 | 26.8084 |
| 100, 85, 1000 | 95.5304 | 28.5762 |
| 100, 90, 1000 | 95.6358 | 30.5728 |
| Number of Nodes (N11, N2, N33) | Test Accuracy (%) | Total Average Time (s) |
|---|---|---|
| 100, 15, 1000 | 95.9970 | 6.4500 |
| 100, 15, 2000 | 96.5613 | 7.1869 |
| 100, 15, 3000 | 95.5982 | 7.5683 |
| 100, 15, 4000 | 90.0000 | 8.0937 |
| 100, 15, 5000 | 80.7374 | 8.9812 |
| 100, 15, 6000 | 93.4989 | 9.2012 |
| 100, 15, 7000 | 95.6810 | 9.9691 |
| 100, 15, 8000 | 96.5162 | 10.7368 |
| 100, 15, 9000 | 97.0880 | 11.6575 |
| 100, 15, 10000 | 97.1257 | 12.7143 |
| 100, 15, 11000 | 97.2611 | 13.6536 |
| 100, 15, 12000 | 97.3589 | 14.8280 |
| 100, 15, 13000 | 97.4643 | 16.0800 |
| 100, 15, 14000 | 97.6072 | 17.3710 |
| 100, 15, 15000 | 97.5320 | 18.6380 |
| 100, 15, 16000 | 97.7200 | 20.8649 |
| 100, 15, 17000 | 97.7351 | 22.2932 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Yuan, Y.; Zou, L.; Deng, W.; Guo, C.; Zhao, H. Study on a Novel Fault Diagnosis Method Based on VMD and BLM. Symmetry 2019, 11, 747. https://doi.org/10.3390/sym11060747
Zheng J, Yuan Y, Zou L, Deng W, Guo C, Zhao H. Study on a Novel Fault Diagnosis Method Based on VMD and BLM. Symmetry. 2019; 11(6):747. https://doi.org/10.3390/sym11060747
Chicago/Turabian StyleZheng, Jianjie, Yu Yuan, Li Zou, Wu Deng, Chen Guo, and Huimin Zhao. 2019. "Study on a Novel Fault Diagnosis Method Based on VMD and BLM" Symmetry 11, no. 6: 747. https://doi.org/10.3390/sym11060747
APA StyleZheng, J., Yuan, Y., Zou, L., Deng, W., Guo, C., & Zhao, H. (2019). Study on a Novel Fault Diagnosis Method Based on VMD and BLM. Symmetry, 11(6), 747. https://doi.org/10.3390/sym11060747





