Abstract
K-Means is a well known and widely used classical clustering algorithm. It is easy to fall into local optimum and it is sensitive to the initial choice of cluster centers. XK-Means (eXploratory K-Means) has been introduced in the literature by adding an exploratory disturbance onto the vector of cluster centers, so as to jump out of the local optimum and reduce the sensitivity to the initial centers. However, empty clusters may appear during the iteration of XK-Means, causing damage to the efficiency of the algorithm. The aim of this paper is to introduce an empty-cluster-reassignment technique and use it to modify XK-Means, resulting in an EXK-Means clustering algorithm. Furthermore, we combine the EXK-Means with genetic mechanism to form a genetic XK-Means algorithm with empty-cluster-reassignment, referred to as GEXK-Means clustering algorithm. The convergence of GEXK-Means to the global optimum is theoretically proved. Numerical experiments on a few real world clustering problems are carried out, showing the advantage of EXK-Means over XK-Means, and the advantage of GEXK-Means over EXK-Means, XK-Means, K-Means and GXK-Means (genetic XK-Means).
1. Introduction
Clustering algorithms are a class of unsupervised classification methods for a data set (cf. [1,2,3,4,5]). Roughly speaking, a clustering algorithm classifies the vectors in the data set such that distances of the vectors in the same cluster are as small as possible, and the distances of the vectors belonging to different clusters are as large as possible. Therefore, the vectors in the same cluster have the greatest similarity, while the vectors in different clusters have the greatest dissimilarity.
A clustering technique called K-Means is proposed and discussed in [1,2] among many others. Because of its simplicity and fast convergence speed, K-Means is widely used in various research fields. For instance, K-Means is used in [6] for removing the noisy data. A disadvantage of K-Means is that it is easy to fall into local optima. As a remedy, a popular trend is to integrate the genetic algorithm [7,8] with K-means to obtain genetic K-means algorithms [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. K-Means is also combined with fuzzy mechanism to obtain fuzzy C-Means [24,25].
A successful modification of K-Means is proposed in [26], referred to as XK-Means (eXploratory K-Means). It adds an exploratory disturbance onto the vector of the cluster centers so as to jump out of the local optimum and to reduce the sensitivity to the initial centers. However, empty clusters may appear during the iteration of XK-Means, which violates the condition that the number of clusters should be a pre-given number K and causes damage to the efficiency of the algorithm (see Remark 1 in Section 2.3 below for details). As a remedy, we propose in this paper to modify XK-Means in terms of an empty-cluster-reassignment technique, resulting in an EXK-Means clustering algorithm.
The involvement of the exploratory disturbance in EXK-Means helps to jump out of the local optimum during the iteration. However, in order to guarantee the convergence of the iteration process, the exploratory disturbance has to decrease and tend to zero in the iteration process. Therefore, it is still possible for EXK-Means to fall into local optimum. To further resolve this problem, we follow the aforementioned strategy to combine the genetic mechanism with our EXK-Means, resulting in a clustering algorithm called GEXK-Means.
Numerical experiments on thirteen real world data sets are carried out, showing the higher accuracies of our EXK-Means over XK-Means, and our GEXK-Means over GXK-Means, EXK-Means, XK-Means and K-Means: first, our GEXK-Means achieves the highest S, and the lowest MSE, DB and XB (see the next section for definitions of these evaluation tools) for all of the thirteen data sets. Therefore, GEXK-Means performs better than the other four algorithms. Second, the overall performance of our EXK-Means is a little bit better than that of XK-Means, which shows the benefit of the introduction of our empty cluster reassignment technique.
The numerical experiments also show that the execution times of EXK-Means are a little bit longer than those of K-Means and XK-means, and the execution times of GEXK-Means are the longest in the five algorithms. This is a disadvantage of EXK-Means and GEXK-Means. However, the computer speed is getting high and high in nowadays, and sometimes the computational time does not matter very much in practice if the data set is not very large. In case we do not mind a bit of an increase in the computational time and we care very much about the accuracy, our algorithm may be of value.
A probabilistic convergence of our GEXK-Means to the global optimum is theoretically proved.
This paper is organized as follows. In Section 2, we describe the K-Means, XK-Means, GXK-Means, and our proposed EXK-Means and GEXK-Means. In Section 3, numerical experiments are shown on GEXK-Means and its comparison with K-Means, XK-Means, GXK-Means and EXK-Means. The convergence of GEXK-Means to a globally optimal solution is theoretically proved in Section 4. Some short conclusions are drawn in Section 5.
2. Algorithms
In this section, we first give some notations and describe some evaluation tools. Then, we define the clustering algorithms used in this paper.
2.1. Notations
Let us introduce some notations. Our task is to cluster a set of n genes into K clusters. Each gene is expressed as a vector of dimension D: . For and , we define
In addition, we define the label matrix . We require that each gene belongs to precisely one cluster, and each cluster contains at least one gene. Therefore,
Denote the center of the k-th cluster by , defined as
The Euclidean norm will be used in our paper. Then, for any two D-dimensional vectors and in , the distance is
2.2. Evaluation Strategies
In our numerical simulation, we will use the following evaluation tools: the mean squared error (MSE), the Xie–Beni index (XB) [12], the Davies–Bouldin index (DB) [13,27], and the separation index (S) [4]. The aim of the clustering algorithms discussed in this paper is to choose the optimal centers ’s and the optimal label matrix so as to minimize the mean square error MSE. Then, MSE together with the indexes XB, DB and S will be applied to evaluate the outcome of the clustering algorithms.
MSE is defined by
MSE will be used as the evaluation function in the genetic operation of the numerical simulation later on. Generally speaking, lower MSE means better clustering result.
The XB index [12] is defined as follows:
where is the shortest distance between cluster centers. Higher means better clustering result. As we mentioned above, the MSE is the lower the better. Therefore, lower XB implies better clustering results.
To define the DB index [13,27], we first defined the within-cluster separation as
where (resp. ) denotes the set (resp. the number) of the samples belonging to the cluster k. Next, we define a term for cluster as
Then, the DB index is defined as
Generally speaking, lower DB implies better clustering results.
The separation index S [4] is defined as follows:
Generally speaking, higher S implies better clustering results.
The Nemenyi test [28,29,30] will be used for evaluating the significance of differences of XK-Means vs. EXK-Means and GXK-Means vs. GEXK-Means, respectively. The function cdf.chisq of SPSS software (SPSS Statistics 17.0, IBM, New York, USA) is used to compute the significance probability Pr. The value of Pr is in between 0 and 1. The smaller value of Pr implies the bigger significance of the difference of the two groups. One can say that the difference of the two groups is significant if Pr is less than a particular threshold value. The most often used threshold values are 0.01, 0.05 and 0.1. The threshold value 0.05 will be adopted in this paper.
The relative error defined below will be used for a stop criterion in our numerical iteration process:
where and denote the values of MSE in the current and previous iteration steps, respectively.
2.3. XK-Means
Trying to jump out of the local minimum, the XK-Means algorithm is proposed in [26], where the usual K-Means is modified by adding an exploratory vector onto each cluster center as follows:
where is a D-dimensional exploratory vector at the current step. It is used to disturb the center produced by K-Means operation, and its component is randomly chosen as
where is a given positive number, and
with a given factor . In general, the disturbance should be decreased with the increase of the iteration step. Thus, for a new iteration step, the new value of is set to be
with a given factor .
Remark 1.
Empty cluster will not appear in a usual K-Means iteration process. However, it is possible for XK-Means to produce an empty cluster in the iteration process. This happens when the exploratory vector in Formula (13) drives the center away from the genes in the k-th cluster, such that all these genes join another cluster in the re-organization stage of the XK-Means and leave the k-th cluster empty. Then, the XK-Means iteration will end up with the number of clusters less than K, which violates the condition that the number of clusters should be K.
2.4. EXK-Means
Due to the disturbance , the XK-Means algorithm may produce empty clusters during the iteration process, which violates condition . The reason for such a cluster to become empty is that it is too close to, and is attracted into other cluster when the centers are disturbed by the ’s. In this sense, it seems reasonable for such a cluster to “disappear”. However, on the other hand, the empty clusters will damage the clustering efficiency due to the decrease of the number of working clusters.
To resolve this problem, our idea is to re-assign such an empty cluster by a vector that is farthest to its center. Specifically, our EXK-Means modifies the XK-means by applying the following Empty-cluster-reassignment procedure when empty clusters appear after an XK-Means iteration step.
Empty-cluster-reassignment procedure:
- Let be the number of empty clusters, .
- Find the most marginal point of each non-empty cluster: , where is the set of genes in the k-th cluster.
- Sort in descending order according to their distances to the corresponding centroids to get .
- Take the first genes from to form new centers .
- Adjust the partition of genes according to original centers and the new centers.
2.5. Genetic Operations
As we argued in the Introduction, although EXK-Means and XK-Means algorithms improve the K-Means on the local minimum issue, but the possibility remains for them to fall into local optimum. We try to combine a genetic mechanism with the EXK-Means to get the global convergence. In particular, we propose to use the following genetic operations:
2.5.1. Label Vectors
For the convenience of genetic operation, in place of the label matrix , let us introduce the n-dimensional label vector
where each component represents the cluster label of , as in [10]. Let N denote the population size. Then, we write the population set as .
2.5.2. Initialization
To avoid empty clusters in the initialization stage, we initialize the population as follows. First, the top K components of each are randomly assigned as a permutation of . Secondly, the other components of are assigned as random cluster numbers respectively selected from the uniform distribution of the .
2.5.3. Selection
The usual roulette strategy is used for the random selection. The probability that an individual is selected from the existing population to breed the next generation is given by
where is the reciprocal of MSE and represents the fitness value of the individual in the population.
2.5.4. Mutation
The mutation probability is denoted by , which determines whether an individual will be mutated. If an individual is to be mutated, the translation probability of its component to be k is defined as
where . To avoid empty individuals after mutation operation, is mutated only when the -th cluster contains more than two genes.
2.5.5. Three Steps EXK-Means
A three-step EXK-Means is applied for rapid convergence. For an individual , it is updated through the following operations: calculate the cluster centers by using for the given ; add the exploratory vector and update the cluster centers by using ; reassign each gene to the cluster with the closest cluster center to form a new individual ; correct the new by using the Empty-cluster-reassignment procedure in Section 2.4 if it contains empty cluster(s) at this moment. Repeat the process three times, and finally form an individual of the next generation.
2.6. Genetic XK-Means ( GXK-Means )
The GXK-Means is briefly described as follows:
- Initialization: Set the population size N, the maximum number of iterations T, the mutation probability , the number of clusters K and the error tolerance . Let , and choose the initial population according to Section 2.5.2. In addition, choose the best individual from and denote it as super individual .
- Selection: Select a new population from according to Section 2.5.3, and denote it by .
- Mutation: Mutate each individual in according to Section 2.5.4, and get a new population denoted by .
- XK-Means: Perform XK-Means on three times to get the next generation population denoted by .
- Update the super individual: choose the best individual from and compare it with to get .
- Stop if either or (see ), otherwise go to 2 with .
2.7. GEXK-Means (Genetic EXK-Means)
The process of GEXK-Means proposed in this paper is as follows:
- Initialization: Set the population size N, the maximum number of iterations T, the mutation probability , the number of clusters K and the error tolerance . Let , and choose the initial population according to Section 2.5.2. In addition, choose the best individual from and denote it as super individual .
- Selection: Select a new population from according to Section 2.5.3, and denote it by .
- Mutation: Mutate each individual in according to Section 2.5.4, and get a new population denoted by .
- EXK-Means: Perform the three steps EXK-Means on according to Section 2.5.5 to get the next generation population denoted by .
- Update the super individual: choose the best individual from and compare it with to get .
- Stop if either or (see ), otherwise go to 2 with .
Let us explain the functions of the four operations in the GEXK-Means: selection, mutation, EXK-Means and updating of the super individual. The selection operation encourages the population to have a good evolution direction. The function of the EXK-Means operation is local search for better individuals. The mutation operation guarantees the ergodicity of the evolution process, which in turn guarantees the appearance of a global optimal individual in the evolution process. Finally, the updating operation of the super individual will catch forever the global optimal individual once it appears.
3. Experimental Evaluation and Results
3.1. Data Sets and Parameters
Thirteen data sets shown in Table 1 are used for evaluating our algorithms. The first five data sets are gene expression data sets, including Sporulation [31], Yeast Cell Cycle [32], Lymphoma [33], and two UCI data sets Yeast and Ecoli. The other eight are UCI data sets, which are not gene express data sets.

Table 1.
Data sets used in experiments.
As shown in Table 1, Sporulation, Yeast Cell Cycle and Lymphoma data sets contain some sample vectors with missing component values. To rectify these defective data, we follow the strategy adopted in [34,35,36]: the sample vectors with more than 20% missing components are removed from the data sets. In addition, for the sample vectors with less than 20% missing components, the missing component values are estimated by the KNN algorithm with the parameter as in [35], where k is the number of the neighboring vectors used to estimate the missing component value (see [34,35,36] for details). Here, we point out that this parameter k here is different from the index k we have used in this paper for denoting the k-th cluster.
The values of the parameters used in the computation are set as follows:
| Population size | (cf. Section 2.6 and Section 2.7) |
| Mutation probability | (cf. Section 2.6 and Section 2.7) |
| Error tolerance | (cf. Section 2.2, Section 2.6 and Section 2.7) |
| (cf. , ) | |
| (cf. , ) | |
| (cf. Section 2.6 and Section 2.7) |
In the experiments, we use two different computers: M1 (Intel (R), Core (TM) i3-8100 CPU and 4 GB RAM, Santa Clara, CA, USA) and M2 (Intel (R), Core (TM) i5-7400 CPU and 8 GB RAM). The software Matlab (Matlab 2017b, Math Works, Natick, MA, USA) is used to implement the clustering algorithms.
3.2. Experimental Results and Discussion
We divide this subsection into three parts. The first part concerns with the performances of the algorithms in terms of MSE, S, DB and XB. The second part demonstrates the significance of differences of the algorithms in terms of Nemenyi Test. The third part presents the computational times of the algorithms. We shall pay our attention mainly on the comparisons of EXK-Means vs. XK-Means and GEXK-Means vs. GXK-Means, respectively, so as to show the benefit of the introduction of our empty-cluster-reassignment technique.
3.2.1. MSE, S, DB and XB Performances
Each of the five algorithms conducted fifty trials on the thirteen data sets. The averages over the fifty trials for the four evaluation criteria (MSE, S, DB and XB) are listed in Table 2 and Table 3, devoted to the five gene expression data sets and the other eight UCI data sets, respectively.

Table 2.
Average MSE, S, DB and XB on the gene data sets.

Table 3.
Average MSE, S, DB and XB on the non-gene data sets.
From Table 2 and Table 3, we see that our GEXK-Means achieves the highest S, and the lowest MSE, DB and XB for all the thirteen data sets. Therefore, GEXK-Means performs better than the other four algorithms.
We also observe that the overall performance of our EXK-Means is a bit better than that of XK-Means: EXK-Means is better than XK-Means in terms of all the four clustering criteria (MSE, S, XB and DB) for three of the thirteen data sets; EXK-Means is better in terms of three criteria for three data sets; EXK-Means is better in terms of two criteria for four data sets; and EXK-Means is better in terms of one criteria for three data sets. This means that EXK-Means performs better than XK-Means in nearly two thirds of the cases. (In the total cases, EXK-Means is better than XK-Means for cases.) The better case is marked by black face number in Table 2 and Table 3.
To see more clearly the overall performance, in Figure 1, Figure 2, Figure 3 and Figure 4 for MSE, DB, XB and S evaluations respectively, we further present the average performances of the five algorithms over the thirteen data sets. These figures clearly show that, in the sense of average performance, the proposed GEXK-Means outperforms the other four algorithms, and EXK-Means outperforms K-Means and XK-Means.
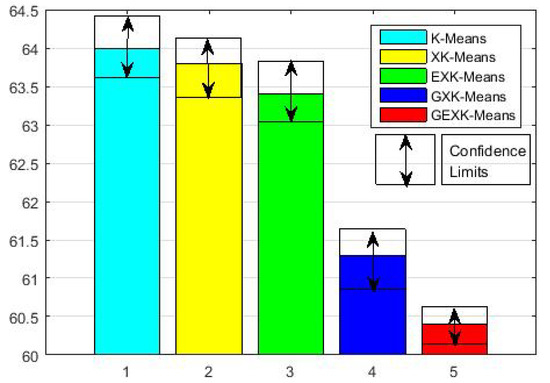
Figure 1.
Average MSE of thirteen data sets (The value of MSE is the lower the better).
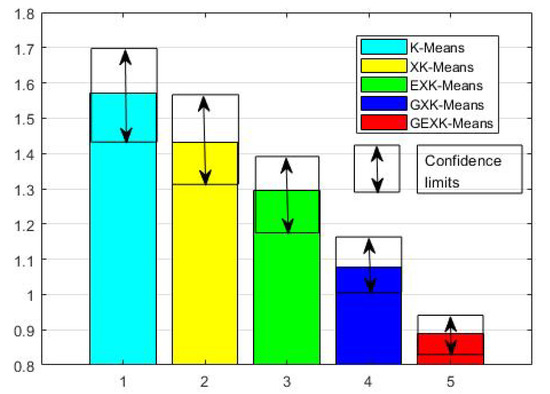
Figure 2.
Average DB of thirteen data sets (The value of DB is the lower the better).
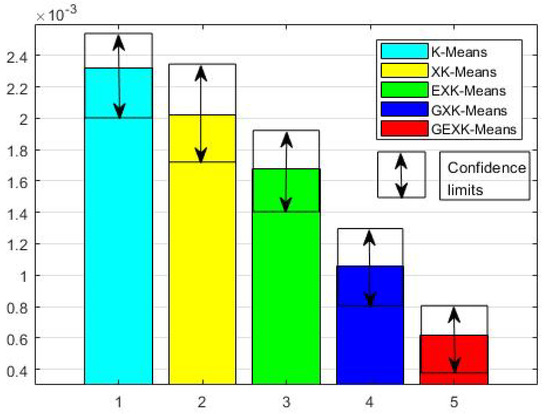
Figure 3.
Average XB of thirteen data sets (The value of XB is the lower the better).
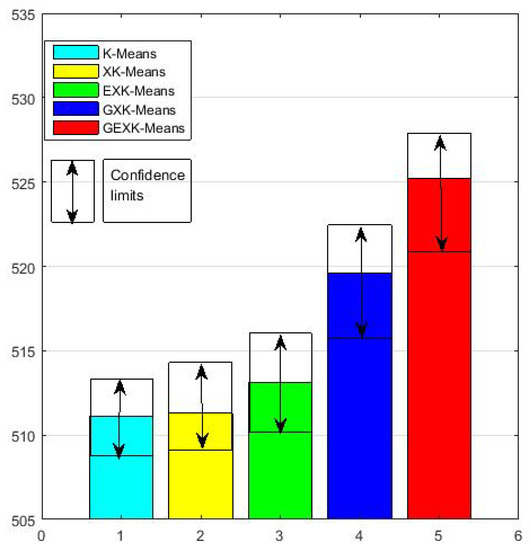
Figure 4.
Average S of thirteen data sets (The value of S is the higher the better).
As an example to show what happens in the iteration processes, a typical iteration process on Yeast Cell Cycle data set is shown in Figure 5, Figure 6, Figure 7 and Figure 8, presenting the MSE, XB, DB and S curves respectively for the five algorithms.
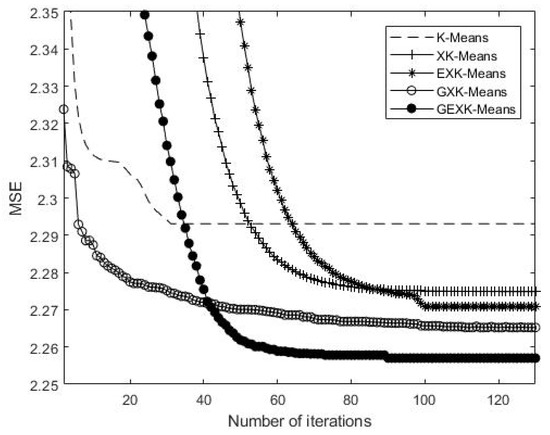
Figure 5.
MSE curves of the algorithms for Yeast Cell Cycle (The value of MSE is the lower the better).
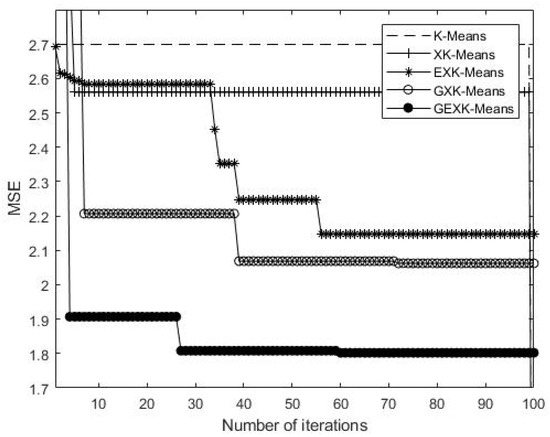
Figure 6.
DB curves of the algorithms for Yeast Cell Cycle (The value of DB is the lower the better).
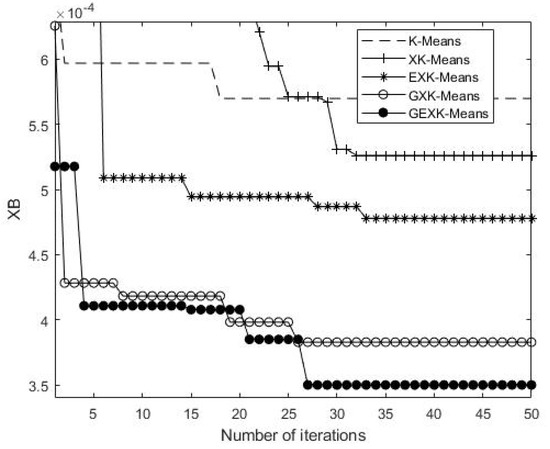
Figure 7.
XB curves of the algorithms for Yeast Cell Cycle (The value of XB is the lower the better).
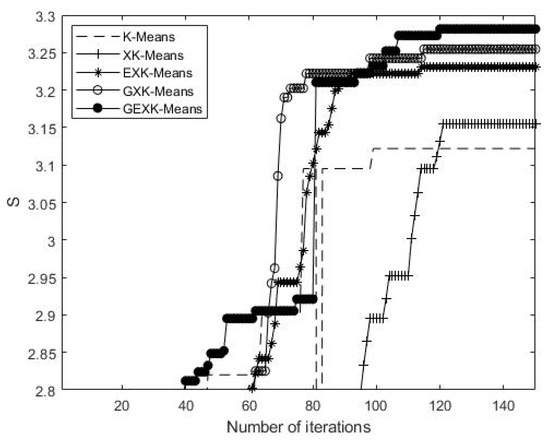
Figure 8.
S curves of the algorithms for Yeast Cell Cycle (The value of S is the higher the better).
3.2.2. Nemenyi Test
Table 4 shows the results of Nemenyi Test on MSE, S, DB and XB indexes. We use the threshold value 0.05 for the significance evaluation. For DB index, EXK-Means shows significant difference compared with XK-Means, while EXK-Means does not show significant difference compared with XK-Means for the other three indexes. For all four of the indexes, GEXK-Means shows a significant difference compared with GXK-Means.

Table 4.
Nemenyi Test for multiple comparisons.
3.2.3. Computational Time
Table 5 gives the average computational times over the fifty runs for each data set. It shows that the computational times of EXK-Means are a little bit longer than those of K-Means and XK-means, and the computational times of GEXK-Means are a little bit longer than those of GXK-Means. This indicates that the introduction of our empty-cluster-reassignment technique increases the computational time. However, our algorithms are better if we do not mind a bit of increase in the computational time and we care very much about the accuracy.

Table 5.
Average running times (in seconds).
4. Convergence
In this section, the convergence properties of GEXK-Means are analyzed. It is clear that there exist possible solutions when classifying n genes into K clusters. As mentioned in Section 2.5, every possible solution can be denoted as a label vector . Therefore, the number of all possible individuals is m. Let be the set of global optimal individuals with maximum fitness value.
For an individual that will to be mutated, according to Eqution , we have
where , and . Therefore, , and . We note that the number of genes and the number of clusters are finite. Therefore, has lower bound denoted by . This means that every gene can be mutated into any one cluster with positive probability. In particular, can be mutated into any other individuals with positive probability. Recall that is the population at step t. Let stand for the probability in which is mutated to one of the global optimal individuals. Then
Let stand for the probability generating the optimal individual in by mutation operation. Then,
where is the mutation probability, is the selection probability defined by Equation , and .
Theorem 1.
When the GEXK-Means defined in Section 2.7 is applied for the classification of a given data set, the global optimal classification result for the data set will appear and will be caught with probability 1 in an infinite evolution iteration process of the GEXK-Means.
Proof.
Along with the evolution process, the updating operation of the super individual will keep the super individual denoted by of every generation . According to , we know that the may become a global optimal individual with positive probability. According to the Small Probability Event Principle [37,38], the global optimum individual will appear in the super individual sequence with probability 1 when the evolution iteration process goes to infinity. This proves the global convergence of GEXK-Means. □
We remark that the global convergence stated above is of a theoretical and probabilistic nature. It does not guarantee that the convergence to a global optimum can be reached in finite number of GEXK-Means iterations.
5. Conclusions
XK-Means (eXploratory K-Means) is a popular data clustering algorithm. However, empty clusters may appear during the iteration of XK-Means, which violates the condition that the number of clusters should be K and causes damage to the efficiency of the algorithm. As a remedy, we define an empty-cluster-reassignment technique to modify XK-Means when empty clusters appear, resulting in an EXK-Means clustering algorithm. Furthermore, we combine the EXK-Means with genetic mechanism to form a GEXK-Means clustering algorithm.
Numerical simulations are carried out on the comparison of K-Means, XK-Means, EXK-Means and GXK-Means (genetic XK-Means) and GEXK-Means. The evaluation tools include the mean squared error (MSE), the Xie–Beni index (XB), the Davies–Bouldin index (DB) and the separation index (S). The Nemenyi Test for multiple comparisons is also done on MSE, S, DB and XB, respectively. Thirteen real world data sets are used for the simulation. The running times of these algorithms are also considered.
The conclusions we draw from the simulation results are as follows: first, the overall performances of EXK-Means in terms of the four indexes outperform those of XK-Means, and the overall performances of GEXK-Means outperform those of GXK-Means. This shows the effectiveness of the introduction of the empty-cluster-reassignment technique. Secondly, if we take the threshold value as 0.05 for the Nemenyi Test, then GEXK-Means shows a significant difference compared with GXK-Means for all four of the indexes. However, EXK-Means shows a significant difference compared with XK-Means only for the DB index. Thirdly, our EXK-Means and GEXK-Means take a little bit more computational time than XK-Means and GXK-Means, respectively.
The following global convergence of the GEXK-Means is also theoretically proved: the global optimum will appear and will be caught in the evolution process of GEXK-Means with probability 1.
Author Contributions
C.H. developed the mathematical model, carried out the numerical simulations and wrote the manuscript; W.W. advised on developing the learning algorithms and supervised the work; F.L. contributed to the theoretical analysis; C.Z. and J.Y. helped in the numerical simulations.
Funding
This research was supported by the National Science Foundation of China (No: 61473059), and the Fundamental Research Funds for the Central Universities of China.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Steinhaus, H. Sur la division des corp materiels en parties. Bull. Acad. Polon. Sci. 1956, 3, 801–804. [Google Scholar]
- Macqueen, J. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Los Angeles, CA, USA, 21 June–18 July 1967. [Google Scholar]
- Wlodarczyk-Sielicka, M. Importance of Neighborhood Parameters During Clustering of Bathymetric Data Using Neural Network. In Proceedings of the 22nd International Conference, Duruskininkai, Lithuania, 13–15 October 2016. [Google Scholar]
- Du, Z.; Wang, Y. PK-Means: A New Algorithm for Gene Clustering. Comput. Biol. Chem. 2008, 32, 243–247. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Du, Z. A Novel Parallelization Approach for Hierarchical Clustering. Parallel Comput. 2005, 31, 523–527. [Google Scholar]
- Santhanam, T.; Padmavathi, M.S. Application of K-Means and Genetic Algorithms for Dimension Reduction by Integrating SVM for Diabetes Diagnosis. Procedia Comput. Sci. 2015, 47, 76–83. [Google Scholar] [CrossRef]
- Deep, K.; Thakur, M. A New Mutation Operator for Real Coded Genetic Algorithms. Appl. Math. Comput. 2007, 193, 211–230. [Google Scholar] [CrossRef]
- Ming, L.; Wang, Y. On Convergence Rate of a Class of Genetic Algorithms. In Proceedings of the World Automation Congress, Budapest, Hungary, 24–26 July 2006. [Google Scholar]
- Maulik, U. Genetic Algorithm Based Clustering Technique. Pattern Recognit. 2000, 33, 1455–1465. [Google Scholar] [CrossRef]
- Jones, D.R.; Beltramo, M.A. Solving Partitioning Problems with Genetic Algorithms. In Proceedings of the 4th International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991. [Google Scholar]
- Zheng, Y.; Jia, L.; Cao, H. Multi-Objective Gene Expression Programming for Clustering. Inf. Technol. Control 2012, 41, 283–294. [Google Scholar] [CrossRef][Green Version]
- Xie, X.L.; Beni, G. A Validity Measure for Fuzzy Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- Liu, Y.G. Automatic Clustering Using Genetic Algorithms. Appl. Math. Comput. 2011, 218, 1267–1279. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-Means Algorithm. IEEE Trans. Syst. Man Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef]
- Bouhmala, N.; Viken, A. Enhanced Genetic Algorithm with K-Means for the Clustering Problem. Int. J. Model. Optim. 2015, 5, 150–154. [Google Scholar] [CrossRef][Green Version]
- Sheng, W.G.; Tucker, A. Clustering with Niching Genetic K-means algorithm. In Proceedings of the 6th Annual Genetic and Evolutionary Computation Conference (GECCO 2004), Seattle, WA, USA, 26–30 June 2004. [Google Scholar]
- Zhou, X.B.; Gu, J.G. An Automatic K-Means Clustering Algorithm of GPS Data Combining a Novel Niche Genetic Algorithm with Noise and Density. ISPRS Int. J. Geo-Inf. 2017, 6, 392. [Google Scholar] [CrossRef]
- Islam, M.Z.; Estivill-Castro, V.; Rahman, M.A.; Bossomaier, T. Combining K-Means and a Genetic Algorithm through a Novel Arrangement of Genetic Operators for High Quality Clustering. Expert Syst. Appl. 2018, 91, 402–417. [Google Scholar] [CrossRef]
- Michael, L.; Sumitra, M. A Genetic Algorithm that Exchanges Neighboring Centers for k-means clustering. Pattern Recognit. Lett. 2007, 28, 2359–2366. [Google Scholar]
- Ishibuchi, H.; Yamamoto, T. Fuzzy Rule Selection by Multi-objective Genetic Local Search Algorithms and Rule Evaluation Measures in Data Mining. Fuzzy Sets Syst. 2004, 141, 59–88. [Google Scholar] [CrossRef]
- Zubova, J.; Kurasova, O. Dimensionality Reduction Methods: The Comparison of Speed and Accuracy. Inf. Technol. Control 2018, 47, 151–160. [Google Scholar] [CrossRef]
- Wozniak, M.; Polap, D. Object Detection and Recognition via Clustered Features. Neurocomputing 2018, 320, 76–84. [Google Scholar] [CrossRef]
- Anusha, M.; Sathiaseelan, G.R. Feature Selection Using K-Means Genetic Algorithm for Multi-objective Optimization. Procedia Comput. Sci. 2015, 57, 1074–1080. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R. FCM: The Fuzzy C-Means Clustering Algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Indrajit, S.; Ujjwal, M. A New Multi-objective Technique for Differential Fuzzy Clustering. Appl. Soft Comput. 2011, 11, 2765–2776. [Google Scholar]
- Lam, Y.K.; Tsang, P.W.M. eXplotatory K-Means: A New Simple and Efficient Algorithm for Gene Clustering. Appl. Soft. Comput. 2012, 12, 1149–1157. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Liu, Y.W.; Chen, W.H. A SAS Macro for Testing Differences among Three or More Independent Groups Using Kruskal-Wallis and Nemenyi Tests. J. Huazhong Univ. Sci. Tech.-Med. 2012, 32, 130–134. [Google Scholar] [CrossRef] [PubMed]
- Nemenyi, P. Distribution-Free Multiple Comparisons. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1963. [Google Scholar]
- Fan, Y.; Hao, Z.O. Applied Statistics Analysis Using SPSS, 1st ed.; China Water Conservancy and Hydroelectricity Publishing House: Beijing, China, 2003; pp. 138–152. [Google Scholar]
- Chu, S.; DeRisi, J. The Transcriptional Program of Sporulation in Budding Yeast. Science 1998, 282, 699–705. [Google Scholar] [CrossRef] [PubMed]
- Spellman, P.T. Comprehensive Identification of Cell Cycle-regulated Genes of the Yeast Saccharomyces Cerevisiae by Microarray Hybridization. Mol. Biol. 1998, 9, 3273–3297. [Google Scholar] [CrossRef]
- Alizadeh, A.A.; Eisen, M.B. Distinct Types of Diffuse Large B-cell Lymphoma Identified by Gene Expression Profiling. Nature 2000, 403, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Yoon, D.; Lee, E.K. Robust Imputation Method for Missing Values in Microarray Data. BMC Bioinform. 2007, 8, 6–12. [Google Scholar] [CrossRef] [PubMed]
- Troyanskaya, O.; Cantor, M. Missing Value Estimation Methods for DNA Microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef]
- Corso, D.E.; Cerquitelli, T. METATECH: Meteorological Data Analysis for Thermal Energy CHaracterization by Means of Self-Learning Transparent Models. Energies 2018, 11, 1336. [Google Scholar] [CrossRef]
- Liu, G.G.; Zhuang, Z.; Guo, W.Z. A novel particle swarm optimizer with multi-stage transformation and genetic operation for VLSI routing. Energies 2018, 11, 1336. [Google Scholar]
- Rudolph, G. Convergence Analysis of Canonical Genetic Algorithms. IEEE Trans. Neural Netw. 1994, 5, 96–101. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).